An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control
Abstract
:1. Introduction
2. System Model

2.1. Vehicle Dynamics Model
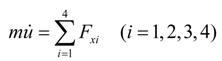
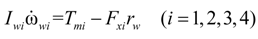
2.2. Tyre Model
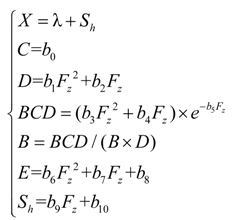
| No. | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| bi | 1.02316 | 21.80968 | 526.2336 | 0.09624 | 250.33146 | 0.00906 |
| No. | 6 | 7 | 8 | 9 | 10 | – |
| bi | −0.00255 | 0.03726 | 0.87693 | −0.00009 | −0.00033 | – |
2.3. Motor Model
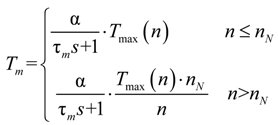
2.4. Slip Rate Calculation Model
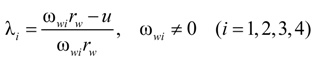
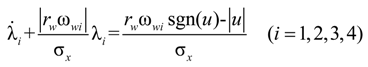
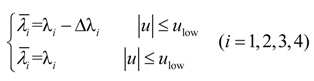
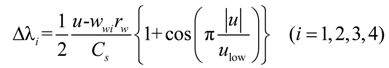

3. Control Strategies
- (1)
- Td ≤ 2 × Tmax ≤ Troad, generally corresponds to a condition of high road adhesion. In this case, the drive wheel slip will not happen over the entire range of the accelerator pedal, and it’s not necessary to perform a complex torque distribution for the front and rear axles, just let αf = αr = αpedal. Although the slip rates of the front and rear axles will be different with the same drive torque due to the different vertical loads of front and rear axles, the vehicle dynamic performance and driving stability will not be influenced.
- (2)
- Td ≤ Troad ≤ 2 × Tmax, generally corresponds to the condition of middle road adhesion. In this case, although the driver-desired torque Td is smaller than Troad, the slip phenomenon may happen on the driving shaft with a smaller axle load due to the bad road conditions. So a reasonable allocation of the drive torque of the front and rear axles is required to ensure Tf + Tr = Td, thereby avoiding slipping under the condition of avoiding vehicle dynamics loss.
- (3)
- 2 × Tmax ≥ Td ≥ Troad, generally corresponds to the condition of low road adhesion. In this case, the driver-desired torque Td is bigger than Troad, and the inter-axle torque distribution will cause an unavoidable slip phenomenon. In order to make full use of the road adhesion, the independent control for front and rear axles is the best control plan, thus the slip rates of the front and rear axles can be controlled to be equal to the optimal rate slip. In this way Tf + Tr = Troad, and the vehicle can acquire the biggest power at this moment.

3.1. Mode 1: Average Distribution of Inter-Axle Torque
3.2. Mode 2: Optimal Distribution of Inter-Axle Torque
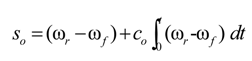
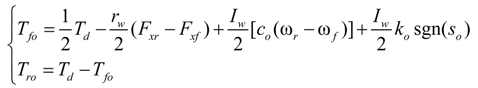
3.3. Mode 3: Independent Control of Optimal Slip Rate
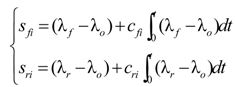
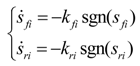
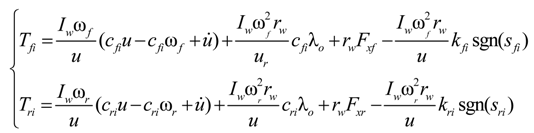
4. Simulation Results and Analysis
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| co | 500 | kri | 80 |
| cfi | 50 | m | 5000 kg |
| cri | 500 | nN | 4000 |
| Cs | 1.81 kg·m2 | rw | 0.447 m |
| Cx | 1.65 kg·m2 | ulow | 1.83 m/s |
| Iw | 2.035 kg·m2 | τm | 200 |
| ko | −100 | σx | 0.91 |
| kfi | −200 | – | – |
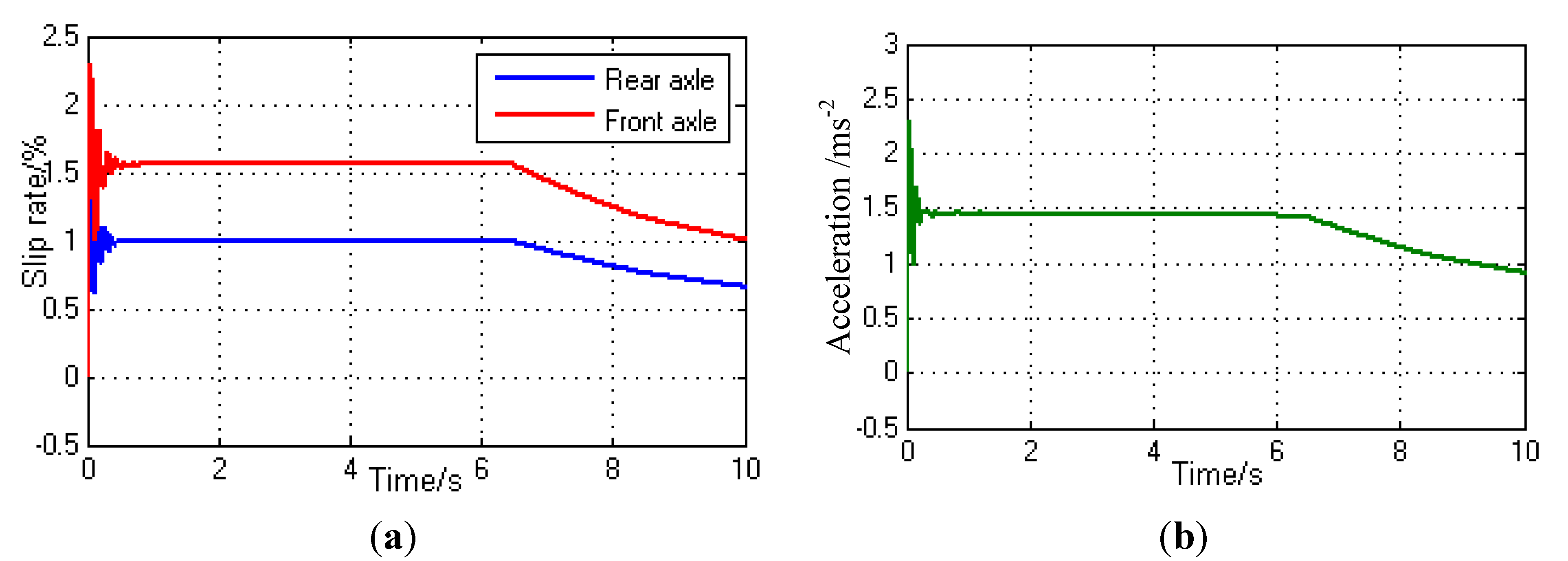
4.1. Simulation on Average Distribution of Inter-Axle Torque
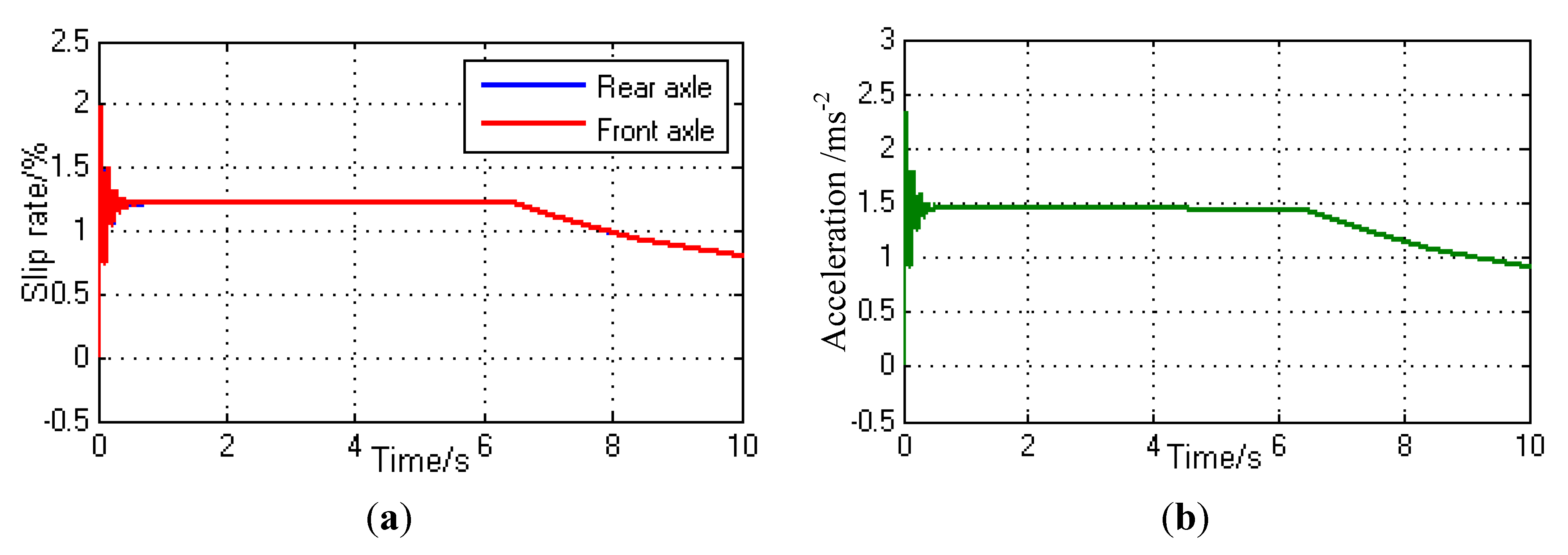
4.2. Simulation of Optimal Distribution of Inter-Axle Torque
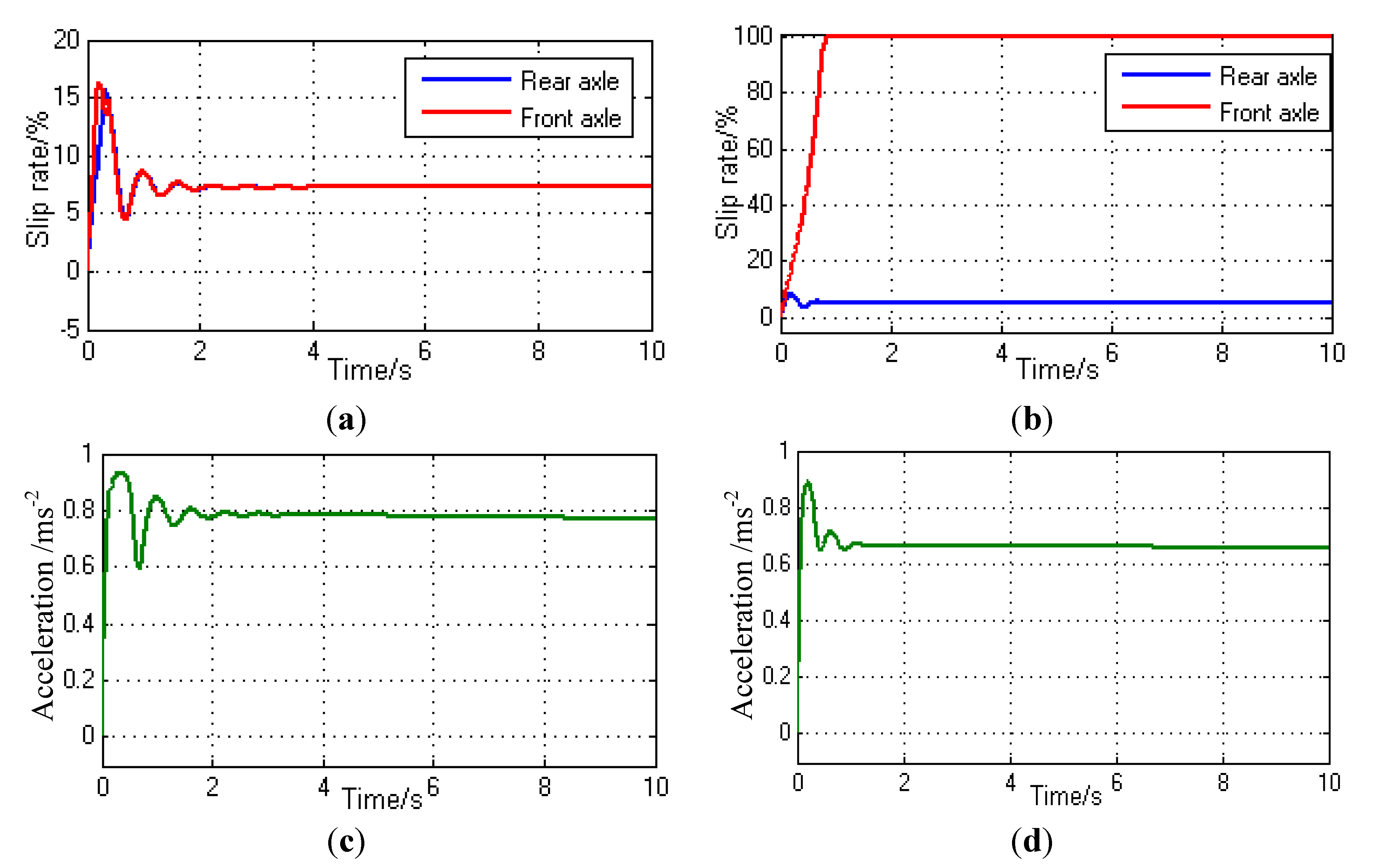

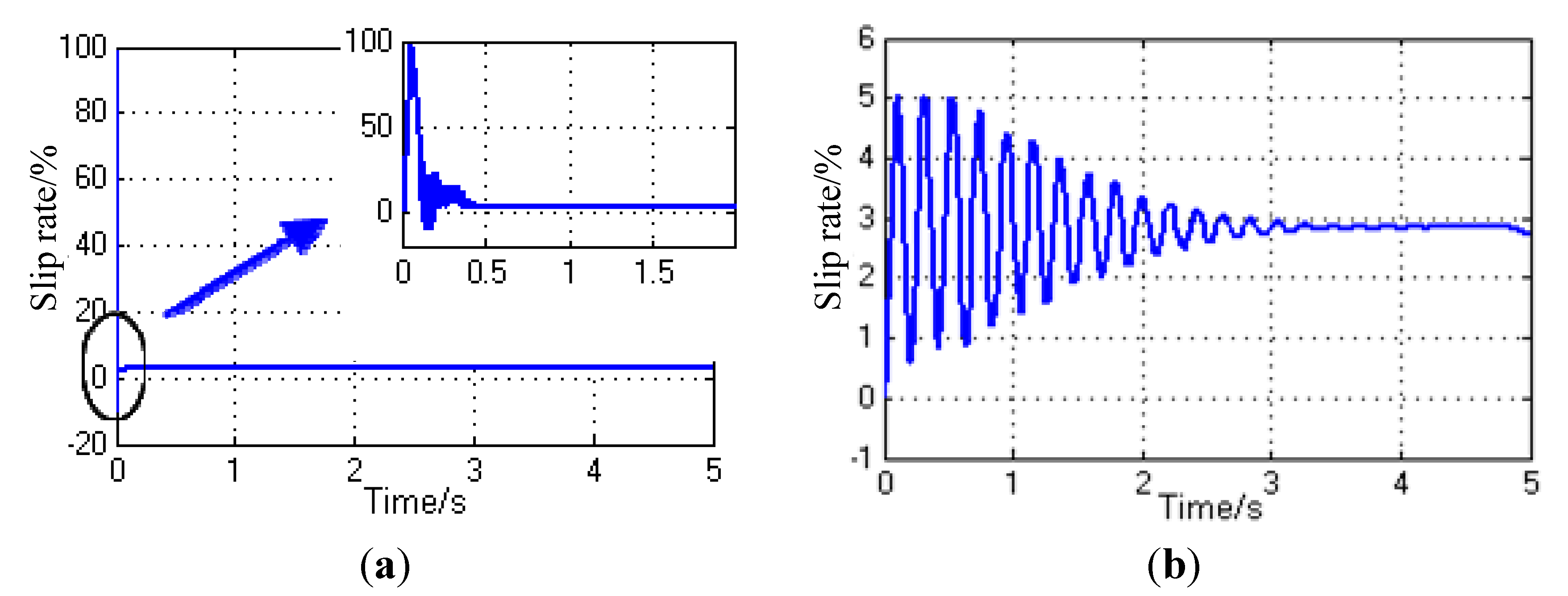
4.3. Simulation of Independent Control of Optimal Slip Rate
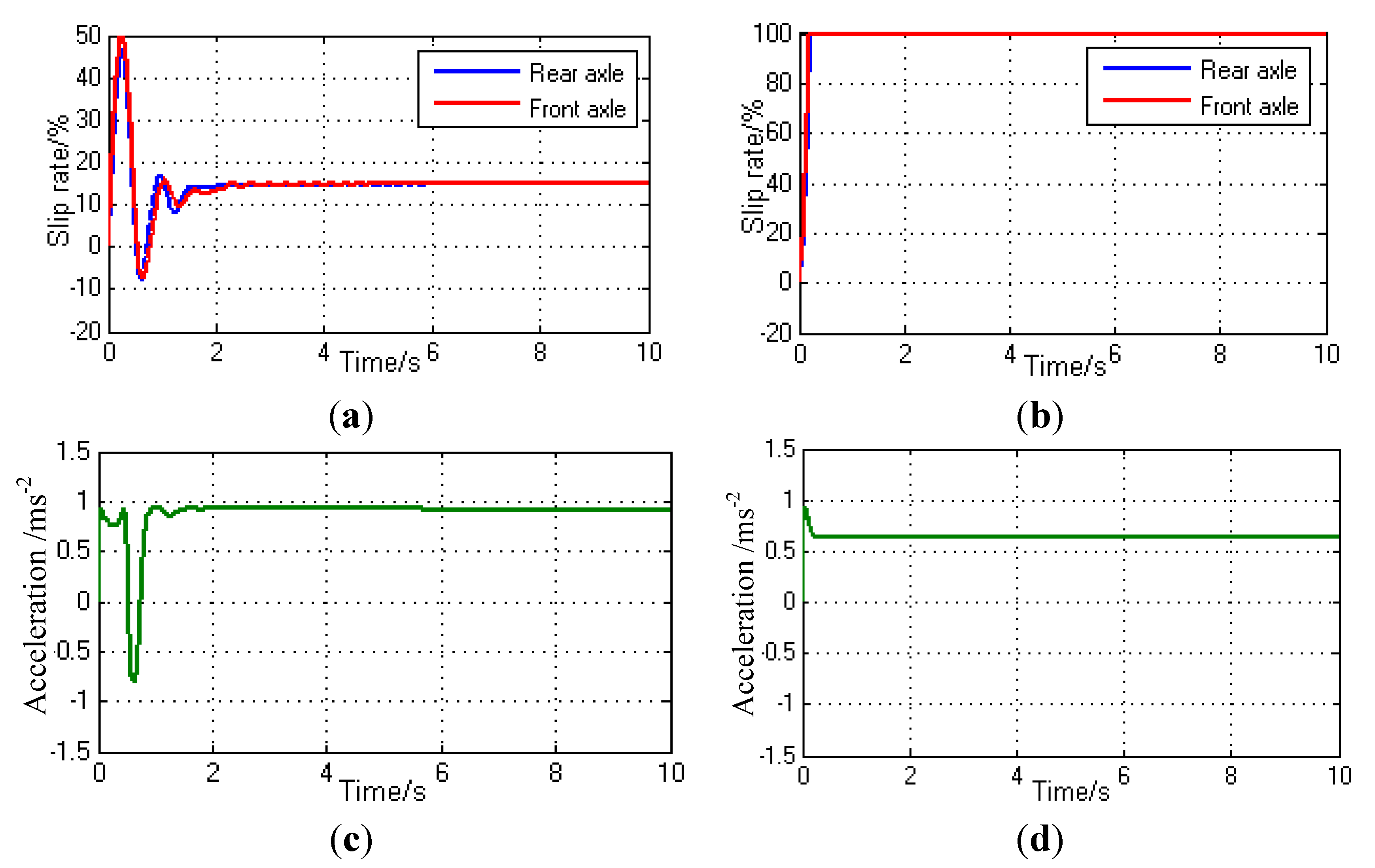

4.4. Comprehensive Simulation and Analysis of the Acceleration Slip Regulation Control Strategy

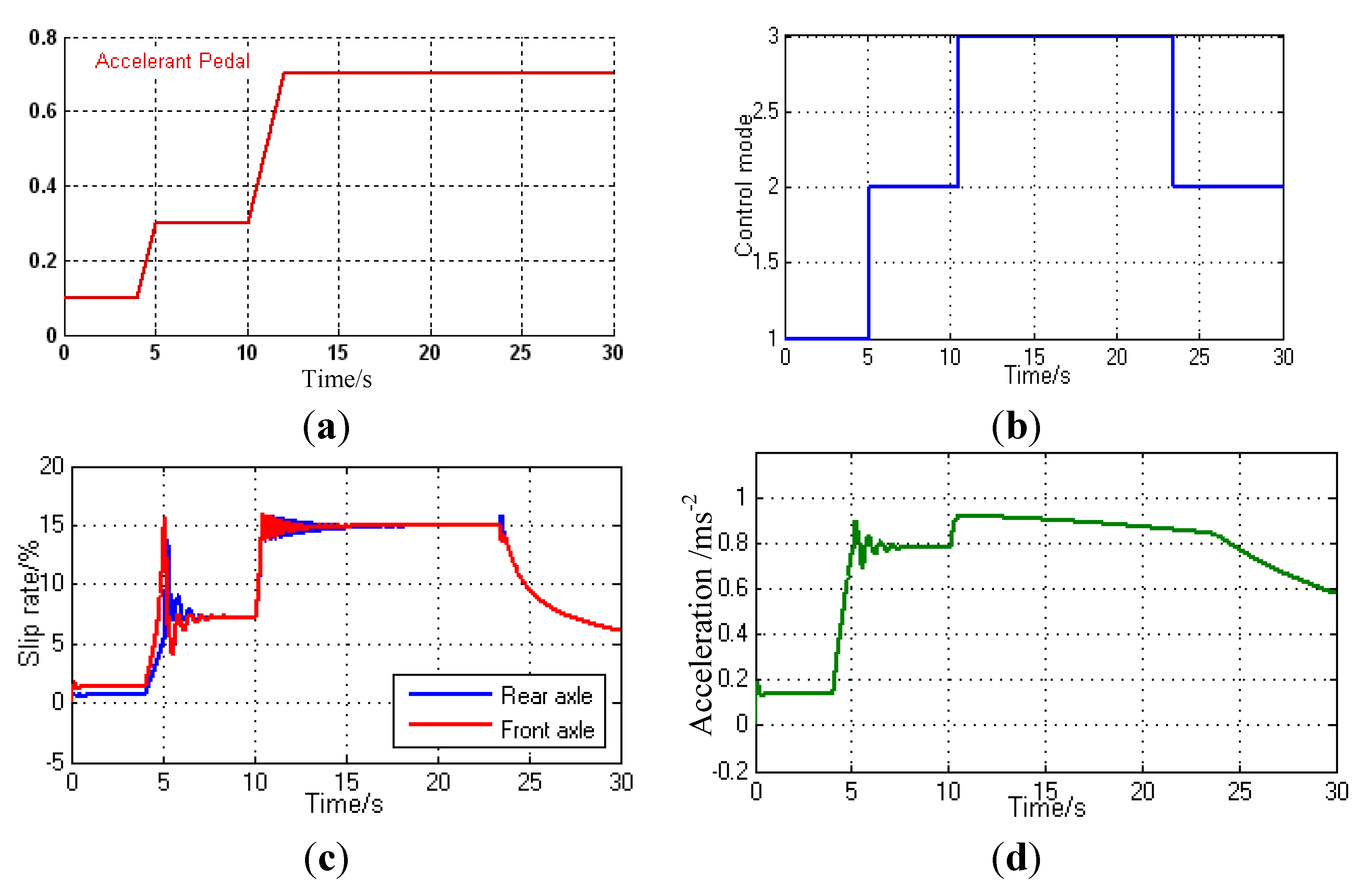
5. Conclusions
- (1)
- Aiming at the 4WD electric vehicle, which was driven by front and rear independent motors, a model of the ASR system was established.
- (2)
- Compared with the conventional method of slip rate calculation, using the state equation of slip rate can be more accurate to describe the tyre slip process in a low vehicle velocity situation.
- (3)
- An ASR control strategy which contains three torque distribution mode was designed, namely average distribution of inter-axle torque for high road adhesion, optimal distribution of inter-axle torque for middle road adhesion and independent control of optimal slip rate for low road adhesion. Several simulations were carried out with MATLAB/Simulink, and the simulation results with some comparisons show that, the proposed strategy could realize the transformation among different control modes, thus fully use the road adhesion conditions, make the vehicle’s dynamic performance to follow the driver’s wishes. As a result, the vehicle longitudinal drive stability and dynamic performance are ensured.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, J.; Wang, Q.; Jin, L.; Song, C. Independent wheel torque control of 4WD electric vehicle for differential drive assisted steering. Mechatronics 2011, 21, 63–76. [Google Scholar] [CrossRef]
- Kang, J.; Yoo, J.; Yi, K. Driving control algorithm for maneuverability, lateral stability, and rollover prevention of 4WD electric vehicles with independently driven front and rear wheels. IEEE Trans. Veh. Technol. 2011, 60, 2987–3001. [Google Scholar] [CrossRef]
- Dasgupta, K. Analysis of a hydrostatic transmission system using low speed high torque motor. Mech. Mach. Theory 2000, 35, 1481–1499. [Google Scholar] [CrossRef]
- Gasbaoui, B.; Nasri, A. A Novel 4WD Electric Vehicle Control Strategy Based on Direct Torque Control Space Vector Modulation Technique. Intell. Control. Autom. 2012, 3, 236–242. [Google Scholar] [CrossRef]
- Xue, X.; Cheng, K.; Ng, T.; Cheung, N.C. Multi-objective optimization design of in-wheel switched reluctance motors in electric vehicles. IEEE Trans. Ind. Electron. 2010, 57, 2980–2987. [Google Scholar] [CrossRef]
- Tong, Q. Simulation Study on the Longitudinal Dynamics of a Full Drive Vehicle with Two Separated Motors. Master’s Thesis, Beijing Institute of Technology, Beijing, China, 2013. [Google Scholar]
- Jalali, K.; Uchida, T.; McPhee, J.; Lambert, S. Development of a Fuzzy Slip Control System for Electric Vehicles with In-wheel Motors. SAE Int. J. Altern. Powertrains 2012, 1, 46–64. [Google Scholar]
- Liu, W.; He, H.; Peng, J. Driving Control Research for Longitudinal Dynamics of Electric Vehicles with Independently Driven Front and Rear Wheels. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Zhao, Z. Study of acceleration slip regulation strategy for four wheel drive hybrid electric car. Chin. J. Mech. Eng. 2011, 47, 83–98. [Google Scholar] [CrossRef]
- Sakai, S.; Hori, Y. Advantage of electric motor for anti-skid control of electric vehicle. Eur. Power Electron. Drives J. 2001, 11, 26–32. [Google Scholar]
- Yin, D.; Oh, S.; Hori, Y. A novel traction control for EV based on maximum transmissible torque estimation. IEEE Trans. Ind. Electron. 2009, 56, 2086–2094. [Google Scholar] [CrossRef]
- Chen, F.W.; Liao, T.L. Nonlinear linearization controller and genetic algorithm based fuzzy logic controller for ABS systems and their comparison. Int. J. Veh. Des. 2000, 24, 334–349. [Google Scholar] [CrossRef]
- Nakakuki, T.; Shen, T.; Tamura, K. Adaptive control approach to uncertain longitudinal tire slip in traction control of vehicles. Asian J. Control. 2008, 10, 67–73. [Google Scholar] [CrossRef]
- Liu, J.K. Sliding Mode Control Design and MATLAB Simulation, 2nd ed.; Tsinghua University Press: Beijing, China, 2012. [Google Scholar]
- Ameodeo, M.; Ferrara, A.; Terzaghi, R.; Vecchio, C. Wheel Slip Control via Second–Order Sliding-Model Generation. IEEE Trans. Intell. Trans. Syst. 2010, 11, 122–131. [Google Scholar] [CrossRef]
- Bashash, S.; Fathy, H.K. Transport-based load modeling and sliding mode control of plug-in electric vehicles for robust renewable power tracking. IEEE Trans. Smart Grid 2012, 3, 526–534. [Google Scholar] [CrossRef]
- Subudhi, B.; Ge, S.S. Sliding-Mode-Observer-Based Adaptive Slip rate Control for Electric and Hybrid Vehicles. IEEE Trans. Intell. Trans. Syst. 2012, 13, 1617–1626. [Google Scholar] [CrossRef]
- Kim, J.; Park, C.; Hwang, S.; Hori, Y. Control algorithm for an independent motor-drive vehicle. IEEE Trans. Veh. Technol. 2010, 59, 3213–3222. [Google Scholar] [CrossRef]
- Austin, L.; Morrey, D. Recent advances in antilock braking systems and traction control systems. Proc. Inst. Mech. Eng. Part D 2000, 214, 625–638. [Google Scholar] [CrossRef]
- Peng, J.K.; He, H.W.; Feng, N.L. Simulation Research on an Electric Vehicle Chassis System Based on a Collaborative Control System. Energies 2013, 6, 312–328. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Veh. Syst. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Clover, C.; Bernard, J. Longitudinal tire dynamics. Veh. Syst. Dyn. 1998, 29, 231–260. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
He, H.; Peng, J.; Xiong, R.; Fan, H. An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control. Energies 2014, 7, 3748-3763. https://doi.org/10.3390/en7063748
He H, Peng J, Xiong R, Fan H. An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control. Energies. 2014; 7(6):3748-3763. https://doi.org/10.3390/en7063748
Chicago/Turabian StyleHe, Hongwen, Jiankun Peng, Rui Xiong, and Hao Fan. 2014. "An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control" Energies 7, no. 6: 3748-3763. https://doi.org/10.3390/en7063748
APA StyleHe, H., Peng, J., Xiong, R., & Fan, H. (2014). An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control. Energies, 7(6), 3748-3763. https://doi.org/10.3390/en7063748






