A Single Phase Doubly Grounded Semi-Z-Source Inverter for Photovoltaic (PV) Systems with Maximum Power Point Tracking (MPPT)
Abstract
:1. Introduction
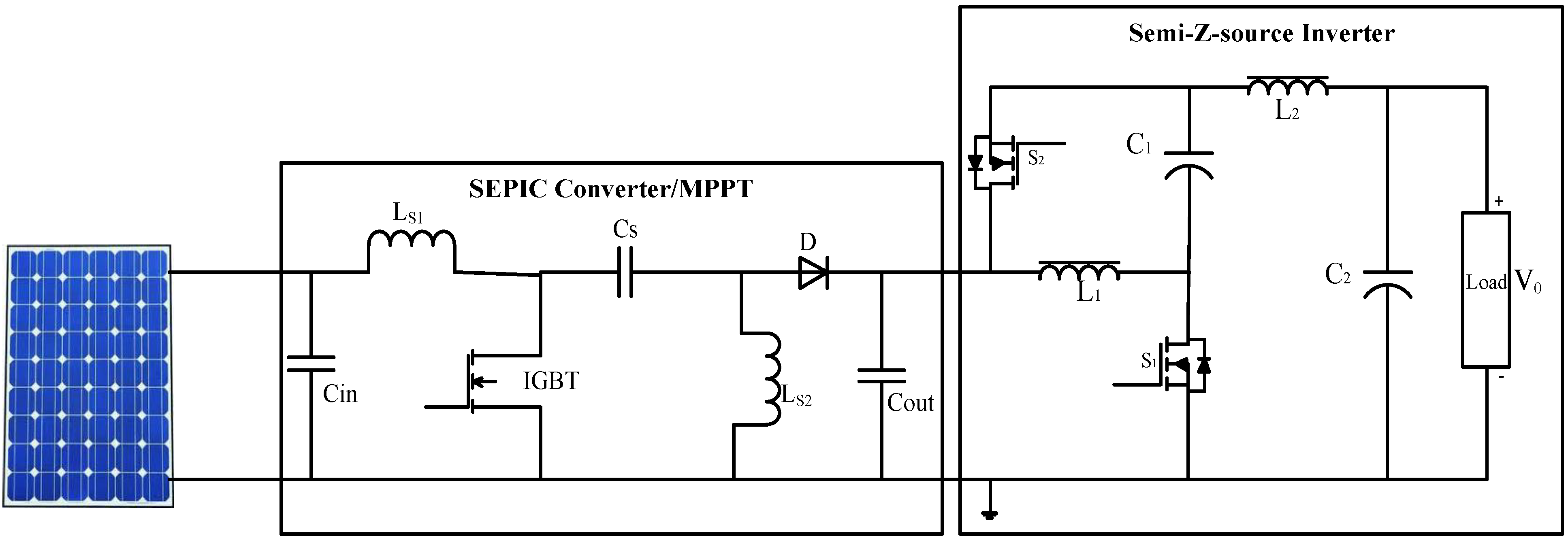
2. Working Principle
2.1. MPPT Working Principle
2.1.1. PV System with DC-DC Converter
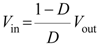
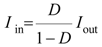
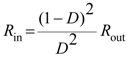
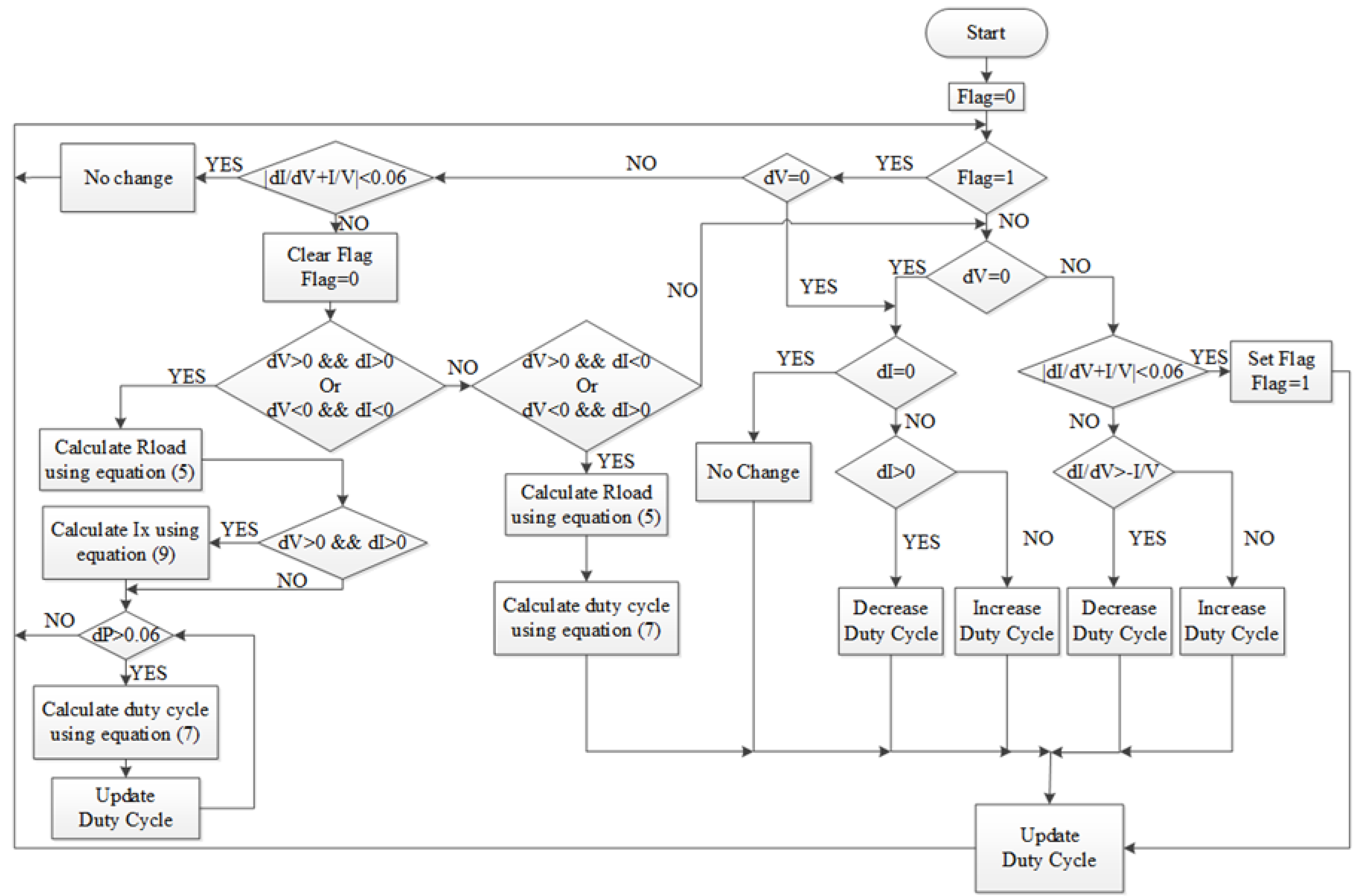
2.1.2. MPPT Algorithm
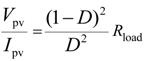
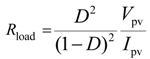
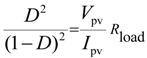
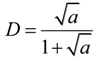
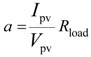 .
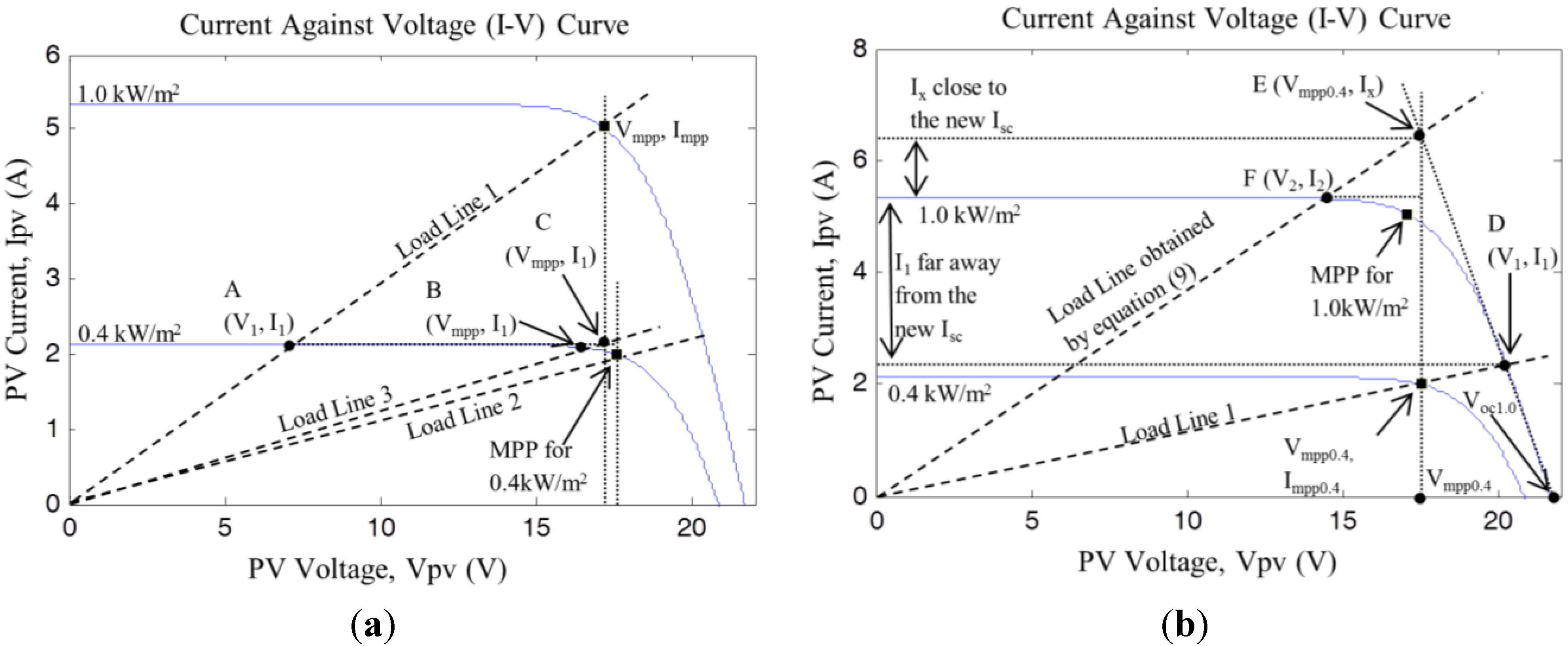
.2.1.2.1. Decrease in Solar Irradiation Level
2.1.2.2. Increase in Solar Irradiation Level
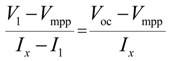
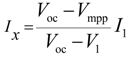
2.1.2.3. Load Variation
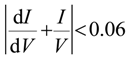
2.2. Semi-Z-Source Inverter Working Principle
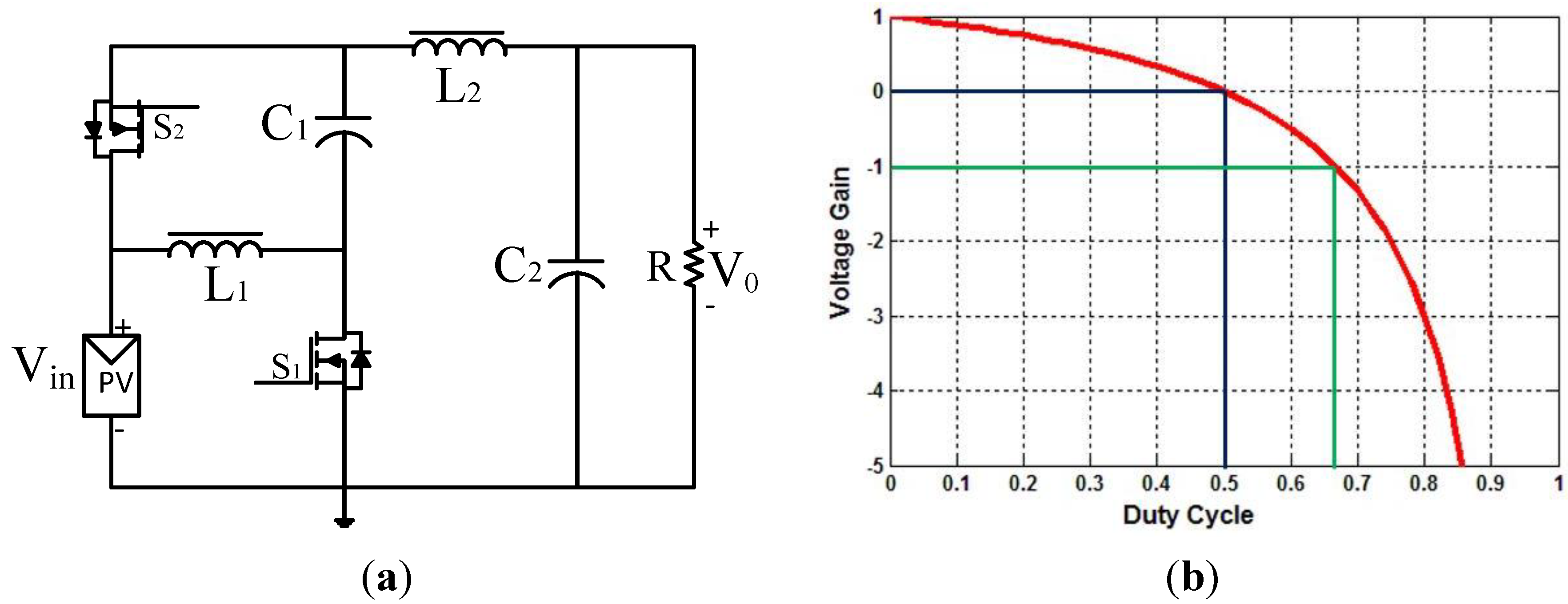
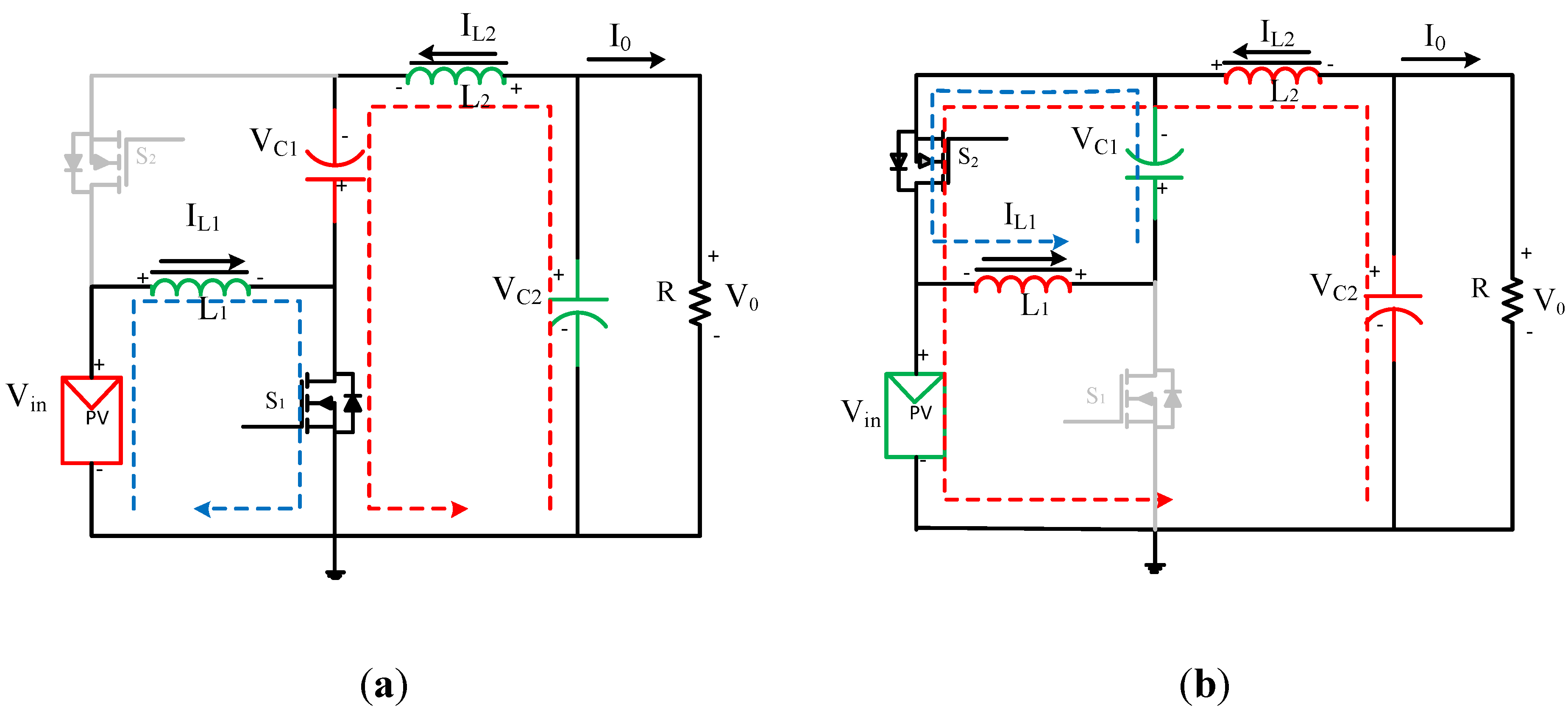
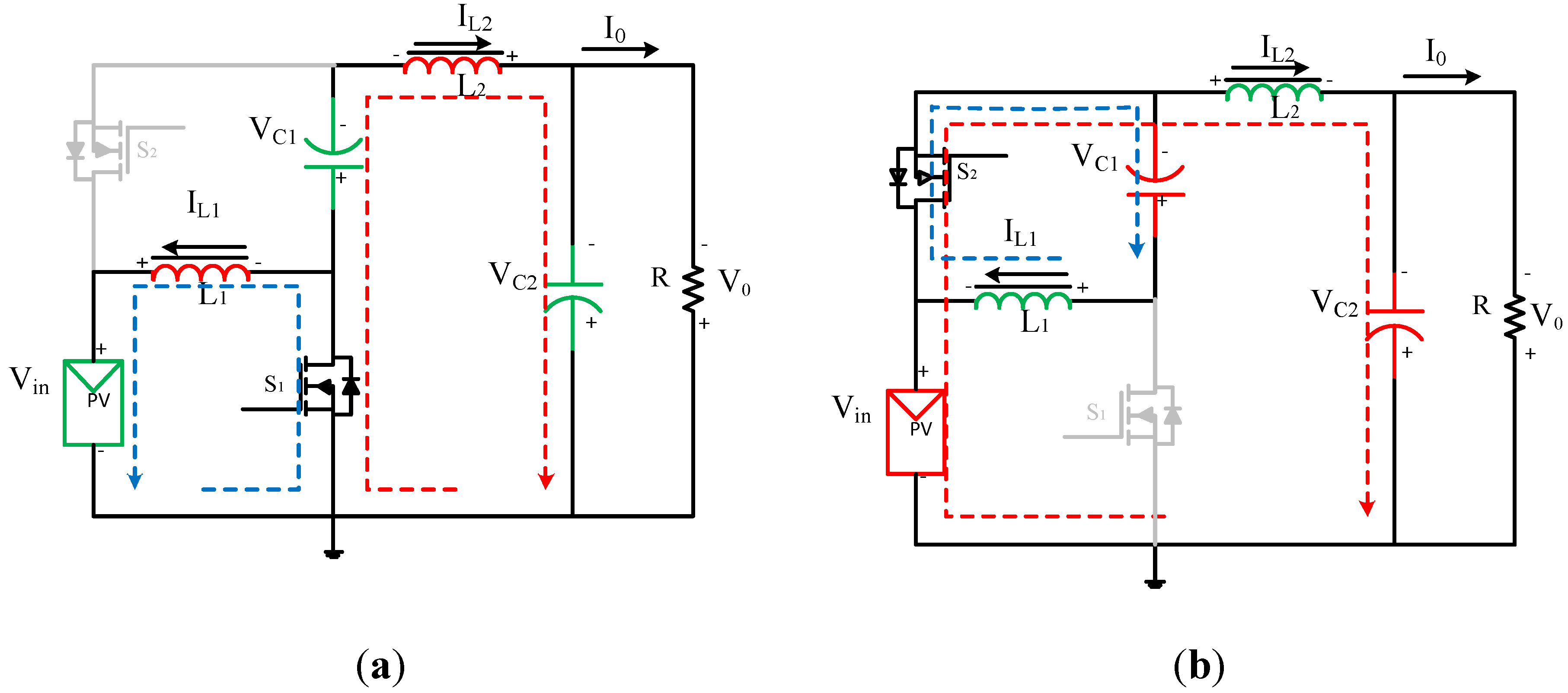
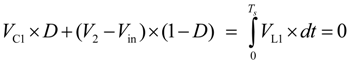
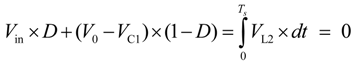
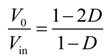
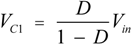
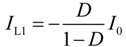
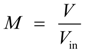
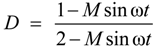
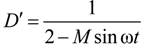

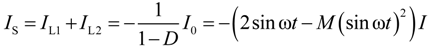

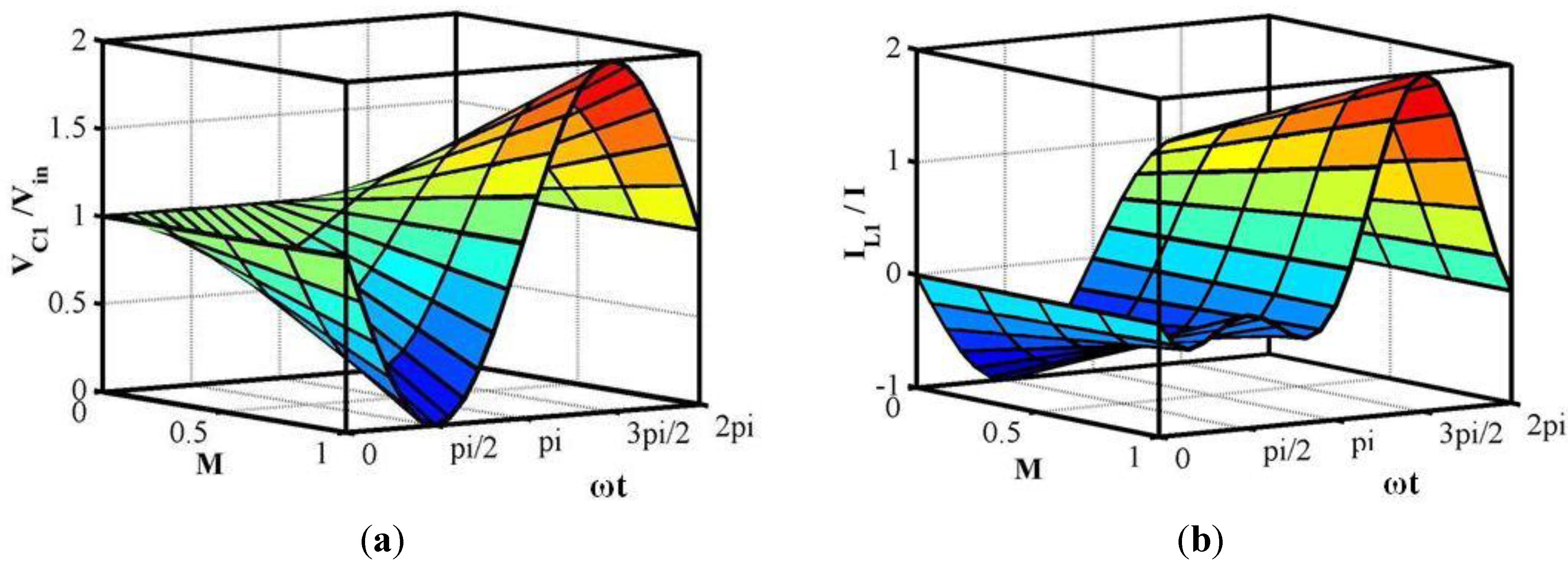
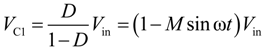
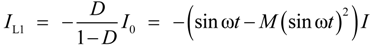
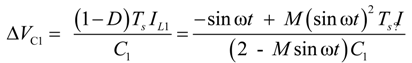
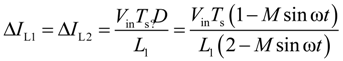
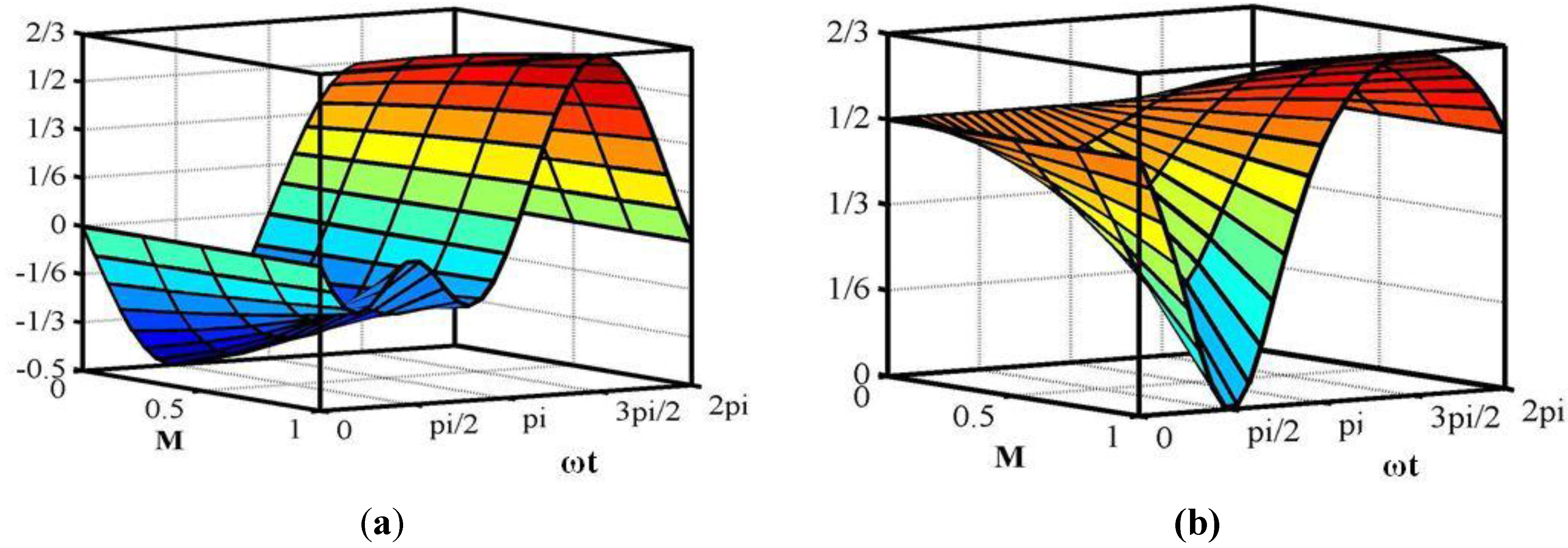
2.3. Semi-Z-Source Inverter Modulation Principle
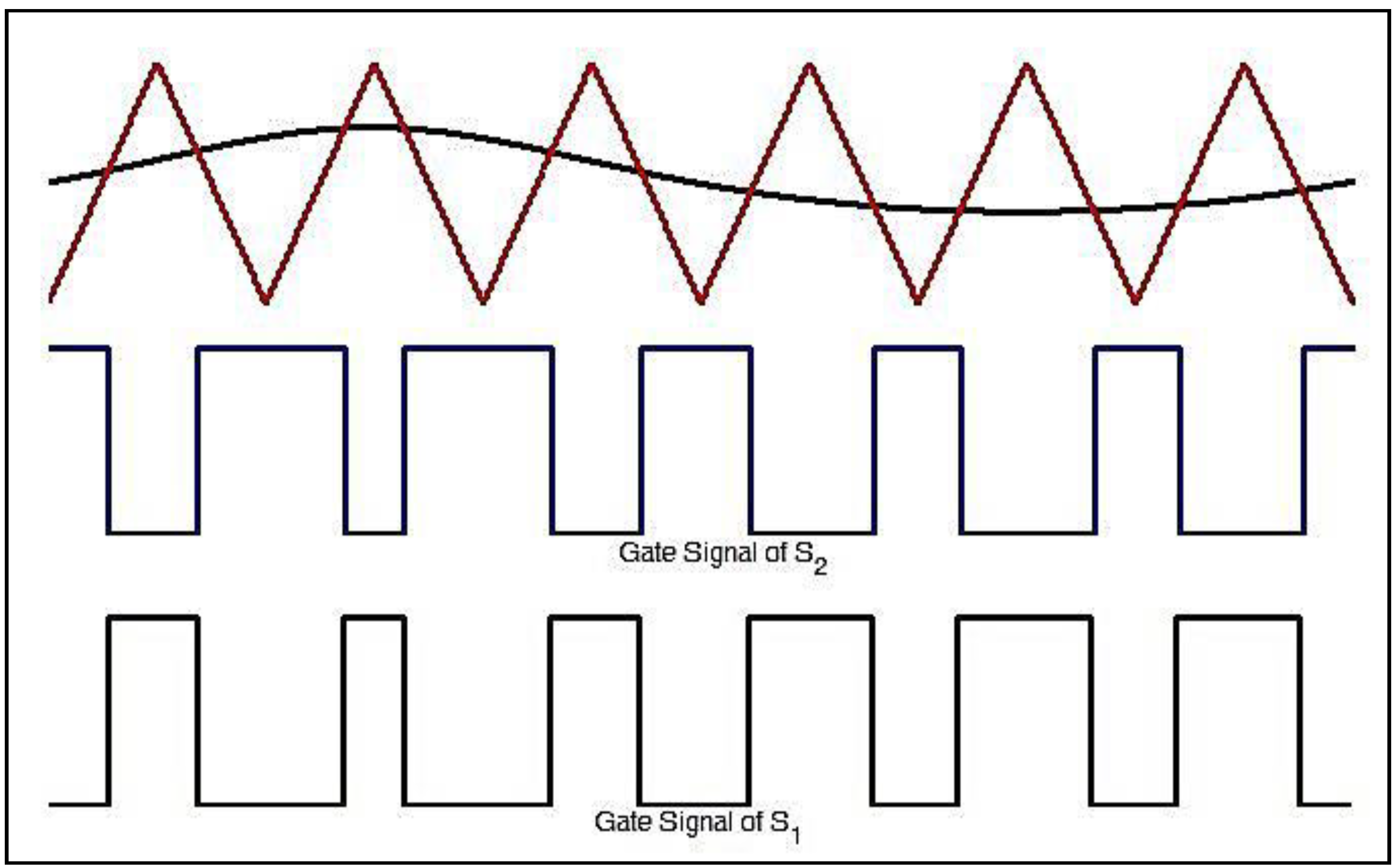
2.4. Experimental Validation of Semi-Z-Source Inverter


3. Experimental Validation of Single Phase Semi-Z-Source Inverter for PV System with MPPT
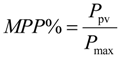

| Parameters | Conventional Incremental Conductance algorithm [20] | Modified incremental conductance algorithm [20] | Proposed fast convergence algorithm |
|---|---|---|---|
| Steady state oscillation | Yes | No | No |
| Response under fast varying solar irradiation | Slow | Fast | Fast |
| MPP efficiency (%) | 98.49 | 99.89 | 99.94 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Desai, H.P.; Patel, H. Maximum power point algorithm in PV generation: An overview. In Proceedings of the 2007 7th International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; pp. 624–630.
- Xiao, L.; Yaoyu, L.; Seem, J.E. Maximum power point tracking for photovoltaic system using adaptive extremum seeking control. IEEE Trans. Control Syst. Technol. 2013, 21, 2315–2322. [Google Scholar] [CrossRef]
- Shen, J.-M.; Jou, H.-L.; Wu, J.-C. Novel transformerless grid-connected power converter with negative grounding for photovoltaic generation system. IEEE Trans. Power Electron. 2012, 27, 1818–1829. [Google Scholar] [CrossRef]
- Kasem Alaboudy, A.H.; Zeineldin, H.H.; Kirtley, J.L. Microgrid stability characterization subsequent to fault-triggered islanding incidents. IEEE Trans Power Deliv. 2012, 27, 658–669. [Google Scholar] [CrossRef]
- Meneses, D.; Blaabjerg, F.; Garcia, O.; Cobos, J.A. Review and comparison of step-up transformerless topologies for photovoltaic AC-module application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef]
- Ahmed, M.E.-S.; Orabi, M.; AbdelRahim, O.M. Two-stage micro-grid inverter with high-voltage gain for photovoltaic applications. IET Power Electron. 2013, 6, 1812–1821. [Google Scholar] [CrossRef]
- Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of perturb and observe MPPT algorithm implementation techniques for PV pumping applications. IEEE Trans. Sustain. Energy 2012, 3, 21–33. [Google Scholar] [CrossRef]
- Sera, D.; Mathe, L.; Kerekes, T.; Spataru, S.V.; Teodorescu, R. On the perturb-and-observe and incremental conductance MPPT methods for PV systems. IEEE J. Photovolt. 2013, 3, 1070–1078. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and hardware implementation of incremental conductance mppt with direct control method using CUK converter. IEEE Trans. Ind. Electron. 2011, 58, 1154–1161. [Google Scholar]
- Ishaque, K.; Salam, Z.; Amjad, M.; Mekhilef, S. An improved particle swarm optimization (PSO)-based MPPT for PV with reduced steady-state oscillation. IEEE Trans. Power Electron. 2012, 27, 3627–3638. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Huang, S.-C.; Huang, J.-W.; Liang, W.-C. A particle swarm optimization-based maximum power point tracking algorithm for PV systems operating under partially shaded conditions. IEEE Trans. Energy Convers. 2012, 27, 1027–1035. [Google Scholar] [CrossRef]
- El Khateb, A.; Rahim, N.A.; Selvaraj, J.; Uddin, M.N. Fuzzy logic controller based SEPIC converter for maximum power point tracking. IEEE Trans. Ind. Appl. 2014, PP, 1. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Finney, S.J.; Williams, B.W. Fuzzy-logic-control approach of a modified hill-climbing method for maximum power point in microgrid standalone photovoltaic system. IEEE Trans. Power Electron. 2011, 26, 1022–1030. [Google Scholar] [CrossRef]
- Lin, W.-M.; Hong, C.-M.; Chen, C.-H. Neural-network-based MPPT control of a stand-alone hybrid power generation system. IEEE Trans. Power Electron. 2011, 26, 3571–3581. [Google Scholar] [CrossRef]
- Zhang, F.; Thanapalan, K.; Maddy, J.; Guwy, A. Development of a novel hybrid maximum power point tracking methodology for photovoltaic systems. In Proceedings of the 18th IEEE International Conference on Automation and Computing, Loughborough, UK, 7–8 September 2012; pp. 1–6.
- Al-Diab, A.; Sourkounis, C. Variable step size P&O MPPT algorithm for PV systems. In Proceedings of the 12th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 20–22 May 2010; 2010; pp. 1097–1102. [Google Scholar]
- Chao, K.-H.; Li, C.-J. An intelligent maximum power point tracking method based on extension theory for PV systems. Expert Syst. Appl. 2010, 37, 1050–1055. [Google Scholar] [CrossRef]
- Liu, F.; Duan, S.; Liu, F.; Liu, B.; Kang, Y. A variable step size INC MPPT method for PV systems. IEEE Trans. Ind. Electron. 2008, 55, 2622–2628. [Google Scholar] [CrossRef]
- Zbeeb, A.; Devabhaktuni, V.; Sebak, A. Improved photovoltaic MPPT algorithm adapted for unstable atmospheric conditions and partial shading. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; pp. 320–323.
- Tey, K.S.; Mekhilef, S. Modified incremental conductance MPPT algorithm to mitigate inaccurate responses under fast-changing solar irradiation level. Solar Energy 2014, 101, 333–342. [Google Scholar] [CrossRef]
- Kerekes, T.; Teodorescu, R.; Liserre, M.; Klumpner, C.; Sumner, M. Evaluation of three-phase transformerless photovoltaic inverter topologies. IEEE Trans. Power Electron. 2009, 24, 2202–2211. [Google Scholar] [CrossRef]
- Haeberlin, H.; Borgna, L.; Kaempfer, M.; Zwahlen, U. New Tests at Grid-Connected PV Inverters: Overview over Test Results and Measured Values of Total Efficiency ηtot. In Proceedings of the 21st European Photovoltaic Solar Energy Conference, Dresden, Germany, 4–8 September 2006.
- Martínez-Moreno, F.; Lorenzo, E.; Muñoz, J.; Moretón, R. On the testing of large PV arrays. Prog. Photovolt.: Res. Appl. 2012, 20, 100–105. [Google Scholar] [CrossRef]
- Araújo, S.V.; Zacharias, P.; Mallwitz, R. Highly efficient single-phase transformerless inverters for grid-connected photovoltaic systems. IEEE Trans. Ind. Electron. 2010, 57, 3118–3128. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. Grid-connected photovoltaic power systems: Technical and potential problems—A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Lopez, O.; Freijedo, F.D.; Yepes, A.G.; Fernandez-Comesana, P.; Malvar, J.; Teodorescu, R.; Doval-Gandoy, J. Eliminating ground current in a transformerless photovoltaic application. IEEE Trans. Energy Convers. 2010, 25, 140–147. [Google Scholar]
- Xiao, H.F.; Xie, S.J. Leakage current analytical model and application in single-phase transformerless photovoltaic grid-connected inverter. IEEE Trans. Electromagn. Compat. 2010, 52, 902–913. [Google Scholar] [CrossRef]
- Yang, B.; Li, W.H.; Gu, Y.J.; Cui, W.F.; He, X.N. Improved transformerless inverter with common-mode leakage current elimination for a photovoltaic grid-connected power system. IEEE Trans. Power Electron. 2012, 27, 752–762. [Google Scholar]
- Zhang, F.; Yang, S.; Peng, F.Z.; Qian, Z. A zigzag cascaded multilevel inverter topology with self voltage balancing. In Proceedings of the Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition 2008, Austin, TX, USA, 24–28 February 2008; pp. 1632–1635.
- Ahmed, T.; Mekhilef, S.; Nakaoka, M. Single phase transformerless semi-Z-source inverter with reduced total harmonic distortion (THD) and DC current injection. In 5th Annual International Energy Conversion Congress and Exibition for the Asia Pacific Region (IEEE ECCE Asia DownUnder), Melbourne, Australia, 3–6 June, 2013; pp. 1322–1327.
- Blewitt, W.M.; Atkinson, D.J.; Kelly, J.; Lakin, R.A. Approach to low-cost prevention of DC injection in transformerless grid connected inverters. IET Power Electron. 2010, 3, 111–119. [Google Scholar] [CrossRef]
- Calais, M.; Ruscoe, A.; Dymond, M. Transformerless PV inverter issues revisited–are australian standards adequate? In Proceedings of 2009 the 47th Annual Conference ANZSES Annual Conference, Townsville, Australia, 29 September–2 October 2009.
- IEEE. IEEE Standard for Interconnecting Distributed Resourceswith Electric Power Systems; IEEE Standard 1547–2003; IEEE: New York, NY, USA, 2003; pp. 1–16. [Google Scholar]
- British Standards Institution. Characteristics of the Utility Interface for Photovoltaic (PV) SystemsIEC 61727, 2nd ed.; British Standards Institution: London, UK, 2004. [Google Scholar]
- IEEE. Recommended Practice for Utility Interface of Photovoltaic (PV) Systems; IEEE Standard 929–2000; IEEE: New York, NY, USA, 2000. [Google Scholar]
- IEEE. Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; IEEE 519–1992; IEEE: New York, NY, USA, 1992. [Google Scholar]
- Alajmi, B.N.; Ahmed, K.H.; Adam, G.P.; Williams, B.W. Single-phase single-stage transformer less grid-connected PV system. IEEE Trans. Power Electron. 2013, 28, 2664–2676. [Google Scholar] [CrossRef]
- Wu, T.-F.; Chang, C.-H.; Lin, L.-C.; Kuo, C.-L. Power loss comparison of single-and two-stage grid-connected photovoltaic systems. IEEE Trans. Energy Convers. 2011, 26, 707–715. [Google Scholar]
- Patel, H.; Agarwal, V. A single-stage single-phase transformer-less doubly grounded grid-connected PV interface. IEEE Trans. Energy Convers. 2009, 24, 93–101. [Google Scholar] [CrossRef]
- Singh, B.; Jain, C.; Goel, S. Ilst control algorithm of single-stage dual purpose grid connected solar PV system. IEEE Trans. Power Electron. 2013, PP, 1. [Google Scholar]
- Wensong, Y.; Jih-Sheng, L.; Hao, Q.; Hutchens, C. High-efficiency MOSFET inverter with H6-type configuration for photovoltaic nonisolated AC-module applications. IEEE Trans. Power Electron. 2011, 26, 1253–1260. [Google Scholar] [CrossRef]
- Li, Y.; Oruganti, R. A low cost flyback CCM inverter for AC module application. IEEE Trans. Power Electron. 2012, 27, 1295–1303. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, Q.; Liang, B.; Liu, X.; Cui, S. Analysis of a single-phase Z-source inverter for battery discharging in vehicle to grid applications. Energies 2011, 4, 2224–2235. [Google Scholar] [CrossRef]
- Kasa, N.; Iida, T.; Iwamoto, H. Maximum power point tracking with capacitor identifier for photovoltaic power system. In Proceedings of the Eighth International Conference on Power Electronics and Variable Speed Drives, London, UK, 18–19 September 2000; pp. 130–135.
- Shimizu, T.; Hashimoto, O.; Kimura, G. A novel high-performance utility-interactive photovoltaic inverter system. IEEE Trans. Power Electron. 2003, 18, 704–711. [Google Scholar] [CrossRef]
- Cao, D.; Jiang, S.; Yu, X.; Peng, F.Z. Low-cost semi-Z-source inverter for single-phase photovoltaic systems. IEEE Trans. Power Electron. 2011, 26, 3514–3523. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ahmed, T.; Soon, T.K.; Mekhilef, S. A Single Phase Doubly Grounded Semi-Z-Source Inverter for Photovoltaic (PV) Systems with Maximum Power Point Tracking (MPPT). Energies 2014, 7, 3618-3641. https://doi.org/10.3390/en7063618
Ahmed T, Soon TK, Mekhilef S. A Single Phase Doubly Grounded Semi-Z-Source Inverter for Photovoltaic (PV) Systems with Maximum Power Point Tracking (MPPT). Energies. 2014; 7(6):3618-3641. https://doi.org/10.3390/en7063618
Chicago/Turabian StyleAhmed, Tofael, Tey Kok Soon, and Saad Mekhilef. 2014. "A Single Phase Doubly Grounded Semi-Z-Source Inverter for Photovoltaic (PV) Systems with Maximum Power Point Tracking (MPPT)" Energies 7, no. 6: 3618-3641. https://doi.org/10.3390/en7063618
APA StyleAhmed, T., Soon, T. K., & Mekhilef, S. (2014). A Single Phase Doubly Grounded Semi-Z-Source Inverter for Photovoltaic (PV) Systems with Maximum Power Point Tracking (MPPT). Energies, 7(6), 3618-3641. https://doi.org/10.3390/en7063618






