Online Parameter Identification of Ultracapacitor Models Using the Extended Kalman Filter
Abstract
: Ultracapacitors (UCs) are the focus of increasing attention in electric vehicle and renewable energy system applications due to their excellent performance in terms of power density, efficiency, and lifespan. Modeling and parameterization of UCs play an important role in model-based regulation and management for a reliable and safe operation. In this paper, an equivalent circuit model template composed of a bulk capacitor, a second-order capacitance-resistance network, and a series resistance, is employed to represent the dynamics of UCs. The extended Kalman Filter is then used to recursively estimate the model parameters in the Dynamic Stress Test (DST) on a specially established test rig. The DST loading profile is able to emulate the practical power sinking and sourcing of UCs in electric vehicles. In order to examine the accuracy of the identified model, a Hybrid Pulse Power Characterization test is carried out. The validation result demonstrates that the recursively calibrated model can precisely delineate the dynamic voltage behavior of UCs under the discrepant loading condition, and the online identification approach is thus capable of extracting the model parameters in a credible and robust manner.1. Introduction
In order to address serious concerns over energy sustainability and environmental impact, governments, the automotive industry, and academia are endeavoring to expedite a paradigm shift to a green transportation system [1]. Electric vehicles have been widely recognized as an integral part of such a high-efficiency system, owing to the fact that the use of electricity can potentially diversify the power sources for vehicle propulsion systems [2]. The performance of electric vehicles is heavily influenced by their energy storage systems (ESSs). Thus, the drivability, fuel economy, and recuperation efficiency of electric vehicles are highly dependent on the specific power and energy of their ESSs [3,4]. Electrochemical devices, including fuel cells [5], rechargeable batteries [6], and ultracapacitors (UCs) [7] are among the most appropriate components for vehicular ESSs, each with strengths and limitations [8].
Ultracapacitors, also known as supercapacitors or double-layer capacitors, have high power density, low internal resistance, high efficiency, and exceedingly long cycle life, while possessing the merits of wide operating temperature range and fast charging [9,10]. However, their drawbacks, such as low energy density and relative high price, limit the possibility of deploying UCs as the single energy storage for electric vehicles. At present, rechargeable batteries, especially Li-ion batteries, are commonly used for energy storage in electric vehicles since they have a much higher energy density in comparison to UCs. Nevertheless, their cycle-life expectancy is still far less than can be expected in the ideal case, and they are highly sensitive to the charging/discharging current rate and the operating temperature. Therefore, one promising alternative is to combine UCs and batteries to constitute a hybrid energy storage system (HESS) with synergistically improved performance [4,11–13].
A model that can simulate the dynamics of an UC with high precision is vital for energy management design in electric vehicles equipped with UCs or HESSs. The modeling of UCs has a rich history. This research can be generally grouped into three categories: electrochemical models, artificial neural networks (ANNs), and equivalent circuit models. Electrochemical models are developed from first principles and depict the real physical-chemical reactions within an ultracapacitor utilizing partial differential equations [14,15]. They are suitable for providing insights into the distributed physical-electrochemical reactions and for related ultracapacitor design/synthesis purposes. However, the large number of model parameters and the inaccessibility of these parameters in terms of the measurability deter their usage for real-time management and power control design. ANN-based models can accurately describe the transient behavior of energy storage units such as batteries and UCs, as long as the model has been well trained beforehand [16–20]. However, the training process may be time-consuming and require a considerable quantity of training data. Furthermore, the model should be retrained if the real characteristics of the UC drift significantly with aging. Therefore, the above mentioned causes make ANN-based models unsuitable for online energy management implementation.
Equivalent circuit models have been carefully developed, especially for the energy management design and power control; these have been extensively reported in the literature [21–23]. The key advantage of these equivalent models lies in their relatively small number of parameters. For example, Buller et al. proposed an equivalent circuit model composed of a bulk capacitor, a second-order capacitance-resistance network, and a series resistance. This was adopted in [24] to delineate the voltage behavior of an UC. The bulk capacitor mainly accounts for the capacitance behavior while the second-order capacitance-resistance network contributes to better capturing the voltage response under dynamic scenarios. The accuracy of the parameterization is significant in terms of the electric vehicle context. A large body of literature exists pertaining to parameter extraction methods. For example, Spyker and Nelms [25] presented a classical equivalent circuit that comprises an equivalent series resistance, an equivalent parallel resistance, and a main capacitor. The model parameters were derived by measuring the voltage responses during charge and rest. However, the accuracy of this method is highly dependent on the measurement precision so it is sensitive to measurement noise. Gualous et al. [26] used electrochemical impedance spectroscopy (EIS) to characterize a second-order equivalent circuit model for UCs. EIS is a commonly used approach for the measurement of the complex impedances of energy storage devices such as batteries and UCs. This is done for a wide range of frequencies by imposing a known bias voltage upon the terminals of the tested storage device and detecting the corresponding excitation current [27,28]. The obtained frequency spectrum can be modeled with interleaved RC circuits by analyzing the frequency dependency of the real and imaginary parts of impedance, thus resulting in an equivalent circuit model [22]. However, the precision of an identified model when obtained using the EIS method may be compromised under the varying loading conditions due to offline implementation. This should attribute to the fact that the lumped equivalent circuit model parameters are largely dependent on the loading conditions, which makes the offline EIS-obtained model incapable of representing the dynamics of batteries or UCs accurately in the real implementation. The majority of the methods presented in the literature are subject to the similar drawbacks, i.e., susceptibility to measurement precision and noise and offline implementation. In order to tackle these problems, this paper employs the extended Kalman filter (EKF) to recursively estimate the model parameters. The EKF has the advantages of being closed-loop, online, and the availability of error bounds. Hence has been widely used to perform the model calibration for batteries in real time. For example, Hu et al. presented a second-order equivalent circuit model for Li-ion batteries whose parameters were calibrated using the EKF [29]. However, there is a lack of literature reporting the application of the EKF technique to identify online UC model parameters.
This paper is arranged as follows: Section 2 reviews the equivalent circuit model used to describe the voltage response of UCs. Then, the formulation for the extended Kalman filter for model parameter estimation is detailed. Section 3 describes a test rig that was specially developed in order to carry out the experimental UC tests. Section 4 discusses the modeling results, followed by key conclusions in Section 5.
2. Modeling and Parameter Estimation for Ultracapacitors
2.1. Ultracapacitor Model Structure
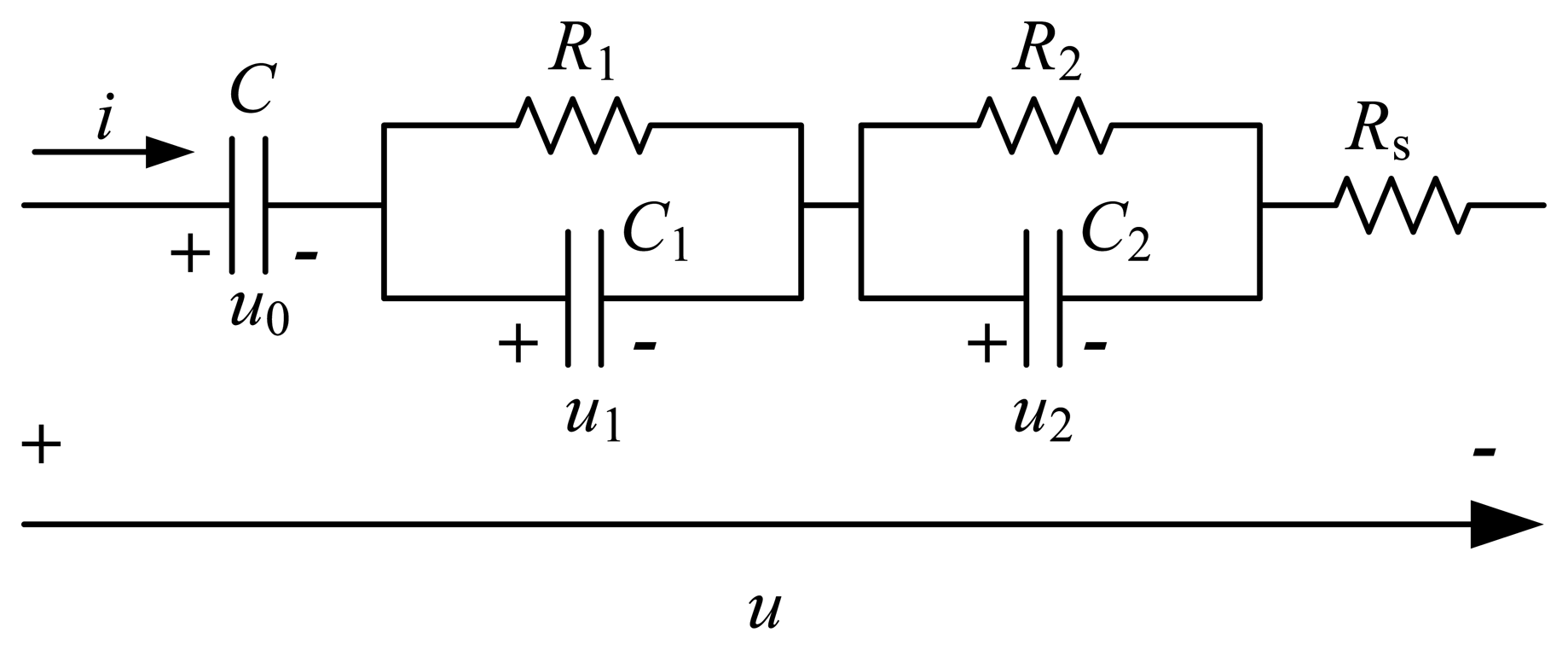
There are a variety of equivalent circuit model structures for UCs as reported in the literature. This paper selects the one that consists of a bulk capacitor, a second-order capacitance-resistance network and a series resistance. The second-order capacitance-resistance network is composed of two parallel RC circuits. The model originates from an impedance model in the frequency domain [30]. The detailed structure is shown in Figure 1 where u0 denotes the voltage across the bulk capacitor C, u1 and u2 denote the voltages of the two RC circuits, respectively, u denotes the output voltage, and Rs denotes the series resistance.
According to basic electrical circuit principles, the continuous state equation can be derived as:
The state equation can be further transformed into the discrete state equation so that:
Where ΔT is the sampling time; The output equation can be derived as:
2.2. Parameter Estimation Using the Extended Kalman Filter
Recently, the Kalman filtering has gained more popularity in the field of state estimation, parameter estimation and dual estimation due to its inherent merits [31,32]. That is, it can be implemented online and automatically provides the estimation error bound. In order to implement extended Kalman filtering to recursively estimate the parameters, the process of parameter evolution can be formulated into a state equation so that:
Time update
where θ̂kk−1 is the priori estimate of the parameter vector θ at time interval k before the measurement uk is taken into consideration, θ̂k is the a posteriori estimate of the parameter vector at time interval k−1, Pk|k−1 represents the a priori estimation error of parameter vector θ̂ at time interval k, and Pk−1 represents the posteriori estimation error of parameter vector θ̂ at time interval k−1.Measurement update:
and:where W represents the covariance of the measurement noise υ and L is the Kalman gain at time interval k. x̂k can be computed given x̂k−1 and θ̂k−1 according to Equation (2). Updates in the time and measurement equations at each time interval means that the parameter vector θ̂k can be recursively estimated. Since x̂k acts as a function of the parameter vector θ̂k, Ck can be computed by performing recurrent differentiations, which are:where:It is obvious that the derivative calculation is recursive, and can be initiated by:
3. Experimental Setup
In order to collect experimental data for the parameter estimation, a test rig was developed. A block diagram is shown in Figure 2, while components of the actual rig are illustrated in Figure 3. It consists of a Digtron Battery Test System (BTS-600), a thermal chamber, a host computer and an UC. The BTS-600 is assigned to charge the UC according to a pre-designed program with a maximum voltage of 500 V and a maximum charging/discharging current of 300 A. It has the capability of recoding the real-time testing parameters such as terminal voltage, load current and accumulative capacity loss. The terminal voltage and load current are logged and used to perform the parameter estimation. The thermal chamber is used to maintain an ambient temperature of 20 °C during all the tests; this reduces the influence of temperature on the variation of the model parameters. The host computer is responsible for controlling the load profile and logging the measured data from the BTS-600. A commercially available UC was selected to conduct the experimental tests. It has a nominal capacitance of 3000 F and a rated voltage of 2.7 V.
4. Results and Discussion
4.1. Parameter Estimation in the DST Test
In order to validate the proposed estimation algorithm, a transient power test based on the standard Dynamic Stress Test (DST) was conducted on the established test rig. The DST-based test can represent the dynamic load conditions of a UC during daily driving of an electric vehicle with UCs as the single or complementary energy storage. The voltage and current of the UC in the DST test are shown in the Figure 4 while a magnified part of the voltage curve is also shown.
It is well-known that Kalman filters require a priori knowledge about the process and the measurement noise statistics. When it comes to the algorithm, the process and measurement noise covariance, namely Q and W, should be carefully selected. Based on the knowledge of the test UC, the parameters for the extended Kalman filter algorithm are specified by:
Given the specified parameters, the proposed extended Kalman filter was implemented in order to estimate online the model parameters of the UC. The evolution of the estimated model parameters is shown in Figure 5. It is clear that all the estimated parameters tend to converge at the end of the test. It can be seen that the value of R1 is bigger than that of R2 while C1 is just slightly smaller than C1. It means that the first RC circuit has a larger time constant than the second RC network in the selected model. It can be observed that the value of the main capacitor of C exhibits a gently decline, which indicates the capacitance varies with the terminal voltage. It can also be seen that the estimated resistance Rs increases along with the decline of the voltage in the test. The variations of C and Rs reveal the internal characteristics are also dependent on the external loading conditions [33].
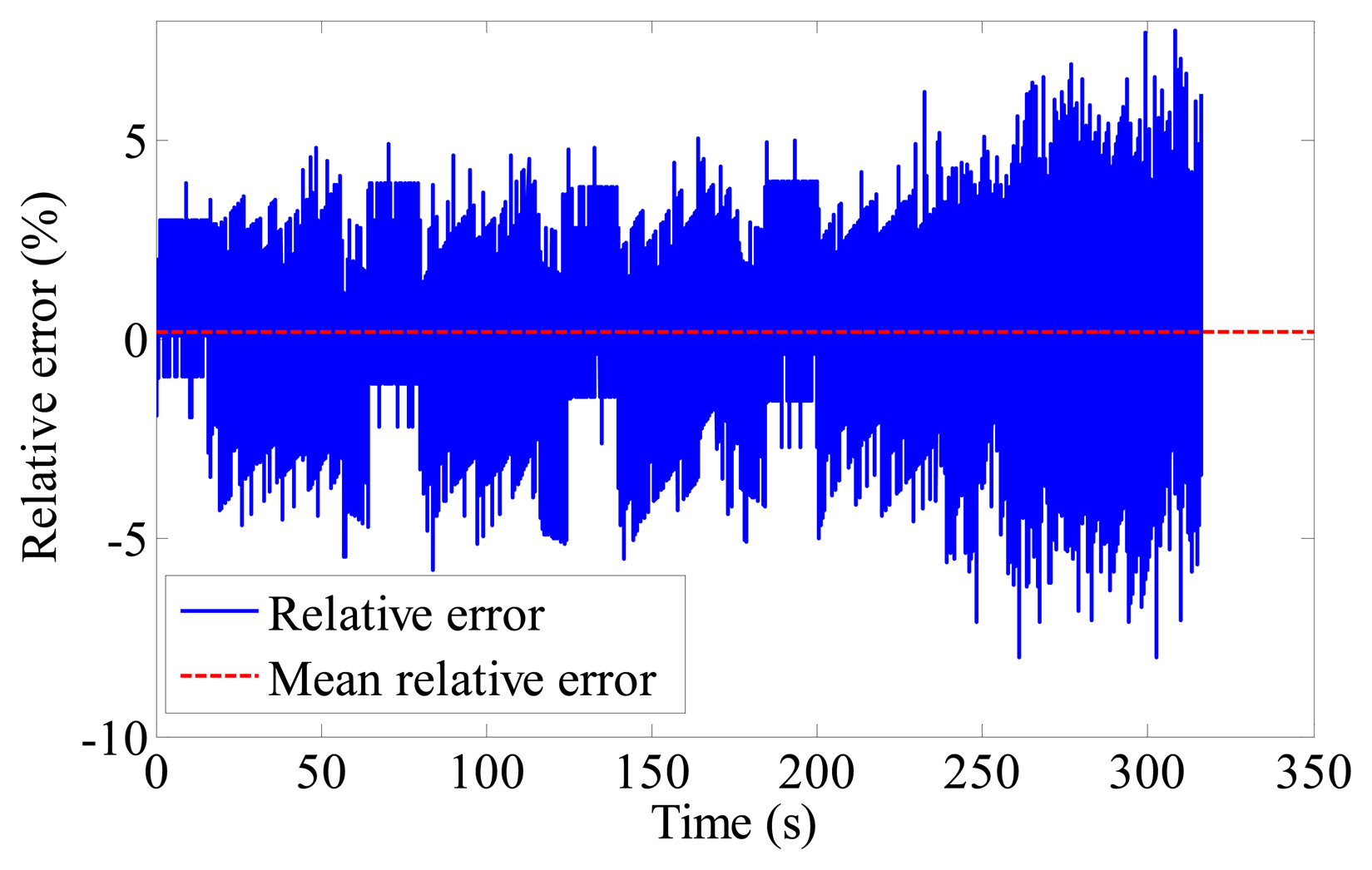
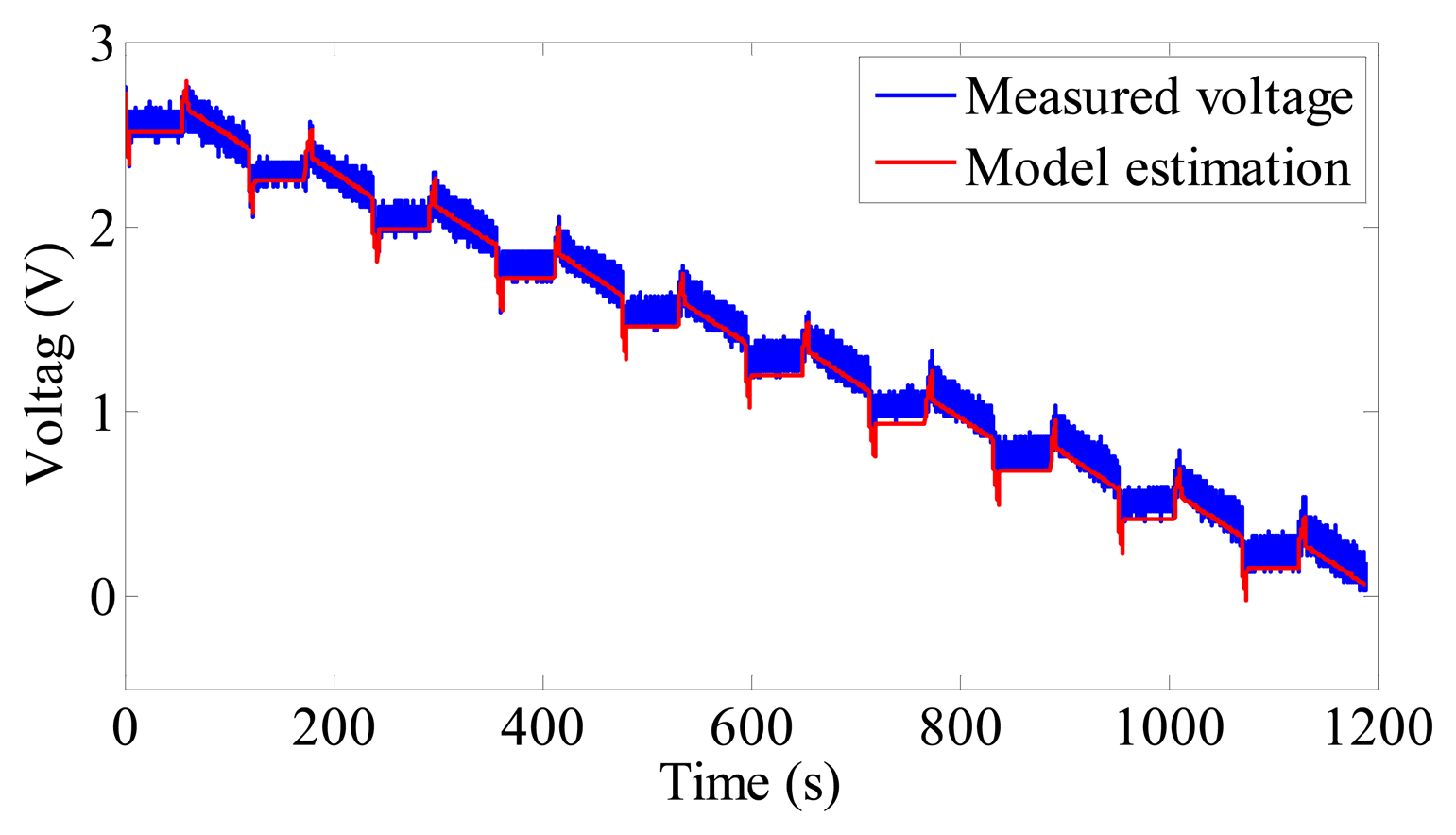
The evolution of the measured and estimated voltages is shown in Figure 6. It can be seen that the estimated voltage shows good agreement with the measured voltage in the DST test. This proves that the recursively identified model can precisely capture the voltage response after compensating for the initial model error. The relative voltage error is illustrated in Figure 7 which further demonstrates the model performance. The converged estimation result is shown in Table 1. According to Equations (3) to (6), the model parameters can be computed and these are shown in Table 2.
4.2. Model Validation in the HPPC
In order to validate the derived model, a Hybrid Pulse Power Characterization (HPPC) was conducted. The voltage and current profiles in the HPPC test are shown in Figure 8, while a magnified part of the voltage curve is also shown. The simulated and measured voltages are illustrated in Figure 9. It is obvious that the model with the previously estimated parameters can well represent the voltage behavior under the HPPC test. The error, instead of the relative error between the simulated and measured voltages, is used to indicate the accuracy of the identified model because the voltage of the UC generally decreases to 0 V at the end of the test. The error curve is shown in Figure 10. The mean error is 0.058 V, indicating the high accuracy of the model. It verified that proposed estimation algorithm can achieve robust parameter estimation and be used to derive a model that can predict the dynamics of a UC under different load profiles. Owing to that the DST and HPPC loading profiles are highly dynamic and representative of the real driving conditions of vehicles, it is reasonable to conclude that the derived model is applicable to the real driving scenarios with sufficient accuracy. That is to say, the proposed method can identify the model with robustness and precision in real implementation.
5. Conclusions
This paper presents an online model identification method for a UC model based on the well-known Kalman filter. An equivalent circuit model was used to represent the dynamics of a UC. It was composed of a bulk capacitor, a second-order RC network and a series internal resistance. The rationale for the use of this model is that it can sufficiently capture the transient voltage response without introducing heavy computation load. The evolution of the model dynamics was depicted by a body of discrete state equations according to electrical principles. The equation parameters were extracted and used as the targets for the proposed estimation method. The extended Kalman filter was formulated and applied to recursively identify the parameters through a DST test conducted on the test rig. The results show that the recursively calibrated model can precisely represent the transient voltage behavior under the dynamic operating conditions. In order to further validate the accuracy of the model, the HPPC test was implemented. The result shows that the model can also depict the voltage behavior under the HPPC operating scenarios with high fidelity. This verifies that the proposed method can identify a model in a robust manner against different load profiles.
Acknowledgments
Lei Zhang is grateful to the funding from the China Scholarship Council as well as the University of Technology Sydney and Beijing Institute of Technology for his studies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, X.; Murgovski, N.; Johannesson, L.; Egardt, B. Energy efficiency analysis of a series plug-in hybrid electric bus with different energy management strategies and battery sizes. Appl. Energy 2013, 111, 1001–1009. [Google Scholar]
- Waraich, R.; Galus, M.; Dobler, C.; Balmer, M.; Andersson, G.; Axhausen, K. Plug-in hybrid electric vehicles and smart grid: Investigations based on a microsimulation. Transp. Res. Part C Emerg. Technol. 2013, 28, 74–86. [Google Scholar]
- Cao, J.; Emadi, A. A New Battery/UltraCapacitor Hybrid Energy Storage System for Electric, Hybrid, and Plug-In Hybrid Electric Vehicles. IEEE Trans. Power Electron. 2012, 27, 122–132. [Google Scholar]
- Hu, X.; Murgovski, N.; Johannesson, L.; Egardt, B. Comparison of three electrochemical energy buffers applied to a hybrid bus powertrain with simultaneous optimal sizing and energy management. IEEE Trans. Intell. Transp. Syst. 2014. Available online: http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6708463 (accessed on 10 March 2014). [Google Scholar] [CrossRef]
- Messagie, M.; Boureima, F.-S.; Coosemans, T.; Macharis, C.; Van Mierlo, J. A Range-Based Vehicle Life Cycle Assessment Incorporating Variability in the Environmental Assessment of Different Vehicle Technologies and Fuels. Energies 2014, 7, 1467–1482. [Google Scholar]
- Bo, L.; Ji, H.R.; Shin, T.L.; Kil, T.C. Design and Control of a Multi-Functional Energy Recovery Power Accumulator Battery Pack Testing System for Electric Vehicles. Energies 2014, 7, 1376–1392. [Google Scholar]
- He, H.-W.; Xiong, R.; Chang, Y.-H. Dynamic Modeling and Simulation on a Hybrid Power System for Electric Vehicle Applications. Energies 2010, 3, 1821–1830. [Google Scholar]
- Li, Q.; Chen, W.; Li, Y.; Liu, S.; Huang, J. Energy management strategy for fuel cell/battery/ultracapacitor hybrid vehicle based on fuzzy logic. Int. J. Electr. Power Energy Syst. 2012, 43, 514–525. [Google Scholar]
- Lee, D.; Kim, U.; Shin, C.; Lee, B.; Kim, B.; Kim, Y. Modelling of the thermal behaviour of an ultracapacitor for a 42-V automotive electrical system. J. Power Sources 2008, 175, 664–668. [Google Scholar]
- Schiffer, J.; Linzen, D.; Sauer, D. Heat generation in double layer capacitors. J. Power Sources 2006, 160, 765–772. [Google Scholar]
- Bentley, P.; Stone, D.; Schofield, N. The parallel combination of a VRLA cell and supercapacitor for use as a hybrid vehicle peak power buffer. J. Power Sources 2005, 147, 288–294. [Google Scholar]
- Ortúzar, M.; Moreno, J.; Dixon, J. Ultracapacitor-Based Auxiliary Energy System for an Electric Vehicle: Implementation and Evaluation. IEEE Trans. Power Electron. 2007, 54, 2147–2156. [Google Scholar]
- Amjadi, Z.; Williamson, S. Prototype Design and Controller Implementation for a Battery-Ultracapacitor Hybrid Electric Vehicle Energy Storage System. IEEE Trans. Smart Grid 2012, 3, 332–340. [Google Scholar]
- Wang, C.; Srinivasan, V. Computational battery dynamics (CBD)—Electrochemical/thermal coupled modeling and multi-scale modeling. J. Power Sources 2002, 110, 364–376. [Google Scholar]
- Schmidt, A.; Bitzer, M.; Imre, Á.; Guzzella, L. Experiment-driven electrochemical modeling and systematic parameterization for a lithium-ion battery cell. J. Power Sources 2010, 195, 5071–5080. [Google Scholar]
- Chan, C.C.; Lo, E.W.C.; Shen, W. The available capacity computation model based on artificial neural network for lead-acid batteries in electrical vehicles. J. Power Sources 2000, 87, 201–204. [Google Scholar]
- Shen, W.X.; Chau, K.T.; Chan, C.C. Neural network-based residual capacity indicator for nickel-metal hydride batteries in electric vehicles. IEEE Trans. Veh. Technol. 2005, 54, 1705–1712. [Google Scholar]
- Morita, Y.; Yamamoto, S.; Lee, S.H.; Mizuno, N. On-line detection of state-of-charge in lead acid battery using radial basis function neural network. Asian J. Control. 2006, 8, 268–273. [Google Scholar]
- Cheng, B.; Bai, Z.F.; Cao, B.G. State of charge estimation based on evolutionary neural network. Energy Convers. Manag. 2008, 49, 2788–2794. [Google Scholar]
- Marie-Francoise, J.; Gualous, H.; Berthon, A. Supercapacitor thermal- and electrical-behaviour modelling using ANN. IEE Proc. Electr. Power Appl. 2006, 153, 255–260. [Google Scholar]
- Nelms, R.; Cahela, D.; Tatarchuk, B. Modeling double-layer capacitor behavior using ladder circuits. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 430–438. [Google Scholar]
- Zhang, Y.; Yang, H. Modeling and characterization of supercapacitors for wireless sensor network applications. J. Power Sources 2011, 196, 4128–4135. [Google Scholar]
- Bertrand, N.; Sabatier, J.; Briat, O.; Vinassa, J. Fractional non-linear modelling of ultracapacitors. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1327–1337. [Google Scholar]
- Buller, S.; Karden, E.; Kok, D.; Doncker, R. Modeling the dynamic behavior of supercapacitors using impedance spectroscopy. Proceedings of Conference Record of the 2001 IEEE Industry Applications Conference, Thirty-Sixth IAS Annual Meeting, Chicago, IL, USA, 30 September–4 October 2001; pp. 2500–2504.
- Spyker, R.; Nelms, R. Classical equivalent circuit parameters for a double-layer capacitor. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 829–836. [Google Scholar]
- Gualous, H.; Bouquain, D.; Berthon, A. Experimental study of supercapacitor serialresistance and capacitance variations with temperature. J. Power Sources 2003, 123, 86–93. [Google Scholar]
- Kötz, R.; Hahn, M.; Gallay, R. Temperature behavior and impedance fundamentals of supercapacitors. J. Power Sources 2006, 154, 550–555. [Google Scholar]
- Rafik, F.; Gualous, H.; Gallay, R.; Crausaz, A.; Berthon, A. Frequency, thermal and voltage supercapacitor characterization and modeling. J. Power Sources 2007, 165, 928–934. [Google Scholar]
- Hu, X.; Sun, F.; Cheng, X. Recursive calibration for a lithium iron phosphate battery for electric vehicles using extended Kalman filtering. J. Zhejiang Univ. Sci. A 2011, 12, 818–825. [Google Scholar]
- Chiang, C.; Yang, J.; Cheng, W. Temperature and state-of-charge estimation in ultracapacitors based on extended Kalman filter. J. Power Sources 2013, 234, 234–243. [Google Scholar]
- Plett, G. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 1. Background. J. Power Sources 2004, 134, 252–261. [Google Scholar]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar]
- Wu, C.; Hung, Y.; Hong, C. On-line supercapacitor dynamic models for energy conversion and management. Energy Convers. Manag. 2012, 53, 337–345. [Google Scholar]







| a1 | b1 | a2 | b2 | C_recip | Rs |
|---|---|---|---|---|---|
| 0.9677 | 1.55 × 10−5 | 0.8767 | 8.77 × 10−6 | 3.85 × 10−4 | 6.93 × 10−4 |
| C(F) | C1(F) | C2(F) | R1(Ω) | R2(Ω) | Rs(Ω) |
|---|---|---|---|---|---|
| 2601 | 628 | 1065 | 4.85 × 10−4 | 7.14 × 10−4 | 6.93 × 10−4 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, L.; Wang, Z.; Sun, F.; Dorrell, D.G. Online Parameter Identification of Ultracapacitor Models Using the Extended Kalman Filter. Energies 2014, 7, 3204-3217. https://doi.org/10.3390/en7053204
Zhang L, Wang Z, Sun F, Dorrell DG. Online Parameter Identification of Ultracapacitor Models Using the Extended Kalman Filter. Energies. 2014; 7(5):3204-3217. https://doi.org/10.3390/en7053204
Chicago/Turabian StyleZhang, Lei, Zhenpo Wang, Fengchun Sun, and David G. Dorrell. 2014. "Online Parameter Identification of Ultracapacitor Models Using the Extended Kalman Filter" Energies 7, no. 5: 3204-3217. https://doi.org/10.3390/en7053204





