Experimental Study on Influence of Pitch Motion on the Wake of a Floating Wind Turbine Model
Abstract
: Wind tunnel experiments were performed, where the development of the wake of a model wind turbine was measured using stereo Particle Image Velocimetry to observe the influence of platform pitch motion. The wakes of a classical bottom fixed turbine and a streamwise oscillating turbine are compared. Results indicate that platform pitch creates an upward shift in all components of the flow and their fluctuations. The vertical flow created by the pitch motion as well as the reduced entrainment of kinetic energy from undisturbed flows above the turbine result in potentially higher loads and less available kinetic energy for a downwind turbine. Experimental results are compared with four wake models. The wake models employed are consistent with experimental results in describing the shapes and magnitudes of the streamwise velocity component of the wake for a fixed turbine. Inconsistencies between the model predictions and experimental results arise in the floating case particularly regarding the vertical displacement of the velocity components of the flow. Furthermore, it is found that the additional degrees of freedom of a floating wind turbine add to the complexity of the wake aerodynamics and improved wake models are needed, considering vertical flows and displacements due to pitch motion.1. Introduction
Wind energy has become a major contributor to energy from renewable sources and is still projected to increase its portion to the overall energy supply in the future. Offshore wind energy is found to have the highest potential to fulfill these demands, due to sustained winds which are unaffected by complex terrain [1]. Offshore wind turbines, which have been installed recently, use monopiles or tripods as foundations, which are feasible in shallow water up to a depth of 50 m. Such shallow areas are rare and are often already exploited [2], therefore, solutions have to be found to produce wind energy in deeper water areas. Floating support structures for offshore wind turbines are possible alternatives to current bottom fixed foundations. A limited amount of field and experimental data in regards to the operational conditions of floating wind turbines is available.
The additional degrees of freedom of a floating platform will cause different operational conditions compared to fixed foundations. A detailed understanding of the influence of the added degrees of freedom on aerodynamic performance, fatigue loads and finally the costs of floating wind turbines would allow an optimized design of floating wind turbines [3].
The influence of various motions such as pitch, sway and heave on the aerodynamics of the rotor and the wake characteristics are important in determining the design space for proper load and fatigue calculations [4]. Most wind turbines are operated in arrays so proper modeling of wake development plays an important role in order to reduce fatigue loads of turbines positioned downstream and maximize power output of the turbine ensemble [5]. Experimental data is needed to validate the performance of computational models.
Feasibility studies have been performed to define the constraints for floating turbines installations [6]. The critical constraints as outlined are to establish a design basis for offshore turbines, reliable offshore substructures as well as low cost anchors and moorings. Simulations of the structural response have been performed by Jonkman et al. [7,8]. The approach used consisted of expanding the FAST (Fatigue, Aerodynamics, Structures and Turbulence) code for classical turbines with hydrodynamic wave-body interaction programs such as WAMIT (Wave Analysis at Massachusetts Institute of Technology), that covers hydrodynamic damping and wave excitation of the platform. A comparison of three concepts of floating platforms with land-based turbines showed an overall increase of loadings on all turbine components due to the floating platform, so a mechanically more robust design is required [9]. Further combinations of platform and turbine design have to be tested and economic aspects must be considered in order determine an optimal design.
Matsukama et al. [10] performed motion analysis of a spar floating wind turbine under steady wind conditions. The effect of rotor rotation on the response of the floating platform was taken into account using blade element momentum theory and multibody dynamics theory, thus splitting the turbine into rotor, nacelle, tower and platform. It was found that motions like sway, roll and yaw are influenced by the gyroscopic moment of the rotor and that these motions drive variations in loads and power output of a turbine. A 9° static pitch of the platform was calculated for the rated wind speed of the turbine. The dynamic pitch of the platform was found to be the same on average, but oscillating around this value. Yaw and roll movement were estimated as well and found to drive the loads on the turbine and changes in variation in the power output.
Experimental investigations have been done on the structural response of floating support structures by Utsunomiya et al. [11]. The equation as posed by Morison, which accounts for inertia and drag force on a body in a flow, was used to determine the wave force on a the spar body and to estimate response amplitudes of a spar bouy. Qualitative agreement was found between estimates from the equation and experiments performed in a wave basin but the need for further improvements was stressed. A review of current literature on floating wind turbines is given in [12].
A preliminary study using the time averaged Unsteady Reynolds Averaged Navier-Stokes (URANS) method to simulate the aerodynamic interaction of the flow and pitch platform motion was performed by Matha et al. [13]. The effects of the mooring system dynamics on the turbine wake was explored for a case where the turbine pitched upwind and downwind in a uniform flow. Findings indicated that the wake of the floating turbine is susceptible to the floating conditions and the dynamics of the surrounding waves. Furthermore, results showed a stronger expansion of the wake and that vortices shed from the blade led to a rippled boundary layer in the upper wake.
Sebastian and Lackner [14] found current analysis methods based on blade element momentum theory did not capture the unsteady flow generated at the blades by strong variations in angle of attack. Large angle of attack changes were due to the additional motion of the floating platforms. These aerodynamic analysis methods use ad hoc formulations to cover the unsteadiness due to tip losses, high tip speed ratios and yawed flows. Motion induced unsteadiness violates assumptions of standard blade element momentum theory and leads to inaccurate predictions of unsteady aerodynamic loads. Spectral analysis of the kinematic behavior of various types of floating platforms were performed and the pitch aerodynamics was found to dominate unsteady flow effects and structural loading. It was shown that pitching motions of the wind turbine cause the turbine to change from the windmill state, where the turbine extracts energy from the flow, and the propeller state, under which the turbine drops energy into the flow [4]. The state of the turbine can be determined by observing the bound vorticity of the blades, where high vorticity represents a windmill state and low, negative vorticity represents a propeller state. It was found that vorticity change follows pitch motions of the platform and the variation in bound vorticity will lead to varying loads and fatigue on the rotor.
Jonkman et al. [7] performed simulations of fully coupled aero-hydro-servo-elastic responses of floating platform concepts and compared the results in special cases with other simulation frequency-domain analysis methods to test their reliability. None of the simulation results were validated against experimental data since no such data was freely available.
Wake measurements of offshore wind turbines were performed and compared with six different wake models [15]. The results showed a wide spread of predicted wake deficits.
The objective of this study is to investigate the influence of pitch motion on the wake of a model wind turbine. Wake measurements have been performed in a wind tunnel using stereoscopic particle image velocimetry (SPIV). The flow field, including mean and fluctuating components of the flow, are analyzed for a fixed versus an oscillating turbine under the same inflow. These results are then compared with existing wake models to determine their ability to capture such pitch motion effects.
2. Theory and Models
2.1. Mean Momentum and Kinetic Energy Equations
For steady, incompressible and inviscid flows, the Reynolds-averaged Navier-Stokes (RANS) equations are given by:
Multiplication of Equation (1) by the mean velocity Ui results in the mean kinetic energy equation:
Several terms of the momentum in Equation (1) and the mechanical energy in Equation (2) will be analyzed and related to the extraction of power, as it has been found that their balance yields the power production [16,17]. For further details on the derivation, see [16].
2.2. Wake Models
Both the mean momentum in Equation (1) and the mean kinetic energy in Equation (2) contain the Reynolds stress tensor . As a consequence of the dynamic equation that can be derived for this quantity, the Reynolds stress tensor is not fully determined by the averaged velocity Ui and pressure P alone [18]. In addition, information about the average over products of three velocity fluctuation components in the Reynolds stress equation is needed, otherwise called the triple correlation. The fact that this problem repeats for all moments of the velocity fluctuation is the closure problem of turbulence. This issue is circumvented by the application of a turbulence model which imposes a closed expression for in terms of Ui, P and possibly additional variables. These additional variables are often governed by partial differential equations similar to Equation (1) in that such equations balance convection with source, sink and stress terms.
Wake models that solve systems of partial differential equations are often summarised as field models. While the numerical solution of the continuity and momentum equations in three dimensions with a turbulence model and viscosity effects is obtained in computational fluid dynamics (CFD), also systems of reduced complexity are often considered. The model by Ainslie [19] is often employed, which imposes axial symmetry and an eddy viscosity model for turbulence closure. Consequently, this allows the formulation of a closed, two dimensional system of partial differential equations describing the far wake behind a single wind turbine.
Further simplified descriptions are given by analytical wake models. These follow from momentum balance considerations in a specific control volume, together with model-specific assumptions. One widely used example is the model by Jensen [20], which relies on the restriction to one velocity component and linear wake expansion. Often such models include parameters that are determined empirically. Note that if enough data is available, it is also possible to build wake models that are entirely empirical [21].
Herein, short summaries of the Jensen model, the Larsen model, the Ainslie model and a CFD actuator disk model are provided, before comparing the results to data obtained from wind tunnel experiments. The governing equations of the wake models can be found in Appendix A.
For the calculation of the wake models, flapFOAM [22] is used. This follows a similar approach as the wind farm layout program FLaP [23], but is fully embedded into the framework of OpenFOAM [24], thus extending the modeling capabilities. The resulting velocity deficits were added to the measured inflow profile, which was extended for low and high vertical coordinates by fitting standard log-profiles:
2.2.1. Jensen Model
The Jensen model wake is characterised by linear wake expansion as a function of the downstream distance from the rotor plane [20], with a proportionality constant usually chosen in the range of k = 0.04−0.07. Only the axial velocity deficit is modeled, with the magnitude obtained by momentum conservation. The deficit profile is hat-shaped in that it is constant in the radial direction within the wake and abruptly drops to zero at its boundary.
2.2.2. Larsen Model
The Larsen model [25] assumes an axisymmetric wake, reducing the RANS equations to two dimensions. For the Reynolds stresses, Prandtl's mixing length theory is used to model the eddy viscosity [26]. Model constants are determined empirically using measurements at 9.5D behind an isolated turbine. The wake radius is given as an explicit non-linear function of the downwind coordinate in this model. Descriptions of the horizontal and radial velocity components are given, which possess dependencies on the downstream and radial coordinates. The wake expansion and decay are determined by the thrust coefficient and the ambient turbulence intensity. The Larsen model has analytical solutions at first and second order with respect to an expansion in the axial velocity deficit.
2.2.3. Ainslie Model
Like the Larsen model, the Ainslie model [19] is based on the assumption of an axisymmetric wake. Viscous effects are taken into account using an eddy-viscosity model to obtain turbulence closure. Up to a distance of 2D downwind from the rotor the wake is prescribed using to a Gaussian profile, before it starts evolving according to the two coupled partial differential equations in the radial and downwind coordinates. Chosen parameters are the thrust coefficient and ambient turbulence, the latter entering the eddy viscosity components. The solutions for the axial and radial velocity components are obtained numerically on a two-dimensional grid.
2.2.4. Actuator Disk Rotor Model
Discretised versions of the RANS equations can be solved on a three-dimensional mesh with methods from computational fluid dynamics. The simplest representation of the rotor is the actuator disk approach with uniform forcing [27]. For turbulence modeling, i.e., modeling the eddy viscosity to estimate Reynolds stresses, the k − ε model with increased dissipation near the rotor is applied [28]. The inflow boundary condition for the velocity is described in Section 2.2. Likewise, the measured inflow profile for the turbulent kinetic energy (TKE) is extrapolated linearly for low and high vertical coordinates. The inflow turbulent dissipation ε could not be measured with sufficient accuracy, therefore it is interpolated using the Richards-Hoxey solution [29], which corresponds to the local log-profile approximation. In the simulations, all effects due to laboratory walls, apart from the ground, were ignored. The latter is represented by wall functions with roughness length z0 = 0.0046 m.
3. Methods
3.1. Wind Tunnel Facility
The experiments were performed in the wind tunnel at Portland State University. The test section of this closed-circuit tunnel is 5 m in length with a height of 0.8 m and a width of 1.2 m. The free stream velocity can be set between 2 m/s and 40 m/s with low turbulence intensity. Figure 1 shows a schematic view of the wind tunnel and setup used during the experiments. The inflow conditions were modified by a passive grid to generate a mean turbulence intensity level of 9%. Behind the grid, vertical strakes made of plexiglas were placed, shaped in such way, that the velocity profile resembles atmospheric-like conditions. For more details on the wind tunnel see [30].
The hub height of the turbine was 25 cm. The wind tunnel speed was set to 6.05 m/s at hub height of the turbine and the model wind turbine was placed 2.01 m downstream of the passive grid.
3.2. Model Wind Turbine
The model wind turbine shown in Figure 2 is a 1:400 scale model of a typical horizontal axis wind turbine with a 80 m rotor diameter. The model turbine consists of an aluminum tower with a diameter of 16 mm and a nacelle with a diameter of 28 mm. The rotor has a diameter D of 200 mm and is produced with a rapid prototyping method. The blockage ratio of rotor area to wind tunnel cross-section is below 3.3% so blockage effects can be neglected [31]. The blades are designed using Blade Element Momentum theory to perform efficiently at low wind speeds and therefore at low Reynolds numbers. The design tip speed ratio λ is approximately 6 which corresponds to common tip speed ratios of full scale turbines. The blades had a twist of 31° from root to tip and a pitch angle of 6° set at blade tip with respect to rotor plane. The hub height of the turbine is at 1.25D from the floor of the test section. Inside of the nacelle, a small direct current (DC) motor (Faulhaber 1331T006SR) is mounted, which is operated as a generator. The power output of the turbine was measured mechanically, therefore the torque T is measured by a sensor based on strain gauges with a design following the concept of the torque sensor of Kang et al. [32]. The rotational frequency ω is given by a magnetic encoder which is attached to the motor (Faulhaber IE2-400). The output of the encoder are 400 pulses per revolution. The measurements are performed using a National Instruments A/D converter of model NI USB 6211 and in-house software written in LabView. The turbine was loaded by resistors to operate at its highest efficiency. The turbine is mounted in an gimbal support which allows oscillations in streamwise direction. The turbine is stabilized by a cylindrical weight of 650 g below the gimbal. The pitch motion was characterized using video analysis. The analysis consisted of 300 s video recorded at 30 Hz of the floating turbine. The nacelle of the turbine was marked with a dot of high contrast and a video tracking tool was used to create a time series of the nacelle movement. The resulting mean pitch angle for the floating case is 17.6° with a standard deviation of 0.4°. The range of oscillations was between 16° and 19°. A Fourier transformation of the time series indicates that the dominant frequencies of the oscillation are in the range of 1.2–1.8 Hz. A range for the frequency has to be given since the oscillations of the turbine are not controlled and are induced by the inflow of the turbine. In part due to the lower rotor frontal area in the inclined turbine position, the power coefficient, cp, in the floating case was 0.26 whereas a higher cp of 0.29 was observed for the fixed case. Thrust coefficients, cT , were estimated from the induction factor and found to be 0.89 and 0.85 for the fixed and floating cases, respectively. Induction factors were, in turn, calculated from the corresponding power coefficients [33]. Motion of the model was restricted to one-dimensional pitching oscillations, which is indeed the dominant motion in real conditions. Therefore, it is recognized that some aspects of the wake may differ from that of full-scale as sway and heave are not considered. Furthermore, in studies capturing the structural response of floating bodies to wave excitations as in offshore structures, the Froude number is taken into consideration [34]. In this study, given that the movement of the mast is restricted to pitch, Froude number is not considered. Scaled parameters for the model wind turbine that are taken into account are the tip speed ratio, thrust and power coefficient. The gimbal can be blocked at a straight position, so the turbine is operated as classic non-floating turbine and the performance of the turbine and surrounding flow conditions can be compared between fixed and floating with minor changes in the setup. Measurements were taken first for the fixed case, followed directly by measurements for the floating case.
3.3. SPIV
The SPIV setup consisted of a LaVision system with a Nd:YAG (532 nm, 1200 mJ, 4 ns duration) double pulsed laser and two 2 k × 2 k pixel CCD cameras. The time delay between exposures of the cameras was 150 μs. The seeding fluid was neutrally buoyant in air atomized diethylhexyl sebecate. To allow consistent resolution, the seeding density was kept constant during the measurements and seeding particles were well mixed within the wind tunnel. The thickness of the laser sheet was approximately 1 mm throughout the measurement plane. Before each experiment, the cameras were calibrated using a standard LaVision two-plane measurement plate with known geometries which are recognized by the DaVis measurement software. The resulting measurement plane was approximately 0.2 m × 0.2 m with a vector resolution of approximately 1.5 mm. To estimate the vector fields from the raw images, a multi-pass FFT based correlation algorithm was used. Interrogation windows of 64 × 64 pixels was used twice and a 32 × 32 window was used once, each with an overlap of 50%.
The freestream inflow conditions without the turbine present were measured using SPIV 1.5D to 0.5D upstream of the turbine position at a height of −0.5D to 0.4D with 0D being hub height. For the wake measurements, the SPIV data was collected directly downstream of the centerline of the turbine. The height of the planes was positioned from −0.25D to 0.75D, so the averaged development of the blade tip vortices was captured. The planes were taken at distances of 0.7D, 1.6D, 2.5D, 4.3D and 6D. The first three planes were obtained with an overlap of approximately 0.1D to ensure a continuous plane throughout the near wake. SPIV allows for measurements of three velocity components in a two dimensional plane, where U is streamwise wind speed in the x direction, V the wall normal wind speed in the y direction and W is the spanwise wind speed in the z direction, as denoted in Figure 1.
For each measurement plane, 2500 samples were taken for the fixed and floating case. A convergence test was carried out by calculating ensemble averages of 500, 1500 and 2500 samples. The results between 1500 and 2500 samples match very well so statistical convergence of means and higher order moments is assured. Spurious vectors were excluded from statistical calculation using a normalized median test according to [35]. For all planes, the percentage of spurious vectors for U and V were below 1% and below 1.2% for W.
This work compares the wake development of the fixed case and the floating case. The fixed case represents the wake of a classical bottom-fixed turbine. The floating case represents the same turbine which has the freedom to incline in the streamwise direction (pitch motion). Due to the mean inflow velocity and its fluctuations, the turbine pitches downstream and oscillates, as described earlier in this work. Therefore, only the influence of dynamic pitch on the wake is discussed.
For the fixed turbine, the sampling frequency for the SPIV system of 1 Hz was used. In the floating case, the image acquisition was triggered to a fixed amplitude of oscillations in the downstream direction to ensure the same influence of the oscillation on wake structures for each image. Therefore, a reflective strip was placed on the tower of the oscillating turbine. A Monarch optical tracker was positioned in such way, that every time the turbine reached a fixed pitch angle the SPIV system was triggered for data collection. The angle was chosen to be close to maximum pitch angle (∼18.5°).
4. Results
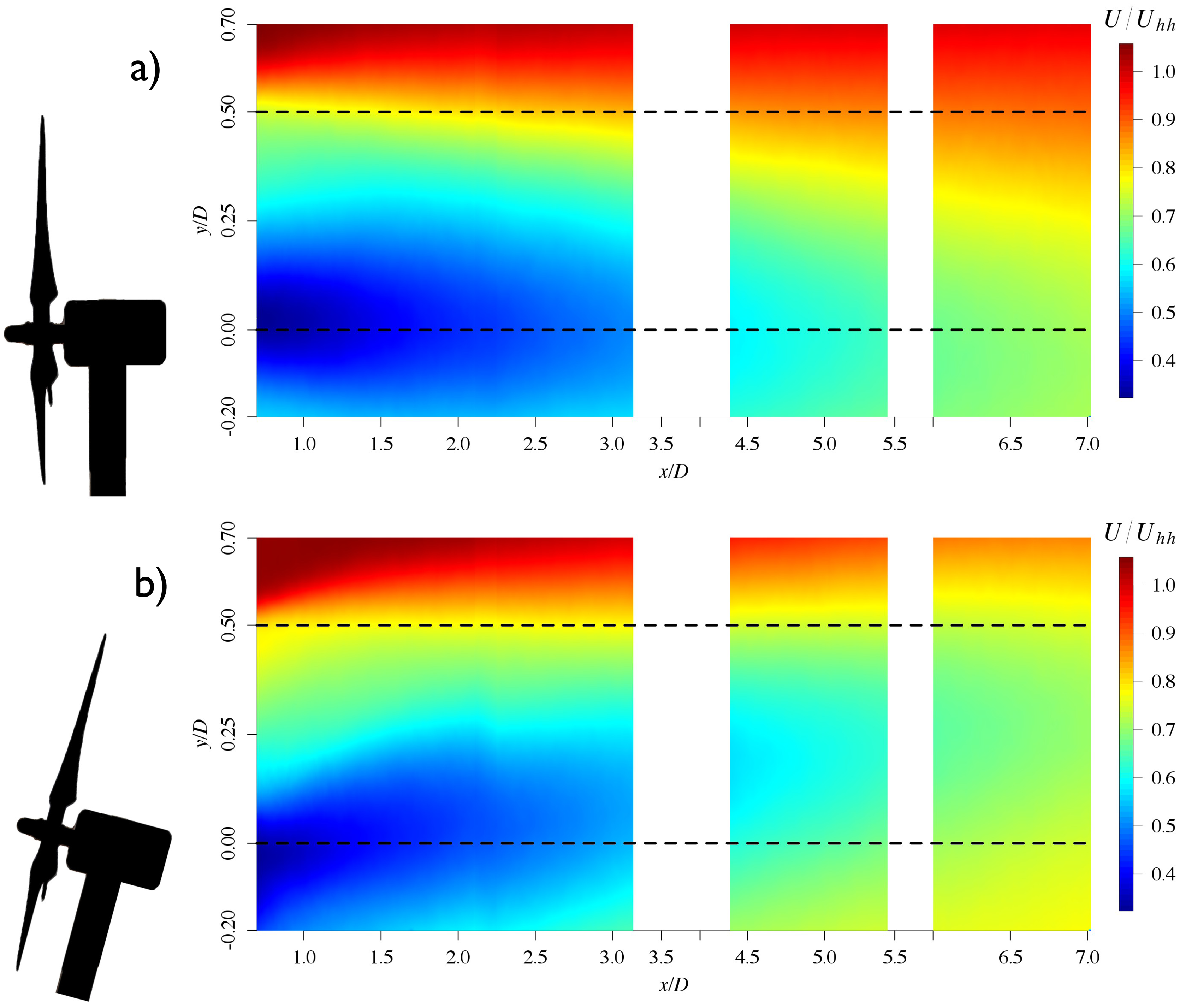
Measurements of the flow field obtained via SPIV for the fixed and floating turbine cases are compared. Contour plots are presented pairwise where the upper plot (Figure 3a) shows the result of the fixed turbine and the lower plot (Figure 3b) shows the result of the floating turbine. The planes from 0.6D to 3.3D were taken with an geometrical overlap so the results of these planes are merged using a linear weight function. Thereafter, average profiles for the mean velocity, Reynolds stresses and terms in the mean kinetic energy equation are analyzed. Profile plots, which represent intersections of the wake at different downstream distances, are presented to emphasize the quantitative differences in the development of the wake.
4.1. Mean Flow
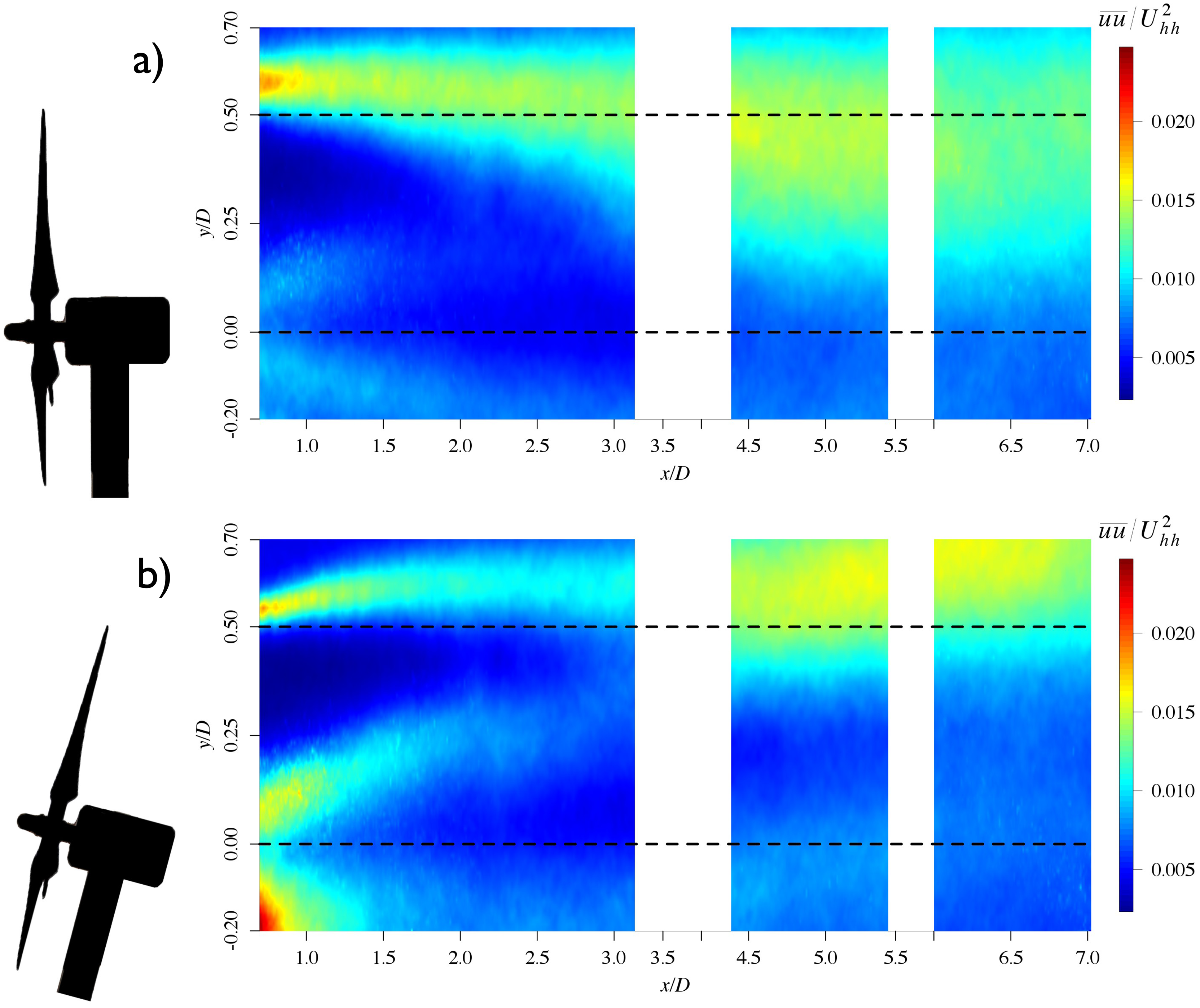
Figure 3 shows contour plots of the averaged streamwise velocity component U normalized by the inflow wind speed at hub height Uhh = 6 m/s. The velocity ranges are similar in both cases. In Figure 3a, U/Uhh behind the fixed turbine is plotted for a range of downstream distances encompassing both the near and far wake. Similarly, this is done in Figure 3b for the floating turbine, where the SPIV system is locked to a fixed pitch angle of the turbine. This angle represents a strong downstream pitching of the turbine due to its oscillations.
Figure 3a shows the wake of the fixed turbine which has the typical shape of a wake of a classical horizontal axis wind turbine [36,37]. The shape of the deficit is symmetric around hub height. From −0.2D to 0.25D in the y/D dimension, a strong velocity deficit (∼30% of Uhh) is observed due to the blockage of the nacelle. The deficit is pronounced mainly up to 3D and recovers up to 75% of Uhh at 7D downstream. These results correspond to the findings of Chamorro et al. [37] for a single turbine in an neutral boundary layer.
Figure 3b shows that, for the floating case, the deficit is no longer symmetric about the hub height in the wall normal direction, y/D. This is in stark contrast with the symmetry observed in the fixed case. The deficit is shifted down by 0.1D, due to the pitch angle of the turbine. The area with the strongest deficit (below 0.5 Uhh) is by 25% smaller in the floating case compared to the fixed case. The wake pattern of the floating turbine is skewed upward by approximately 3° due to the pitch motion of the turbine. Similar wake deflections, due to non-axial momentum extraction of the turbine, were observed for turbines in yaw conditions, but in the spanwise direction [38,39]. The flow pattern in the shear layer above blade tip is more compact in the floating case than in the fixed case. At 6.5–7D downstream, the low speed area (blue/green) is shifted up by approximately 0.25D towards the top tip. In addition, due to the overall upward shift of the wake, Figure 3b shows that the mean streamwise wind speed between the hub height and blade tip is 10% lower with 0.7 Uhh in the floating case by 6.5–7D.
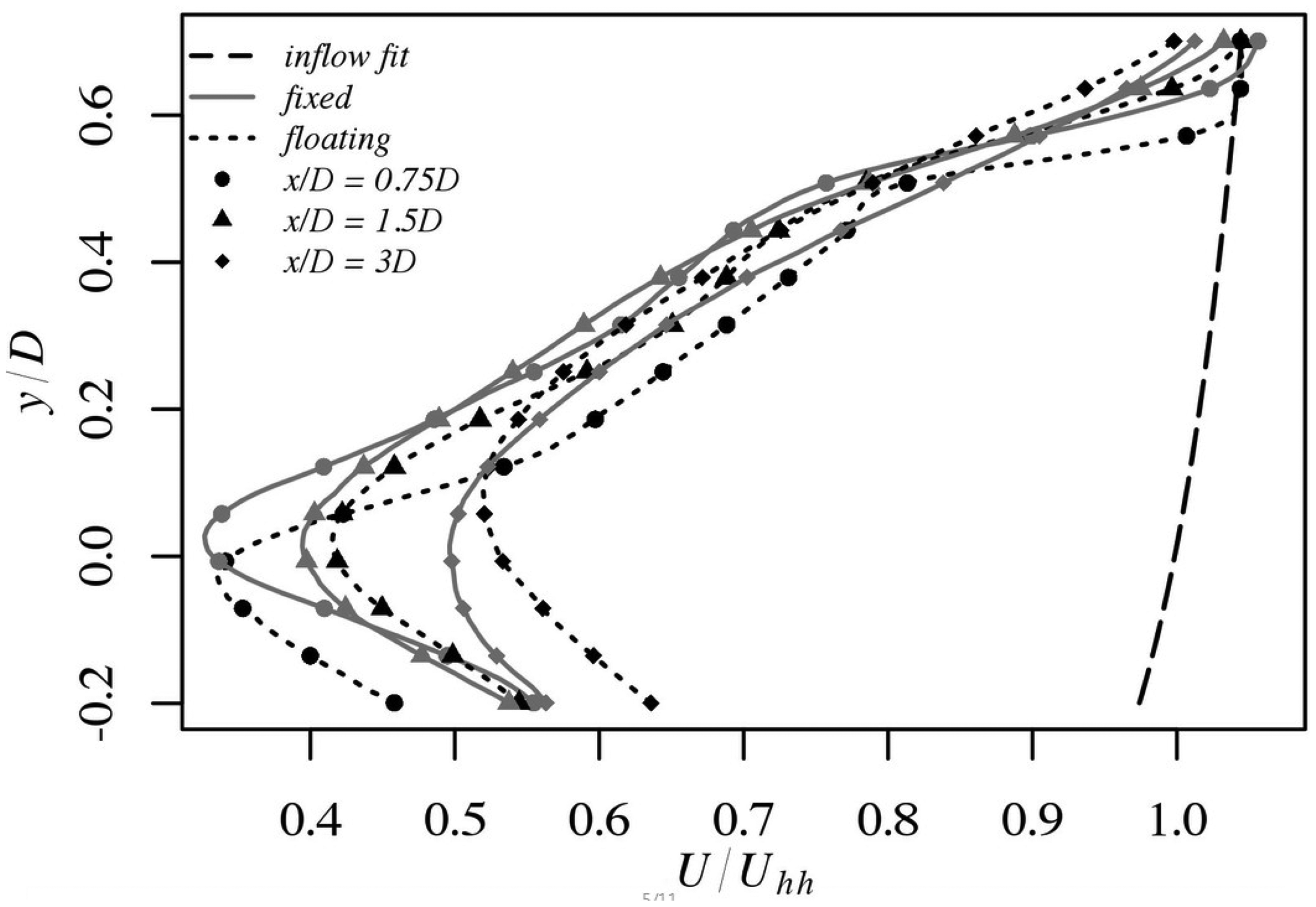
Figure 4 provides vertical profiles of U/Uhh at downstream distances x/D of 0.75D, 1.5D and 3D for both the fixed and floating cases in order to allow a more detailed comparison. A logarithmic fit to the inflow profile is added to visualize the effect of the turbines on the flow. The fit extends the measured inflow profile to y/D = 0.7, since the measurement plane for the inflow was set to y/D of −0.5D to 0.5D. At x/D of 0.75D, the shift of the deficit in the floating case is very pronounced. At x/D of 1.5D, the profiles for both cases have similar shapes, but the wind speed is lower in the fixed case. At x/D of 3D, a strong upwards shift by 0.1D in the y/D dimension is observed in the profile for the fixed case. In addition, the deficit is again weaker in the floating case than the fixed case. Comparing the fixed and floating cases, two main differences exist in the location of the inflection points and profile crossings near the top tip. First, the inflection point and crossings near the top tip are shifted vertically away from the tunnel floor for the fixed case with profile crossings located at y/D = 0.57D for the fixed case and at y/D = 0.55D for the floating case. Second, the magnitude of the deficit at which the profile crossing is located is smaller in the fixed case. The profiles for the fixed turbine tend to intersect at the lowest point whereas this does not occur for the floating turbine. This is attributed to the movement induced via the pitch motion of the turbine.
Figure 5 shows profiles at 4.5D, 6.1D and 7D downstream positions. The streamwise velocity component at blade tip height and above is smaller by 5%–15% for the fixed and by 10%–25% for the floating case as compared with Uhh, which is due the mast of the turbine being rigid and, consequently, further enhances mixing and recovery particularly in the shear layer of the wake. In the fixed case, the flow is recovering at hub height gradually, but has not fully recovered by 5–7D, which compares well to [37,40]. The profiles of the floating case are shifted up by 0.2–0.3D. In order to quantify the differences between the fixed and floating cases, the resultant thrust force (thrust force ∼ U2) from y/D = −0.2D to 0.5D was calculated. In the floating case, the thrust force on a downwind turbine is reduced 9%–10% compared to the fixed case. Also, the available power at downstream distances x/D = 4.5D, 6.1D and 7D is compared, by integrating the cubed velocity profiles from y/D = −0.2D to 0.5D. The available power to be extracted in the floating case is 14%–16% lower compared to the fixed case.
Figure 6 presents contours of mean wall normal velocity V/Uhh for both cases. In the fixed case (Figure 6a), the average wind speed hovers around 0 m/s, except directly behind the nacelle at hub height and below, where an area with −0.04 Uhh is present, thus entraining fluid downwards on the downstream range of 1–3D. As expected, the flow becomes increasingly homogeneous as x/D increases.
In the floating case (Figure 6b), the average wall normal velocity of the whole field is 0.035 Uhh. A small enclosed deficit area behind the nacelle with negative wind speed is present up to 1D downstream. A positive wind speed up to 0.08 Uhh is shown from y/D = 0.25 and upwards toward the blade top tip. With increasing downstream distance, the wall normal velocity increases to an average of 0.04 Uhh in the region from 6.1D to 7D. Notably, a wall normal velocity of 0.04 Uhh for the floating case represents 980% of V/Uhh for the same location in the fixed case.
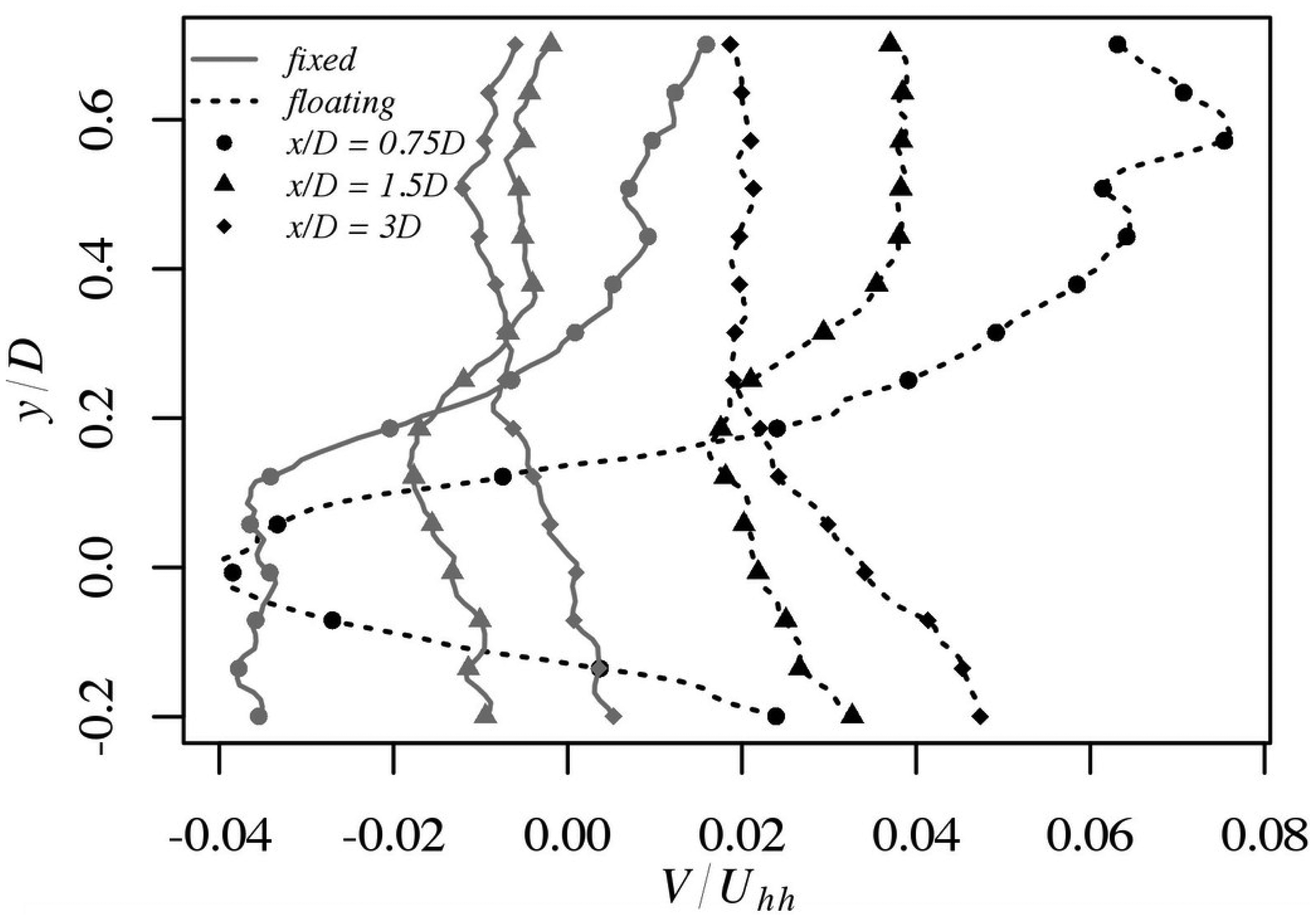
Profiles of V/Uhh at downstream distances x/D of 0.75D, 1.5D and 3D are shown in Figure 7 for both cases. Above hub height, the profile shapes at x/D of 0.75D are similar for the two cases but the absolute velocities are much higher for the floating case. A well defined area of reversed flow behind the nacelle at hub height is evident in the wall normal velocity profile at x/D = 0.75D for the floating case. In contrast, the area of reversed flow in the corresponding location is more diffused in the fixed case. A faster recovery is observed in the floating case than the fixed case.
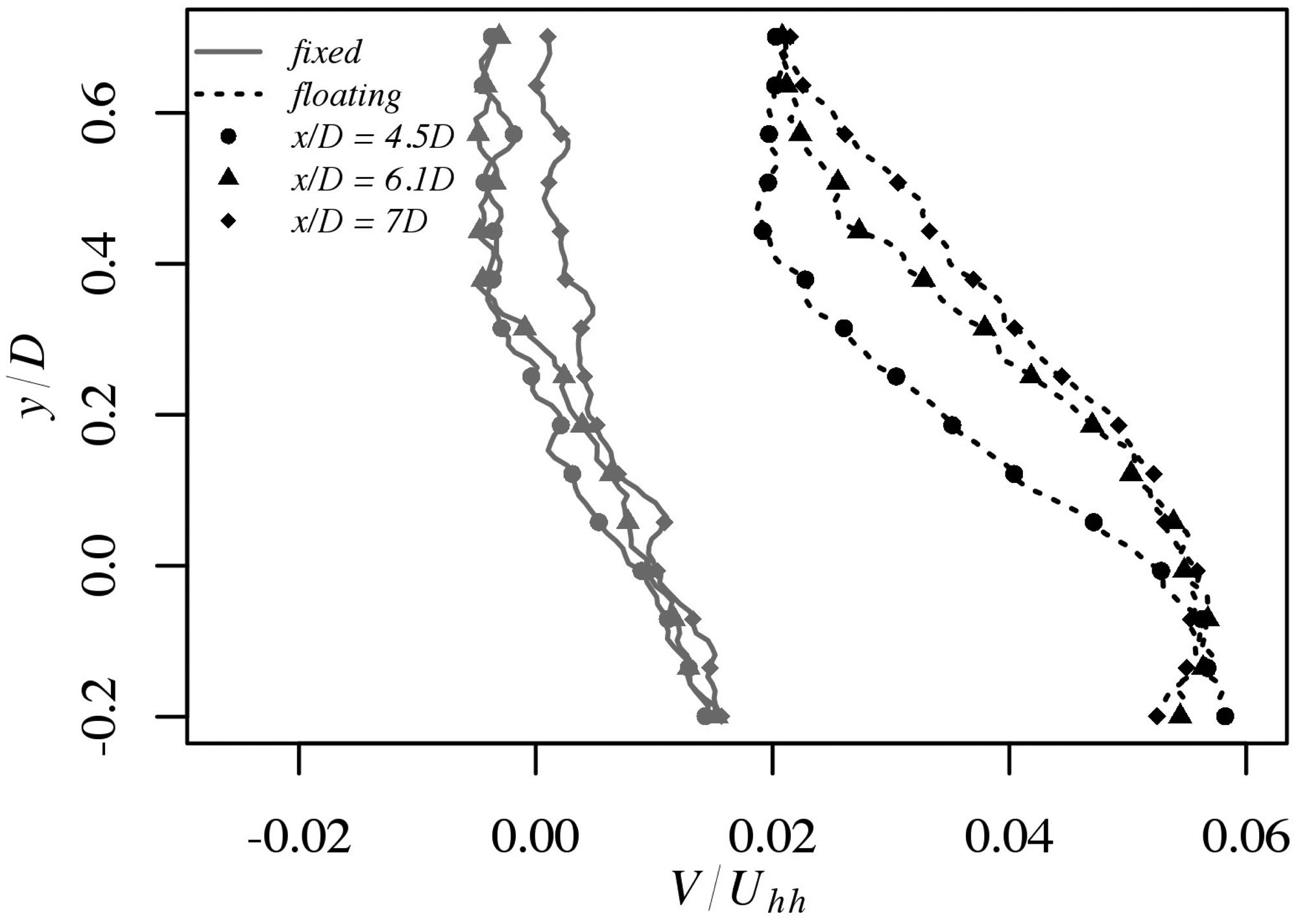
Figure 8 presents far wake profiles for the wall normal velocity component at x/D of 4.5D, 6.1D and 7D downstream. For the fixed case, not only are the trends in the velocity profiles at all three streamwise positions similar, but the absolute velocities observed are comparable. As observed in the wall normal velocity contour plots, the overall velocity is larger in the floating case.
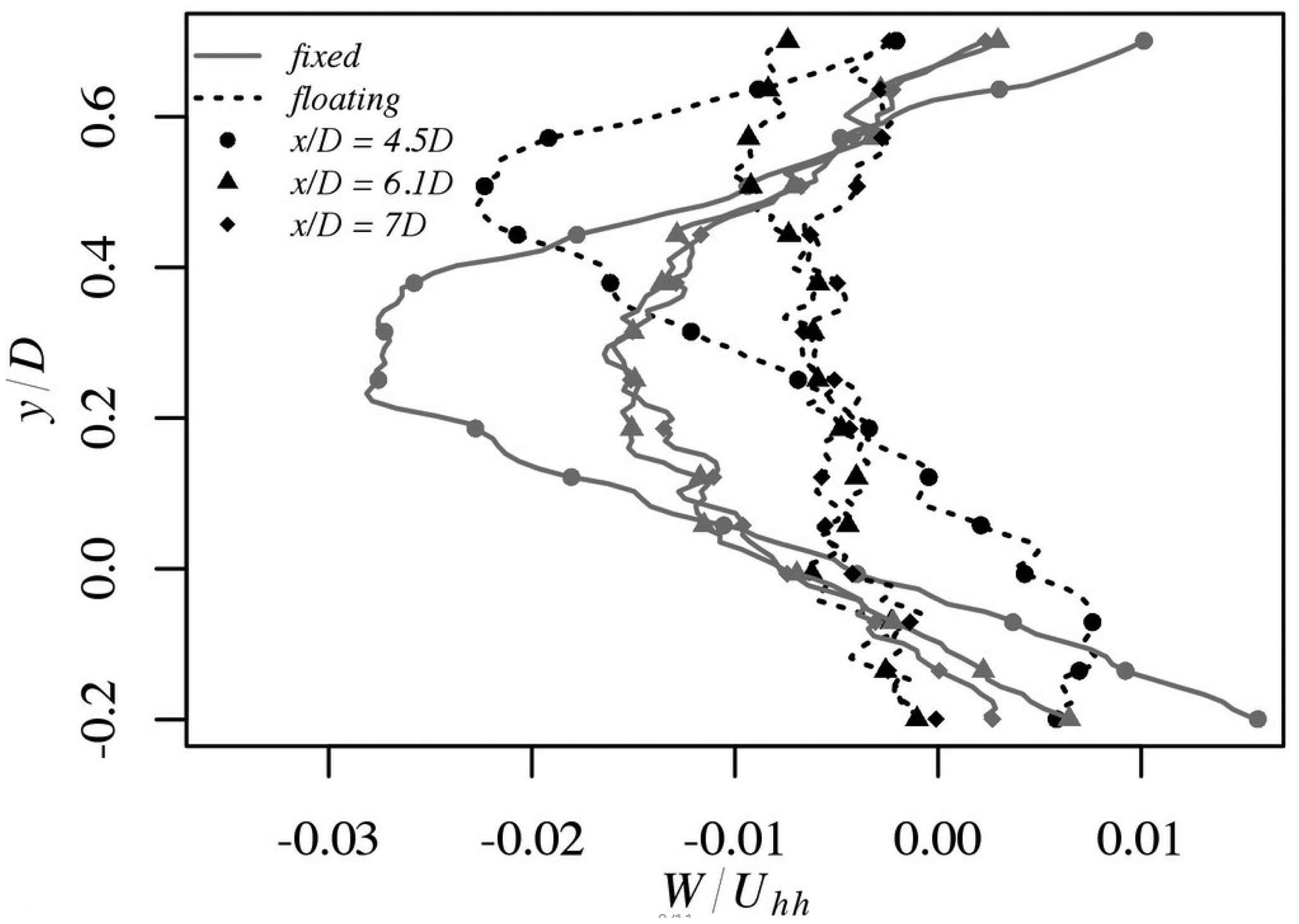
Figure 9 presents contours of the mean spanwise velocity W/Uhh. The velocity ranges of both contours are comparable in magnitude although the shape of the contours differ from one another. In both cases, there is a clear visible divide between positive and negative spanwise velocity at hub height, which is due to the clockwise rotation of the blades. In the floating case, this point is shifted upwards by 0.03D due to the inclined turbine as a consequence of the oscillatory motion of the mast. In the fixed case, the area with negative velocity is cone-shaped and extends to 3D downstream of the rotor. In the fixed case, the line dividing areas of positive and negative velocities is roughly horizontal while the line dividing positive and negative velocities shows a positive slope with increasing downstream distance in the floating case.
Near wake profiles of spanwise velocity are presented in Figure 10. The profiles at x/D = 0.75D have a similar shape for both cases, but the profiles develop differently with increasing distance. At x/D = 1.5D and 3D, the shift of the peak negative speed in the floating case to higher wall normal position becomes evident. At 1.5D, the velocity magnitudes are shifted towards negative speeds in the floating case. The shape of the fixed profiles is symmetric, while the profiles in the floating case smear out with distance due to the oscillation of the turbine.
Figure 11 shows the far wake profiles of W/Uhh. The minimum spanwise velocity occurs at 4.5D in the wall normal dimension for the fixed case whereas the minimum is shifted upward 0.2D in the wall normal dimension for the floating case. At x/D = 6–7D, the flow in the floating case is homogeneous and closer to zero, whereas in the fixed case the flow is negative from hub height to the tip of the blades and positive below hub height and above the tip. Such observations at x/D = 6–7D suggest that the flow shedding due to the rotation of the blades is persisting further downstream in the fixed case even at 7D downstream.
4.2. Reynolds Stresses and Flux of Mean Kinetic Energy
Figure 12 shows the contours of the normalized normal component of the Reynolds stress tensor. Overall, the average stress over the measurement area is 8% smaller in the floating case compared to the fixed case. In the fixed case, the largest magnitude of is produced in the shear layer above the top tip. Directly behind the hub at hub height, roughly v-shaped regions with elevated magnitudes of are evident for both cases. However, smaller magnitudes of the Reynolds stress are found in this v-shaped region in the fixed case. Furthermore, in the non-moving turbine, these features diminish after x/D = 1.5–2D. In the case of the oscillating turbine, the presence of a higher stress behind and above hub height is advected towards the shear layer and at this wall-normal location with a downstream distance of x/D ≈ 3, it merges. In the near wake of the floating case, the magnitudes of in the shear layer as well as behind the hub are comparable to the magnitudes of the fixed case.
Above the top tip, in the shear layer is 20% higher in the fixed case for downstream distances up to x/D ≈ 3.1D and, in the far wake, the stress in the upper segment (y/D > 0.5) is 26% higher in the floating case. The maximum amplitude of is at y/D ≈ 0.57D in the fixed case.
In the floating case, the peak above top tip is lower with at y/D ≈ 0.54D whereas the peak below hub height is the highest streamwise Reynolds normal stress with at y/D ≈ −0.18D.
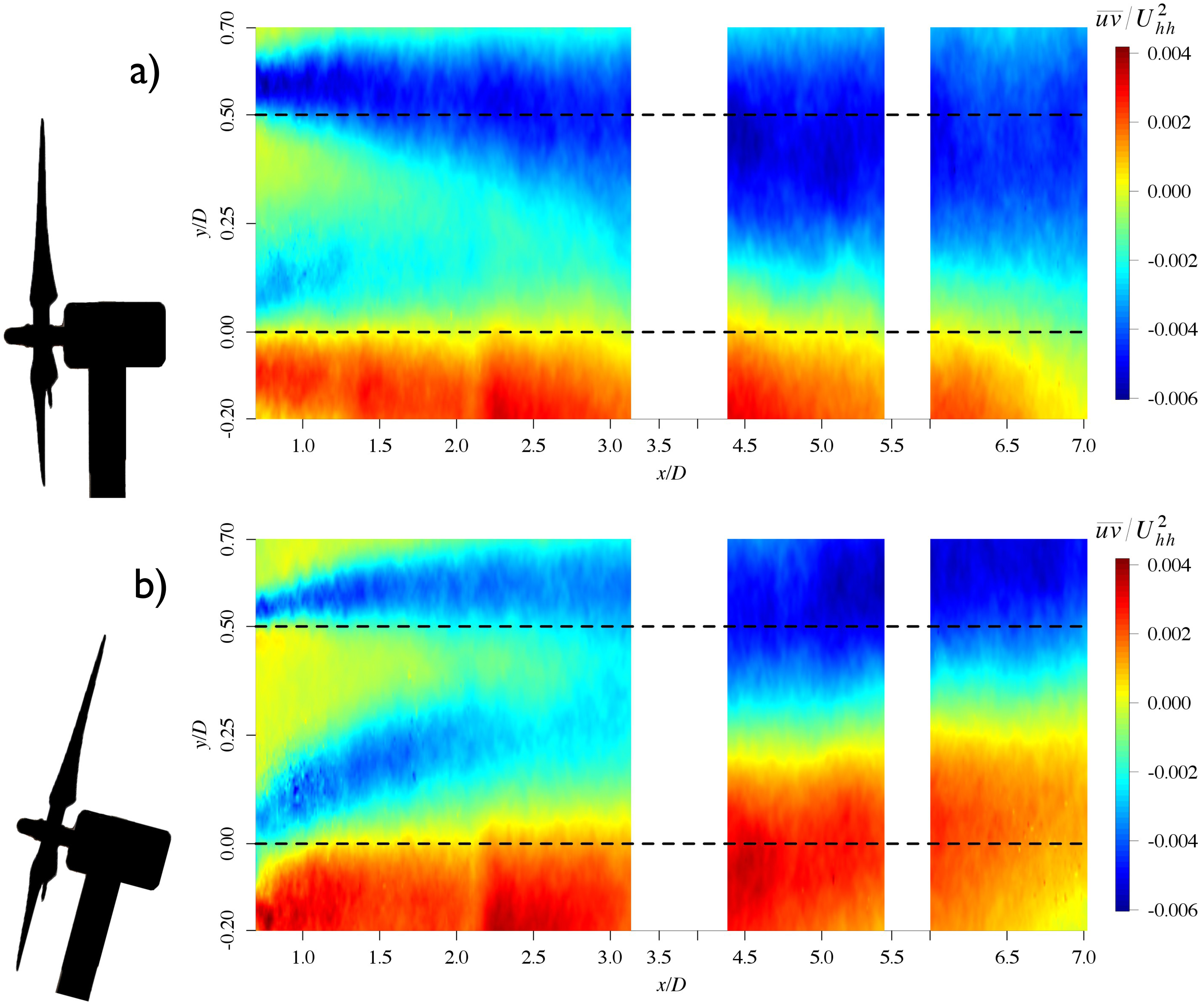
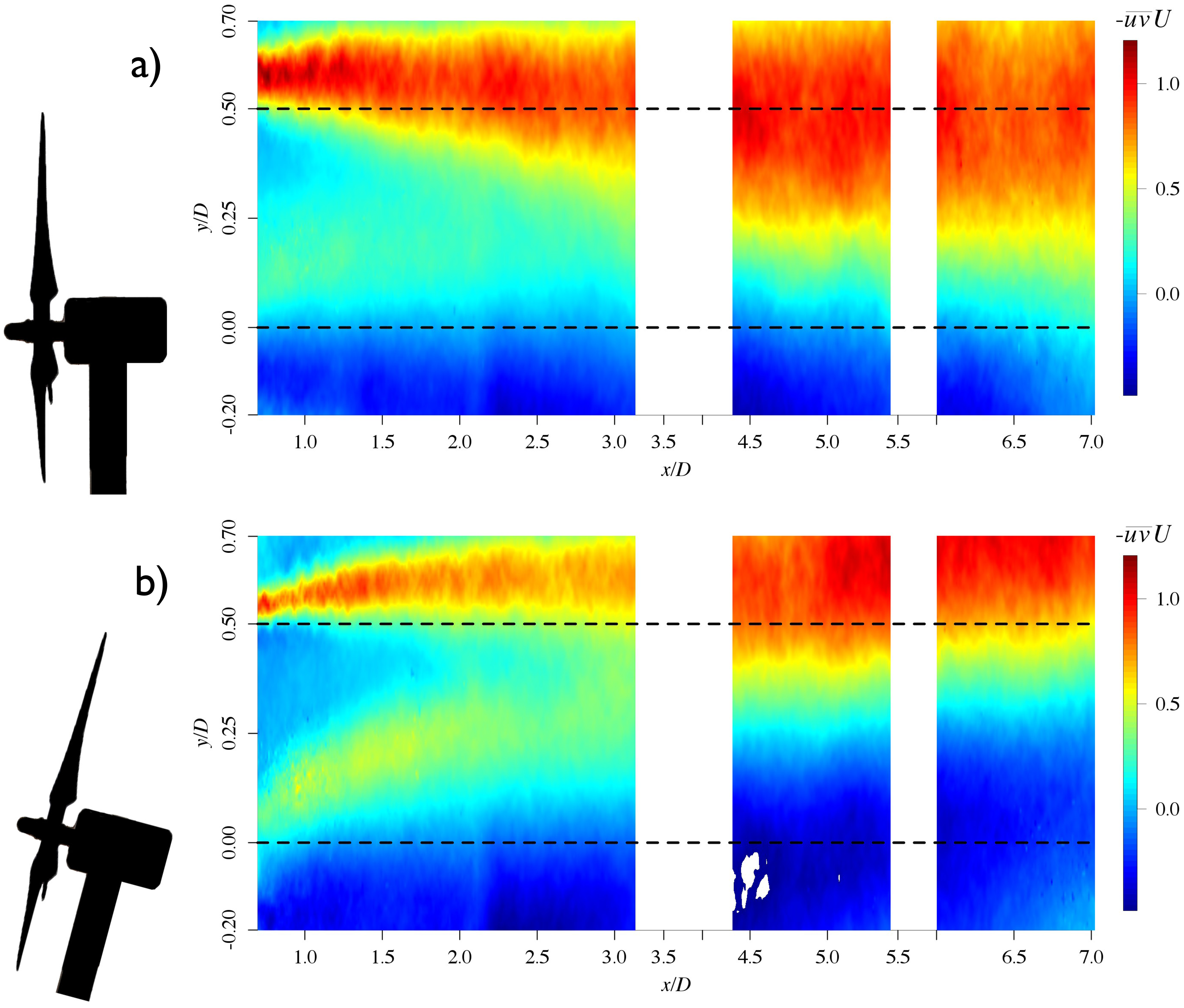
In Figure 13, the Reynolds shear stress, , is presented. This quantity is an indicator for the transport of momentum. The development of is of high interest as it is responsible for the energy being extracted from the turbine [16]. In both cases, the ranges of turbulent shear stress are close in magnitude. The range and shape of the contours in the fixed case is comparable to the results found by Chamorro et al. [37]. A large negative turbulent stress above hub height and a positive turbulent stress below hub height is present, which is attributed to mixing effects of the wake.
In the fixed case, positive is mostly present below hub height. In the floating case, the oscillations of the turbine cause a stronger positive shear stress in the far wake. Positive shear stress becomes less significant in the far wake region, x/D ≈ 6.1–7D, in the fixed case. In the floating case, positive shear stress dominates in this same far wake region. Furthermore, the positive Reynolds shear stress region below hub height remains constant in magnitude with x/D for the fixed case whereas this region is shifted upwards in the floating case. The pitch motion of the turbine causes a larger variation of the shear stress in the floating case and therefore stronger changes in the momentum flux are observed.
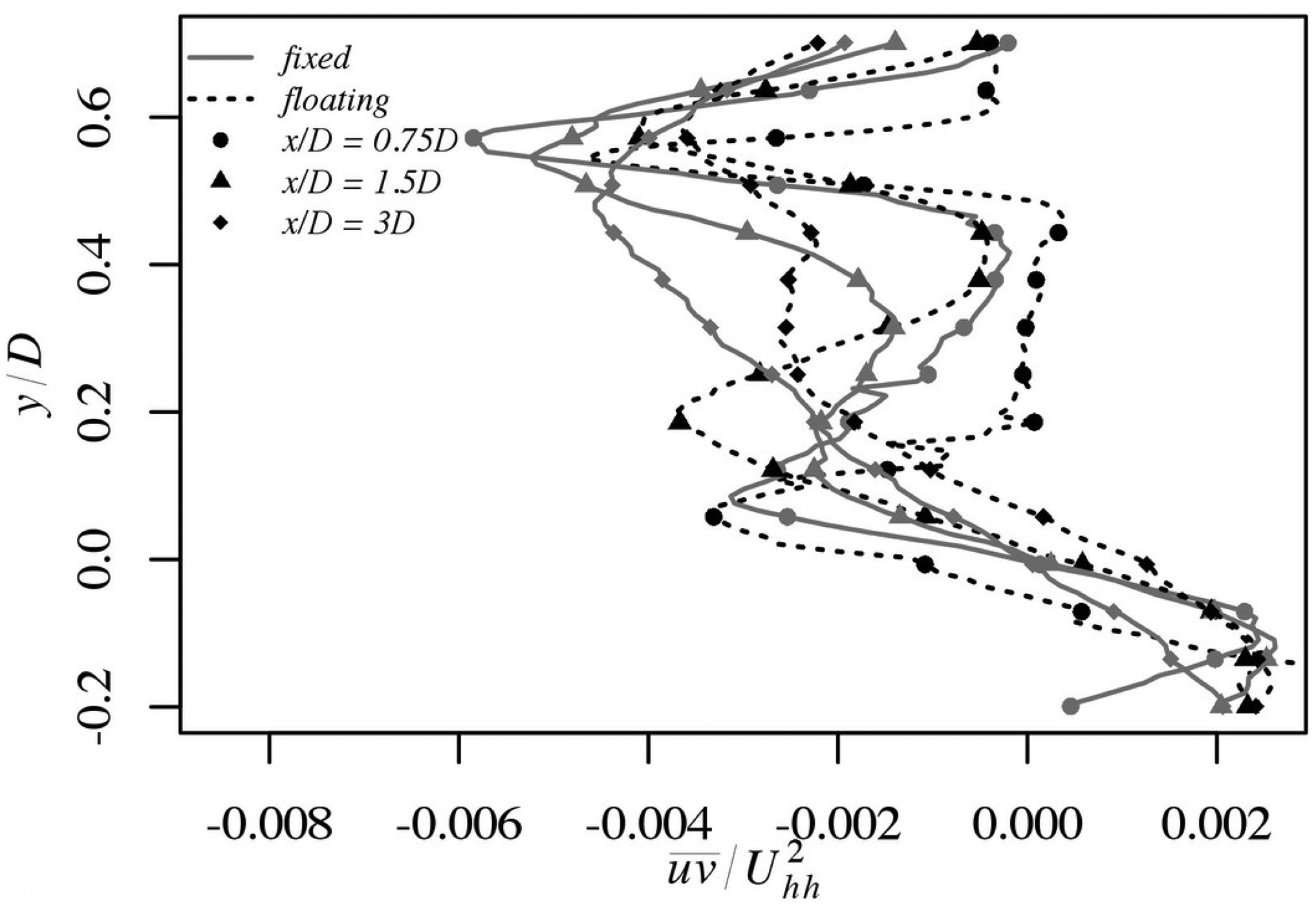
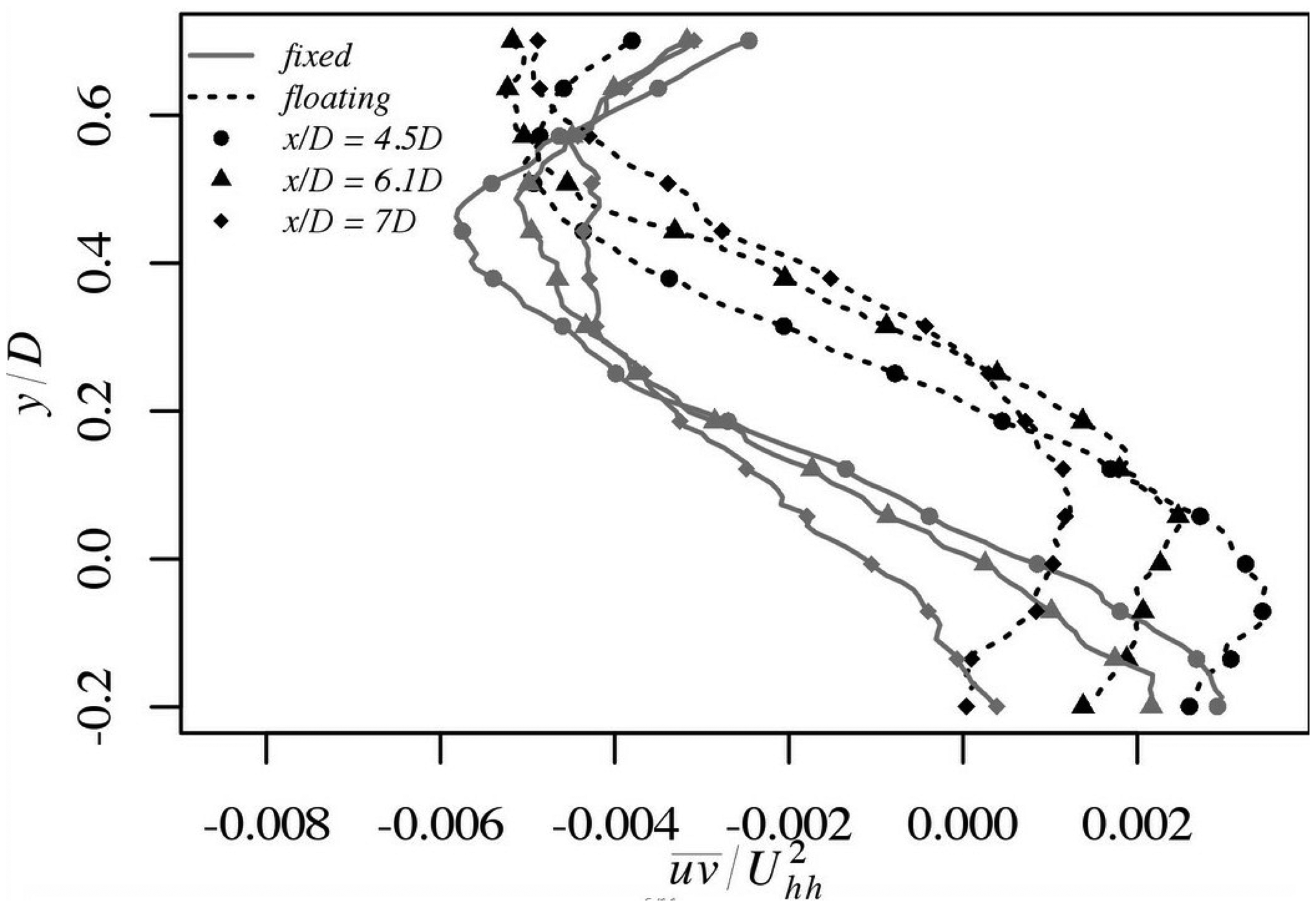
Figure 14 shows the near wake profiles of the Reynolds shear stress . For the fixed case, the profiles cross just above the hub height whereas in the floating case they tend to monotonically increase with downstream position. Right behind the rotor (x/D = 0.75), the Reynolds shear stress magnitudes are also greater for the fixed turbine.
Figure 15 shows far wake profiles of for fixed and floating cases. Although the shapes of the profiles for both case evolve similarly with increasing distance downstream, there is a systematic upward shift in the profiles for the floating case. The negative peaks of the stress at 6.1D and 7D are similar in magnitude in both cases.
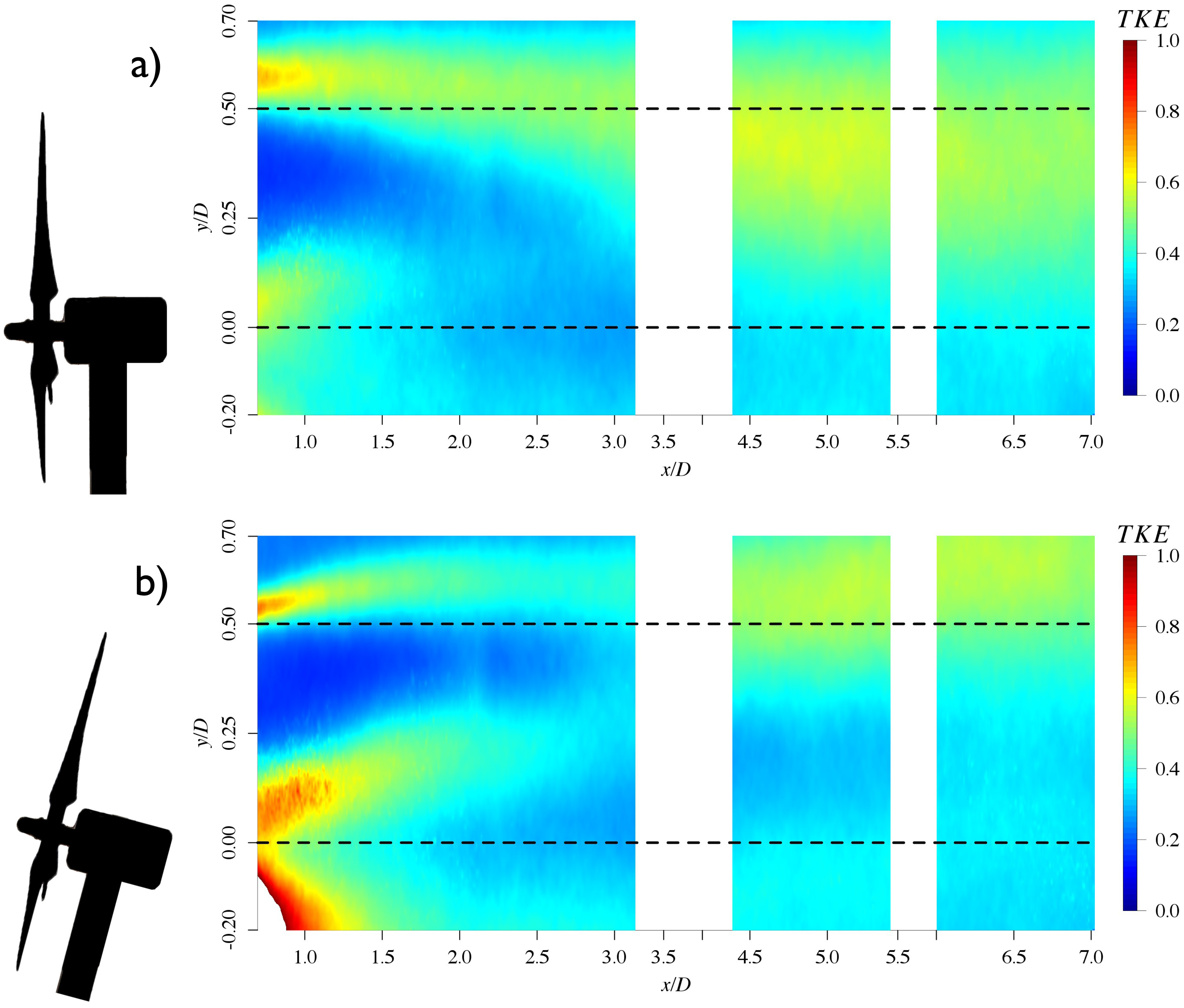
Figure 16 shows the contours of TKE, which has shapes that develop similar to the normal stress component in Figure 12. This quantity is important, since for the first turbine, the convective terms in the turbulent kinetic energy equation are significant. For both cases, turbulent kinetic energy has high values above top tip and and behind the hub. The maximum magnitudes in the floating case are higher, especially behind the hub, where TKE has its maximum with 1.4 m2/s2, while for the fixed case, the highest TKE is in the shear layer with 0.7 m2/s2. For the fixed case, the turbulent kinetic energy from above tip top spreads and moves downward with increasing x/D with decaying magnitude in the near wake and increases from 4.5 < x/D < 5.5. In the floating case, the magnitude of TKE behind the hub decreases quickly with increasing downstream distance x/D = 0.7–2.2. The TKE above hub height spreads slightly with increasing x/D, but the structure remains close to the top tip height and moves upwards in the far wake.
Figure 17 shows the development of the flux of the Reynolds shear stress , which has been found to be important for the energy being extracted by the turbine [16]. For y/D < 0, is negative for both cases. In the floating case, this region shifts away from the wall with increasing downstream distance. In the fixed case, a positive flux is observed in the shear layer and the quantity grows over a larger area with increasing downstream distance. At the top tip of the rotor, the magnitude remains relatively constant at about 0.9 m3/s3. In contrast, in the floating case, the area of positive flux increases more slowly with increasing distance. Also at the top tip of the rotor, the flux of mean kinetic energy increases in magnitude as the flow advects downstream for the floating case as well as moving away from the top tip rotor location. The large negative blue area is restricted to y/D < 0 on the fixed case. This is contrary to the floating case where the flux crosses the y/D < 0 into the top half of the rotor and it is permanent even at x/D = 7D.
The contours of vertical flux of this normal Reynolds stress component for the fixed and floating cases in Figure 18a,b, respectively. For the fixed case, the largest magnitudes of the mean vertical flux exist behind the hub, but the overall mean vertical flux of is close to zero with −0.004 m3/s3. For the floating case, is mostly positive with an average value of 0.04 m3/s3. Although these components are small compared to , a remarkable difference exists between the two cases, which is consequently attributed to the oscillations of the turbine, thus contributing to enhanced transport due to the vertical fluctuations.
4.3. Comparison with Models
Measured profiles of U/Uhh are compared to wake models as proposed by [19,20,24,27–29,41] at positions of x/D = 1.5D, 3D, 4.5D and 7D and the models are described in Section 2.2. These are shown in Figures 19 and 20 for the fixed and floating turbine cases, respectively.
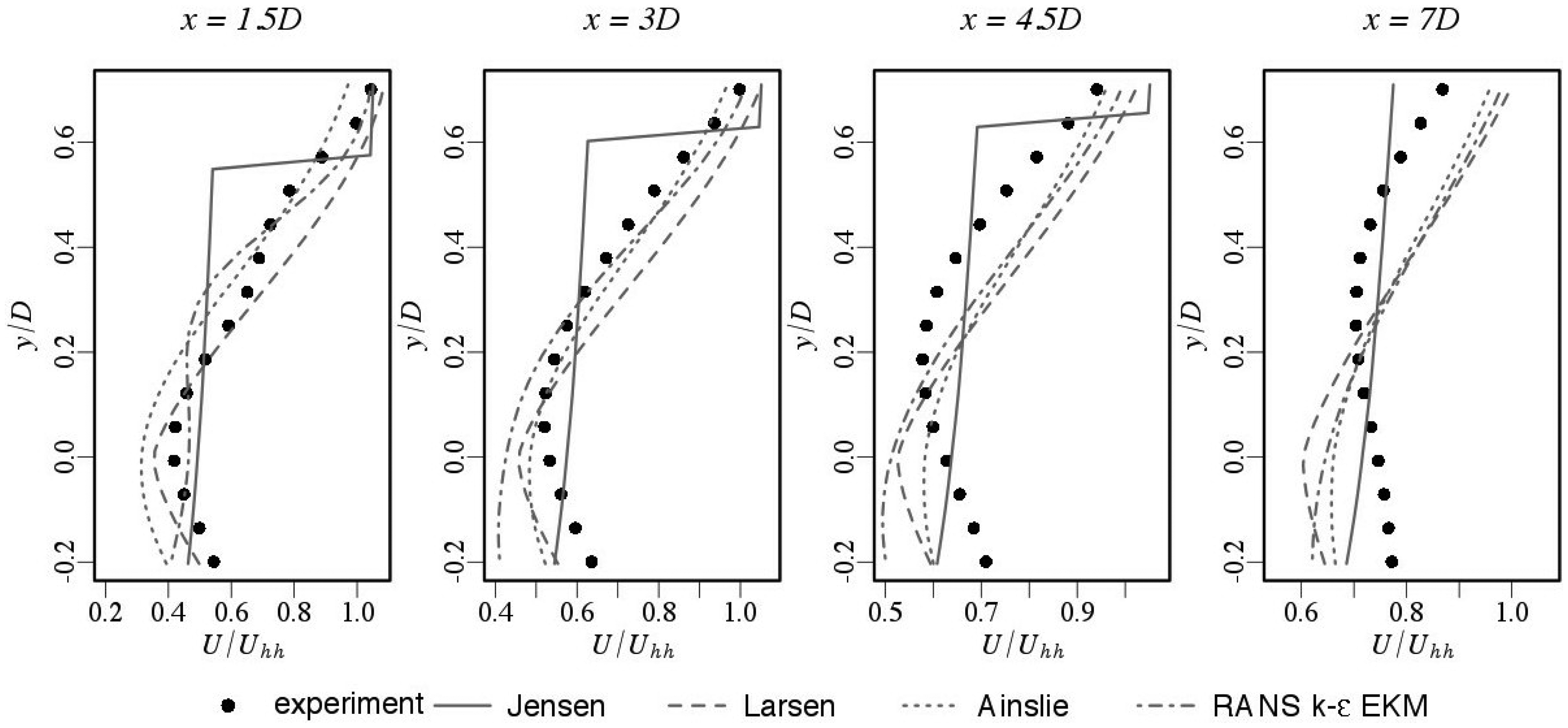
For the fixed case, all wake models with the exception of the Larsen model overestimate the wake expansion at 1.5D. For the Jensen model, which has a hat-shaped profile, the output of the model does not match the experimental data. Since the prescription of the model is solely determined by k in the far wake behavior, this difference is expected. The Ainslie model is set to a constant Gaussian profile for distances less than 2D and hence at x/D = 1.5D, the deficit is greater than the experimental data. The uniform actuator disk RANS model results in a wake that is comparable to the diameter of the disk. This disk acts like a porous bluff body, and ignores aerodynamic details like tip vortices, nacelle and tower effects, that causes, once again, the profile of the wake to be more affected by the rotor than the experimental data.
At larger distances x/D of 4.5D and 7D location of the maximum of the predicted wake deficit coincides with the experimental data for the fixed case. Nevertheless, the rest of the profile does not collapse with the experimental data due to inherent shape of the profile (i.e., top-hat shape). Furthermore, the Ainslie and RANS models improve considerably in comparison at these downstream distances although the maximum is slightly over-predicted. Taking into account all of the employed models, the RANS model best matches the experimental data as it takes into account additional terms compared with the other models. Of particular interest is the influence due to the wall, which is related to the influence of the developing boundary layer. Notably, the models tend to over-predict the velocity deficit for the fixed case when compared to the acquired data. This is due to the assumption built into the Jensen, Larsen and Ainslie models that the total wake deficit is calculated based on the concept of superposition of the inflow profile in addition to the modeled deficit. It is well understood that the inflow profile is not constant as it advects downstream. On the other hand, the RANS simulation captures the changes in the development of the wake and more realistically predicts the shape of the velocity deficit. However, an offset at all measured distances is clearly present, which can be attributed to either the parameterization of the wall and/or the turbulence closure. The latter inherently follows from the use of an eddy viscosity in the wake region that tends to be a larger sink that otherwise prescribed.
In stark contrast to what was observed for the fixed case, the models do not manage to capture the vertical shift to higher y/D of the measured wake of the floating case. Figure 20 shows that these discrepancies become more apparent as downstream distance increases. It is of no surprise that the velocity profiles generated via the Jensen, Larsen and Ainslie models do not collapse with the experimental data since these models have not been constructed to represent a wind turbine with induced pitch due to the incoming flow.
In fact, both the Jensen and Ainslie models assume an axial symmetry in the wake. As a result of the pitch motion not being well represented in the models, the wake is then directed towards the wall. Therefore, the overall effect is reduced to a change in both thrust and power coefficients. The RANS model was implemented differently than the other models in that the RANS model was tilted by 15° and the rotor position was shifted accordingly. Even though these changes are implemented, the RANS model still is not able to capture the behavior as that observed in the experimental data. This disparity is then attributed to the fact that rotation was not represented in the applied actuator disk model. Consequently, it cannot capture the anisotropy as observed by the wake.
5. Discussion
Platform pitch and streamwise oscillations have a strong impact on the mean shape of the wake as well as the magnitudes of all velocity components. Due to the oscillations in the floating case, the turbine experiences a variable shear flow. The pitch motion of the platform with an average inclination angle of 17.6° skews the mean streamwise velocity component in the wake with a positive slope, with an angle of approximately 3°. This observation is comparable to results observed in yawed turbines with a yaw misalignment of 20° [38,39]. Extending the analogy of wake deflection from turbines under a yaw condition, the average skew angle of the wake may be partially explained by momentum theory since the non-axial momentum extraction is due to the pitching effect of the turbine [33]. In order to capture other effects generated by the oscillation of the platform, more complex descriptions are necessary as highlighted by Sebastian et al. [42]. The shift due to the pitch motion/oscillations results in a far wake, which has not fully recovered and thus 14%–16% less power is available for the downwind turbine. Furthermore, the 10% decrease in thrust force observed in the floating turbine is due to the decrease in mean velocity and upward shift of the wake. It is also expected that a completely different load distribution on the rotor of a downwind turbine is observed compared to that of non-floating turbine.
The increase of the wall-normal mean velocity in the floating case is of importance, since vertical flow is often not considered in wake models. This is certainly true considering the development of V/Uhh for the fixed case (Figure 6b), which subsequently, leads to potential, unpredicted fatigue loads on downstream turbines in the floating case. The shape of the V/Uhh wake component is not changed by the oscillations (compare contours in Figure 6a,b), but the magnitudes are increased, resulting in high vertical wind speeds in the floating case. It can then be concluded that the vertical component of the flow field in the wake of an floating turbine cannot be neglected and must be considered for operating conditions of downstream turbines.
When evaluating the out of plane component, that is the spanwise component of the mean velocity, W/Uhh, symmetry in this component between the top and bottom of the rotor (i.e., y/D > 0 and y/D < 0, respectively) for the fixed turbine is entirely disrupted when oscillations are taken into account as seen in the floating case. Although as the flow develops downstream, the signatures due to the out of plane velocity are less pronounced in comparison to the fixed case.
Furthermore, the oscillations and inclination experienced by the turbine have a strong impact on the fluctuations of the flow and on the features of turbulent kinetic energy in the wake, where in the top tip of the fixed case, the features of , and TKE seem to diffuse with increasing distance. These features become more pronounced with increasing downstream distance for the oscillating turbine. The evaluation of the turbulent kinetic energy for the turbine without induced motion is maximum at the top tip of the blade and is shifted upwards in the oscillating case. At hub height, the value of the TKE nearly doubles again pointing towards the influence of the pitch dynamics. This increase can be linked with the increase in the mean vertical velocity component.
From the point of view of a downwind turbine, the shear stress distribution in the fixed case leads to negative fluctuating shear forces above hub height and positive fluctuating shear forces below the hub. Similarly, strong fluctuations are observed at the nacelle. In the floating case, most of a downwind rotor potentially experiences positive fluctuating shear forces, but a strong transition from positive to negative shear force occurs at the blade tips.
Turbulent kinetic energy is a measure for the amount of kinetic energy that is contained in the fluctuations. For the fixed case, the rotor of a downwind turbine would be exposed to strong fluctuations above hub height. In the floating case, the smaller TKE in the far wake results in a steadier inflow situation for a downstream turbine, which is positive from the point of view of loads on a turbine. The vertical shift of the turbulence quantities, on the other hand, affects the power production adversely. When considering the mean kinetic energy flux, , the upwards shift as seen in the floating case results in a lower momentum entrainment from overhead flow, thus resulting in less energy available in the downstream wind and therefore in less power available for a downstream turbine.
Almost no vertical transport of vertical fluctuations can be observed in the fixed case, which compares well to findings of [30], where is several orders of magnitudes smaller than the main contributor to the flux . In the floating case, remains much bigger than , but the pitch motion of the turbine creates high positive transport at the blade tips and a negative transport behind the hub. Due to the overall positive vertical flux, entrainment of kinetic energy from the free stream above the canopy is reduced in the floating case. This corresponds well to the flow in the mean streamwise direction, where the wake recovery is diminished as observed by the far wake, thus contains less kinetic energy for a downstream turbine.
The comparison with wake models shows that for the fixed case, the shape and magnitudes of the streamwise component of the wake in midrange distance (x = 3–7D) can be approximated by the Ainslie, the Larsen and the actuator disk models, even though in the lower half of the wake the models over-predict the deficit. In the floating case, all models fail to capture the vertical displacement of the streamwise component, resulting in an inaccurate wake description. The inflow of a downwind turbine would then be inaccurate leading to erroneous load and power predictions for a downwind turbine.
6. Conclusions
Wind tunnel experiments were performed to compare the wake development of a fixed and a streamwise oscillating wind turbine model using stereo PIV. Statistical analysis of wake development from 0.7D to 7D was performed and differences in their quantities were elaborated for both cases. The pitch motion of the turbine has a strong impact on the development of the mean components as well as on the turbulent quantities. The vertical shift of U/Uhh results in less available kinetic energy for a downwind turbine in offshore conditions, which could be due to the shifted turbulent kinetic flux . The upwards shift of the turbulent kinetic energy reduces potential fatigue loads on a downwind turbine, but the increase in V/Uhh adds to such loads. Comparison of the measurements with wake models reveals minor discrepancies of the model predictions in the fixed case, but these models fail to describe the wake behind a wind turbine with induced dynamic pitch motion. Floating platforms for wind turbines provide the capability for allowing the production of energy offshore. Nevertheless, the pitch motion of the turbine results in new challenges for wake modeling, thus providing the opportunity for furthering the modeling capabilities to a new scenario (i.e., offshore versus onshore). This certainly has great implications in the experienced loads by the turbine as well as the power production capabilities. The article examines the dynamic pitch motion of a wind turbine; it would also be relevant to discern the differences between the dynamic pitching with static pitch in the future.
Acknowledgments
The authors would like to thank Stefan Ivanell for providing the blade design, Carlos Peralta for providing the turbulence model implementation for the actuator disk model simulation. This work was supported in part by grants from the Federal Environmental Foundation (DBU), Germany.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix
A. Wake Model Equations
A.1. Jensen Model
The wake diameter Dw in the Jensen model [20] increases linearly with the downstream distance x behind the rotor:
A.2. Larsen Model
In the Larsen model [25], a two dimensional system of partial differential equations is solved analytically for the first two orders of an expansion in the axial velocity deficit. The resulting wake radius Rw as a function of downwind distance x is [43]:
The effective wake diameter Deff and wake radius R9.5 at distance 9.5D, corrected for finite hub height effects, are:
The latter relation was found empirically, with hub height H and:
The solution for the wake deficit to second order is:
The second order solution contains a sum over functions:
The solution of the radial velocity component was ignored in this work.
A.3. Ainslie Model
The Ainslie model flow has an axial component, denoted as U(x,r), and a radial component V(x,r). The two dimensional system of partial differential equations is then [23]:
The solution of Equations (A16) and (A17) is obtained as follows. First, an initial Gaussian profile is assumed at x = 2D:
The momentum Equation (A17) is solved by discretising it in a Crank-Nicholson scheme, and re-writing it as a tri-diagonal matrix problem. The centre line deficit and the radial velocity field are then updated using the continuity Equation (A16), and the solution is iterated until convergence is obtained.
References
- Zervos, A.; Kjaer, C. Pure Power: Wind Energy Scenarios up to 2030; European Wind Energy Association: Brussels, Belgium, 2008. [Google Scholar]
- Henderson, A.; Witcher, D.; Morgan, C. Floating Support Structures Enabling New Markets for Offshore Wind Energy. Proceedings of the European Wind Energy Conference (EWEC), Marseille, France, 16–19 March 2009.
- Butterfield, C.; Musial, W.; Jonkman, J. Engineering Challenges for Floating Offshore Wind Turbines; National Renewable Energy Laboratory: Golden, CO, USA, 2007. [Google Scholar]
- Sebastian, T.; Lackner, M. Analysis of the induction and wake evolution of an offshore floating wind turbine. Energies 2012, 5, 968–1000. [Google Scholar]
- Barthelmie, R.J.; Pryor, S.C.; Frandsen, S.T.; Hansen, K.S.; Schepers, J.G.; Rados, K.; Schlez, W.; Neubert, A.; Jensen, L.E.; Neckelmann, S. Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos. Ocean. Technol. 2010, 27, 1302–1317. [Google Scholar]
- Musial, W.; Butterfield, S.; Renewable, N. Energy from Offshore Wind. Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1–4 May 2006; pp. 18355:1–18355:11.
- Jonkman, J. Dynamics of offshore floating wind turbines—Model development and verification. Wind Energy 2009, 12, 459–492. [Google Scholar]
- Jonkman, J.; Matha, D. A Quantitative Comparison of the Responses of Three Floating Platforms; National Renewable Energy Laboratory: Golden, CO, USA, 2010. [Google Scholar]
- Jonkman, J.; Matha, D. Dynamics of offshore floating wind turbines—Analysis of three concepts. Wind Energy 2011, 14, 557–569. [Google Scholar]
- Matsukuma, H.; Utsunomiya, T. Motion analysis of a floating offshore wind turbine considering rotor-rotation. IES J. Part A Civ. Struct. Eng. 2008, 1, 268–279. [Google Scholar]
- Utsunomiya, T.; Matsukuma, H.; Minoura, S. On Sea Experiment of a Hybrid SPAR for Floating Offshore Wind Turbine Using 1/10 Scale Model. Proceedings of the ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; Volume 3, pp. 529–536.
- Wang, C.M.; Utsunomiya, T.; Wee, S.C.; Choo, Y.S. Research on floating wind turbines: A literature survey. IES J. Part A Civ. Struct. Eng. 2010, 3, 267–277. [Google Scholar]
- Matha, D.; Schlipf, M.; Cordle, A.; Pereira, R.; Jonkman, J. Challenges in Simulation of Aerodynamics, Hydrodynamics, and Mooring-Line Dynamics of Floating Offshore Wind Turbines. Proceedings of the 21st Offshore and Polar Engineering Conference, Maui, HI, USA, 19–24 June 2011.
- Sebastian, T.; Lackner, M. Characterization of the unsteady aerodynamics of offshore floating wind turbines. Wind Energy 2013, 16, 339–352. [Google Scholar]
- Barthelmie, R.J.; Larsen, G.C.; Frandsen, S.T.; Folkerts, L.; Rados, K.; Pryor, S.C.; Lange, B.; Schepers, G. Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar. J. Atmos. Ocean. Technol. 2006, 23, 888–901. [Google Scholar]
- Cal, R.B.; Lebrón, J.; Castillo, L.; Kang, H.S.; Meneveau, C. Experimental study of the horizontally averaged flow structure in a model wind-turbine array boundary layer. J. Renew. Sustain. Energy 2010, 2. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22. [Google Scholar] [CrossRef]
- Davidson, P.A. Turbulence: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK; New York, NY, USA, 2004. [Google Scholar]
- Ainslie, J.F. Development of an Eddy Viscosity Model for Wind Turbine Wakes. Proceedings of the 7th BWEA Wind Energy Conference, Oxford, UK, 23–25 March 1983; pp. 61–66.
- Jensen, J.O. A Note on Wind Generator Interaction; Technical Report Risø-M-2411; Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Nygaard, N.G. Construction and Validation of a New Offshore Wake Model. Proceedings of the International Conference on Aerodynamics of Offshore Wind Energy Systems and Wakes (ICOWES) Conference, Lyngby, Danmark, 17–19 June 2013.
- Schmidt, J.; Stoevesandt, B. Wind Farm Layout Optimisation Using Wakes from Computational Fluid Dynamics Simulations. Proceedings of the EWEA Conference, Barcelona, Spain, 10–13 March 2014.
- Lange, B.; Waldl, H.P.; Guerrero, A.G.; Heinemann, D.; Barthelmie, R.J. Modelling of offshore wind turbine wakes with the wind farm program FLaP. Wind Energy 2003, 6, 87–104. [Google Scholar]
- OpenFOAM, 2013. Available online: http://www.openfoam.org (accessed on 5 November 2013).
- Larsen, G.C. A Simple Wake Calculation Procedure; Technical Report Risø-M-2760; Risø National Laboratory: Roskilde, Denmark, 1988. [Google Scholar]
- Swain, L.M. On the turbulent wake behind a body of revolution. Proc. R. Soc. Lond. A 1929, 125, 647–659. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained; Wiley and Sons: Chichester, UK, 2009. [Google Scholar]
- El Kasmi, A.; Masson, C. An extended k-є model for turbulent flow through horizontal-axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2008, 96, 103–122. [Google Scholar]
- Richards, P.J.; Hoxey, R.P. Appropriate boundary conditions for computational wind engineering models using the k-є turbulence model. J. Wind Eng. Ind. Aerodyn. 1993, 46–47, 145–153. [Google Scholar]
- Hamilton, N.; Melius, M.; Cal, R.B. Wind turbine boundary layer arrays for Cartesian and staggered configurations—Part I, flow field and power measurements. Wind Energy 2014. [CrossRef]
- Simms, D.; Schreck, S.; Hand, M.; Fingersh, L. NREL Unsteady Aerodynamics Experiment in the NASA-Ames Wind Tunnel: A Comparison of Predictions to Measurements; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
- Kang, H.S.; Meneveau, C. Direct mechanical torque sensor for model wind turbines. Meas. Sci. Technol. 2010, 21. [Google Scholar] [CrossRef]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M. Summary of Conclusions and Recommendations Drawn from the DeepCWind Scaled Floating Offshore Wind System Test Campaign. Proceedings of the ASME 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; Volume 8. [CrossRef]
- Westerweel, J.; Scarano, F. Universal outlier detection for PIV data. Exp. Fluids 2005, 39, 1096–1100. [Google Scholar]
- Vermeer, L.; Sø rensen, J.; Crespo, A. Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar]
- Chamorro, L.P.; Porté-Agel, F. Effects of thermal stability and incoming boundary-layer flow characteristics on wind-turbine wakes: A wind-tunnel study. Bound.-Layer Meteorol. 2010, 136, 515–533. [Google Scholar]
- Medici, D. Experimental Studies of Wind Turbine Wakes Power Optimisation and Meandering. Ph.D. Thesis, Royal Institute of Technology, Stockholm, Sweden, December 2005. [Google Scholar]
- Parkin, P.; Holm, R.; Medici, D. The Application of PIV to the Wake of a Wind Turbine in Yaw. Proceedings of the Particle Image Velocimetry, Gottingen, Germany, 17–19 September 2001; pp. 155–162.
- Wu, Y.T.; Porté-Agel, F. Large-eddy simulation of wind-turbine wakes: Evaluation of turbine parametrisations. Bound.-Layer Meteorol. 2010, 138, 345–366. [Google Scholar]
- Larsen, G.C. A Simple Stationary Semi-Analytical Wake Model; Technical Report Risø-R-1713; Risø National Laboratory: Roskilde, Denmark, 2009. [Google Scholar]
- Sebastian, T.; Lackner, M.A. Development of a free vortex wake method code for offshore floating wind turbines. Renew. Energy 2012, 46, 269–275. [Google Scholar]
- Renkema, D.J. Validation of Wind Turbine Wake Models. Master's Thesis, Delft University of Technology, Delft, The Netherlands, June 2007. [Google Scholar]








© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rockel, S.; Camp, E.; Schmidt, J.; Peinke, J.; Cal, R.B.; Hölling, M. Experimental Study on Influence of Pitch Motion on the Wake of a Floating Wind Turbine Model. Energies 2014, 7, 1954-1985. https://doi.org/10.3390/en7041954
Rockel S, Camp E, Schmidt J, Peinke J, Cal RB, Hölling M. Experimental Study on Influence of Pitch Motion on the Wake of a Floating Wind Turbine Model. Energies. 2014; 7(4):1954-1985. https://doi.org/10.3390/en7041954
Chicago/Turabian StyleRockel, Stanislav, Elizabeth Camp, Jonas Schmidt, Joachim Peinke, Raúl Bayoán Cal, and Michael Hölling. 2014. "Experimental Study on Influence of Pitch Motion on the Wake of a Floating Wind Turbine Model" Energies 7, no. 4: 1954-1985. https://doi.org/10.3390/en7041954




