Conditional Methods in Modeling CO2 Capture from Coal Syngas
Abstract
: Gasification of coal or biomass with in-situ CO2 capture is an emerging technology aiming to address the problem of climate change. Development of a CO2 sorbent with desirable properties and understanding the behavior of such a material in carbonation/calcination reactions is an important part of developing the technology. In this paper, we report experimental results describing the carbonation behavior of three synthetic CaO-based sorbents. We also present a physically-based model of the reactive transport processes in sorbent particles, which have complicated pore structures. This modeling is based on the conditional approach (i.e., conditional moment closure (CMC)), which has proven to be successful in modeling reactive transport phenomena in porous media. The model predictions are in good agreement with the experimental data.1. Introduction
Extensive efforts have been devoted worldwide to developing CO2 mitigation technologies in order to address the problem of climate change. Gasification of coal/biomass with in-situ CO2 capture is an emerging technology aimed at addressing this issue. The technology simultaneously allows production of clean hydrogen at relatively low cost while reducing the release of CO2 into the atmosphere. The process is carried out using two reactors: the gasifier and the calciner. Coal/biomass reacts with steam in the gasifier to produce hydrogen (H2). The heat required for this reaction is supplied by the exothermic carbonation reaction (CaO + CO2 = CaCO3), in which CO2 is also consumed. In this way, high purity H2 is generated. The reacted sorbent particles are separated from the product gas and transferred into the calciner for regeneration.
Carbonation/calcination of CaO-based sorbents, which is also known as the calcium looping cycle, is considered to be an economically viable CO2-capture technology [1]. The performance of the sorbent is one of the key issues in this calcium looping cycle, as it significantly affects the economics of the whole process. Naturally occurring limestone is cheap and abundant. Nevertheless, its performance in the cycling process rapidly decreases due to sintering, attrition and ash fouling [2]. To overcome the loss in CO2 sorption capacity over cycles, synthetic CaO based sorbents have been developed [3,4] and tested in a laboratory scale process [4]. Note that relatively low CaO content in these samples allows for substantial improve the performance of the synthetic sorbents over many cycles. The carbonation behavior of three sorbent samples has been experimentally investigated and the results are reported below.
In order to assist in selecting optimal parameters of the carbonation process, which is an illustrative example of a reactive flow through complex porous media, a comprehensive, physically-based model of such processes is required. Traditionally, a porous medium is characterised by two phases: the fluid β-phase and the solid σ-phase [5]. Heterogeneous reactions occur on the β/σ-interface. The intrinsic (taken over the β-phase only) and superficial (taken over both phases) averages are used to characterise the gaseous reactants [5].
The regime of the heterogeneous reaction is determined by the balance between the reaction kinetics and the rate of transport of the reactant to the reactive surface. This balance is described in terms of the Damköhler number Da, which is defined as the ratio of the characteristic fluid transport time to the characteristic reaction time. Depending on the Da, the reaction regime can vary from kinetics-controlled to diffusion-controlled. Traditional averaging works well for the kinetics-controlled regime (Da ≪ 1). It has been demonstrated [6], however, that the traditional volume averaging approach gives poor predictions for the diffusion-controlled (Da ≫ 1) and intermediate regimes (Da ≈ 1).
Another approach is one—which, by analogy with other areas of Fluid Mechanics, we call direct numerical simulation (DNS). In this approach, the reactive flow is simulated over the gas phase only, while the boundary conditions are defined on gas-solid interface. The prerequisite for this approach is the ability to represent the pore structure in a way suitable for such simulations. This approach does not include averaging and allows simulating reactive flows as accurately as possible. Clearly, exact simulation of real porous media is problematic. As a result, some models have to be used. Accuracy of DNS method comes at an enormous computational cost. This cost makes the DNS method practically inapplicable for large domains and for porous media with complicated porous structures. Determining and simulating the structure of pores in such media, where the pore size can vary over many orders of magnitude, is an extremely difficult problem by itself.
Practically, the exact pore structure can be approximated by an artificially created system of relatively simple pores, which is intended to reproduce some characteristics of the realistic pores. Such simulations, which can be referred to as incomplete DNS (IDNS), still deal with non-averaged quantities and should be distinguished from the methods based on averaging. IDNS allows for a substantial reduction in computational cost. In this case, however, one could not expect the same accuracy due to incomplete reproduction of the realistic pore structure and, possibly, other simplifications.
An alternative approach, which addresses these challenges, has been recently introduced [6–9]. This approach is based on conditional averaging. In contrast to traditional (or unconditional) models, where the averaging is taken over all points in physical space, conditional averages are taken over only those points where some conditional variable attains a specified value. As a result, conditional averaging is much more detailed than its unconditional kin. Conditional closures represent a generalisation of the concept of multiple porosities and can be interpreted as having continuously varying porosity grades. At the same time, the conditional approach is much more computationally affordable than DNS. From this standpoint, conditional models are in many respects intermediate between those based on unconditional averaging and DNS.
Conditional models become the most effective when traditional volume averaging is replaced by more mathematically sound and convenient ensemble averaging. The ensemble-spatial averaging theorem, which is the ensemble analogue of the spatial averaging theorem [10], has been proven in [7]. The ensemble-spatial averaging theorem justifies the use of ensemble averaging, both conditional and unconditional, in porous media applications.
It is important to note that the presented CMC methodology is general and independent of the sub-models used to describe diffusive characteristics of a porous medium or kinetics of heterogeneous and homogeneous reactions. In fact, one can use virtually any sub-models, which are dictated by real conditions or regarded as appropriate from separate considerations. The approach is applicable to a variety of reacting flows through porous media.
Below we present a spectrum of models that can be effectively used to accurately model a wide range of reacting flows through porous media. In this paper, we briefly summarise theoretical developments of the previous studies and also present the results of computational modelling of the carbonation process in sorbent particles, while comparing these results to experimental data. Before presenting the conditional approach we briefly discuss the phenomena involved in the carbonation process.
2. Phenomena to be Considered
2.1. Complex Transport
The CaO based sorbents are porous materials with complicated porous structures with fractal properties. Such media are characterised by geometrical similarity of pore structures at different scales (micro-, meso- and macro-pores) and by the predominant location of the reactive surface (CaO) within the smallest pores. Transport in such porous media involves complex cascade diffusion through pores of different sizes (micro-, meso- and macro-pores). In the experiments described in Section 4.1, the pressure at the outer border of spherical sorbent particles remains approximately constant. However, the convective transport could not be neglected a priori. Indeed, the consumption of CO2 at the reactive surfaces inside a sorbent particle can cause non-zero pressure gradients and, therefore, non-zero gas velocities. Although convective transport predominantly occurs through the largest pores and fractures, the convective term should also be taken into account.
2.2. Different Regimes of the Heterogeneous Carbonation Reaction
Traditionally [10,11], the equations that govern the transport in the gas phase are averaged using intrinsic (over the β-phase) or superficial (over the entire porous medium) averages. The averaging is performed by taking the convolution integral with a bell-shaped weighting function. The characteristic length scale of this function is much larger than the characteristic pore size but much smaller than the length scale of flow parameter variations. As a result, models based on traditional averaging disregard the variations in species concentrations within a pore and variations between pores of different sizes.
The traditional approach is suitable for modelling the reactive transport if the heterogeneous reaction is in the kinetics-controlled regime (Da ≫ 1) and all pores are of approximately the same size. As demonstrated [6,9], the traditional averaging gives poor predictions for the intermediate (Da ≈ 1) and diffusion-controlled (Da ≪ 1) regimes. Since the reaction regime is not known a priori, more advanced treatment is required for accurate modelling of the sorbent carbonation behavior. Note that conditional methods presented below reduce to traditional averaging when (Da ≫ 1).
2.3. Formation of the Product Layer
The reactive transport in porous sorbent particles is complicated by the formation of the product layer (CaCO3) over the reactive surface. Such a layer alters the pore structure and, more importantly, substantially reduces the apparent rate of the carbonation reaction by slowing down the transport of the gaseous reactant to the reactive surface [12–14]. These effects have to be taken into account in modelling of carbonation behavior. It is also important to take into account the temperature dependence of the product layer diffusivity reported in [14]. Below we present our approach, which is capable of incorporating all the above mentioned phenomena.
3. Conditional Methods
The conditional moment closure (CMC) methodology was proposed in the early nineties [15,16] for modelling of turbulent reacting flows. A detailed description of this methodology is given in [17]. Since then, the methodology has been successfully applied to a variety of problems in turbulent reacting flows as well as in reacting flows through porous media.
As discussed above, the traditional approach [10,11], which is based on unconditional averages, is unable to take into account variations in species concentrations along the distance to the reactive surface. An additional variable that describes these variations has to be introduced in order to treat heterogeneous gas-solid reactions more accurately. Two such variables have been proposed so far: the diffusive tracer and the distance tracer. The porous CMC (PCMC) model for the diffusive tracer is presented in [6]. PCMC treatment of the case where the product layer is formed due to heterogeneous reactions is given in [9]. The model for the distance tracer, which is called porous distance-conditioned moment closure (PDCMC), is presented in [8]. Properties of the diffusive and the distance tracers in fractal porous media are comparatively analyzed in [7], where the interplay between interface and network fractalities is also discussed. The effective transport coefficients for conventional and conditional models can be evaluated using a generalized Effective Medium Approximation, combined with an approximation similar to the Fokker-Planck equation (non-uniform single-bond effective medium approximation (NEMA)-diffusional continuum approximation (DCA)) [18]. Below, we present the major equations of these models following the notations used in [19]. We refer an interested reader to the previous publications [6–9,18,19] for more details.
3.1. Interface and Network Fractality
The conditional approach distinguishes two types of fractality in porous media: interface and network (see Section 10 in [7] for more details). The former affects transport of species and heterogeneous reactions within each pore, while the latter induces variations between pores of different sizes that form a complex network of pores. A typical network of pores would have most of its pore volume contained in the largest pores, while most of the phase interface surface would be hidden in the smallest pores. Thus, transport between pores of different sizes is essential for flows with heterogeneous reactions. Generally, as discussed below, the PCMC model is more suitable for the treatment of interface fractality, while PDCMC and NEMA-DCA models are preferable in the case where network fractality plays the major role. If the heterogeneous reaction is in the diffusion-controlled regime (Da ≫ 1), the interface fractality is the primary issue, while network fractality dominates for the kinetics-controlled regime (Da ≪ 1).
We note, however, that the regime of the heterogeneous reaction is not known a priori. Furthermore, the true rate of the carbonation reaction (on clean CaO surface) is, practically, not accessible to measurements. Instead, information about the true rate can be inferred from modeling of the carbonation behavior of real samples. Below we describe the conditional modeling of the carbonation behavior of the sample CaAlWM.
3.2. Diffusive Tracer (PCMC)
The main idea utilised in the PCMC model is linking transport of different reactive scalars to and from the phase interface to a single scalar—the tracer scalar Z—whose characteristics are easier to find. The interface surface can be complex and possess fractal properties, affecting the transport to and from the surface; hence the tracer scalar needs to be selected in such a way that Z possesses a topological similarity with other main species. The species' diffusion to and from the interfaces then can be interpreted as diffusion in the space of variable Z, which in conditional models plays the role of an additional independent variable. The PCMC treatment covers both kinetics-limited and diffusion-limited cases as well as any case in between these limiting cases. Even if the problem is homogeneous in physical space, the PCMC model still involves diffusive transport in Z-space, which becomes most important when reaction rates are fast.
The reactive flow within the β-phase is governed by the continuity:
Here, ρ and v are the gas density and velocity; while Yi and Wi are the mass fraction and the production rate of the species “i”, respectively; and D is the diffusion coefficient in the gas phase.
The diffusive tracer Z can be introduced in [6] as follows. The tracer Z is assumed to be produced at the constant rate WZ in the β-phase. It is transported in the same way as gaseous species. That is, Z satisfies the conventional species transport equation with the same diffusion coefficient D:
This ensures that Z emulates transport of gaseous species. The value of the constant source term WZ can be arbitrarily selected without loss of generality and we put WZ = 1. As demonstrated in [7], the diffusive tracer can be interpreted as a distance from a given point in the β-phase to the reactive surface measured by the average time required for a random walk process to reach the surface.
The tracer is instantaneously consumed at the reactive surface, so that Z is positive in the β-phase and monotonically decreases to zero at the reactive surface. In this way, Z parameterises the distance from the reactive surface and the condition Z = 0 defines the surface. That is, conditioning on Z resolves the phase interface. Furthermore, the instantaneous consumption of Z on the surface emulates the diffusion-controlled regime of heterogeneous reactions.
The equations of the PCMC model are expressed in terms of conditional Favre averages. For an arbitrary function F, the conditional Favre average (F̄)z is defined as (F̄)z = 〈Fρβ∣Z = z〉/〈ρβ∣Z = z〉. The angular brackets conventionally denote superficial averages and z is the variable in the Z-dimension, while β is the indicator of the β-phase so that β = 1 in the β-phase and β = 0 elsewhere. If Z resolves the interface, the indicator β does not affect conditional averaging and can be omitted.
Averaging Equations (1) and (2) with the help of the technique described in [17], while omitting the terms which are conventionally neglected in the CMC approach [6], and conventionally denoting Qi ≡ (Ȳ1)z, we arrive at the following equations of the PCMC model:
If the reactive surface is not resolved by the conditioning variable, the source terms Wi involve the effect of both volumetric and surface reactions. If the surface is resolved by Z = 0 (or by a similar condition), then the surface reactions are treated separately with boundary conditions for the Z-dimension [8]. This case of the phase interface resolved by Z = 0 is specifically considered in this section. The boundary conditions are obtained using an ensemble average [6], which generalizes the spatial averaging theorem [14]. Following [6], we assume that the reactive surface is quasi-stationary and the Z-field is developed. Then, the boundary conditions for Z → 0 read:
Thus, Equation (7) takes into account the heterogeneous reactions and provides one of the major advances of CMC models over the conventional (unconditional) approach. In Equation (7), the surface reaction rates Ψi are functions of Qi, which are linked to the distance to the reactive surface via conditioning on Z. In contrast, only unconditional averages, which are independent of that distance, are available in conventional models.
Note that consistent modelling of both PZ and (N̄)z is required to close Equations (4) and (5). Generally, PZ is not known and needs to be reasonably approximated. In the test case considered in [6], such an approximation was obtained by matching the DNS results. This approach, however, is computationally expensive and requires additional modelling of the structure of a porous medium, which can be an extremely difficult problem by itself. A more practical method for a medium with fractal properties, which is based on the result obtained in [7], is suggested in [9]. This more practical method is utilised in the present study.
3.3. Distance Tracer (PDCMC)
Alternatively, the distance to the phase interface can be parameterised by the distance tracer R. The distance tracer is defined as the minimal distance from a point within a pore to the reactive surface [7]. The sample variable in the R-dimension is r. The tracer R appears to be a more natural parameterisation. Averages conditioned on R are independent of the flow parameters. The PDCMC model equations, however, involve an additional velocity component u corresponding to the R-direction, as well as other additional terms.
The PDCMC model equations are formulated in terms of conditional averages [8] as follows. For an arbitrary function F we define 〈F〉r ≡ 〈F∣R = r〉 and (F̄)r ≡ 〈Fρ〉r/ρr where ρr ≡ 〈ρ∣R = r〉 is conditional average of the density. Let PR be the PDF of R. As demonstrated in [7], PR asymptotically follows the power-law. That is, PR ∼ 1/rα. Similarly to the diffusive tracer, the distance tracer is positive in the β-phase and the condition R = 0 defines the reactive surface.
In terms of the averages conditioned on R, Equation (1) reads:
A superficial PDF, normalised as in Equation (9), is implied here. Using an over-tilde to distinguish the conditioning on R from that on Z and denoting Q̃i ≡ (Ȳl)r, Equation (2) takes the form:
The last terms in Equations (10) and (11) are needed only if R = 0 does not resolve the phase interface (in practice, as discussed below, this occurs with network fractality). If conditional averaging resolves the boundary these terms are not present in the conditional equations but, instead, enter the boundary conditions on the reactive surface (r = +0), which are given by:
In the case of interface fractality, the PCMC and PDCMC models are equivalent at the modeling level. This means that with a consistent choice of the parameters of the models, PCMC and PDCMC can be obtained from each other by replacement of variables. The interface-resolving versions of the models (i.e., R = 0 and Z = 0 at the interface) are recommended for interface fractality. In the case of network fractality the PDCMC approach is preferable as in this case the distance tracer can be interpreted as a proxy for pore sizes [9,19]. Indeed, the distance R is typically found in a pore of size slightly larger than R. This is because R cannot be found in a pore smaller than R, while the probability of being located in a pore much larger than R is low, since smaller pores contain most of the interface surface. Hence, as demonstrated in [19], conditioning on the distance tracer can also be interpreted as conditioning on the pore size. In the network version of the PDCMC model R = 0 does not correspond to the interface and conditional averages of the interface reaction terms are present as source terms—the last terms in Equations (10) and (11). In principle the PCMC model may also have a network version using the maximal value of Z within the pore as a proxy for the pore size (see discussion in [7]), but this does not seem to offer any advantages over network-PDCMC. Conditional methods allow for double conditioning (i.e., distance to the wall and pore size), although at this stage this seems to be impractical and excessively complicated.
Determining transport coefficients for conditional models is a problem, which can be solved by performing DNS on a small test volume or by adjusting the coefficients in according with experimental data. The NEMA-DCA approach, which can constructively determine transport coefficients for network fractality while taking into account percolation effects for arbitrary irregular networks of pores, seems most promising.
3.4. Generalized Effective Medium Approximation
Determining transport coefficients in realistic porous media is a challenging problem, especially under conditions when network fractality plays a significant role and percolation effects may become prominent. The goal of determining transport properties in porous media with irregular structure and varying percolations can be achieved by using NEMA-DCA, which represents a merger of a DCA with a generalized, NEMA. The generalisation is needed since Kirkpatrick's original single-bond EMA [20] was only capable of dealing with regular lattices; we, on the other hand, must deal with networks that can be irregular in many ways, including pores of a wide variety of sizes, which can be arranged in ways that are anisotropic and heterogeneous. A full description of this approach is given in [18], but a quick summary is given in this section.
For this approach, the porous medium is seen as a random network, in which the pores are the nodes of the network; each pore has an associated random vector of properties yi, with shared distribution f(y). This vector includes the co-ordinates of the pore in the physical space (x1,x2,x3), and can also contain other pore properties. In particular, the inclusion of pore size as one of the properties denoted by y = (x1,x2,x3,r) gives rise to equations for transport properties conditioned on pore size. The behavior of the pore connections is adequately described by a single effective quantity—conductance—which is described by the conditional PDF f(g ∣ yi, yj). While conductance g, quantities m, and concentrations c may be interpreted differently depending on the exact problems under consideration, transport within a single instance of such a random network is described by the generic master equation, which can be written in the form:
The proposed method derives a continuous transport equation from this model via an averaging approach, but with two steps. The first step employs an effective medium approximation in order to account for the network's connectivity in a continuous model. If this step was skipped, the continuous model would simply neglect such effects, resulting in significant inaccuracy. The latter step consists of a conditional ensemble average over possible realizations of the network structure; as with the CMC approaches discussed in other sections, this average is conditional and retains dependence on parameters of the pore network. Most notably, the distance tracer R can be considered as a proxy for the pore size and hence can reasonably be used within this model.
For the EMA, each throat conductance distribution f(g ∣ yi, yj) is replaced by an effective conductance g̃(yi, yj) according to the self-consistent condition of effective medium theory:
After taking the generalised effective medium approximation, conditional ensemble averaging gives the effective diffusion tensor D; this tensor determines the overall transport properties of the medium, and is described by:
The NEMA-DCA approach has been shown to give accurate results even under conditions when a conventional diffusional approximation would become highly inaccurate due to percolation effects, or diverge without producing a finite value for the coefficients [18].
4. Experimental Investigation and Modelling of the Carbonation Process
4.1. Materials
Three synthetic CaO sorbents denoted as CaCSG, CaCPM and CaAlWM were studied here. The samples CaCSG and CaCPM were made from calcium hydroxide and high aluminate cement by the simplified sol-gel and physical mixing methods respectively. They both contain around 15% CaO in the final sorbent. The sample CaAlWM was made from calcium d-gluconate monohydrate and aluminium nitrate nonahydrate by the wet mixing method. The final sorbent contains 6.5% CaO as the active component and 93.5% mayenite-Ca12Al14O33 as inert support. The chemical compositions of the cement and the detailed preparation procedure used to make the sorbents are given in [21].
Adsorption of N2 on a sorbent was performed on a TriStar 3000 instrument (Micromeritics Instrument Corporation, Norcross, GA, USA) in order to evaluate its Brunauer, Emmett and Teller (BET) surface area and pore volume, parameters of which were used to calculate the initial surface area and porosity of CaO and CaCO3. Before the test, the fresh sorbent was degassed at 250 °C overnight. Then adsorption of N2 was accomplished at −196 °C in liquid nitrogen. The properties of the samples are summarised in Table 1.
4.2. Experimental Procedure
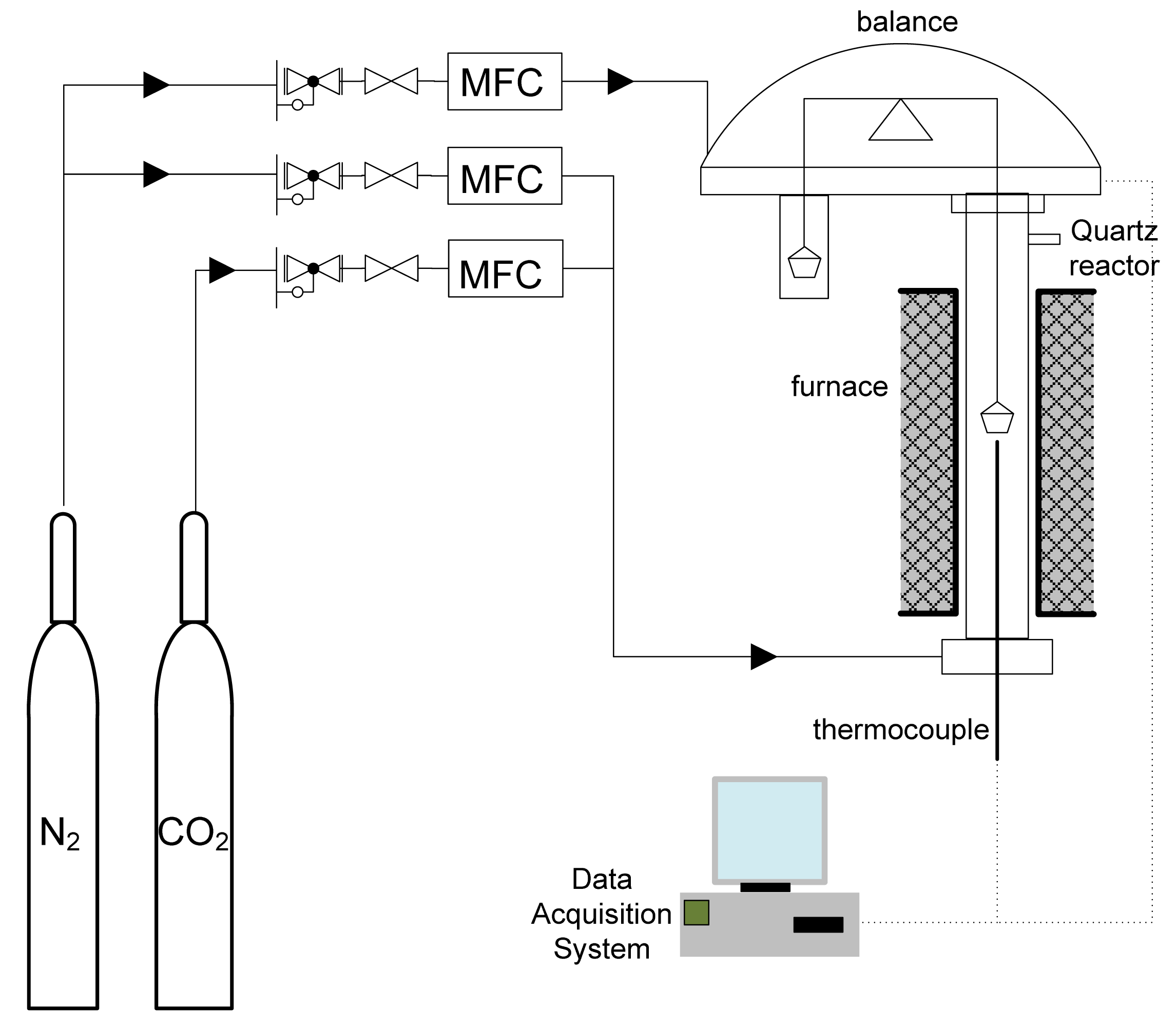
The carbonation behavior of the samples was measured using a Cahn-131 thermogravimetric analyser (TGA) (Thermo Fisher Scientific, Newington, NH, USA) at five different temperatures in the range of 550–750 °C. The schematic diagram of the experimental setup is shown in Figure 1. In each run about 20 mg sorbent was loaded into a quartz holder hanging from the balance on a platinum wire that passes through the inside pipe of the cooling section. The furnace was then heated up to 900 °C at a ramp rate of 20 °C/min in a pure N2 stream with volumetric flow rate of 85 mL/min. After 10 min holding at 900 °C, the furnace was cooled down to the desired temperature for carbonation under 15 vol% CO2 (N2 balance) for 30 min. A thermocouple was placed about 5 mm below the sample hold to represent the solid temperature. The mass of the sample was recorded by the balance every 10 s.
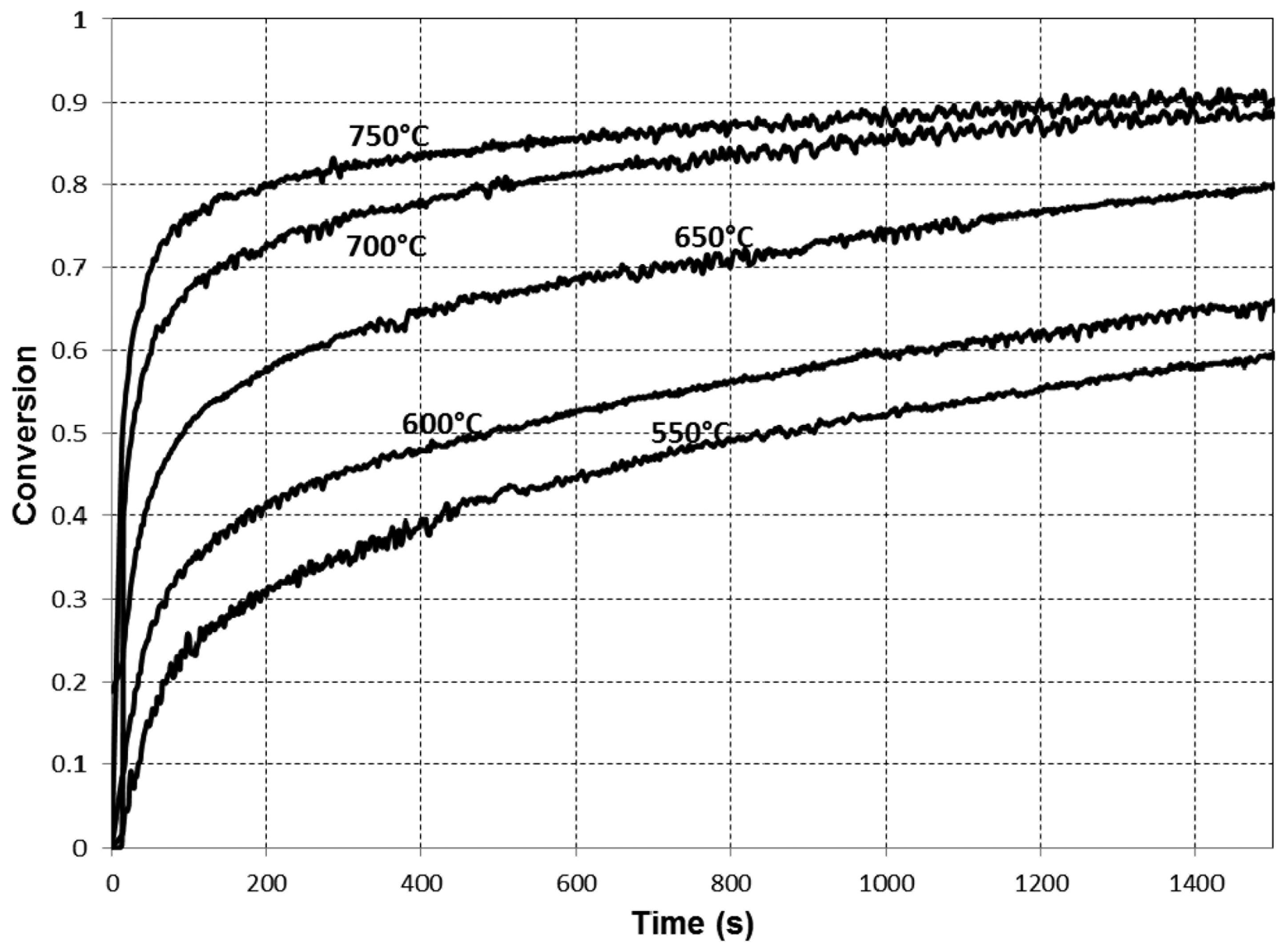
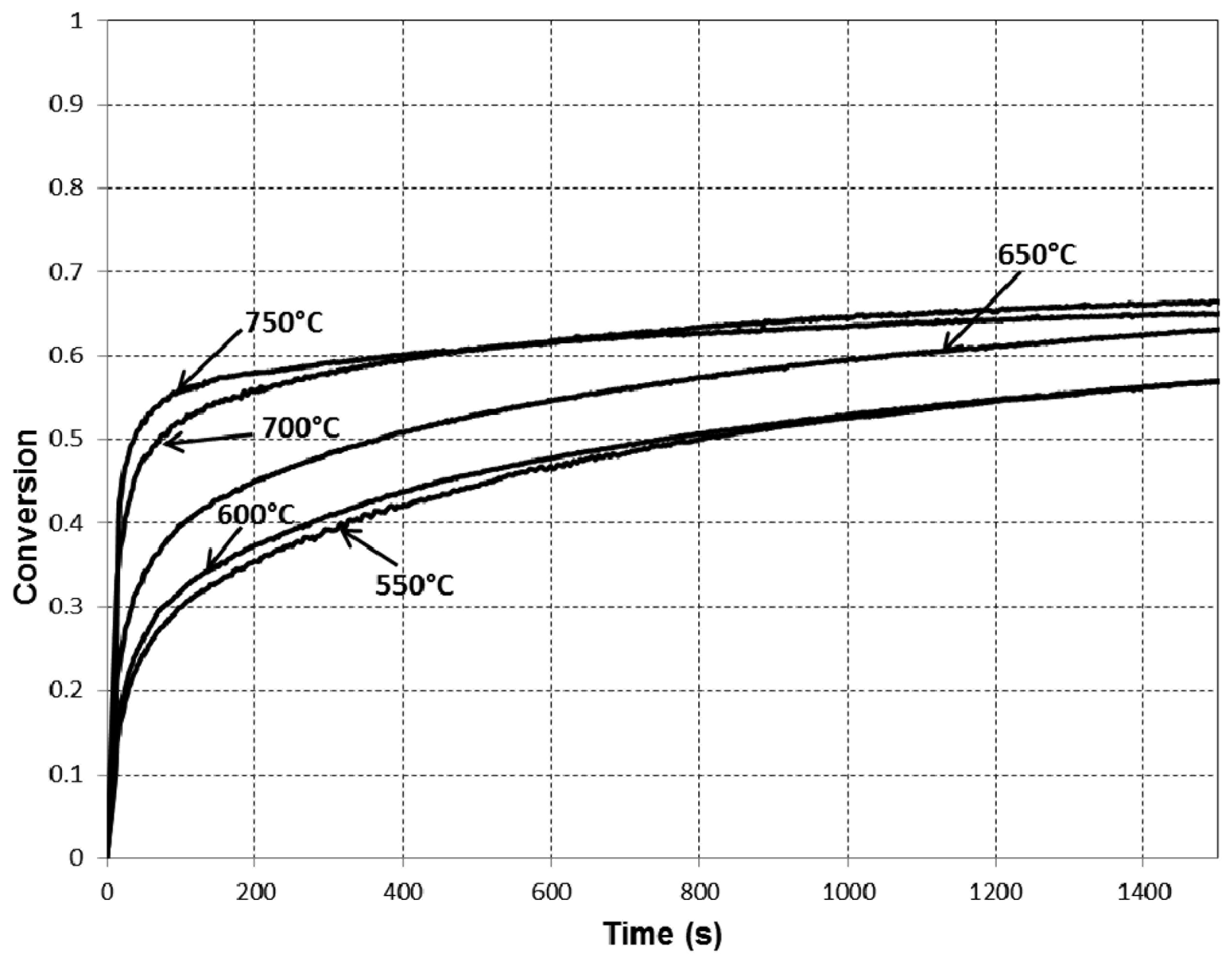
The experimental results are presented in Figures 2, 3 and 4.
4.3. Product Layer and Its Diffusivity
The carbonation of CaAlWM sample has been simulated using the PCMC model. In this simulation, the parameters of the sorbent particles and initial conditions were selected to match those in experiments (see Table 1 and the description of the experiment).
As discussed above, the carbonation reaction results in a formation of a product layer over the reactive surface. Such a layer imposes additional resistance to the transport of gaseous species towards the reaction surface. This effect has been taken into account in the present treatment, as described in [9]. Following [9,13], we assume that the thickness of the product layer δ is small compared to the characteristic size of the reactive surface S. That is, . We note that, for this sorbent sample, the variation in porosity caused by the formation of the product layer is negligibly small due to low content of CaO (6.5 wt%). For this reason, we assume that the product layer affects the effective reaction rate, while the porosity of sorbent particles remains unchanged in the process.
The rate-controlling mechanisms of the carbonation reaction have been discussed in [14]. The authors pointed out that in the later stages the carbonation reaction is controlled by the diffusion through the product layer. The authors also investigated the temperature dependence of product layer diffusivity and observed that the dependence of the diffusion coefficient on temperature can be described by the conventional Arrhenius-type equation. Following [14], we assume that the diffusion coefficient in the product layer DP is given by:
4.4. Computational Algorithm
The above described PCMC model has been implemented in the form of MATLAB code that utilises the Newton–Raphson method. The code allows for simulation of the reactive transport within spherical porous particles, while taking into account the formation of the product layer over the reactive surface. The usage of spherical symmetry of the particles reduces the dimension of the problem to one spatial coordinate ξ (radial direction) and one additional coordinate (z-direction). This, in its turn, substantially reduces the computational burden compared to a non-spherical case with three special coordinates. The other assumptions used in the presented simulation are summarised below.
The PDF PZ is presumed to have the form given by Equation (13) in Reference [9]. The conditional dissipation of the tracer (N̄)z is modelled as described in [9]. Z-field is assumed to be fully developed at each time step and the temporal partial derivative in Equation (4) is neglected. The reactive surface is assumed to be predominantly located in smallest pores, where the convective transport is negligibly small, and the second term in Equation (4) is neglected. This allows analytical expression for (N̄)z. See Reference [9] for more details.
The Qi are calculated on a rectangular domain (ξ × z) 50 by 50 points. Initially, the values of Qi are equated with those in the surrounding atmosphere for the entire domain. No-flux boundary conditions are employed for ξ = 0 (the centre of the particle) and for z = zmax. The boundary conditions at the reactive surface z = 0 are defined by Equation (7). The boundary conditions on the surface of the particle (ξ = ξmax) are defined as follows. We note that the gas exchange between the inner space of the particle and the surrounding atmosphere occurs mainly through the largest pores. To simulate this, Qi are equated with those in the surrounding atmosphere for ten percent of the points with the largest values of z, while no-flux conditions are used for other points. The utilised value for the time step is 0.2 s.
The algorithm used in this code can be briefly described as follows:
As the preliminary step, all the necessary variables are initialised and the values of the model parameters as well as initial and boundary conditions are assigned to match those in experiment. Then, the time advancing procedure is carried out.
Firstly, the values of Qi for the next time step are calculated using a finite difference scheme for Equation (6). Although the hybrid scheme (partly explicit and partly implicit) is implemented in the code, we utilised only the implicit part in order to avoid computational instabilities. The linear equations for the scheme are solved using the embedded MATLAB matrix solver.
Secondly, the obtained values of Qi are used to calculate new values of the gas mixture molar mass M for each node in the computational domain (both in ξ- and in z-direction), using the values of the gas density ρ from the previous time step. The new value of the gas density ρ is calculated for the entire domain, using the equation of state for ideal gas. Then, these values are averaged over z-direction using the values of PZ from the previous time step.
Thirdly, the new values of the gas velocity in radial direction uξ are recalculated from the continuity Equation (1). Here we use previous values of uξ and both previous and new values of the gas density. In z-direction, the velocity is approximated as a linear function of z. In this approximation, we set uZ(0) = 0 (non-slipping conditions) and select the slope to equate the average value (over z) with uξ.
Fourthly, the new values of the gas pressure p are calculated from Darcy's law, which, in our case, is given by:
Finally, the new value of the product layer thickness δ, as well as the parameters PZ and (N̄)z, are calculated as described in [9]. Then, the time-cycle continues.
4.5. Simulation Results
The value for the diffusivity in the gas phase (z-direction) was selected from [22]. The other adjustable parameters of the model were selected by fitting the experimental data using a trial-and-error procedure. The values of the adjustable parameters used in the modelling CaAlWM sample carbonation are given in Table 2.
The results of the modeling and their comparison with experimental data are presented in Figure 5. Figure 5 shows that, except for the lowest temperature of 550 °C, very good agreement of the model prediction with the experimental data has been achieved. In this work, we followed [14] and utilise the Arrhenius equation with a constant pre-exponential factor to describe the dependence of the product layer diffusivity on temperature. In reality, however, this dependence can be more complex. According to Figure 9 in [14], the Arrhenius-type dependence of the diffusivity on temperature has been reported only for high temperatures (more than 850 °C), while the behavior of the diffusivity in the lower temperature region remains unclear. It is reasonable to assume that one should use the modified Arrhenius equation (with a temperature-dependent pre-exponential factor) to describe the product layer diffusivity for lower temperatures. Therefore, the discrepancy between the model predictions and experimental data observed for the temperature of 550 °C can be explained by the use of a simplified equation for product layer diffusivity.
It is important to investigate the regime of the heterogeneous reaction in order to clarify which type of fractality dominates in this particular case. To do this, we examine the variation of the gaseous reactant (CO2) mass fraction in z-direction and compare it with that in the ξ-direction. The computational results show that the CO2 mass fraction varies substantially in the ξ-direction. Due to diffusion toward the centre of a sorbent particle, this variation decreases with time. In contrast, the CO2 mass fraction varies insignificantly as functions of the diffusive tracer even at the initial stage of the process. This implies that, under the conditions used in the experiments, the heterogeneous carbonation reaction is in the kinetics-controlled regime (Da ≪ 1) and the interface fractality plays a less important role than network fractality.
5. Conclusions
The paper expose the family of conditional models specifically designed to simulate reacting flows in complex porous media. The presented methods—PCMC, PDCMC and NEMA-DCA—allow for the simultaneous and consistent treatment of both homogeneous reactions in the gas phase and heterogeneous reactions on complex phase interface in various reaction regimes coupled with the transport through an irregular pore networks. The methods are designed to take into account percolation effects, irregular or fractal natures of porous media, fast heterogeneous reactions, and transport between pores of very different sizes. In contrast to previously used models, which utilize the volume averaging technique and, therefore, neglect inter-pore variations in gaseous reactant concentrations, the new models utilize conditional averaging and take these variations into account. The conditional models are computationally affordable and should escape the prohibitive computational cost associated with DNS.
The carbonation behavior of the CaO-based sorbents has been experimentally investigated and simulated using the discussed conditional approach. The simulation results are in a good agreement with the experimental data. The carbonation process is an important instrumental part of the gasification technology with in-situ CO2 capture and the ability to accurately model this process is important for optimization of this emerging gasification technology.
Acknowledgments
The authors gratefully acknowledge the financial support of the Department of Resources, Energy and Tourism under the Australia-China Joint Coordination Group on Clean Coal Technology grant scheme and the Australian Research Council.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dean, C.C.; Blamey, J.; Florin, N.H.; Al-Jeboori, M.J.; Fennell, P.S. The calcium looping cycle for CO2 capture from power generation, cement manufacture and hydrogen production. Chem. Eng. Res. Des. 2011, 89, 836–855. [Google Scholar]
- Lu, H.; Khan, A.; Pratsinis, S.E.; Smirniotis, P.G. Flame-made durable doped-CaO nanosorbents for CO2 capture. Energy Fuels 2009, 23, 1093–1100. [Google Scholar]
- Liu, W.Q.; Feng, B.; Wu, Y.Q.; Wang, G.X.; Barry, J.; da Costa, J.C.D. Synthesis of sintering-resistant sorbents for CO2 capture. Environ. Sci. Technol. 2010, 44, 3093–3097. [Google Scholar]
- An, H.; Song, T.; Shen, L.; Qin, C.; Yin, J.; Feng, B. Coal gasification with in situ CO2 capture by the synthetic CaO sorbent in a 1 kV dual fluidised-bed reactor. Int. J. Hydrog. Energy 2012, 37, 14195–14204. [Google Scholar]
- Quintard, M.; Whitaker, S. Transport in ordered and disordered porous media I: The cellular average and the use of weighting functions. Transp. Porous Media 1994, 14, 163–177. [Google Scholar]
- Klimenko, A.Y.; Abdel-Jawad, M.M. Conditional methods for continuum reacting flows in porous media. Prog. Energy Combust. Sci. 2007, 31, 2107–2115. [Google Scholar]
- Vladimirov, I.G.; Klimenko, A.Y. Tracing diffusion in porous media with fractal properties. Multiscale Model. Simul. 2010, 8, 1178–1211. [Google Scholar]
- Klimenko, A.Y.; Saulov, D.N.; Massarotto, P.; Rudolph, V. Conditional model for sorption in porous media with fractal properties. Transp. Porous Media 2012, 92, 745–765. [Google Scholar]
- Saulov, D.N.; Chodankar, C.; Cleary, M.J.; Klimenko, A.Y. Coupling the porous conditional moment closure with the random pore model: Applications to gasification and CO2 capture. Front. Chem. Sci. Eng. 2012, 6, 84–93. [Google Scholar]
- Whitaker, S. The Method of Volume Averaging; Kluwer Academic Publishers: Berlin, Germany, 1999. [Google Scholar]
- Lichtner, P.C. Continuum Formulation of Multicomponent-Multiphase Reactive Transport. In Reviews in Mineralogy: Reactive Transport in Porous Media; Lichtner, P.C., Steefel, C.I., Oelkers, E.H., Eds.; Mineralogical Society of America: Chantilly, VA, USA, 1996; Volume 34, pp. 1–82. [Google Scholar]
- Barker, R. The reversibility of the reaction CaCO3 ⇄ CaO+CO2. J. Appl. Chem. Biotechnol. 1973, 23, 733–742. [Google Scholar]
- Bhatia, S.K.; Perlmutter, D.D. Effect of the product layer on the kinetics of the CO2-lime reaction. AIChE J. 1983, 29, 79–86. [Google Scholar]
- Mess, D.; Sarofim, A.F.; Longwell, J.P. Product layer diffusion during the reaction of calcium oxide with carbon dioxide. Energy Fuels 1999, 13, 999–1005. [Google Scholar]
- Klimenko, A.Y. Multicomponent diffusion of various scalars in turbulent flow. Fluid Dyn. 1990, 25, 327–333. [Google Scholar]
- Bilger, R.W. Conditional moment closure for turbulent reacting flow. Phys. Fluids A 1993, 5, 436–444. [Google Scholar]
- Klimenko, A.Y.; Bilger, R.W. Conditional moment closure for turbulent combustion. Prog. Energy Combust. Sci. 1999, 25, 595–687. [Google Scholar]
- Klimenko, D.A.; Hooman, K.; Klimenko, A.Y. Evaluating transport in irregular pore networks. Phys. Rev. E 2012, 86, 011112:1–011112:11. [Google Scholar]
- Saulov, D.N.; Zhao, M.M.; Cleary, M.J.; Klimenko, D.A.; Hooman, K.; Klimenko, A.Y. General approach for modelling of reactive transport in porous media. Int. J. Chem. Eng. Appl. 2012, 3, 471–476. [Google Scholar]
- Kirkpatrick, S. Percolation and conduction. Rev. Mod. Phys. 1973, 45, 574–588. [Google Scholar]
- Yin, J.; Qin, C.; An, H.; Liu, W.; Feng, B. High-temperature pressure swing adsorption process for CO2 separation. Energy Fuels 2012, 26, 169–175. [Google Scholar]
- Incropera, F.P.; Dewitt, D.P.; Bergmann, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Willey & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]


| Property | CaAlWM | CaCSG | CaCPM |
|---|---|---|---|
| CaO Content (%) | 6.5 | 15 | 15 |
| Sorbent density (g/cm3) | 2.73 | 1.965 | 1.965 |
| Porosity | 0.327 | 0.186 | 0.565 |
| Surface area of CaO (m2/cm3) | 0.47 | 0.88 | 0.47 |
| Total surface area of solid (m2/cm3) | 11.49 | 10.0 | 5.35 |
| Pore volume (cm3/g) | 0.024 | 0.031 | 0.016 |
| Particle diameter (mm) | 0.54 | 0.54 | 0.54 |
| Parameter | Value | |
|---|---|---|
| Diffusivity in z-direction (m2/s) | 1.6 × 10−5 | |
| Effective diffusivity in ξ-direction (m2/s) | 5.0 × 10−4 | |
| Excess fractal dimension | 0.9 | |
| Permiability (d) | 0.001 | |
| Gas viscosity (Pa s) | 2.93 × 10−5 | |
| Size of the largest pores (mm) | 0.54 | |
| Diffusivity through the product layer | Pre-exponential factor (m2/s) | 0.065 |
| Activation energy (J/mol) | 1.94 × 105 | |
| Intrinsic rate of the carbonation reaction | Pre-exponential factor (kg/m2) | 0.7773 |
| Activation energy (J/mol) | 4.3 × 104 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Saulov, D.N.; Watanabe, S.; Yin, J.; Klimenko, D.A.; Hooman, K.; Feng, B.; Cleary, M.J.; Klimenko, A.Y. Conditional Methods in Modeling CO2 Capture from Coal Syngas. Energies 2014, 7, 1899-1916. https://doi.org/10.3390/en7041899
Saulov DN, Watanabe S, Yin J, Klimenko DA, Hooman K, Feng B, Cleary MJ, Klimenko AY. Conditional Methods in Modeling CO2 Capture from Coal Syngas. Energies. 2014; 7(4):1899-1916. https://doi.org/10.3390/en7041899
Chicago/Turabian StyleSaulov, Dmitry N., Shuhei Watanabe, Junjun Yin, Dimitri A. Klimenko, Kamel Hooman, Bo Feng, Matthew J. Cleary, and Alexander Y. Klimenko. 2014. "Conditional Methods in Modeling CO2 Capture from Coal Syngas" Energies 7, no. 4: 1899-1916. https://doi.org/10.3390/en7041899






