Temperatures and Heat Flows in a Soil Enclosing a Slinky Horizontal Heat Exchanger
Abstract
: Temperature changes and heat flows in soils that host “slinky”-type horizontal heat exchangers are complex, but need to be understood if robust quantification of the thermal energy available to a ground-source heat pump is to be achieved. Of particular interest is the capacity of the thermal energy content of the soil to regenerate when the heat exchangers are not operating. Analysis of specific heat flows and the specific thermal energy regime within the soil, including that captured by the heat-exchangers, has been characterised by meticulous measurements. These reveal that high concentrations of antifreeze mix in the heat-transfer fluid of the heat exchanger have an adverse impact on heat flows discharged into the soil.1. Introduction
The basic low-potential sources of energy for heat pump evaporators used for heating and cooling are air, water, and ground, i.e., soil. When air is used, the installation of the energy system is easier and cheaper. A disadvantage here is the lower amount of energy savings resulting from the lower seasonal performance factor (SPF). The use of surface or ground water as the source for heat pumps is very advantageous in view of the energy effect of the system. Installations of such systems, however, are limited especially by environmental requirements for the protection of such water sources. Soil or rock mass appears efficient, especially in relation to the ambient temperature. In winter, the mass temperature is higher than the ambient temperature and, conversely, lower in summer. This mass and ambient temperature ratio is useful in winter when the heat pump is employed for heating and in summer for cooling. The performance and economic comparison of air, soil and rock mass acting as low-potential sources of energy for heat pumps has been addressed by Petit and Meyer [1]. They state that the highest performance is achieved with vertical rock mass exchangers. Horizontal ground heat exchangers deliver a better heating factor and the best economic parameters of all three sources of energy. Air has received the worst rating as the source of energy for heat pumps.
Lund et al. [2] prepared an overview of the use of geothermal energy for direct consumption in 78 countries. The total installed thermal power capacity of geothermal sources amounted to 48,493 MW in 2009. Those sources delivered 423,830 TJ of heat energy per year. Approximately 47.2% of that energy was acquired from ground-to-water heat pumps. The total installed output of ground-to-water heat pumps was 33,134 MW in 2009. The number of installed energy systems with ground-to-water heat pumps in 2009 was double and quadruple compared to 2005 and 2000, respectively.
Heat from the soil or rock mass is removed using horizontal or vertical heat exchangers. Vertical ground heat exchangers deliver a high efficiency in performance and have the minimum requirements for the ground area. However, they present an investment that is considerably higher than that of horizontal heat exchangers, due to design and installation of vertical borehole heat exchangers. Horizontal ground heat exchangers represent a compromise between high efficiency and investment costs of the heat exchanger. They are available in three basic configurations: linear, spiral and coil type [3]. The 30–50 mm pipes of these heat exchangers are buried at a depth of 1.5–2.0 m under the surface, depending on the thermal characteristics of the ground mass. The results of measurement of ground mass temperature [4] have indicated that the area up to 1 m deep is highly sensitive even to short-term variations of weather. In the summer months (July–September), the density of transferred heat flow from the ground mass surface to deeper strata amounts to 3.6 W·m−2. At the end of September, the temperature gradient drops to zero and the heat flow reverses. Heat is transferred towards the surface of the mass.
A number of publications have explored the experimental as well as numerical analyses over the last several years. De Swardt and Meyer [5] compared two low-potential sources of energy for heat pumps: air and water from the community water mains. Water mains may be regarded as a horizontal ground heat exchanger. The results demonstrated lower consumption of electricity and higher seasonal performance factor when mains water was used. The Research Center for Energy and Environment in Lecce [6] verified the basic configuration of horizontal ground source heat exchangers. Throughout the year the researchers there measured the temperatures of the soil and the thermal output discharged by the heat exchangers. The results of the test showed that the primary parameters fundamentally affecting heat transfer in the soil are the thermal conductivity coefficient of the soil and the speed at which the heat-transfer fluid flows through the pipes of the heat exchanger. The spacing of the heat exchanger pipes and the depth at which they were laid did not play a significant role.
Song et al. [7] analysed the most important parameters affecting the thermal conductivity coefficient of the soil. Their experiments have shown that within the temperature range of 10–40 °C in a dry state the thermal conductivity coefficient of the soil is 0.55–0.6 W·m−1·K−1; with normal moisture content the average is 2.3 W·m−1·K−1 and with wet soil the figure is 2.7 W·m−1·K−1. When the moisture content of the soil increases, the coefficient also increases to a certain specific figure. When the moisture content rises above this specific level, the thermal conductivity coefficient of the mass is almost constant. The differing thermal conductivity coefficients of water in a liquid state (0.58 W·m−1·K−1) and of ice (2.25 W·m−1·K−1) show that the properties of the frozen soil are different. Experimental measurements [7], for example, have shown that the thermal conductivity coefficient of clay at plus-zero temperatures is 1.616 W·m−1·K−1, but while the clay is frozen it is 2.454 W·m−1·K−1. Leong et al. [8] have demonstrated a strong correlation of heat pump performance to moisture content and mineralogical composition of the ground mass. The findings of their experiments have proven that any reduction of moisture in the ground mass below 12.5% has a devastating impact on the performance of the heat pump. Ground mass moisture above 25% significantly improves the heat pump performance, albeit moisture levels in excess of 50% have an insignificant impact on the pump performance. The effect of the flow of the heat-transfer fluid in the pipes of the heat exchangers on the heat-transfer process in the soil is described by Tarnawski [9]. He has conducted computer simulations of horizontal linear heat exchangers installed at depths of 0.5 m and 1.0 m in single and two overlapping layers. He states that with the laminar flow of the heat-transfer fluid the heat-transfer process depends on the flow rate and the pipe diameter, as well as on the density, thermal conductivity and specific heat capacity of the heat-transfer fluid. He also states that heat transfer between the fluid and the pipe wall is more intense at lower temperatures and concentrations of the water and anti-freeze mixture, with shorter heat exchanger pipes, wider pipe diameters and faster fluid flow rates. He also confirms that horizontal ground heat exchangers have little impact on thermal degradation of the ground mass.
Researchers at the Department of Earth Resources Engineering at Kyushu University in Japan [10] checked various configurations of slinky-type horizontal heat exchangers. They checked heat exchangers with a loop diameter of 0.8 m, pipe diameters of 0.034 m and 0.024 m and with a spacing of 0.4 m, 0.6 m and 0.8 m; in order to assess the heat-transferring process between the soil and the heat exchanger pipes they used the ratio Δt/qτ, where Δt = /tk – t0/ (K), tk (°C) is the average temperature of the heat-transfer fluid, t0 (°C) is the temperature of the reference soil measured at a distance of at least 5 m from the heat exchanger and at the same depth as the heat exchanger, and qτ (W·m−1) is the specific thermal output of the ground source heat exchanger. They also used the finite element method and FEFLOW simulator to simulate the thermal output of a horizontal slinky-type ground source heat exchanger. During the simulation, attention was focused on the energy balance on the surface of the soil, the temperatures of the heat-transfer medium and the surrounding soil. The accuracy of the simulation model was confirmed by calculations and the results of the test.
Rezaei et al. [11] investigated the effect of surface cover on soil containing a horizontal heat exchanger on temperature distribution and heat flows discharged to the soil. When the surface of the soil is covered by an insulating layer of recycled tyres, the heat flux discharged from the soil during winter increased by 17%.
Researchers at the Department of Civil, Geological and Mining Engineering, École Polytechnique de Montréal [12] presented a new analytical model of a ground source heat exchanger based on the line source of heat method applicable for all types of horizontal ground source heat exchangers, including spiral and slinky heat exchangers. The model also takes account of possible changes in the water phase in the soil around the pipe of the horizontal heat exchanger. This model monitors the impact that the length of the pipe, the depth it is placed at and the spacing of the heat exchanger pipes have on the discharged thermal output and the risk of the soil thawing around the heat exchanger pipes.
Slinky-type horizontal heat exchangers require much smaller area of land. So it is assumed a greater interest in their implementation. Another motive for pursuing this type of horizontal exchangers, compared to linear horizontal exchangers is the relative lack of published knowledge.
The aim of our work was to monitor temperatures and analyse temperature changes in soil enclosing a slinky horizontal heat exchanger. Also, to assess the potential regeneration of the energy potential of the soil when the heat exchangers are not operational, and to determine the specific heat flows and specific thermal energy discharged from the soil.
2. Material and Methods
2.1. Theoretical Analysis
The basic equation for heat transfer by a cylindrical linear source in a solid mass was published by Carslaw and Jaeger [13]. Their aim was to determine the temperature t at any point at a distance of r from the linear source at the time τ after the source was started up. The equation at the coordinates x, y, z has the following basic form:
In Equation (1):
C: volumetric specific heat capacity of mass (J·m−3·K−1);
λ: thermal conductivity coefficient of mass (W·m−1·K−1).
For the following conditions the authors give Equation (1) in the form:
Equation (2) applies for the following conditions:
- *
at time τ = 0 t = t0 for all r values (at the beginning of the measurement the temperature of the soil is constant at all distances from the linear source of heat);
- *
for r → ∞ t = t0 for all τ values (the distance from a linear source of heat approaching infinity, the temperature of the soil is constant independently of the operating line source).
In Equation (2):
t0: constant temperature of thermally unaffected mass (°C);
q: constant discharged (supplied) specific heat flux (W·m−1);
E(u): exponential integral function u.
If the specific thermal resistance of the heat exchanger pipes Rp (K·m·W−1) is taken into account, Equation (2) becomes:
After the heat exchanger has been started up, the pipes start to discharge heat from the soil in a radial direction into the heat-transfer medium in a pipe. After a certain amount of time, the heat exchanger begins to react to the temperature of the soil surface. The temperature of the soil surface thus becomes the dominant boundary condition. It may take several months for this to take effect with horizontal ground source heat exchangers.
To determine heat conduction through a semi-defined mass with a number of pipes the resources methods and the principles of superposition of the temperature field as described by Šorin [14] and later applied in the fundamental publication by Banks [15] should be used. This method is based on the above assumption that after a certain amount of time a pipe at a depth of z discharges heat flux qτ corresponding to heat flux qτ on the surface of the soil. When the superposition method is used, the heat flux qτ on the surface of the soil is expressed with an imaginary pipe at a distance of z above the surface of the soil. According to Banks [15], Equation (3) then becomes:
In Equations (4) to (6):
rp: is the outer radius of the heat exchanger pipe (m);
τ: time after starting the heat exchanger (s);
tk: average temperature of the heat-transfer fluid (°C).
When using a logarithmic approximation, according to Banks, Equation (6) then becomes:
The thermal resistance of the heat exchanger pipe Rp may be expressed using the equation:
In Equation (8):
Rt: thermal resistance of conduction through pipe wall (K·m·W−1);
Rα: thermal resistance of convection between pipe wall and heat-transfer fluid (K·m·W−1).
The calculation of the thermal resistances Rt and Rα is shown in the article by Šedová et al. [16].
2.2. Measurement Methods
The ground source heat exchangers tested are sources of energy for three heat pumps. Prior to 10 July 2012 these were 2× IVT Greenline HT PLUS E17 (Industriell Värme Teknik, Tnanas, Sweden) with a heat output of 16.2 kW and 1× IVT Premiumline X15 with a heat output of 11.7 kW. The IVT Premiumline X15 heat pump was replaced on 10 July 2012 with an IVT Premiumline EQ13 with a heat output of 13.3 kW. Heat output is determined at temperatures of 0/35 °C. These and another three heat pumps are used to heat the administrative building and operational halls of VESKOM s.r.o., based in Dolní Měcholupy.
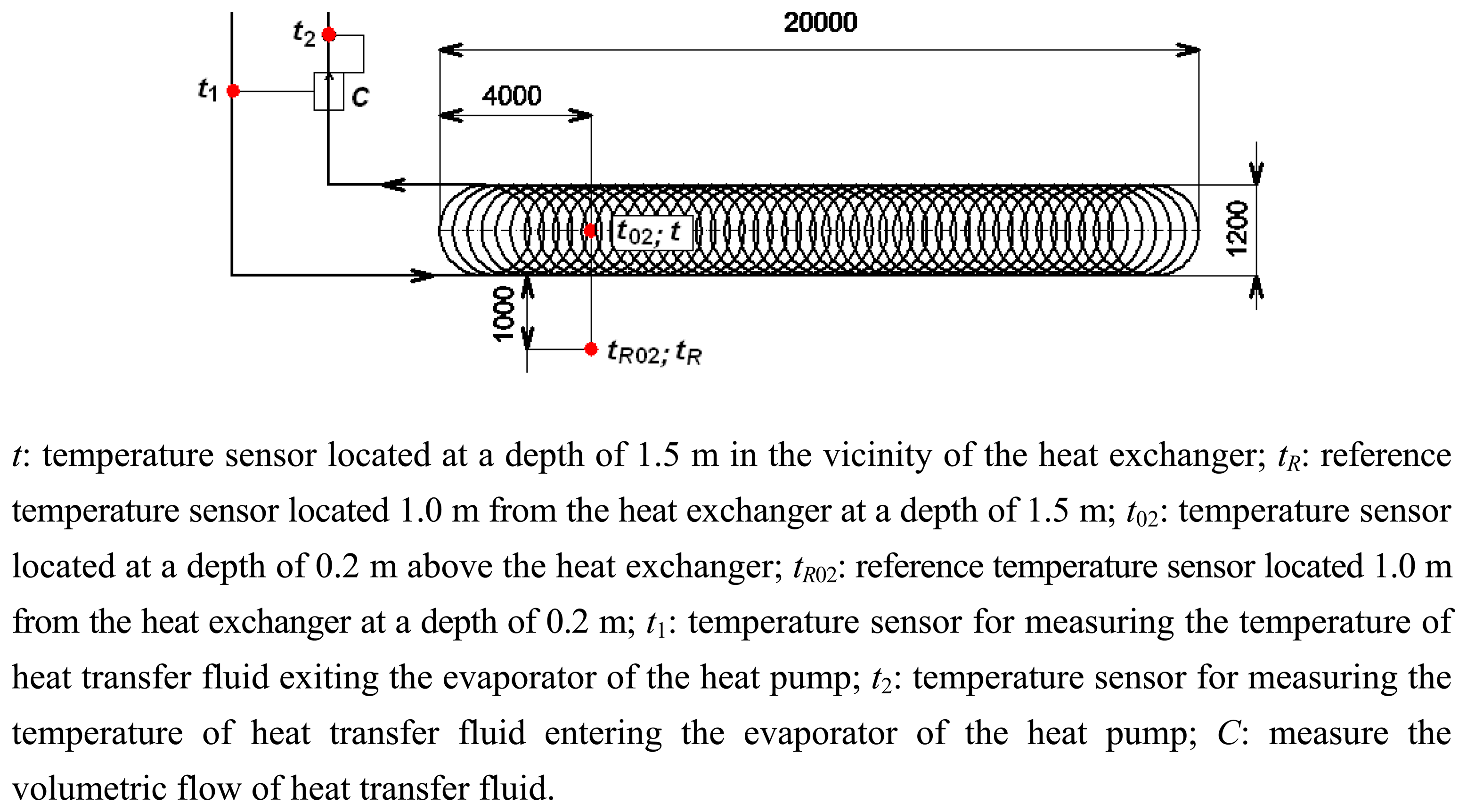
A plan of a horizontal slinky-type ground source heat exchanger is shown in Figure 1. The heat exchanger was made from PE 100RC 32 × 2.9 mm polyethylene tubing (Luna Plast a.s., Hořín, Czech Republic) resistant to point loads and cracking. It is not laid in a sand bed. The heat exchanger pipes, 200 m in total length, are installed at a depth of 1.5 m in 53 loops twisted into a circle with a loop spacing of 0.38 m. The soil to a depth of approximately 2 m consists of dark-brown sandy loam soil, coarse gravel, rubble and brick fragments. The sensors for measuring the temperature of the soil were installed at a distance of 4 m from the start of the heat exchanger. The heat transfer fluid flowing through the heat exchanger is a mixture of 33% (volumetric) ethanol and 67% water.
The temperatures of the soil were measured using PT 1000A RTD temperature sensors (manufactured by Greisinger Electronic GmbH, Regenstauf, Germany) and recorded in 15-min intervals. The ambient temperatures te were measured at a height of 2 m above the ground and at a distance of 20 m from the horizontal ground source heat exchangers. MTW 3 electronic heat consumption meters (manufactured by Itron Inc., Liberty Lake, WA, USA) were used to measure the total heat flow discharged by the horizontal heat exchangers. Electronic meter heat consumption works on the principle of integration of the heat transfer fluid flow and heat transfer fluid temperature difference between the inlet and the outlet of the evaporator of the heat pump.
The thermal characteristics of the soil, thermal conductivity coefficient λ (W·m−1·K−1), volumetric specific heat capacity C (J·m−3·K−1) and temperature conductivity coefficient a (m2·s−1) were determined using an Isomet 2104 (manufactured by Applied Precision, Bratislava, Slovakia) at temperature t (°C) and volumetric moisture w (%). Isomet 2104 is a portable instrument designed for the direct measurement of the thermal conductivity and specific volumetric heat capacity. For the measurement uses replaceable needle or a flat probe with integrated memory and the known calibration constants. Soil moisture in the ground heat exchanger was measured PR2—Profile Probe (manufacturer Delta-T Devices, Cambridge, UK).
The primary aim was to monitor the temperature of the soil and the environment during the heating period and the period of stagnation of ground heat exchanger. Furthermore, to determine in the following heating season (with valid recorded data) temperature of the heat transfer medium and the specific heat dissipated from soil.
3. Results and Discussion
The results of the measurement of the thermal characteristics of the soil are given in Table 1. The measurements were taken directly in the soil, when the heat exchanger was idle during the summer, on 6 June 2012. The thermal characteristics are within a range corresponding to Cambisol, the most widespread type of soil [17] in the Czech Republic.
This article presents results of the tests of a horizontal slinky-type ground source heat exchanger performed between 7 September 2011 and 22 April 2013. The graph in Figure 2 shows the average daily temperature trends of the soil t and the temperature of the surrounding air te when the heat exchanger is operational in the period τ 7 September 2011–16 September 2012. The temperatures t02 (°C) and reference temperatures tR (°C) of the soil are not shown for reasons of clarity. These dependences may be expressed using an equation based on the equation for the free undamped oscillation of a mass point [18]:
t : temperature (°C);
t̄ : average temperature (°C);
ΔtA : oscillation amplitude around temperature t̄ (°C);
τ : number of days from start of measurement (days);
φ : initial phase of oscillation (rad);
Ω : angular velocity = 2·π·365−1 (rad·day−1).
This is the non-linear regression of y to x, and is therefore used to determine the degree of dependence between two random variables of the determination index (-), [19].
The trend in the temperature of the soil mass and that of the surrounding air when the heat exchanger is operational may be expressed using following equations:
The period in question (376 days) may be divided up into the heating part of period A (7 September 2011–26 April 2012, 233 days) and that part of the period in which the system was idle B (27 April 2012–16 September 2012, 143 days). In part of period B the energy potential of the soil regenerates for the next heating season. The temperatures measured and Equations (10) and (12) show that the temperature difference Δt = tR − t was insignificant in both parts of the period, Δtp,A = −0.1 ± 0.7 K, Δtp,B = 0.1 ± 0.3 K. The negligible temperature difference Δt is, however, affected by the position of the reference temperatures sensor in the soil a mere 1 m from the heat exchanger. One important finding is that during part of period A the temperature of the soil around the heat exchanger was above zero. Lower temperatures of the soil result in lower-temperature evaporation in the evaporator, which may have an adverse effect on the heat pump performance factor.
The minimal temperature of the soil mass in vicinity of the heat exchanger tmin = 0.83 °C was determined as the average of four temperatures measured between 10:00 to 11:00 am 13 February 2012 (τ = 160 days). The minimal average daily temperatures of the soil in the vicinity of the heat exchanger tmin. day = 1.27 °C also occurred on 13 February 2012.
The temperature of the soil t02 at a depth of 0.2 m above the heat exchanger is influenced particularly by the temperature and speed of the surrounding air, the intensity of incident solar radiation, and falls of rain and snow. The heat flux discharged by the heat exchanger also has a massive effect on the temperature, however. This is confirmed by Equations (10), (11) and (13). t̄ < t̄02 < t̄e is applicable for the average temperature of the soil at a depth of 0.2 m and ΔtA < Δ tA02 < ΔtAe for the oscillation amplitude. The initial phase of temperature oscillation at a depth of 0.2 m (φ02 = 2.24 rad) is influenced by the surrounding environment (φe = 2.493 rad). In the vicinity of the heat exchanger and at the reference point the difference in the initial phases (Δφ = 0.039 rad) may be considered insignificant.
The minimal average daily temperatures calculated from Equations (10) to (13) are shown in Table 2.
From the summary in Table 2 it is apparent that the minimal temperatures occur in a logical sequence. The graph in Figure 3 displays the results of measuring the temperature of the soil in the vicinity of the heat exchanger t, the ambient temperature te and specific heat qd discharged from the soil in the heating season 17 September 2012–22 April 2013. The temperatures of the soil in the vicinity of the heat exchanger and the ambient temperatures are given by the equations:
During the heating period 17 September 2012–22 April 2013, Δt = tR – t = 1.2 ± 0.6 K. The temperature difference is thus slightly higher than in the previous heating season 7 September 2011–26 April 2012, when it was Δtp,A = tR – t = −0.1 ± 0.7. It is assumed that the cause of higher temperature difference is lower average temperature te (about 1.53 K) in the heating period 17 September 2012–22 April 2013 than in the period 7 September 2011–26 April 2012. There is thus a higher heat transfer of the earth mass, resulting in a lower average temperature of the soil mass t (about 2.79 K).
As Equation (14) only portrays the temperatures of the soil in the vicinity of the heat exchanger during the heating season, the average daily temperature t̄ is lower than in Equation (10), which also includes the idle period. The oscillation amplitudes ΔtA around the temperature t̄ are almost the same in both equations. The same is true of Equations (13) and (15) describing the ambient temperature te. However, the oscillation amplitudes show greater differences.
In Equation (15) the determination index is <0.8, which is below the normal level of dependence. The lower determination index is caused by the considerable dispersion of the ambient temperature.
As in the 2011–2012 heating season, during this period the temperature of the soil in the vicinity of the heat exchanger was above zero. The minimum temperature of the soil mass in vicinity of the heat exchanger tmin. = 0.44 °C was determined as the average of four temperatures measured from 8:00 to 9:00 am 2 April 2013 (τ = 197 days). The minimal average daily temperature of the soil tmin.day = 0.83 °C occurred on 28 March 2013. During the 2012–2013 heating season the minimal temperature of the soil in the vicinity of the heat exchanger occurred 37 days later than in the 2011–2012 heating season. The graphs in Figure 2 and Figure 3 show that the ambient temperature dropped in a single wave in the 2011–2012 heating season, after the heat exchanger had been operational for approximately 153 days.
The temperature of the soil in the vicinity of the heat exchanger subsequently also fell to the minimum. In the 2012–2013 heating season the ambient temperature dropped to higher than in the previous heating season in three waves. It was not until after the third wave that the temperature of the soil fell to the minimum with a relatively large discharge of heat.
The energy potential regeneration capacity when the heat exchanger is idle may be gauged on the basis of the starting and final temperatures of the soil in the vicinity of the heat exchanger over several heating seasons. In particular, a reduction in the temperature of the soil at the start of the heating season would be a clear sign of the gradual reduction of the energy potential of the mass and also therefore of the amount of time the mass could be used to power a heat pump. The energy potential of the soil could be increased during the summer by modulating the operation of the heat pump, i.e., by the site cooling and the generated heat accumulating in the soil. The measurements are given in Table 3.
The differences in the temperature of the soil at the start and end of the heating seasons are within the range of measurement accuracy. The results of more than three years of validation indicate that the slinky-type horizontal ground heat exchanger can be considered as stable energy source for heat pumps.
The heat qd (Wh·m−1·day−1) discharged by the ground source heat exchanger is displayed in the columns in Figure 3. Average value of heat discharged during the period in question was 26.57 Wh·m−1·day−1; the maximum was 109.93 Wh·m−1·day−1. During the entire heating season of 217 days, 1 m of heat exchanger pipe discharged 5831.54 Wh·m−1 of heat to the soil. A water storage tank was connected to the condenser of the heat pump, meaning that it is impossible to assess the direct link between the heat discharged and the temperature of the surrounding air.
During the heating period 17 September 2012–22 April 2013 the average temperature of the heat transfer fluid at the outlet of the ground heat exchanger was 4.17 °C, minimal temperature was 0.39 °C. The average temperature of the heat-transfer fluid at the heat pump outlet was 2.52 °C; the minimal temperature was −2.02 °C.
An example of average thermal outputs qτ (W·m−1) discharged to the soil by the heat exchanger, the temperature t (°C) of the soil in the vicinity of the heat exchanger and the ambient temperature te (°C) is shown in the graph in Figure 4. During the 24 h of that day 1 m of heat exchanger pipe discharged 109.87 Wh·m−1 to the soil. The average specific thermal output of the heat exchanger was qτ = 4.58 W·m−1; the maximum was 8.21 W·m−1. The circulation pump pumping the ground source heat exchanger's heat-transfer fluid worked at a higher rate (1.72·10−4 m3·s−1) at the intervals 3–7 a.m., 5–10 p.m. and at 12 a.m. (a total of 12 h). The pump was switched off or worked at a lower rate at the intervals 1–2 a.m., 8 a.m.–5 p.m. and at 11 p.m. (also a total of 12 h). Although the operation of the circulation pumps was influenced by the accumulation of heat from the heat pump condenser, the graph in Figure 4 clearly shows a link between the specific heat flux qτ (W·m−1) discharged by the ground source heat exchanger and the ambient temperature te (°C). The temperature of the soil in the vicinity of the heat exchanger reacts to changes in specific thermal output only within the range t = 4.48 ± 0.4 °C.
Validity of the Equation (7) designed for the linear type of heat exchanger, was in case of example depicted in Figure 4 verified for the Slinky-type heat exchanger. Towards determination of flow type of the heat transfer fluid, form of the criteria equation and calculation of the heat transfer coefficient α between the tube wall of heat exchanger and heat transfer fluid was used Reynolds and Nusselt criteria. The Reynolds criterion Re (-) of the heat-transfer fluid was in the range (586.6–1544.4). Computation of the Nusselt criterion Nu (-) is based on the equation given by Prof. Schramek [20], which is applicable for the laminar fluid flow in the pipe:
In Equation (17):
Nu: Nusselt criterion (-);
α: convective heat-transfer coefficient between the wall of the heat exchanger pipe and the heat-transfer fluid (W·m−2·K−1);
dh: hydraulic diameter of pipe (m);
λk: thermal conductivity coefficient of heat-transfer fluid (W·m−1·K−1);
Pr: Prandtl criterion (-);
L: length of heat exchanger pipe (m).
Equation (17) shows Nu within the range (4.507–4.508). Spitler [21], using the GHELPRO software for laminar calculation of the thermal resistance between heat transfer fluid and the inner wall of the exchanger tube in laminar flow conditions (Re ≤ 2,100), achieves Nu = 4.364. Determining the thermal conductivity of the soil for the Equation (7) we used the established relationship between change of the thermal conductivity λ (W·m−1·K−1) and volumetric moisture of soil mass w (%), the soil type Cambisol in the area. For the estimated volumetric moisture soil mass, in vicinity of the heat exchanger, w = 35%–45% (control measurement), the thermal conductivity of the soil, for a given soil type Cambisol, is in the range of λ = 1.45–1.61 W·m−1·K−1. In the calculation of the Equation (7) is considered λ = 1.54 W·m−1·K−1.
The temperature difference (t0 − tk) (K) computed from Equation (7) and the measured temperatures are within the range Δ(t0 − tk) = 0.85 ± 0.90 K. If the secondary circulation of the heat-transfer fluid caused by the centrifugal force generated by the curvature of the pipe is taken to the account, the heat-transfer coefficient α calculated from Equation (17) is multiplied by the pipe curvature coefficient [22]:
In Equation (18):
d: diameter of heat exchanger pipe (m);
r: loop radius of heat exchanger (m).
The curvature coefficient εR calculated from Equation (18) is 1.0944. Curvature thus increases the heat-transfer coefficient α by approximately 10%. The temperature difference is then Δ(t0 − tk) = 0.92 ± 0.90 K. Both these differences Δ(t0 − tk) (K) show that Equation (7) may be applied with sufficient accuracy to slinky-type heat exchangers.
The thermal resistance of convection Rα (m·K·W−1) between the wall of the pipe and the heat-transfer fluid is, together with the thermal conductivity coefficient of the soil λ (W·m−1·K−1), a crucial factor affecting heat flux qτ (W·m−1) discharged to the soil. If Rα (m·K·W−1) increases excessively, qτ (W·m−1) is reduced and the temperature of the heat-transfer fluid tk (°C), may drop to unfavourable minus temperatures. In the horizontal heat exchanger (measurement 8 December 2012) in question the relatively high Rα value (0.165–0.166) m·K·W−1 is due to the low heat-transfer coefficient α (73.28–73.81) W·m−2·K−1 caused by the laminar flow of the heat-transfer fluid. A better turbulent flow will be achieved by increasing the flow rate, although this consumes more energy to drive the circulation pump, which reduces the SPF (seasonal performance factor). It seems more effective to reduce the concentration of anti-freeze in the heat-transfer fluid. Reducing this concentration would reduce kinematic viscosity, which, especially at low temperatures, would have a positive impact on Re (-) and thus also on Nu (-) and Rα (-). According to The Engineering ToolBox [23], the freezing point of the heat-transfer fluid (33% C2H6O + 67% H2O) is −17.4 °C. The results of our measurements showed that the minimal temperature of the heat-transfer fluid at the outlet of the heat pump was −2.02 °C. Therefore, for the heat exchanger in question a lower concentration would be more suitable, e.g., 20% ethanol, when the freezing point of the mixture is −9.0°C. At the same volumetric flow of the heat-transfer fluid (8 December 2012 measurement) the thermal resistance Rα (-) would be (0.145–0.146) m·K·W−1. Convective heat transfer coefficient α may increase for 13.62%. Decrease of concentration of ethyl alcohol in heat transferring liquid from 33% to 20% results in rise of specific heat capacity for 5.41% as well as rise of density for 1.22%. This will positively influence thermal output of ground heat exchanger. Xu and Spitler [24] state that with a 20% concentration of propylene glycol in the heat-transfer fluid and with a fluid temperature of −5 °C, the Re (-) figure would be a mere 39% of the figure achieved at the same flow rate and at a temperature of 20 °C.
4. Conclusions
The temperature trends in soil containing a slinky heat exchanger, the temperature of the reference mass and the ambient temperature as shown in the graphs in Figures 2 and 3 may be expressed using Equations (10)–(16). During the entire heating season (217 days) the amount of heat discharged to the soil through 1 m of heat exchanger pipe totalled a relatively significant 5831.54 Wh·m−1. Therefore, if the total length of the heat exchanger pipes is 200 m, 1166.30 kWh was discharged to the soil in the heating season. The maximum specific thermal output of the heat exchanger was 12.33 W·m−1. The meaning of work for design practice and implementation of Slinky-type horizontal heat exchangers can be summarized in the following points:
The results of the test showed that in both the heating seasons in question the temperatures of the soil in the vicinity of the heat exchanger were above zero. The temperatures of the heat-transfer fluid at the heat pump outlet also dropped to below zero in the second half of the heating season (minimum −2.02 °C);
The results of more than three years of validation indicate that the slinky-type horizontal ground heat exchanger can be considered as stable energy source for heat pumps. The temperature difference at the beginning and end of the heating seasons (Table 3) did not exceed 2 K in the four years that measurements were taken;
Equation (7), designed for a linear heat exchanger, may also be used for slinky-type heat exchangers with a sufficient degree of accuracy.
The thermal performance of horizontal ground heat exchanger has a dominant influence to thermal conductivity of the soil λ and thermal resistance Rα between the pipe wall and the heat transfer fluid;
The maximum specific thermal output of the heat exchanger was 12.33 W·m−1;
The temperatures of the heat-transfer fluid at the heat pump outlet proved that the concentration of ethanol (33%) in the heat-transfer fluid is unnecessarily high. High concentration of ethanol is due to the higher value of kinematic viscosity and a lower value of thermal conductivity of heat transfer fluid the predominant cause of laminar flow of heat transfer fluid, and high values of thermal resistance of convection Rα (m·K·W−1) between the tube wall and the heat transfer fluid;
Further research phase of horizontal ground slinky-type heat exchanger will focus on:
- *
Creating a mathematical model of the temperature field in the ground mass exchanger;
- *
Verification of lower concentrations of ethanol in the heat transfer fluid to the heat exchanger performance;
- *
Verification of use of ground heat exchanger for cooling the building in summer on the energy potential of the soil mass and heat transfer rate in the heating season.
Acknowledgments
Authors acknowledge the financial support of the Technology Agency of the Czech Republic (Project No. TA02020991 “Optimization of the energetic parameters of the horizontal ground heat exchangers with respect to soil and hydrological conditions at the specific location”).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Petit, P.J.; Meyer, J.P. Techno-economic analysis between the performances of heat source air conditioners in South Africa. Energy Convers. Manag 1998, 39, 661–669. [Google Scholar]
- Lund, J.W.; Freeston, D.H.; Boyd, T.L. Direct utilization of geothermal energy 2010 worldwide review. Geothermics 2011, 40, 159–180. [Google Scholar]
- Brandl, H. Energy foundations and other therma-active ground structures. Géotechnique 2006, 2, 81–122. [Google Scholar]
- Popiel, C.; Wojtkowiak, J.; Biernacka, B. Measurements of temperature distribution in ground. Exp. Therm. Fluid Sci 2001, 25, 301–309. [Google Scholar]
- De Swardt, C.A.; Meyer, J.P. A performance comparison between an air-coupled and a ground-coupled reversible heat pump. Int. J. Energy Res 2001, 25, 810–899. [Google Scholar]
- Congedo, P.M.; Colangelo, G.; Starace, G. CFD simulations of horizontal ground heat exchangers: A comparison among different configurations. Appl. Therm. Eng. 2012, 33–34, 24–32. [Google Scholar]
- Song, Y.; Yao, Y.; Na, W. Impacts of Soil Pipe Thermal Conductivity on Performance of Horizontal Pipe in a Ground-Source Heat Pump. Energy Systems Laboratory. Available online: http://hdl.handle.net/1969.1/5465 (accessed on 12 November 2006).
- Leong, W.H.; Tarnawski, V.R.; Aittomaki, A. Effect of soil type and moisture content on ground heat pump performance. Int. J. Refrig 1998, 21, 595–606. [Google Scholar]
- Tarnawski, V.R.; Leong, W.H.; Momose, T.; Hamada, Y. Analysis of ground source heat pumps with horizontal ground heat exchangers for northern Japan. Renew. Energy 2009, 34, 127–134. [Google Scholar]
- Fujii, H.; Nishia, K.; Komaniwaa, Y.; Choub, N. Numerical modeling of slinky-coil horizontal ground heat exchangers. Geothermics 2012, 41, 55–62. [Google Scholar]
- Rezaei, B.A.; Kolahdouz, E.M.; Dargush, G.F.; Weber, A.S. Ground source heat pump pipe performance with tire derived aggregate. Int. J. Heat Mass Transfer 2012, 55, 2844–2853. [Google Scholar]
- Fontainea, P.O.; Marcottea, D.; Pasquiera, P.; Thibodeaub, D. Modeling of horizontal geoexchange systems for building heating and permafrost stabilization. Geothermics 2011, 40, 211–220. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: London, UK, 1948; pp. 239–272. [Google Scholar]
- Šorin, S.N. Transmission of Heat, 1st ed.; State Publishing of Technical Literature: Prague, Czech Republic, 1968; pp. 142–148, in Czech. [Google Scholar]
- Banks, D. An Introduction to Thermogeology: Ground Source Heating and Cooling, 2nd ed.; John Wiley & Sons: Chichester, West Sussex, UK, 2012; pp. 332–344. [Google Scholar]
- Šeïová, M.; Adamovský, R.; Neuberger, P. Analysis of ground massif temperatures with horizontal heat exchanger. Res. Agric. Eng 2013, 59, 91–97. [Google Scholar]
- Němeček, J.; Vokoun, J.; Smejkal, J.; Macků, J.; Kozák, J.; Němeček, K.; Borůvka, L. Taxonomic Classification System of Soils in the Czech Republic. Available online: http://klasifikace.pedologie.czu.cz/index.php?ac (accesed on 10 October 2013). in Czech.
- Beer, F.P.; Johnston, E.R., Jr. Vector Mechanics for Engineers: Statics and Dynamics, 5th ed.; McGraw-Hill: New York, NY, USA, 1988; pp. 943–946. [Google Scholar]
- Bowerman, B.L.; O'Connell, R.T. Applied Statistics: Improving Business Processes, 1st ed.; Richard D. Irwin Inc.: Boston, MA, USA, 1997; pp. 712–723. [Google Scholar]
- Recknadel, H.; Sprenger, E.; Schramek, E.R. Handbook for Heating and Air Conditioning, 73rd ed.; Oldenbourg Industrieverlag: München, Germany, 2007; pp. 150–156, in Deutsch. [Google Scholar]
- Spitler, J.D. GLHEPRO 4.0 for Windows User'S Guide. International Ground Source Heat Pump Association, Oklahoma State University, Stillwater. Available online: http://www.hvac.okstate.edu (accesed on17 July 2007).
- Kalčík, J.; Sýkora, K. Technical Thermodynamics, 1st ed.; Academia: Prague, Czech Republic, 1973; pp. 448–453, in Czech. [Google Scholar]
- The Engineering ToolBox: Ethanol Freeze Protected Water Solutions. online: http://www.engineeringtoolbox.com/ethanol-water-d_989.html (accesed on 2 July 2013).
- Xu, X.; Spitler, J. Modeling of Vertical Ground Loop Heat Exchangers with Variable Convective Resistance and Thermal Mass of the Fluid. Proceedings of 10th International Conference on Thermal Energy Storage Ecostock 2006, Stockton, NJ, USA, 31 May– 2 June 2006.



| Depth(m) | t(°C) | w(%) | λ(W·m−1·K−1) | 106·C(J·m−3·K−1) | 10−6·a(m2·s−1) |
|---|---|---|---|---|---|
| 0.06 | 13.36 | 36.65 | 1.21 | 2.08 | 0.583 |
| 0.22 | 12.76 | 26.25 | 1.29 | 2.15 | 0.602 |
| 0.30 | 12.42 | 30.70 | 1.35 | 2.11 | 0.640 |
| 0.60 | 12.66 | 31.55 | 1.24 | 1.82 | 0.678 |
| 0.90 | 12.73 | 29.30 | 1.48 | 2.15 | 0.688 |
| 1.20 | 12.65 | 31.60 | 1.39 | 2.08 | 0.672 |
| 1.50 | 13.64 | 39.00 | 1.58 | 2.24 | 0.704 |
| 1.60 | 13.83 | - | 1.57 | 2.16 | 0.727 |
t: temperature of the soil; w: volumetric moisture; λ: thermal conductivity coefficient; C: volumetric specific heat capacity; a: temperature conductivity coefficient.
| Temperature | Minimal temperature(°C) | Time of heat exchanger operationτ (days) |
|---|---|---|
| te | 1.09 | 129 |
| t02 | 1.14 | 144 |
| t | 3.34 | 164 |
| tR | 3.36 | 164 |
te: average daily temperature of the surrounding air; t02: temperature of the soil at a depth of 0.2 m; t: average daily temperature of the soil at a depth of 1.5 m; tR: average daily reference temperature of the soil at a depth of 1.5 m.
| Phase of heating season | Heating season | Date | t (°C) | Δt (K) |
|---|---|---|---|---|
| Start of heating season | 2010–2011 | 30 August 2010 | 18.40 | −0.04 |
| 2011–2012 | 7 September 2011 | 18.44 | ||
| 2012–2013 | 17 September 2012 | 16.90 | ||
| 1.54 | ||||
| End of heating season | 2010–2011 | 22 March 2011 | 4.45 | −1.58 |
| 2011–2012 | 22 March 2012 | 6.03 | ||
| 2012–2013 | 22 April 2013 | 5.30 | ||
| 0.73 | ||||
t: temperature of the soil; Δt: temperature difference.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Neuberger, P.; Adamovský, R.; Šeďová, M. Temperatures and Heat Flows in a Soil Enclosing a Slinky Horizontal Heat Exchanger. Energies 2014, 7, 972-987. https://doi.org/10.3390/en7020972
Neuberger P, Adamovský R, Šeďová M. Temperatures and Heat Flows in a Soil Enclosing a Slinky Horizontal Heat Exchanger. Energies. 2014; 7(2):972-987. https://doi.org/10.3390/en7020972
Chicago/Turabian StyleNeuberger, Pavel, Radomír Adamovský, and Michaela Šeďová. 2014. "Temperatures and Heat Flows in a Soil Enclosing a Slinky Horizontal Heat Exchanger" Energies 7, no. 2: 972-987. https://doi.org/10.3390/en7020972




