An FMEA-Based Risk Assessment Approach for Wind Turbine Systems: A Comparative Study of Onshore and Offshore
Abstract
: Failure mode and effects analysis (FMEA) has been extensively used by wind turbine assembly manufacturers for analyzing, evaluating and prioritizing potential/known failure modes. However, several limitations are associated with its practical implementation in wind farms. First, the Risk-Priority-Number (RPN) of a wind turbine system is not informative enough for wind farm managers from the perspective of criticality; second, there are variety of wind turbines with different structures and hence, it is not correct to compare the RPN values of different wind turbines with each other for prioritization purposes; and lastly, some important economical aspects such as power production losses, and the costs of logistics and transportation are not taken into account in the RPN value. In order to overcome these drawbacks, we develop a mathematical tool for risk and failure mode analysis of wind turbine systems (both onshore and offshore) by integrating the aspects of traditional FMEA and some economic considerations. Then, a quantitative comparative study is carried out using the traditional and the proposed FMEA methodologies on two same type of onshore and offshore wind turbine systems. The results show that the both systems face many of the same risks, however there are some main differences worth considering.1. Introduction
Wind energy has become an attractive source of renewable energy, and its installed capacity worldwide has grown significantly in recent years. For instance, the cumulative installations of wind power in the EU has increased from 23.1 GW in the end of 2002 to 106.0 GW in the year 2012, which represents an annual growth of 16.5% [1].
Basically, there are two main alternatives for wind energy, onshore and offshore. Offshore wind farms are constructed on the continental shelf area, usually about 10–40 km away from the coast. Comparing with onshore wind power, offshore winds tend to flow at a higher speed, thus allowing turbines to produce more electricity. However, a wind power system located at sea comes with higher failure rates, lower reliability and availability, and higher operation and maintenance (O&M) costs [2], so with the development of wind farms in remote areas, the need for an efficient tool to identify and then limit or avoid risk of failures is of increasing importance.
Failure mode and effects analysis (FMEA) is a widely used engineering technique for designing, identifying and eliminating potential/known system failures. FMEA was first proposed by NASA in 1963 for their obvious reliability requirements. Then, it was adopted and implemented by Ford Motor [3] in 1977. Since then, it has become a powerful tool for risk and reliability analysis of systems in a wide range of industries including automotive [4], foundry [5], nuclear [6], construction [7], etc.
FMEA is a structured, bottom-up approach that starts with potential/known failure modes at one level and investigates the effect on the next sub-system level [8]. Hence, a complete FMEA analysis of a system often spans all the levels in the hierarchy from bottom to top (see Figure 1).
A failure mode is defined as the way in which a component, sub-system or system could potentially fail to perform its desired function. A failure cause is defined as a weakness that may result in a failure. For each identified failure mode, their ultimate effects need to be determined, usually by a cross-functional team which is formed by specialists from various functions. A failure effect is defined as the result of a failure mode on the function of the system as perceived by the user.
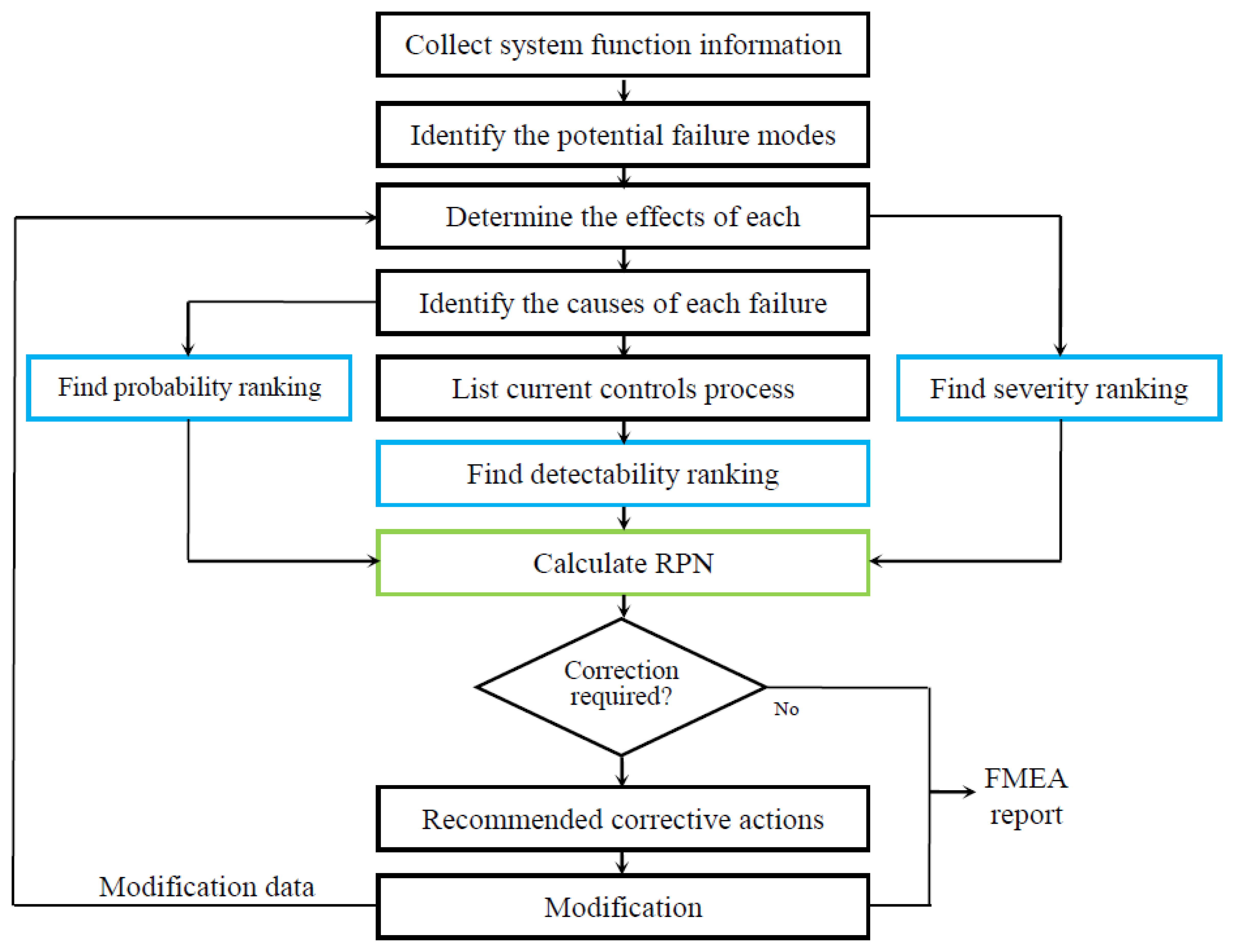
As outlined by Pillay and Wang [9], the process for carrying out an FMEA can be divided into several steps as shown in Figure 2. These steps are briefly explained here:
Collect the system function information: first, develop a good understanding of what the system is supposed to do when it is operating properly; then, divide the system into sub-divisions and use schematics and flow charts to identify relations among sub-assemblies; lastly, prepare a complete part list for each sub-assembly.
Identify the failure modes of each sub-assembly.
Consider how the failure modes might affect the performance of sub-assemblies, sub-divisions, and the entire system.
Identify the operational and environmental stresses that cause failures.
Estimate the probability of failure occurrence, and find the occurrence ranking (O) using the 10-point scale described in appendix, Table A1.
Categorize the hazard level of each failure, and find the severity ranking (S) using the 10-point scale described in appendix, Table A2.
Identify the current control schemes to detect or prevent a given cause of failure, and find the detection ranking (D) using the 10-point scale described in appendix, Table A3.
Calculate the risk-priority-number (RPN) which is defined as the product of the occurrence (O), severity (S) and detection (D) of a failure, i.e., RPN = O × S × D.
Rank the RPN values that are between 1 and 1000 to find out the failures with higher risks for correction.
Develop recommendations (preventive or corrective actions) to enhance the system performance.
Prepare FMEA report by summarizing the analysis in a tabular form as shown in Table 1.
The traditional FMEA methodology has been extensively used by wind turbine assembly manufacturers for analyzing, evaluating and prioritizing the potential/known failure modes [11]. However, a brief review of the literature shows that only a few researchers have worked on improving the traditional FMEA methodology to make it more practical for wind turbine systems (see [12–16]). Recently, Tavner and his colleagues presented a design-stage FMEA methodology for prioritization of failures in a 2-MW wind turbine system (named as R80) within the Reliawind project [17,18]. The authors' methodology used four-point scales for occurrence rating (see Table 2), severity rating (see Table 3), and detection of a failure (see Table 4) to represent the risk priorities of the sixty-four occurrence–severity–detection combinations.
Even though it is shown that the proposed FMEA methodology was more efficient than the traditional one, several limitations are still associated with its practical implementation in wind farms:
- (i)
the RPN value of a wind turbine system is not informative enough for wind farm managers from the perpective of criticality;
- (ii)
there are variety of wind turbines with different structures, and hence, it is not true to compare the RPN values of different wind turbines with each other for prioritization purposes;
- (iii)
RPN values are not continuous with many holes and heavily distributed at the bottom of the scale from 1 to 100. As a matter of fact, in the proposed FMEA methodology 161 RPN values (11, 13, 17, …, 151–199) cannot be obtained from multiplication of the three risk factors;
- (iv)
various sets of Sf, S and Sd may produce an identical RPN value, however, their hidden risk implications may be totally different. For example, two different failure modes with values of 5, 4, 4 and 2, 4, 10 for Sf, S and Sd, respectively, will have the same RPN value of 80. However, the hidden risk implications of these two failure modes may not necessarily be the same, and this could entail a waste of resources and time;
- (v)
the methodology only considers three factors in terms of safety, and some important economical aspects such as production losses, logistics and transportation are not taken into account in the RPN value. So, the result may not necessarily represent the true risk priorities of the failure modes.
In order to overcome these drawbacks, we extend our works in [15,19], and develop a mathematical tool for risk and failure mode analysis of wind turbine systems (both the onshore and offshore) based on three main factors: failure probability, incurred failure costs, and the fault detection possibility. The proposed methodology is applied to the two same type of onshore and offshore wind turbine systems, and the results are compared with the existing prioritization approaches. Our results show that the proposed methodology can have a high potential to improve the safety as well as mitigate the operational risks associated with an unexpected failure within the wind farms (i.e., costly repair or replacement, lack of spare parts, transportation means and manpower, and loss of power production).
The rest of this paper is organized as follows: Section 2 describes the wind turbine system considered in this study. In Section 3, the proposed FMEA methodology is described. In Section 4, a quantitative study is carried out on two same types of onshore and offshore wind turbines, and some useful comparisons and analyses are conducted. Finally, in Section 5, we conclude this study with a brief discussion on topics for future research.
2. Wind Turbine System Considered in this Study
Nowadays, many kinds of wind turbine systems compete in the market. According to Li and Chen [20] and Pinar et al. [21], wind turbines can be categorized by their generator, gearbox, and their power converter types as shown in Table 5.
Fixed speed wind turbines which operate with constant speed “Danish concept” were produced until the late 1990s with power ratings below 1 MW. They used a multi-stage gearbox, and a standard squirrel-cage induction generator directly connected to the grid through a transformer. From the late 1990s, fully variable speed wind turbines were introduced in wind power industry. The first generation of fully variable speed wind turbines (with power ratings of approximately 1 MW) used a multi-stage gearbox, a relatively low-cost standard wound rotor induction generator, and a power electronic converter feeding the rotor [22]. The doubly fed induction generator (DFIG) technology is currently the most widely used in the wind turbine industry because of its low investment cost and good energy yield [23]. Since the mide-1990s, there have also been variable speed wind turbines with gearless generator systems which are equipped with a direct-drive generator and a fully-rated power electronic converter. The brushless doubly fed induction generator (BDFIG) is a well known drive technology which eliminates the need for brushes and slip rings, increases the lifetime of the machine, and ultimately reduces the maintenance costs [24].
This paper focuses on a wind turbine system which is available in both onshore and offshore types. This wind turbine features a non-integrated drive train with a rotor shaft supported by two bearings, a combined planetary/spur wheel gearbox, and a double-fed asynchronous generator. The three-blade rotor is also equipped with an electrical blade angle adjustment and a cast iron rotor hub.
The wind turbine has a condition monitoring system that measures a wide range of temperature, noise and vibration parameters (for more see [25]). This system monitors major components of wind turbine (such as the main gearbox, gear teeth and the generator bearings) to provide early diagnosis of potentially damaging changes.
After recognizing the wind turbine type, we define a general set of sub-assemblies and main parts. In this study, sixteen sub-assemblies and components with higher failure probabilities and serious consequences have been considered: brake system, cables, gearbox, generator, main frame, main shaft, nacelle housing, pitch system, power converter, rotor bearings, rotor blades, rotor hub, screws, tower, transformer, yaw system. It may be apparent that not all of these components may be available in some types of wind turbine systems.
After subdivision of the wind turbine system, the potential failure modes of sub-assemblies are identified using the information gathered from four experts. These experts have experience, ranging from three to six years, within the reliability, availability, maintainability and safety (RAMS) of wind energy industry. The experts used the “fault tree analysis” (FTA) to describe the complete set of potential system failures. The FTA is one of the most popular and diagrammatic techniques to analyze the undesired states of a system using AND gate (the output occurs only if all inputs occur) and OR gate (the output occurs if any input occurs) [26].
Figure 3 depicts the fault tree diagram for three important sub-assemblies of the wind turbine system: gearbox, generator and the blades, starting with the top event “sub-assembly failure”. The main identified failure modes in the wind turbine sub-assemblies are as follows: fatigue, collapse, cracked, deterioration, deformed, stripped, worn, corroded, binding, buckled, sag, loose, misalignment.
Any of these failure modes or their combination can become a cause of system failure. Each failure in the wind turbine system may result in a high production loss, poor power quality to the grid, and a significant audible noise. Evidently, each one of the failure modes has a root cause that the probability of failure mode is directly related to the probability of occurrence of its root cause. Table 6 shows the common root causes of the failure modes for the wind turbine systems in four different categories: external, structural, electrical, and wear.
3. Proposed Methodology
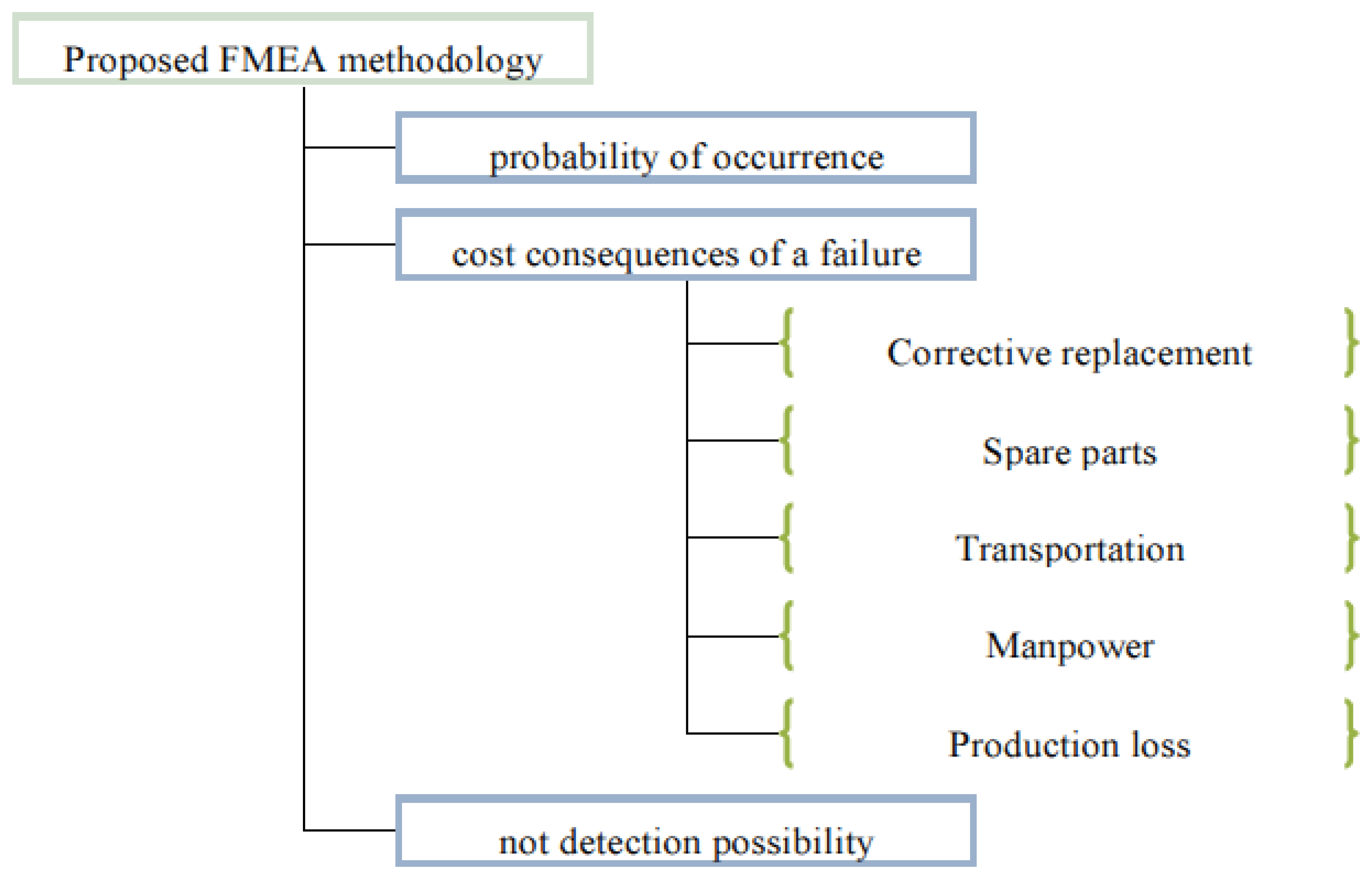
In this section, a new tool for risk and failure mode analysis of wind turbine systems is presented. In the proposed methodology, the risk of each failure mode is evaluated by three factors as shown in Figure 4.
“probability of occurrence (O)” is a value between 0 and 1 that can be obtained from the field failure data. The probability of occurrence for the failure mode i is given by:
Assume that the failures resulted from the failure mode i occur statistically independent according to a homogeneous Poisson process with parameter λi > 0. This assumption can be applied in practice to the systems that are in their useful life period, where the underlying failure distribution is the negative exponential distribution. Accepting that the sub-assemblies of wind turbine are arranged in series and have no redundancy, the probability of occurrence for the failure mode i is calculated as follows:
where k represents the total number of potential/known failure modes.“cost consequence of failure (C)” is a positive value including all costs associated with a failure due to repair or replacement, logistics and spare parts, transportation, manpower, and production loss. Then, the cost consequence of a failure resulted from the failure mode i is given by:
where:(€) is the cost of the sub-assembly which needs to be repaired/replaced due to the failure;
CS (€) is the cost of equipping the maintenance crew, hiring the service vessels, and ordering the spare parts;
CT (€) is the expected cost of transporting the maintenance crew to the wind farm, that can be calculated using the following equation:
where d (km) is the average distance between the repair shop and the wind farm, and cT (€/km) is the transportation cost per unit distance (including the cost of bio-diesel fuels used in the service vessels and helicopters, cost of CO2 emissions associated with the maintenance expeditions, etc).(€) is the manpower cost for the inspections and corrective maintenance tasks on the failed sub-assembly, and is given by:
where mi is the number of technicians required to repair/replace the failed sub-assembly, cL (€/day) is the daily rate of manpower for eight working hours per day, tT (day/km) is the transportation time per unit distance, t0 (day) is the expected time required to setup the maintenance actions, and (day) is the expected time required to repair/replace the failed sub-assembly.(€) is the expected cost of production loss due to the failure, that can be calculated using the following equation:
where L (day) is expected time required to equip the maintenance crew, and cP (€) is the fixed cost of production loss per unit downtime which is given by [11], that is:where W is the wind turbine power rating (MW), E is the unit cost of energy (€/MW), and f is the capacity factor of wind farm. We assume that the time interval between failure occurrence and the failure detection is negligible and can be ignored.
“not detection possibility (D)” is a value between 0 and 1 that can be obtained by dividing the number of actual failures (NF) to the total number of failure vulnerabilities (NFV) [13]. NFV is defined as the sum of number of actual failures (NF) and the number of detected possible failures prior to their occurrences (ND), for any given period of time. Then, the not detection possibility of the failure mode i is given by:
For each failure mode with several root causes, multiplying the occurrence (O), cost (C) and detectability (D) values results in related cost-priority-number (CPN), i.e., the CPN value for the failure mode i is calculated as:
The CPN value is continuous and is expressed in monetary unit (€), and hence, it can be easily used for comparison purposes. The failure modes with higher CPNs are assumed to be more important and will be given higher priorities for correction.
By aggregating the sub-assembly CPNs, the wind turbine's overall CPN is obtained as follows:
The share of each failure mode in the overall CPN can be evaluated by dividing its CPN value to the wind turbine's overall CPN. Then, the share of failure mode i in the overall CPN, %CPN, is given by:
A simple tool that can help managers to prioritize the main factors causing failures in the wind farm is pareto analysis (for more see [27]). Pareto analysis can provide a mechanism for identifying a set of sub-assemblies that have significant impact on the overall CPN. It can also be used to calculate the percentage reduction in the overall CPN of system when the CPN of one of the critical sub-assemblies is reduced. In this study, we use the cumulative %CPN to classify the wind turbine subassemblies into three main groups. The main features of the three groups are the following:
- Group A.
Significant savings can be obtained by reducing their failure frequency and/or the downtime length. These failure modes comprise around 70% of the overall CPN.
- Group B.
A medium CPN reduction can be obtained using an effective preventive maintenance strategy. These failure modes comprise around 20% of the overall CPN.
- Group C.
Low levels of savings can be obtained through reduction of failure consequences. These failure modes comprise around 10% of the overall CPN.
It is very often observed that a wind farm consists of “different types” of wind turbines produced by the same manufacturer, or different brands from different manufacturers [28]. Different wind turbines have generally different capacities and structures. A main feature of the proposed methodology is that the CPN analysis can be applied to any type of wind turbines with different structures. In order to compare the different types from criticality perspective, the wind turbines's “annual” CPN should be considered. The annual CPN for a wind turbine system with k potential/known failure modes is defined as:
4. A Comparative Study
In this section, a quantitative comparative study is carried out using the traditional and the proposed FMEA methodologies on two onshore and offshore wind turbine systems of the same type. Both the wind turbines have the same power rating, structure, and same condition monitoring system to detect failures. The only difference between the turbines is in their geographical features (such as location, weather conditions, wind speed and temperature).
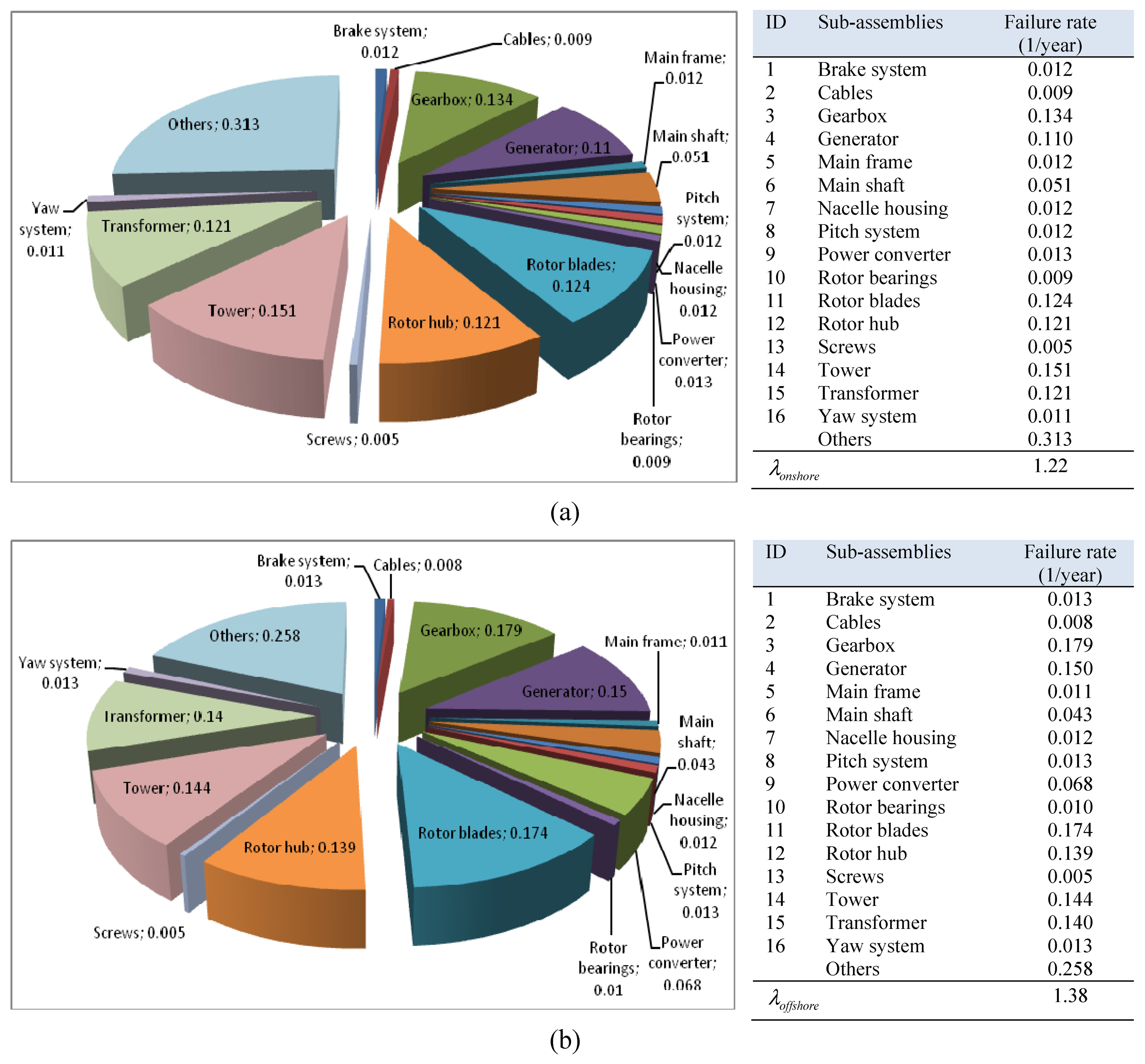
In order to make comparison of the results fair, the same database has been used for two methodologies. Our failure data has been collected from ten-minute Supervisory control and data acquisition (SCADA) database, automated fault logs, O&M reports, and supplemented with data from references [11,29–31]. Figure 5 represents the failure rate of the sixteen sub-assemblies of the onshore/offshore wind turbine system. Since the wind turbines considered for this study are in their useful lifetime, we assumed that their failure rates are constant. However, we tested our dataset and it did not provide enough evidence to reject our hypothesis that the underlying failure distribution is the negative exponential distribution. As shown, the average failure rate of the onshore (offshore) wind turbine system (i.e., the expected number of failures per year) is equal to 1.22 (1.38)/year. In the onshore wind turbine system, the most frequent failures are related, respectively, to the tower, gearbox, rotor blades, rotor hub and the transformer, whereas in the offshore wind turbine system, the gearbox, rotor blades, generator, tower and the transformer possess the highest failure rates.
The software reliability analysis tool used for this study is Windchill Quality Solutions (formerly Relex), version 10.0 [32]. This software can be used for a variety of purposes such as reliability prediction, FTA, Markov modeling, Weibull analysis and drawing the reliability block diagrams.
4.1. Traditional FMEA
On the basis of collected information from the experts and the criteria explained in Tables 2, 3 and 4, the traditional FMEA methodology is applied to both the onshore and offshore wind turbine systems.
Table 7 gives the RPN values obtained from PTC Windchill FMEA module [33] for the sixteen sub-assemblies of wind turbine systems considered in this study. Since we assumed that both the wind turbines have been equipped with the same condition monitoring system, the same scores were assigned for detection of a failure (Sd) in sub-assemblies.
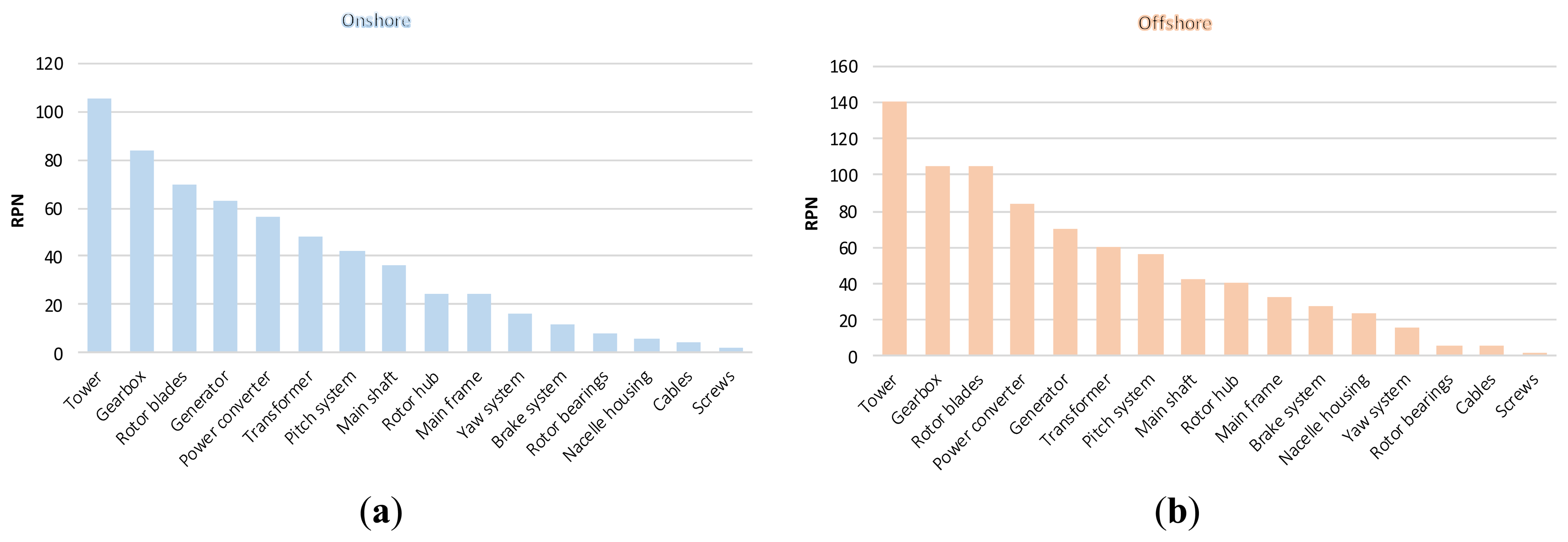
From Table 7, the tower (sub-assembly #14) is identified as the most critical part in both the onshore and offshore wind turbine systems. However, the tower's RPN value in offshore system is 35 units higher than that of onshore counterpart. Also, the screws (sub-assembly #13) are the least critical part in both systems with the same RPN value of 2.
The ranking order of all sub-assemblies with their scores is shown in Figure 6, where the vertical axis represents the RPN values. As shown, in the onshore wind turbine system, the gearbox has a higher RPN value compared to the rotor blades, whereas, in the offshore wind turbine system, the RPN values of these two sub-assemblies are equal. Also, in the onshore wind turbine system, the generator and the power converter are ranked, respectively, as the forth and the fifth critical sub-assemblies, while this ranking order is reversed in offshore type.
It also should be noted that the ranking orders of some individual sub-assemblies (such as transformer, pitch system and main frame) in both systems are the same. One reason for this event might be the restricted number of severity-occurrence-detection combinations to assige to the three risk factors in traditional methodology. Figure 7 illustrates the RPN values, out of the thirty-nine different RPN values, obtained for each sub-assembly of onshore/offshore wind turbine system.
The difference between the risk levels of the two wind turbine systems will become more obvious when the proposed methodology is applied.
4.2. Proposed FMEA
The distance between the onshore platform and the repair shop is negligible and can be ignored, but the offshore platform is located approximately 20 km from the repair shop. The onshore (offshore) wind turbine's capacity factor is 0.3 (0.4). This implies that the onshore (offshore) wind turbine system is expected to generate ∼13.14 (17.52) gigawatt hours (GWh) of electricity per year. This is equivalent to the annual electricity consumption of about 3000 (4000) households. The average electricity purchase rate is equal to 48 €/MW.
The expected time required to equip the maintenance crew is 0.5 days. The expected cost to order the spare parts and hire service vessels (ship and lifting crane) is 10,000 €. The expected transportation time per kilometer is 0.02 days, and the expected transportation cost per kilometer is 500 €. The expected time required to setup the maintenance is 0.5 days. The expected time to perform the maintenance actions on the failed sub-assembly in onshore (offshore) wind turbine is 0.5 days (one day). Daily rate of a skilled worker for maintenance tasks is 200 €.
Table 8 gives the CPN values for the sixteen sub-assemblies of the onshore/offshore wind turbine system considered in this study. As can be seen, the tower (sub-assembly #14) has the highest CPN value in both the onshore and offshore wind turbine systems. However, the tower's CPN value in offshore wind turbine system is 432.77 € higher than that in onshore counterpart. Also, the cables (sub-assembly #2) possess the lowest CPN value in the both systems.
From Table 8, the CPN value of gearbox in the onshore wind turbine system is 35.84 € higher than that of rotor blades. This order becomes reverse in the offshore wind turbine system, where the rotor blades' CPN value is 2833.45 € higher than that for gearbox. The main reason might be that the offshore wind turbine blades are more under “stress” in harsh maritime environments because of the extreme weather conditions as well as seasonal affects (such as icing and thunderstorms) [34]. In addition, conducting the maintenance tasks for an offshore wind turbine blade is more expensive since it requires hiring specialized equipment (e.g., lifting cranes) and transportation means (ships, helicopters).
It is also observed that the overall CPN value for onshore wind turbine system is 24,069 €, whereas, this is 30,500 € for the offshore type. This implies that the wind power system located on sea comes with 27% higher O&M costs compared to its onshore counterpart. Definitely, this cost ratio will become greater for those offshore wind turbines located in cold, icy or remote areas. Now, the share of each subassembly's failure in the overall CPN is calculated using Equation (11). In Figure 8, the sub-assemblies have been sorted in descending order with regard to their %CPNs, where the vertical axis represents the cumulative %CPN.
From the criticality point of view, the wind turbine sub-assemblies were classified into three main groups. In onshore wind turbine, the seven most critical sub-assemblies of tower, gearbox, rotor blades, transformer, main frame, generator and pitch system comprise around 70% of the overall CPN, whereas, their frequency of failure accounts for 54% of the system failures. Similarly, in the offshore type, the five most critical sub-assemblies tower, rotor blades, gearbox, power converter and transformer are included in Group A. The failures due to these five sub-assemblies comprise around 51% of the total system failures.
In order to estimate the annual CPN of the wind turbine systems, Equation (12) is used. Table 9 gives the annual CPNs for the sixteen sub-assemblies of the onshore/offshore wind turbine system. The column of failure vulnerability specifies the expected frequency that each sub-assembly has been detected with a risk of failure or has actually been failed.
From Table 9, it can be seen that the annual CPN for the onshore (offshore) wind turbine system is 38,386 € (52,908 €), which implies an expected annual failure vulnerability of 1.59 (1.73) for the onshore (offshore) wind turbine system.
4.3. Analysis of Results
4.3.1. Comparisons
In this section, some comparisons are made between the quantitative results of the proposed FMEA methodology and the existing prioritization approaches in wind farms. Then, the results are analyzed to establish some relationships that might be useful for future wind turbine designs.
A useful outcome of the proposed methodology could be a comparison between the ranking orders obtained from the sub-assemblies' CPNs and the field failure rates. Such a comparison between field failure rate data (in Figure 5) and CPN values (in Table 8) for the offshore wind turbine system is shown in Table 10.
From Table 10, it is observed that both the approaches (failure rate and CPN) obtain the same ranking orders for three of the individual sub-assemblies (i.e., rotor blades, transformer and rotor bearings). Nevertheless, there is a noticeable difference between the results obtained using two approaches for some major sub-assemblies such as the tower, gearbox, power converter, and the generator.
Also, as the failure rates of the three sub-assemblies brake, pitch system and the yaw system are almost equal, they are put in the same priority level from the failure rate perspective. However, the yaw system's failures are more detectable than the brake or pitch system's failures. For instance, in Table 7, the detection rating of 4 was assigned to the yaw system, while it was 7 for both the brake and the pitch system. Similarly, according to Table 8, the not detection possibility of yaw system was obtained equal to 0.8, while it was 0.9 for both the brake and the pitch system.
Even though the detection possibility is linked to failure rate (because if a root cause is hard to detect, a failure is more likely to occur), it might seem more reasonable to compare the ranking orders with the product of failure rate and detection possibility. Such a comparison between “failure rate × not detection possibility” data (from Figure 5 and Table 8), and CPN values (in Table 8) for the offshore wind turbine system is shown in Table 11.
Table 11 shows more similarity between the results obtained from the “failure rate × not detection possibility” point of view and the CPN approach. For instance, the difference between the ranking orders of some sub-assemblies such as the tower and the generator has been less. In addition, as it was expected, the brake and the pitch system are ranked ahead of the yaw system from the “failure rate × not detection possibility” perspective. Nevertheless, there is still some noticeable difference between the ranking orders of some critical sub-assemblies such as the gearbox and the power converter. The main reason is that the severity information cannot be concluded from “failure rate × not detection possibility”. Therefore, it seems more reasonable to multiply the “failure rate × not detection possibility” data by some measures of severity (such as the mean-time-to-repair, logistics lead-time, or cost consequences of a failure). In Table 12, the results obtained for the offshore wind turbine system from the CPN perspective is compared with the results obtained from the traditional FMEA using RPN method.
As can be seen, two methodologies are in agreement about the tower being the most critical sub-assembly of wind turbine. Also, the results obtained from two approaches (RPN and CPN) are very similar to each other for most of the major sub-assemblies (such as the rotor blades, gearbox, power converter, generator and the transformer).
The main problem in the traditional FMEA methodology is that it puts two critical sub-assemblies of the gearbox and the rotor blades as having the same priority. The nacelle housing and the cables are also placed at the same ranking level. But, applying the proposed methodology reveals that there is a significant difference between these sub-assemblies' CPN values.
4.3.2. CPN Reduction
Offshore wind farm managers are under an increasing pressure to reduce their O&M costs. One effective way to reduce O&M costs of the wind turbine systems is by improving the fault detection capability. This improvement can be achieved through using new monitoring techniques such as acoustic emission, ultrasonic testing, strain measurement, radiographic inspection, thermography and signal processing methods [35].
As mentioned earlier, the proposed FMEA methodology can be used in order to find out the percentage reduction in the overall CPN of system when the CPN value of one of the sub-assemblies is reduced. Table 13 gives the amount of reduction in each sub-assembly's annual CPN that can be achieved by ten percent improvement in the fault detection capability.
From Table 13, it can be seen that ten percent improvement in fault detection capability of the group A's sub-assemblies will result, respectively, in 6.61 and 7.69 percent reduction in the onshore and offshore wind turbine's annual CPN. This implies that using a condition monitoring system that be able to improve the detection possibility of these sub-assemblies by ten percent and costs less than this amount of saving, is beneficial to be purchased.
4. Conclusions
In this paper, we developed a new tool for risk and failure mode analysis of wind turbine systems (both onshore and offshore) by integrating the aspects of traditional FMEA and some economic considerations. Some important features of the proposed methodology, for application to FMEA of wind turbine systems, can be summarized as follows:
The traditional FMEA methodology is based on the risk-priority-number (RPN) index which is calculated by multiplying the occurrence (O), severity (S), and detection (D) of a failure. While, the proposed FMEA methodology is built on the cost-priority-number (CPN) index which is defined as the product of the probability of failure (O), it's likely cost consequences (C) and detection possibility (D).
The proposed FMEA methodology provides an organized framework to combine the qualitative (expert experience) and quantitative (SCADA field data) knowledge for use in an FMEA study;
The building blocks of RPN method are discrete, and therefore cannot represent effectively the strength of criticality. But, the CPN method is based on the cost consequences of failures which are expressed in monetary unit. So, it makes the proposed FMEA methodology more understandable, realistic and practical for wind farm managers;
The relative importance weights of the risk factors need to be taken into account in the traditional methodologies (see [36]), but in the CPN method, there is no need to include any weighting factors for O, C and D;
The use of CPN analysis enables the wind farm managers to compare different wind turbine systems with different structures from criticality point of view;
The CPN method supports wind farm managers' decision making on whether and how much to invest in reliability improvement programs (such as upgrading the monitoring system) in order to reduce the O&M costs;
The CPN method can be utilized when the field failure data and the cost parameters are available. Since our analysis showed a meaningful similarity between the results of the traditional FMEA and the CPN method, the use of the traditional FMEA is recommended only in situations where there is a lack of the field data;
The traditional FMEA methodology could be suitable for use in “risk screening” phase, or during the “design” stage of a new wind turbine configuration. During the risk-screening phase, only a relative ranking order is needed. This will distinguish the failure modes with a high risk level from those with a low-risk level. The proposed FMEA methodology would be suitable for use in “risk analysis and evaluation” phase, or during the “operation” stage. At this stage, a more detailed analysis of each failure mode is required to evaluate their ultimate effects on the system performance.
There is a wide scope for future research in the area of FMEA for wind turbine systems. In this study, we only considered the economic dependence that exists between the components in a multi-component system and focused on an economical risk assessment approach of the wind turbine systems. The generalization of the model in order to include the structural and stochastic dependencies between components will be an interesting topic for future research. It is also observed sometimes that the FMEA team members, because of their different expertise and backgrounds have different opinions. The diversity and uncertainty of FMEA team members' assessment information will be well modeled and analyzed using some existing belief structures in our future research.
Acknowledgments
The authors would like to thank the guest editor Frede Blaabjerg and four anonymous referees for their valuable comments and suggestions that appreciably improved the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
| Rating | Occurrence | Meaning | Possible failure rate |
|---|---|---|---|
| 1 | remote | Failure in unlikely. | ≤1/1,500,000 |
| 2 | low | Relatively few failures. | 1/150,000 |
| 3 | - | - | 1/15,000 |
| 4 | moderate | Occasional failures. | 1/2,000 |
| 5 | - | - | 1/400 |
| 6 | - | - | 1/80 |
| 7 | high | Repeated failures. | 1/20 |
| 8 | - | - | 1/8 |
| 9 | very high | Failure is almost inevitable. | 1/3 |
| 10 | - | - | ≥1/2 |
| Rating | Severity effect | Meaning |
|---|---|---|
| 1 | none | No effect. |
| 2 | very minor | Cosmetic defect in finish, fit and finish/squeak or rattle item that does not conform to specifications. Defect noticed by discriminating customers. |
| 3 | minor | Cosmetic defect in finish, fit and finish/squeak or rattle item that does not conform to specifications. Defect noticed by average customer. |
| 4 | very low | Cosmetic defect in finish, fit and finish/squeak or rattle item that does not conform to specifications. Defect noticed by most customers. |
| 5 | low | Item operable, but comfort/convenience item(s) operable at reduced level of performance. Customer experiences some dissatisfaction. |
| 6 | moderate | Item operable, but comfort/convenience item(s) inoperable. Customer experiences discomfort. |
| 7 | high | Item operable, but at reduced level of performance. Customer dissatisfied. |
| 8 | very high | Item inoperable, with loss of primary function. |
| 9 | hazardous with warning | Very High severity ranking when a potential failure mode affects safe operation and/or involves noncompliance with government regulations with warning. |
| 10 | hazardous without warning | Very High severity ranking when a potential failure mode affects safe operation and/or involves noncompliance with government regulations without warning. |
| Rating | Detection | Meaning |
|---|---|---|
| 1 | almost certain | Design control will almost certainly detect a potential cause/mechanism and subsequent failure mode. |
| 2 | very high | Very High chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 3 | high | High chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 4 | moderately high | Moderately high chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 5 | moderate | Moderate chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 6 | low | Low chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 7 | very low | Very Low chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 8 | remote | Remote chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 9 | very remote | Very remote chance the design control will detect a potential cause/mechanism and subsequent failure mode. |
| 10 | absolutely impossible | Design control will not and/or cannot detect a potential cause/mechanism and subsequent failure mode; or there is no design control. |
References
- European Wind Energy Association. Wind in Power, 2012 European Statistics; EWEA: Brussels, Belgium, 2013. Available online: http://www.ewea.org/fileadmin/files/library/publications/statistics/Wind_in_power_annual_statistics_2012.pdf (accessed on 4 March 2013).
- Hameed, Z.; Vatn, J. Role of grouping in the development of an overall maintenance optimization framework for offshore wind turbines. Proc. IMechE Part O J. Risk Reliab. 2012, 226, 584–601. [Google Scholar]
- Gilchrist, W. Modeling failure mode and effect analysis. Int. J. Qual. Reliab. Manag. 1993, 10, 16–23. [Google Scholar]
- Teng, S.-H.; Ho, S.-Y. Failure mode and effects analysis: An integrated approach for design and process control. Int. J. Qual. Reliab. Manag. 1996, 13, 8–26. [Google Scholar]
- Kumar, A.; Poonia, M.P.; Pandel, U.; Jethoo, A.S. FMEA: Methodology, design and implementation in a foundry. Int. J. Eng. Sci. Technol. 2011, 3, 5288–5297. [Google Scholar]
- Guimaraes, A.C.F.; Lapa, D.M.F.; Moreira, M.L. Fuzzy methodology applied to probabilistic safety assessment for digital system in nuclear power plants. Nucl. Eng. Des. 2011, 241, 3967–3976. [Google Scholar]
- Liu, H.-T.; Tsai, Y.-L. A fuzzy risk assessment approach for occupational hazard in the construction industry. Saf. Sci. 2012, 50, 1067–1078. [Google Scholar]
- Sharma, R.K.; Kumar, D.; Kumar, P. Systematic failure mode effect analysis (FMEA) using fuzzy linguistic modelling. Int. J. Qual. Reliab. Manag. 2005, 22, 986–1004. [Google Scholar]
- Pillay, A.; Wang, J. Modified failure mode and effects analysis using approximate reasoning. Reliab. Eng. Syst. Saf. 2003, 79, 69–85. [Google Scholar]
- Liu, H.-C.; Liu, L.; Bian, Q.-H.; Lin, Q.-L.; Dong, N.; Xu, P.-C. Failure mode and effects analysis using fuzzy evidential reasoning approach and grey theory. Expert Syst. Appl. 2011, 38, 4403–4415. [Google Scholar]
- Andrawus, J. Maintenance Optimization for Wind Turbines. Ph.D. Thesis, School of Engineering, Robert Gordon University, Aberdeen, UK, 2008. [Google Scholar]
- Fischer, K.; Besnard, F.; Bertling, L. Reliability-centered maintenance for wind turbines based on statistical analysis and practical experience. IEEE Trans. Energy Convers. 2012, 27, 184–195. [Google Scholar]
- Kahrobaee, S.; Asgarpoor, S. Risk-Based Failure Mode and Effect Analysis for Wind Turbines (RB-FMEA). Proceedings of the North American Power Symposium (NAPS), Boston, MA, USA, 4–6 August 2011; pp. 1–7.
- Das, M.K.; Panja, S.C.; Chowdhury, S.; Chowdhury, S.P.; Elombo, A.I. Expert-Based FMEA of Wind Turbine System. Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, Singapore, 6–9 December 2011; pp. 1585–1589.
- Dinmohammadi, F.; Shafiee, M. A fuzzy-FMEA risk assessment approach for offshore wind turbines. Int. J. Progn. Health Manag. 2013, 4, pp. 1–10. Available online: http://www.phmsociety.org/sites/phmsociety.org/files/phm_submission/2013/ijphm_13_013.pdf (accessed on 1 July 2013). [Google Scholar]
- Sunder, T.S.; Kesavan, R. Failure modes and effects analysis system deployment in a wind turbine at high uncertain wind environment. Adv. Sci. Lett. 2013, 19, 2166–2169. [Google Scholar]
- Tavner, P.J.; Higgins, A.; Arabian-Hoseynabadi, H.; Long, H.; Feng, Y. Using an FMEA Method to Compare Prospective Wind Turbine Design Reliabilities. Proceedings of the European Wind Energy Conference, Warsaw, Poland, 20–23 April 2010; pp. 1–7.
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure modes and effects analysis (FMEA) for wind turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar]
- Dinmohammadi, F.; Shafiee, M. An Economical FMEA-Based Risk Assessment Approach for Wind Turbine Systems. Proceedings of the European Safety, Reliability and Risk Management (ESREL), Amsterdam, The Netherlands, 30 September–2 October 2013; pp. 2127–2136.
- Li, H.; Chen, Z. Overview of different wind generator systems and their comparisons. IET Renew. Power Gener. 2008, 2, 123–138. [Google Scholar]
- Pinar, J.M.; García, F.P.; Tobias, A.M.; Papaelias, M. Wind turbine reliability analysis. Renew. Sustain. Energy Rev. 2013, 23, 463–472. [Google Scholar]
- Carlin, P.W.; Laxson, A.S.; Muljadi, E.B. The history and state of the art of variable-speed wind turbine technology. Wind Energy 2003, 6, 129–159. [Google Scholar]
- Muller, S.; Deicke, M.; de Doncker, R.W. Doubly fed induction generator systems for wind turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar]
- Carlson, R.; Voltolini, H.; Runcos, F.; Kuo-Peng, P. A Performance Comparison between Brush and Brushless Doubly Fed Asynchronous Generators for Wind Power Systems. Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ), Balearic Island, Spain, 5–7 April 2006; pp. 1–5.
- Márquez, F.P.G.; Tobias, A.M.; Pérez, J.M.P.; Papaelias, M. Condition monitoring of wind turbines: Techniques and methods. Renew. Energy. 2012, 46, 169–178. [Google Scholar]
- Andrews, J.D.; Moss, T.R. Reliability and Risk Assessment, 2nd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2002. [Google Scholar]
- Herbert, G.M.J.; Iniyan, S.; Goic, R. Performance, reliability and failure analysis of wind farm in a developing country. Renew. Energy 2010, 35, 2739–2751. [Google Scholar]
- Amayri, A.; Tian, Z.; Jin, T. Condition Based Maintenance of Wind Turbine Systems Considering Different Turbine Types. Proceedings of the International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (ICQR2MSE), Chengdu, China, 15–18 June 2011; pp. 596–600.
- Karyotakis, A. On the Optimization of Operation and Maintenance Strategies for Offshore Wind Farms. Ph.D. Thesis, Department of Mechanical Engineering, University College London, London, UK, 2011. [Google Scholar]
- Besnard, F. On Maintenance Optimization for Offshore Wind Farms. Ph.D. Thesis, Department of Energy and Environment, Chalmers University of Technology, Gothenburg, Sweden, 2013. [Google Scholar]
- Shafiee, M.; Patriksson, M.; Strömberg, A.-B.; Bertling, L. A Redundancy Optimization Model Applied to Offshore Wind Turbine Power Converters. Proceedings of the IEEE PowerTech Conference, Grenoble, France, 16–20 June 2013. [CrossRef]
- Windchill Quality Solution. Available online: http://www.ptc.com/products/windchill/quality/ (accessed on 18 March 2013).
- Windchill FMEA Software. Available online: http://www.ptc.com/product/windchill/fmea (accessed on 18 March 2013).
- Shafiee, M.; Patriksson, M.; Strömberg, A.-B. An optimal number-dependent preventive maintenance strategy for offshore wind turbine blades considering logistics. Adv. Oper. Res. 2013. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Crabtree, C.J.; Feng, Y.; Qiu, Y. Wind turbine condition monitoring: Technical and commercial challenges. Wind Energy 2012. [Google Scholar] [CrossRef]
- Braglia, M. MAFMA: Multi-attribute failure mode analysis. Int. J. Qual. Reliab. Manag. 2000, 17, 1017–1033. [Google Scholar]




| System | FMEA No. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Subsystem | Page | |||||||||||||
| Component | Prepared by | |||||||||||||
| Core team | FMEA Date (org.) | |||||||||||||
| Existing conditions | Action results | |||||||||||||
| Component/process | Potential failure mode | Potential effects of mode | Potential causes of mode | Present control mechanisms | Severity | Occurrence | Detection | Risk Priority Number (RPN) | Recommend actions | Action taken | S | O | D | RPN |
| Rank | Description | Criteria |
|---|---|---|
| 1 | Level E (extremely unlikely) | A single failure mode probability of occurrence is less than 0.001. |
| 2 | Level D (remote) | A single failure mode probability of occurrence is more than 0.001 but less than 0.01. |
| 3 | Level C (occasional) | A single failure mode probability of occurrence is more than 0.01 but less than 0.10. |
| 5 | Level A (frequent) | A single failure mode probability of occurrence is greater than 0.10. |
| Rank | Description | Criteria |
|---|---|---|
| 1 | Category IV (minor) | Electricity can be generated but urgent repair is required. |
| 2 | Category III (marginal) | Reduction in ability to generate electricity. |
| 3 | Category II (critical) | Loss of ability to generate electricity. |
| 4 | Category I (catastrophic) | Major damage to the Turbine as a capital installation. |
| Rank | Description | Criteria |
|---|---|---|
| 1 | Almost certain | Current monitoring methods almost always will defect the failure. |
| 4 | High | Good likelihood current monitoring methods will detect the failure. |
| 7 | Low | Low likelihood current monitoring methods will defect the failure. |
| 10 | Almost impossible | No known monitoring methods available to detect the failure. |
| Type of generation system | Turbine concept | Gearbox | Converter |
|---|---|---|---|
| Single Cage Induction Generator (SCIG) | fixed speed | multiple stage | - |
| variable speed | multiple stage | full scale | |
| Permanent Magnet Synchronous Generator (PMSG) | variable speed | - | full scale |
| variable speed | single or multiple stage | full scale | |
| Doubly Fed Induction Generator (DFIG) | variable speed | multiple stage | partial scale |
| Electrically Excited Synchronous Generator (EESG) | variable speed | - | partial & full scale |
| Wound Rotor Induction Generator (WRIG) | limited variable speed | multiple stage | partial scale |
| Brushless Doubly Fed Induction Generator (BDFIG) | variable speed | multiple stage | partial scale |
| External | Structural | Electrical | Wear |
|---|---|---|---|
| High/low wind | Installation defects | Calibration error | Aging |
| Environmental shocks | Manufacturing and material defect | Connection fault | Corrosion |
| Icing | Maintenance errors | Overload | Fatigue |
| Lightning strike | Mechanical overload | Insulation failure | Insufficient lubrication |
| - | - | Software failure | Aging |
| # ID | Sub-assembly | Some components | Onshore | Offshore | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sf | S | Sd | RPN | Rank | Sf | S | Sd | RPN | Rank | |||
| 1 | Brake system | Brake disk, Spring, Motor | 2 | 1 | 7 | 14 | 13 | 2 | 2 | 7 | 28 | 11 |
| 2 | Cables | Cable | 2 | 2 | 1 | 4 | 15 | 2 | 3 | 1 | 6 | 14 |
| 3 | Gearbox | Toothed gear wheels, Pump, Oil heater/cooler, Hoses | 3 | 4 | 7 | 84 | 2 | 5 | 3 | 7 | 105 | 2 |
| 4 | Generator | Shaft, Bearings, Rotor, Stator, Coil | 3 | 3 | 7 | 63 | 4 | 5 | 2 | 7 | 70 | 5 |
| 5 | Main frame | - | 2 | 3 | 4 | 24 | 10 | 2 | 4 | 4 | 32 | 10 |
| 6 | Main shaft | Shaft, Bearings, Couplings | 2 | 2 | 7 | 28 | 9 | 3 | 2 | 7 | 42 | 8 |
| 7 | Nacelle housing | Nacelle | 2 | 3 | 1 | 6 | 14 | 2 | 3 | 1 | 6 | 14 |
| 8 | Pitch system | Pitch motor, Gears | 2 | 3 | 7 | 42 | 7 | 2 | 4 | 7 | 56 | 7 |
| 9 | Power converter | Power electronic switch, cable, DC bus | 2 | 4 | 7 | 56 | 5 | 3 | 4 | 7 | 84 | 4 |
| 10 | Rotor bearings | - | 2 | 2 | 4 | 16 | 11 | 2 | 3 | 4 | 24 | 12 |
| 11 | Rotor blades | Blades | 5 | 2 | 7 | 70 | 3 | 5 | 3 | 7 | 105 | 2 |
| 12 | Rotor hub | Hub, Air brake | 3 | 3 | 4 | 36 | 8 | 5 | 2 | 4 | 40 | 9 |
| 13 | Screws | Screw | 2 | 1 | 1 | 2 | 16 | 2 | 1 | 1 | 2 | 16 |
| 14 | Tower | Tower, Foundation | 5 | 3 | 7 | 105 | 1 | 5 | 4 | 7 | 140 | 1 |
| 15 | Transformer | - | 3 | 4 | 4 | 48 | 6 | 5 | 3 | 4 | 60 | 6 |
| 16 | Yaw system | Yaw drive, Yaw motor | 2 | 2 | 4 | 16 | 11 | 2 | 2 | 4 | 16 | 13 |
| ID | Sub-assembly | Onshore | Offshore | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| O | C | D | CPN | Rank | O | C | D | CPN | Rank | ||
| 1 | brake system | 0.0100 | 35,880 | 0.9 | 322.92 | 15 | 0.00942 | 47,488 | 0.9 | 402.60 | 12 |
| 2 | cables | 0.0071 | 61,299 | 0.7 | 304.66 | 16 | 0.00580 | 72,118 | 0.7 | 292.80 | 16 |
| 3 | gearbox | 0.1102 | 30,657 | 0.9 | 3,040.56 | 2 | 0.12971 | 33,730 | 0.9 | 3,937.55 | 3 |
| 4 | generator | 0.0901 | 12,410 | 0.7 | 782.70 | 6 | 0.10870 | 13,789 | 0.7 | 1,049.20 | 6 |
| 5 | main frame | 0.0097 | 113,849 | 0.8 | 883.47 | 5 | 0.00797 | 133,940 | 0.8 | 854.00 | 7 |
| 6 | main shaft | 0.0418 | 17,657 | 0.9 | 664.26 | 8 | 0.03116 | 20,773 | 0.9 | 582.55 | 9 |
| 7 | nacelle housing | 0.0100 | 57,469 | 0.7 | 402.28 | 9 | 0.00870 | 67,611 | 0.7 | 411.75 | 11 |
| 8 | pitch system | 0.0100 | 81,341 | 0.9 | 732.07 | 7 | 0.00942 | 95,695 | 0.9 | 811.30 | 8 |
| 9 | power converter | 0.0110 | 37,883 | 0.8 | 333.37 | 11 | 0.04928 | 38,759 | 0.8 | 1,528.05 | 4 |
| 10 | rotor bearings | 0.007 | 78,709 | 0.6 | 330.58 | 13 | 0.00725 | 85,540 | 0.6 | 372.10 | 14 |
| 11 | rotor blades | 0.1017 | 42,207 | 0.7 | 3,004.72 | 3 | 0.12609 | 76,714 | 0.7 | 6,771.00 | 2 |
| 12 | rotor hub | 0.0990 | 4,208 | 0.8 | 333.27 | 12 | 0.10072 | 5,186 | 0.8 | 417.85 | 10 |
| 13 | screws | 0.0044 | 124,135 | 0.6 | 327.72 | 14 | 0.00362 | 146,041 | 0.6 | 317.20 | 15 |
| 14 | tower | 0.1234 | 68,330 | 0.9 | 7,588.73 | 1 | 0.10435 | 85,412 | 0.9 | 8,021.50 | 1 |
| 15 | transformer | 0.0990 | 11,467 | 0.8 | 908.19 | 4 | 0.10145 | 13,491 | 0.8 | 1,094.95 | 5 |
| 16 | yaw system | 0.0090 | 48,002 | 0.8 | 345.61 | 10 | 0.00942 | 50,590 | 0.8 | 381.25 | 13 |
| - | others | 0.2566 | 14,668 | 1 | 3,763.81 | - | 0.18696 | 17,407 | 1 | 3,254.35 | - |
| - | overal CPN (€) | - | - | - | 24,069 | - | - | - | - | 30,500 | - |
| ID | Sub-assembly | Onshore | Offshore | |||
|---|---|---|---|---|---|---|
| Failure vulnerability | Annual CPN | Failure vulnerability | Annual CPN | |||
| 1 | brake system | 0.14 | 43.77 | 0.14 | 58.15 | |
| 2 | cables | 0.12 | 37.70 | 0.11 | 33.46 | |
| 3 | gearbox | 1.49 | 4,542.06 | 1.99 | 7,831.35 | |
| 4 | generator | 1.57 | 1,229.08 | 2.14 | 2,248.29 | |
| 5 | main frame | 0.15 | 130.69 | 0.14 | 117.43 | |
| 6 | main shaft | 0.57 | 376.38 | 0.48 | 278.33 | |
| 7 | nacelle housing | 0.17 | 70.11 | 0.17 | 70.59 | |
| 8 | pitch system | 0.14 | 99.24 | 0.14 | 117.19 | |
| 9 | power converter | 0.17 | 55.92 | 0.85 | 1,298.84 | |
| 10 | rotor bearings | 0.14 | 47.05 | 0.17 | 62.02 | |
| 11 | rotor blades | 1.77 | 5,325.82 | 2.49 | 16,830.77 | |
| 12 | rotor hub | 1.51 | 503.15 | 1.74 | 726.01 | |
| 13 | screws | 0.09 | 29.32 | 0.08 | 26.43 | |
| 14 | tower | 1.67 | 12,694.09 | 1.60 | 12,834.40 | |
| 15 | transformer | 1.51 | 1,371.14 | 1.75 | 1,916.16 | |
| 16 | yaw system | 0.14 | 47.43 | 0.16 | 61.95 | |
| - | others | 3.13 | 11,782.68 | 2.58 | 8,396.22 | |
| Rank | Failure rate | Proposed FMEA |
|---|---|---|
| 1 | Gearbox | Tower |
| 2 | Rotor blades | Rotor blades |
| 3 | Generator | Gearbox |
| 4 | Tower | Power converter |
| 5 | Transformer | Transformer |
| 6 | Rotor hub | Generator |
| 7 | Power converter | Main frame |
| 8 | Main shaft | Pitch system |
| 9 | Brake system/ Pitch system/Yaw system | Main shaft |
| 10 | - | Rotor hub |
| 11 | - | Nacelle housing |
| 12 | Nacelle housing | Brake system |
| 13 | Main frame | Yaw system |
| 14 | Rotor bearings | Rotor bearings |
| 15 | Cables | Screws |
| 16 | Screws | Cables |
| Rank | “Failure rate × not detection possibility” | Proposed FMEA |
|---|---|---|
| 1 | Gearbox | Tower |
| 2 | Tower | Rotor blades |
| 3 | Rotor blades | Gearbox |
| 4 | Transformer | Power converter |
| 5 | Rotor hub | Transformer |
| 6 | Generator | Generator |
| 7 | Power converter | Main frame |
| 8 | Main shaft | Pitch system |
| 9 | Brake system/Pitch system | Main shaft |
| 10 | - | Rotor hub |
| 11 | Yaw system | Nacelle housing |
| 12 | Main frame | Brake system |
| 13 | Nacelle housing | Yaw system |
| 14 | Rotor bearings | Rotor bearings |
| 15 | Cables | Screws |
| 16 | Screws | Cables |
| Rank | Traditional FMEA | Proposed FMEA |
|---|---|---|
| 1 | Tower | Tower |
| 2 | Gearbox/Rotor blades | Rotor blades |
| 3 | - | Gearbox |
| 4 | Power converter | Power converter |
| 5 | Generator | Transformer |
| 6 | Transformer | Generator |
| 7 | Pitch system | Main frame |
| 8 | Main shaft | Pitch system |
| 9 | Rotor hub | Main shaft |
| 10 | Main frame | Rotor hub |
| 11 | Brake system | Nacelle housing |
| 12 | Rotor bearings | Brake system |
| 13 | Yaw system | Yaw system |
| 14 | Nacelle housing/Cables | Rotor bearings |
| 15 | - | Screws |
| 16 | Screws | Cables |
| ID | Sub-assembly | Redunction in annual CPN | |
|---|---|---|---|
| onshore | offshore | ||
| 1 | brake system | 4.37 | 5.81 |
| 2 | cables | 3.77 | 3.34 |
| 3 | gearbox | 454.21 | 783.14 |
| 4 | generator | 122.90 | 224.83 |
| 5 | main frame | 13.07 | 11.75 |
| 6 | main shaft | 37.63 | 27.83 |
| 7 | nacelle housing | 7.01 | 7.06 |
| 8 | pitch system | 9.93 | 11.72 |
| 9 | power converter | 5.59 | 129.88 |
| 10 | rotor bearings | 4.70 | 6.21 |
| 11 | rotor blades | 532.58 | 1683.08 |
| 12 | rotor hub | 50.31 | 72.60 |
| 13 | screws | 2.93 | 2.64 |
| 14 | tower | 1269.41 | 1283.44 |
| 15 | transformer | 137.11 | 191.61 |
| 16 | yaw system | 4.74 | 6.19 |
| others | 1178.27 | 839.62 | |
| Group A | 2539.21 | 4071.15 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shafiee, M.; Dinmohammadi, F. An FMEA-Based Risk Assessment Approach for Wind Turbine Systems: A Comparative Study of Onshore and Offshore. Energies 2014, 7, 619-642. https://doi.org/10.3390/en7020619
Shafiee M, Dinmohammadi F. An FMEA-Based Risk Assessment Approach for Wind Turbine Systems: A Comparative Study of Onshore and Offshore. Energies. 2014; 7(2):619-642. https://doi.org/10.3390/en7020619
Chicago/Turabian StyleShafiee, Mahmood, and Fateme Dinmohammadi. 2014. "An FMEA-Based Risk Assessment Approach for Wind Turbine Systems: A Comparative Study of Onshore and Offshore" Energies 7, no. 2: 619-642. https://doi.org/10.3390/en7020619





