Distributed Load-Shedding System for Agent-Based Autonomous Microgrid Operations
Abstract
: A microgrid is an eco-friendly power system because renewable sources are used as main power sources. In the islanded operation mode of a microgrid, maintaining the balance between power supply and power demand is a very important problem. In the case of surplus supply, decreased generation output and/or charge of distributed storages can be applied to solve the imbalance between power supply and demand. In the case of supply shortages, increased generation output and/or discharge of distributed storages can be applied. Especially in the case of critical supply shortages, load shedding should be applied. In a distributed load-shedding approach, microgrid components need to make decisions autonomously. For autonomous microgrid operation, a multi-agent system has been investigated. In this paper, a distributed load-shedding system for agent-based autonomous operation of a microgrid is designed. The designed system is implemented and tested to show the functionality and feasibility of the proposed system.1. Introduction
A microgrid is an emerging frontier in meeting the challenges of providing reliable power supplies in small communities [1]. Microgrids can be described as a set of distributed generations (DGs), distributed storages (DSs), and Loads [2–5]. DG is a power generator such as diesel generators, wind turbines, PV systems, micro turbines and/or fuel cell systems based on combined heat and power (CHP). DS can absorb and supply power by charge and discharge actions. Load is a power consumer such as a residential or commercial building. The load requirement is the amount of power demanded. Hereafter, “Load” indicates a power consumer as one of components in a microgrid and “load” indicates the amount of power to be demanded by a “Load”. Normally, a microgrid is connected to an upstream power grid. Recently, many microgrid technologies, such as microgrid operation and control, protection schemes, simulators, and field tests, have been studied [6,7].
A microgrid should maintain a constant frequency, such as 50 Hz or 60 Hz, as an operational requirement in a permitted range. The frequency depends on a balance between power supply and power demand. A microgrid is operated in either a grid-connected mode or an islanded mode. In a grid-connected mode, a microgrid is connected to an upstream power grid. In this mode, a microgrid can exchange energy with the power grid. In other words, the difference between the power generated and the power demanded is balanced by trading with the power grid. Islanded mode means an intentional isolated operation from an upstream power grid for maintenance purposes or due to a fault occurrence on the power grid. In this mode, if load requirements are less than the power generation, the amount of power generated by DGs decreases and/or DSs charge the amount of excess power to solve the power imbalance problem. On the other hand, if load requirements are larger than the generation, DSs discharge the amount of the shortage and/or a load-shedding scheme is used.
A load shedding is defined as a coordinated set of controls which results in a decrease of the electric load in a microgrid [8]. Load shedding has two approaches: a centralized load-shedding approach and a distributed load-shedding approach. In a centralized load-shedding approach, all components in a microgrid cooperate for a common goal, e.g., the maximization of system performance. It is suitable if the components have the same owner or a very strong operational or legal connection. In this case, a control center [we call it MicroGrid Operation and Control Center (MGOCC)] determines the amount of load to be shed for each Load. In a distributed load-shedding approach, microgrid components have different owners and operating policies. In this case, instead of making a decision by MGOCC, several decisions should be taken autonomously by each component of a microgrid. Auctions are a great way to represent and solve distributed resource allocation problems [9]. They require all components to send their bids to a centralized auctioneer who then determines the winners. There are basically three issues: bidding, allocation, and strategy. For bidding, each bidder should be able to express its own bid on a resource. The bidding algorithm determines how to express the bid and how to communicate the bid with a centralized auctioneer. For auction, once the bids are all in, resource in the auction should be allocated among the difference bidders. The allocation will attempt the optimization of a target function, usually the auctioneer's revenue or the bidders' revenue. However, in most cases, this optimization is computationally intractable (NP-complete) and heuristics should be used. For strategy, each bidder determines its own bid through its bidding strategy. A well designed auction ensures that the intended goals of the auction are met when all bidders act according to their strategies. In this paper, each Load bids for the power supplied by DGs through a bidding process. In an islanded operation mode, since the power supply from the power grid is interrupted, a microgrid has to rely on its own local DGs. If the maximum capacity of the local DGs is not enough to satisfy the total power demands, then a load shedding is initiated to satisfy the minimum power demands of Loads. Thus, in our load shedding, we assume that DGs provide their maximum power output and Loads bid for the supplied power as bidders. Then an auctioneer gathers the bids from Loads and allocates the power to Loads according to their bids in order to determine the amount of load to be shed. We extend MGOCC to include the function of the auctioneer for simplicity, but it is not necessary. It can be implemented without MGOCC. To implement the functions of components in a microgrid, intelligent agent technologies can be a good solution because each agent has a certain degree of intelligence to make a decision locally. An intelligent agent (abbreviated as an agent) senses external environmental changes, effectively makes decisions against the changes based on its operational goal, and acts autonomously according to its decision. A multi-agent system is an autonomous system composed of multiple agents [10–12].
In this paper, for a distributed load-shedding approach, a multi-agent system is designed for autonomous microgrid operation in an islanded mode. First of all, a control architecture for a distributed load shedding is defined and the functionalities of agents in the architecture are defined. Then, a power allocation algorithm for a bidding process is presented. The designed load-shedding system is implemented by using a multi-agent system platform to show its feasibility and functionality.
This paper is organized as follows: Section 2 introduces a multi-agent system in a microgrid as a research background. In Section 3, we define a multi-agent system for load shedding, propose a power allocation algorithm by using proportional fairness, and design a distributed load-shedding system. In Section 4, performance analysis of our system is given. Finally, conclusions are drawn in Section 5.
2. Research Background
2.1. Microgrid Operation
Generally, it is difficult to find literature to explain the detailed procedures of real microgrid operation. Thus, it is assumed that like conventional power systems, a microgrid is operated in two steps: planning and implementation. Under the assumption, MGOCC makes an operational plan for the next interval (e.g., interval i) at interval I − 1. The operational plan to be made at interval I − 1 is implemented during interval i. The length of an interval depends on operation rules. In this paper, we employ the following operational rules for an islanded microgrid [3]:
At the beginning of an operational interval, MGOCC announces the start of operational planning for the next interval to microgrid components;
DG proposes the amount of power supplied with a price per unit to MGOCC;
Load proposes the amount of load demanded with its bidding price to MGOCC;
DS selects one among three actions: no action, charge, or discharge. In the case of charge, DS proposes the amount of load demanded with its bidding price to MGOCC as a Load. In the case of discharge, DS proposes the amount of power supplied with a price per unit to MGOCC as a DG;
If the amount of total power supplied is greater than the amount of total power demanded, MGOCC selects the final power suppliers among DGs considering the total power demand and it determines the final amount of power generated by the final power suppliers;
If the amount of total power supplied is less than the amount of total power demanded, MGOCC initiates a load shedding to determine the amount of load to be shed;
MGOCC announces its decision to microgrid components;
According to the operational plan announced by MGOCC, each component implements the plan during the next interval.
A microgrid is intrinsically distributive in nature. In order to improve the performance of a microgrid, an autonomous and cooperative control is required. Agent technology is one of techniques for achieving the objectives of autonomous control of a microgrid.
2.2. Multi-Agent System for Load Shedding
A multi-agent system (MAS) [10–12] is a collection of autonomous computational entities (agents) that possess the ability to perceive changes of their environment and take an action to deal with those changes. Agents have varying degrees of intelligence, based on their roles within the architecture. Agents pursue goals to optimize certain performance measures within an environment which can be hard to define analytically. Additionally, agents have the capability to interact with other agents. This communication may be simply for the purposes of information passing, or may be more complex schemes involving negotiation or cooperation towards a common goal. This includes interaction whereby agents converge on a course of action by proposing, counter-proposing, accepting, or rejecting operational choices.
Load shedding is defined as a coordinated set of controls which results in decrease of the electric load in a microgrid. An optimal load-shedding scheme finds the best stable equilibrium operating point for the system with the minimum amount of load to be shed.
In conventional under frequency load-shedding scheme, whenever frequency of the system falls below predetermined thresholds, parts of the system load are shed in some predetermined steps [7]. In the first step, the anticipated overload (L) is determined as below:
All of the required loads to be disconnected can be shed simultaneously, however this approach may lead to overshedding for small disturbances. A suitable alternative is to divide the loads to be dropped among several steps and shed a portion in each step. Thus, the second step is to select the number of load shedding steps. In the third step, the total amount of load to be shed is calculated to maintain frequency above minimum permissible frequency for the maximum anticipated overload, as below [13]:
A distributed constraint optimization problem (DCOP) [18] is a fundamental problem that can formalize various applications related to MAS. A DCOP consists of a set of agents, each of which needs to decide the value assignment of its variables so that the sum of the resulting rewards/costs is optimized. Many application problems in MAS can be formalized as DCOPs, e.g., distributed resource allocation problems, including microgrids. The microgrid optimization problem has been shown to subsume several classical power systems sub-problems such as load shedding, demand response, and restoration. The objective of the microgrid optimization problem is composed of three parts: the agents' consumption preference, the agents' generation preference, and a global cost function.
In the islanded mode, since the main power supply from the power grid to a microgrid is interrupted, a microgrid has to rely on its own local DGs and DSs. If the sum of power storage capacity of the local DSs and the power generation capacity of the local DGs is not enough to satisfy the total power demands, then the load shedding is initiated to satisfy the minimum power demands of Loads. Thus, researches on a load shedding focus on how to minimize the difference between the largest amount of possible power consumed and the largest amount of possible power produced [18,19].
3. Design of Agent-Based Load-Shedding System
Our load-shedding process is composed of three parts. The first part is a bidding strategy for a Load. The bidding strategy determines a bidding price and quantity, learns from experience of the previous bidding, and updates its bidding strategy through the learning. The second part is an allocation algorithm. When the bids from Loads are gathered, the clearing prices and quantities are determined by using allocation algorithm. The third part is about how to express the bid and how to communicate the bid among components. In this paper, we assume that a Load has its own bidding strategy which is our next research topic. We focus on presenting an allocation algorithm by using a proportional fairness algorithm and actually implementing the load-shedding system to express and communicate the bids.
3.1. Design of Multi-Agent System
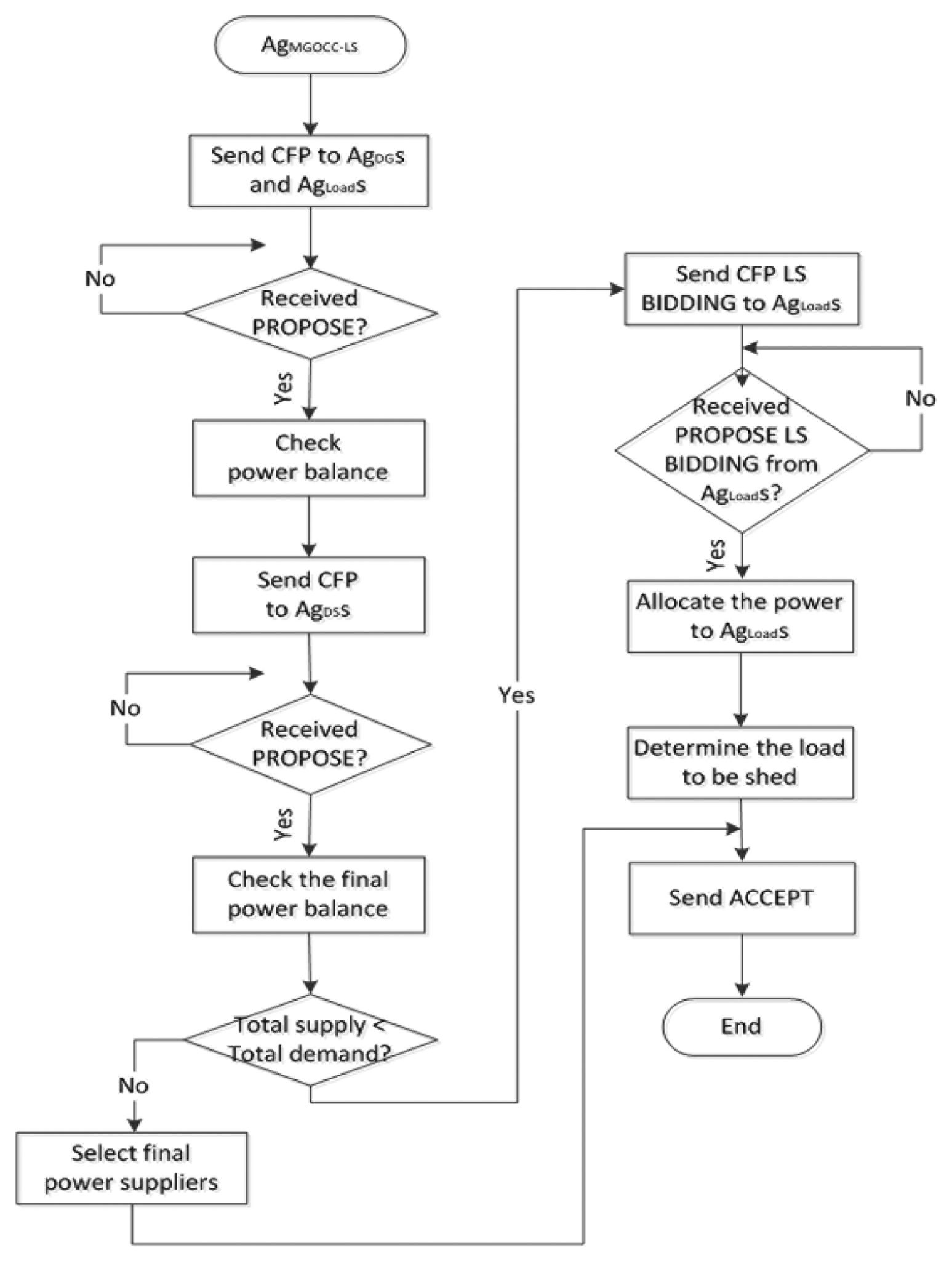
For the purpose of agent design for our load shedding in a microgrid, we divide microgrid components into four classes. Diverse microgrid components are grouped according to operational capabilities and assigned appropriate control agents: AgDG, AgLoad, AgDS, and AgMGOCC-LS. For simplicity, we extend MGOCC [3] to include load-shedding functionalities (i.e., the functionalities of auctioneer) and we call it MGOCC-LS. The following describes agent types and responsibilities associated with load shedding (The extended functionalities for the load shedding are specified by the sentence “when the load shedding is initiated”).
AgDG
- -
Determine of the amount of available power supplied and a price per unit for the next operational interval;
- -
Inform AgMGOCC-LS of the amount of available power supplied with the price per unit;
- -
Informed of the final amount of supply power granted by AgMGOCC-LS;
- -
Manage its power output according to the informed final supply amount;
- -
Monitor the amount of power supplied by attached components.
AgLoad
- -
Anticipate and determine the amount of power demanded by attached components for the next operational interval;
- -
Inform AgMGOCC-LS of the amount of load demanded;
- -
(When the load shedding is initiated) Determine a bidding price and quantity according to its bidding strategy;
- -
Informed of the final amount of load granted by AgMGOCC-LS;
- -
Manage its load amount.
AgDS
- -
Informed of the power balance by AgMGOCC-LS for the next operational interval;
- -
Determine the amount of state of charge (SOC) of attached components;
- -
Determine its role as a power supplier or a power consumer;
- -
(When the load shedding is initiated) if its role is a power consumer, determine its bidding price and quantity according to its bidding strategy;
- -
Inform AgMGOCC-LS of the amount of power supplied with the price per unit as a power supplier, or (when the load shedding is initiated) the bidding price and quantity as a power consumer;
- -
Informed of the final amount of power generated or the final amount of power consumed;
- -
Manage charging/discharging according to the final amount to be informed from AgMGOCC-LS;
AgMGOCC-LS
- -
Initiate operational planning of a microgrid every operational interval;
- -
Communicate with other agents to gather the information for the operational plan of the next interval;
- -
Check a power balance by using the gathered information;
- -
When total power supply is less than total power demand, initiate our load shedding;
- -
(When the load shedding is initiated) start a bidding process for the load shedding;
- -
(When the load shedding is initiated) communicate with AgLoads to gather their bidding information for the power;
- -
(When the load shedding is initiated) make a decision on the allocation of the power;
- -
When total power supply is more than total power demand, select the final power suppliers and determine the final amount of power to be generated by the final power suppliers;
- -
Inform other agents of the final amount of supply power or the final amount of load;
- -
Monitor operational implementation of a microgrid;
3.2. Proportional Fairness Algorithm for Power Allocation
We consider a system model for our load shedding in an islanded operation of a microgrid. The system is defined as a pair (L, P), where P is a vector of the supplied power by N DGs and L is a vector of load demands of M Loads, i.e., P = (P1, P2…, PN) and L =(L1, L2…, LM). When AgMGOCC-LS gathers bids from AgLoads, it allocates the power to AgLoads. We devise a load-shedding scheme by using the optimization solution to fairly allocate the power to Loads. The power allocation is determined according to a proportional fairness criterion [20] applied to the allocation per unit charge. It is shown that the system optimum is achieved when Loads' choices of bidding prices and system's choice of allocations are in equilibrium. Suppose that if xm is the power to be allocated to Load m (1 ≤ m ≤ M) in our load-shedding scheme, then this has utility Um(xm) to the Load at each interval. The time-dependent utility models a general situation where the Load may have different load demands at different time intervals. We assume that Um(xm) as a function of xm s continuously differentiable, strictly concave, increasing, over the range xm ≥ 0 [21]. Under this model, the optimization problem is given by:
Suppose that a bidding price of Load m in unit to buy the power is wm. Using the utility function , (3) is rewritten as:
A vector of the power to be allocated to Loads, x is proportionally fair if it is feasible, that is 0 ≤ xm ≤ Lm and , and if for any other feasible vector x*, the aggregate of proportional changes is zero or negative:
The utility function Um (xm) is not required by the system, and only appears in the optimization problem faced by Load m. Lagrangian techniques [22] are used to solve these maximization problems efficiently in polynomial time. These bounds can significantly improve linear programming run-times, as the pruning via linear programming happens over a restricted belief space [23]. The Lagrangian for the problem is:
We solve , λ2 (Lm−xm) = 0 and (9) and get the following as the optimal for the problem:
3.3. Design of Distributed Load-Shedding System
One of key functionalities of a multi-agent system (MAS) is the communication among the distributed agents. By utilizing the Foundation for Intelligent Physical Agents (FIPA) guidelines for agent-based communication, the interoperability and communication protocols for MAS, i.e., FIPA-Contract Net Protocol (CNP) performatives are standardized [24]. The performatives include CFP, PROPOSE, REFUSE, ACCEPT, REJECT, FAILURE, and INFORM, as shown in Table 1. In the literature [3], FIPA-CNP performatives are extended for agent communication in a microgrid. It has split a PROPOSE message into two different messages, i.e., PROPOSE SUPPLY for power suppliers and PROPOSE LOAD for power consumers. It is because the information sent from power suppliers and the information sent from power consumers are different. In other words, agents of power suppliers send their supply amounts and prices per unit and agents of power consumers send their load demands. In this paper, based on [3], we add performatives for a bidding process in our load shedding of a microgrid, i.e., CFP LS BIDDING and PROPOSE LS BIDDING. CFP LS BIDDING message is sent by AgMGOCC-LS to initiate a bidding process. PROPOSE LS BIDDING message is sent by AgLoad to bid for the power supplied. In Table 1, the purpose of the extended performatives for the load shedding is described.
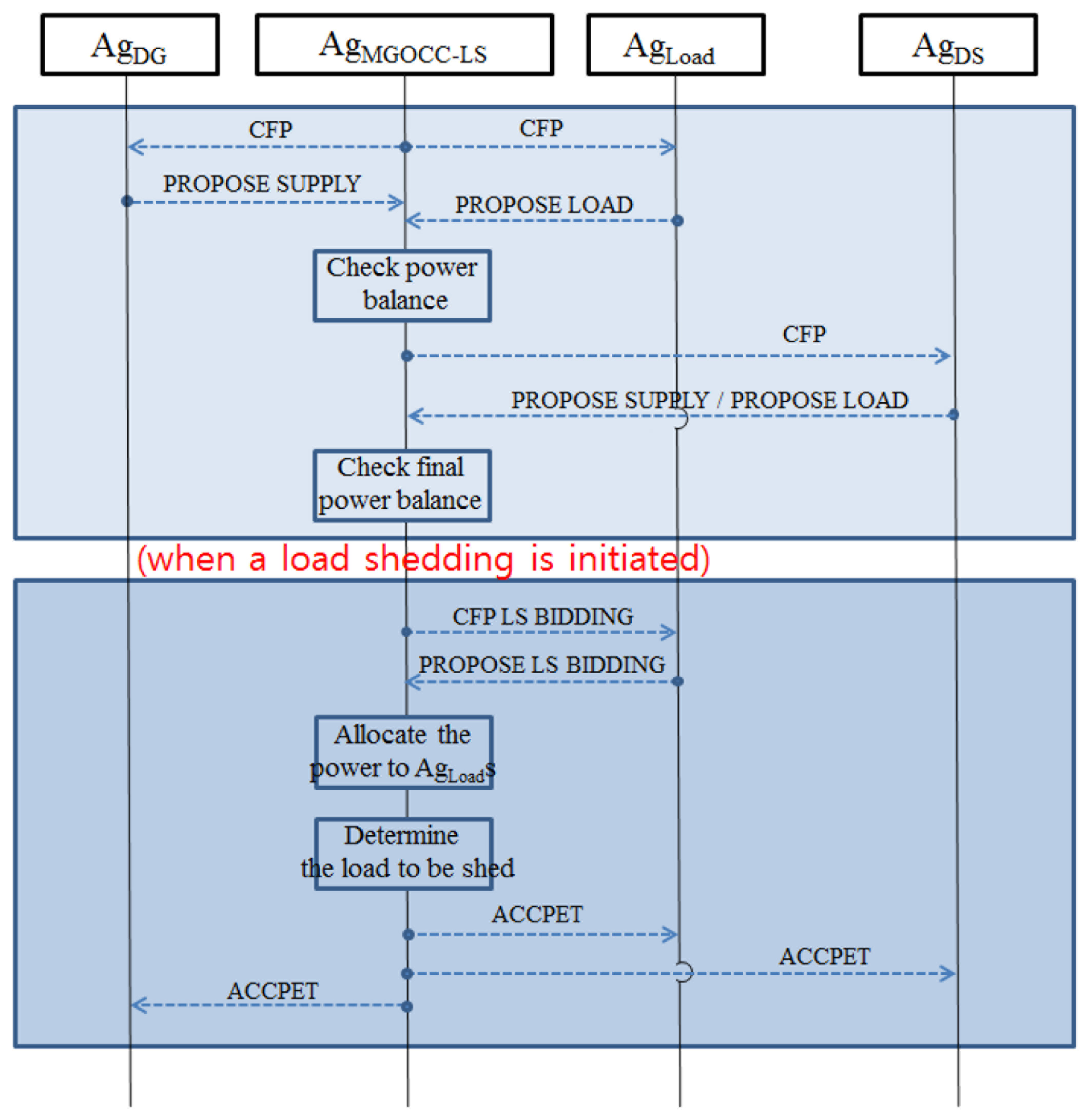
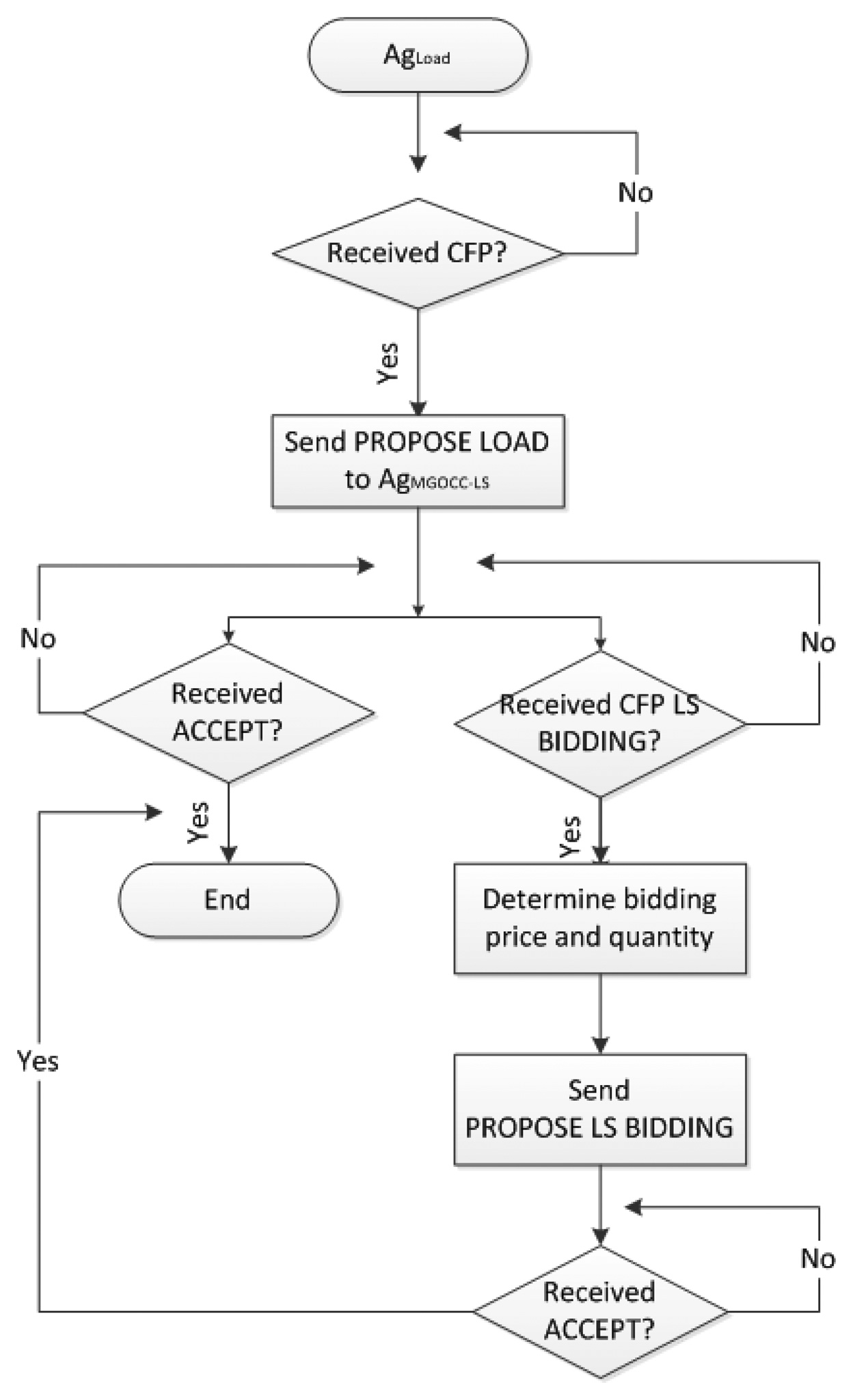
Figure 1 shows the message flows based our extended FIPA-CNP performatives. In the figure, the upper box is for the microgrid operation defined by [3], and the lower box is for the load shedding proposed by this paper. First of all, AgMGOCC-LS sends CFP messages to AgDGs and AgLoads to make an operational plan of the next interval. AgDGs and AgLoads respond with PROPOSE SUPPLY and PROPOSE LOAD messages, respectively. Once AgMGOCC-LS receives the messages from AgDGs and AgLoads, it checks the balance between power supply and power demand. Then, AgMGOCC-LS informs AgDSs of the information of power balance by sending CFP messages. AgDSs decide their roles as power suppliers or power consumers and send PROPOSE SUPPLY (as power suppliers) or PROPOSE LOAD (as power consumers) messages. When AgMGOCC-LS receives the messages from AgDSs, it finally checks the power balance. If the total power supply is less than the total power demand, AgMGOCC-LS initiates the load shedding. For the load shedding, AgMGOCC-LS starts a bidding process by sending CFP LS BIDDING messages to AgLoads. When AgLoads receive the messages, AgLoads determine the bidding prices and quantities though their bidding strategies. Then, they send PROPOSE LS BIDDING messages including their bidding prices and quantities to AgMGOCC-LS. Once AgMGOCC-LS gathers the bidding information from AgLoads, it allocates the power to AgLoads and decides the amount of load to be shed. Lastly, AgMGOCC-LS notifies the final amount of power generated and power consumed to AgDGs and AgLoads respectively by sending ACCEPT messages. When AgLoads receive ACCEPT messages as the results of the bidding, AgLoads learn from experience of the previous bidding and update their bidding strategies through the learning. The process repeats at each interval. Figures 2 and 3 show the detailed algorithms of AgMGOCC-LS and AgLoad for the load shedding in a microgrid.
For communication among agents, a modified version of the Knowledge Query and Manipulation Language (KQML) [25] is employed and the following message format is used:
4. Implementation of Distributed Load-Shedding System
In this paper, we implement the proposed system by using the Agent-based Architecture of Distributed Information Processing System (ADIPS)/Distributed Agent System based on Hybrid Architecture (DASH) framework as an agent development platform [26]. The main features of the ADIPS/DASH framework are summarized as below:
The ADIPS/DASH is a repository-based MAS framework which consists of a distributed agent workplace and an agent repository;
A repository manages various DASH agents and is responsible to design and realize MAS based on the users' requests;
A workplace is an agent execution environment on a distributed computer platform and it is responsible to monitor and control a behavior of agents realized by a repository;
An agent is designed and implemented to describe the agent's behavior knowledge for cooperative problem solving together with the agent's meta-knowledge for managing an agent in a repository;
The ADIPS/DASH framework provides a wrapping mechanism to utilize the external software module such as a Java program as a procedural knowledge of an agent;
Agents can communicate with different types of agents, such as FIPA-compliant JADE agents, by using the Agent Communication Language (ACL) messages of DASH agents.
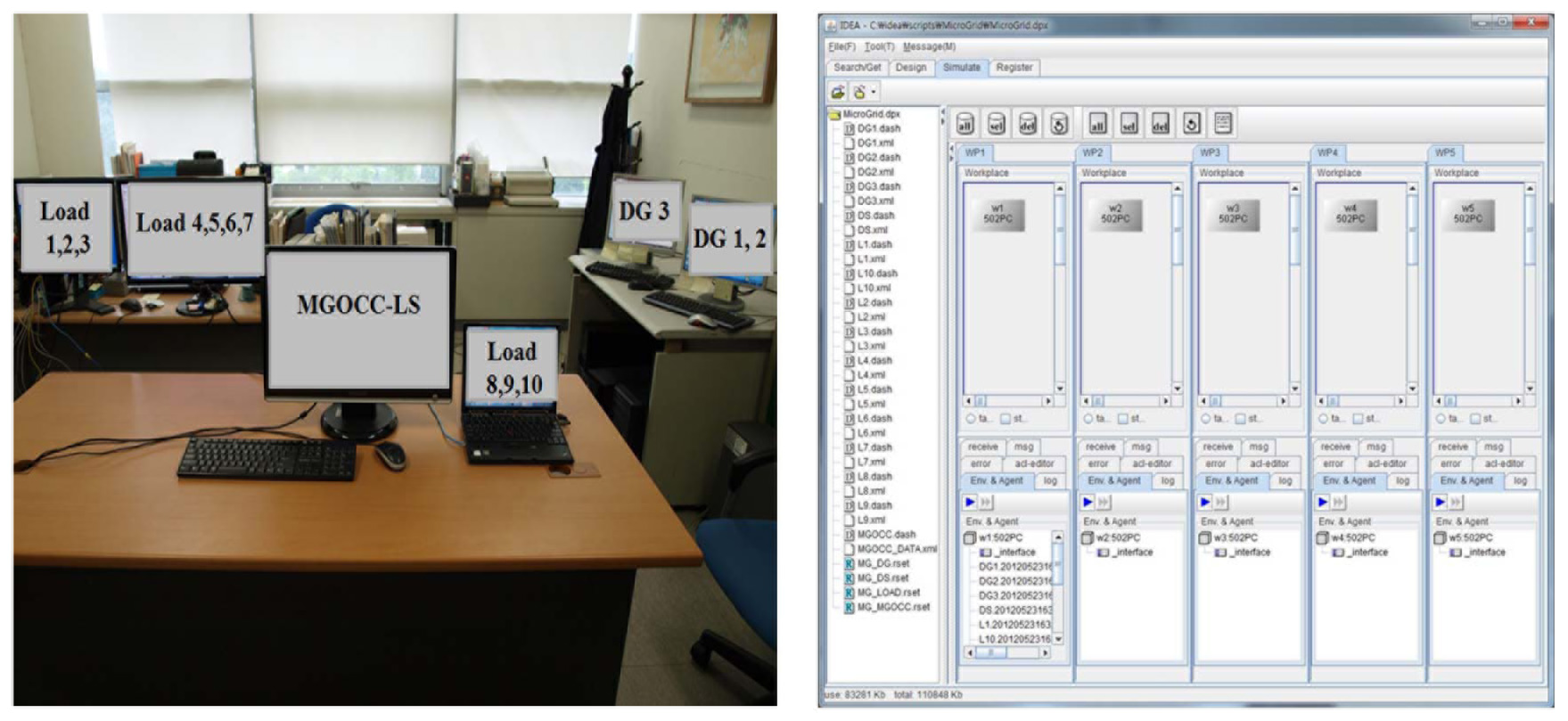
In order to show the functionality and feasibility of the proposed system, we configure our system with one MGOCC-LS, three DGs, and ten Loads. Figure 5 indicates our system in a distributed environment based on six PCs. The left picture of the figure shows the test environment of our laboratory. As you can see, AgMGOCC-LS is on one PC, three AgDGs are on two PCs, and 10 AgLoads are on three PCs. Agents use the Internet for communications. The right picture of the figure shows the start-up screen to configure a test scenario. In our system, the total load demand (i.e., ) is 1300 kWh. The total supply (i.e., ) is set to 25%, 50%, and 75% of the total load demand, respectively. In other words, the total supply is set to 325 kWh for 25% (we call it “25% test scenario”), the supply is set to 650 kWh for 50% (we call it “50% test scenario”), and the supply is set to 975 kWh for 75% (we call it “75% test scenario”). For example, in the case of 50% test scenario, 650 kWh is composed of 200 kWh, 200 kWh, and 250 kWh for three DGs. We divide the time in a day to 24 intervals for a microgrid operation, and the length of each interval is one hour. The amount of load demand of an AgLoad for each interval follows a Poisson distribution. Besides, for each interval, each AgLoad randomly selects its bidding price within a reasonable range between $29 and $38. The range is according to average market values of the previous month of the PJM (Pennsylvania, New Jersey, Maryland) power market [27]. When AgMGOCC-LS gathers bids from 10 AgLoads, it allocates the power to the AgLoads according to the proportional fairness algorithm. In other words, as a AgLoad has the high bidding price, it gets more power to be allocated.
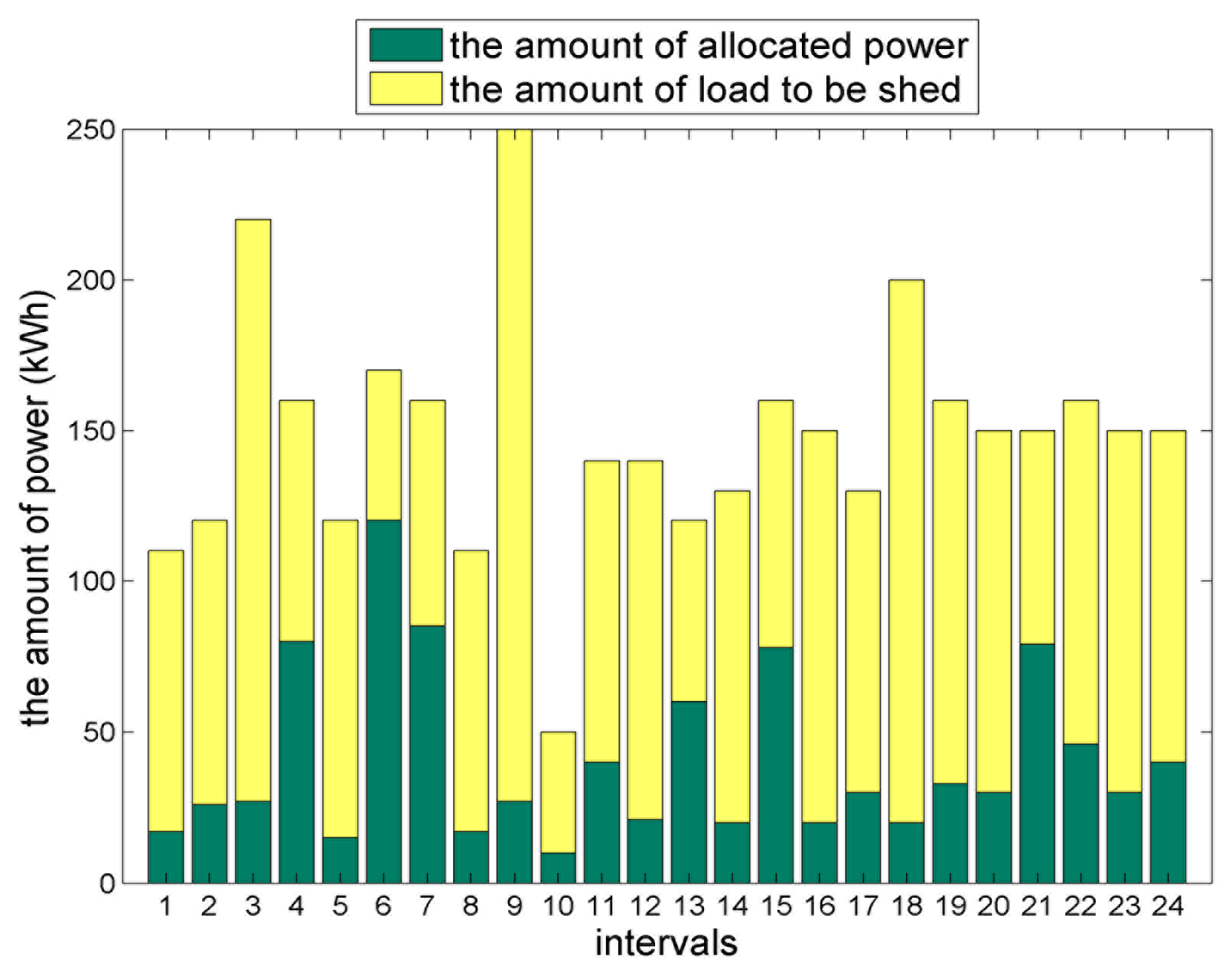
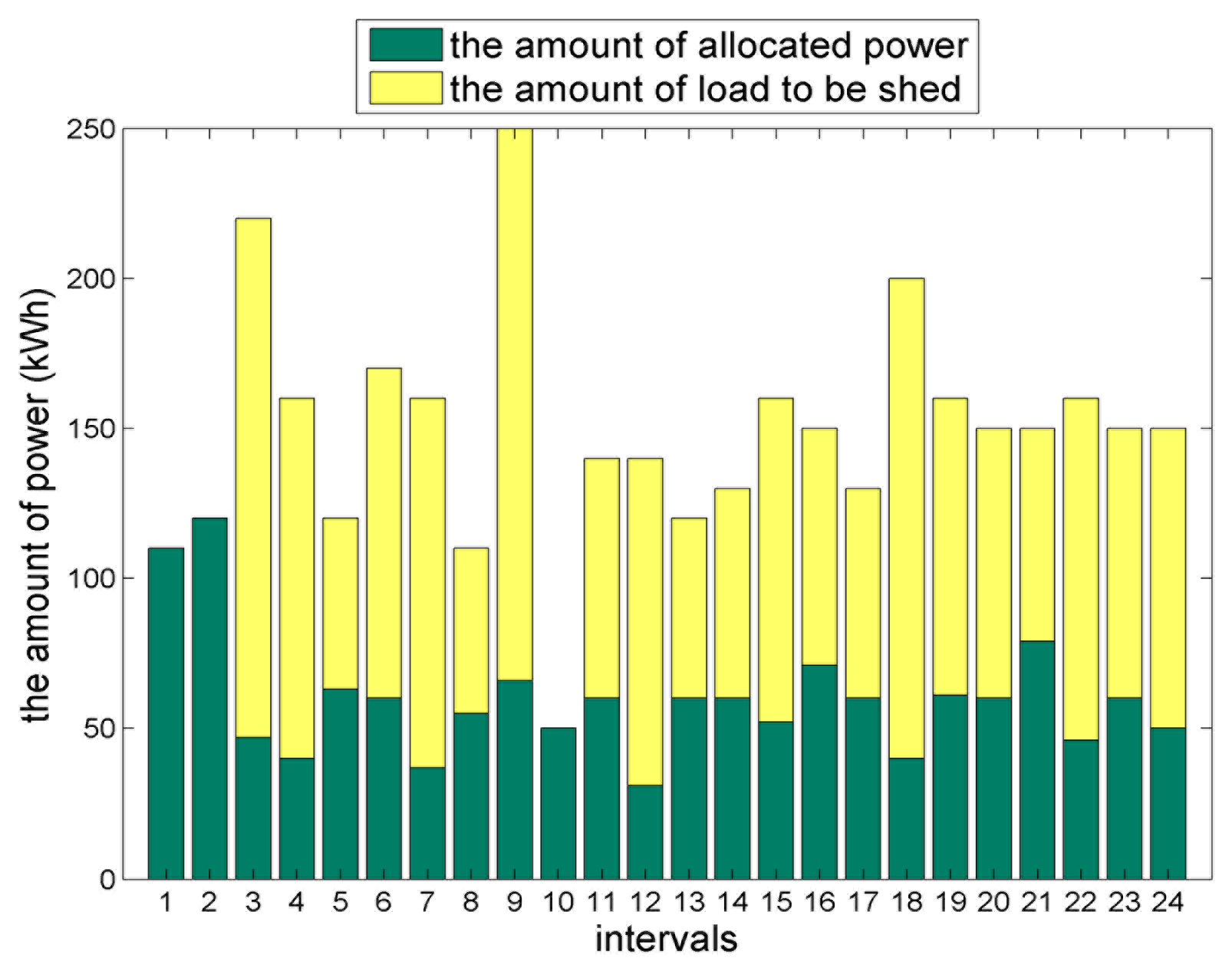
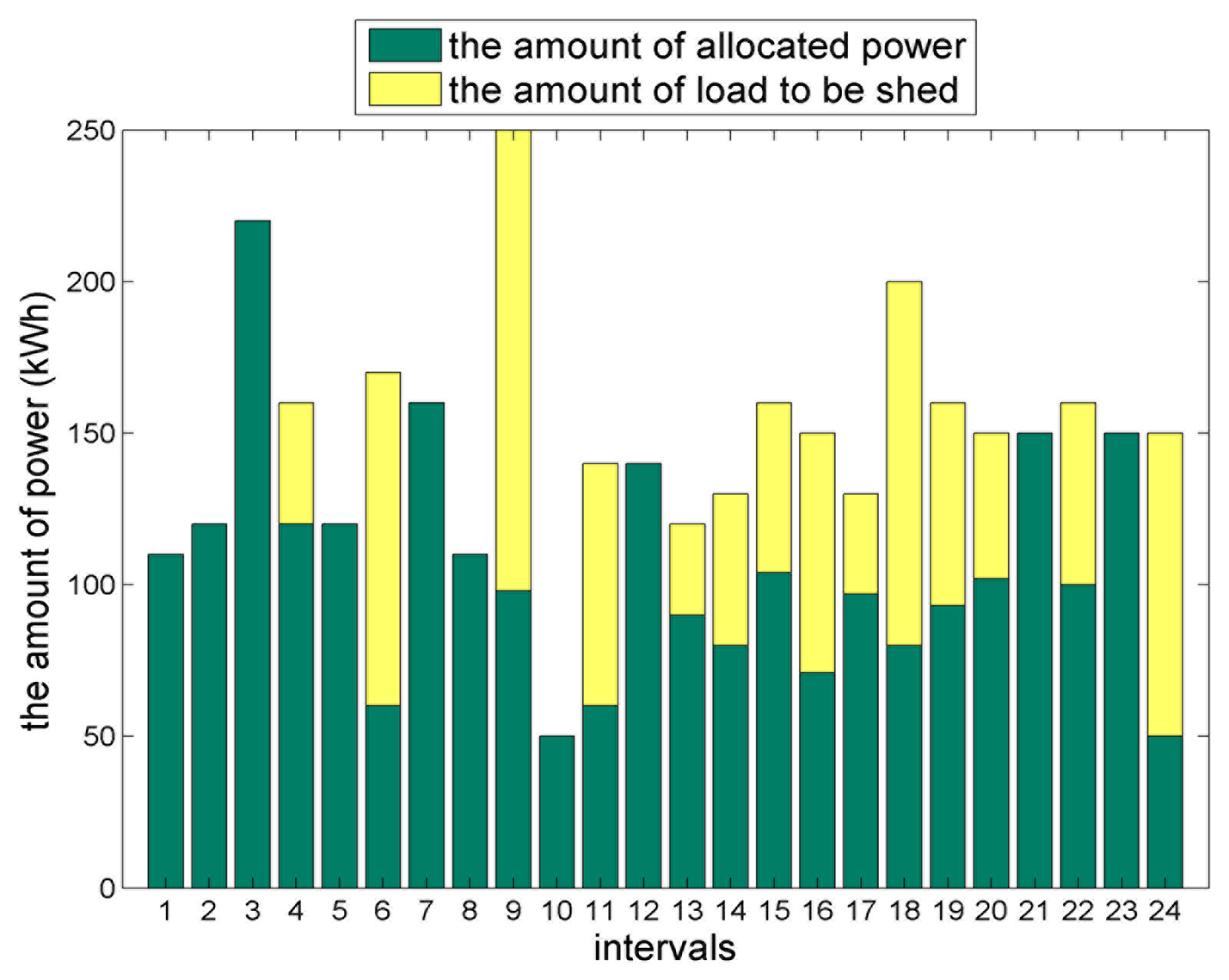
Figures 6, 7 and 8 show the functionality of our system in three test scenarios. The figures show the amount of load to be shed of Load 5 for 24 intervals. In the figures, the height of each bar indicates the amount of load to be demanded, and the dark green color of each bar indicates the amount of load to be allocated. At each interval, the amount of load demand and bidding price of Load 5 are changed, so the amount of load to be allocated is changed according to the bidding price. As shown in Figure 6, since the total power supply is much less than the total power demand, much of load demand is shed. On the other hands, as shown in Figures 7 and 8, as the total power supply increases, the amount of load to be shed decreases.
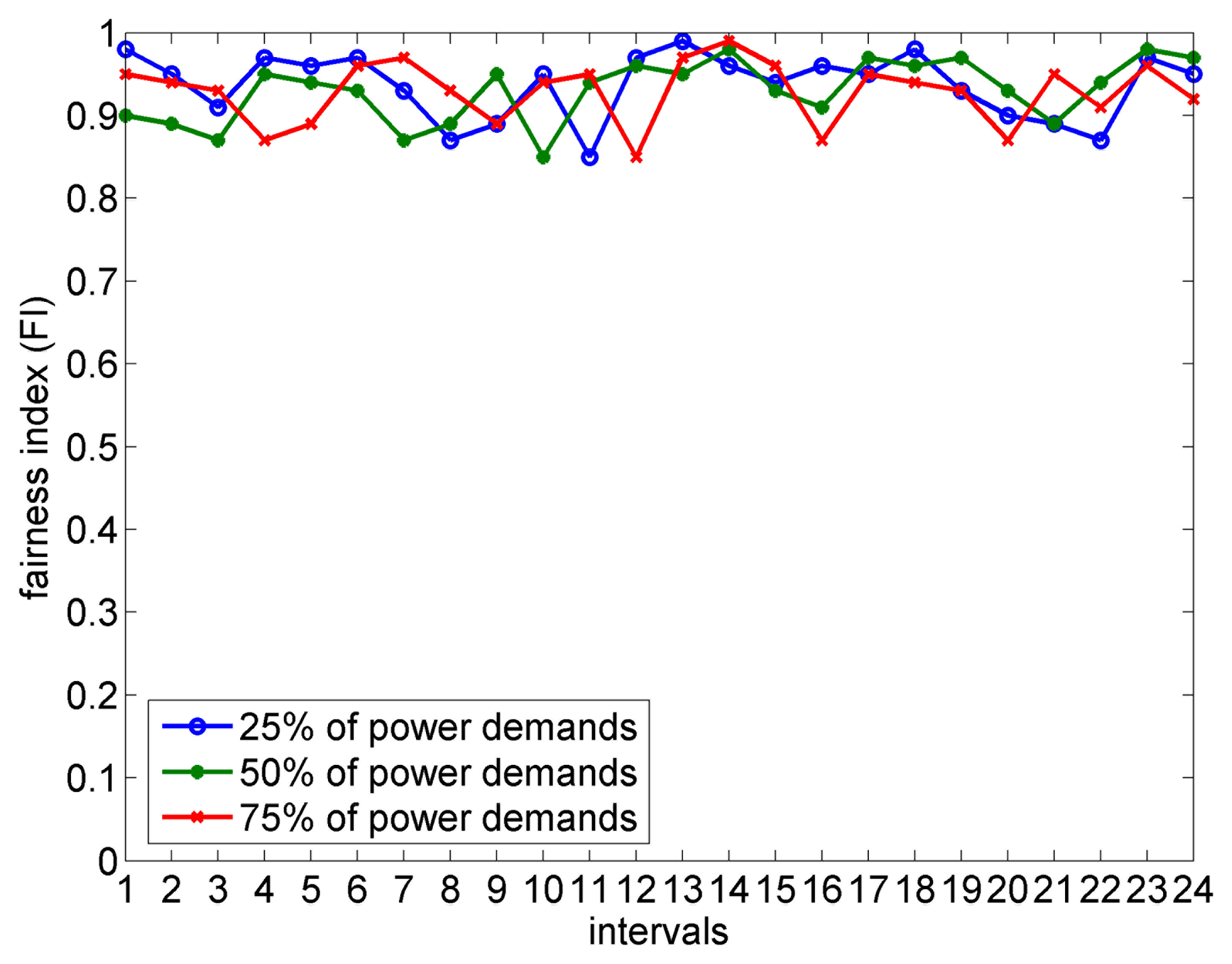
Generally, in order to determine whether users are receiving a fair share of resources, fairness metrics or measures are used. Jain's fairness index (FI) [28] is the most popular fairness metrics:
Figure 9 shows FI in three test scenarios. Fair allocating of resources achieves index of 1. As you can see, the values of FI in all scenarios indicate that Loads are receiving a fair share of power. Figure 10 shows the running time of our load-shedding process. The dominant factor of the running time of our load-shedding process is the time to run the proportional fairness algorithm. In the figure, we change the amount of total supply to show the feasibility of our system. We can see the running time of our system is less than 0.04 s in three test scenarios.
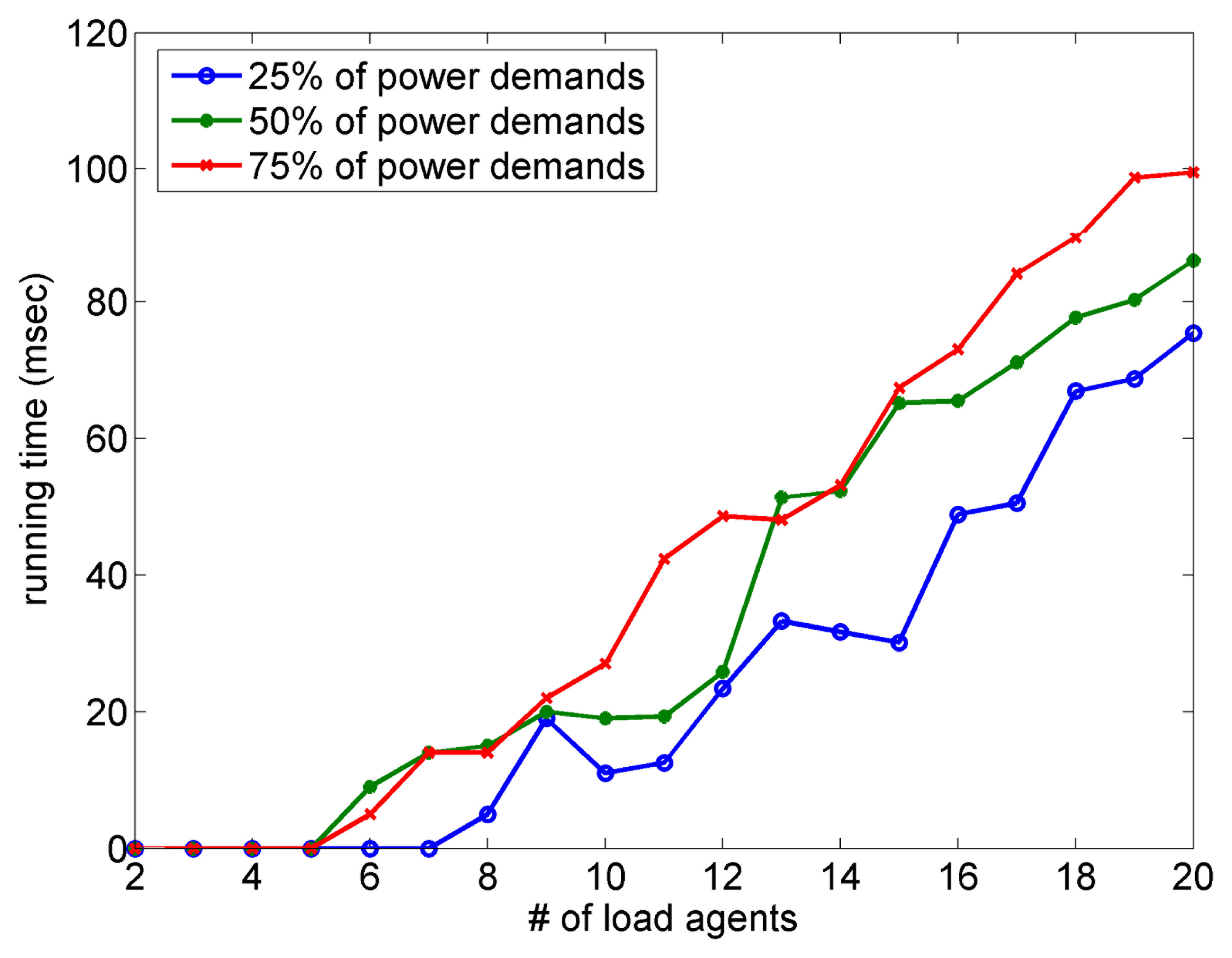
Figure 11 shows the running time with varying the number of agents in a microgrid. In the figure, we change the number of AgLoads from 2 to 20 in order to show the feasibility of our system in various scenarios. We can see that the running time of our system is less than 0.1 s in the various scenarios.
5. Conclusions
We have presented a distributed load-shedding system for an agent-based autonomous operation in an islanded microgrid. We have defined the functionalities of agents for components of a microgrid and interaction protocols to share the information among agents. The system includes a power allocation algorithm for a bidding process as a step of distributed load-shedding system. We have implemented the proposed system using ADIPS/DASH framework as an agent development platform. The implemented system has been tested on a distributed environment to evaluate the functionality and feasibility of our system.
The proposed system serves to bring out the numerous avenues for research in a load shedding field of a microgrid. Many challenges remain to be overcome in terms of reliability, bidding strategy, and interoperability. We plan to find an optimal bidding strategy of a Load to maximize the profit of the Load in a long run.
Acknowledgments
This work was supported by the GRRC program of Gyeonggi province. [(GRRC SUWON2013-B4), Research on Precision Location Tracking System for Real-Time Situation]
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hatziargyriou, N.D. Microgrids. IEEE Power Energy 2008, 6, 26–29. [Google Scholar]
- IEEE SCC21 Standards Coordinating Committee on Fuel Cells, Photovoltaics, Dispersed Generation, and Energy Storage. In Guide for Design, Operation, and Integration of Distributed Resource Island Systems with Electric Power Systems; IEEE Standard 1574.4; IEEE: Washington, DC, USA, 2011; pp. 1–54.
- Kim, H.-M.; Kinoshita, T. A multiagent system for microgrid operation in the grid-interconnected mode. KIEE J. Electr. Eng. Technol. 2011, 5, 246–254. [Google Scholar]
- Kim, H.-M.; Lim, Y.; Kinoshita, T. An intelligent multiagent system for autonomous microgrid operation. Energies 2012, 5, 3347–3362. [Google Scholar]
- Xiao, Z.; Li, T.; Huang, M.; Shi, J.; Yang, J.; Yu, J.; Wu, W. Hierarchical MAS based control strategy for microgrid. Energies 2010, 3, 1622–1638. [Google Scholar]
- Khodayar, M.E.; Barati, M.; Shahidehpour, M. Integration of high reliability distribution system in microgrid operation. IEEE Trans. Smart Grid 2012, 3, 1997–2006. [Google Scholar]
- Saffarian, A.; Sanaye-Pasand, M.; Asadi, H. Performance Investigation of New Combinational Load Shedding Schemes. Proceedings of the IEEE International Conference on Power System Technology and IEEE Power India Conference (POWERCON) 2008, New Delhi, India, 12–15 October 2008; pp. 1–8.
- Hong, Y.-Y.; Hsiao, M.-C.; Chang, Y.-R.; Lee, Y.-D.; Huang, H.-C. Multiscenario underfrequency load shedding in a microgrid consisting of intermittent renewables. IEEE Trans. Power Deliv. 2013, 28, 1610–1617. [Google Scholar]
- Patodi, P.; Ray, A.K. GA Based Winner Determination in Combinatorial Reverse Auction. Proceedings of the IEEE International Conference on Emerging Applications of Information Technology, Kolkata, India, 19–20 February 2011; pp. 361–364.
- Wooldridge, M. An Introduction to Multiagent Systems, 2nd ed.; Wiley: Chichester, UK, 2008. [Google Scholar]
- Weiss, G. Multiagent Systems (Intelligent Robotics and Autonomous Agents series), 2nd ed.; The MIT Press: Boston, MA, USA, 2013. [Google Scholar]
- Rusell, S.; Norvig, P. Aritificial Intelligence: A Modern Approach, 3rd ed.; Pearson: London, UK, 2010. [Google Scholar]
- Seyedi, H.; Sanaye-Pasand, M.; Dadashzadeh, M.R. Design and Simulation of an Adaptive Load Shedding Algorithm Using a Real Network. Proceedings of the IEEE Power India Conference, New Delhi, India, 10–12 April 2006; pp. 1–5.
- Delfino, B.; Massucco, S.; Morini, A.; Scalera, P.; Silvestro, F. Implementation and Comparison of Different Underfrequency Load Shedding Schemes. Proceedings of the IEEE Power Engineering Society Summer Meeting, Vancouver, BC, Canada, 15–19 July 2001; pp. 307–312.
- Saffarian, A.; Sanaye-Pasand, M. Enhancement of power system stability using adaptive combinational load shedding methods. IEEE Trans. Power Syst. 2011, 26, 1010–1020. [Google Scholar]
- Tomsic, T.; Verbic, G.; Gubina, F. Revision of the Underfrequency Load Shedding Scheme of the Slovenian Power System. Proceedings of the IEEE Power Engineering Society General Meeting, 12–16 June 2005; pp. 1782–1787.
- Seyedi, H.; Sanaye-Pasand, M. Design of new load shedding special protection schemes for a double area power system. Am. J. Appl. Sci. 2009, 6, 317–327. [Google Scholar]
- Modi, P.; Shen, W.-M.; Tambe, M.; Yokoo, M. ADOPT: Asynchronous distributed constraint optimization with quality guarantees. Artif. Intell. 2005, 161, 149–180. [Google Scholar]
- Guptay, S.; Jainz, P.; Yeohy, W.; Ranadez, S.J.; Pontelliy, E. Solving Customer-Driven Microgrid Optimization Problems as DCOPs. Proceedings of the International Workshop on Distributed Constraint Reasoning (DCR), Beijing, China, 4 August 2013; pp. 45–59.
- Nguyen, T.-D.; Han, Y. A proportional fairness algorithm with QoS provision in downlink OFDMA systems. IEEE Commun. Lett. 2006, 10, 760–762. [Google Scholar]
- Chen, L.; Li, N.; Low, S.H.; Doyle, J.C. Two Market Models for Demand Response in Power Networks. Proceedings of the IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersburg, MD, USA, 4–6 October 2010; pp. 397–402.
- Jain, P.; Gupta, S.; Ranade, S.; Pontelli, E. Optimum Operation of a Customer-Driven Microgrid: A Comprehensive Approach. Proceedings of the IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Bangalore, India, 16–19 December 2012; pp. 1–6.
- Varakantham, P.; Maheswaran, R.T.; Gupta, T.; Tambe, M. Towards Efficient Computation of Error Bounded Solutions in POMDPs: Expected Value Approximation and Dynamic Disjunctive Beliefs. Proceedings of the International Joint Conference on Artificial Intelligence, Hyderabad, India; 2007; pp. 2638–2643. [Google Scholar]
- Foundation for Intelligent Physical Agents (FIPA). Available online: http://www.fipa.org (accessed on 31 August 2012).
- Wu, X.; Sun, J. Study on a KQML-Based Intelligent Multi-Agent System. Proceedings of the IEEE International Conference on Intelligent Computation Technology and Automation, Changsha, China, 11–12 May 2010; pp. 466–469.
- IDEA/DASH Tutorial. Available online: http://www.ka.riec.tohoku.ac.jp/idea/index.html (accessed on 10 April 2013).
- PJM Operational Data. Available online: http://www.pjm.com (accessed on 16 May 2013).
- Guo, C.; Sheng, M.; Zhang, Y.; Wang, X. A Jain's index perspective on α-fairness resource allocation over slow fading channels. IEEE Commun. Lett. 2013, 17, 705–708. [Google Scholar]


| Performative | Purpose |
|---|---|
| CFP | sent by AgMGOCC-LS to initiate a microgrid operation process |
| CFP LS BIDDING | sent by AgMGOCC-LS to AgLoad in order to initiate a bidding process for the load shedding |
| PROPOSE SUPPLY | sent by AgDG to AgMGOCC-LS in order to propose the amount of power supplied with a price per unit |
| PROPOSE LOAD | sent by AgLoad to AgMGOCC-LS in order to propose the amount of load demanded |
| PROPOSE LS BIDDING | sent by AgLoad to AgMGOCC-LS in order to propose its bidding price and quantity to buy the power supplied |
| REFUSE | sent by AgDG, AgLoad, or AgDS to refuse to send a proposal |
| ACCEPT | sent by AgMGOCC-LS to accept a proposal |
| REJECT | sent by AgMGOCC-LS to reject a proposal |
| FAILURE | sent by AgDG, AgLoad, or AgDS to tell the requested action failed |
| INFORM | sent by AgDG, AgLoad, or AgDS to tell results of action carried out |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lim, Y.; Kim, H.-M.; Kinoshita, T. Distributed Load-Shedding System for Agent-Based Autonomous Microgrid Operations. Energies 2014, 7, 385-401. https://doi.org/10.3390/en7010385
Lim Y, Kim H-M, Kinoshita T. Distributed Load-Shedding System for Agent-Based Autonomous Microgrid Operations. Energies. 2014; 7(1):385-401. https://doi.org/10.3390/en7010385
Chicago/Turabian StyleLim, Yujin, Hak-Man Kim, and Tetsuo Kinoshita. 2014. "Distributed Load-Shedding System for Agent-Based Autonomous Microgrid Operations" Energies 7, no. 1: 385-401. https://doi.org/10.3390/en7010385






