Ventilation Heat Recovery from Wood-Burning Domestic Flues. A Theoretical Analysis Based on a Triple Concentric Tube Heat Exchanger
Abstract
:1. Introduction


2. Theoretical Analysis
- -
- The system operates under steady-state conditions;
- -
- Phase change does not take place;
- -
- Bulk mean temperatures only depend on axial (x) direction;
- -
- The thermo-physical properties of the fluid streams are constant and uniform;
- -
- Thermal conduction is not assumed in fluids or walls parallel to the fluid flow direction;
- -
- Heat transfer coefficients are independent of time and axial position;
- -
- Temperature of the outside remains constant.
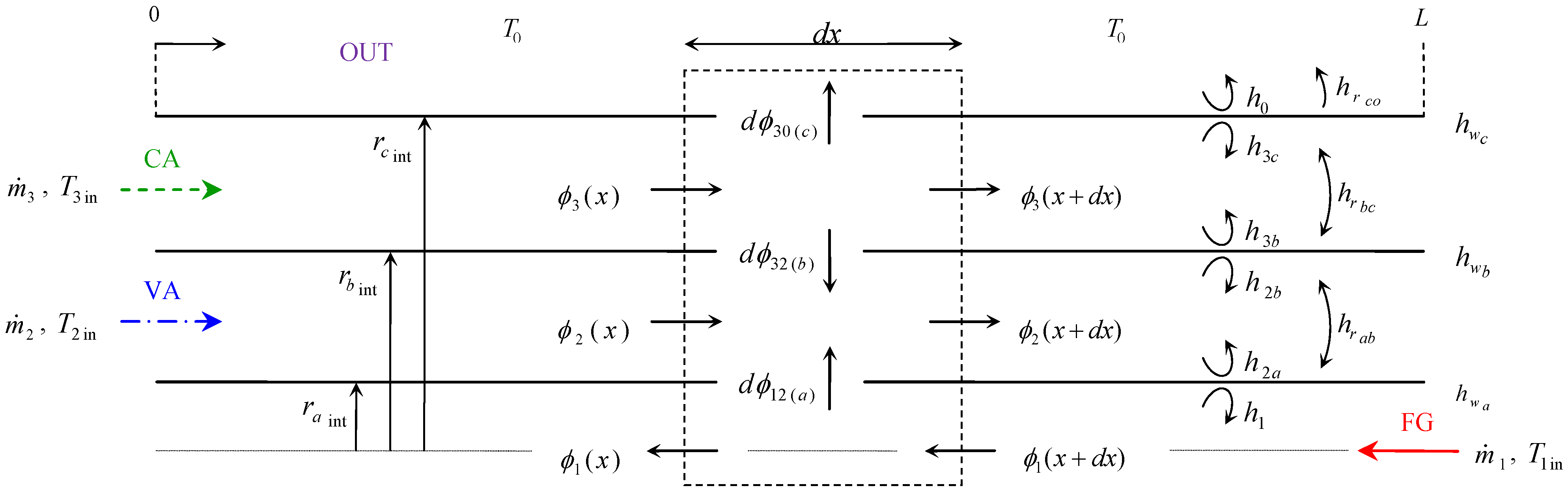
2.1. Mathematical Model
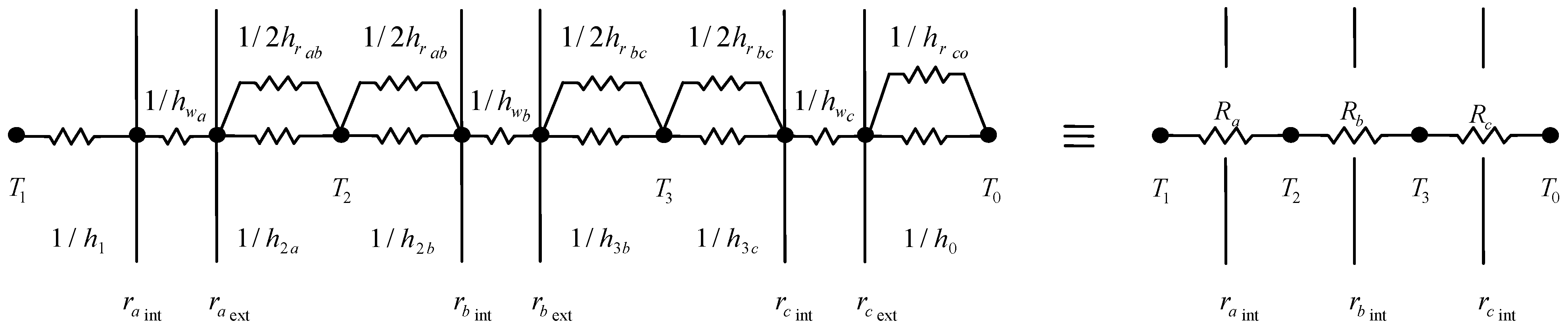
- Conductive heat transfer coefficient
- Convective heat transfer coefficient
| Inner tube: | Nu = 0.023 Re4/5 Pr1/3 | |
| Annulus: | Nu = 0.020 Re4/5 Pr1/3 (Douter / Dinner)0,53 | for the inner wall |
| Nu = 0.027 Re4/5 Pr1/3 | for the outer wall |
| Laminar flow: | 104 ≤ Ra ≤ 109 | Nu = 0.59 Ra1/4 |
| Turbulent flow: | 109 ≤ Ra ≤ 1013 | Nu = 0.10 Ra1/3 |
- Radiant heat transfer coefficient
2.2. Analytical Solutions
2.3. Effectiveness Relation
3. Parametric Study
3.1. Original Set of Input Data and Results
| L = 1.5 m | T0 = 25 °C | Fluid 1 | Fluid 2 | Fluid 3 | |
|---|---|---|---|---|---|
| FG | VA | CA | |||
| Input data | Da, b, c | (mm) | 80 | 180 | 230 |
| Tin 1, 2, 3 | (°C) | 180 | 15 | 60 | |
| C1, 2, 3 | (W/K) | 10 | 20 | 5 | |
| Computed data | Ua, b, c | (W/(m2 K)) | 5.0 | 3.2 | 2.0 |
| TCTHE-NI | Tout 1, 2, 3 | (°C) | 153.09 | 31.6 | 38.2 |
| TCTHE-PI | Tout 1, 2, 3 | (°C) | 153.13 | 32.1 | 45.2 |

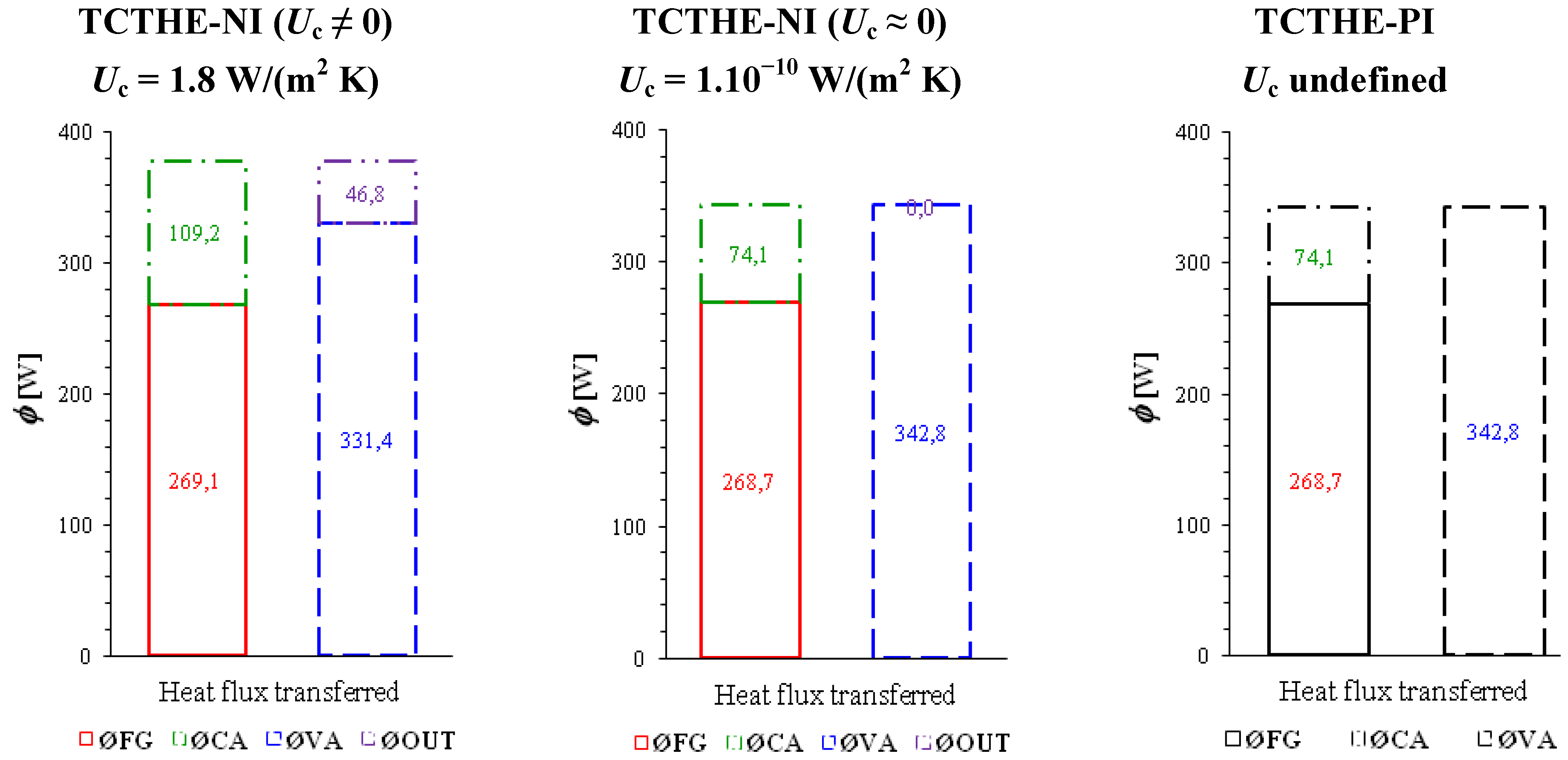
3.2. Influence of Increasing Length
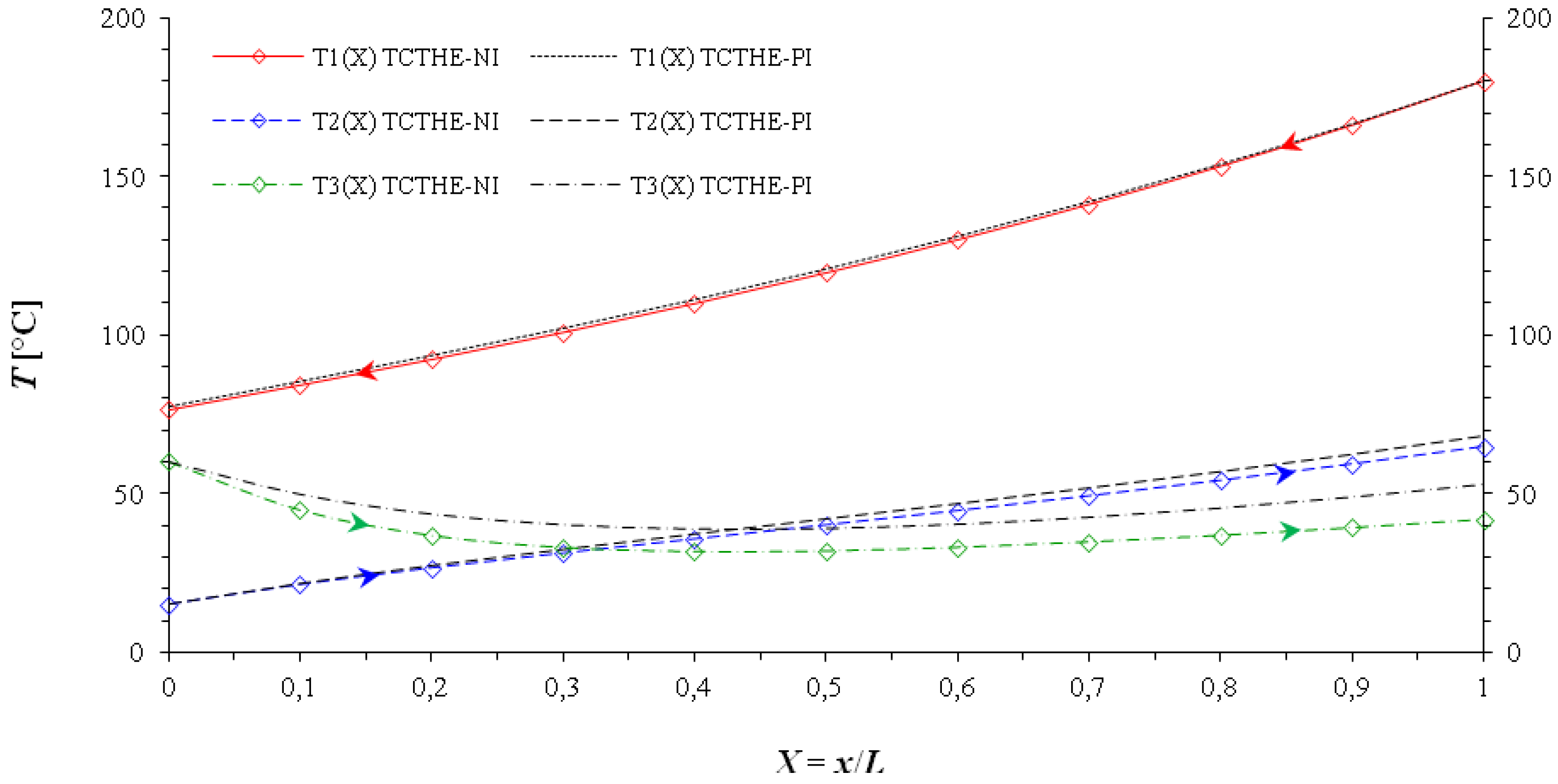
| L = 10 m | T0 = 25 °C | Fluid 1 | Fluid 2 | Fluid 3 | |
|---|---|---|---|---|---|
| FG | VA | CA | |||
| Computed data | Ua, b, c | (W/(m2 K)) | 5.0 | 2.5 | 1.5 |
| TCTHE-NI | Tout 1, 2, 3 | (°C) | 76.5 | 64.7 | 42.0 |
| TCTHE-PI | Tout 1, 2, 3 | (°C) | 77.5 | 68.0 | 53.0 |
3.3. Influence of Adding Fins
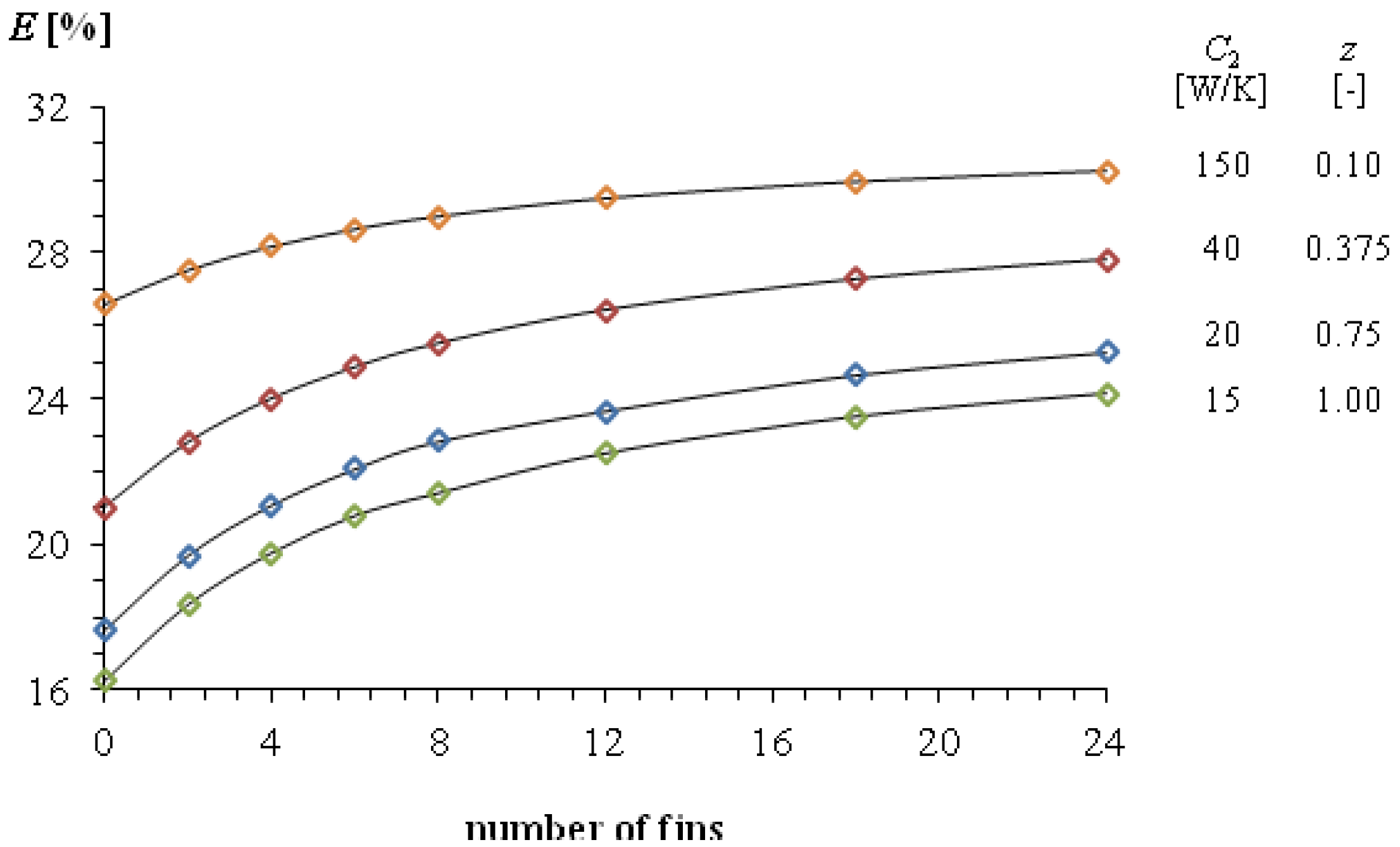
3.4. Effectiveness Charts
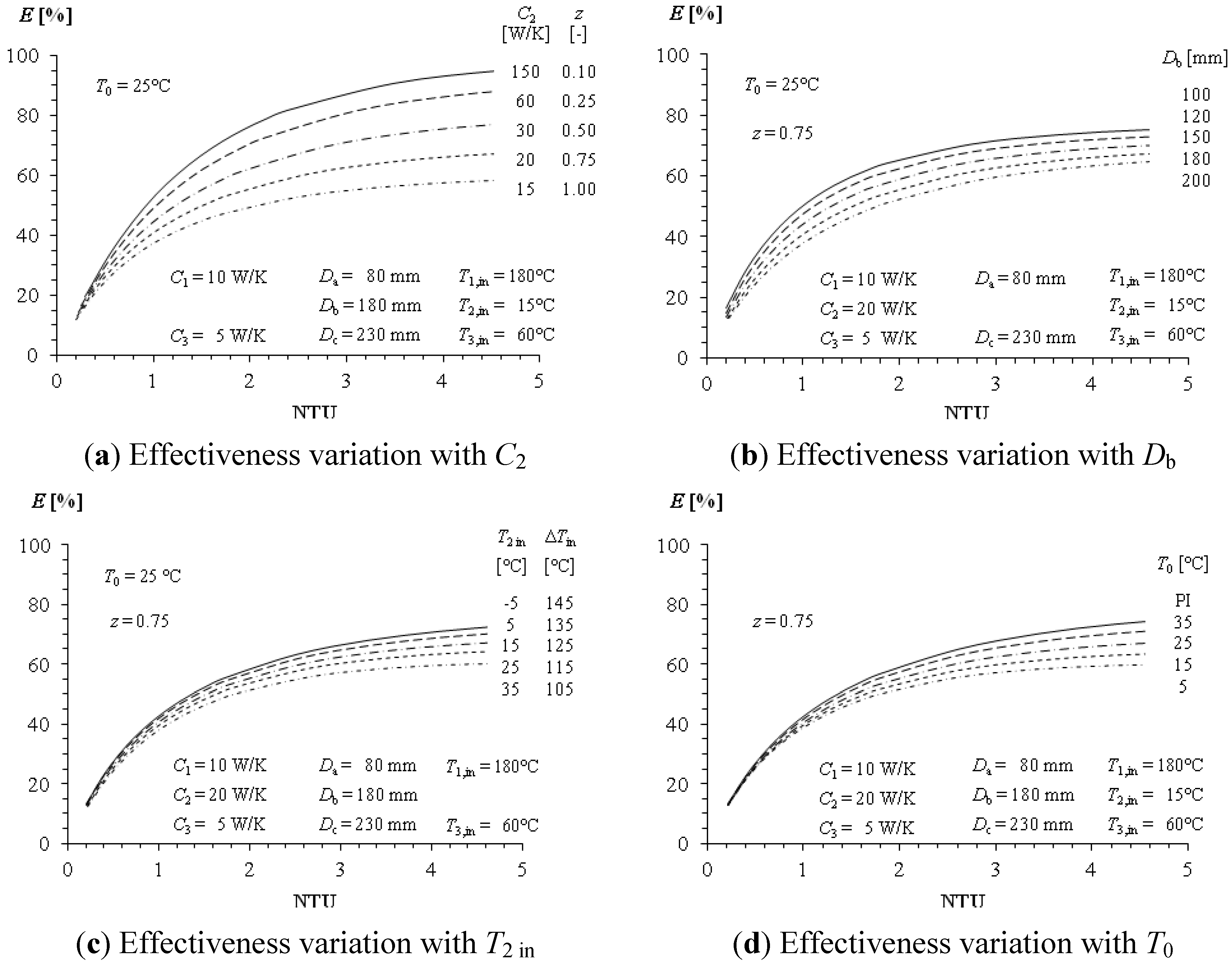
3.5. Importance of Heat Losses
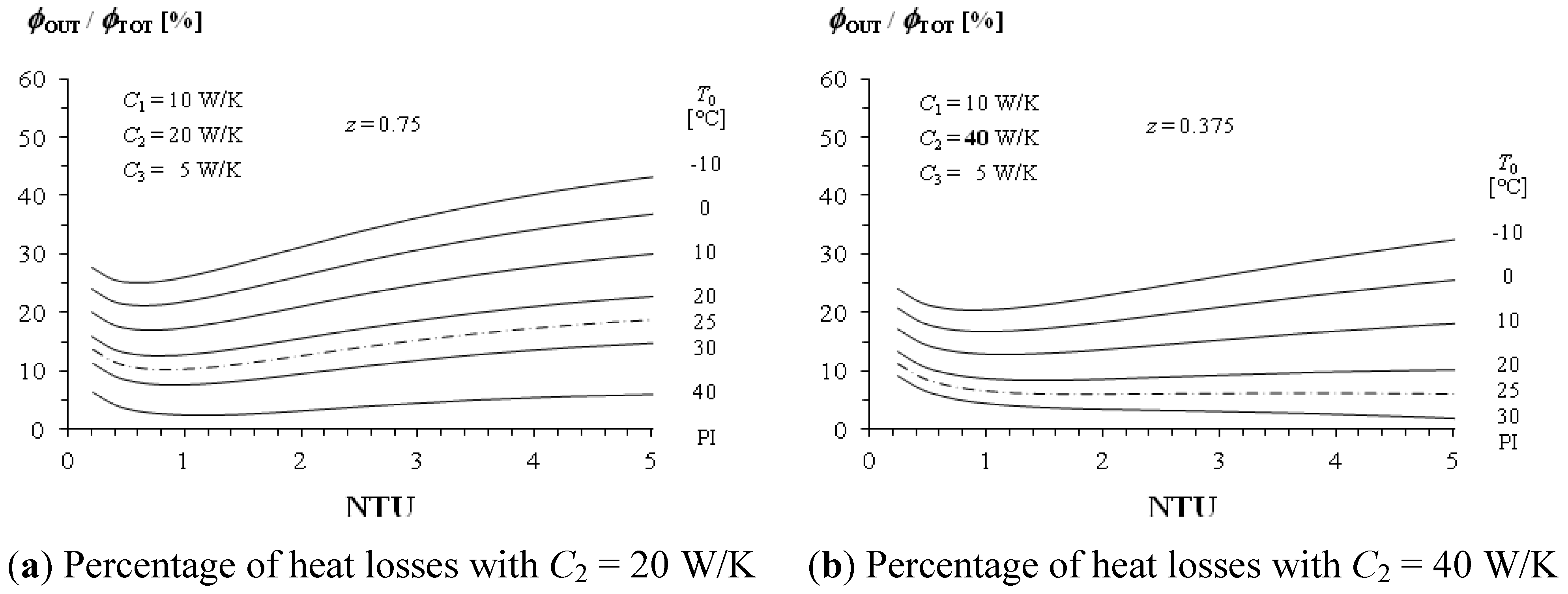
4. Conclusions
Nomenclature
| A | heat transfer area (m2) |
| cp | specific heat capacity at constant pressure [J/(kg·K)] |
| C | heat capacity rate (J/K) |
| Cr | dimensionless heat capacity ratio (-) |
| dA | differential heat transfer area (m2) |
| dϕ | differential heat flow rate (W) |
| dx | axial discretization step (m) |
| D | diameter (m) |
| Dh | hydraulic diameter (m) |
| e | thickness (m) |
| E | effectiveness (%) |
| h | convective heat transfer coefficient [W/(m2·K)] |
| hr | radiant heat transfer coefficient (W/(m2 K)) |
| hw | conductive heat transfer coefficient [W/(m2·K)] |
| L | length (m) |
mass flow rate (kg/s) | |
| N | dimensionless ratio of overall conductance UA and heat capacity rate C (-) |
| Nu | Nusselt number (-) |
| NTU | number of transfer units (-) |
| P | perimeter (m) |
| Pr | Prandtl number (-) |
| r | radius (m) |
| Ra | Rayleigh number (-) |
| Re | Reynolds number (-) |
| T | temperature (K) |
| U | overall heat transfer coefficient [W/(m2·K)] |
| X | dimensionless length coordinate (-) |
| x | axial coordinate (m) |
| z | heat capacity rate ratio (min/max) (-) |
Greek Symbols
| ε | emissivity (-) |
| λ | thermal conductivity [W/(m·K)] |
| σ | Stephan-Boltzmann constant [5.67 × 10−8 W/(m2·K4)] |
| ϕ | heat flow rate (W) |
| ηf | fin efficiency (-) |
| ηo | overall surface efficiency (-) |
| θ | dimensionless temperature (-) |
| ΔT | temperature difference (K) |
| ΔTin | temperature difference depending on inlet temperatures and heat capacity rates (K) |
Subscripts
| 0 | ambient air (surroundings) |
| 1 | first fluid (flue gases) |
| 2 | second fluid (ventilation air) |
| 3 | third fluid (combustion air) |
| a | internal tube |
| b | intermediate tube |
| c | external tube |
| o | outside (surroundings) |
| f | fin(s) |
| in | inlet |
| out | outlet |
| ext | external |
| int | internal |
| inner | inner |
| outer | outer |
| actual | actual |
| m | mean |
| max | maximum |
| min | minimum |
| tot | total |
Acronyms
| FG | flue gases |
| VA | ventilation air |
| CA | combustion air |
| OUT | outside |
| TOT | total |
| RSWPS | room-sealed wood pellet stove |
| MVHR | mechanical ventilation heat recovery |
| TCTHE | triple concentric tube heat exchanger |
| TCTHE-PI | triple concentric tube heat exchanger with perfect insulation |
| TCTHE-NI | triple concentric tube heat exchanger with no insulation |
| DCTHE-NI | double concentric tube heat exchanger with no insulation |
Acknowledgments
References
- Plateforme de Recherche et D'expérimentation sur l'Energie dans le Bâtiment (PREBAT); International Building and Energy Comparison—Final Report; PREBAT: Paris, France, 2007.
- Mardiana-Idayu, A.; Riffat, S.B. Review on heat recovery technologies for building applications. Energy Buildings 2012, 16, 1241–1255. [Google Scholar]
- El Fouih, Y.; Stabat, P.; Rivière, P.; Hoang, P.; Archambault, V. Adequacy of air-to-air heat recovery ventilation system applied in low energy buildings. Energy Buildings 2012, 54, 29–39. [Google Scholar] [CrossRef]
- Laverge, J.; Janssens, A. Heat recovery ventilation operation traded off against natural and simple exhaust ventilation in Europe by primary energy factor, carbon dioxide emission, household consumer price and exergy. Energy Buildings 2012, 50, 315–323. [Google Scholar] [CrossRef]
- Feist, W.; Schnieders, J.; Dorer, V.; Haas, A. Re-inventing air heating: Convenient and comfortable within the frame of the Passive House concept. Energy Buildings 2005, 37, 1186–1203. [Google Scholar] [CrossRef]
- Pfluger, R. Wood Stoves in Passive Houses—Strategies for Comfort. In Proceedings of the 12th International Conference on Passive House, Nuremberg, Germany, 11–12 April 2008.
- Consumer Safety Commission. Recommendation on Hot Air Redistribution Systems. Available online: http://www.securiteconso.org/article230.html (assessed on 16 September 2012).
- Peigné, P. Étude d'un système combiné de ventilation et de chauffage au bois dans les bâtiments à basse consommation d'énergie. Ph.D. Thesis, Université La Rochelle, La Rochelle, France, 2012. [Google Scholar]
- Morley, T.B. Exchange of heat between three fluids. Engineer 1933, 155, 314–316. [Google Scholar]
- Rabinovich, G.D. Steady state heat transfer among three streams in a parallel flow recuperator. [in Russian]. Inzh.-Fiz. Zh. 1961, 4, 37–43. [Google Scholar]
- Wolf, J. General solution of the equations of parallel flow multichannel heat exchangers. Int. J. Heat Mass Tran. 1964, 7, 901–919. [Google Scholar] [CrossRef]
- Aulds, D.D.; Barron, R.F. Three-fluid heat exchanger effectiveness. Int. J. Heat Mass Tran. 1967, 10, 1457–1462. [Google Scholar] [CrossRef]
- Sorlie, T. Three Fluid Heat Exchanger Design Theory: Counter and Parallel Flow; Department of Mechanical Engineering, Stanford University: Stanford, CA, USA, 1962. [Google Scholar]
- Zuritz, C.A. On the design of triple concentric-tube heat exchangers. J. Food Process Eng. 1990, 12, 113–130. [Google Scholar] [CrossRef]
- Shpil’rain, E.E.; Yakimovich, K.A. Heat transfer between three media in triple countercurrent pipe flow. Inzh.-Fiz. Zh. 1982, 43, 1028–1033. [Google Scholar]
- Shpil’rain, E.E.; Yakimovich, K.A. Heat exchange between three streams in pipes of variable cross section. J. Eng. Thermophys. 1983, 45, 937–939. [Google Scholar]
- Krishnamurty, V.V.G.; Rao, C.V. Heat transfer in three-fluid heat exchangers. Indian J. Technol. 1964, 2, 325–327. [Google Scholar]
- Krishnamurty, V.V.G. Heat transfer in multi-fluid heat exchangers. Indian J. Technol. 1966, 4, 167–169. [Google Scholar]
- Sekulic, D.P. A compact solution of the parallel flow three-fluid heat exchanger problem. Int. J. Heat Mass Tran. 1994, 37, 2183–2187. [Google Scholar] [CrossRef]
- Sekulic, D.P.; Shah, R.K. Thermal design theory of three-fluid heat exchangers. Adv. Heat Tran. 1995, 26, 219–328. [Google Scholar]
- Prasad, R.C. Analytical solution for a double-pipe heat exchanger with non-adiabatic condition at the outer surface. Int. Commun. Heat Mass. 1987, 14, 665–672. [Google Scholar] [CrossRef]
- Prasad, R.C. Generalized solution and effectiveness for concentric tube heat exchangers. Int. J. Heat Mass Tran. 1988, 31, 2571–2578. [Google Scholar] [CrossRef]
- Ünal, A. Theoretical analysis of triple concentric-tube heat exchangers, Part 1: Mathematical modelling. Int. Commun. Heat Mass. 1998, 25, 949–958. [Google Scholar] [CrossRef]
- Ünal, A. Theoretical analysis of triple concentric-tube heat exchangers, Part 2: Case studies. Int. Commun. Heat Mass. 2001, 28, 243–256. [Google Scholar] [CrossRef]
- Ünal, A. Effectiveness-NTU relations for triple concentric-tube heat exchangers. Int. Commun. Heat Mass. 2003, 30, 261–272. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Jakob, M. Heat Transfer; John Wiley & Sons: New York, NY, USA, 1949. [Google Scholar]
- García-Valladares, O. Numerical simulation of triple concentric-tube heat exchangers. Int. J. Therm. Sci. 2004, 43, 979–991. [Google Scholar] [CrossRef]
- Sekulic, D.P.; Kmecko, L. Three-fluid heat exchanger effectiveness. J. Heat Tran. 1995, 117, 226–227. [Google Scholar] [CrossRef]
Appendix: Explanation of the Mathematical Model Coefficients
 | |||||
 | ||
 | |||||
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Peigné, P.; Inard, C.; Druette, L. Ventilation Heat Recovery from Wood-Burning Domestic Flues. A Theoretical Analysis Based on a Triple Concentric Tube Heat Exchanger. Energies 2013, 6, 351-373. https://doi.org/10.3390/en6010351
Peigné P, Inard C, Druette L. Ventilation Heat Recovery from Wood-Burning Domestic Flues. A Theoretical Analysis Based on a Triple Concentric Tube Heat Exchanger. Energies. 2013; 6(1):351-373. https://doi.org/10.3390/en6010351
Chicago/Turabian StylePeigné, Pierre, Christian Inard, and Lionel Druette. 2013. "Ventilation Heat Recovery from Wood-Burning Domestic Flues. A Theoretical Analysis Based on a Triple Concentric Tube Heat Exchanger" Energies 6, no. 1: 351-373. https://doi.org/10.3390/en6010351





