Dynamic Output Feedback Power-Level Control for the MHTGR Based On Iterative Damping Assignment
Abstract
:1. Introduction
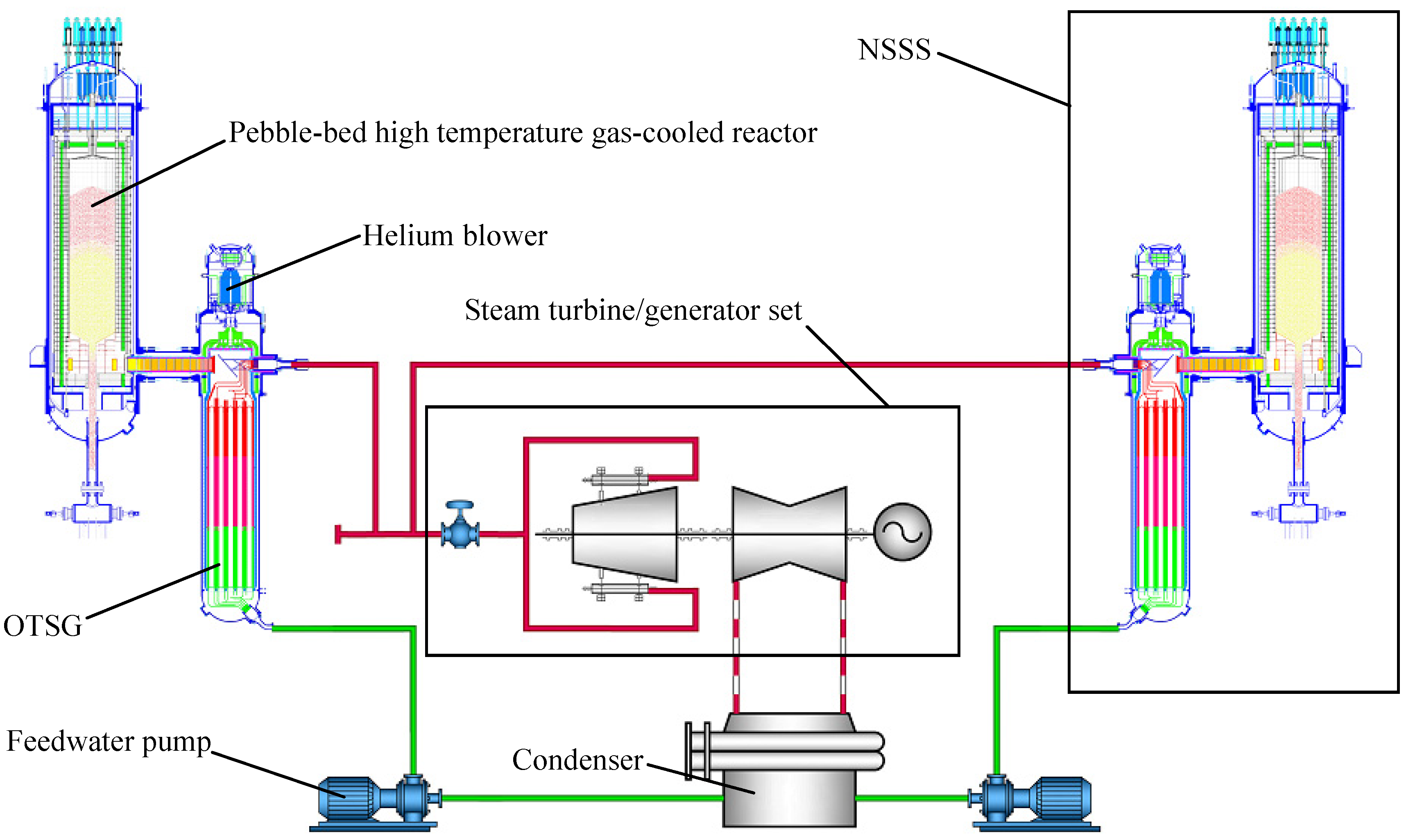
2. Nonlinear State-Space Model and Problem Formulation
2.1. Nonlinear State-Space Model

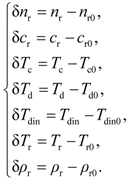
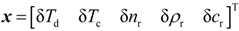
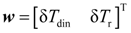

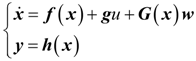

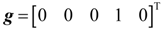
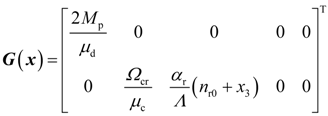
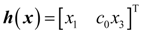
2.2. Problem Formulation
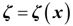
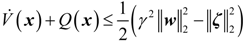
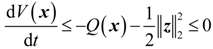
3. Power-Level Control Based on Iterative Damping Assignment
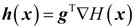
3.1. Introduction to the Concept of Feedback Dissipation Control
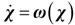
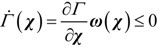
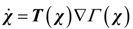
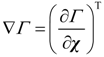 ,and T ∈ Rn×n is called the structure matrix. Moreover, if structure matrix T can be written as:
,and T ∈ Rn×n is called the structure matrix. Moreover, if structure matrix T can be written as:
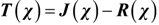
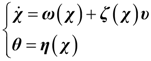


3.2. Design of the Power-Level Control Based on Iterative Damping Assignment
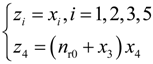
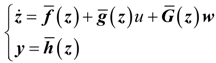
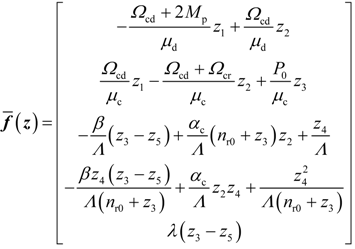
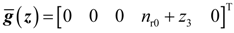
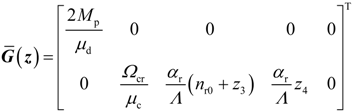
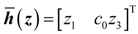
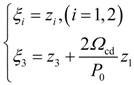
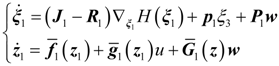

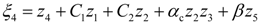
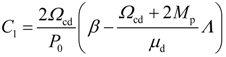
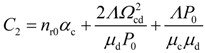
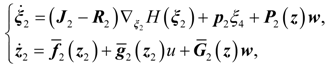

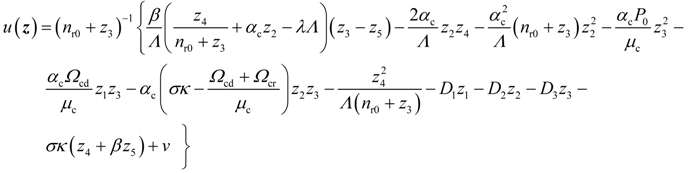

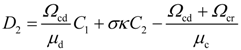
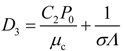
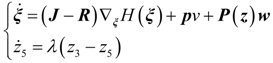
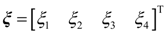

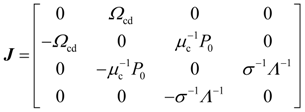
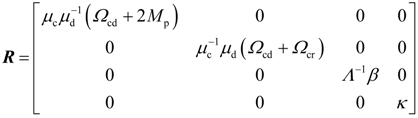
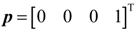
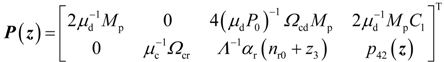
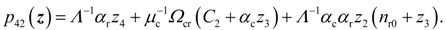
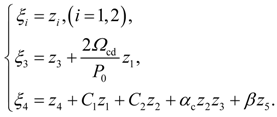
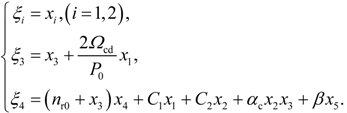

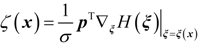
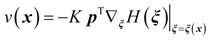

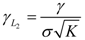
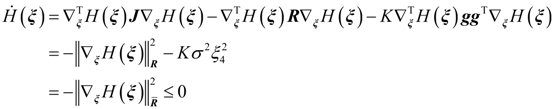
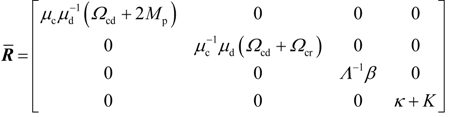
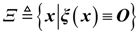
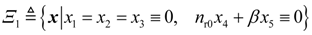
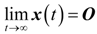
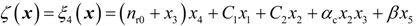
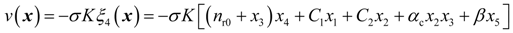
4. Dynamic Output-Feedback Power-Level Control Strategy
4.1. Observation Strategy
 is the state-observation, Fo ∈ Rn×m is the gain matrix of the observer,
is the state-observation, Fo ∈ Rn×m is the gain matrix of the observer,

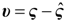
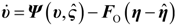
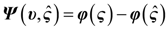
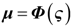
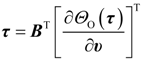
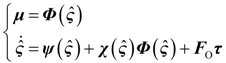
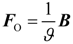
4.2. Design and Analysis of the Dynamic Output-Feedback Power-Level Control Strategy
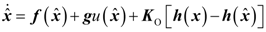
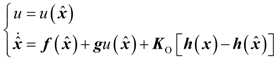
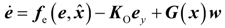
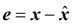
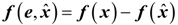
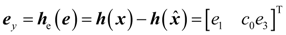
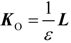
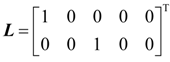
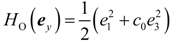
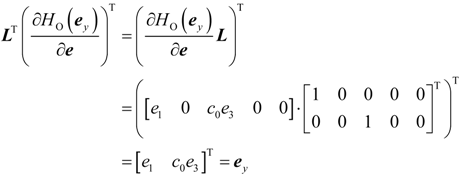
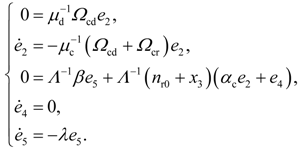
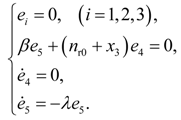

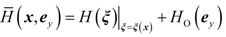
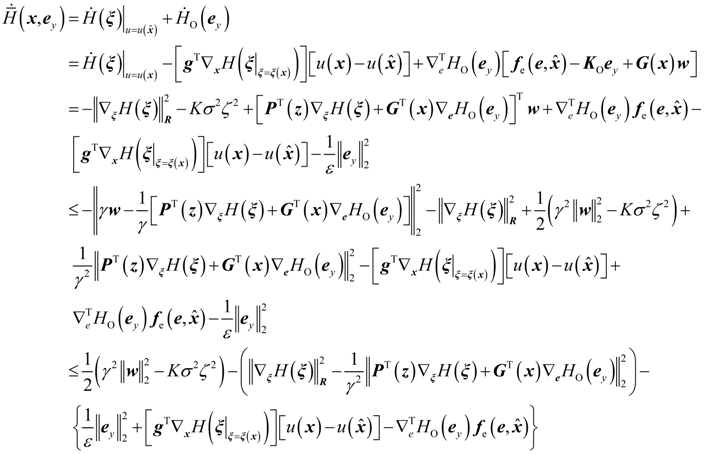
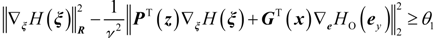

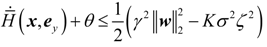
5. Simulation Results with Discussion
5.1. Description of the Numerical Simulation
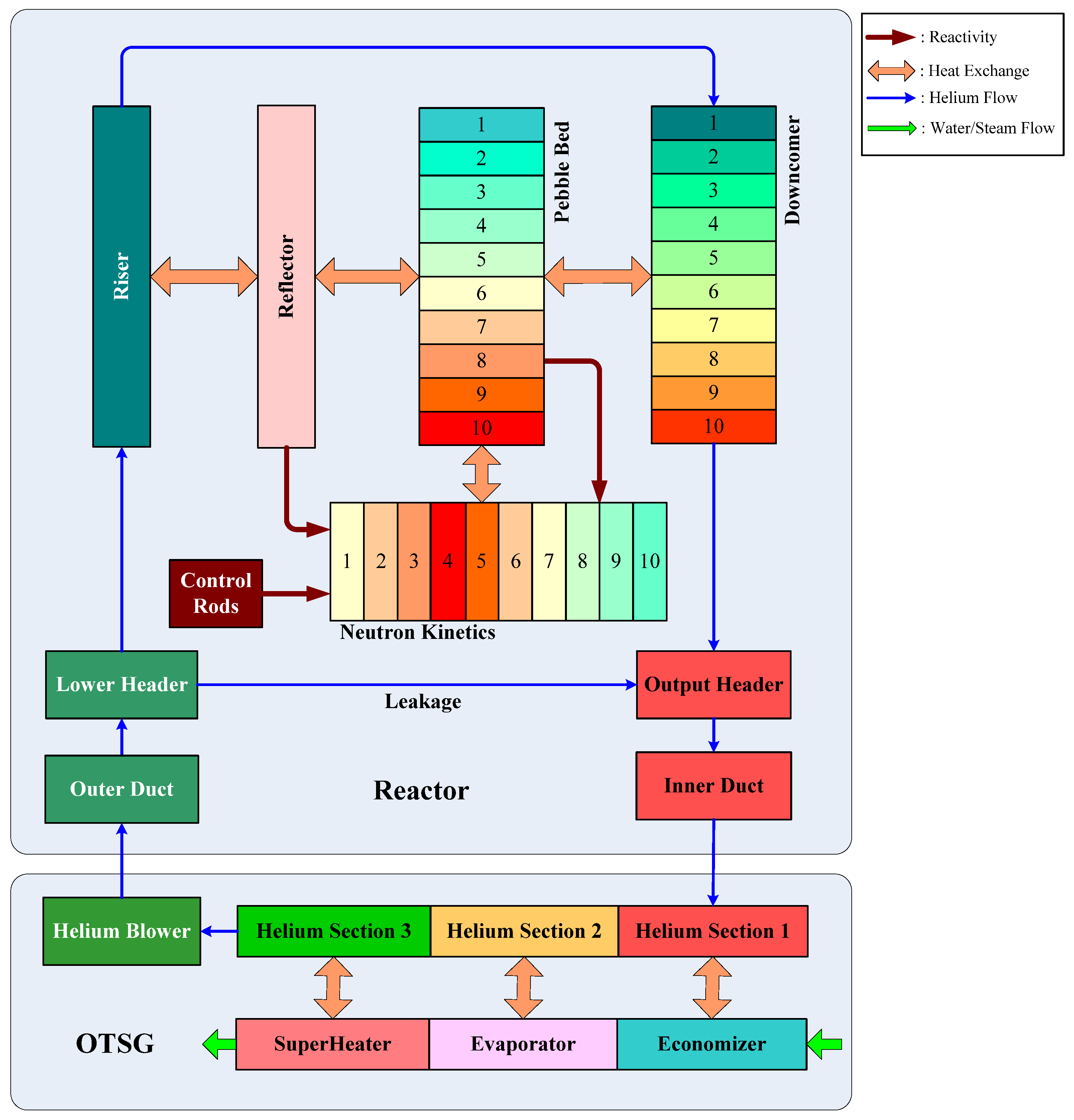
5.2. Simulation Results
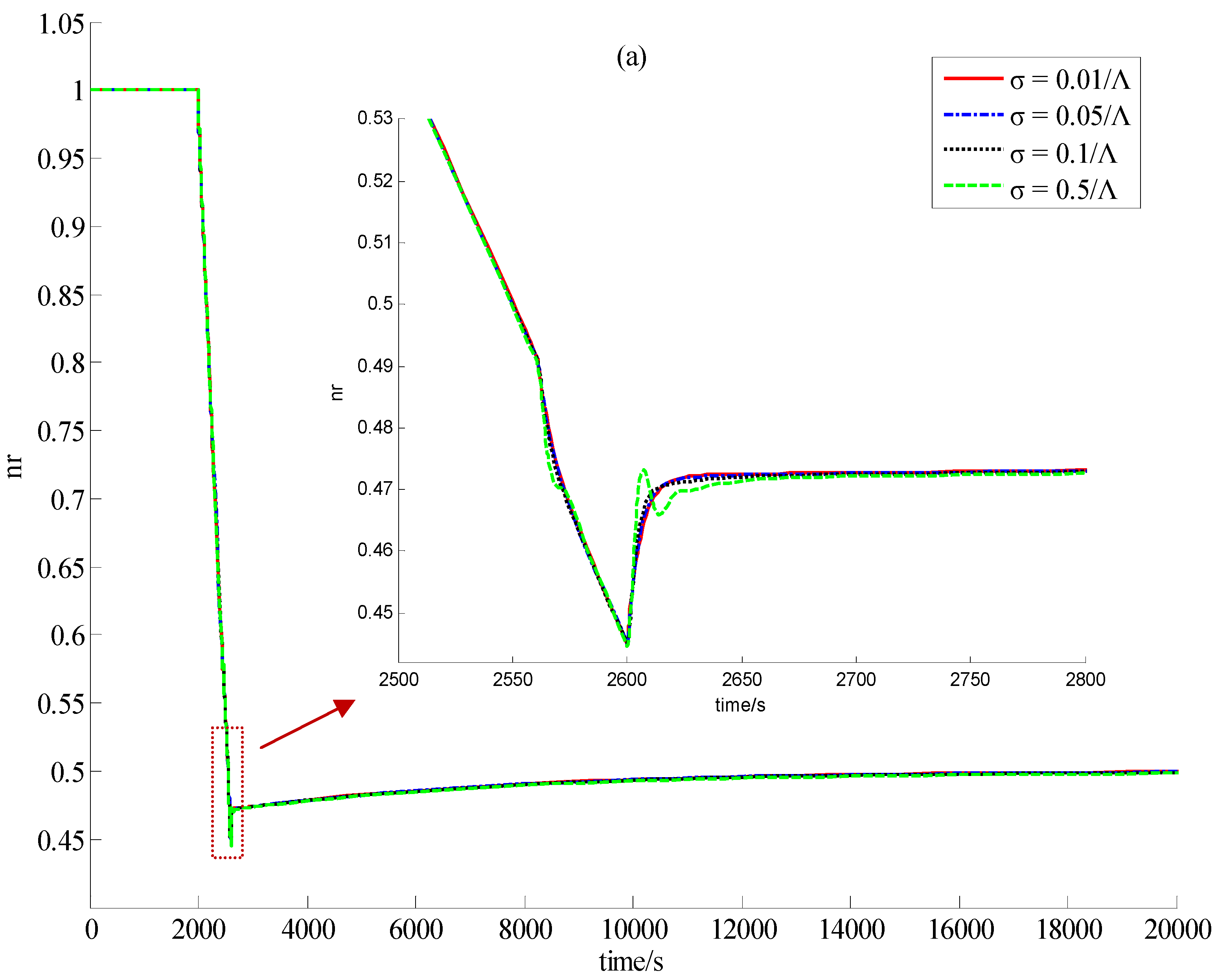
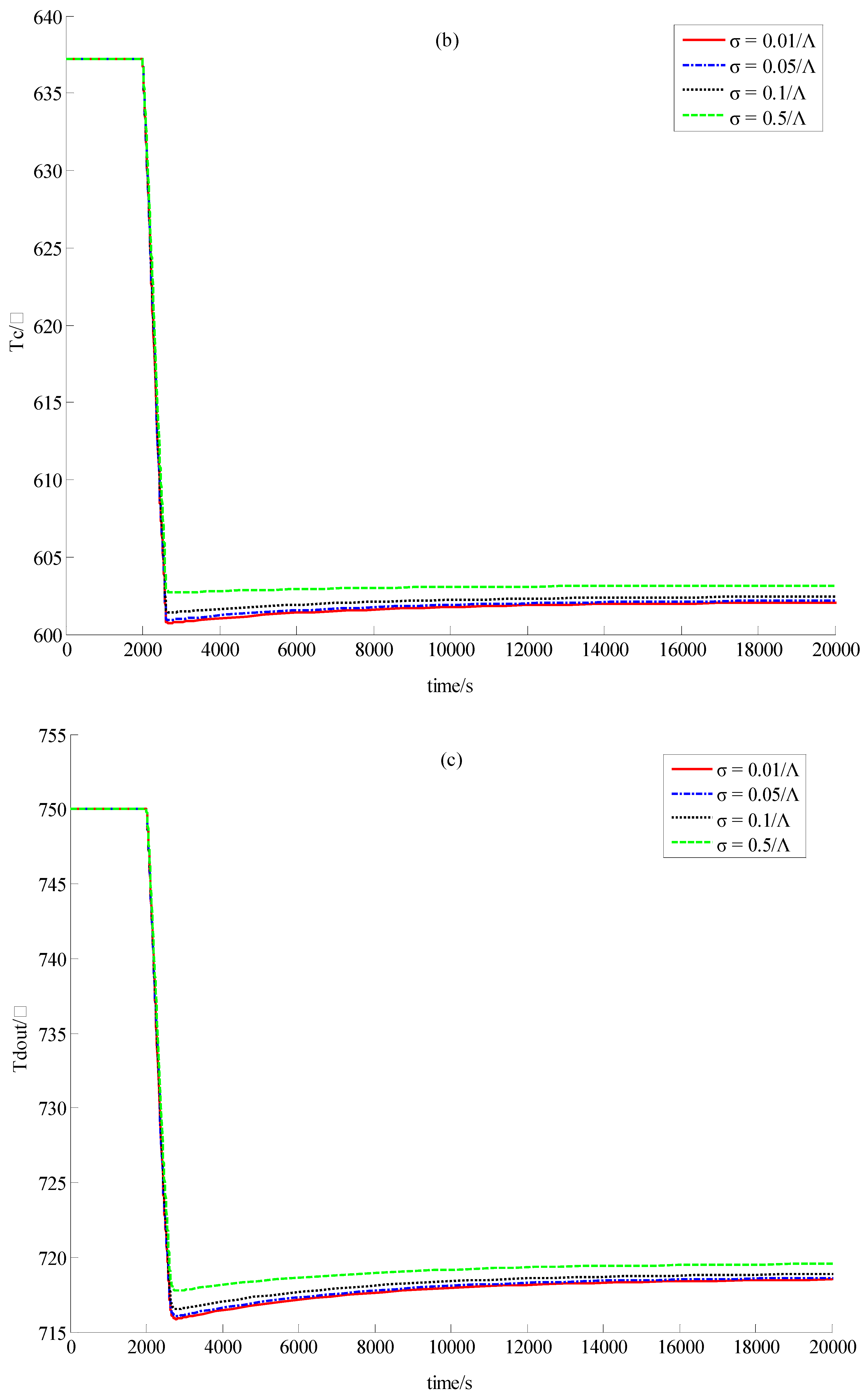
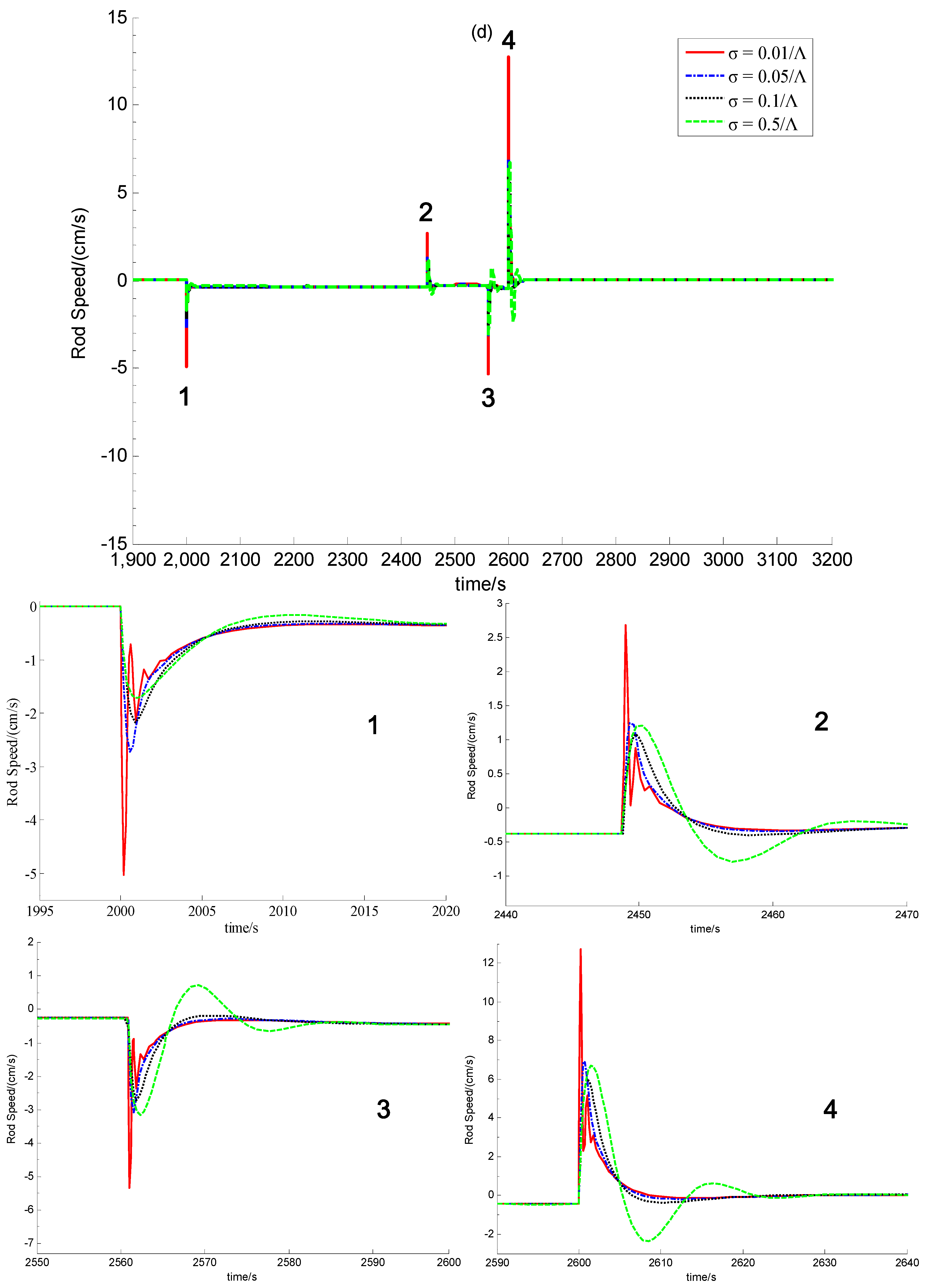
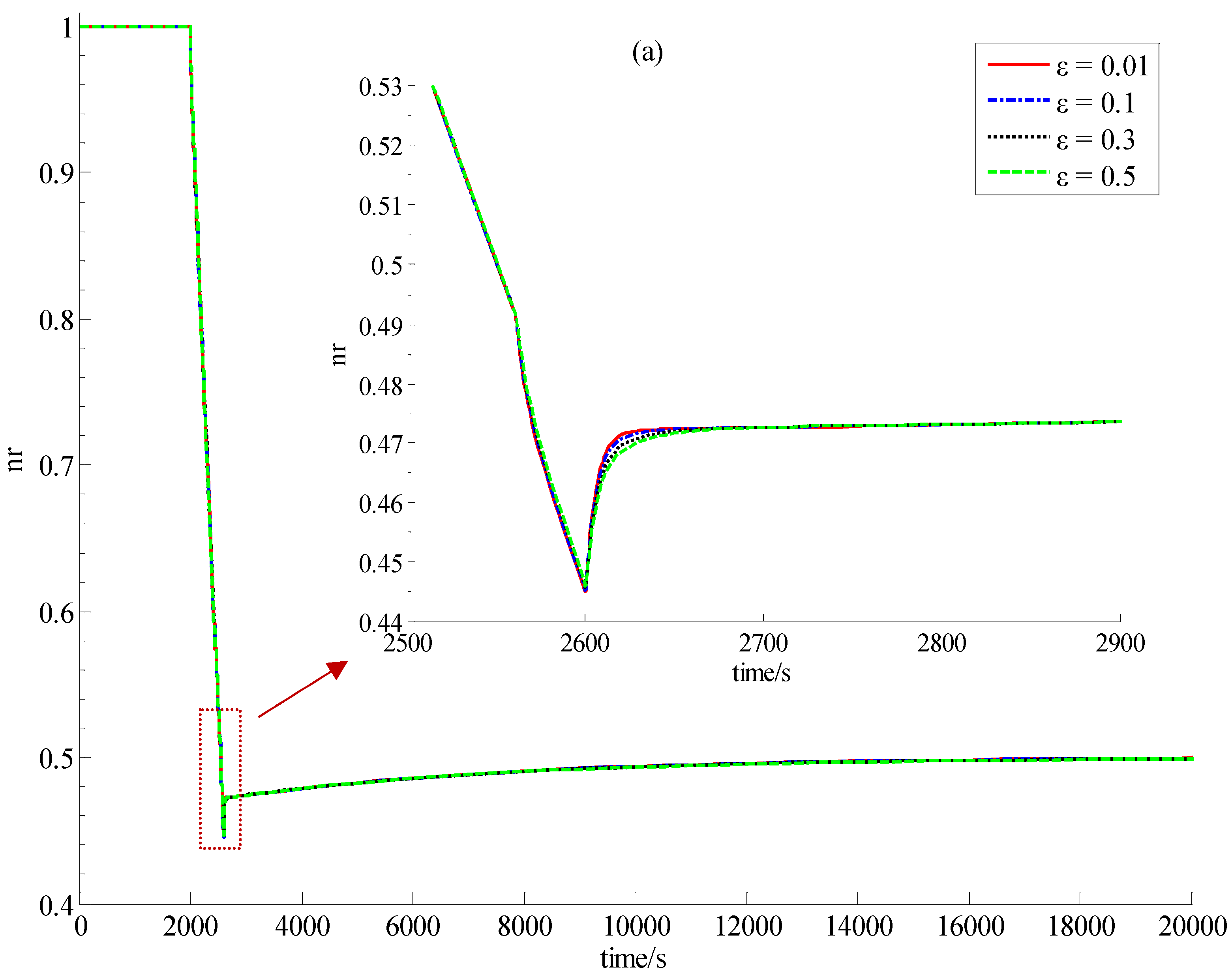
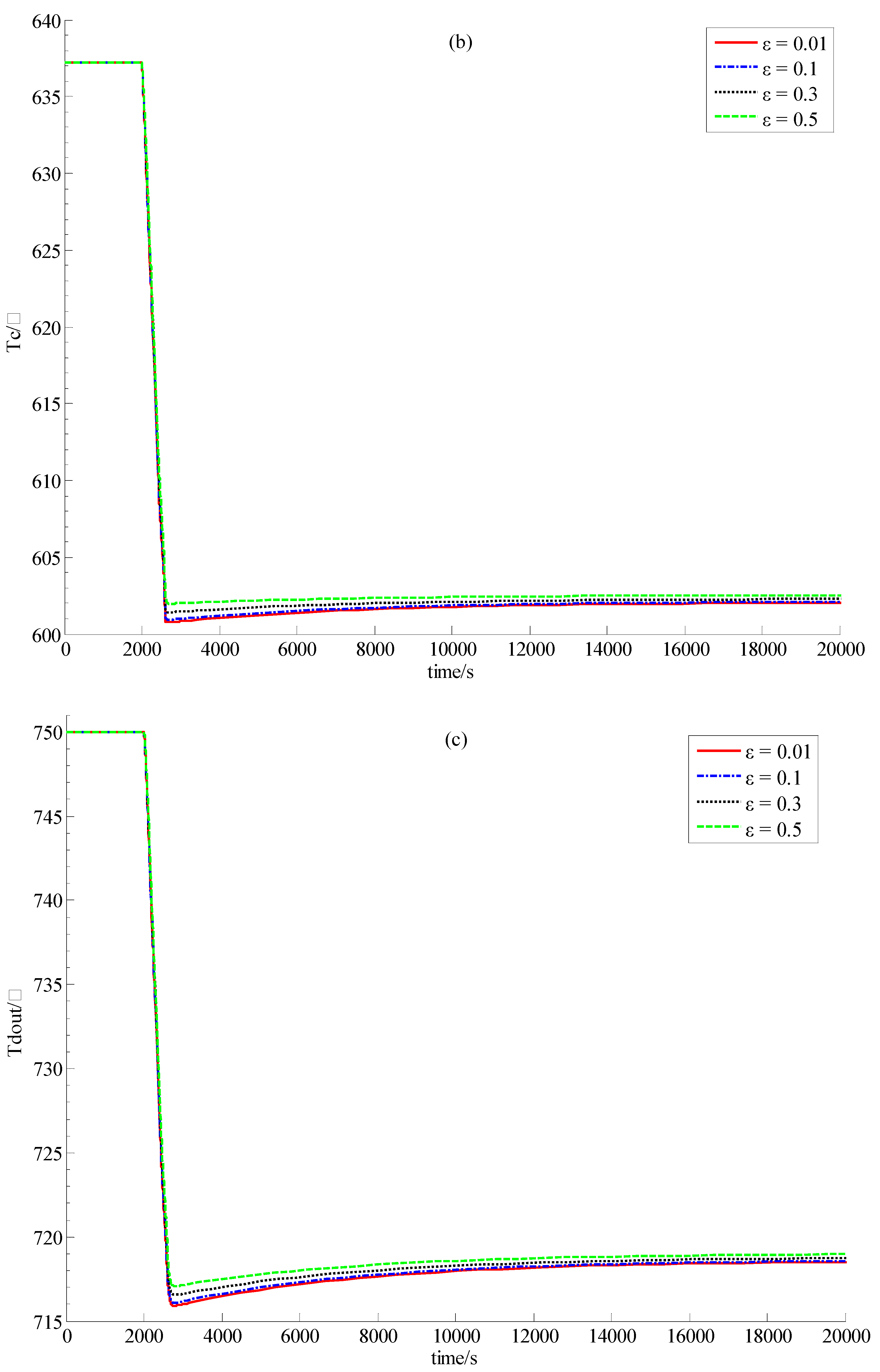
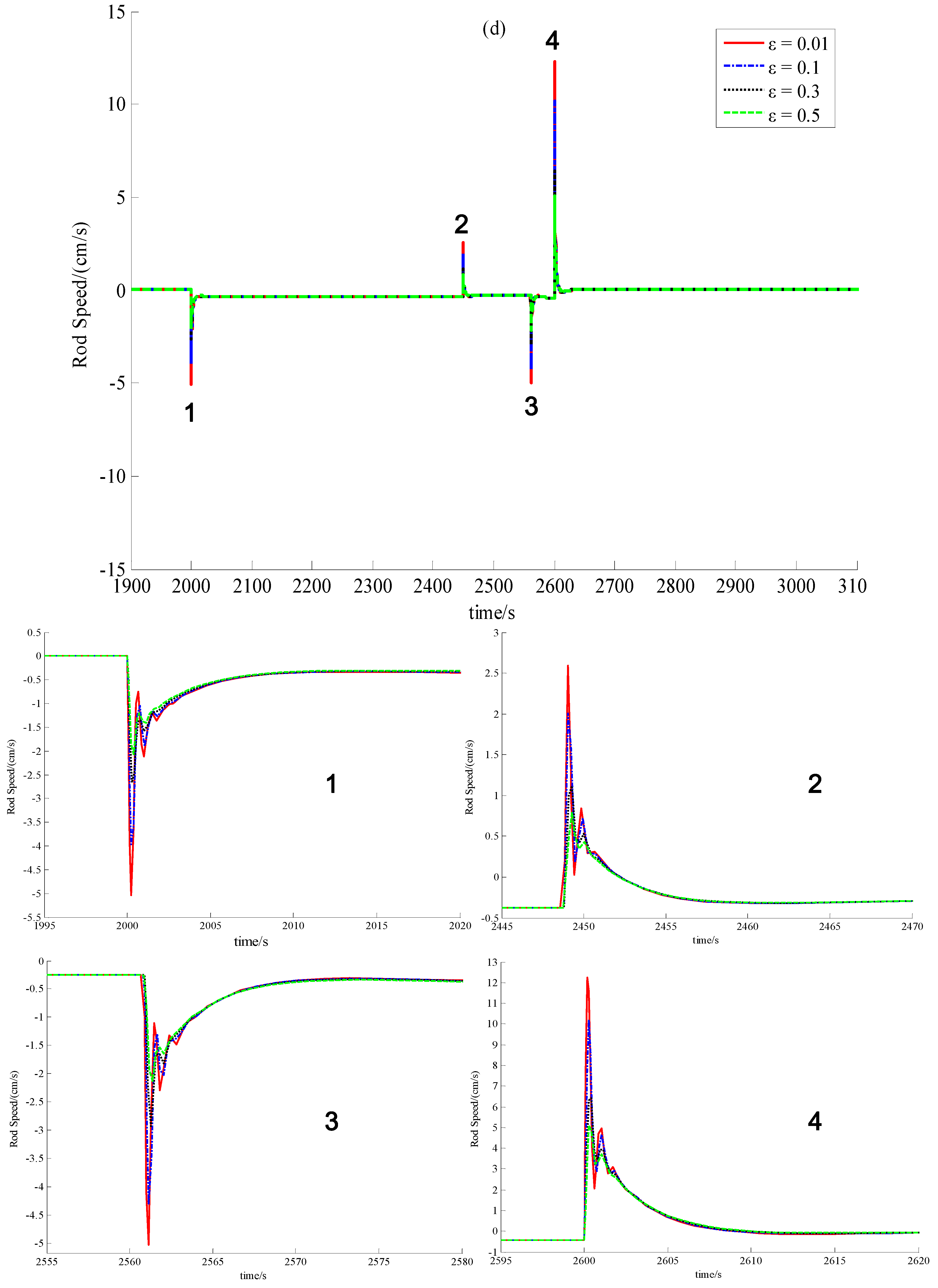
5.3. Discussion
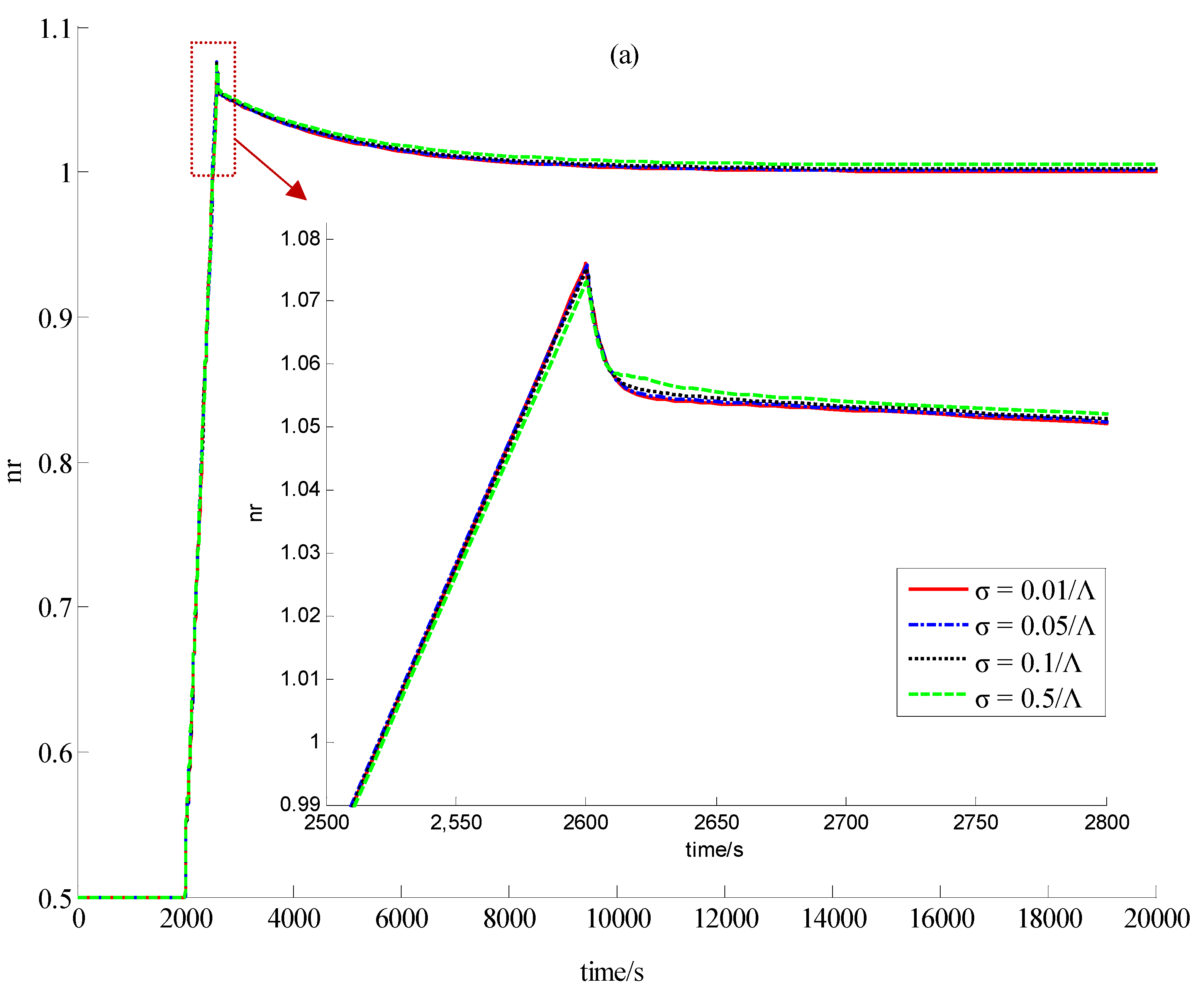
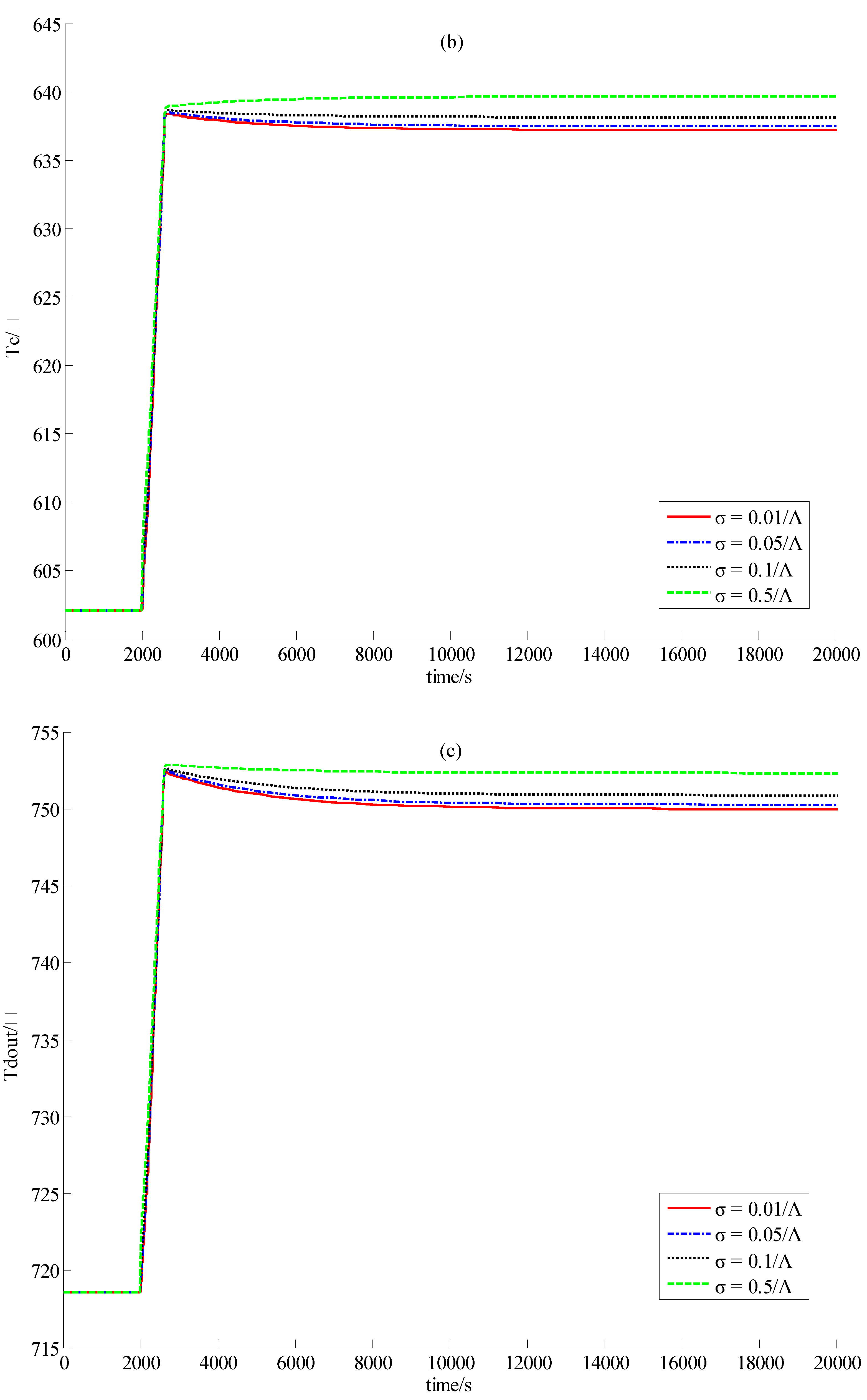
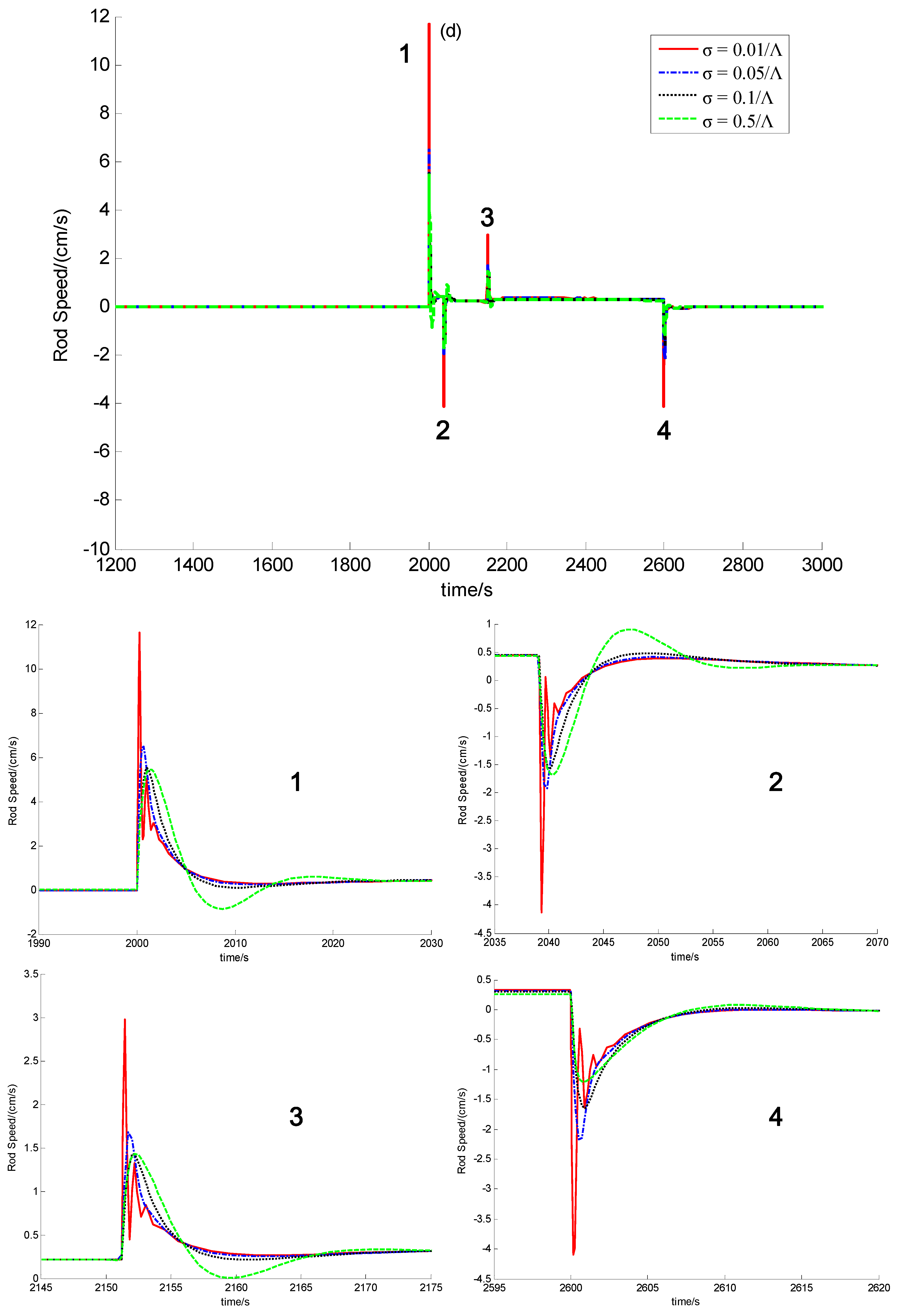
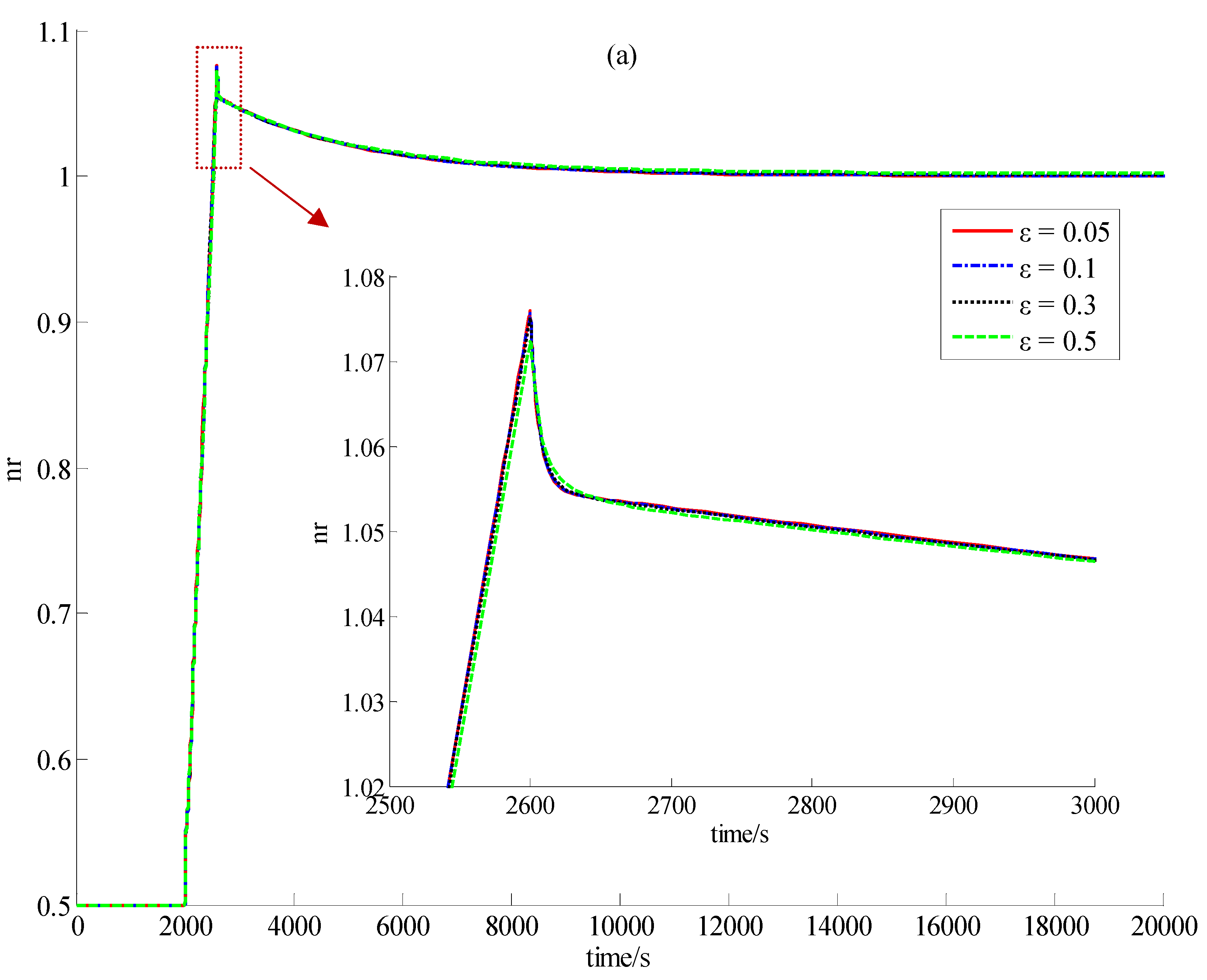
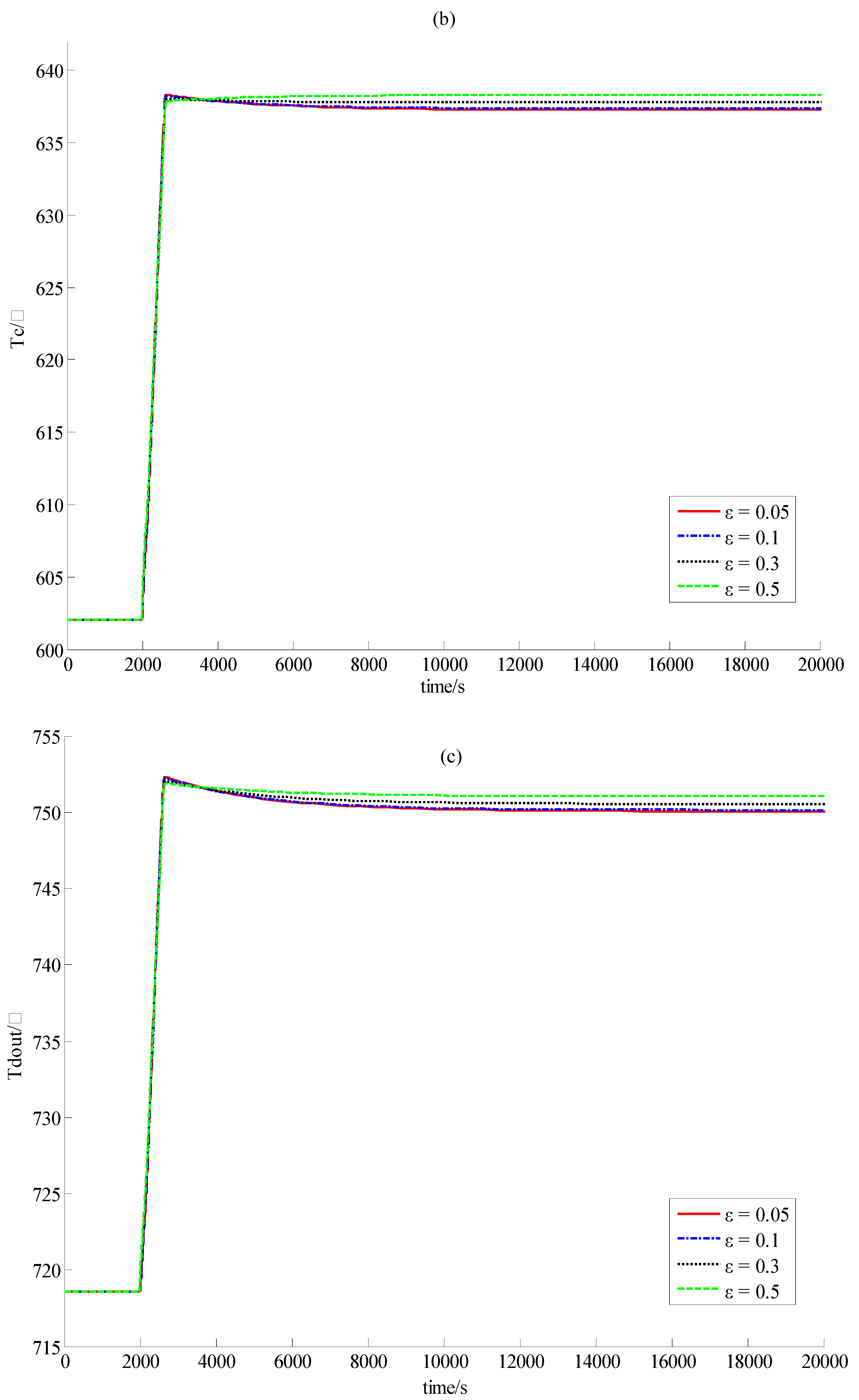
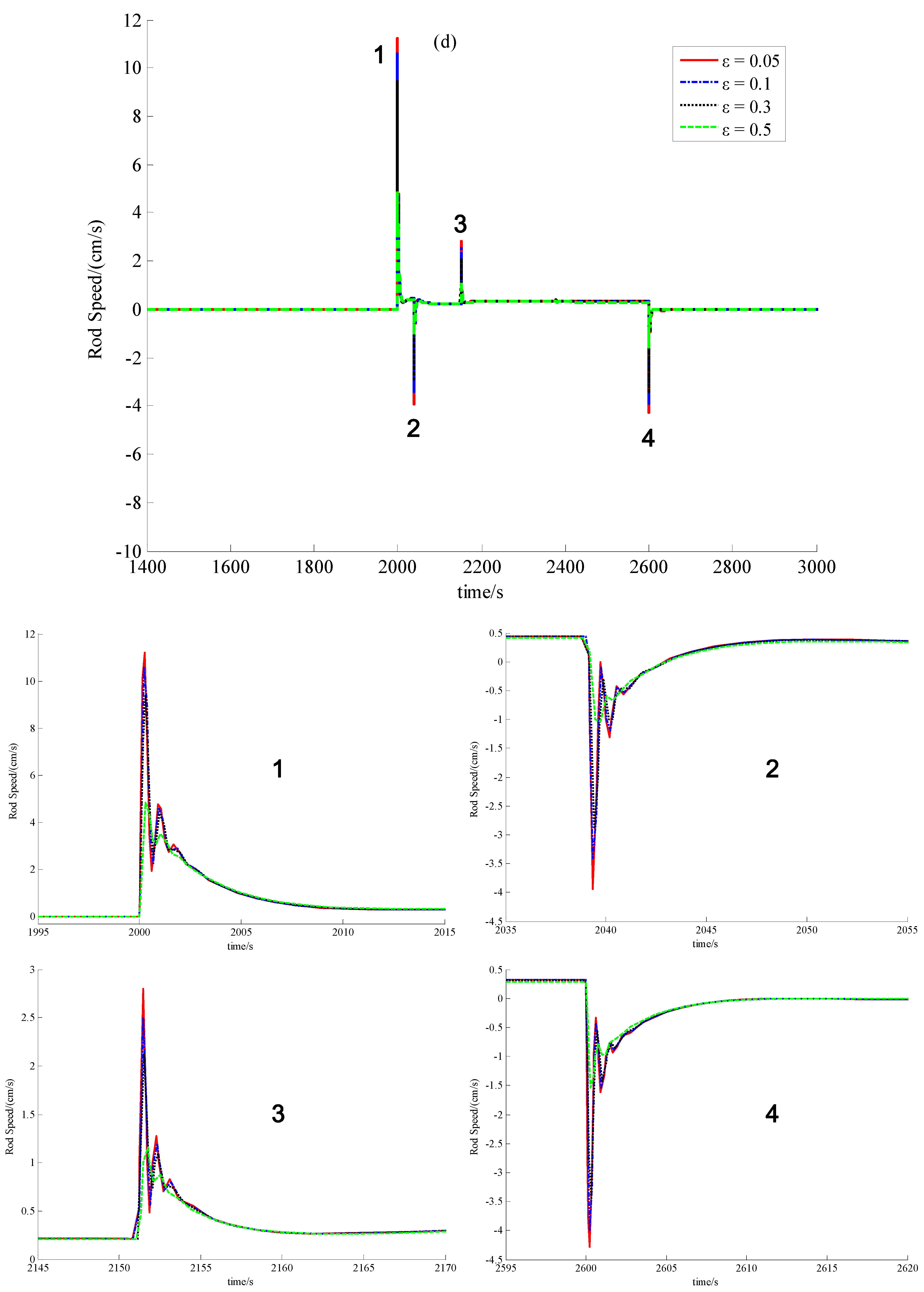
6. Conclusions
Acknowledgement
References
- Reutler, H.; Lohnert, G.H. The modular high-temperature reactor. Nucl. Technol. 1983, 62, 22–30. [Google Scholar]
- Reutler, H.; Lohnert, G.H. Advantages of going modular in HTRs. Nucl. Eng. Des. 1984, 78, 129–136. [Google Scholar] [CrossRef]
- Lohnert, G.H. Technical design features and essential safety-related properties of the HTR-Module. Nucl. Eng. Des. 1990, 121, 259–275. [Google Scholar] [CrossRef]
- Wu, Z.; Lin, D.; Zhong, D. The design features of the HTR-10. Nucl. Eng. Des. 2002, 218, 25–32. [Google Scholar] [CrossRef]
- Hu, S.; Liang, X.; Wei, L. Commissioning and operation experience and safety experiment on HTR-10. In Proceedings of 3rd International Topical Meeting on High Temperature Reactor Technology, Johnanneshurg, South Africa, 1–4 October 2006.
- Zhang, Z.; Wu, Z.; Wang, D.; Xu, Y.; Sun, Y.; Li, F.; Dong, Y. Current status and technical description of Chinese 2 × 250MWth HTR-PM demonstration plant. Nucl. Eng. Des. 2009, 239, 1212–1219. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Y. Economic potential of modular reactor nuclear power plants based on the Chinese HTR-PM project. Nucl. Eng. Des. 2007, 237, 2265–2274. [Google Scholar] [CrossRef]
- Edwards, R.M.; Lee, K.Y.; Schultz, M.A. State-feedback assisted classical control: An incremental approach to control modernization of existing and future nuclear reactors and power plants. Nucl. Technol. 1990, 92, 167–185. [Google Scholar]
- Ben-Abdennour, A.; Edwards, R.M.; Lee, K.Y. LQR/LTR robust control of nuclear reactors with improved temperature performance. IEEE Trans. Nucl. Sci. 1992, 39, 2286–2294. [Google Scholar] [CrossRef]
- Arab-Alibeik, H.; Setayeshi, S. Improved temperature control of a PWR nuclear reactor using LQG/LTR based controller. IEEE Trans. Nucl. Sci. 2003, 50, 211–218. [Google Scholar] [CrossRef]
- Shtessel, Y.B. Sliding mode control of the space nuclear reactor system. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 579–589. [Google Scholar] [CrossRef]
- Ku, C.C.; Lee, K.Y.; Edwards, R.M. Improved nuclear reactor temperature control using diagonal recurrent neural networks. IEEE Trans. Nucl. Sci. 1992, 39, 2298–2308. [Google Scholar] [CrossRef]
- Na, M.G.; Hwang, I.J.; Lee, Y.J. Design of a fuzzy model predictive power controller for pressurized water reactors. IEEE Trans. Nucl. Sci. 2006, 53, 1504–1514. [Google Scholar] [CrossRef]
- Huang, Z.; Edwards, R.M.; Lee, K.Y. Fuzzy-adapted recursive sliding-mode controller design for power plant control. IEEE Trans. Nucl. Sci. 2004, 51, 1504–1514. [Google Scholar] [CrossRef]
- Van der Schaft, A.J. L2-Gain and Passivity Techniques in Nonlinear Control; Springer: Berlin, Germany, 1999. [Google Scholar]
- Maschke, B.M.; Ortega, R.; van der Schaft, A.J. Energy-based Lyapunov functions for forced Hamiltonian systems with dissipation. IEEE Trans. Autom. Control 2000, 45, 1498–1502. [Google Scholar] [CrossRef]
- Ortega, R.; van der Schaft, A.J.; Maschke, B.M.; Escobar, G. Interconnections and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef]
- Ortega, R.; van der Schaft, A.J.; Castaños, F.; Astolfi, A. Control by interconnection and standard passivity-based control of port-Hamiltonian systems. IEEE Trans. Autom. Control 2008, 53, 2527–2542. [Google Scholar] [CrossRef]
- Ortega, R.; Spong, M.W.; Gómez-Estern, F.; Blankenstein, G. Stabilization of a class of underactuated mechanical systems via interconnection and damping assignment. IEEE Trans. Autom. Control 2002, 47, 1218–1233. [Google Scholar] [CrossRef]
- Fujimoto, K.; Sugie, T. Stabilization of Hamiltonian systems with nonholonomic constraints based on time-varying generalized canonical transformations. Syst. Control Lett. 2001, 44, 309–319. [Google Scholar] [CrossRef]
- Liu, Q.J.; Sun, Y.Z.; Shen, T.L.; Song, Y.H. Adaptive nonlinear coordinated excitation and STATCOM controller based on Hamiltonian structure for multimachine power-system stability enhancement. IET Proc. Control Theory Appl. 2003, 50, 285–294. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, D.; Li, C.; Ge, Y. Dissipative Hamiltonian realization and energy-based L2-disturbance attenuation control of multi-machine power systems. IEEE Trans. Autom. Control 2003, 48, 1428–1433. [Google Scholar] [CrossRef]
- Galaz, M.; Ortega, R.; Bazanella, A.S.; Stankovic, A.M. An energy-shaping approach to the design of excitation control of synchronous generators. Automatica 2003, 39, 111–119. [Google Scholar] [CrossRef]
- Dong, Z.; Feng, J.; Huang, X.; Zhang, L. Dissipation-based high gain filter for monitoring nuclear reactors. IEEE Trans. Nucl. Sci. 2010, 57, 328–339. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, X.; Zhang, L. Output feedback power-level control of nuclear reactors based on a dissipative high gain filter. Nucl. Eng. Des. 2011, 241, 4783–4793. [Google Scholar] [CrossRef]
- Li, H.; Huang, X.; Zhang, L. A simplified mathematical dynamic model of the HTR-10 high temperature gas-cooled reactor with control system design purpose. Ann. Nucl. Energy 2008, 35, 1642–1651. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, X.; Zhang, L. A nodal dynamic model for control system design and simulation of an MHTGR core. Nucl. Eng. Des. 2010, 240, 1251–1261. [Google Scholar] [CrossRef]
- Li, H.; Huang, X.; Zhang, L. A lumped parameter dynamic model of the helical coiled once-through steam generator with movable boundaries. Nucl. Eng. Des. 2008, 238, 1657–1663. [Google Scholar] [CrossRef]
- Dong, Z. Output feedback dissipation control for the power-level of modular high-temperature gas-cooled reactors. Energies 2011, 4, 1858–1879. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, X. Real-time simulation platform for the design and verification of the operation strategy of the HTR-PM. In Proceedings of the 19th International Conference on Nuclear Engineering, Chiba, Japan, 16–19 May 2011.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dong, Z. Dynamic Output Feedback Power-Level Control for the MHTGR Based On Iterative Damping Assignment. Energies 2012, 5, 1782-1815. https://doi.org/10.3390/en5061782
Dong Z. Dynamic Output Feedback Power-Level Control for the MHTGR Based On Iterative Damping Assignment. Energies. 2012; 5(6):1782-1815. https://doi.org/10.3390/en5061782
Chicago/Turabian StyleDong, Zhe. 2012. "Dynamic Output Feedback Power-Level Control for the MHTGR Based On Iterative Damping Assignment" Energies 5, no. 6: 1782-1815. https://doi.org/10.3390/en5061782




