Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand
Abstract
:1. Introduction
- A hierarchical control approach is utilized for the collaborative control of an AC/DC hybrid microgrid, which includes primary and secondary control. This approach ensures a stable power supply for the microgrid.
- To optimize uncertain system scenarios resulting from the randomness of power generation and load demand in microgrid systems, the PSO algorithm is utilized. The algorithm generates the optimal operating cost and output power of the system, thereby achieving scheduling optimization of microgrid systems.
- A tertiary control of the microgrid system is proposed based on the optimal power guidance that considers the randomness of power generation and load demand. This control achieves a more stable output with smaller fluctuations in system frequency and bus voltage while also taking economic considerations into account.
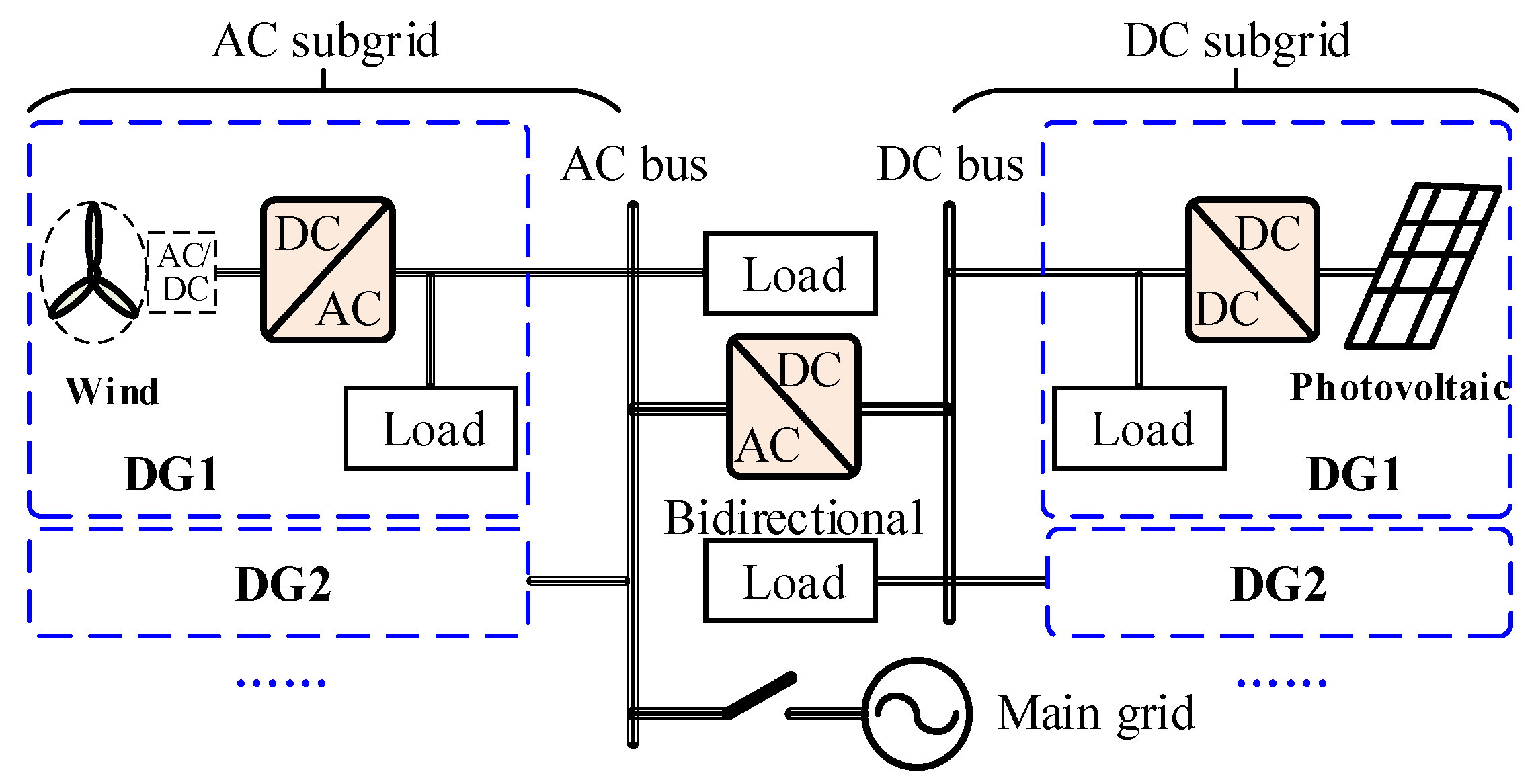
2. Hierarchical Control of Hybrid Microgrid
2.1. Primary Control
2.2. Secondary Control
2.3. Tertiary Control
3. Optimization of Microgrid System
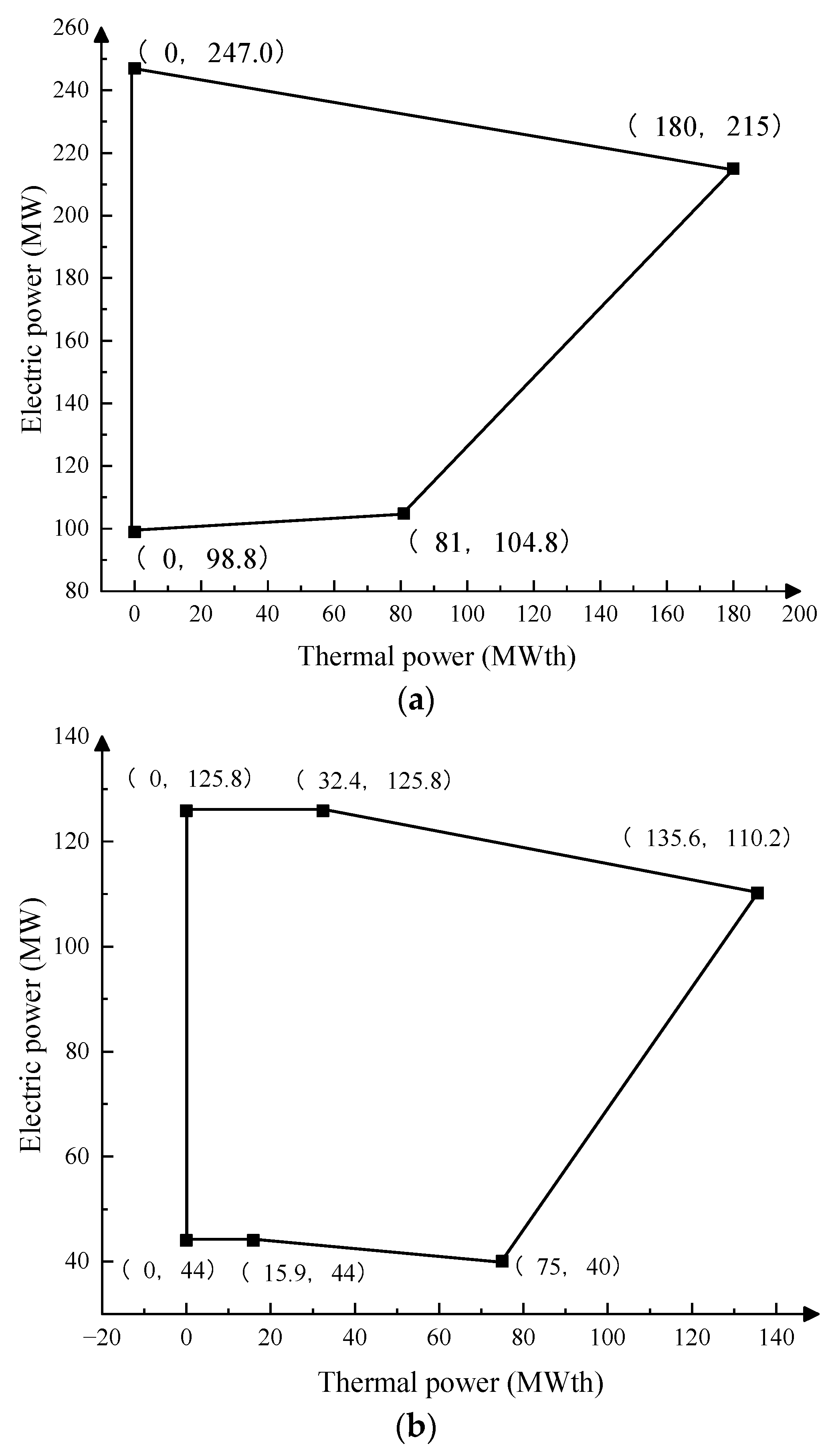
3.1. Dynamic Optimization Modeling
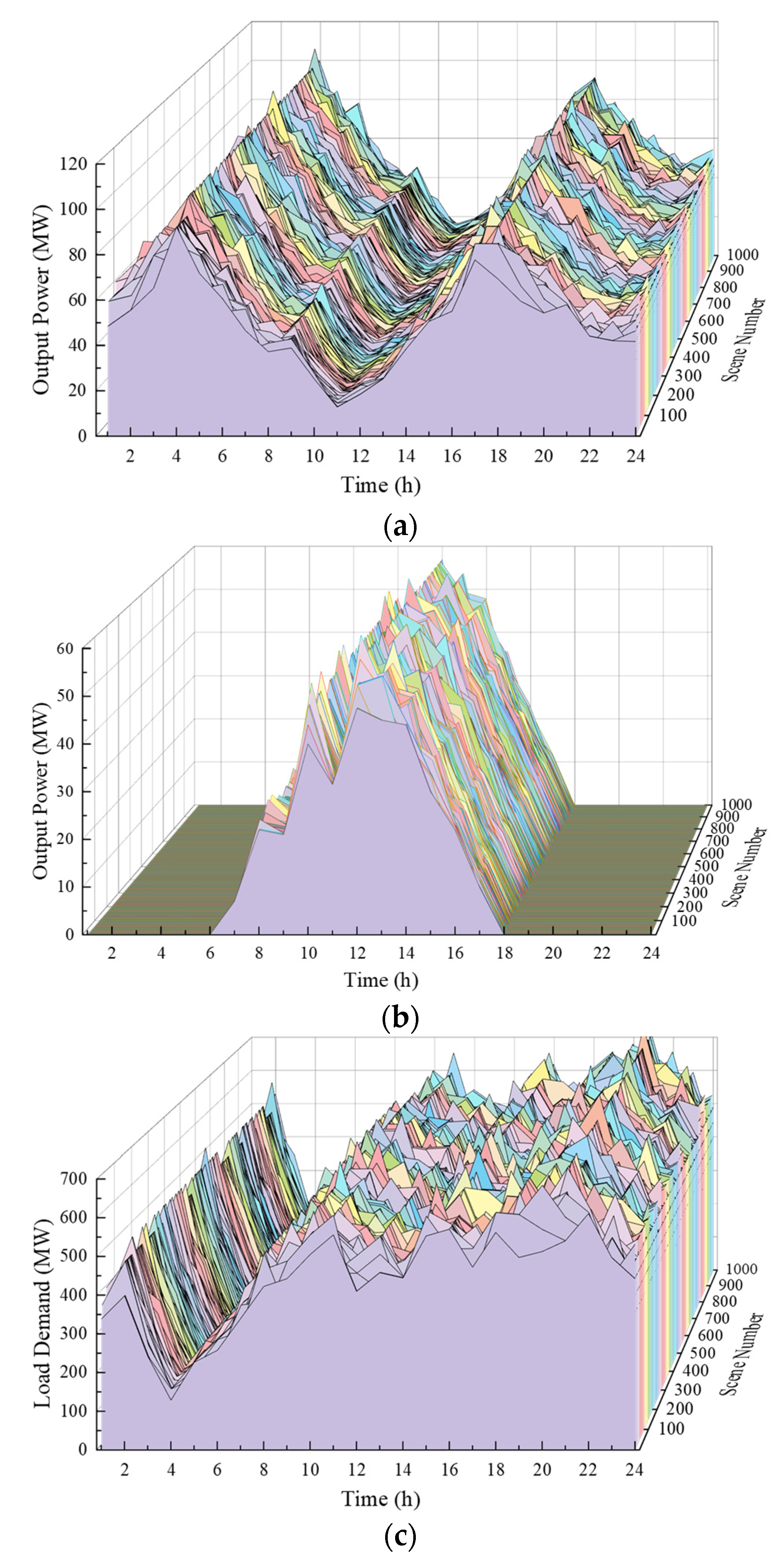
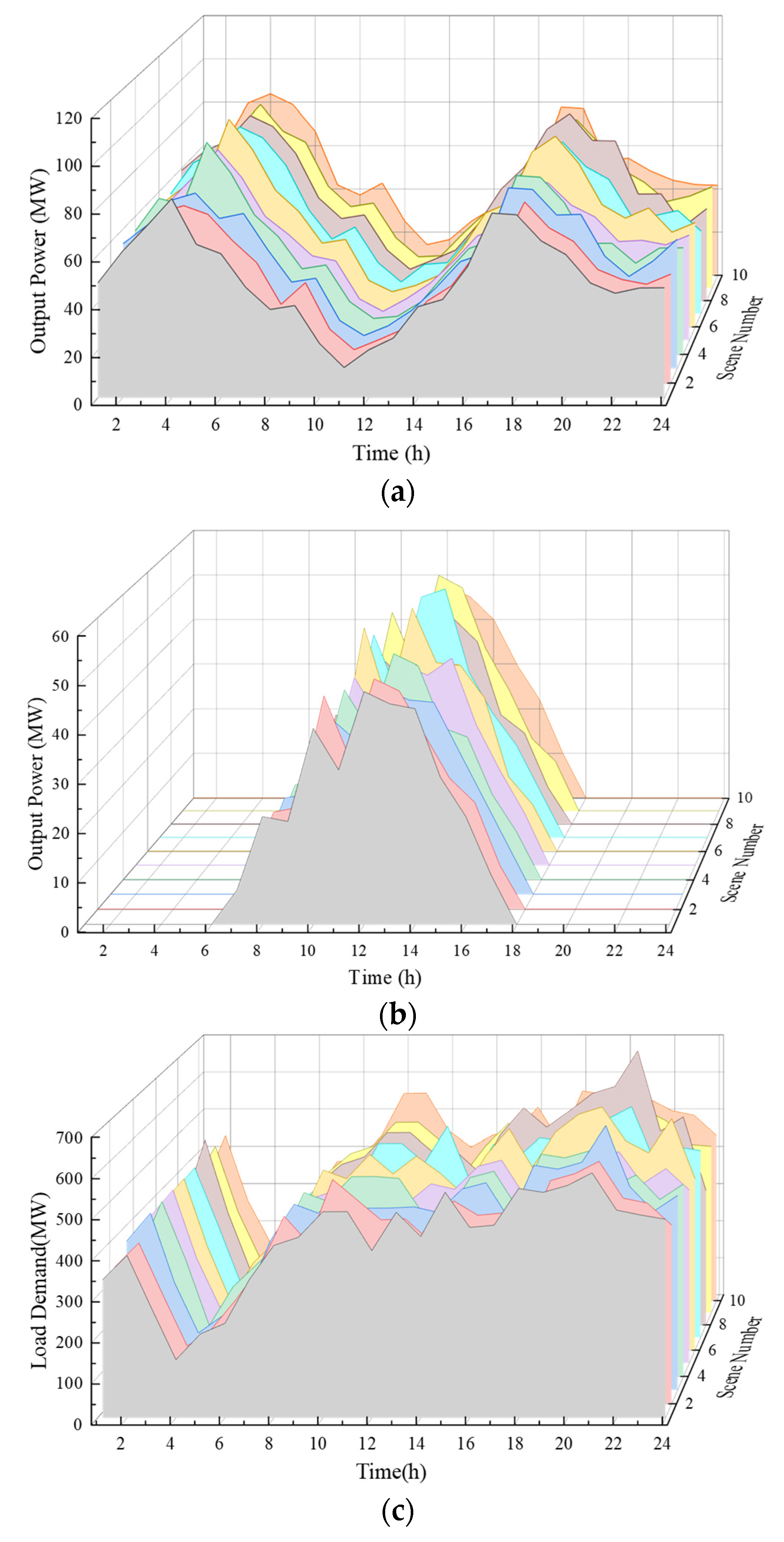
3.2. Scenario Generation and Reduction
3.3. Optimizing Function Creation and Problem Solving
- (a)
- Initialize the particle swarm’s position and velocity.
- (b)
- Determine the fitness value for every particle.
- (c)
- Update the global optimal solution.
- (d)
- Renew each particle’s velocity and position.
- (e)
- Repeat steps 2–4 until the condition is met.
- (f)
- Return the global optimal solution.
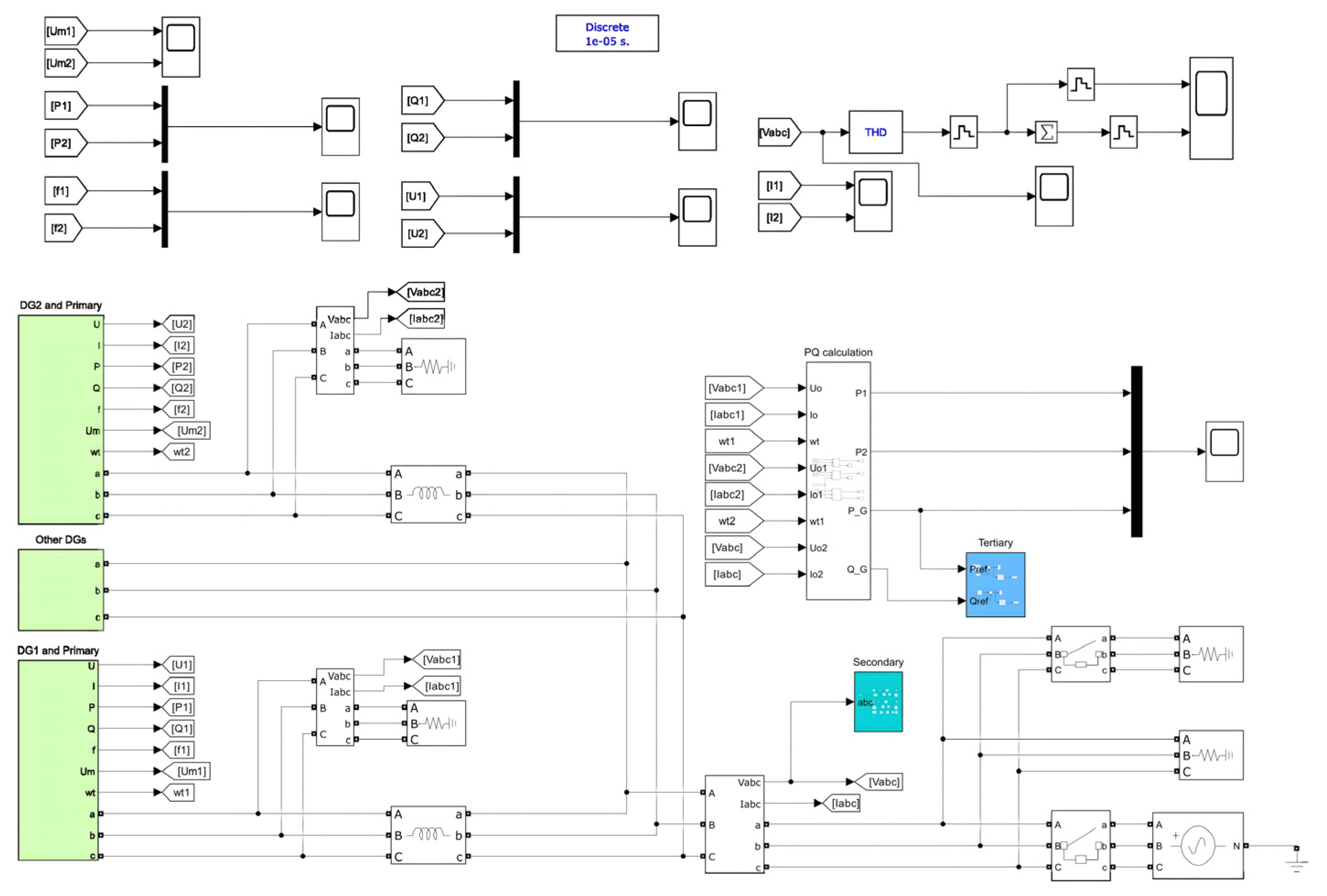
4. Simulation and Result Analysis
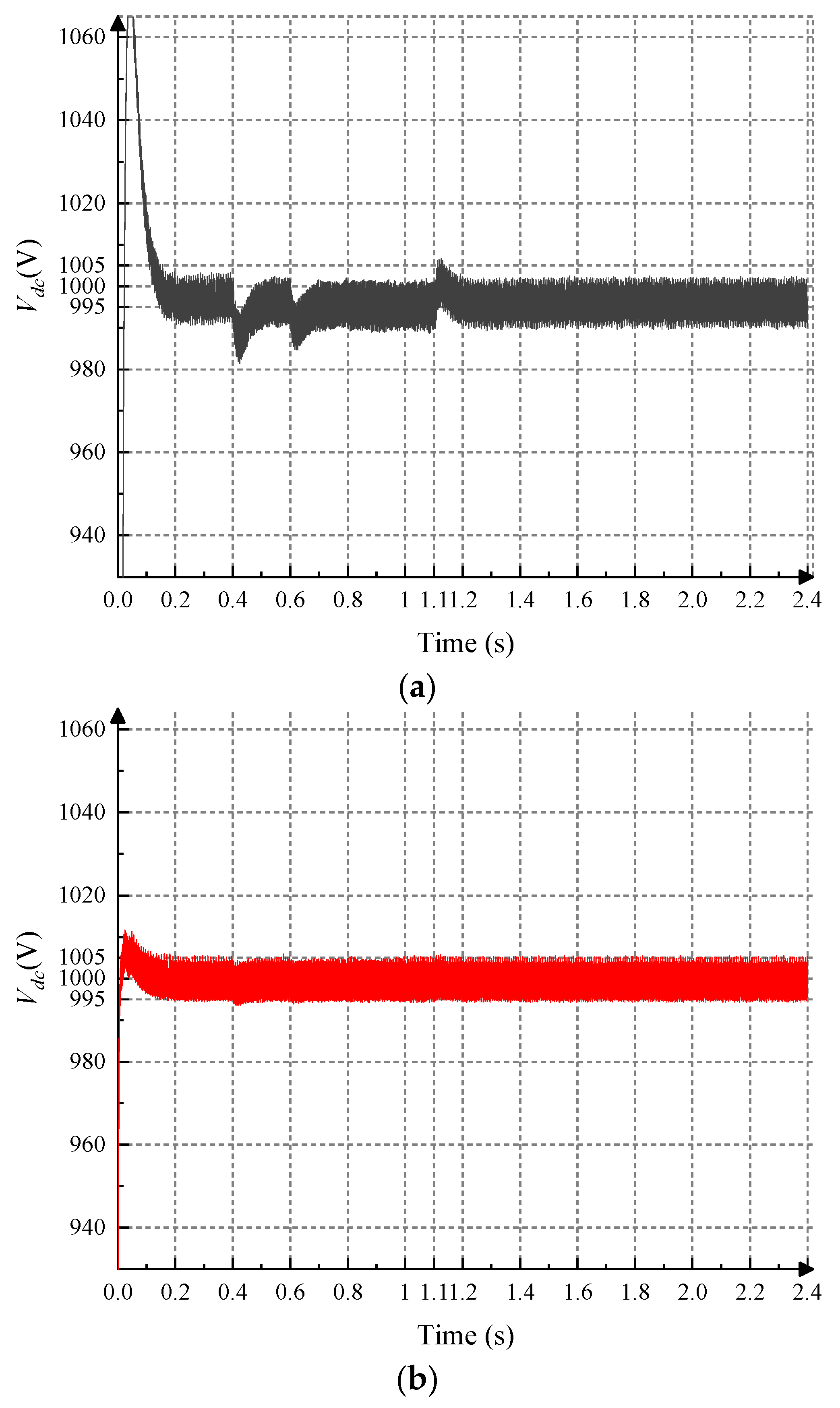
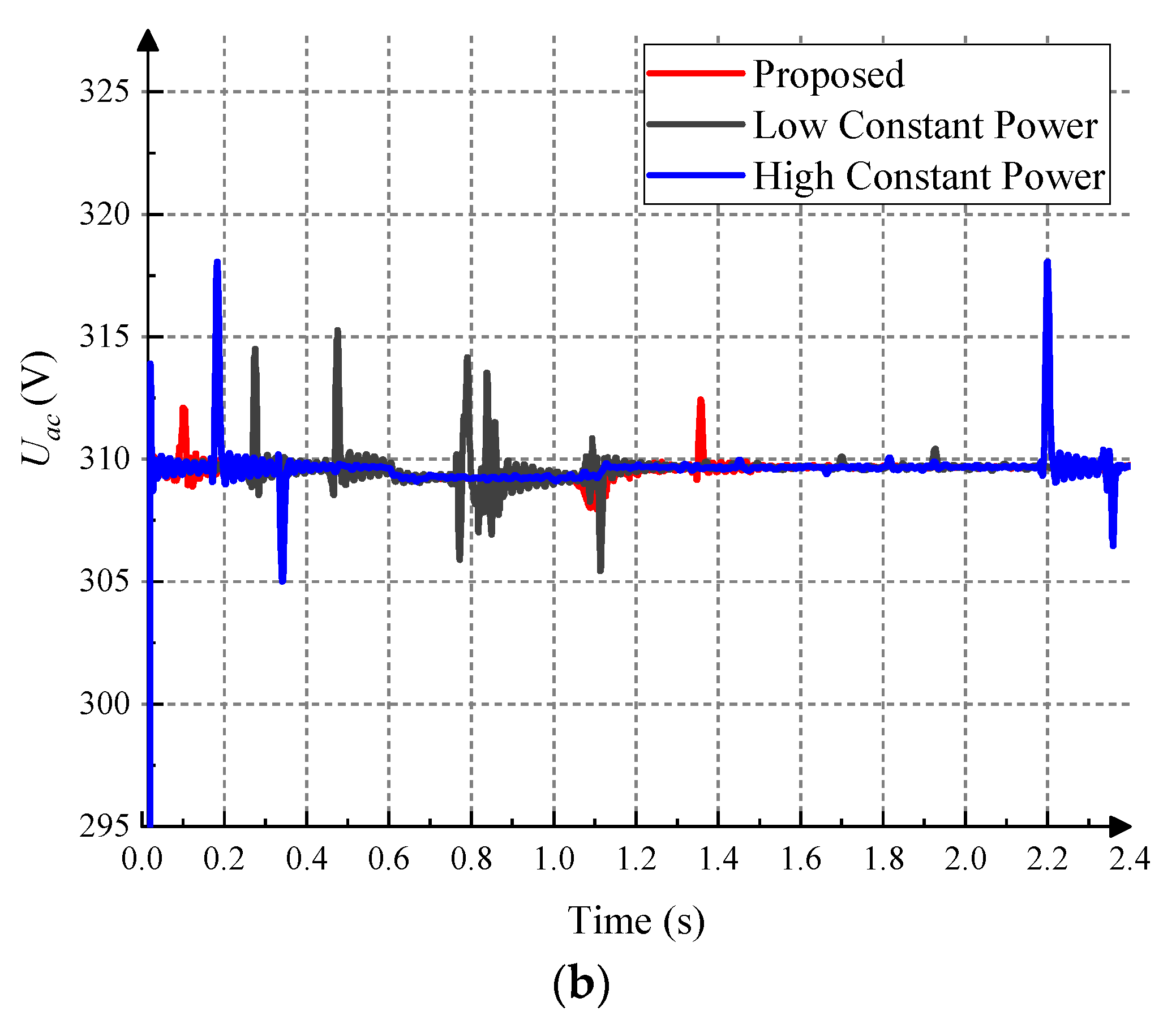
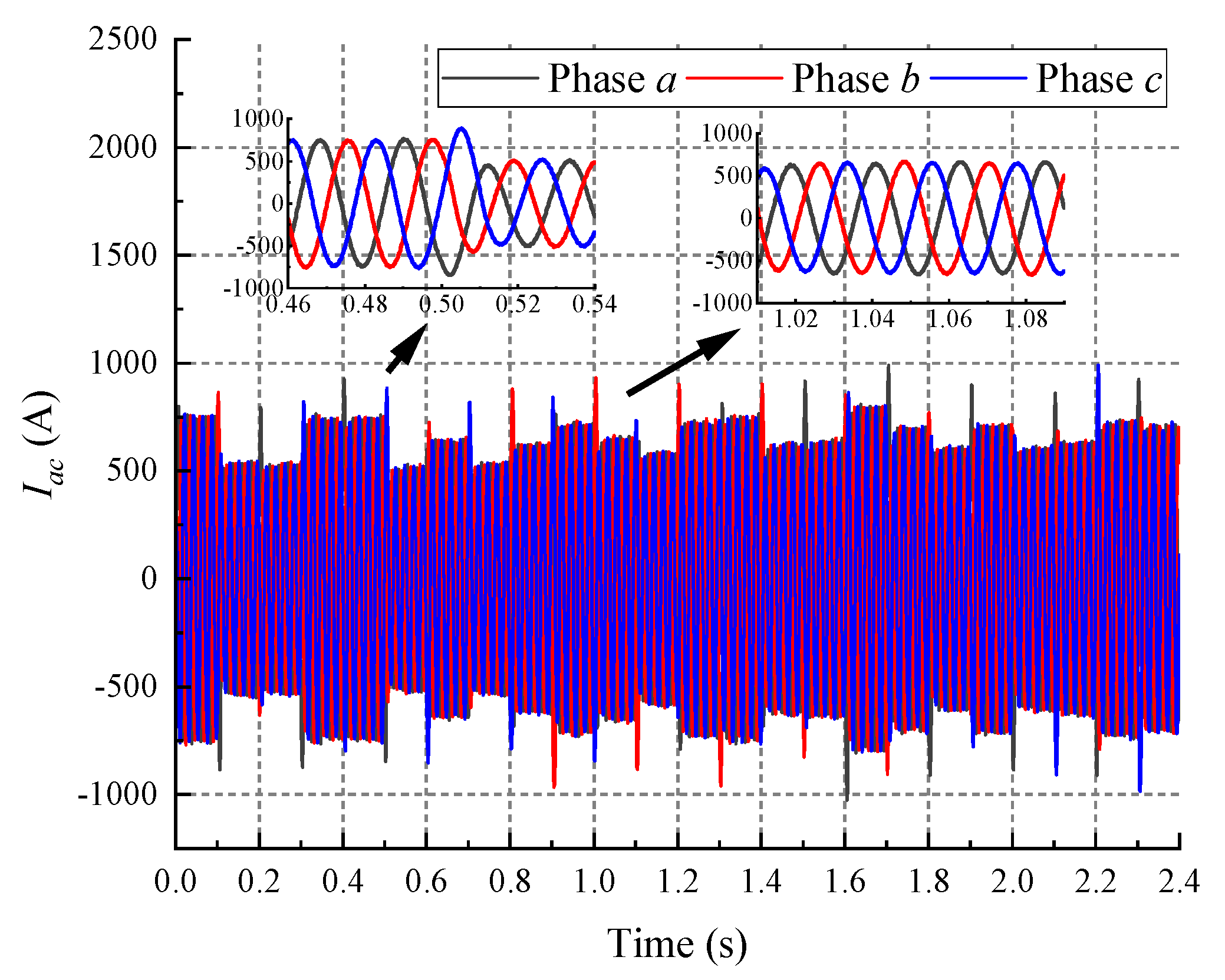
4.1. Hybrid Microgrids’ Hierarchical Control Performance
4.2. Scenario Generation and Reduction
4.3. Case Study and Results Analysis of Microgrid Economic Optimization Model
4.4. Tertiary Control of Microgrid under Optimal Power Guidance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ilyushin, P.; Volnyi, V.; Suslov, K.; Filippov, S. State-of-the-Art Literature Review of Power Flow Control Methods for Low-Voltage AC and AC-DC Microgrids. Energies 2023, 16, 3153. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Vasquez, J.C.; Matas, J.; De Vicuña, L.G.; Castilla, M. Hierarchical Control of Droop-Controlled AC and DC Microgrids—A General Approach toward Standardization. IEEE Trans. Ind. Electron. 2011, 58, 158–172. [Google Scholar] [CrossRef]
- Qin, D.; Chen, Y.; Zhang, Z.; Enslin, J. A Hierarchical Microgrid Protection Scheme Using Hybrid Breakers. In Proceedings of the 2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems, PEDG 2021, Online, 28 June–1 July 2021; Institute of Electrical and Electronics Engineers Inc.: Interlaken, Switzerland, 2021. [Google Scholar]
- Han, Y.; Zhang, K.; Li, H.; Coelho, E.A.A.; Guerrero, J.M. MAS-Based Distributed Coordinated Control and Optimization in Microgrid and Microgrid Clusters: A Comprehensive Overview. IEEE Trans. Power Electron. 2018, 33, 6488–6508. [Google Scholar] [CrossRef] [Green Version]
- Raya-Armenta, J.M.; Bazmohammadi, N.; Avina-Cervantes, J.G.; Sáez, D.; Vasquez, J.C.; Guerrero, J.M. Energy Management System Optimization in Islanded Microgrids: An Overview and Future Trends. Renew. Sustain. Energy Rev. 2021, 149, 111327. [Google Scholar] [CrossRef]
- Zhang, Y.; Gatsis, N.; Giannakis, G.B. Robust Energy Management for Microgrids with High-Penetration Renewables. IEEE Trans. Sustain. Energy 2013, 4, 944–953. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.A.; Crow, M.L. Stochastic Optimization of Renewable-Based Microgrid Operation Incorporating Battery Operating Cost. IEEE Trans. Power Syst. 2016, 31, 2289–2296. [Google Scholar] [CrossRef]
- Hu, W.; Wang, P.; Gooi, H.B. Toward Optimal Energy Management of Microgrids via Robust Two-Stage Optimization. IEEE Trans. Smart Grid 2018, 9, 1161–1174. [Google Scholar] [CrossRef]
- Javed, H.; Muqeet, H.A.; Shehzad, M.; Jamil, M.; Khan, A.A.; Guerrero, J.M. Optimal Energy Management of a Campus Microgrid Considering Financial and Economic Analysis with Demand Response Strategies. Energies 2021, 14, 8501. [Google Scholar] [CrossRef]
- Ahmad, J.; Tahir, M.; Mazumder, S.K. Improved Dynamic Performance and Hierarchical Energy Management of Microgrids with Energy Routing. IEEE Trans. Ind. Inf. 2019, 15, 3218–3229. [Google Scholar] [CrossRef]
- Hai, T.; Zhou, J.; Khaki, M. Optimal Planning and Design of Integrated Energy Systems in a Microgrid Incorporating Electric Vehicles and Fuel Cell System. J. Power Sources 2023, 561, 232694. [Google Scholar] [CrossRef]
- Qin, D.; Sun, Q.; Wang, R.; Ma, D.; Liu, M. Adaptive Bidirectional Droop Control for Electric Vehicles Parking with Vehicle-to-Grid Service in Microgrid. CSEE J. Power Energy Syst. 2020, 6, 793–805. [Google Scholar] [CrossRef]
- Tian, P.; Xiao, X.; Wang, K.; Ding, R. A Hierarchical Energy Management System Based on Hierarchical Optimization for Microgrid Community Economic Operation. IEEE Trans. Smart Grid 2016, 7, 2230–2241. [Google Scholar] [CrossRef]
- Yang, X.; Liu, S.; Zhang, L.; Su, J.; Ye, T. Design and Analysis of a Renewable Energy Power System for Shale Oil Exploitation Using Hierarchical Optimization. Energy 2020, 206, 118078. [Google Scholar] [CrossRef]
- Jani, A.; Karimi, H.; Jadid, S. Multi-Time Scale Energy Management of Multi-Microgrid Systems Considering Energy Storage Systems: A Multi-Objective Two-Stage Optimization Framework. J. Energy Storage 2022, 51, 104554. [Google Scholar] [CrossRef]
- Luo, E.; Cong, P.; Lu, H.; Li, Y. Two-Stage Hierarchical Congestion Management Method for Active Distribution Networks with Multi-Type Distributed Energy Resources. IEEE Access 2020, 8, 120309–120320. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Guo, C. Hierarchical Optimal Configuration of Multi-Energy Microgrids System Considering Energy Management in Electricity Market Environment. Int. J. Electr. Power Energy Syst. 2023, 144, 108572. [Google Scholar] [CrossRef]
- Velasquez, M.A.; Torres-Pérez, O.; Quijano, N.; Cadena, Á. Hierarchical Dispatch of Multiple Microgrids Using Nodal Price: An Approach from Consensus and Replicator Dynamics. J. Mod. Power Syst. Clean Energy 2019, 7, 1573–1584. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Abdou, A.F. Modified PSO Algorithm for Real-Time Energy Management in Grid-Connected Microgrids. Renew. Energy 2019, 136, 746–757. [Google Scholar] [CrossRef]
- Hu, J.; Shan, Y.; Xu, Y.; Guerrero, J.M. A Coordinated Control of Hybrid Ac/Dc Microgrids with PV-Wind-Battery under Variable Generation and Load Conditions. Int. J. Electr. Power Energy Syst. 2019, 104, 583–592. [Google Scholar] [CrossRef] [Green Version]
- Shakiba, F.M.; Shojaee, M.; Azizi, S.M.; Zhou, M. Real-Time Sensing and Fault Diagnosis for Transmission Lines. Int. J. Netw. Dyn. Intell. 2022, 1, 36–47. [Google Scholar] [CrossRef]
- Kreishan, M.Z.; Zobaa, A.F. Optimal Allocation and Operation of Droop-Controlled Islanded Microgrids: A Review. Energies 2021, 14, 4653. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Z.; Mi, Y.; Li, Z.; Li, F. Droop Control for DC Multi-Microgrids Based on Local Adaptive Fuzzy Approach and Global Power Allocation Correction. IEEE Trans. Smart Grid 2018, 10, 5468–5478. [Google Scholar] [CrossRef]
- Meng, L.; Dragicevic, T.; Vasquez, J.C.; Guerrero, J.M. Tertiary and Secondary Control Levels for Efficiency Optimization and System Damping in Droop Controlled DC-DC Converters. IEEE Trans. Smart Grid 2015, 6, 2615–2626. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Cai, H.; Huang, J. The Cooperative Output Regulation by the Distributed Observer Approach. Int. J. Netw. Dyn. Intell. 2022, 1, 20–35. [Google Scholar] [CrossRef]
- Wang, W.; Ikegaya, N.; Okaze, T. Comparing Weibull Distribution Method and Gram–Charlier Series Method within the Context of Estimating Low-Occurrence Strong Wind Speed of Idealized Building Cases. J. Wind Eng. Ind. Aerodyn. 2023, 236, 105401. [Google Scholar] [CrossRef]
- Bagheri, F.; Dagdougui, H.; Gendreau, M. Stochastic Optimization and Scenario Generation for Peak Load Shaving in Smart District Microgrid: Sizing and Operation. Energy Build. 2022, 275, 112426. [Google Scholar] [CrossRef]
- He, Y.; Wu, H.; Ding, M.; Bi, R.; Hua, Y. Reduction Method for Multi-Period Time Series Scenarios of Wind Power. Electr. Power Syst. Res. 2023, 214, 108813. [Google Scholar] [CrossRef]
- Morales, J.M.; Pineda, S.; Conejo, A.J.; Carrión, M. Scenario Reduction for Futures Market Trading in Electricity Markets. IEEE Trans. Power Syst. 2009, 24, 878–888. [Google Scholar] [CrossRef]
- Zhang, Z.; Altalbawy, F.M.A.; Al-Bahrani, M.; Riadi, Y. Regret-Based Multi-Objective Optimization of Carbon Capture Facility in CHP-Based Microgrid with Carbon Dioxide Cycling. J. Clean. Prod. 2023, 384, 135632. [Google Scholar] [CrossRef]
- Dou, C.; Zhou, X.; Zhang, T.; Xu, S. Economic Optimization Dispatching Strategy of Microgrid for Promoting Photoelectric Consumption Considering Cogeneration and Demand Response. J. Mod. Power Syst. Clean Energy 2020, 8, 557–563. [Google Scholar] [CrossRef]
- Lai, J.C.T.; Chung, H.S.H.; He, Y.; Wu, W.; Blaabjerg, F. Wideband Series Harmonic Voltage Compensator Using Look-Ahead State Trajectory Prediction for Network Stability Enhancement and Condition Monitoring. IEEE Trans. Power Electron. 2023, 38, 5266–5282. [Google Scholar] [CrossRef]
- Alahakoon, S.; Roy, R.B.; Arachchillage, S.J. Optimizing Load Frequency Control in Standalone Marine Microgrids Using Meta-Heuristic Techniques. Energies 2023, 16, 4846. [Google Scholar] [CrossRef]
- Abbasi, A.; Sultan, K.; Afsar, S.; Aziz, M.A.; Khalid, H.A. Optimal Demand Response Using Battery Storage Systems and Electric Vehicles in Community Home Energy Management System-Based Microgrids. Energies 2023, 16, 5024. [Google Scholar] [CrossRef]
- Khosravi, N.; Echalih, S.; Hekss, Z.; Baghbanzadeh, R.; Messaoudi, M.; Shahideipour, M. A New Approach to Enhance the Operation of M-UPQC Proportional-Integral Multiresonant Controller Based on the Optimization Methods for a Stand-Alone AC Microgrid. IEEE Trans. Power Electron. 2023, 38, 3765–3774. [Google Scholar] [CrossRef]
- Gonzales-Zurita, O.; Andino, O.L.; Clairand, J.M.; Escriva-Escriva, G. PSO Tuning of a Second-Order Sliding Mode Controller for Adjusting Active Standard Power Levels for Smart Inverter Applications. IEEE Trans. Smart Grid 2023, 1. [Google Scholar] [CrossRef]
- Alomoush, M.I. Optimal Combined Heat and Power Economic Dispatch Using Stochastic Fractal Search Algorithm. J. Mod. Power Syst. Clean Energy 2020, 8, 276–286. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Akhbari, A.; Rahimi, M.; Andresen, B.; Khooban, M.H. Reducing Impact of Constant Power Loads on DC Energy Systems by Artificial Intelligence. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4974–4978. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-Gonzalez, W.; Garces, A. Optimal Power Flow on DC Microgrids: A Quadratic Convex Approximation. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1018–1022. [Google Scholar] [CrossRef]







| Description | Value |
|---|---|
| Primary Control | |
| DC DG1 and 2 | Rd1, Rd2 = 0.3 |
| AC DG1 | m1 = 3/70,000; n1 = 4/11,000 |
| AC DG2 | m2 = 3/80,000; n2 = 1/3000 |
| System frequency | 50 Hz |
| System voltage | 380 V (p-p, rms) |
| Secondary Control | |
| DC DG1 and 2 | KpV = 10; KiV = 70 |
| AC DG1 and 2 frequency | Kpω = 0.447; Kiω = 47 |
| AC DG1 and 2 bus voltage | KpE = 0.18; KiE = 77 |
| Tertiary Control | |
| AC DG1 and 2 frequency | Kpp = 0.003; KiP = 0.8 |
| AC DG1 and 2 bus voltage | KpQ = 100; KiQ = 3000 |
| Unit Number | ||||||
|---|---|---|---|---|---|---|
| CHP1 | 0.0352 | 13.7 | 2650 | 0.028 | 4.3 | 0.029 |
| CHP2 | 0.0423 | 43 | 1250 | 0.032 | 0.7 | 0.009 |
| Unit Number | aip | bip | cip | dip | eip | Pipmin | Pipmax |
|---|---|---|---|---|---|---|---|
| Unit1 | 0.007 | 2.2 | 25 | 100 | 0.045 | 10 | 75 |
| Unit2 | 0.004 | 1.9 | 60 | 140 | 0.038 | 20 | 125 |
| Unit3 | 0.0015 | 2.4 | 100 | 160 | 0.041 | 30 | 175 |
| Unit4 | 0.0012 | 2.1 | 120 | 180 | 0.043 | 40 | 250 |
| Unit Number | akh | bkh | ckh | Hkhmax | Hkhmin |
|---|---|---|---|---|---|
| Thermal power unit | 0.036 | 2.0124 | 950 | 2695.2 | 0 |
| Optimal Cost Value | Average Cost Value | Maximum Cost Value | |
|---|---|---|---|
| Cost (¥) | 452,044.6317 | 525,045.2684 | 643,369.1997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shan, Y.; Ma, L.; Yu, X. Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand. Energies 2023, 16, 5503. https://doi.org/10.3390/en16145503
Shan Y, Ma L, Yu X. Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand. Energies. 2023; 16(14):5503. https://doi.org/10.3390/en16145503
Chicago/Turabian StyleShan, Yinghao, Liqian Ma, and Xiangkai Yu. 2023. "Hierarchical Control and Economic Optimization of Microgrids Considering the Randomness of Power Generation and Load Demand" Energies 16, no. 14: 5503. https://doi.org/10.3390/en16145503




