AC Distributed Winding with Low Higher Spatial Harmonics Content in Mmf Distribution
Abstract
:1. Introduction
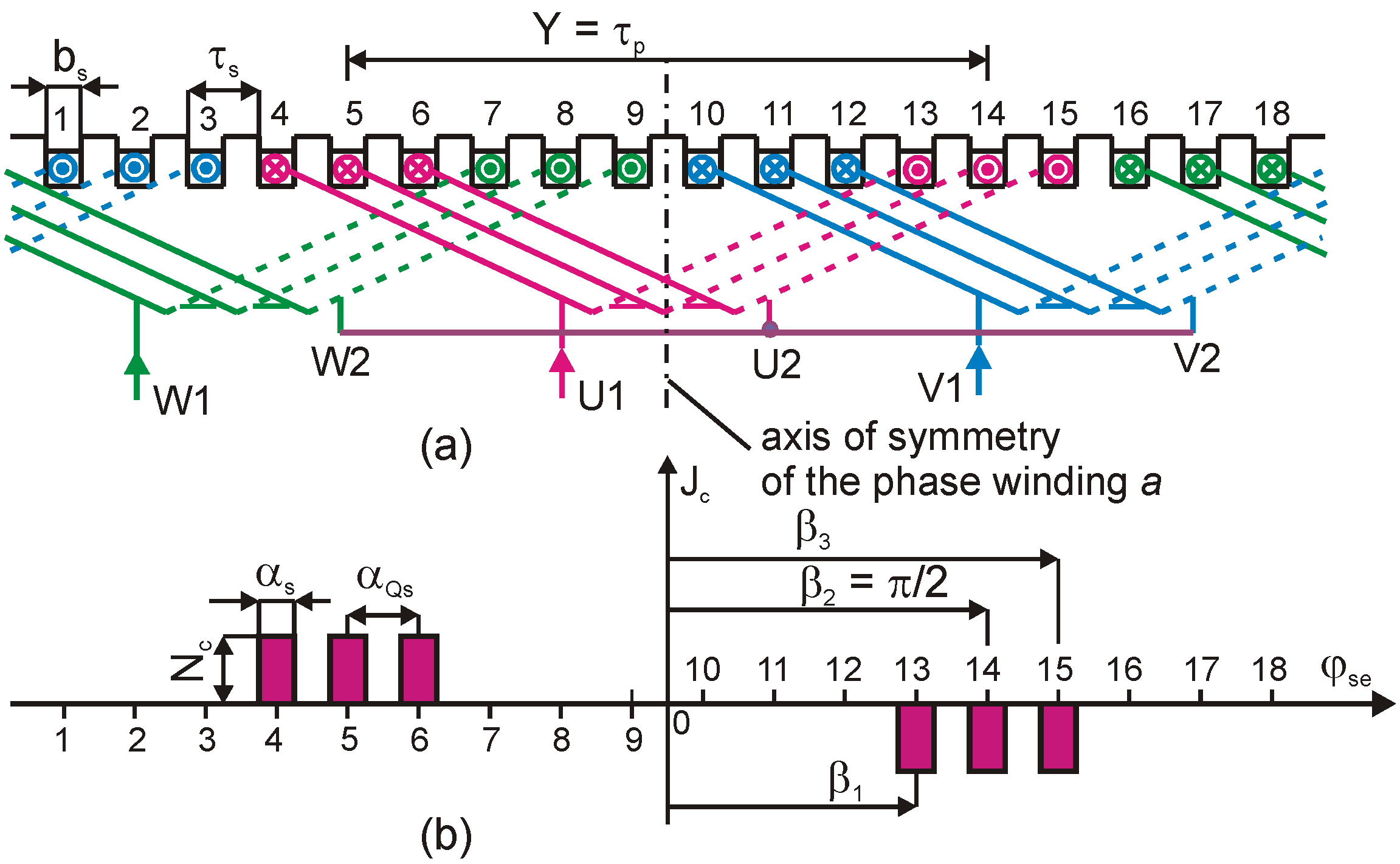
2. Three-Phase Single-Layer Winding
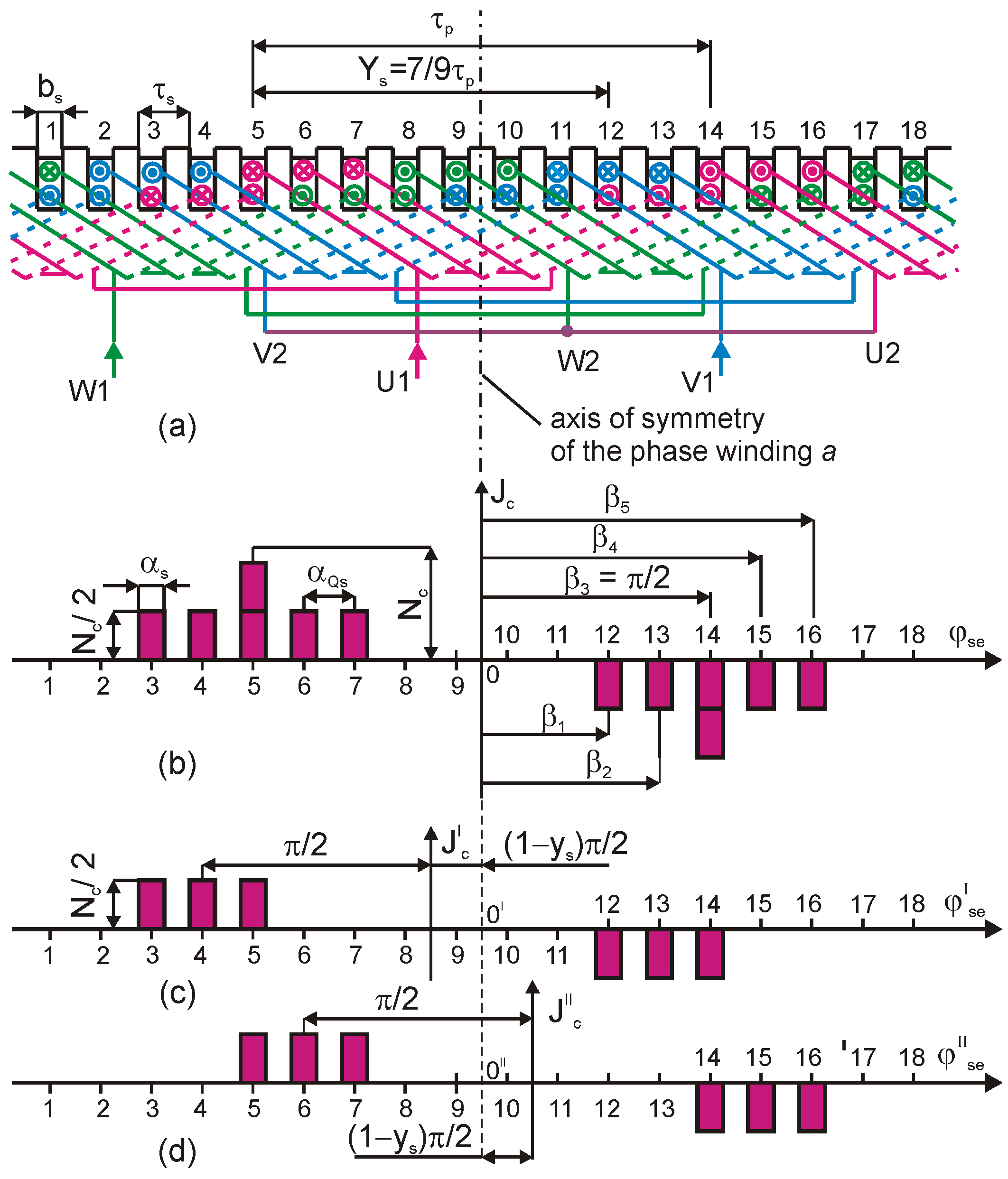
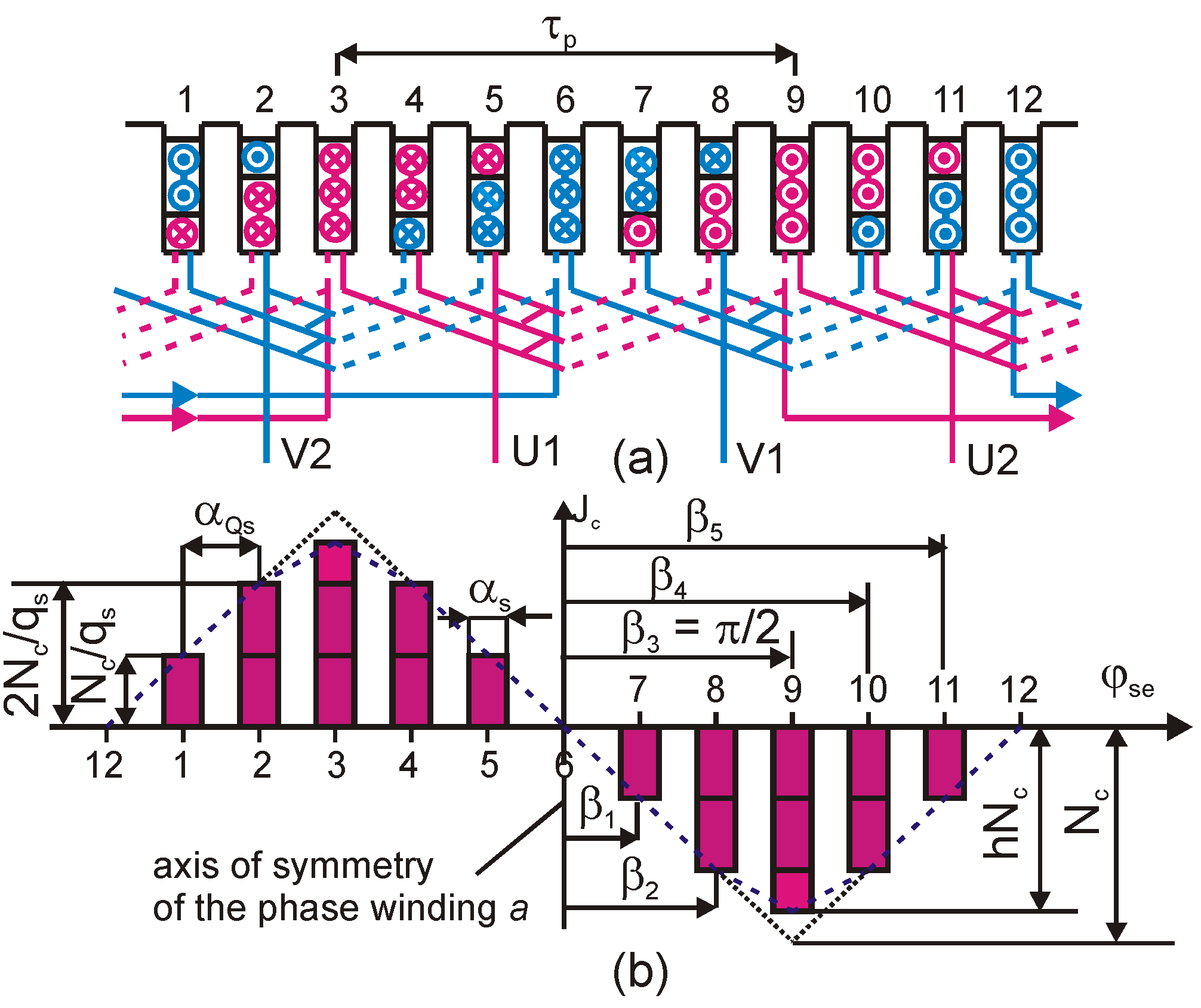
3. Three-Phase Double-Layer Winding
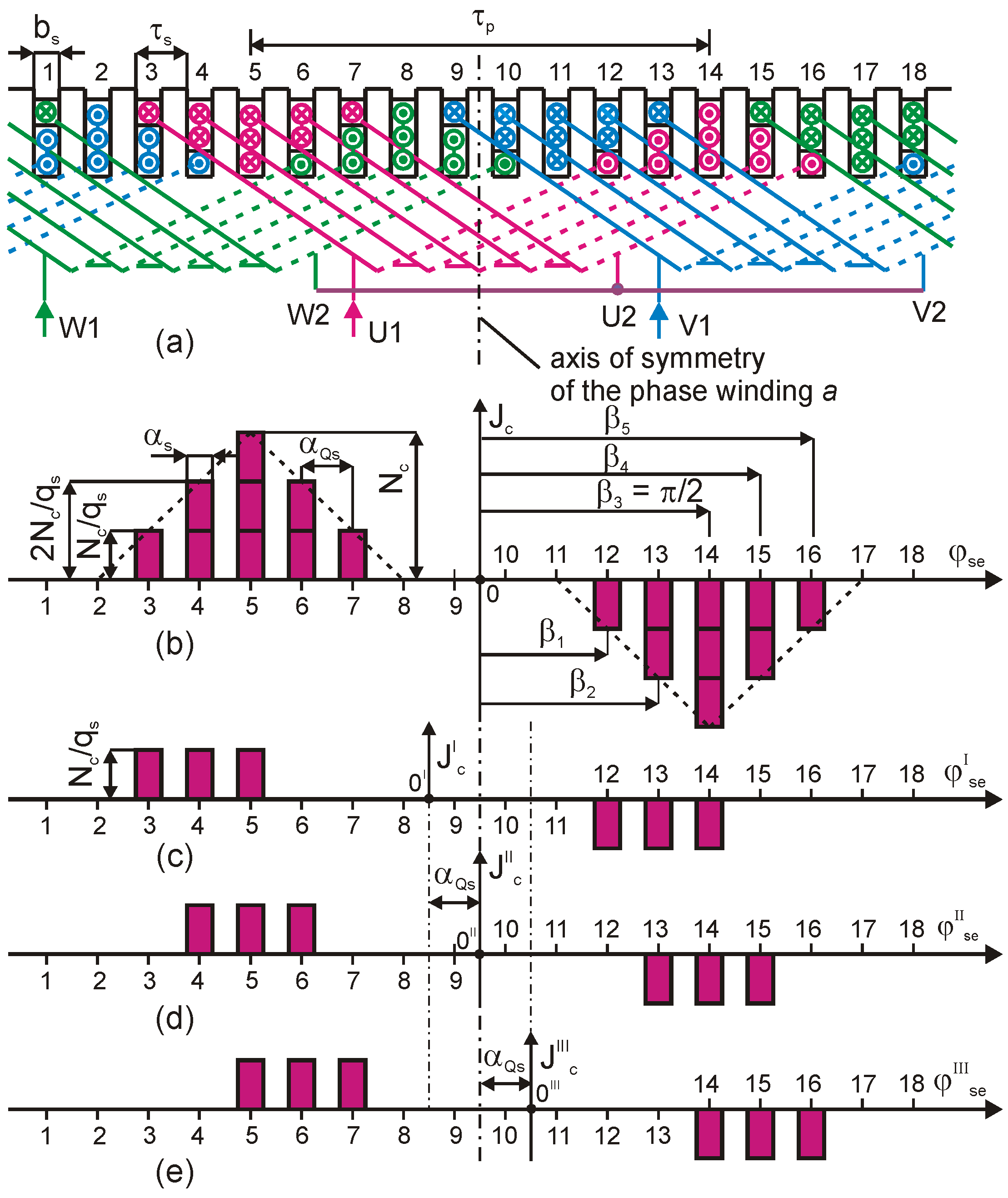
4. Three-Phase Triangle Winding
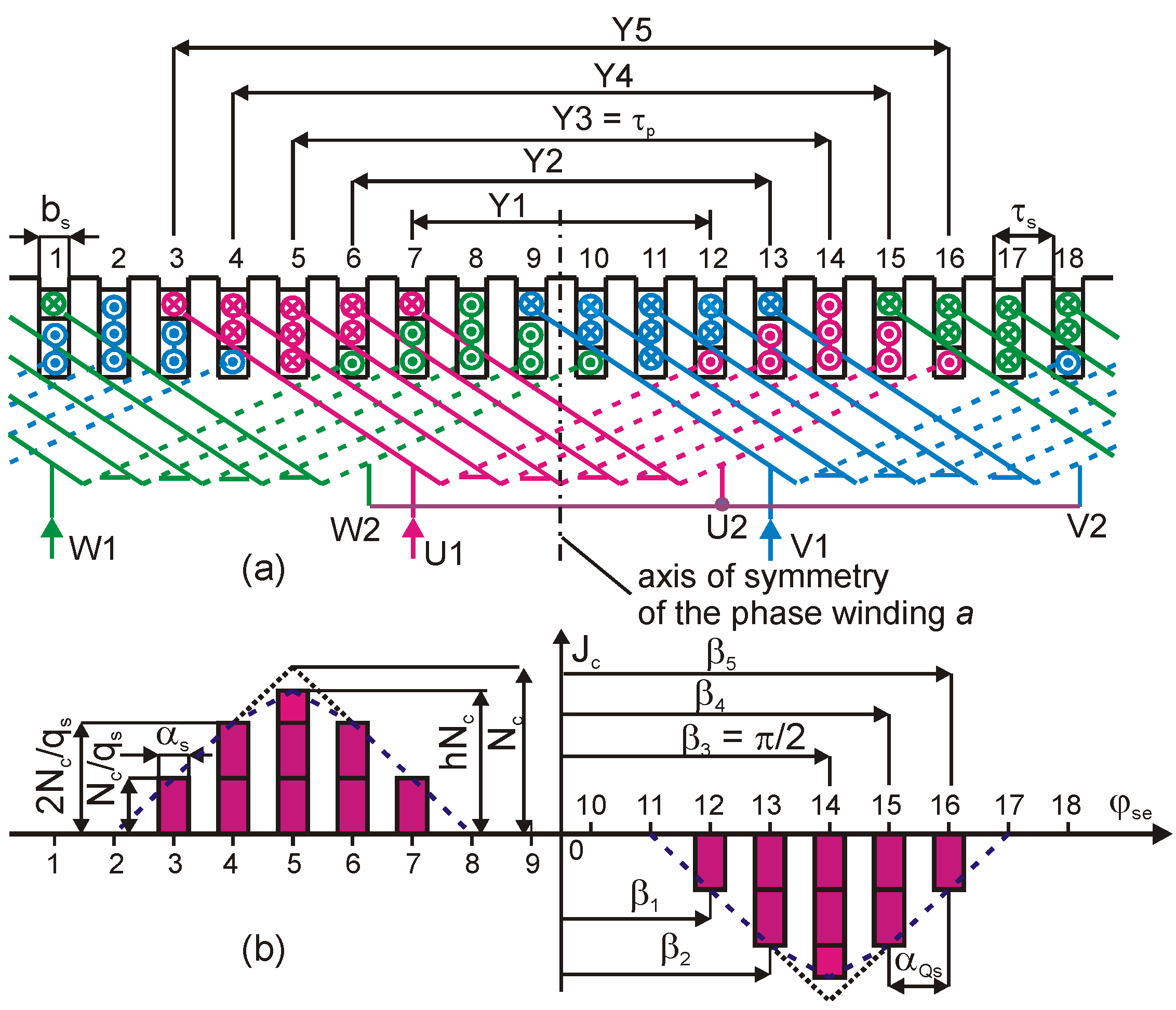
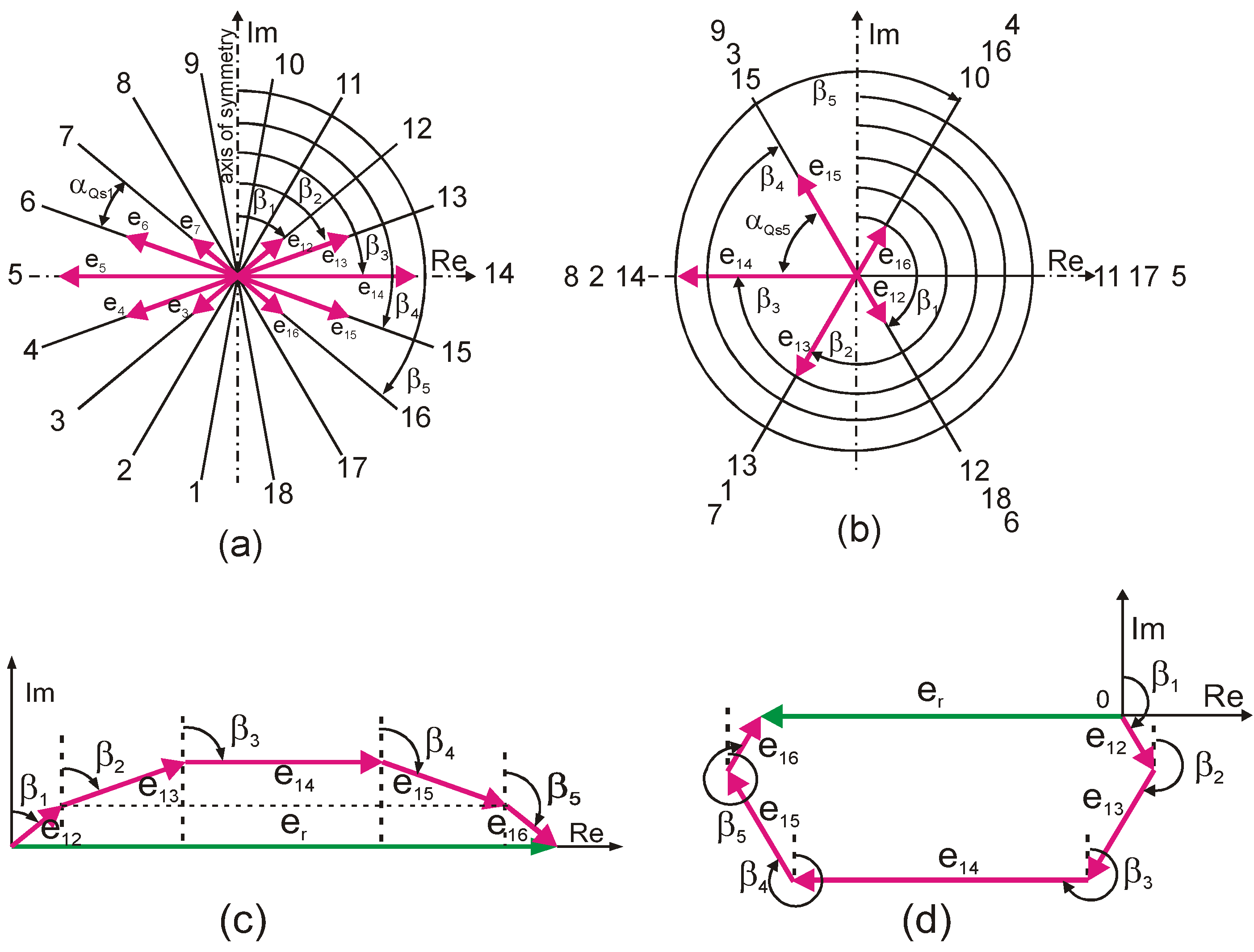
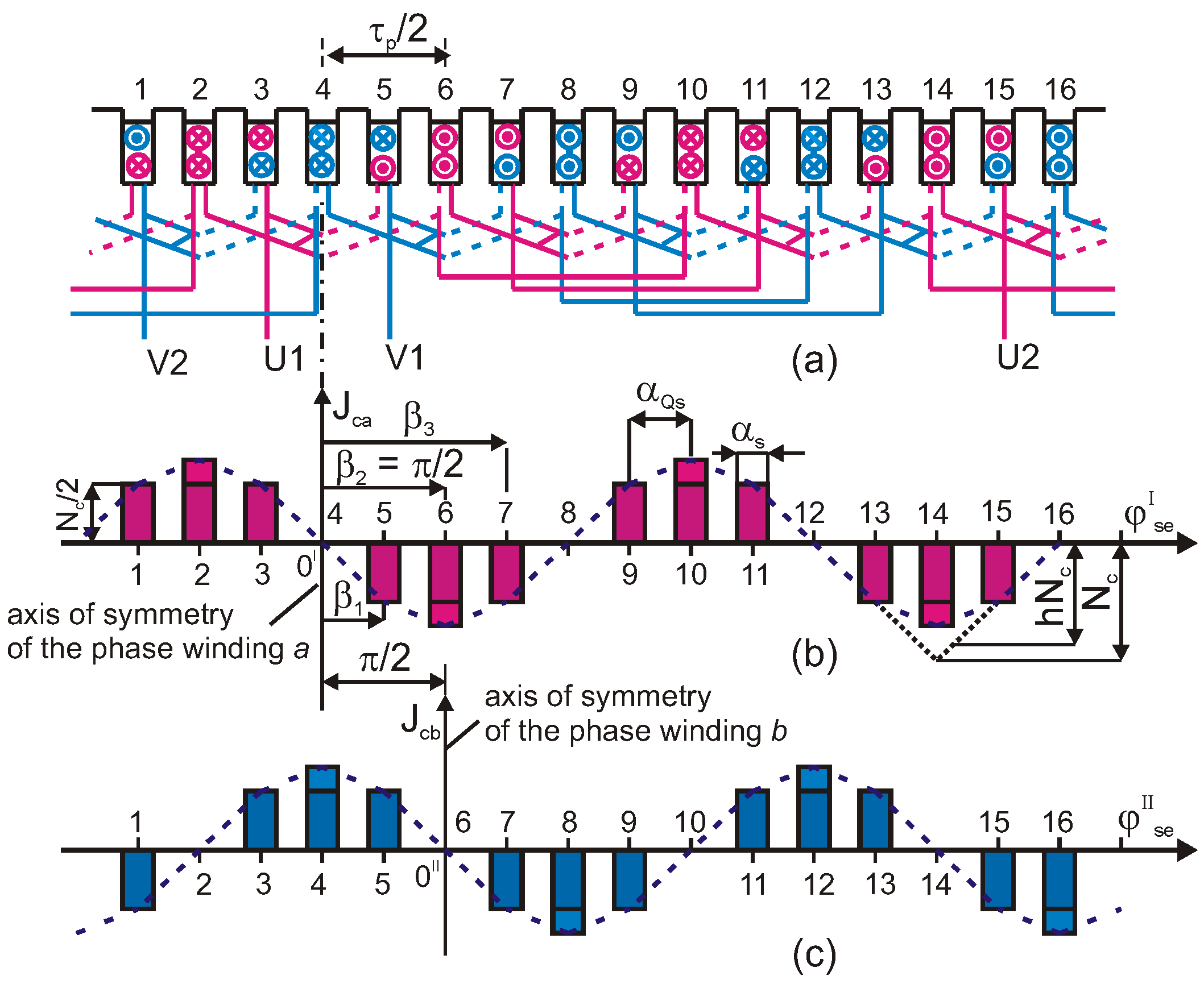
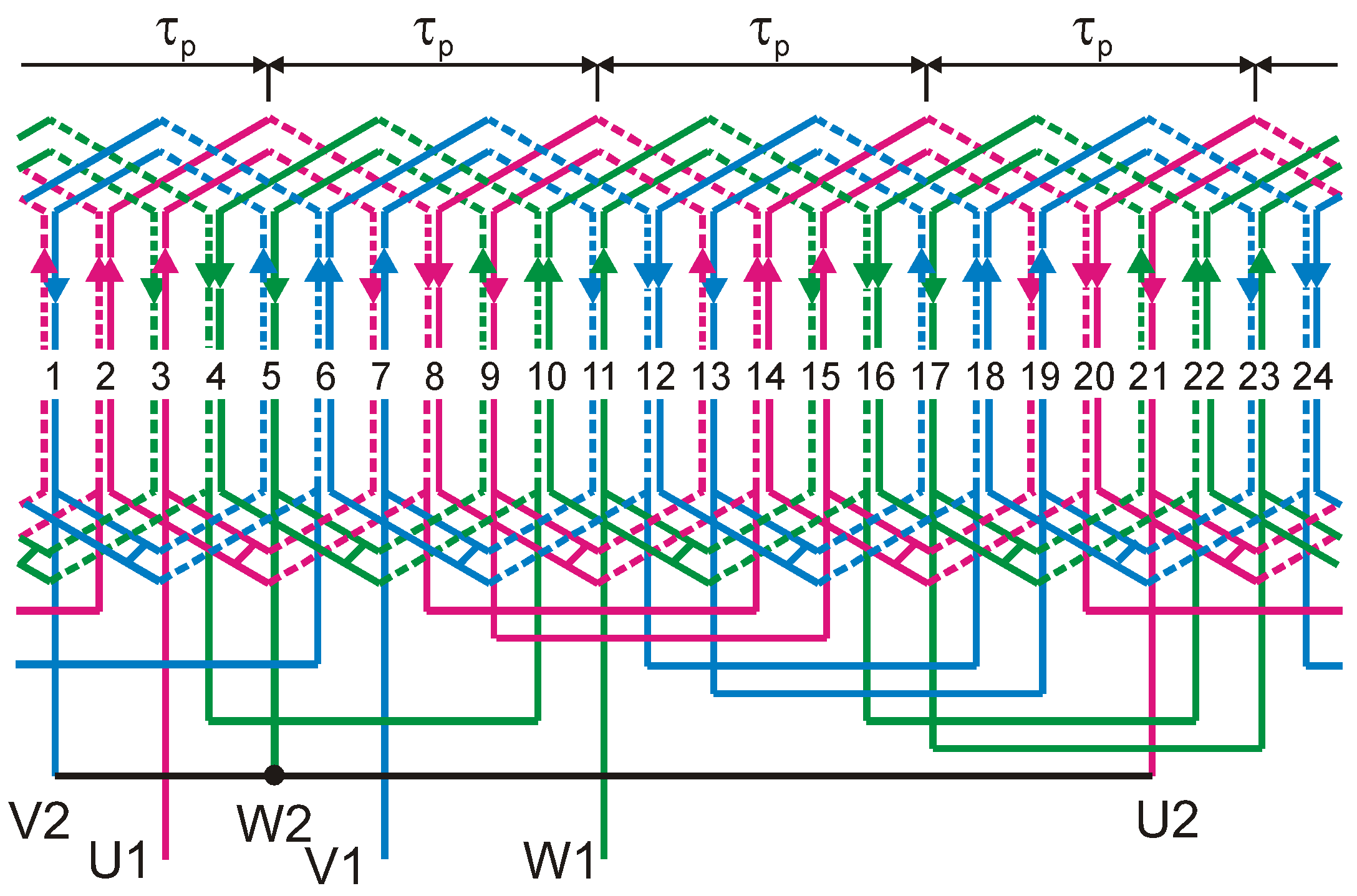
5. Modified Triangle Winding
5.1. Three-Phase Winding
- The number of turns in the slot must be an integer divisible by qs;
- The number of turns in the coil in which the reduction of turns has been made Nh = hNc must be an integer.
- The phase angle, i.e., the electrical angle between the emf of the ν-th harmonic of the sides in adjacent slots:
- The greatest common divisor (g.c.d) of the numbers QS and νp:
- The number of star radii:
- The angle between the radii of the star of slot voltages phasors:
- For the first harmonic:
- For the third harmonic:
5.2. Two-Phase Winding
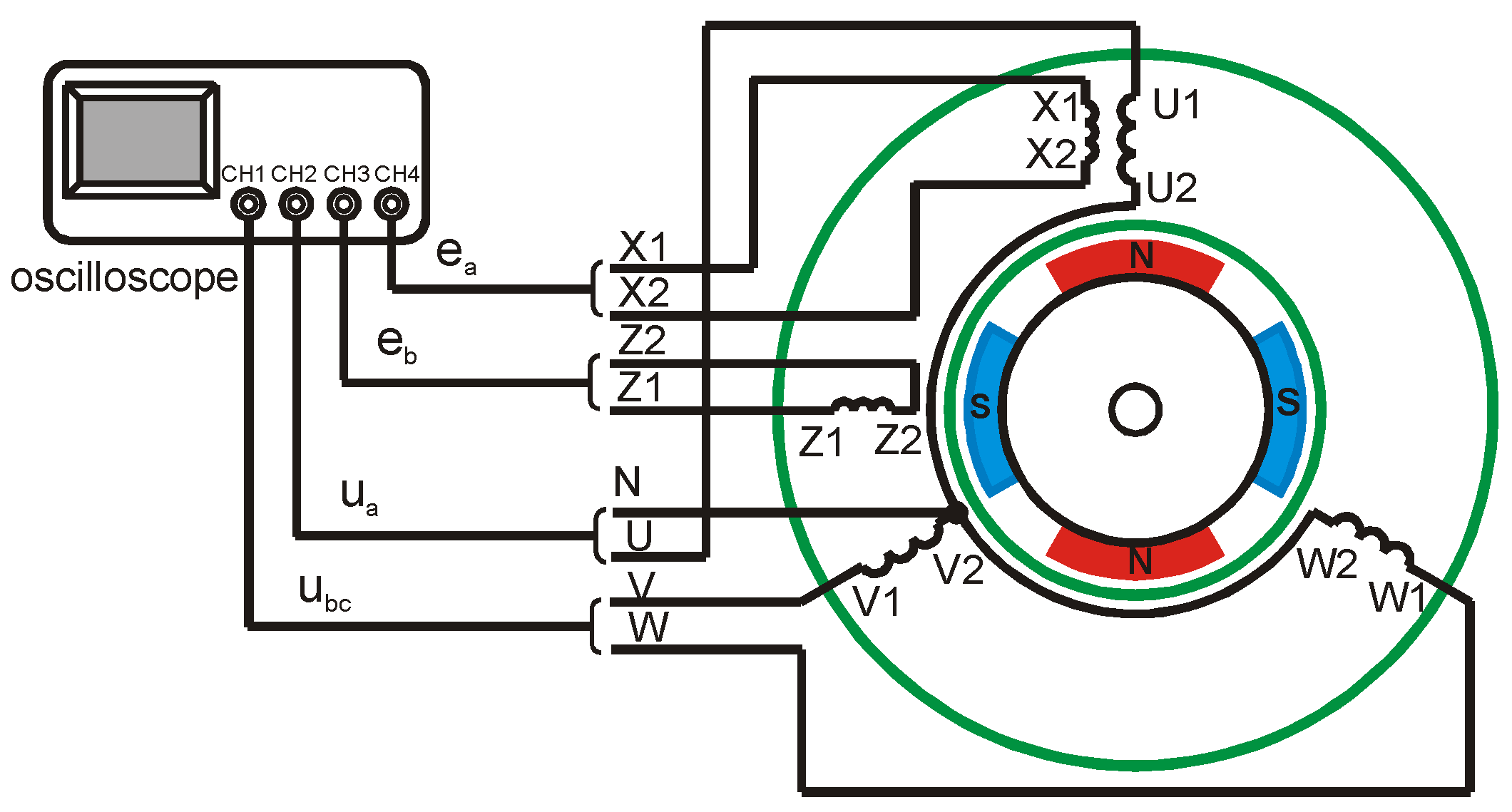
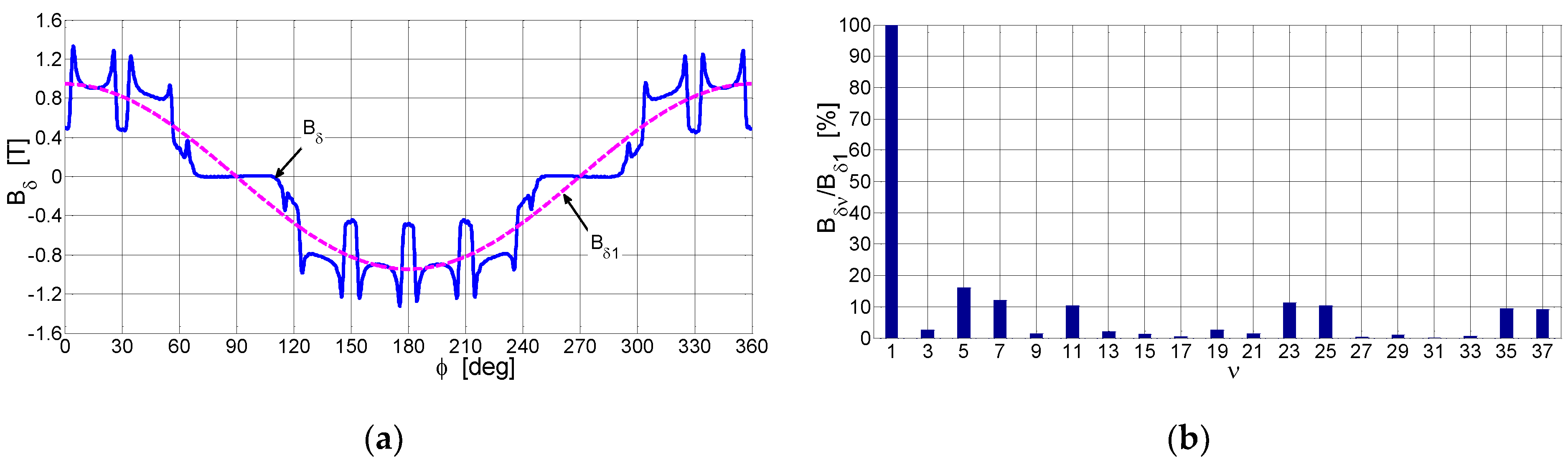
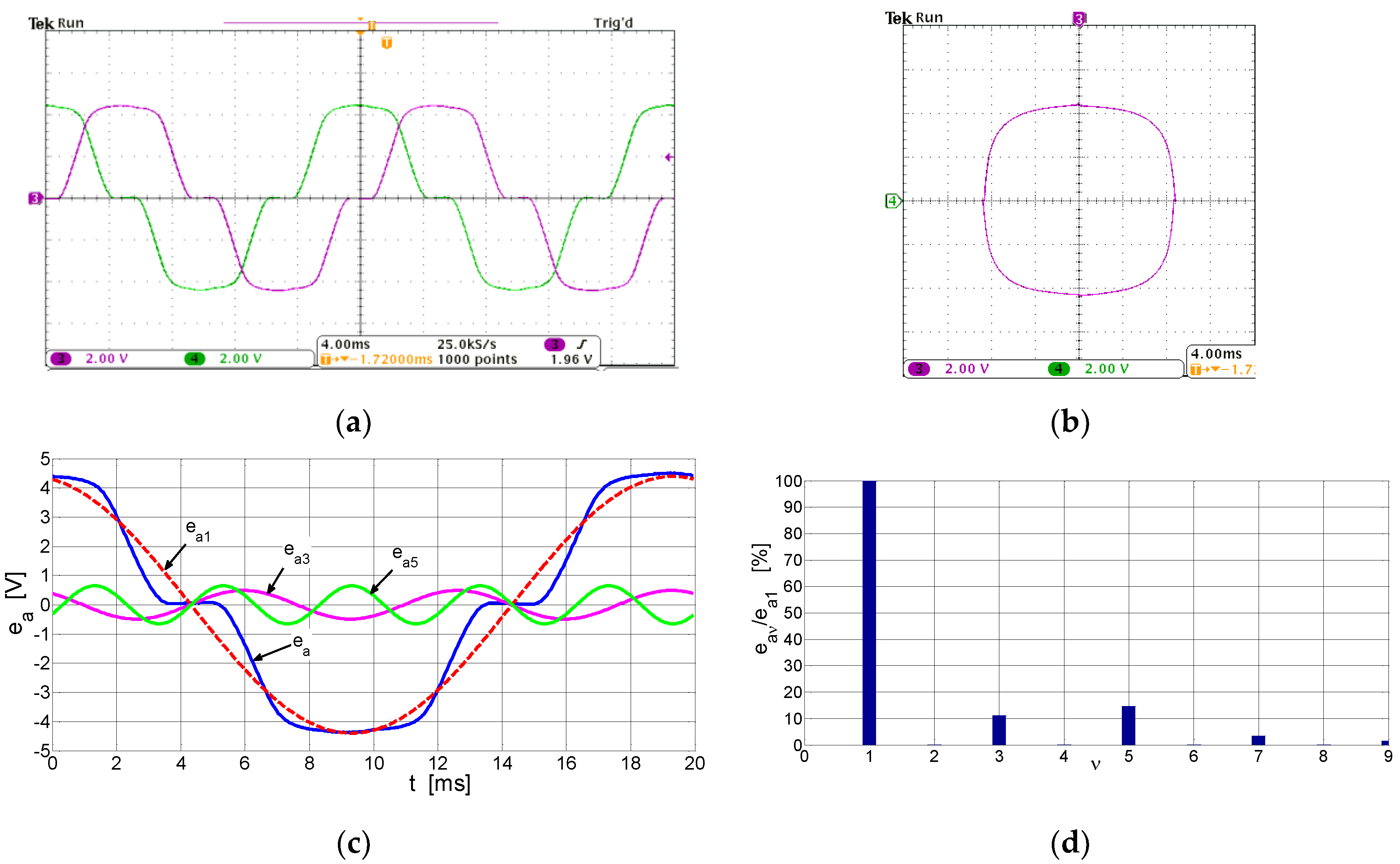
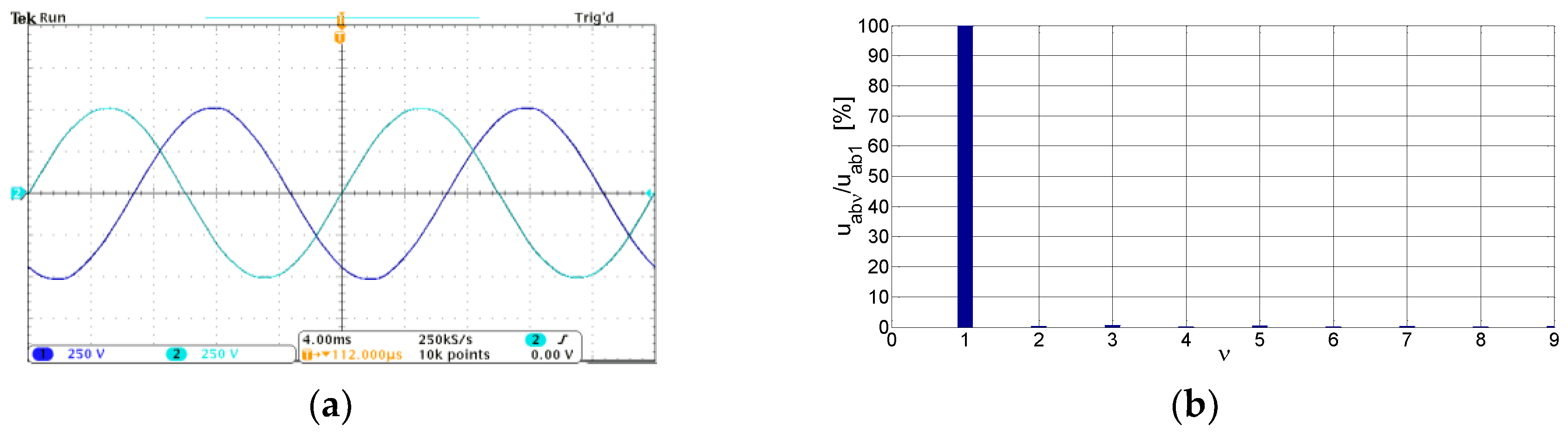
6. Experimental Section
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Heller, B.; Hamata, V. Harmonic Fields Effects in Induction Machines. Academia; Publishing House: Prague, Czech Republic, 1977. [Google Scholar]
- Kluszczyński, K.; Miksiewicz, R. Parasitic Torques in Squirrel-Cage Induction Motors; Polish Society of Theoretical and Applied Electrical Engineering: Warsaw, Poland, 1993. [Google Scholar]
- Carbonieri, M.; Leonardo, L.; Bianchi, N.; Tursini, M.; Villani, M.; Popescu, M. Cage Losses in Induction Motors Considering Harmonics: A New Finite Element Procedure and Comparison With the Time-Domain Approach. IEEE Trans. Ind. Appl. 2022, 58, 1931–1940. [Google Scholar] [CrossRef]
- Schuffenhauer, U.; Kuβ, H. Additional Losses by Magnetic Field Harmonics in the Rotor Bars of Asynchronous Machines and their Influence. Electr. Power Qual. Util. J. 2006, 12, 117–120. [Google Scholar]
- Wang, J.; Cheng, M. No-Load Additional High-order Space Harmonic Losses of Squirrel Cage Induction Motor Based on General Airgap Field Modulation Theory. In Proceedings of the IEEE 12th Energy Congress & Exposition—Asia, Singapore, 24–27 May 2021; pp. 875–880. [Google Scholar]
- Boldea, I.; Nasar, S.J. The Induction Machines Design Handbook; CRC Presss Taylor & Francis: Boca Raton, FL, USA; London, UK, 2010. [Google Scholar]
- Pyrhönen, J.; Jokinen, T.; Hrabovcová, V. Design of Rotating Electrical Machines; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Głowacki, A. Electromagnetic Calculations of Three-Phase Induction Motors; WNT Publishing House: Warsaw, Poland, 1993. (In Polish) [Google Scholar]
- Dąbrowski, M. Design of AC Electrical Machines; WNT Publishing House: Warsaw, Poland, 1993. [Google Scholar]
- Wang, J.; Patel, V.; Wang, W. Fractional-Slot Permanent Magnet Brushless Machines with Low Space Harmonic Contents. IEEE Trans. Magn. 2014, 50, 8200209. [Google Scholar] [CrossRef]
- Huang, J.; Sui, Y.; Yin, Z.; Yuan, Z.; Zheng, P. A Novel High Torque Density Dual Three-Phase PMSM With Low Space Harmonic Content. IEEE Trans. Magn. 2021, 58, 8204007. [Google Scholar] [CrossRef]
- Zhao, B.; Gong, J.; Tong, T.; Semail, E.; Nguyen, N.-K.; Gilon, F. A Novel Five-Phase Fractional Slot Concentrated Winding with Low Space Harmonic Contents. IEEE Trans. Magn. 2021, 57, 8104605. [Google Scholar] [CrossRef]
- Wang, K.; Lin, H. Modular Permanent Magnet Synchronous Machine with Low Space Harmonic Content. Energies 2020, 13, 3924. [Google Scholar] [CrossRef]
- Kocabas, D.A. Novel Winding and Core Design for Maximum Reduction of Harmonic Magnetomotive Force in AC Motors. IEEE Trans. Magn. 2009, 45, 735–746. [Google Scholar] [CrossRef]
- Banchhor, D.K.; Dhabale, A. New Optimized Winding and Core Design for Space Harmonic Reduction in Doubly Fed Induction Machine. In Proceedings of the IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy, Cochin, India, 2–4 January 2020; pp. 1–6. [Google Scholar]
- Tang, N.; Brown, I.P. Framework and Solution Technicues for Suppressing Electric Machine Winding MMF Space Harmonic by Varying Slot Distribution and Coil Turns. IEEE Trans. Magn. 2018, 54, 8103512. [Google Scholar] [CrossRef]
- Gyftakis, K.; Panagiotou, P.; Kappatou, J. Application of Wedges for the Reduction of the Space and Time-Dependent Harmonic Content in Squirrel-Cage Induction Motors. J. Comput. Eng. Hindawi Publ. Corp. 2013, 2013, 657425. [Google Scholar] [CrossRef] [Green Version]
- Staszak, J. Modeling the Electromechanical Characteristics of Three-Phase Squirrel Induction Motor by Selecting the Stator Winding and the Power Supply System. Monograph M31; Publishing House of the Kielce University of Technology: Kielce, Poland, 2012. (In Polish) [Google Scholar]
- Staszak, J.; Nadolski, R. Winding of Low Spatial Harmonic in the Magnetic Field. Patent of Poland PL 213957 B1, 19 October 2012. [Google Scholar]
- Dąbrowski, M. Magnetic Field and Circuits in Electrical Machines; WNT Publishing House: Warsaw, Poland, 1971. [Google Scholar]
- Müller, G. Theorie Rotierender Elektrischer Maschinen; VEB Verlag Technik: Berlin, Germany, 1985. [Google Scholar]
- Zwillinger, D. Standart Mathematical Tables and Formulae; Chapman & Hall: Boca Raton, FL, USA; London, UK; CRC: New York, NY, USA, 2003. [Google Scholar]
- Wach, P. Fractional Winding of AC Machines; Scientific Publishing House PWN: Warsaw, Poland, 1997. (In Polish) [Google Scholar]
- Müller, G.; Vogth, K.; Ponick, P. Berechnung Elektrischen Maschinen; Wiley-VCH: Hoboken, NJ, USA, 2008. [Google Scholar]
- Meeker, D. Finite Element Method Magnetics. User Manual, Version 4.2. 2015. Available online: https://www.femm.info/Archives/doc/manual42.pdf (accessed on 21 June 2023).
- Ivanov-Smolensky, A. Electrical Machines; MEI Publisher: Moscow, Russia, 2004; Volume 1. [Google Scholar]




| ν | Double-Layer Winding | Triangle Winding | Triangle Modified | |||
|---|---|---|---|---|---|---|
| ys = 5/6 | ys = 7/9 | h = 1 | h = 1 | h = 0.866 | h = 0.858 | |
| qs | ||||||
| 2 | 3 | 2 | 3 | 2 | 3 | |
| 1 | 0.933013 | 0.901912 | 0.933013 | 0.921207 | 0.928203 | 0.917292 |
| 3 | −0.500000 | −0.333333 | −0.500000 | −0.444444 | −0.464102 | −0.416840 |
| 5 | 0.066987 | −0.037780 | 0.066987 | 0.047336 | 0 | 0 |
| 7 | −0.066987 | −0.135868 | −0.066987 | −0.031458 | 0 | 0.016667 |
| 9 | −0.500000 | 0.333333 | −0.500000 | 0.111111 | 0.464102 | 0.066944 |
| 11 | −0.933013 | −0.135868 | −0.933013 | −0.031458 | −0.928203 | 0.016667 |
| 13 | 0.933013 | −0.037780 | 0.933013 | 0.047336 | 0.928203 | 0 |
| 17 | 0.066987 | 0.901912 | 0.066987 | 0.921207 | 0 | 0.917292 |
| 19 | −0.066987 | −0.901912 | −0.066987 | −0.921207 | 0 | −0.917292 |
| ν | Double-Layer Winding | Modified Triangle Winding | ||
|---|---|---|---|---|
| ys = 3/4 | ys = 5/6 | h = √3/2 | h = 2/3 | |
| qs | ||||
| 2 | 3 | 2 | 3 | |
| 1 | 0.853553 | 0.879653 | 0.828427 | 0.808013 |
| 3 | −0.146447 | −0.235702 | 0 | 0 |
| 5 | 0.146447 | −0.063156 | 0 | −0.058013 |
| 7 | −0.853553 | −0.063156 | −0.879653 | 0.058013 |
| 9 | 0.853553 | −0.235702 | 0.879653 | 0 |
| 11 | −0.146447 | 0.879653 | 0 | −0.808013 |
| 13 | 0.146447 | −0.879653 | 0 | 0.808013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staszak, J. AC Distributed Winding with Low Higher Spatial Harmonics Content in Mmf Distribution. Energies 2023, 16, 5430. https://doi.org/10.3390/en16145430
Staszak J. AC Distributed Winding with Low Higher Spatial Harmonics Content in Mmf Distribution. Energies. 2023; 16(14):5430. https://doi.org/10.3390/en16145430
Chicago/Turabian StyleStaszak, Jan. 2023. "AC Distributed Winding with Low Higher Spatial Harmonics Content in Mmf Distribution" Energies 16, no. 14: 5430. https://doi.org/10.3390/en16145430






