Using Transfer Learning to Build Physics-Informed Machine Learning Models for Improved Wind Farm Monitoring
Abstract
:1. Introduction
1.1. Objective
- Sample efficiency (i.e., how much data are needed to reach a certain prediction accuracy)
- Robustness (i.e., how much the prediction error varies)
- Ability to detect anomalies (i.e., precision and recall)
1.2. Paper Outline
2. Materials and Methods
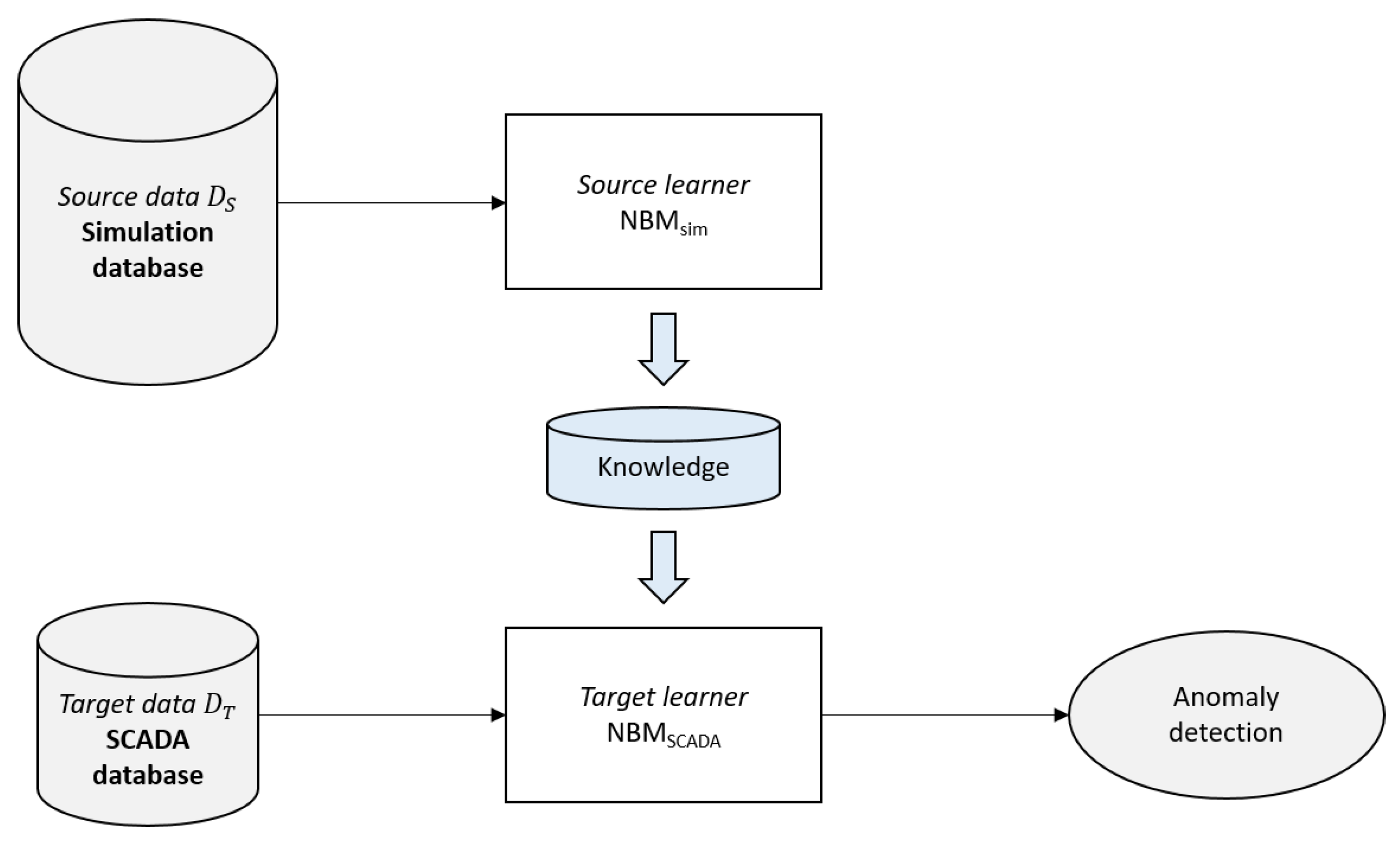
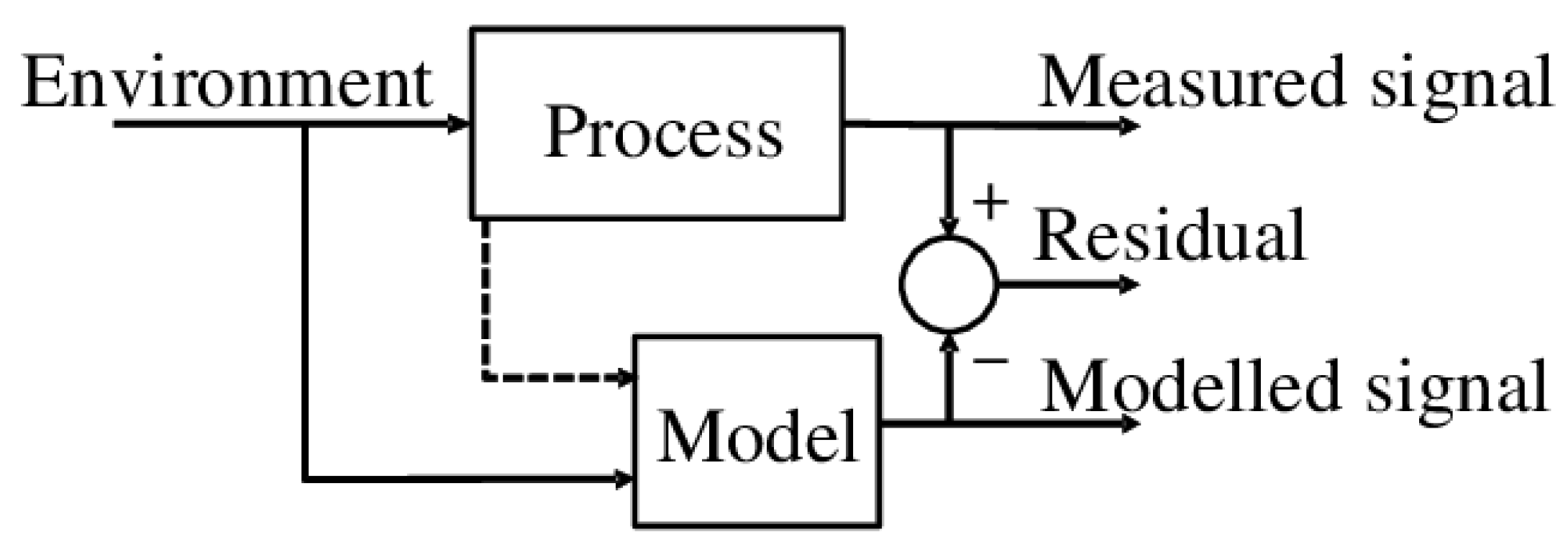
2.1. Transfer Learning for NBM
2.2. Feature Selection
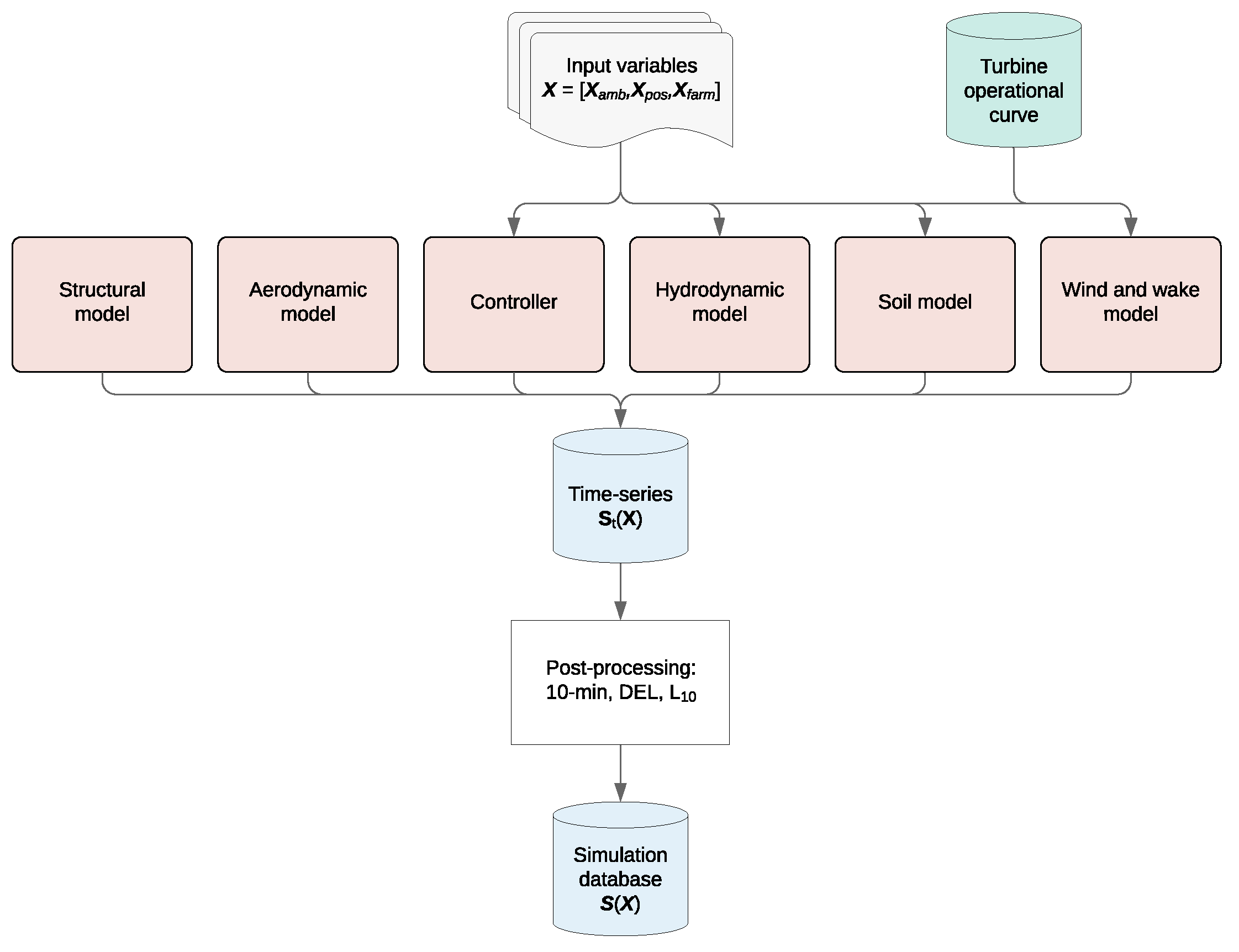
2.3. Creation of Source Data (Simulation)
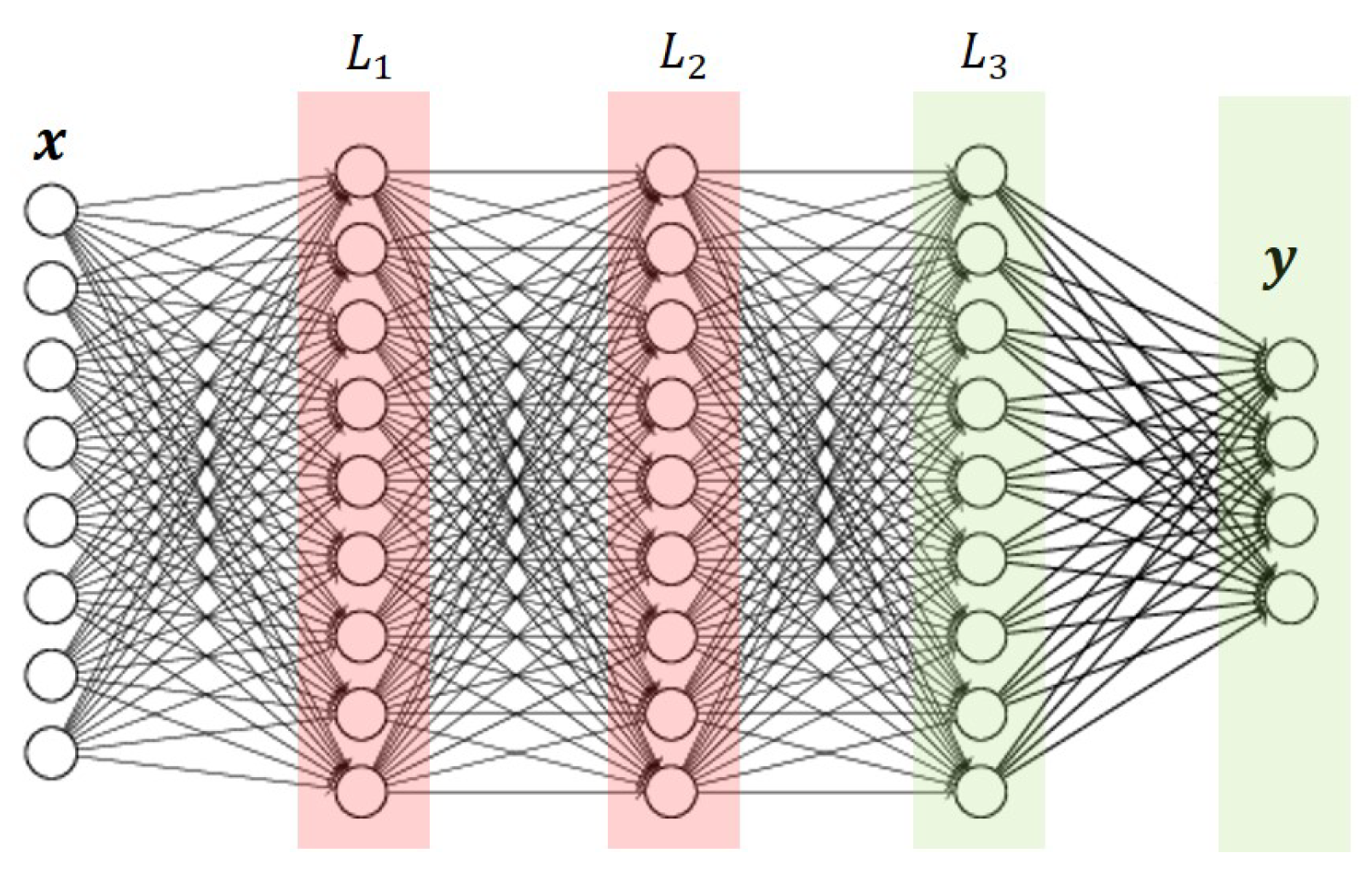
2.4. Method 1: Artificial Neural Network (Parameter Transfer)
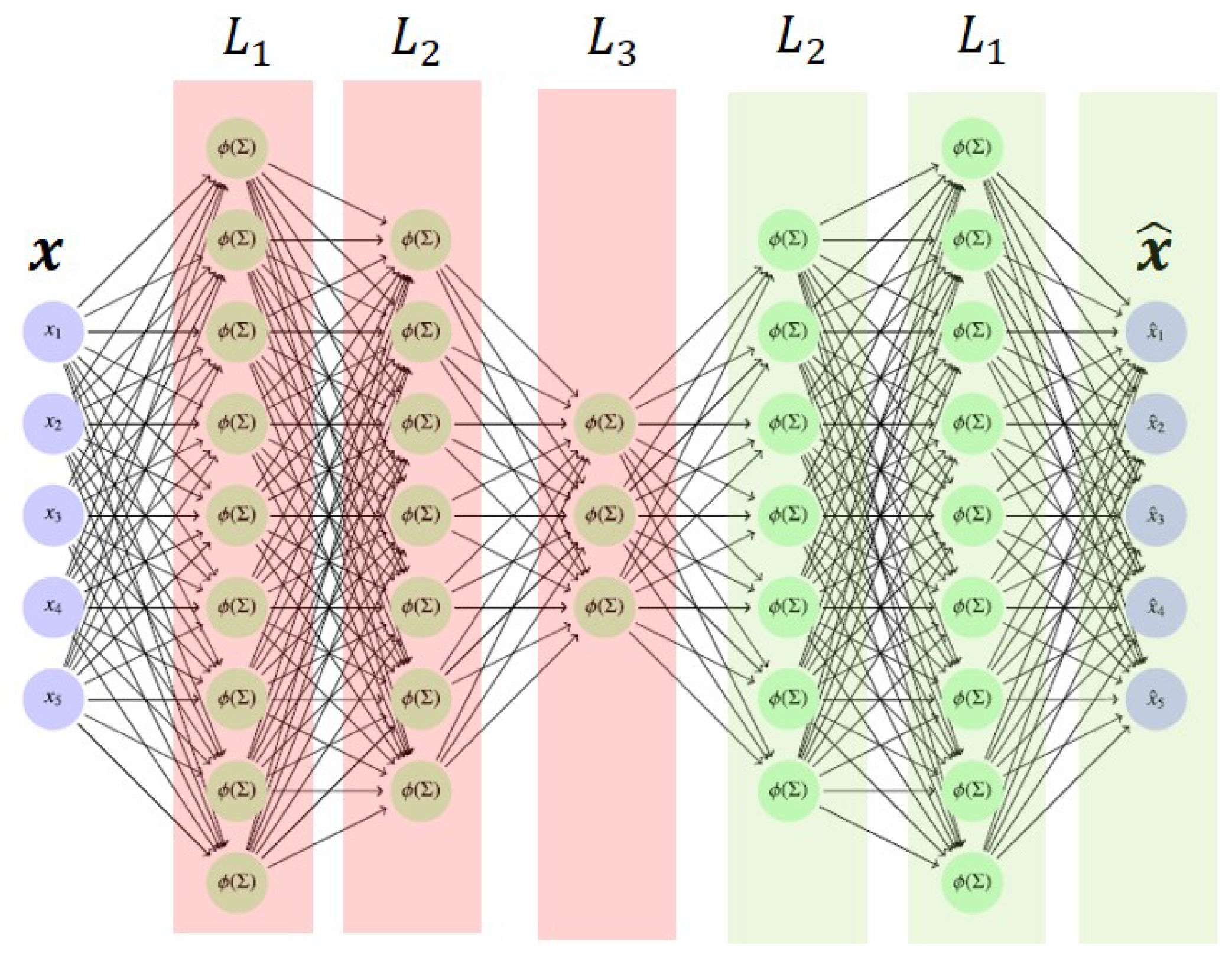
2.5. Method 2: Stacked Denoising Autoencoder (Subspace Transfer)
2.6. Anomaly Detection
3. Results
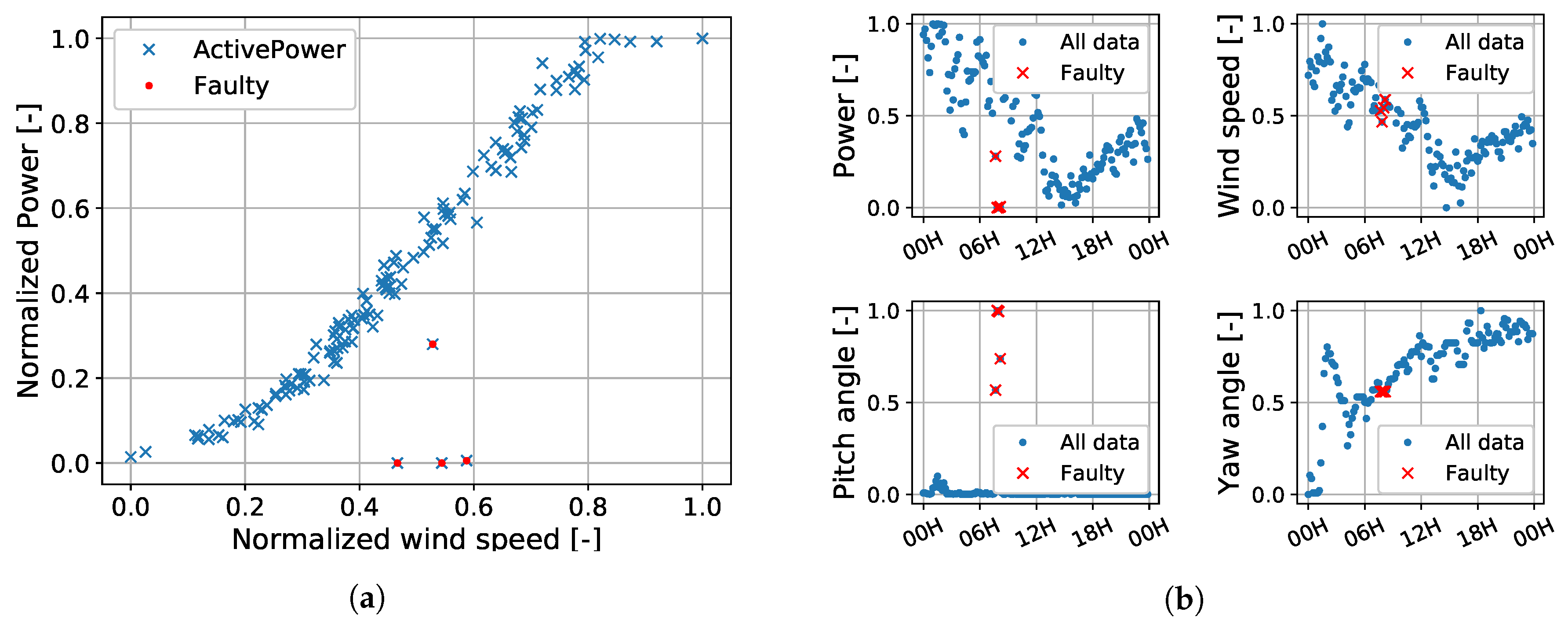
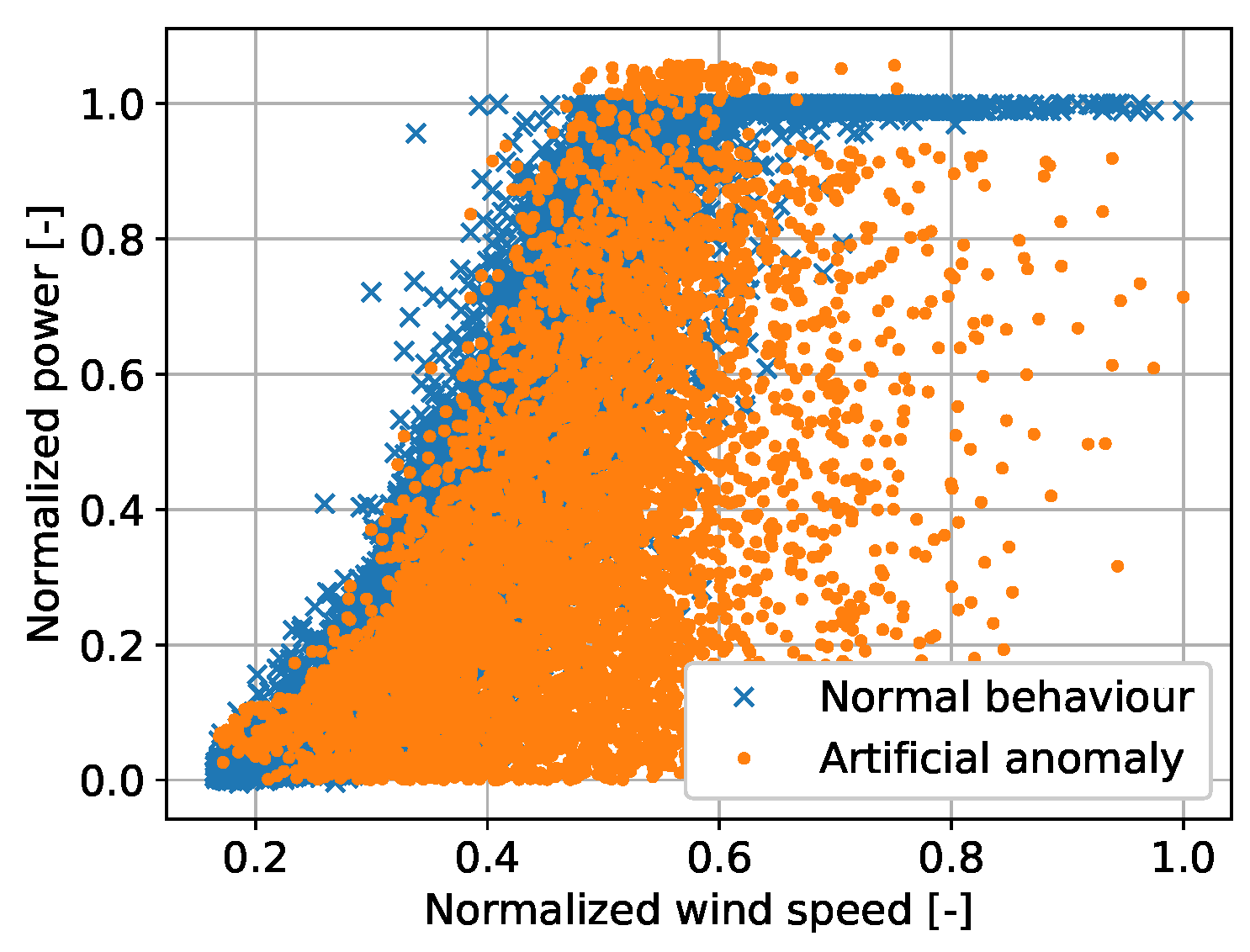
3.1. Data Preparation
3.2. SCADA Data (Target Domain)
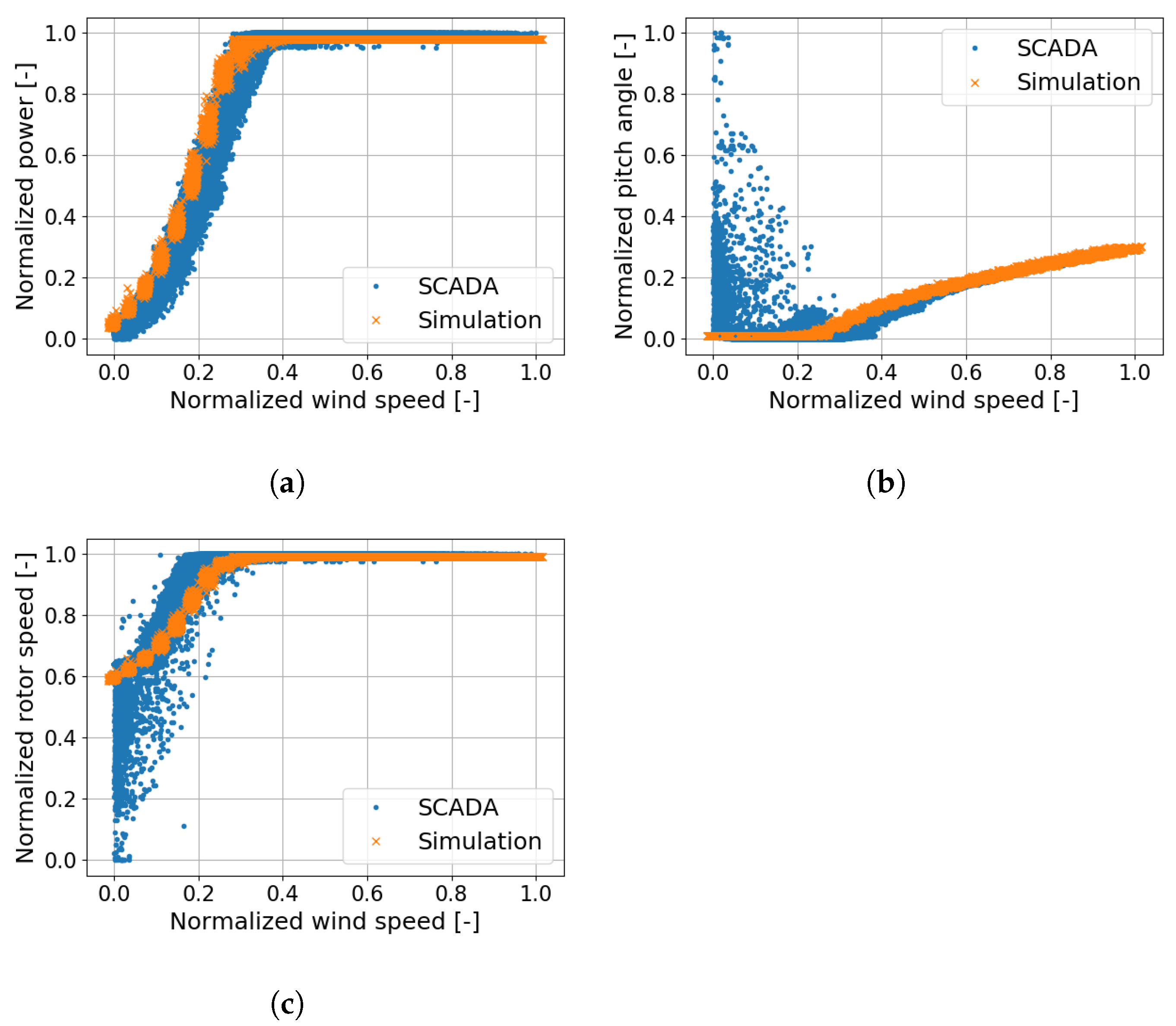
3.3. Simulation Data (Source Domain)
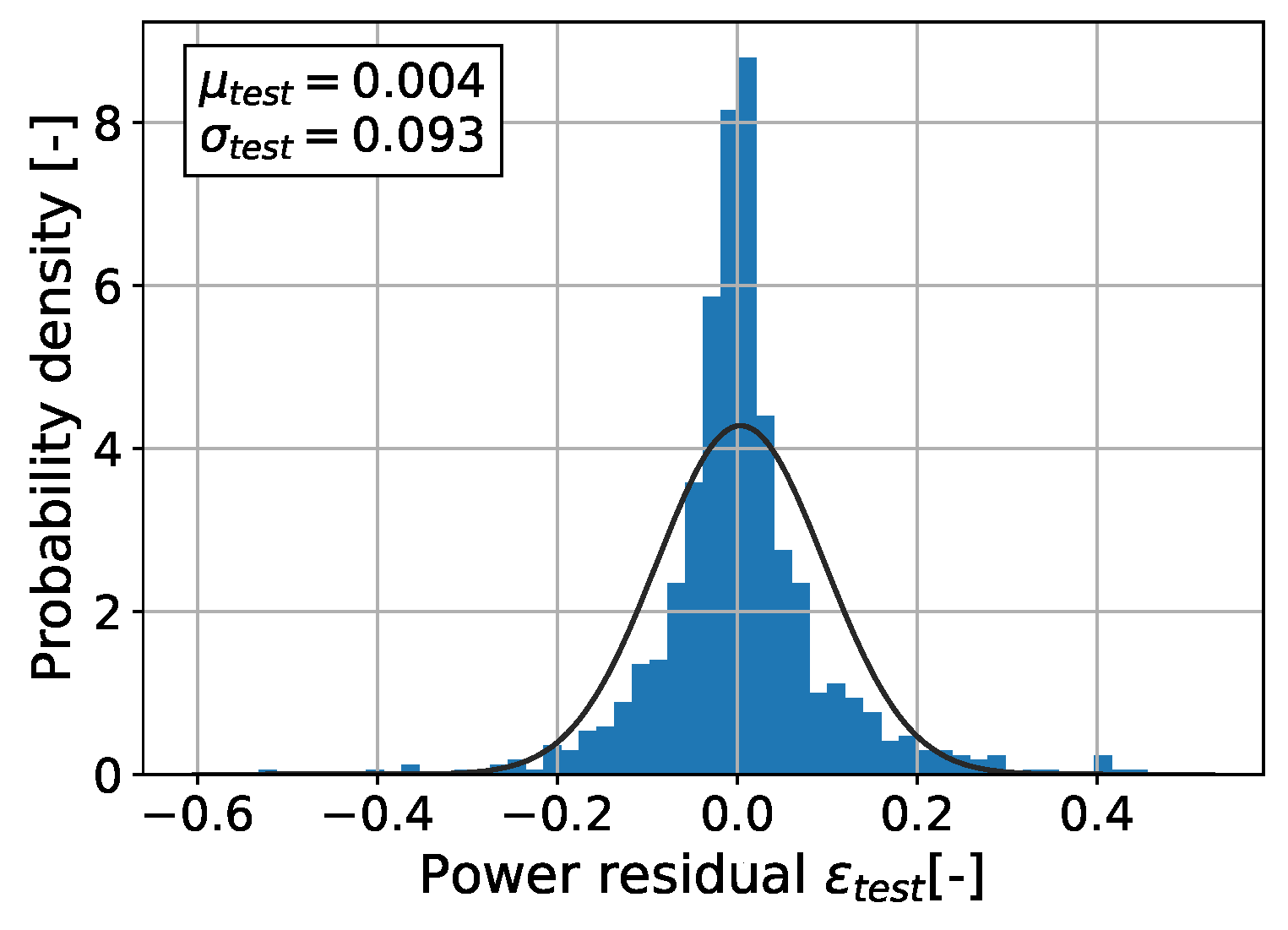
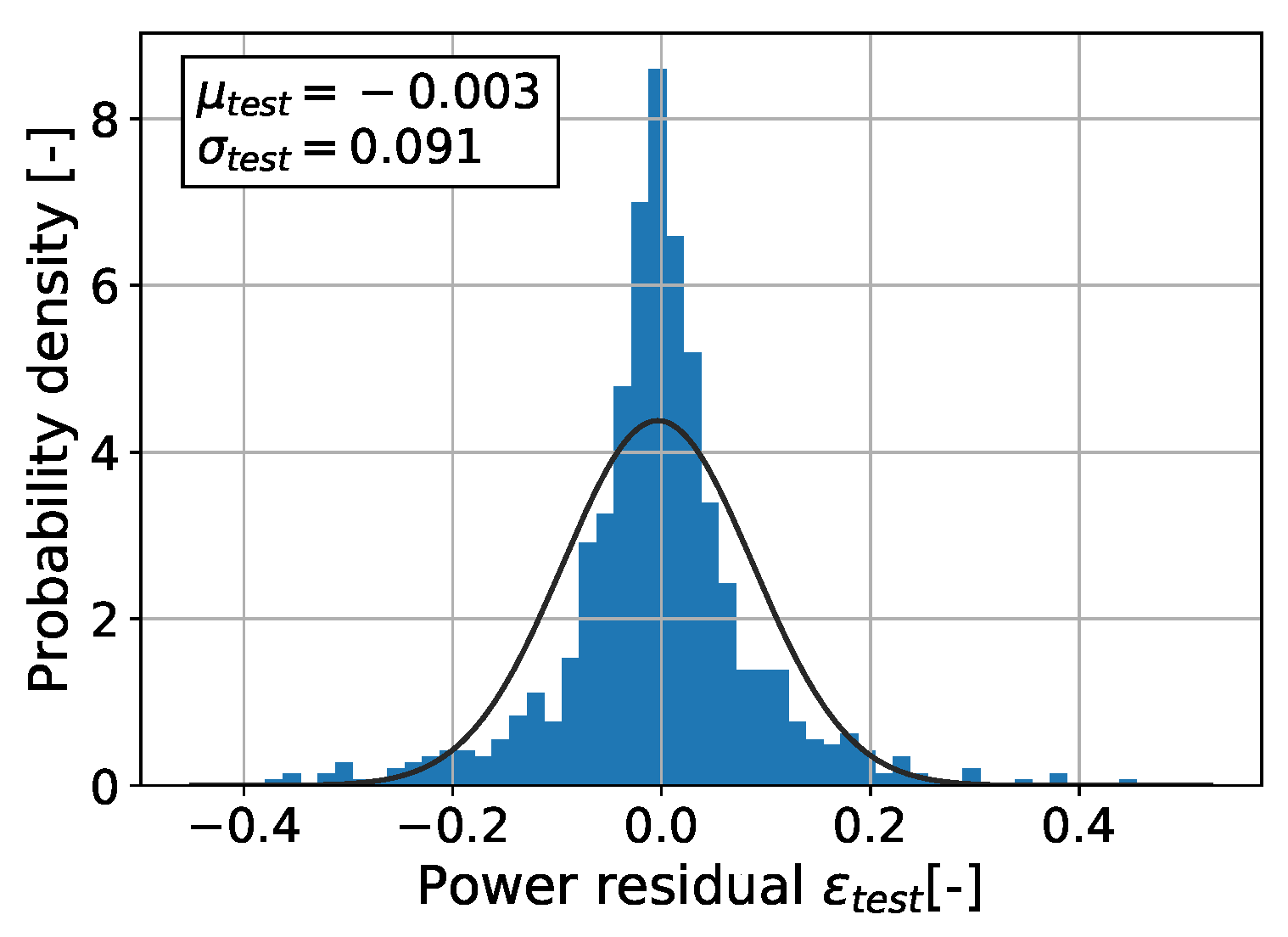
3.4. Model Performance Evaluation
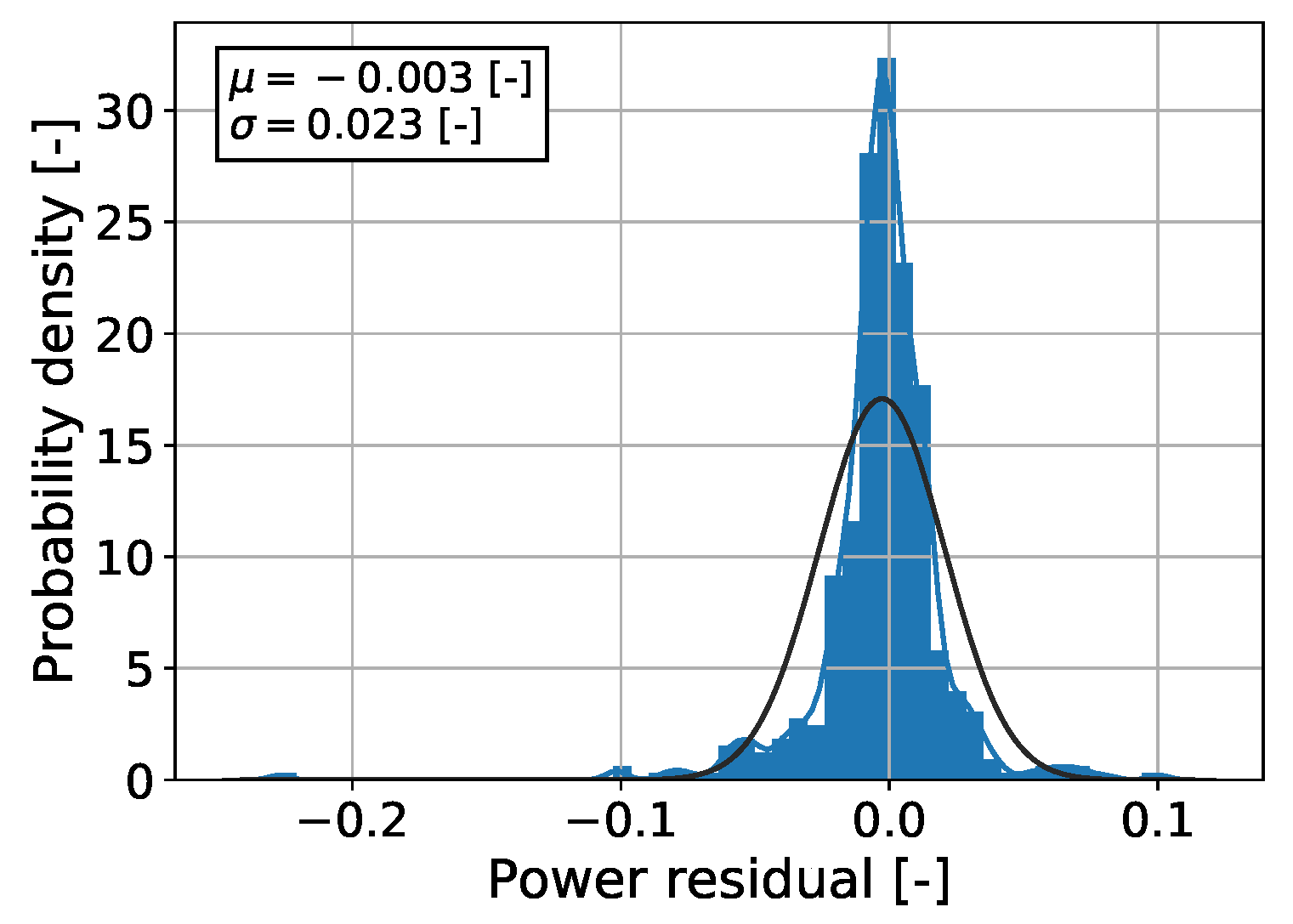
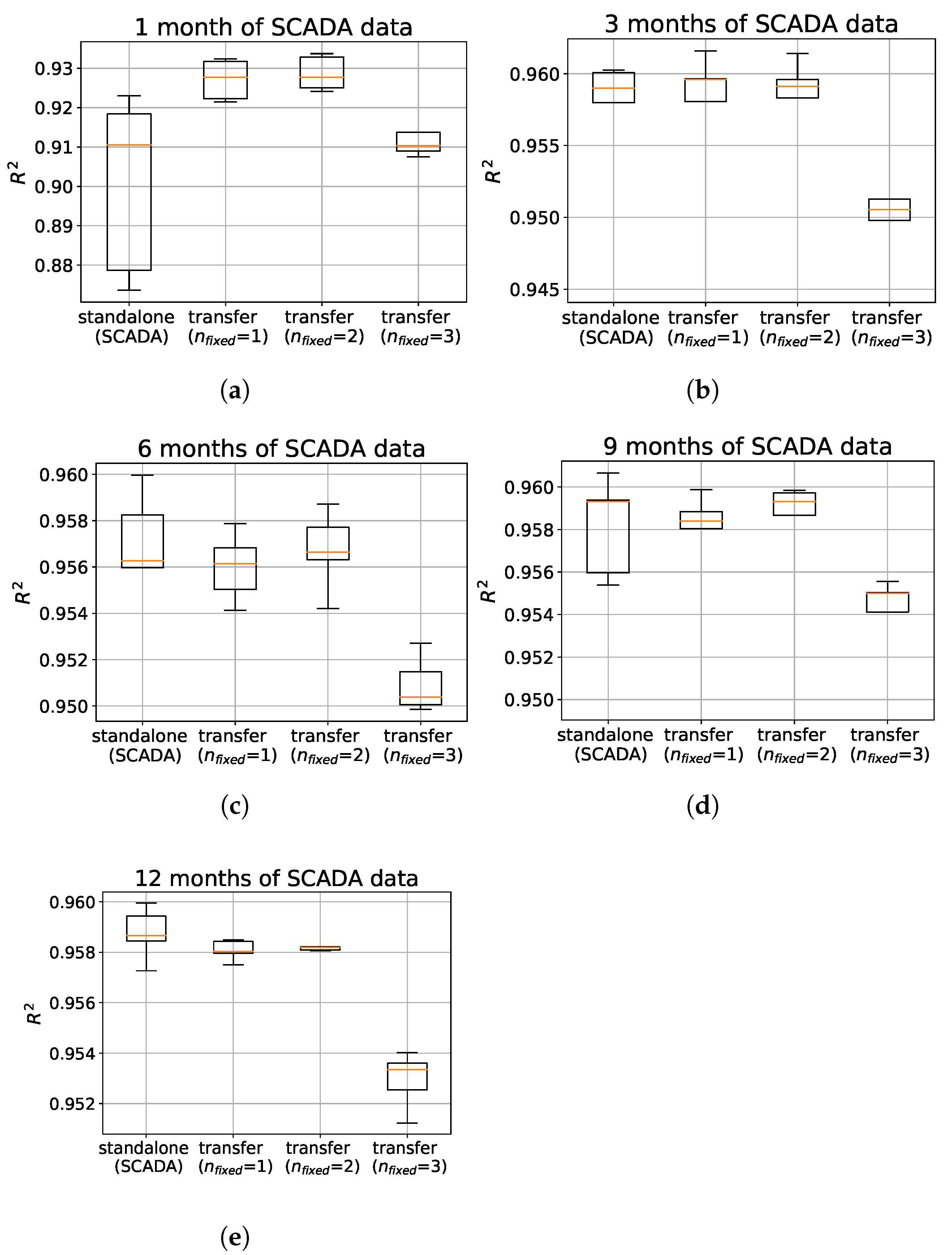
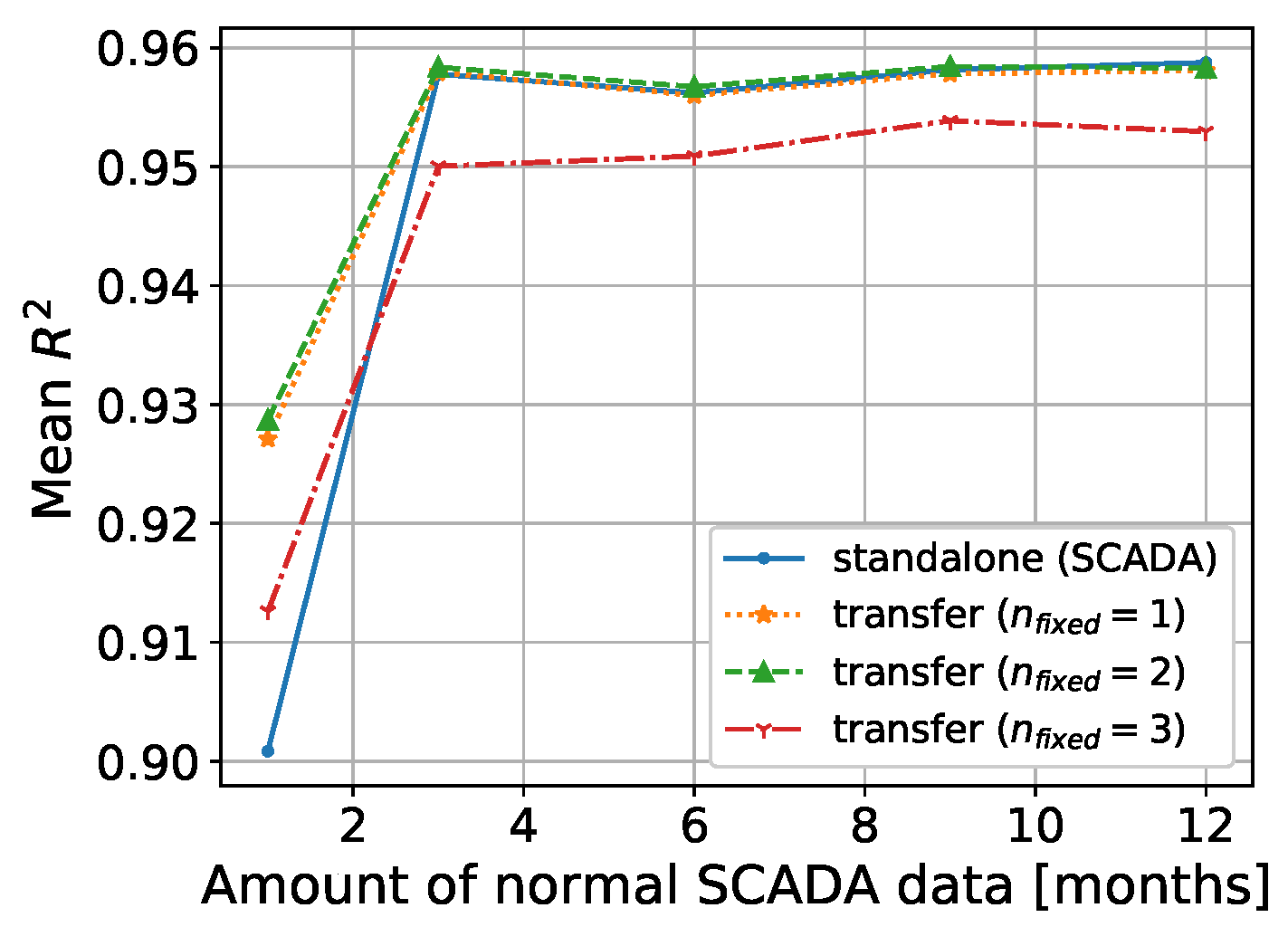
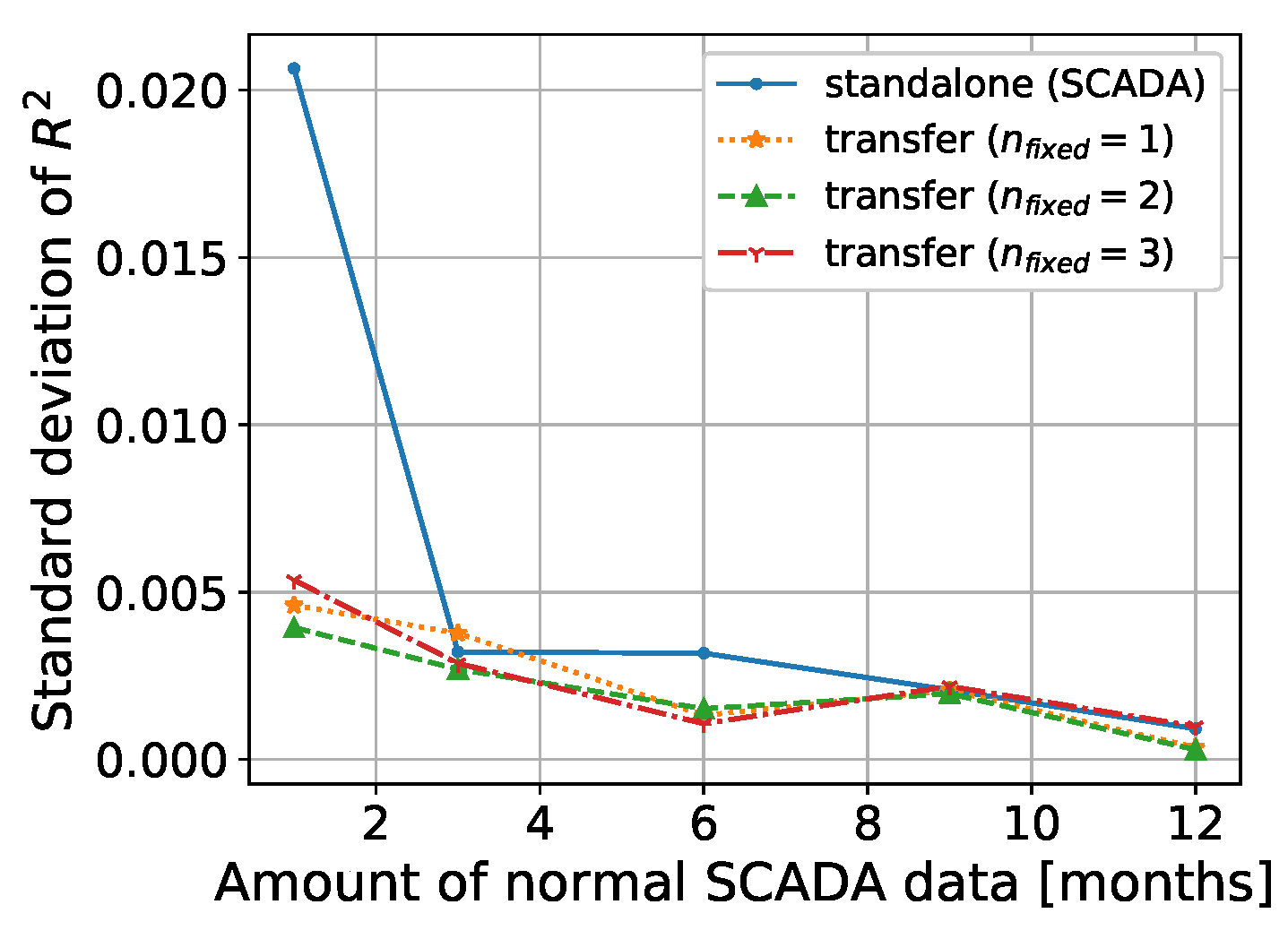
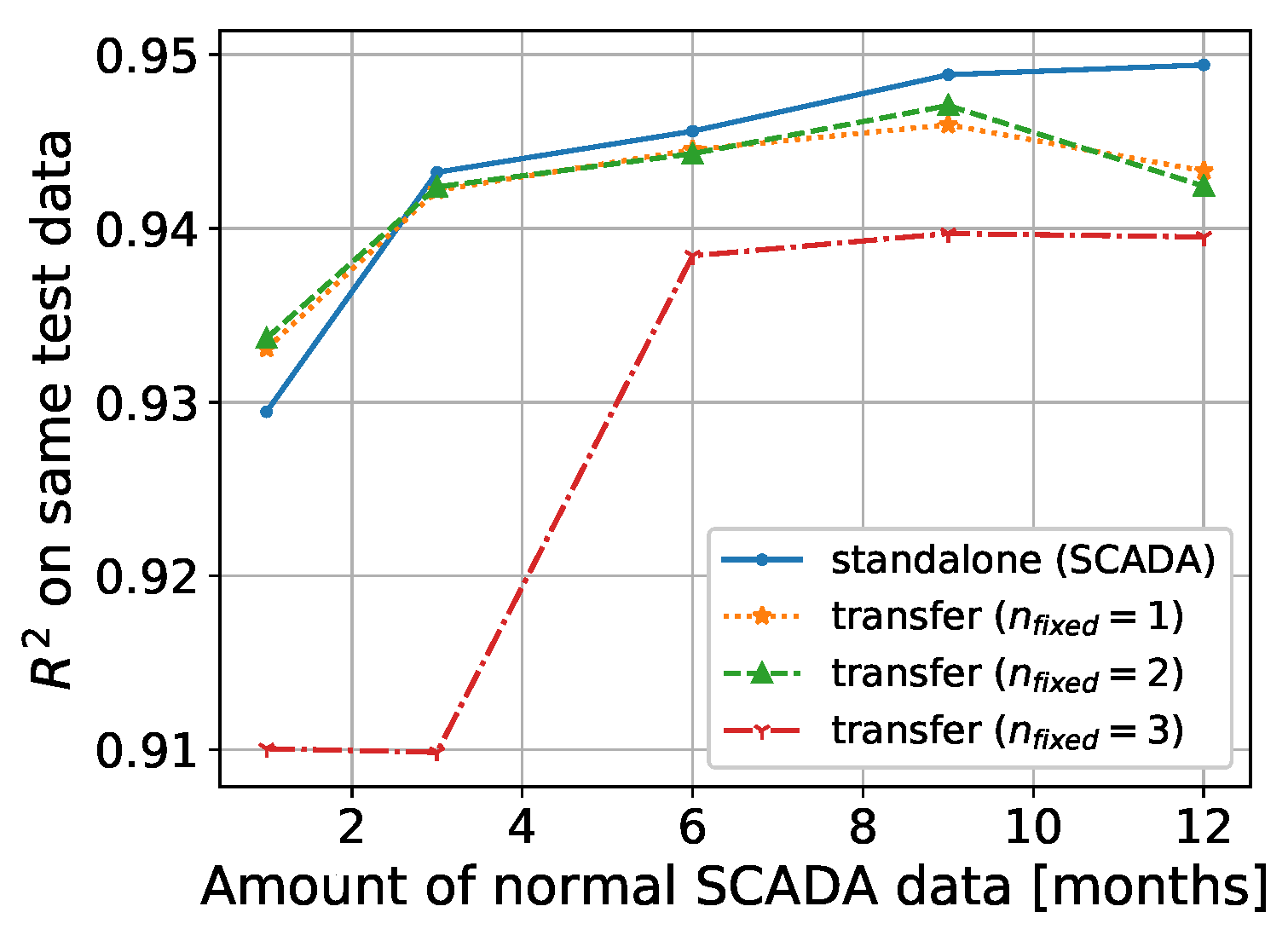
3.5. Artificial Neural Network (Parameter Transfer)
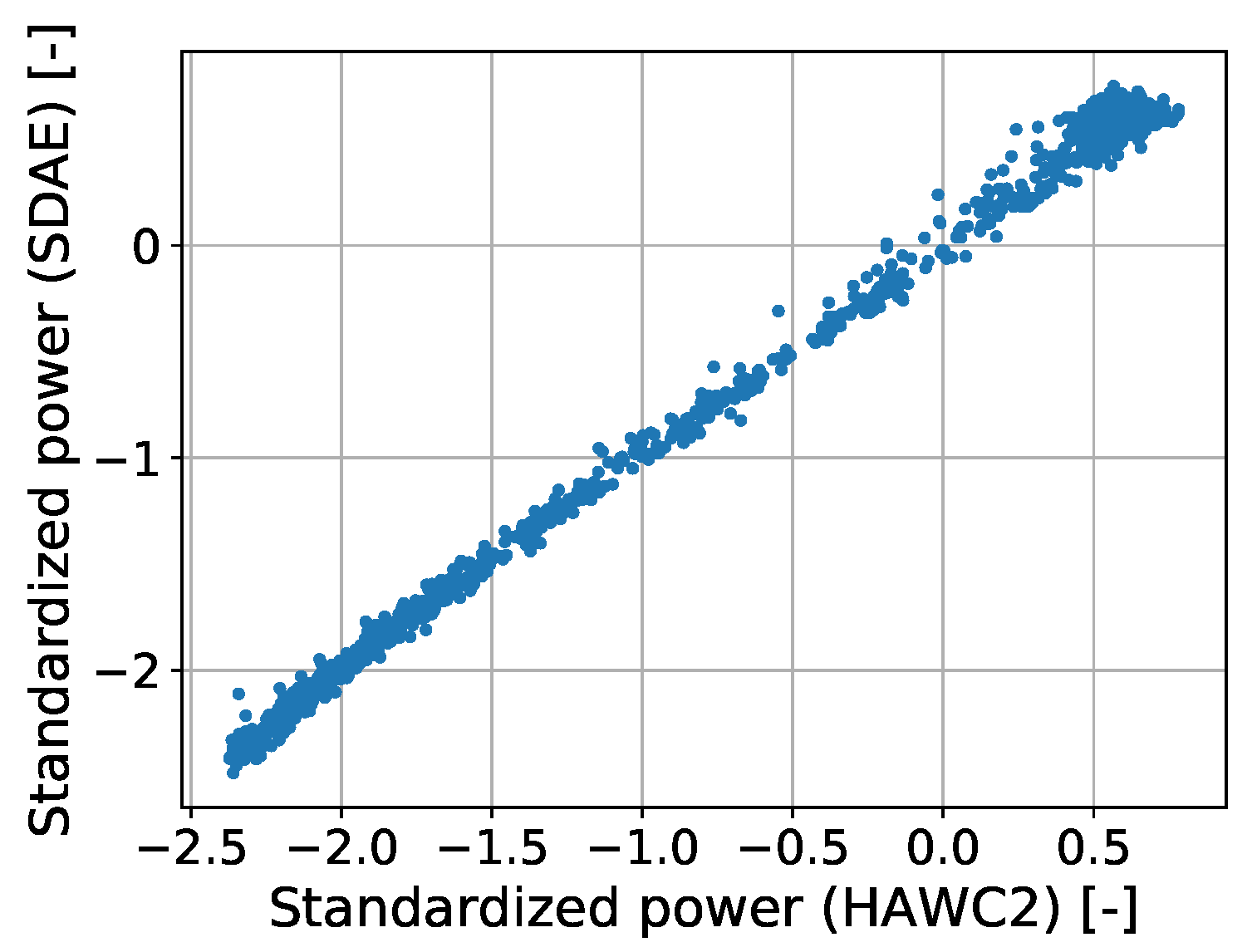
3.6. Autoencoder (Subspace Transfer)
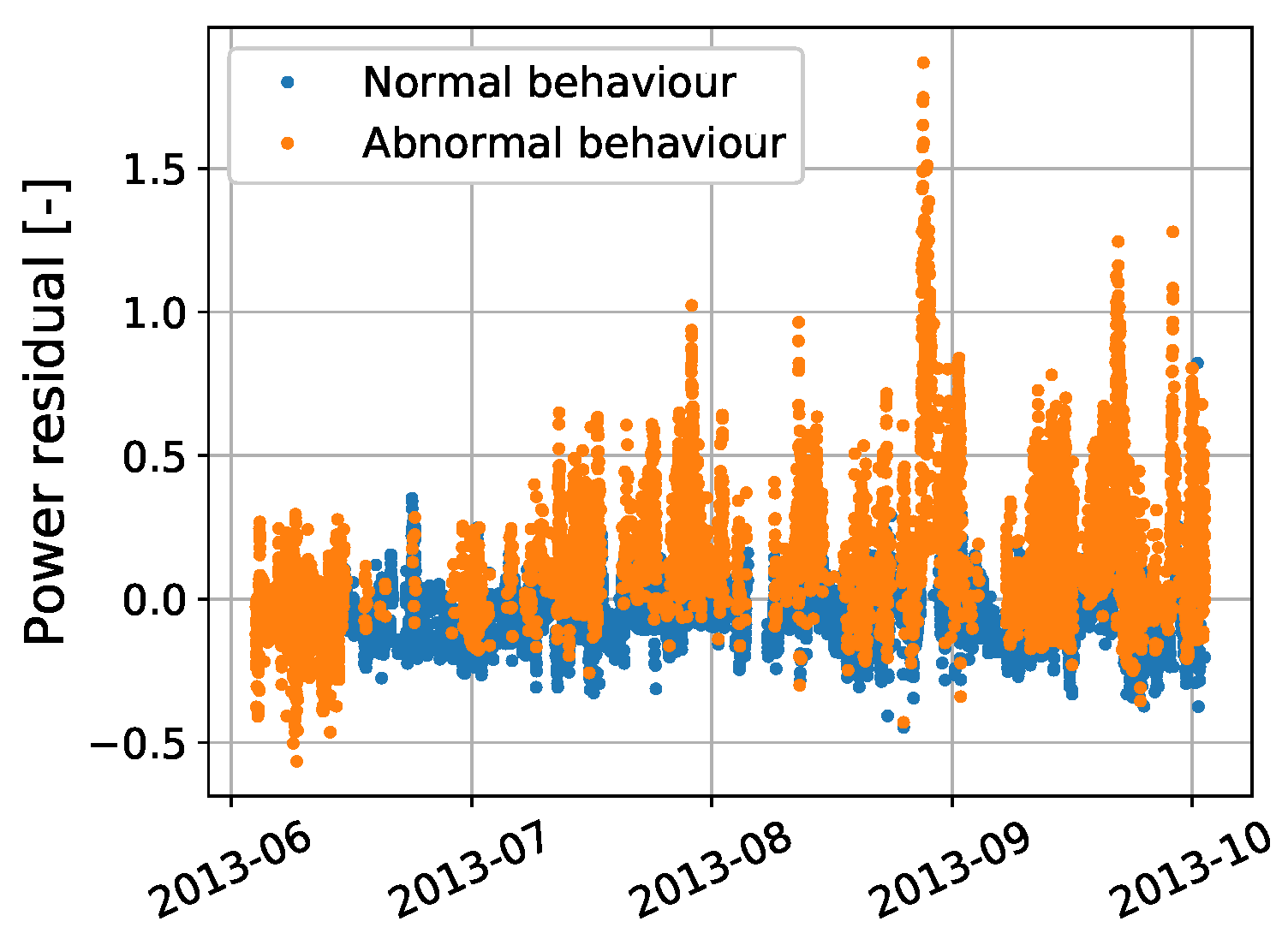
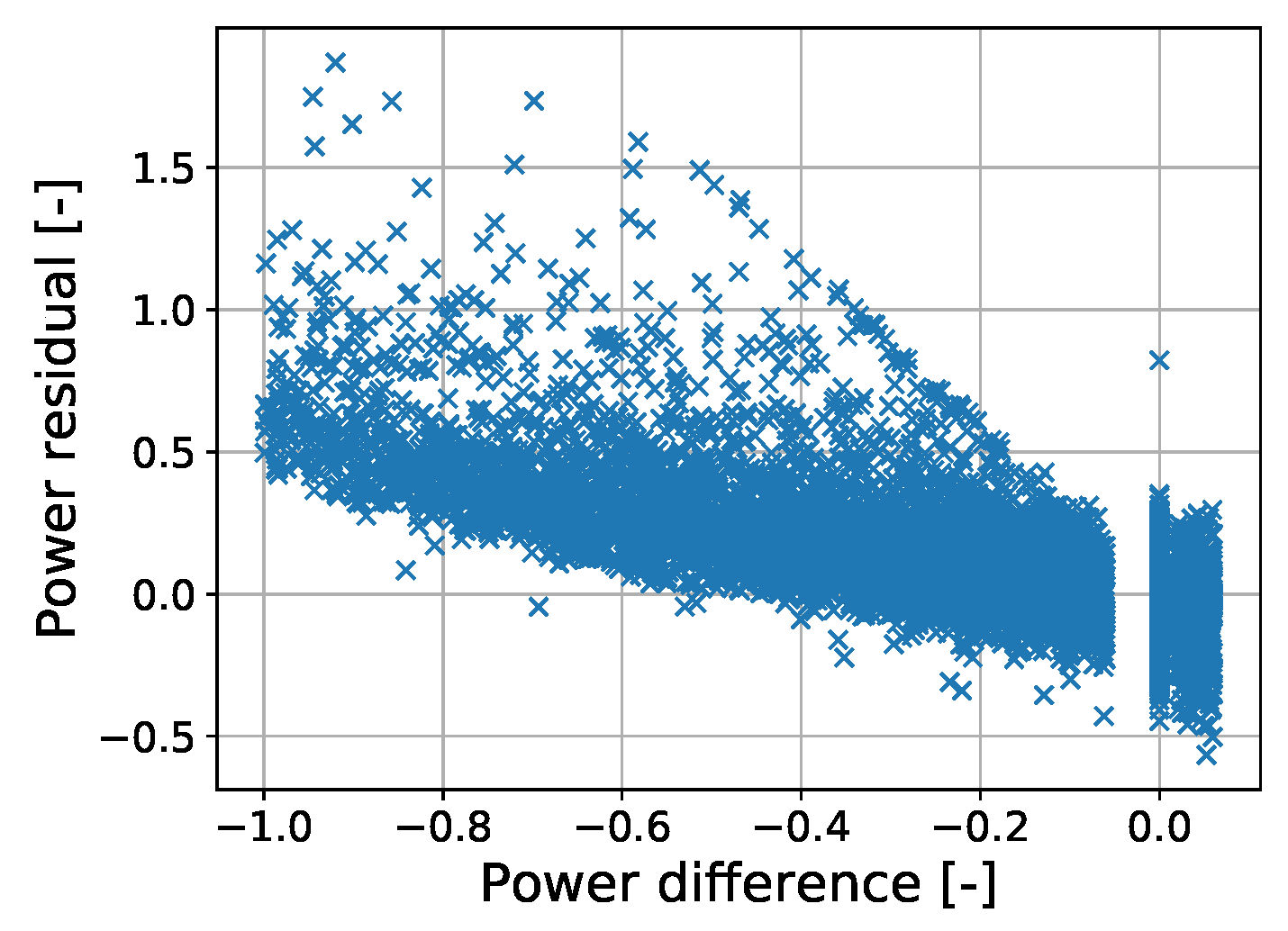
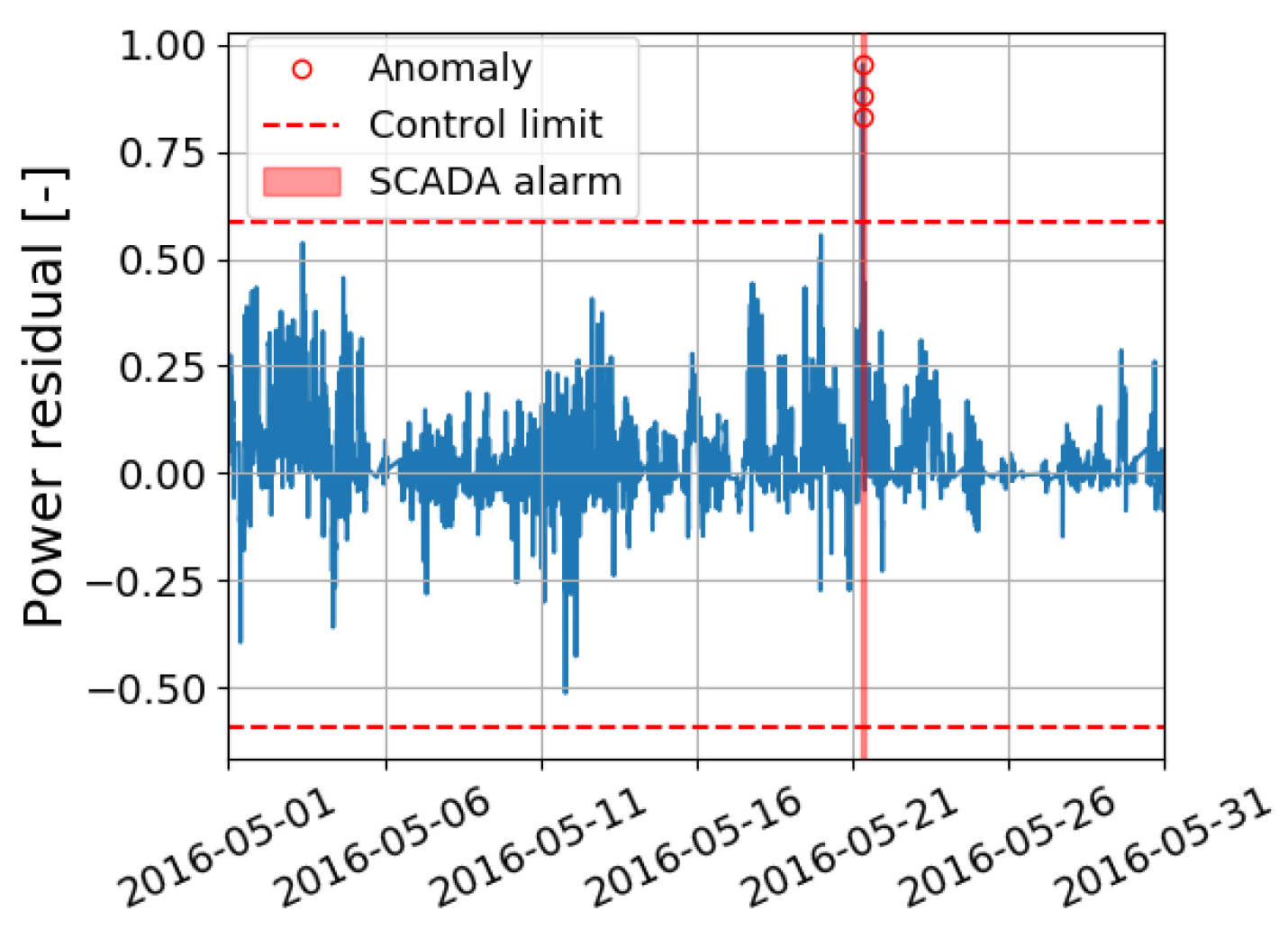
3.7. Anomaly Detection
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- WWEA. Worldwide Wind Capacity Reaches 744 Gigawatts. Germany. 2021. Available online: https://wwindea.org/worldwide-wind-capacity-reaches-744-gigawatts/ (accessed on 10 January 2021).
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F.; Achiche, S. Wind turbine condition monitoring based on SCADA data using normal behavior models. Part 1: System description. Appl. Soft Comput. 2013, 13, 259–270. [Google Scholar] [CrossRef]
- Tautz-Weinert, J.; Watson, S.J. Using SCADA data for wind turbine condition monitoring—A review. IET Renew. Power Gener. 2016, 11, 382–394. [Google Scholar] [CrossRef] [Green Version]
- Zaher, A.; McArthur, S.; Infield, D.; Patel, Y. Online wind turbine fault detection through automated SCADA data analysis. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2009, 12, 574–593. [Google Scholar] [CrossRef]
- Von Rueden, L.; Mayer, S.; Garcke, J.; Bauckhage, C.; Schuecker, J. Informed machine learning–towards a taxonomy of explicit integration of knowledge into machine learning. Learning 2019, 18, 19–20. [Google Scholar]
- Garcia, M.C.; Sanz-Bobi, M.A.; Del Pico, J. SIMAP: Intelligent System for Predictive Maintenance: Application to the health condition monitoring of a windturbine gearbox. Comput. Ind. 2006, 57, 552–568. [Google Scholar] [CrossRef]
- Cross, P.; Ma, X. Model-based and fuzzy logic approaches to condition monitoring of operational wind turbines. Int. J. Autom. Comput. 2015, 12, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Tipireddy, R.; Tartakovsky, A. Physics-informed Machine Learning Method for Forecasting and Uncertainty Quantification of Partially Observed and Unobserved States in Power Grids. arXiv 2018, arXiv:1806.10990. [Google Scholar]
- Nascimento, R.G.; Viana, F.A. Fleet prognosis with physics-informed recurrent neural networks. arXiv 2019, arXiv:1901.05512. [Google Scholar]
- Yucesan, Y.A.; Viana, F.A. Wind Turbine Main Bearing Fatigue Life Estimation with Physics-informed Neural Networks. In Proceedings of the Annual Conference of the PHM Society, Scottsdale, AZ, USA, 23 September 2019; Volume 11. [Google Scholar]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Dimitrov, N. Surrogate models for parameterized representation of wake-induced loads in wind farms. Wind. Energy 2019, 22, 1371–1389. [Google Scholar] [CrossRef]
- Schröder, L.; Dimitrov, N.K.; Verelst, D.R. A surrogate model approach for associating wind farm load variations with turbine failures. Wind. Energy Sci. 2020, 5, 1007–1022. [Google Scholar] [CrossRef]
- Larsen, T.J.; Hansen, A.M. How 2 HAWC2, the user’s manual. Target 2019, 2, 2. [Google Scholar]
- Madsen, H.A.; Larsen, T.J.; Pirrung, G.R.; Li, A.; Zahle, F. Implementation of the blade element momentum model on a polar grid and its aeroelastic load impact. Wind. Energy Sci. 2020, 5, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Mann, J. Wind field simulation. Probabilistic Eng. Mech. 1998, 13, 269–282. [Google Scholar] [CrossRef]
- Larsen, G.C.; Madsen, H.A.; Thomsen, K.; Larsen, T.J. Wake meandering: A pragmatic approach. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2008, 11, 377–395. [Google Scholar] [CrossRef]
- Schlechtingen, M.; Santos, I.F. Comparative analysis of neural network and regression based condition monitoring approaches for wind turbine fault detection. Mech. Syst. Signal Process. 2011, 25, 1849–1875. [Google Scholar] [CrossRef] [Green Version]
- Schröder, L.; Dimitrov, N.K.; Verelst, D.R.; Sørensen, J.A. Wind turbine site-specific load estimation using artificial neural networks calibrated by means of high-fidelity load simulations. J. Phys. Conf. Ser. 2018, 1037, 062027. [Google Scholar] [CrossRef]
- Renström, N.; Bangalore, P.; Highcock, E. System-wide anomaly detection in wind turbines using deep autoencoders. Renew. Energy 2020, 157, 647–659. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Chen, W.; Wang, Y.; Jiang, T. Anomaly detection for wind turbines based on the reconstruction of condition parameters using stacked denoising autoencoders. Renew. Energy 2020, 147, 1469–1480. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. Models for monitoring wind farm power. Renew. Energy 2009, 34, 583–590. [Google Scholar] [CrossRef]
- Reder, M.D.; Gonzalez, E.; Melero, J.J. Wind turbine failures-tackling current problems in failure data analysis. J. Phys. Conf. Ser. 2016, 753, 072027. [Google Scholar] [CrossRef]
- Optis, M.; Perr-Sauer, J.; Philips, C.; Craig, A.E.; Lee, J.C.; Kemper, T.; Sheng, S.; Simley, E.; Williams, L.; Lunacek, M.; et al. OpenOA: An Open-Source Code Base for Operational Analysis of Wind Power Plants. Wind Energ. Sci. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Vorpahl, F.; Popko, W.; Kaufer, D. Description of a Basic Model of the “UpWind Reference Jacket” for Code Comparison in the OC4 Project under IEA Wind Annex XXX; Fraunhofer Institute for Wind Energy and Energy System Technology (IWES): Bremerhaven, Germany, 2011. [Google Scholar]


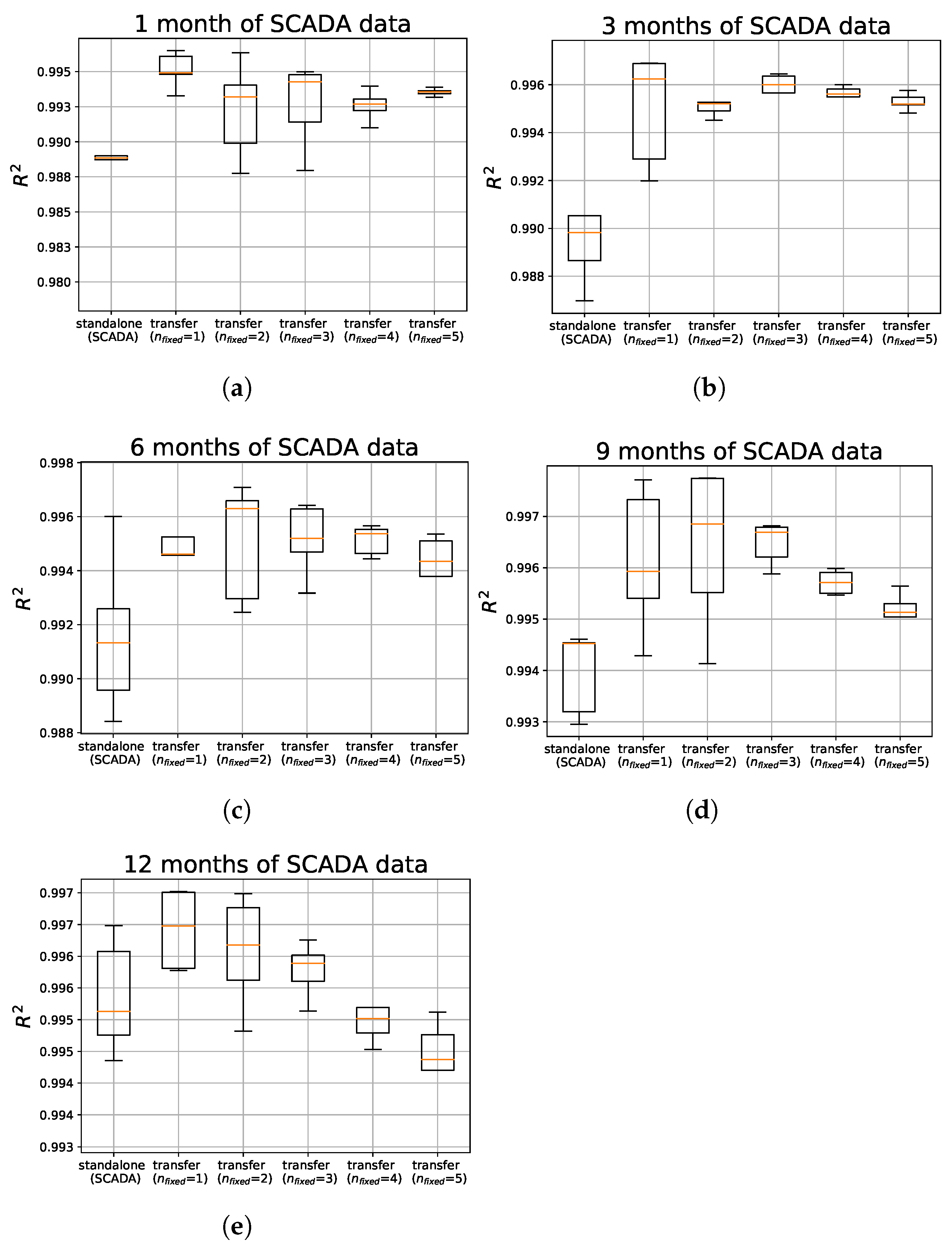
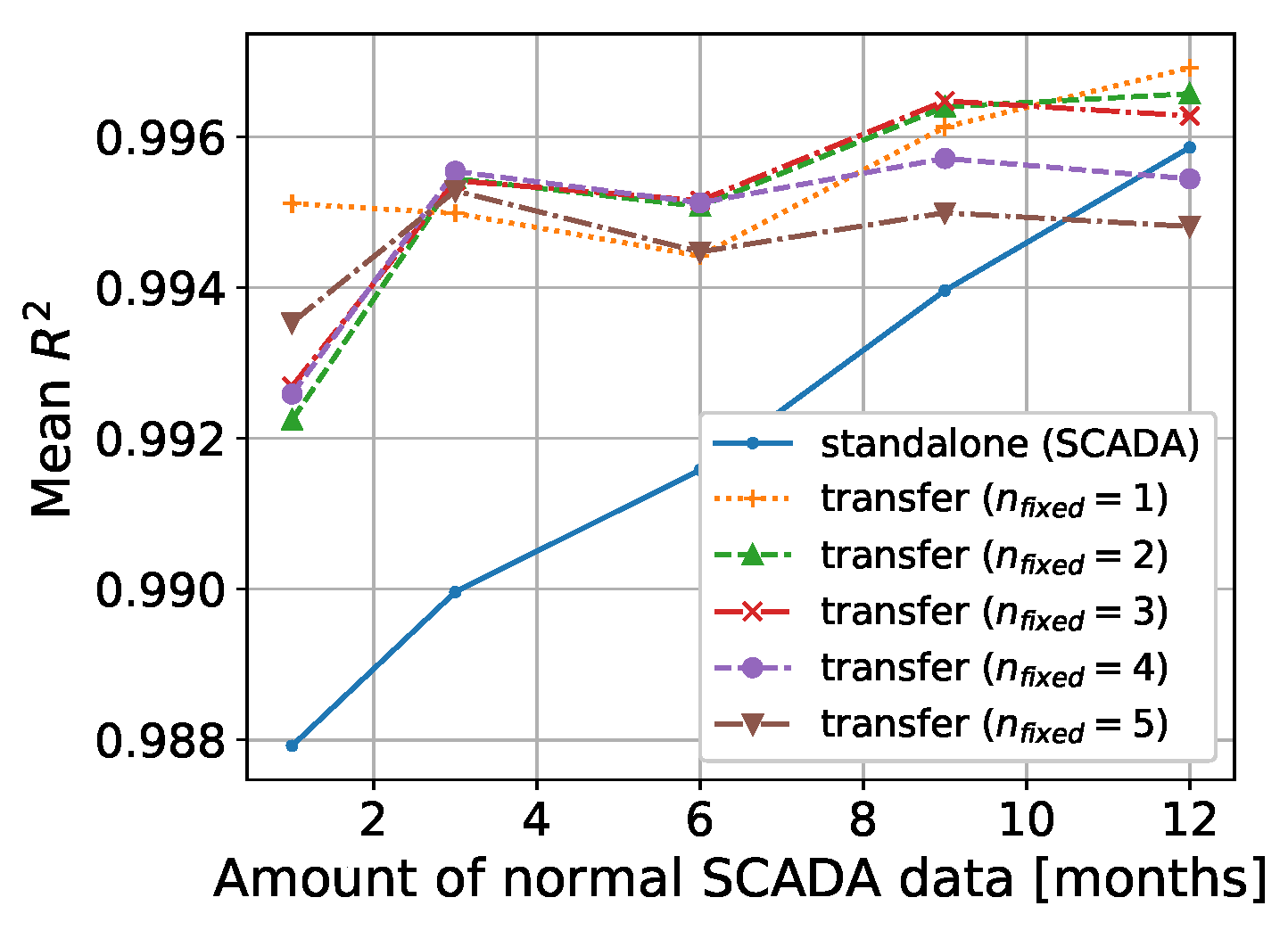
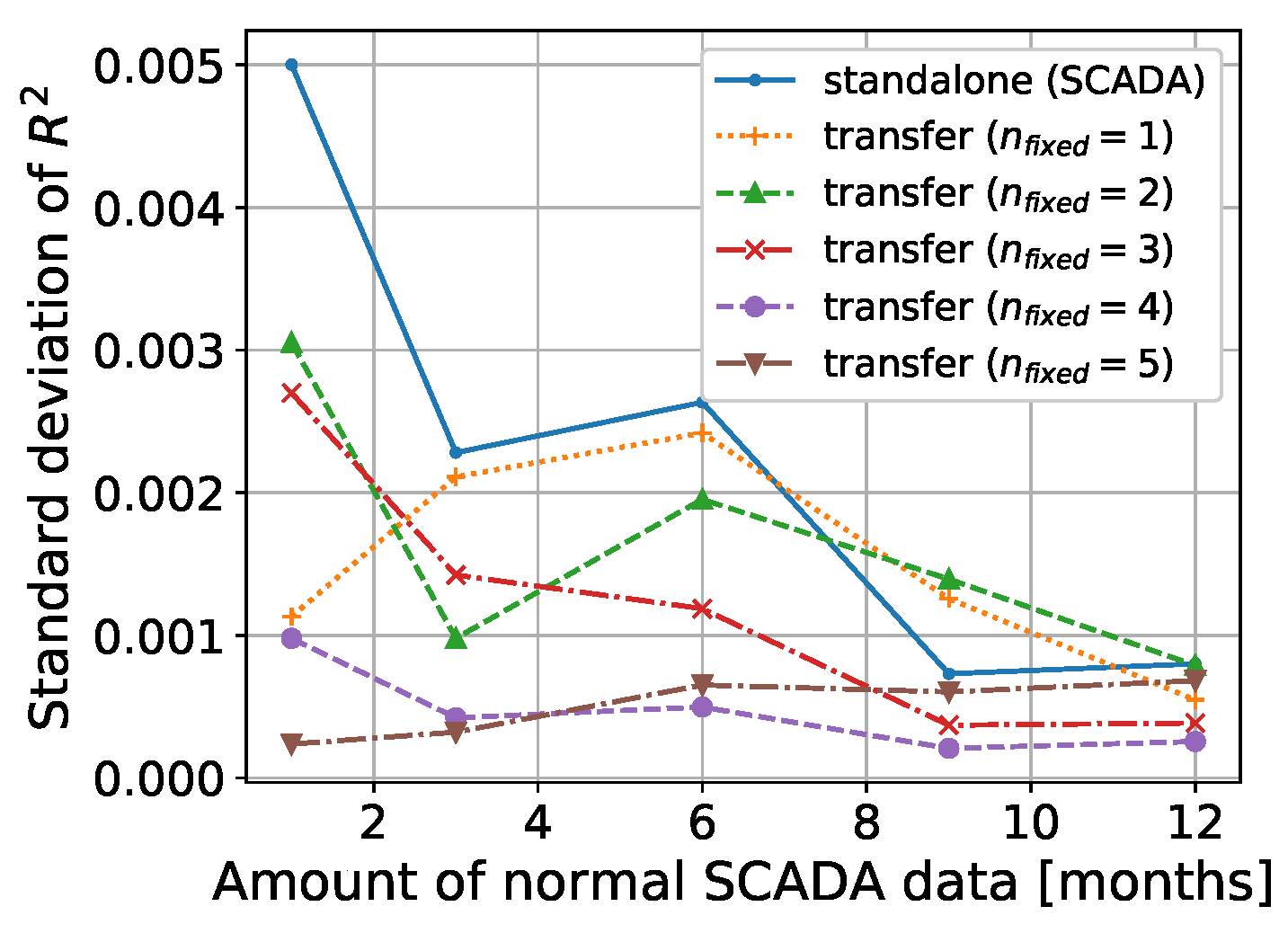
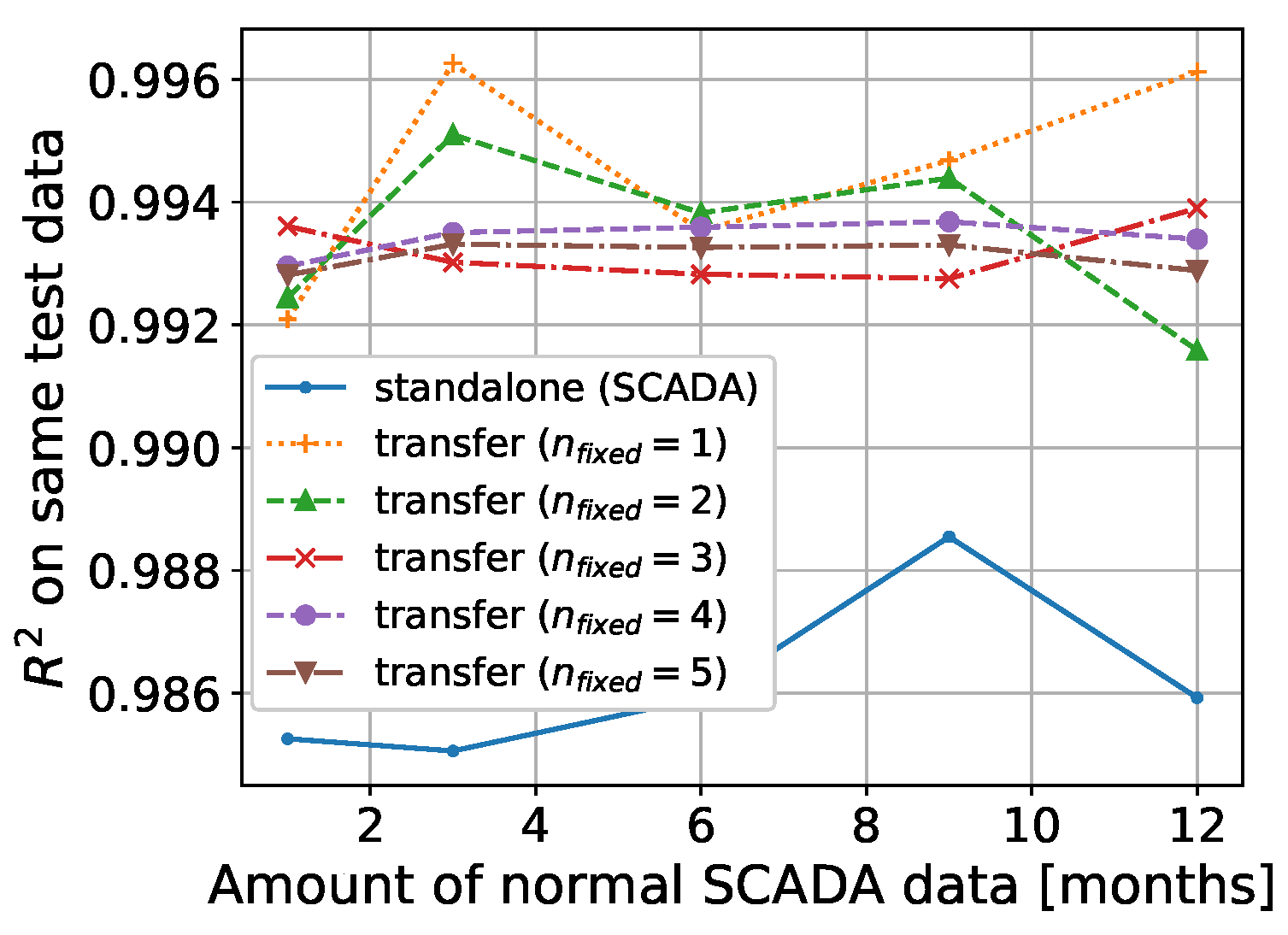

| Mean | Mean NRMSE (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 9 | 12 | 1 | 3 | 6 | 9 | 12 | |
| SCADA | 0.901 | 0.958 | 0.956 | 0.958 | 0.959 | 11.06 | 7.58 | 7.44 | 7.57 | 7.45 |
| = 1 | 0.927 | 0.958 | 0.956 | 0.958 | 0.958 | 9.53 | 7.56 | 7.47 | 7.61 | 7.51 |
| = 2 | 0.929 | 0.958 | 0.957 | 0.958 | 0.958 | 9.42 | 7.53 | 7.40 | 7.55 | 7.50 |
| = 3 | 0.913 | 0.950 | 0.951 | 0.954 | 0.953 | 10.43 | 8.25 | 7.89 | 7.95 | 7.96 |
| NRMSE (‱) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 6 | 9 | 12 | 1 | 3 | 6 | 9 | 12 | |
| standalone | 0.988 | 0.990 | 0.992 | 0.994 | 0.996 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 |
| = 1 | 0.995 | 0.995 | 0.994 | 0.996 | 0.997 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 |
| = 2 | 0.992 | 0.995 | 0.995 | 0.996 | 0.997 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 |
| = 3 | 0.993 | 0.995 | 0.995 | 0.997 | 0.996 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 |
| = 4 | 0.993 | 0.996 | 0.995 | 0.996 | 0.995 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| = 5 | 0.994 | 0.995 | 0.995 | 0.995 | 0.995 | 0.02 | 0.02 | 0.02 | 0.02 | 0.02 |
| SCADA Stanrdalone ANN | Transfer Learning ANN | |
|---|---|---|
| Precision | 50% | 100% |
| Recall | 100% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schröder, L.; Dimitrov, N.K.; Verelst, D.R.; Sørensen, J.A. Using Transfer Learning to Build Physics-Informed Machine Learning Models for Improved Wind Farm Monitoring. Energies 2022, 15, 558. https://doi.org/10.3390/en15020558
Schröder L, Dimitrov NK, Verelst DR, Sørensen JA. Using Transfer Learning to Build Physics-Informed Machine Learning Models for Improved Wind Farm Monitoring. Energies. 2022; 15(2):558. https://doi.org/10.3390/en15020558
Chicago/Turabian StyleSchröder, Laura, Nikolay Krasimirov Dimitrov, David Robert Verelst, and John Aasted Sørensen. 2022. "Using Transfer Learning to Build Physics-Informed Machine Learning Models for Improved Wind Farm Monitoring" Energies 15, no. 2: 558. https://doi.org/10.3390/en15020558






