Stability Analysis of Shunt Active Power Filter with Predictive Closed-Loop Control of Supply Current
Abstract
:1. Introduction
2. Proposed Control System
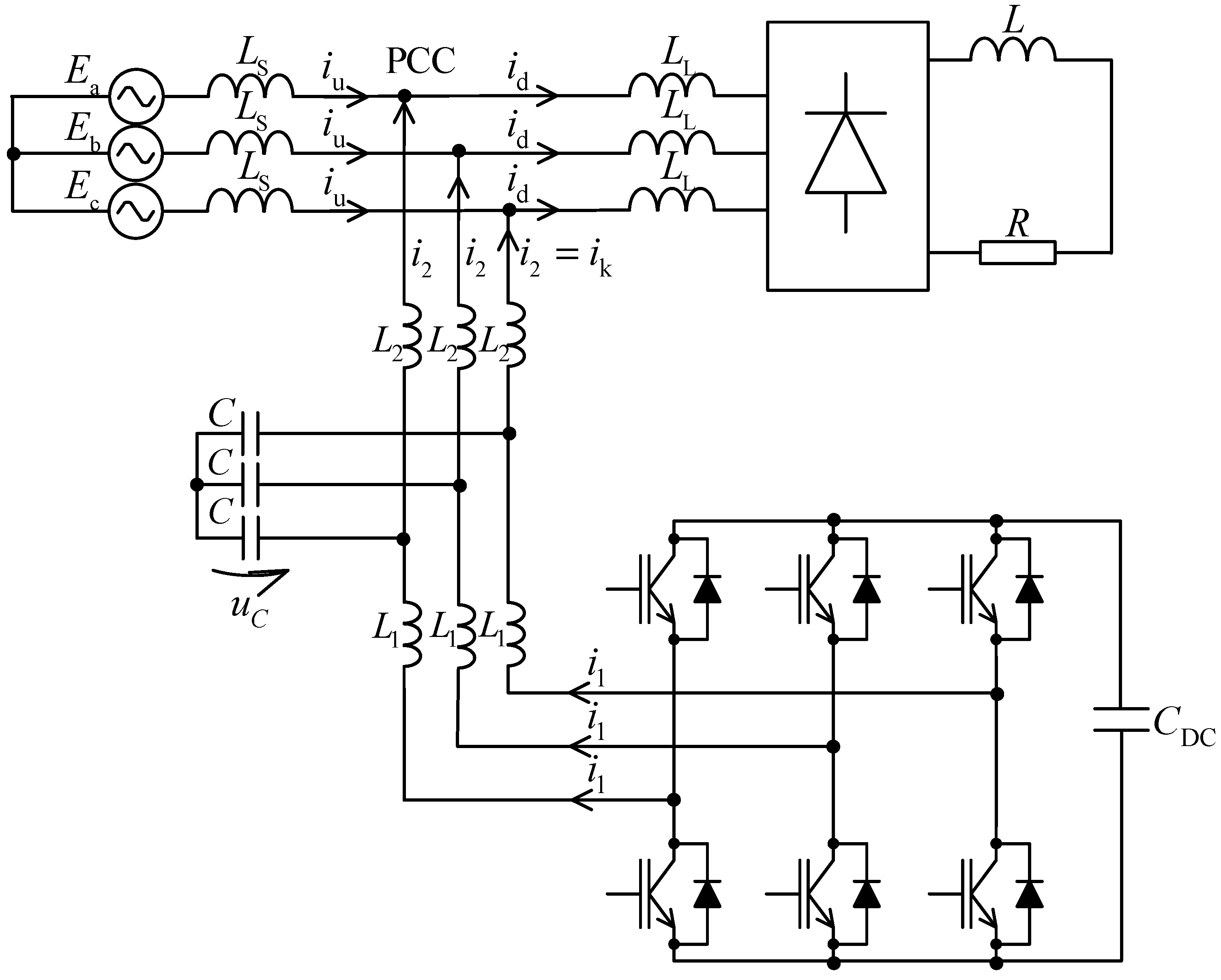
2.1. System Description
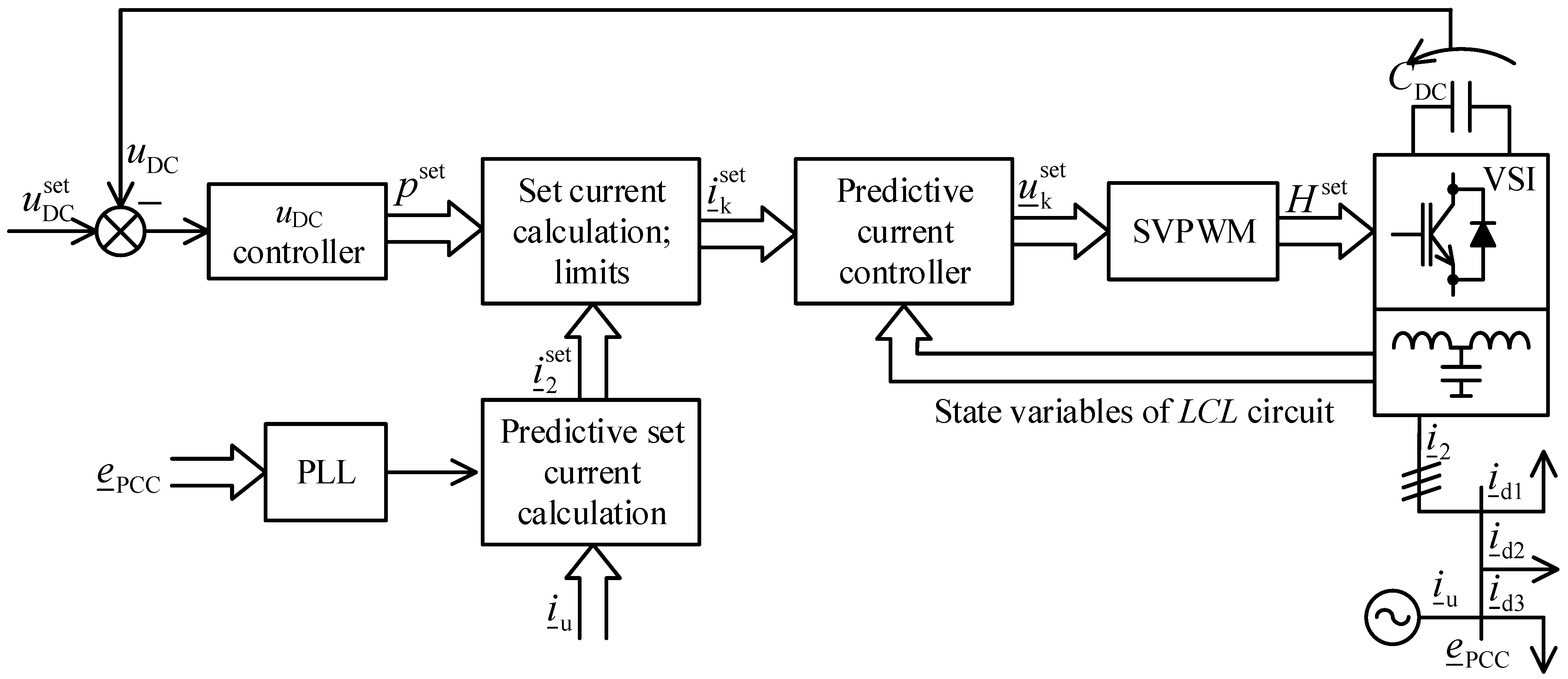
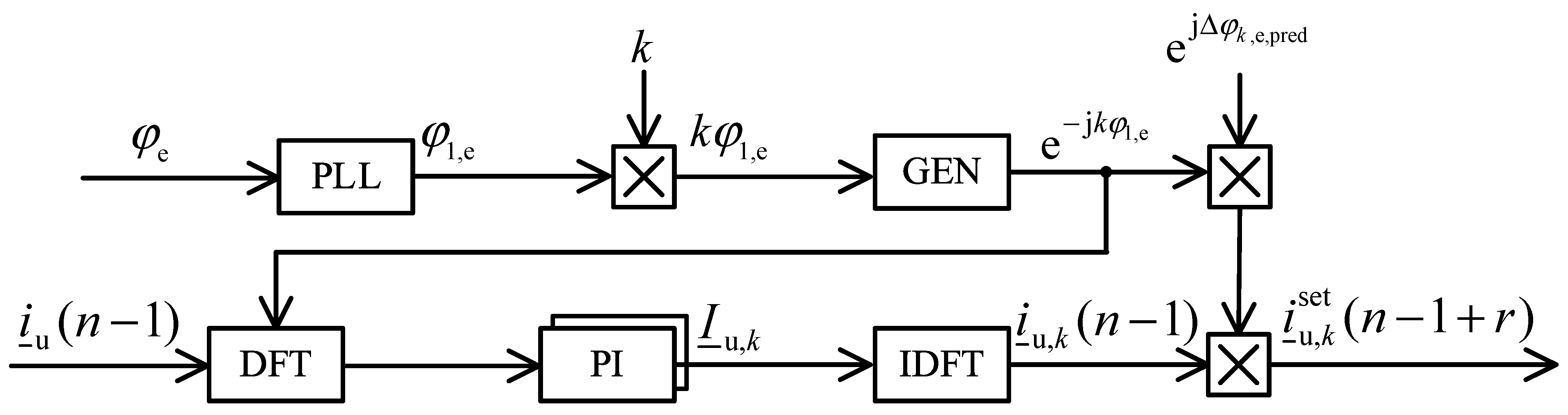
2.2. Control Structure
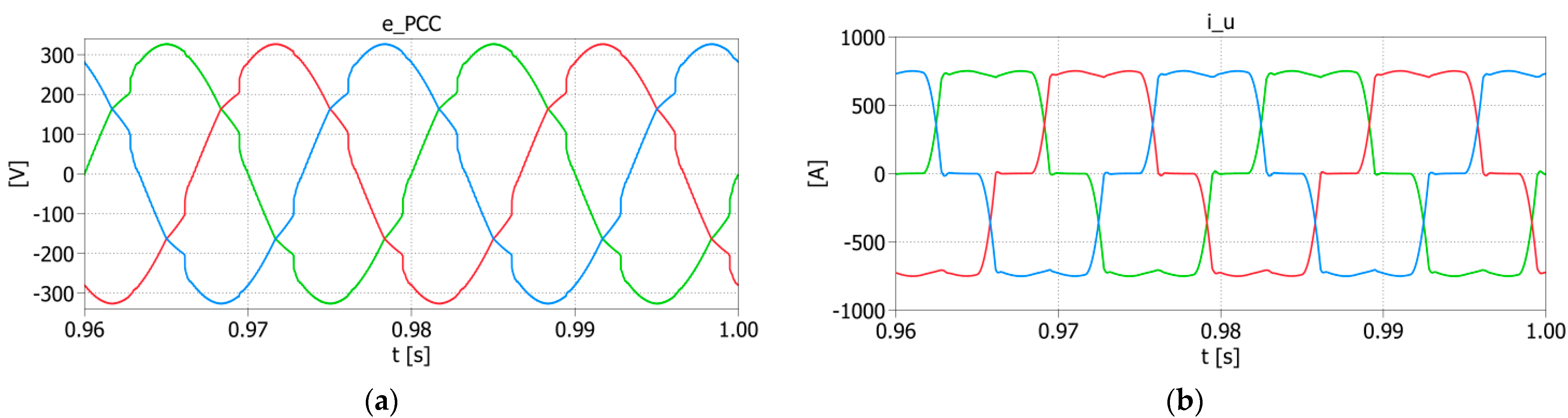
2.3. Sample Waveforms
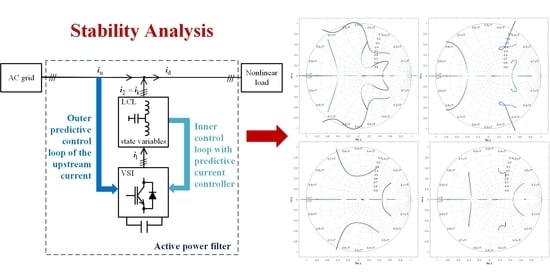
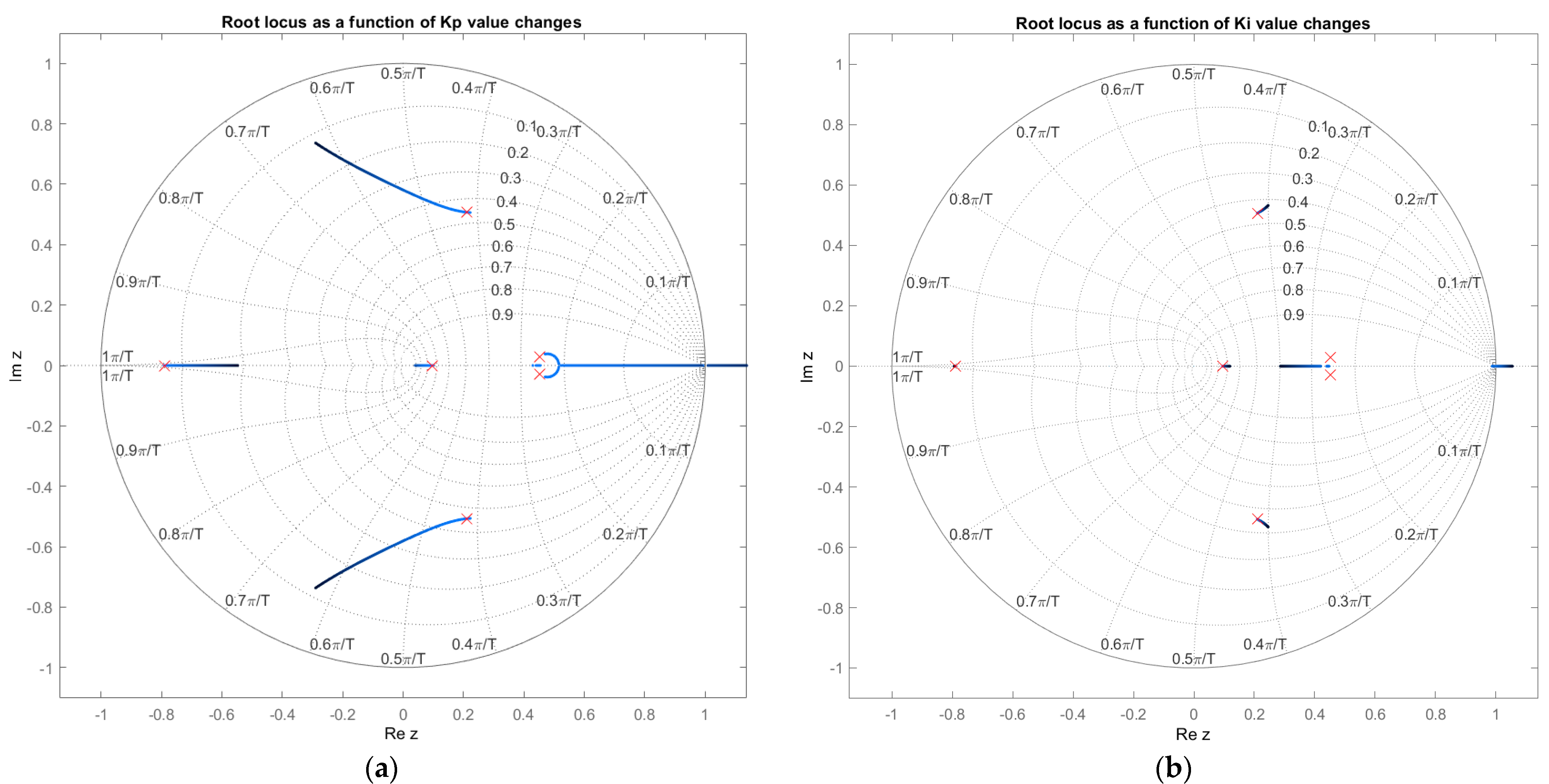
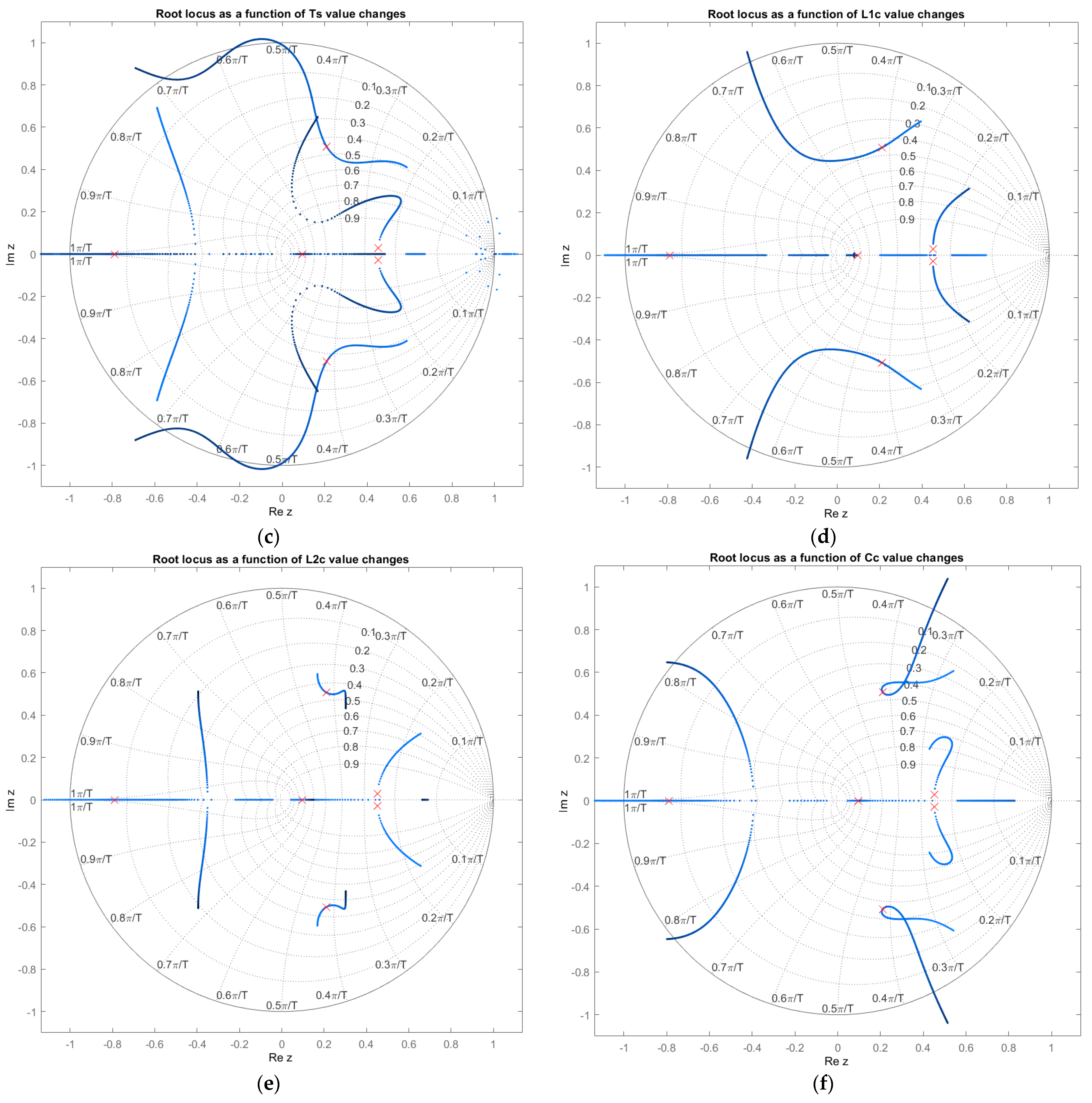
3. Stability Analysis
3.1. Assumptions
3.2. Overall and Partial Transfer Functions
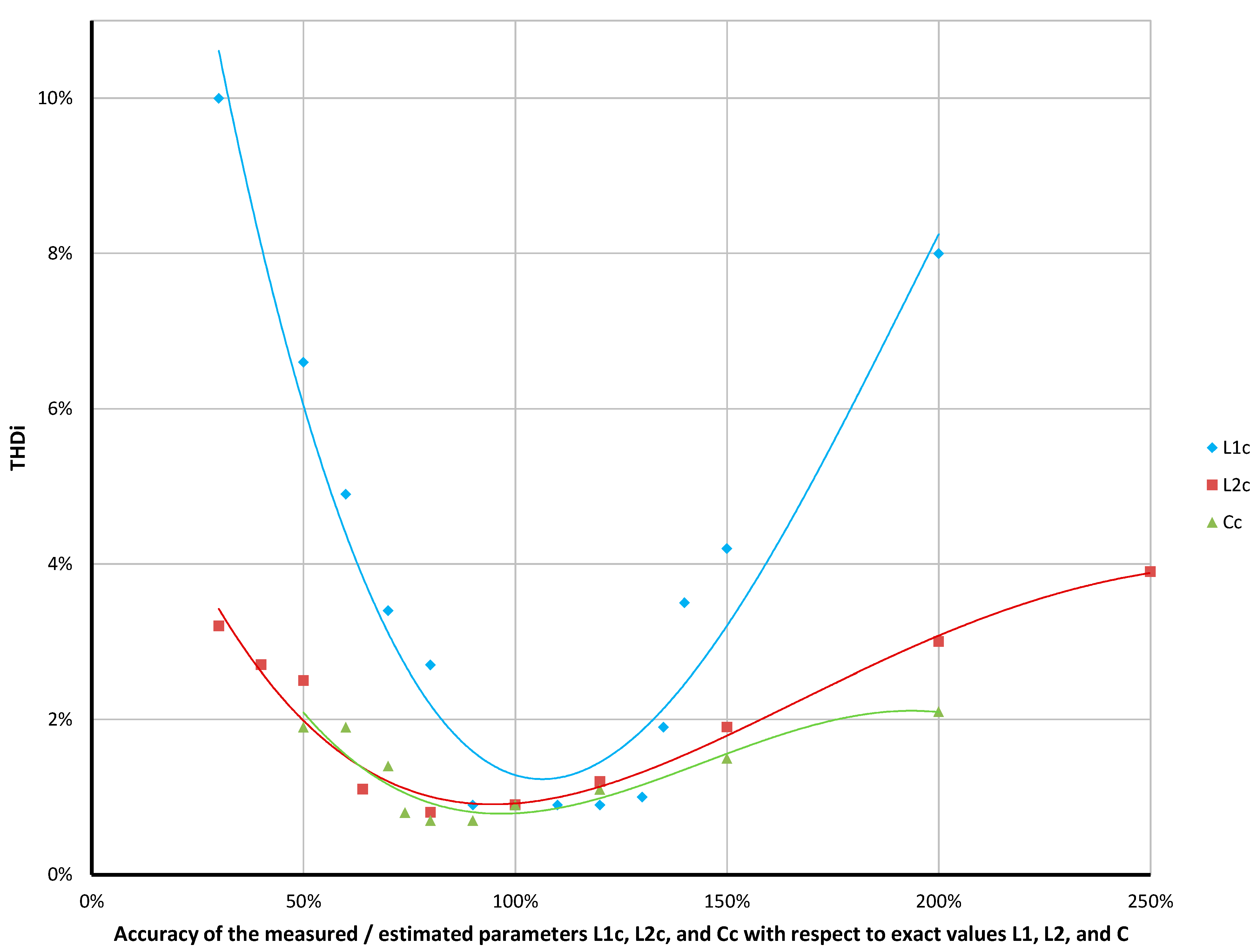
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sleszynski, W.; Cichowski, A.; Mysiak, P. Suppression of Supply Current Harmonics of 18-Pulse Diode Rectifier by Series Active Power Filter with LC Coupling. Energies 2020, 13, 6060. [Google Scholar] [CrossRef]
- Rao, M.U.M.; Rosalina, K.M. Transient stability improvement of Microgrid using Series Active Power Filters. In Proceedings of the 2019 Fifth International Conference on Electrical Energy Systems (ICEES), Chennai, India, 21–22 February 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Sun, B.; Xie, Y.; Ma, H. An enhanced repetitive control strategy for shunt active power filter with LCL output filter. In Proceedings of the IECON 2015 41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 001351–001356. [Google Scholar] [CrossRef]
- Geng, H.; Zheng, Z.; Zou, T.; Chu, B.; Chandra, A. Fast Repetitive Control with Harmonic Correction Loops for Shunt Active Power Filter Applied in Weak Grid. IEEE Trans. Ind. Appl. 2019, 55, 3198–3206. [Google Scholar] [CrossRef]
- Mattavelli, P.; Marafao, F.P. Repetitive-based control for selective harmonic compensation in active power filters. IEEE Trans. Ind. Electron. 2004, 51, 1018–1024. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Xing, Y.; Hu, H.; Sun, K. Analysis and design of enhanced DFT-based controller for selective harmonic compensation in active power filters. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1305–1309. [Google Scholar] [CrossRef]
- Chen, X.; Dai, K.; Xu, C.; Lin, X. Harmonic suppression and resonance damping for shunt APF with selective closed-loop regulation of PCC voltage. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, USA, 20–24 September 2015; pp. 6439–6443. [Google Scholar] [CrossRef]
- Wojciechowski, D. Unified LCL circuit for modular active power filter. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 1985–1997. [Google Scholar] [CrossRef]
- Tumbelaka, H.H.; Borle, L.J.; Nayar, C.V.; Lee, S.R. A grid current-controlling shunt active power filter. In Proceedings of the 2007 7th Internatonal Conference on Power Electronics, Daegu, South Korea, 22–26 October 2007; pp. 956–961. [Google Scholar] [CrossRef]
- Lascu, C.; Asiminoaei, L.; Boldea, I.; Blaabjerg, F. High Performance Current Controller for Selective Harmonic Compensation in Active Power Filters. IEEE Trans. Power Electron. 2007, 22, 1826–1835. [Google Scholar] [CrossRef]
- Mariethoz, S.; Rufer, A.C. Open loop and closed loop spectral frequency active filtering. IEEE Trans. Power Electron. 2002, 17, 564–573. [Google Scholar] [CrossRef]
- Mattavelli, P. A closed-loop selective harmonic compensation for active filters. IEEE Trans. Ind. Appl. 2001, 37, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Zhang, D.; Zhang, H.; Wang, Z.; Sun, M. The Research on Composite Control Strategy of Active Power Filter. In Proceedings of the 2019 34rd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Jinzhou, China, 6–8 June 2019; pp. 431–436. [Google Scholar] [CrossRef]
- Gautam, S.; Aeidapu, M. Sine Cosine Algorithm Based Shunt Active Power Filter For Harmonic Compensation. In Proceedings of the 2019 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 1051–1056. [Google Scholar] [CrossRef]
- Ouchen, S.; Steinhart, H.; Blaabjerg, F.; Benbouzid, M.; Betka, A.; Gaubert, J.P. Performance Analysis of Direct Power Control with Space Vector Modulation for Shunt Active Power Filter. In Proceedings of the IECON 2019 45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 467–472. [Google Scholar] [CrossRef]
- Yang, L.; Yang, J. Robust Current Control Method for LCL-Type Shunt Active Power Filters with Inverter-Side Current Feedback Active Damping. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5706–5712. [Google Scholar] [CrossRef]
- Cao, X.; Dong, K.; Wei, X. An Improved Control Method Based on Source Current Sampled for Shunt Active Power Filters. Energies 2020, 13, 1405. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Pei, Y.; Yi, H.; Zhang, J.L. A New High Control Precision Active Power Filter. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xian, China, 3–6 June 2019; pp. 1109–1112. [Google Scholar] [CrossRef]
- Mysak, T.V.; Shapoval, I.A. A simple control strategy for a three-phase shunt active power filter based on second-order sliding mode. In Proceedings of the 2020 IEEE 4th International Conference on Intelligent Energy and Power Systems (IEPS), Istanbul, Turkey, 7–11 September 2020; pp. 27–32. [Google Scholar] [CrossRef]
- Iturra, R.G.; Cruse, M.; Mütze, K.; Dresel, C.; Soleimani, I.; Thiemann, P. Model Predictive Control for Shunt Active Power Filter with Harmonic Power Recycling Capability. In Proceedings of the 2018 International Conference on Smart Energy Systems and Technologies (SEST), Sevilla, Spain, 10–12 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yi, H.; Zhuo, F.; Wang, X.; Liu, J. Study of closed-loop control scheme for source current detection type Active Power Filter. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 145–150. [Google Scholar] [CrossRef]
- Briz, F.; Díaz-Reigosa, D.; Degner, M.W.; García, P.; Guerrero, J.M. Dynamic behavior of current controllers for selective harmonic compensation in three-phase active power filters. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 2892–2899. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Yang, J.; Gao, M.; Watson, A.; Wheeler, P. Current Control of LCL-Type Shunt APFs: Damping Characteristics, Stability Analysis, and Robust Design Against Grid Impedance Variation. IEEE J. Emerg. Sel. Top. Power Electron. 2020. [Google Scholar] [CrossRef]
- Zhang, Y.; Dai, K.; Chen, X.; Kang, Y.; Dai, Z. Stability Analysis of SAPF by Viewing DFT as Cluster of BPF for Selective Harmonic Suppression and Resonance Damping. IEEE Trans. Ind. Appl. 2019, 55, 1598–1607. [Google Scholar] [CrossRef]
- Hoon, Y.; Mohd Radzi, M.A.; Hassan, M.K.; Mailah, N.F. DC-Link Capacitor Voltage Regulation for Three-Phase Three-Level Inverter-Based Shunt Active Power Filter with Inverted Error Deviation Control. Energies 2016, 9, 533. [Google Scholar] [CrossRef] [Green Version]
- Bing, Y.; Jiang, D.; Liang, Y.; Jiang, C.; He, T.; Yang, L.; Hu, P. Modified Modeling and System Stabilization of Shunt Active Power Filter Compensating Loads with μF Capacitance. Energies 2019, 12, 2084. [Google Scholar] [CrossRef] [Green Version]
- Popescu, M.; Bitoleanu, A.; Suru, C.V.; Linca, M.; Subtirelu, G.E. Adaptive Control of DC Voltage in Three-Phase Three-Wire Shunt Active Power Filters Systems. Energies 2020, 13, 3147. [Google Scholar] [CrossRef]
- Grugel, P. Stability analysis of Parallel Active Power Filter operating on the basis of network voltage distortion. In Proceedings of the 2016 10th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Bydgoszcz, Poland, 29 June–1 July 2016; pp. 240–243. [Google Scholar] [CrossRef]
- Guzman Iturra, R.; Thiemann, P. Asymmetrical Three-Level Inverter SiC-Based Topology for High Performance Shunt Active Power Filter. Energies 2020, 13, 141. [Google Scholar] [CrossRef] [Green Version]
- Imam, A.A.; Sreerama Kumar, R.; Al-Turki, Y.A. Modeling and Simulation of a PI Controlled Shunt Active Power Filter for Power Quality Enhancement Based on P-Q Theory. Electronics 2020, 9, 637. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.; Wong, M. The Analysis of DC-link Voltage, Compensation Range, Cost, Reliability and Power Loss for Shunt (Hybrid) Active Power Filters. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Kota Kinabalu, MA, USA, 7–10 October 2018; pp. 640–645. [Google Scholar] [CrossRef]
- Torabi Jafrodi, S.; Ghanbari, M.; Mahmoudian, M.; Najafi, A.M.G.; Rodrigues, E.; Pouresmaeil, E. A Novel Control Strategy to Active Power Filter with Load Voltage Support Considering Current Harmonic Compensation. Appl. Sci. 2020, 10, 1664. [Google Scholar] [CrossRef] [Green Version]
- Gao, N.; Lin, X.; Wu, W.; Blaabjerg, F. Grid Current Feedback Active Damping Control Based on Disturbance Observer for Battery Energy Storage Power Conversion System with LCL Filter. Energies 2021, 14, 1482. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Line to line grid voltage | 3 × 400 V |
| Grid frequency | f = 50 Hz |
| Grid inductance | LS = 40 µH |
| Non-linear load | 6-pulse diode bridge with RL load (R = 0.7 Ω, L = 1.0 mH) |
| Non-linear load inductor | LL = 40 µH |
| LCL circuit | L1 = 150 µH, L2 = 75 µH, C = 100 µF |
| APF rated power | 120 kVA |
| Deadtime (uncompensated) | 3.0 µs |
| IGBT voltage drop (uncompensated) | 1.5 V |
| Diode voltage drop (uncompensated) | 1.0 V |
| PWM carrier frequency | fPWM = 8 kHz |
| Sampling frequency | fs = 16 kHz |
| L1c Parameter | L2c Parameter | Cc Parameter | Ts Parameter | |
|---|---|---|---|---|
| Stability analysis performed in MATLAB | 88% ÷ 136% of L1 | >64% of L2 | 74% ÷ 290% of C | 150 ÷ 135 µs and <73.8 µs |
| Simulation tests conducted in PLECS | 89% ÷ 136% of L1 | >64% of L2 | 74% ÷ 325% of C | 149 ÷ 130 µs and <73.8 µs |
| Tests performed for the determinants of the experimental system | 13% ÷ 214% of L1 | >16% of L2 | 24% ÷ 315% of C | <150 µs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bielecka, A.; Wojciechowski, D. Stability Analysis of Shunt Active Power Filter with Predictive Closed-Loop Control of Supply Current. Energies 2021, 14, 2208. https://doi.org/10.3390/en14082208
Bielecka A, Wojciechowski D. Stability Analysis of Shunt Active Power Filter with Predictive Closed-Loop Control of Supply Current. Energies. 2021; 14(8):2208. https://doi.org/10.3390/en14082208
Chicago/Turabian StyleBielecka, Agata, and Daniel Wojciechowski. 2021. "Stability Analysis of Shunt Active Power Filter with Predictive Closed-Loop Control of Supply Current" Energies 14, no. 8: 2208. https://doi.org/10.3390/en14082208