Optimum Multi-Mini-Channels Height for Heat Enhancement under Forced Convection Condition
Abstract
:1. Introduction
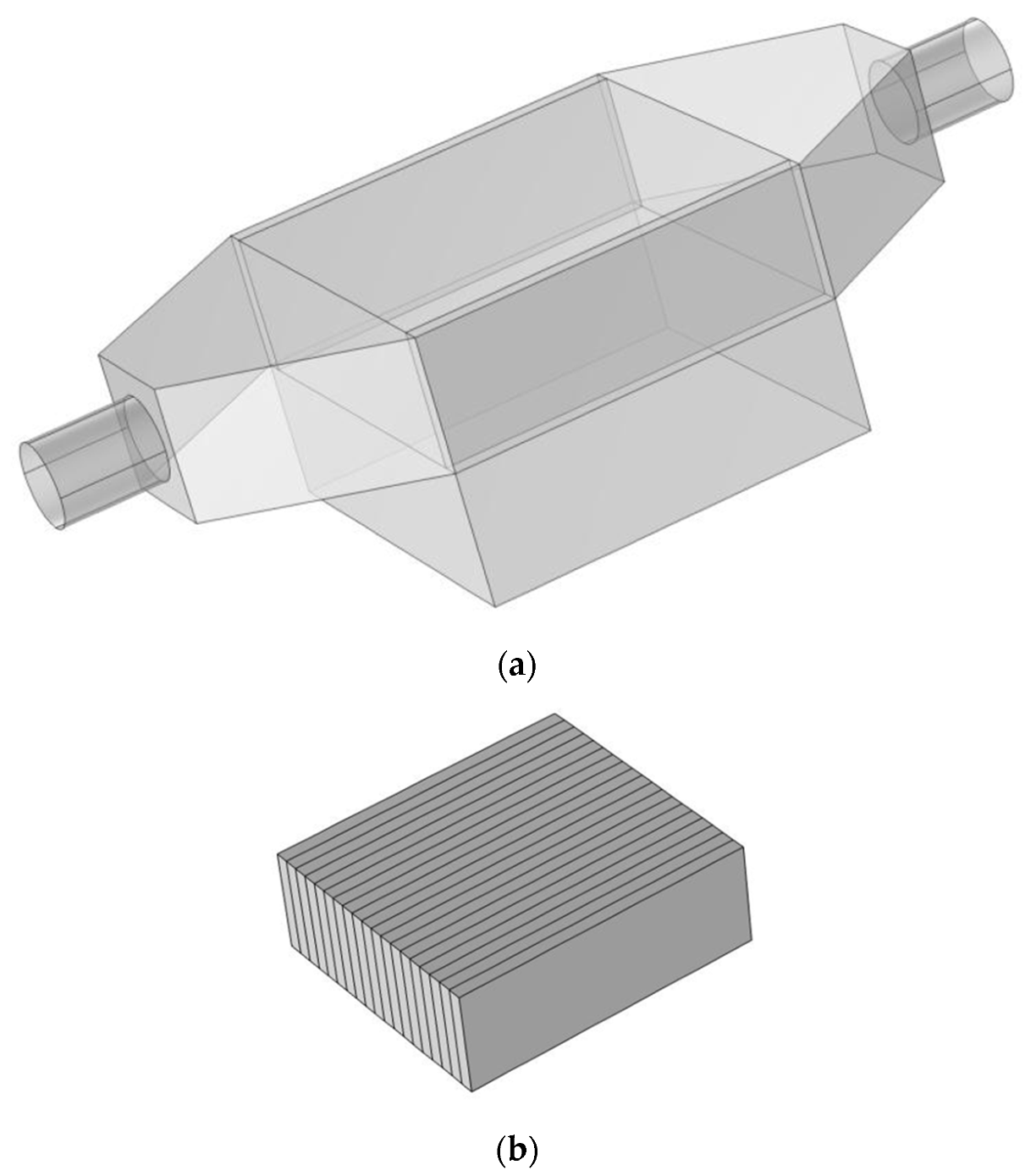
2. Problem Description and Boundary Conditions
3. Finite Element Analysis
3.1. Fluid Flow Formulation
3.2. Heat Transfer Formulation
3.3. Boundary Conditions
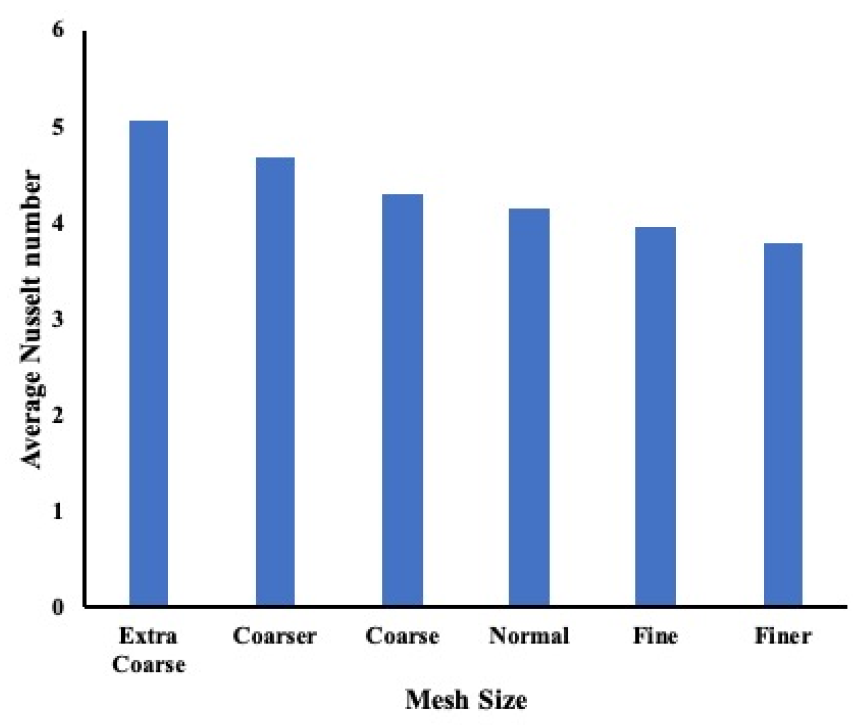
3.4. Mesh Sensitivity
4. Comparison with Experimental Data
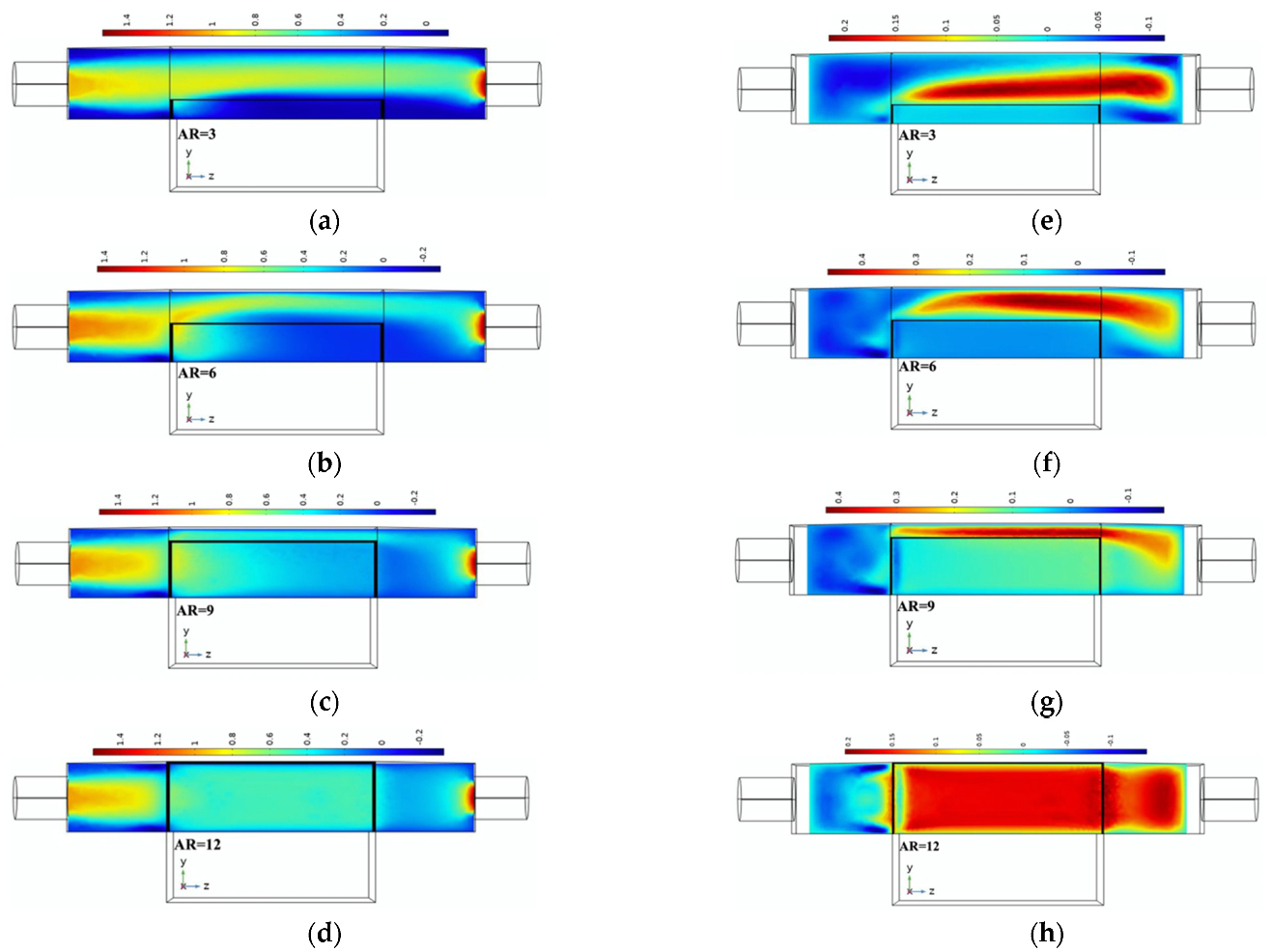
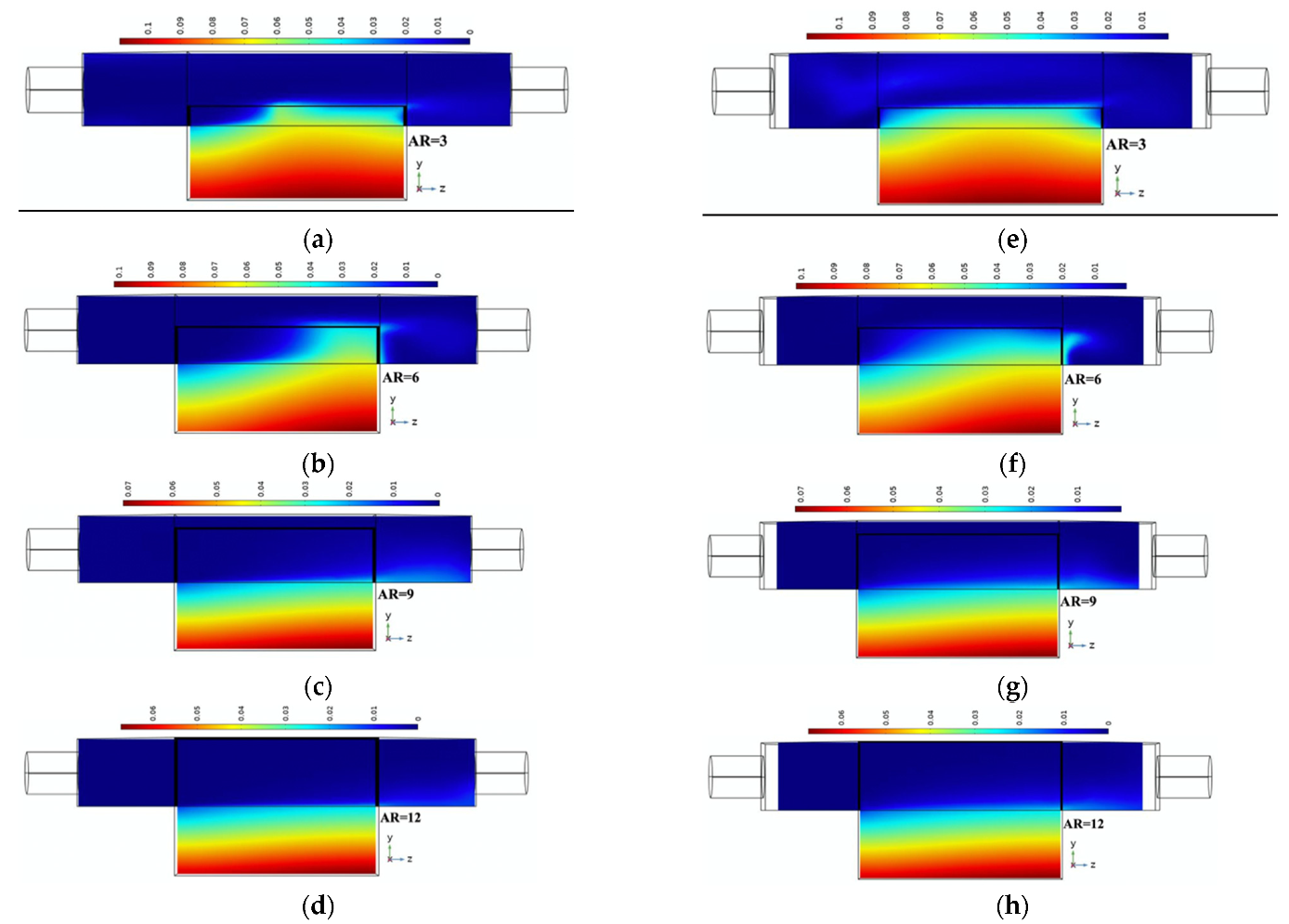
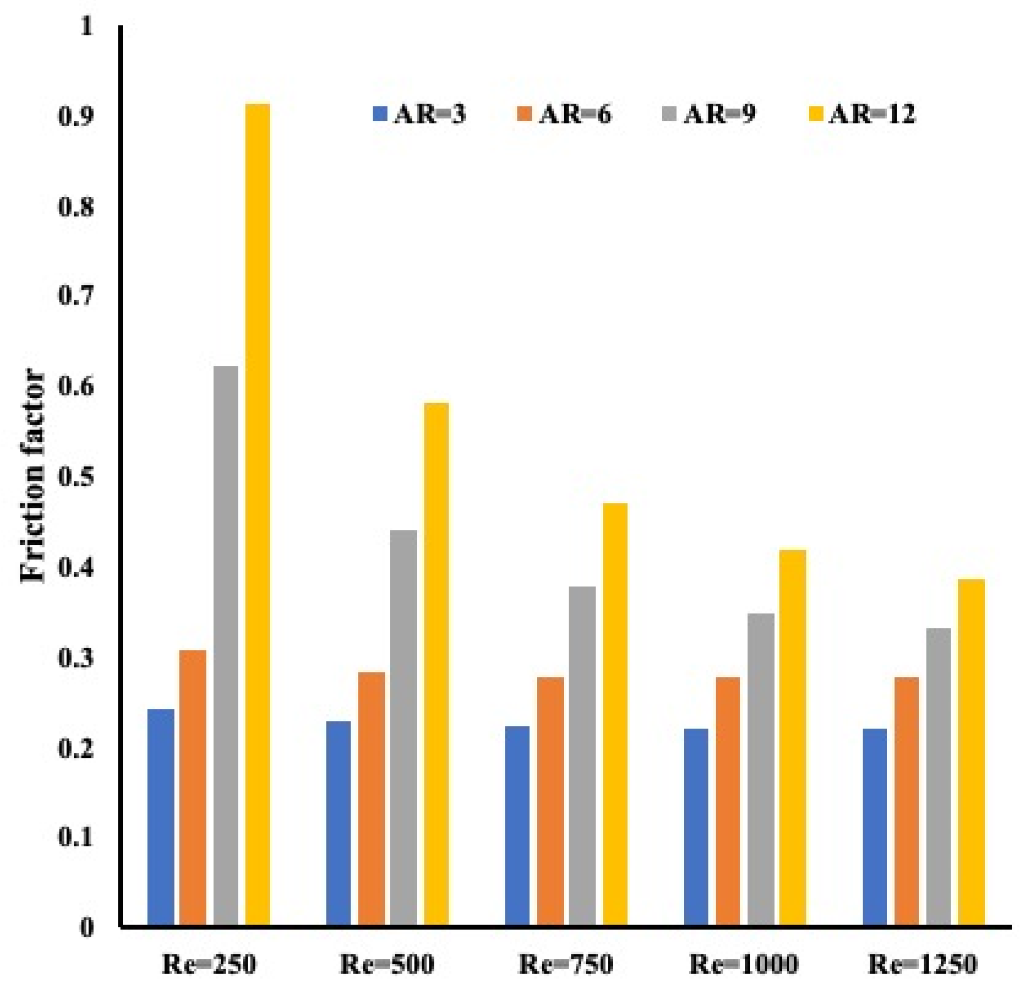
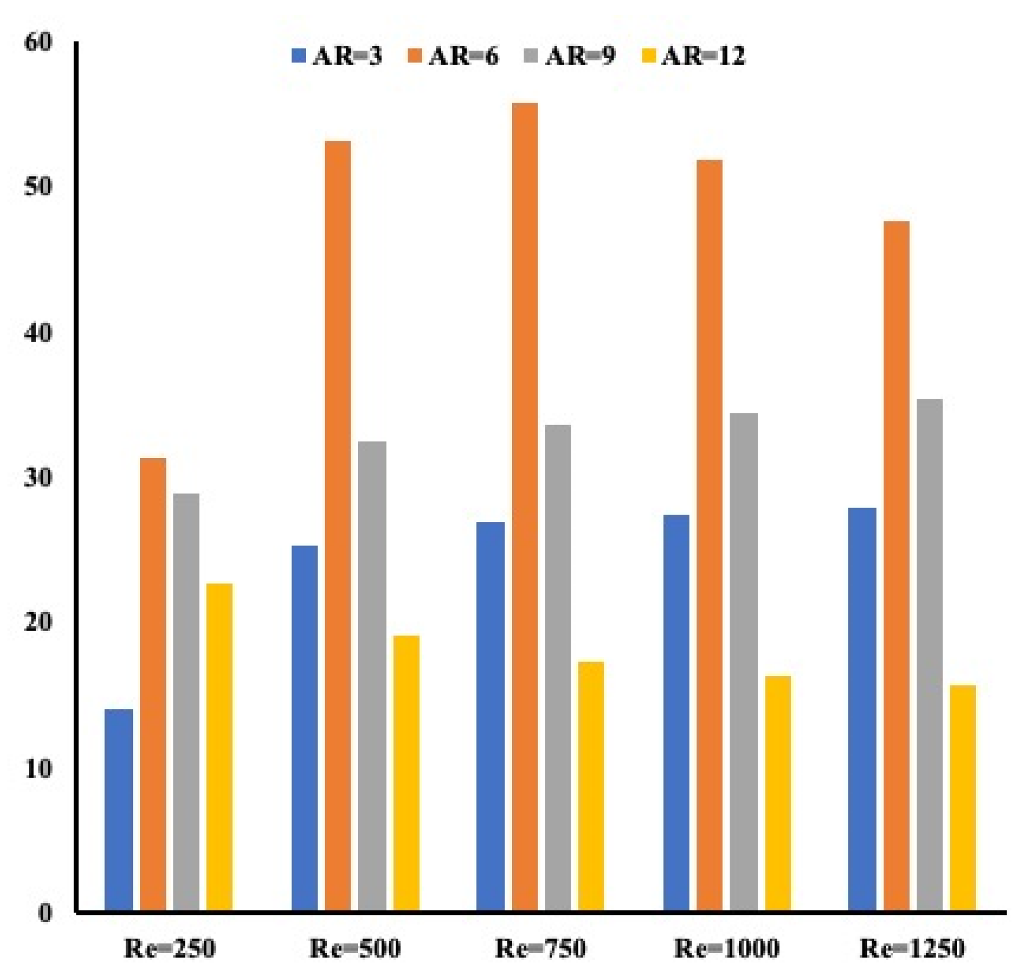
5. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Saghir, M.Z.; Mohamad, A.M. Effectiveness in incorporating Brownian and thermophoresis effects in modeling the convective flow of water-Al2O3 nanoparticles. Int. J. Numer. Methods Heat Fluid Flow 2018, 109, 47–63. [Google Scholar] [CrossRef]
- Welsford, C.; Bayomy, A.M.; Saghir, M.Z. Role of metallic foam in heat storage in the presence of Nanofluid and mcroencapsulated phase change material. Therm. Sci. Eng. Prog. 2018, 7, 61–69. [Google Scholar] [CrossRef]
- Bayomy, A.M.; Saghir, M.Z. Thermal performance of finned Aluminum heat sink filled with ERG Aluminum foam: Experimental and numerical approach. Int. J. Energy Res. 2020, 44, 5217. [Google Scholar] [CrossRef]
- Alhajaj, Z.; Bayomy, A.; Saghir, M.Z.; Rahman, M. Flow of nanofluid and hybrid fluid in porous channels: Experimental and numerical approach. Int. J. Thermofluids 2020, 1–2, 100016. [Google Scholar] [CrossRef]
- Welsford, C.A.; Delisle, C.S.; Plant, R.D.; Saghir, M.Z. Effects of nanofluid concentration and channeling on the thermal effectiveness of highly porous open-cell foam metals: A numerical and experimental study. J. Therm. Anal. Calorim. 2019, 140, 1507–1517. [Google Scholar] [CrossRef]
- Delisle, C.S.; Welsford, C.A.; Saghir, M.Z. Forced convection study with microporous channels and nanofluid: Experimental and numerical. J. Therm. Anal. Calorim. 2019, 140, 1205–1214. [Google Scholar] [CrossRef]
- Saghir, M.Z.; Welsford, C.; Thanapathy, P.; Bayomy, A.M.; Delisle, C. Experimental Measurements and Numerical Computation of Nano Heat Transfer Enhancement Inside a Porous Material. J. Therm. Sci. Eng. Appl. 2019, 12. [Google Scholar] [CrossRef]
- Welsford, C.; Thanapathy, P.; Bayomy, A.M.; Ren, M.; Saghir, M.Z. Heat enhancement using aluminum metal foam: Experimental and numerical approach. J. Porous Media 2020, 23, 249–266. [Google Scholar] [CrossRef]
- Plant, R.D.; Hodgson, G.; Impellizzeri, S.; Saghir, M.Z. Experimental and numerical investigation of heat enhancement using a hybrid nanofluid of copper oxide/alumina nanoparticles in water. J. Therm. Anal. Calorim. 2020, 141, 1951–1968. [Google Scholar] [CrossRef]
- Plant, R.D.; Saghir, M.Z. Numerical and experimental investigation of high concentration aqueous alumina nanofluids in a two and three channel heat exchanger. Int. J. Thermofluids 2020, 9, 100055. [Google Scholar] [CrossRef]
- Dominic, A.; Devahdhanush, V.S.; Suresh, S. An experimental investigation on the effect of relative waviness on performance of minichannel heat sinks using water and nanofluids. Heat Mass Transf. 2021, 1–16. [Google Scholar] [CrossRef]
- Feng, Z.; Ai, X.; Wu, P.; Lin, Q.; Huang, Z. Experimental investigation of laminar flow and heat transfer characteristics in square minichannels with twisted tapes. Int. J. Heat Mass Transf. 2020, 158, 119947. [Google Scholar] [CrossRef]
- Ho, C.J.; Chiu, Y.H.; Yan, Y.M.; Ghalambazd, M. Cooling performance of Al2O3-water nanofluid flow in a minichannel with thermal buoyancy and wall conduction effects. Case Stud. Therm. Eng. 2018, 12, 833–842. [Google Scholar] [CrossRef]
- Ho, C.; Chang, P.-C.; Yan, W.-M.; Amani, P. Efficacy of divergent minichannels on cooling performance of heat sinks with water-based MEPCM suspensions. Int. J. Therm. Sci. 2018, 130, 333–346. [Google Scholar] [CrossRef]
- Ho, C.; Liao, J.-C.; Yan, W.-M.; Amani, M. Experimental study of transient thermal characteristics of nanofluid in a minichannel heat sink with MEPCM layer in its ceiling. Int. J. Heat Mass Transf. 2019, 133, 1041–1051. [Google Scholar] [CrossRef]
- Moraveji, M.K.; Ardehali, R.M.; Ijam, A. CFD investigation of nanofluid effects (cooling performance and pressure drop) in mini-channel heat sink. Int. Commun. Heat Mass Transf. 2013, 40, 58–66. [Google Scholar] [CrossRef]
- Ho, C.J.; Chung, Y.; Lai, C.-M. Thermal performance of Al2O3/water nanofluid in a natural circulation loop with a mini-channel heat sink and heat source. Energy Convers. Manag. 2014, 87, 848–858. [Google Scholar] [CrossRef]
- Rimbault, B.; Nguyen, C.T.; Galanis, N. Experimental investigation of CuO–water nanofluid flow and heat transfer inside a microchannel heat sink. Int. J. Therm. Sci. 2014, 84, 275–292. [Google Scholar] [CrossRef]
- Kumar, V.; Sarkar, J. Two-phase numerical simulation of hybrid nanofluid heat transfer in minichannel heat sink and experimental validation. Int. Commun. Heat Mass Transf. 2018, 91, 239–247. [Google Scholar] [CrossRef]
- Arshad, W.; Ali, H.M. Experimental investigation of heat transfer and pressure drop in a straight minichannel heat sink using TiO2 nanofluid. Int. J. Heat Mass Transf. 2017, 110, 248–256. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, M.; Ahn, C.; Kim, H.U.; Kang, S.-W.; Kim, T. Numerical study on heat transfer and pressure drop in laminar-flow multistage mini-channel heat sink. Int. J. Heat Mass Transf. 2017, 108, 1197–1206. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M.; Sufyan, A.; Rashid, D.; Zahid, S.U.; Rehman, W.U. Experimental investigation of TiO2–water nanofluid flow and heat transfer inside wavy mini-channel heat sinks. J. Therm. Anal. Calorim. 2019, 137, 1279–1294. [Google Scholar] [CrossRef]
- Dominic, A.; Sarangan, J.; Suresh, S.; Devahdhanush, V.S. An experimental study of heat transfer and pressure drop characteristics of divergent wavy minichannels using nanofluids. Heat Mass Transf. 2016, 53, 959–971. [Google Scholar] [CrossRef]
- Plant, R.D.; Hodgson, G.K.; Impellizzeri, S.; Saghir, M.Z. Experimental investigation of heat transfer with various aqueous mono/hybrid Nanofluids in a Multi-channel heat exchanger. Processes 2021. submitted. [Google Scholar]
- Saghir, M.Z.; Bayomy, A.M.; Abdul Rahman, M.D. Heat enhancement effectiveness using multiple twisted tape in rectangular channels. Fluids 2021, 6, 188. [Google Scholar] [CrossRef]






| Fluids | (kg/m/s) | (kg/m3) | cp(J/kg/K) | k(W/m/K) |
|---|---|---|---|---|
| Water | 0.001002 | 998.2 | 4182 | 0.613 |
| Extra coarse mesh | 17,888 total number of elements |
| Coarser mesh | 30,763 total number of elements |
| Coarse mesh | 68,890 total number of elements |
| Normal mesh | 112,088 total number of elements |
| Fine mesh | 321,591 total number of elements |
| Finer mesh | 919,451 total number of elements |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saghir, M.Z.; Alhajaj, Z. Optimum Multi-Mini-Channels Height for Heat Enhancement under Forced Convection Condition. Energies 2021, 14, 7020. https://doi.org/10.3390/en14217020
Saghir MZ, Alhajaj Z. Optimum Multi-Mini-Channels Height for Heat Enhancement under Forced Convection Condition. Energies. 2021; 14(21):7020. https://doi.org/10.3390/en14217020
Chicago/Turabian StyleSaghir, M. Z., and Z. Alhajaj. 2021. "Optimum Multi-Mini-Channels Height for Heat Enhancement under Forced Convection Condition" Energies 14, no. 21: 7020. https://doi.org/10.3390/en14217020







