Reactive Power Control Method for Enhancing the Transient Stability Total Transfer Capability of Transmission Lines for a System with Large-Scale Renewable Energy Sources

Abstract

With the increased proportion of intermittent renewable energy sources (RES) integrated into the sending-end, the total transfer capability of transmission lines is not sufficient during the peak periods of renewable primary energy (e.g., the wind force), causing severe RES power curtailment. The total transfer capability of transmission lines is generally restricted by the transient stability total transfer capability (TSTTC). This paper presents a reactive power control method to enhance the TSTTC of transmission lines. The key is to obtain the sensitivity between TSTTC and reactive power, while the Thevenin equivalent voltage is the link connecting TSTTC and reactive power. The Thevenin theorem states that an active circuit between two load terminals can be considered as an individual voltage source. The voltage of this source would be open-circuit voltage across the terminals, and the internal impedance of the source is the equivalent impedance of the circuit across the terminals. The Thevenin voltage used in Thevenin’s theorem is an ideal voltage source equal to the open-circuit voltage at the terminals. Thus, the sensitivities between TSTTC and the Thevenin equivalent voltages of the sending-end and receiving-end were firstly derived using the equal area criterion. Secondly, the sensitivity between the Thevenin equivalent voltage and reactive power was derived using the total differentiation method. By connecting the above sensitivities together with the relevant parameters calculated from Thevenin equivalent parameter identification and power flow equation, the sensitivity between TSTTC and reactive power was obtained, which was used as the control priority in the proposed reactive power control method. At last, the method was applied to the Gansu Province Power Grid in China to demonstrate its effectiveness, and the accuracy of the sensitivity between TSTTC and reactive power was verified.

1. Introduction

Large-scale renewable energy source (RES) bases in China are mostly located in renewable energy-rich areas far from the load center. The reverse distribution of RES and load leads to large-scale RES power being difficult to consume locally. A large amount of intermittent RES power needs to be delivered to the load center for consumption through long-distance transmission lines. The transfer capability of transmission lines is not sufficient during the peak periods of renewable primary energy, causing a severe RES power curtailment problem [1].

The transfer capability of transmission lines is generally restricted by the transient stability total transfer capability (TSTTC) [2]. TSTTC is the ability of the system to deliver power from the sending-end to the load center through transmission lines, under the condition that the system can stay transiently stable after contingencies occur. Therefore, improving the system transient stability can help in enhancing TSTTC. Several studies proposed methods for improving the system transient stability, as well as enhancing TSTTC from different aspects. One of the effective methods is active power control strategy, which reschedules the generation plans of thermal generation units to improve the system transient stability, thereby enhancing TSTTC [3,4,5]. However, for the sending-end integrated with large-scale RES, the original generation plans of thermal generation units are made considering maximizing the consumption of RES power, and rescheduling generation plans may crowd out the consumption space for RES power. For this reason, studies analyzed the effect of the excitation system parameters of thermal generation units on transient stability, and they proposed methods of increasing the response ratio of excitation voltage and the force excitation threshold voltage to enhance TSTTC without changing generation plans. However, transient excitation enhancement is an open-loop control without feedback; thus, it cannot automatically adapt to the changes of system conditions, and it requires remote transmission of signals, resulting in reducing the reliability of the system [6,7]. In addition, with the application and development of flexible alternating current (AC) transmission systems (FACTS), the utilization of FACTS devices like thyristor-controlled series compensators (TCSC), static var compensators (SVC), and static synchronous compensators (STATCOM) can reduce the energy accumulation in generators during contingencies, thereby improving the system transient stability and enhancing TSTTC [8,9,10]. Furthermore, studies found that superconducting magnetic energy storage (SMES) can also store the excess energy in generators during contingencies with a quicker response and more flexibility [11,12]. However, for systems without FACTS devices or energy storage, installing them needs a long planning time and big investment.

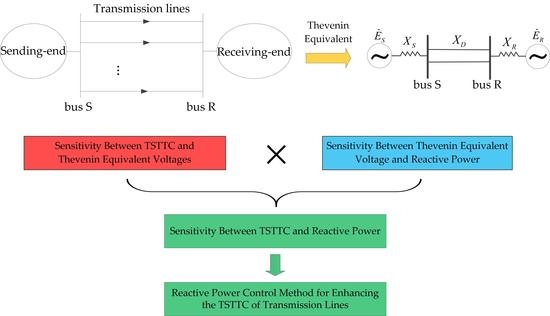
In addition to the methods above, through transient stability analysis, the Thevenin equivalent voltages of the sending-end and receiving-end have a significant influence on the TSTTC, and Thevenin equivalent voltages and reactive power are highly correlated; therefore, reactive power control can also enhance the TSTTC. In a power system, reactive power control is used to control the output of reactive power sources like generators, shunt reactors, and shunt capacitors, thereby adjusting the injecting reactive power into some nodes or the reactive power flow through some lines. At present, reactive power control is mainly used for voltage regulation and voltage stability maintenance [13,14,15]; however, no previous work on enhancing TSTTC using reactive power control was reported.

A new reactive power control method for enhancing the TSTTC of transmission lines for a system with large-scale RES integrated into the sending-end is presented in this paper, with the following main contributions:

• The sensitivity between TSTTC and reactive power is derived, and, with the sensitivity and TSTTC gap, the reactive power adjustment that is needed for filling the TSTTC gap can be calculated. Therefore, the TSTTC of transmission lines can be effectively enhanced by adjusting the reactive power of reactive power devices.
• The proposed reactive power control method is especially useful for enhancing TSTTC for a system with large-scale RES integrated into the sending-end in its existing structure. Because the reactive power adjustment is available from the generators in conventional generation plants and the reactive-load compensation equipment in substations, it needs no further investment in terms of installing new devices.
• Using reactive power control to enhance TSTTC does not involve active power changing; therefore, it will not crowd out the consumption space for RES power. With the enhanced TSTTC, the transmission lines are able to deliver more RES power to the load center, thereby reducing RES power curtailment.

This rest of the paper is organized as follows: in Section 2, the sensitivity between the TSTTC of transmission lines and the Thevenin equivalent voltage is derived using equal area criterion. In Section 3, the sensitivity between the Thevenin equivalent voltage and reactive power is derived using the total differentiation method. By connecting the above sensitivities together, the sensitivity between the TSTTC and reactive power is presented in Section 4, along with the calculation methods to get the relevant parameters needed. In Section 5, using the sensitivity between the TSTTC and reactive power as the control priority, the detailed reactive power control method for enhancing TSTTC is proposed. In Section 6, the method is applied to the Gansu Province Power Grid to demonstrate its effectiveness. Finally, some conclusions are drawn in Section 7.

2. Sensitivity between TSTTC and Thevenin Equivalent Voltages

The schematic diagram of a system composed of a sending-end and receiving-end with transmission lines connecting them is shown in Figure 1, and the sending-end is integrated with large-scale RES.

For the system shown in Figure 1, according to Thevenin’s theorem, at any time, looking from bus S to the sending-end, the sending-end can be equivalent to a generator (Thevenin equivalent voltage ${\dot{E}}_S=E_S\angle {\delta }_S$, Thevenin equivalent reactance $X_S$) [16]. Similarly, the receiving-end is also equivalent to a generator (Thevenin equivalent voltage ${\dot{E}}_R=E_R\angle {\delta }_R$, Thevenin equivalent reactance $X_R$). The equivalent resistance of the system is much lower than the reactance of long-distance transmission lines which is $X_D^{}$; thus, so it is ignored. The equivalent model of the system is shown in Figure 2.

The transmission power through the transmission lines is as follows:

$$P_{SR}^{}=\frac{E_S{E}_R}{X_{\Sigma }}\sin ({\delta }_S-{\delta }_R),$$

(1)

where $X_{\Sigma }=X_S+X_D^{}+X_R$.

Taking the N − 1 fault on the transmission lines as the expected fault, TSTTC is the maximum allowable transmission power through the transmission lines, under the condition that the system can stay transiently stable after an expected fault occurs. Let $\delta ={\delta }_S-{\delta }_R$; then, the transient stability analysis of the two-equivalent-machine system is converted into a single-equivalent-machine system whose rotor motion equation is shown in Equation (2).

$$\frac{d^2\delta (t)}{d{t}^2}=\frac{1}{T_J}(P_m-P_{SR}^{}(t)),$$

(2)

where

$$P_m=P_{SR}^{}(0),$$

(3)

$$P_{SR}^{}(t)=\frac{E_S{E}_R}{X_{\Sigma }(t)}\sin \delta (t),$$

(4)

where $t$ is the transient process moment, $X_{\Sigma }(t)$ is the reactance of different transient phases (pre-fault:$X_{\Sigma }(Ⅰ)$, fault:$X_{\Sigma }(Ⅱ)$, and post-fault:$X_{\Sigma }(Ⅲ)$), and $T_J$ is the system inertia time constant.

According to the equal area criterion, if the system is under the critical condition of transient stability, as shown in Figure 3, the equivalent rotor’s acceleration area A and the biggest possible deceleration area D are equal in the first swing. In this condition, $P_m$ gets its maximum value $P_m^{\max }$, which is the TSTTC of transmission lines [5].

The difference between area D and area A is zero.

$$\mathrm{D}-\mathrm{A}={\displaystyle {\int }_{{\delta }_c}^{{\delta }_u}[\frac{E_S{E}_R}{X_{\sum }(Ⅲ)}\sin \delta (t)-P_m^{\max }}]\mathrm{d}\delta (t)-{\displaystyle {\int }_{{\delta }_0}^{{\delta }_c}[P_m^{\max }-\frac{E_S{E}_R}{X_{\Sigma }(Ⅱ)}\sin \delta (t)}]\mathrm{d}\delta (t)=0,$$

(5)

where ${\delta }_0$, ${\delta }_c$, and ${\delta }_u$ are the initial angle, the fault clearing angle, and the critical angle, which are as follows:

$$\{\begin{array}{l}{\delta }_0=\arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅰ)})\\ {\delta }_c={\delta }_0+\frac{1}{2}\frac{P_m^{\max }}{T_J}{t}_c^2\\ {\delta }_u=\arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅲ)})\end{array},$$

(6)

where $t_c^{}$ is the fault clearing time.

We can then take Equation (6) into Equation (5) to get the expression of the relationship between TSTTC ($P_m^{\max }$) and the Thevenin equivalent voltage ($E_S,E_R$) as follows:

$$\begin{array}{ll}F& (P_m^{\max },E_S,E_R)=0\\ =& \frac{E_S{E}_R}{X_{\sum }(Ⅲ)}\{\cos [\arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅰ)})+\frac{1}{2}\frac{P_m^{\max }}{T_J}{t}_c^2]-\cos \arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅲ)})\}\\ & -\frac{E_S{E}_R}{X_{\sum }(Ⅱ)}\{\cos [\arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅰ)})+\frac{1}{2}\frac{P_m^{\max }}{T_J}{t}_c^2]-\cos \arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅰ)})\}\\ & -P_m^{\max }[\arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅲ)})-\arcsin (P_m^{\max }/\frac{E_S{E}_R}{X_{\Sigma }(Ⅰ)})]\end{array}$$

(7)

Using the implicit function derivative rule with Equation (7), the sensitivity between the TSTTC and the Thevenin equivalent voltage $E_S$ can be calculated as shown in Equation (8). Because $E_R$ has the same position in Equation (7) as $E_S$, the sensitivity between the TSTTC and $E_R$ is similar and omitted.

$$S_{E_S}^{P_m^{\max }}=\frac{\partial P_m^{\max }}{\partial E_S}=-\frac{\partial F(P_m^{\max },E_S,E_R)/\partial E_S}{\partial F(P_m^{\max },E_S,E_R)/\partial P_m^{\max }}.$$

(8)

The detailed expression of $S_{E_S}^{P_m^{\max }}$ is presented in the Appendix A.

3. Sensitivity between Thevenin Equivalent Voltage and Reactive Power

The sensitivity between $E_S$ and reactive power is derived in this section, and the sensitivity between $E_R$ and reactive power is similar and omitted.

In Figure 2, the voltage of bus S is ${\dot{U}}_S=U_S\angle {\theta }_S$, and the complex power injected into bus S from the sending-end is ${\dot{S}}_S^{}=P_S^{}+j{Q}_S^{}$. According to Kirchhoff law, ${\dot{E}}_S$ is as follows:

$${\dot{E}}_S={\dot{U}}_S+j{X}_S{\dot{I}}_S,$$

(9)

where ${\dot{I}}_S=\frac{{\dot{S}}_S^{\ast }}{{\dot{U}}_S^{\ast }}$.

We can take the module value on both sides of Equation (9) as follows:

$$E_S=\sqrt{U_S^2+\frac{X_S}{U_S^2}(P_S^2+Q_S^2)+2X_S{Q}_S^{}}.$$

(10)

While adjusting the reactive power, the active power does not change and is considered as constant. We can then use the total differentiation method on Equation (10) to obtain Equation (11) as follows:

$$\partial E_S=\left[\frac{\partial E_S}{\partial U_S^{}},\frac{\partial E_S}{\partial Q_S^{}}\right]\left[\begin{array}{c}\partial U_S^{}\\ \partial Q_S^{}\end{array}\right],$$

(11)

where, according to Equation (10), $\frac{\partial E_S}{\partial U_S^{}}$ and $\frac{\partial E_S}{\partial Q_S^{}}$ are as follows:

$$\frac{\partial E_S}{\partial U_S^{}}=\frac{U_S^{}-2X_S(P_S^2+Q_S^2)/U_S^2}{\sqrt{U_S^2+\frac{X_S}{U_S^2}(P_S^2+Q_S^2)+2X_S{Q}_S^{}}},$$

(12)

$$\frac{\partial E_S}{\partial Q_S^{}}=\frac{2X_S(1+Q_S^{}/U_S^2)}{\sqrt{U_S^2+\frac{X_S}{U_S^2}(P_S^2+Q_S^2)+2X_S{Q}_S^{}}}.$$

(13)

Through the sensitivity between voltage and reactive power ($S_i^{U_S^{}}$) and the reactive power transfer factor ($D_i^{Q_S^{}}$), $\left[\begin{array}{c}\partial U_S^{}\\ \partial Q_S^{}\end{array}\right]$ in Equation (11) can be converted into reactive power adjustment ($\partial Q_i^{}$) as shown in Equation (14).

$$\left[\begin{array}{c}\partial U_S^{}\\ \partial Q_S^{}\end{array}\right]=\left[\begin{array}{c}{S}_{Q_1}^{U_S^{}},\cdots ,S_{Q_{N_G}}^{U_S^{}}\\ D_{Q_1}^{Q_S^{}},\cdots ,D_{Q_{N_G}}^{Q_S^{}}\end{array}\right]\left[\begin{array}{c}\partial Q_1^{}\\ ⋮\\ \partial Q_{N_G}^{}\end{array}\right].$$

(14)

Taking Equation (14) into Equation (11), we get the expression of the sensitivity between $E_S$ and reactive power as follows:

$$S_{Q_i}^{E_S^{}}=\frac{\partial E_S}{\partial Q_i^{}}=\frac{\partial E_S}{\partial U_S^{}}{S}_{Q_i}^{U_S^{}}+\frac{\partial E_S}{\partial Q_S^{}}{D}_{Q_i}^{Q_S^{}}.$$

(15)

4. Sensitivity between TSTTC and Reactive Power

In Section 2 and Section 3, the sensitivity between the TSTTC and the Thevenin equivalent voltage in Equation (8) and the sensitivity between Thevenin equivalent voltage and reactive power in Equation (15) were derived. By connecting Equation (8) and Equation (15), the sensitivity between the TSTTC and reactive power is given in Equation (16).

$$S_{Q_i}^{P_m^{\max }}=\frac{\partial P_m^{\max }}{\partial E_S}\frac{\partial E_S}{\partial Q_i^{}}+\frac{\partial P_m^{\max }}{\partial E_R}\frac{\partial E_R}{\partial Q_i^{}}=S_{E_S}^{P_m^{\max }}{S}_{Q_i}^{E_S^{}}+S_{E_R}^{P_m^{\max }}{S}_{Q_i}^{E_R^{}}.$$

(16)

According to Equation (16), if the reactive power of node $i$ changes by $\Delta Q_i^{}$, then the TSTTC changes by $S_{Q_i}^{P_m^{\max }}\Delta Q_i^{}$ accordingly. In order to obtain $S_{Q_i}^{P_m^{\max }}$, it is known from Equations (16), (8), and (15) that two kinds of parameters are needed. The first kind can be read directly from the phasor measurement unit (PMU), the supervisory control and data acquisition (SCADA), and the system parameter database, including $P_S^{}$, $Q_S^{}$, $U_S^{}\angle {\theta }_S^{}$, $X_D^{}$, $T_J$ and $t_c^{}$. The second kind of parameter needs to be calculated first, including the Thevenin equivalent parameters ($E_S$,$E_R$,$X_S$,$X_R$), the sensitivity between voltage and reactive power ($S_{Q_i}^{U_S^{}}$), and the reactive power transfer factor ($D_{Q_i}^{Q_S^{}}$). The methods to calculate them are provided below.

4.1. Thevenin Equivalent Parameter Identification

Thevenin equivalent parameters are affected by the grid topology, power generation condition, load condition, etc. Each time the reactive power is adjusted, Thevenin equivalent parameters should be updated. In this paper, the Thevenin equivalent parameters were identified using a tracking algorithm based on variation correction. The algorithm modifies the Thevenin equivalent parameters in the previous condition based on real-time conditions, thereby quickly obtaining those in current conditions [16].

Taking the sending-end shown in Figure 2 as an example, and taking the phase angle of ${\dot{I}}_S$ as reference, which is ${\dot{I}}_S=I_S\angle 0^{\circ }$, by expanding Equation (9) according to the real and imaginary parts, the Thevenin equivalent parameters are expressed as follows:

$$\{\begin{array}{l}{E}_S\cos {\delta }_S^{}=U_S^{}\cos {\theta }_S\\ E_S\sin {\delta }_S^{}=X_S{I}_S+U_S^{}\sin {\theta }_S\end{array}.$$

(17)

The main process is to continuously update $E_S^k$ in the current condition ($k$) through deviation correction, and then use Equation (17) to obtain ${\delta }_S^k$ and $X_S^k$.

The initial $E_S^k$ is

$$E_S^0=\frac{E_S^{\max .0}-E_S^{\min .0}}{2},$$

(18)

where

$$\{\begin{array}{l}{E}_S^{\max .k}=U_S^k\cos {\theta }_S^k/\cos \beta \\ E_S^{\min .k}=U_S^k\\ \beta =\arctan [(Z_S^0{I}_S^0+U_S^0\sin {\theta }_S^0)/(U_S^0\cos {\theta }_S^0)]\\ Z_S^k=\left|U_S^k/I_S^k\right|\end{array}.$$

(19)

We can take $E_S^0$ into Equation (17) to get ${\delta }_S^0$ and $X_S^0$. Then, with the previous values of Thevenin equivalent parameters ($E_S^{k-1}$, ${\delta }_S^{k-1}$, $X_S^{k-1}$) and the present values of $P_S^k$, $Q_S^k$, and ${\dot{U}}_S^k$, we can calculate $E_S^k$ according to the following conditions:

• If $(Z_S^k-Z_S^{k-1})(X_S^{k*}-X_S^{k-1})>0$, then $E_S^k=E_S^{k-1}-{\epsilon }_{}^k$,
• If $(Z_S^k-Z_S^{k-1})(X_S^{k*}-X_S^{k-1})\le 0$, then $E_S^k=E_S^{k-1}+{\epsilon }_{}^k$,

where ${\epsilon }_{}^k=\min (E_S^{k-1}-U_S^k,E_S^{k-1}-E_S^{\max .k},E_S^{k-1}\times \lambda )$ is the variation correction, and $\lambda$ is a pre-specified parameter. $X_S^{k*}$ is an evaluation of $X_S^k$ considering the previous values ($E_S^{k-1}$ and ${\delta }_S^{k-1}$) and the present values ($P_S^k$, $Q_S^k$, and ${\dot{U}}_S^k$).

After obtaining $E_S^k$, we can take it into Equation (17) to get ${\delta }_S^k$ and $X_S^k$, so that all Thevenin equivalent parameters in the sending-end are updated.

4.2. Sensitivity between Voltage and Reactive Power

The sensitivity between voltage and reactive power can be calculated from the Newton–Raphson power flow in Equation (20) [17].

$$\left[\begin{array}{c}\Delta \mathit{P}\\ \Delta \mathit{Q}\end{array}\right]=\left[\begin{array}{cc}{\mathit{J}}_H& {\mathit{J}}_N\\ {\mathit{J}}_J& {\mathit{J}}_L\end{array}\right]\left[\begin{array}{c}\Delta \mathit{\theta }\\ \Delta \mathit{U}/\mathit{U}\end{array}\right],$$

(20)

where ${\mathit{J}}_H$, ${\mathit{J}}_N$, ${\mathit{J}}_J$, ${\mathit{J}}_L$ is the Jacobian block matrix from the power flow equation, $\Delta \mathit{P}$ and $\Delta \mathit{Q}$ are the active and reactive power deviations, $\Delta \mathit{\theta }$ is the voltage phase angle deviation, and $\Delta \mathit{U}/\mathit{U}$ is the ratio of voltage magnitude deviation to voltage magnitude.

The active power is not changed while adjusting the reactive power; thus, $\Delta \mathit{P}=\mathbf{0}$. We can then take it to Equation (20) to get Equation (21).

$$\Delta \mathit{Q}=({\mathit{J}}_L-{\mathit{J}}_J{\mathit{J}}_H^{-1}{\mathit{J}}_N)\Delta \mathit{U}/\mathit{U}.$$

(21)

Thus, the sensitivity between voltage and reactive power is as follows:

$$\mathit{S}={({\mathit{J}}_L-{\mathit{J}}_J{\mathit{J}}_H^{-1}{\mathit{J}}_N)}^{-1}/\mathit{U},$$

(22)

where $\mathit{S}$ is the set of $S_{Q_i}^{U_j^{}}$ in Equation (15).

4.3. Reactive Power Transfer Factor

The sensitivity between the reactive power flowing through line $ij$ (starting node $i$, ending node $j$) and the reactive power injected in node $l$ are defined using the implicit function relationship shown in Equation (23) [18].

$$\frac{\partial Q_{ij}^{}}{\partial Q_l^{}}=\left[\frac{\partial Q_{ij}^{}}{\partial U_i^{}},\frac{\partial Q_{ij}^{}}{\partial U_j^{}},\frac{\partial Q_{ij}^{}}{\partial {\theta }_i^{}},\frac{\partial Q_{ij}^{}}{\partial {\theta }_j^{}}\right]\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\partial U_i^{}/\partial Q_l^{}\\ \partial U_j^{}/\partial Q_l^{}\end{array}\\ \partial {\theta }_i^{}/\partial Q_l^{}\end{array}\\ \partial {\theta }_j^{}/\partial Q_l^{}\end{array}\right],$$

(23)

where

$${\left[\frac{\partial Q_{ij}^{}}{\partial U_i^{}},\frac{\partial Q_{ij}^{}}{\partial U_j^{}},\frac{\partial Q_{ij}^{}}{\partial {\theta }_i^{}},\frac{\partial Q_{ij}^{}}{\partial {\theta }_j^{}}\right]}^T=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{U}_j^{}{Y}_{ij}\sin ({\theta }_i^{}-{\theta }_j^{})\\ U_i^{}{Y}_{ij}\sin ({\theta }_j^{}-{\theta }_i^{})\end{array}\\ -U_i^{}{U}_j^{}{Y}_{ij}\cos ({\theta }_i^{}-{\theta }_j^{})\end{array}\\ U_i^{}{U}_j^{}{Y}_{ij}\cos ({\theta }_i^{}-{\theta }_j^{})\end{array}\right],$$

(24)

where $\partial U_i^{}/\partial Q_l^{}、\partial U_j^{}/\partial Q_l^{}、\partial {\theta }_i^{}/\partial Q_l^{}、\partial {\theta }_j^{}/\partial Q_l^{}$ can be calculated using the Jacobian matrix in Equation (20).

The total injected reactive power ($Q_S^{}$) from the sending-end into bus S is the sum of the reactive power transferring through the lines which are directly connected to bus S in the sending-end; thus, the reactive power transfer factor ($D_{Q_i}^{Q_S^{}}$) in Equation (25) is as follows:

$$D_{Q_i}^{Q_S^{}}=\frac{\partial Q_S^{}}{\partial Q_l^{}}={\displaystyle \sum _{i\in S}\frac{\partial Q_{iS}^{}}{\partial Q_l^{}}}.$$

(25)

5. Reactive Power Control Method for Enhancing the TSTTC of Transmission Lines

The goal of reactive power control is to enhance the TSTTC of transmission lines effectively, under circumstances where the RES power is curtailed due to the insufficiency of TSTTC. The detailed reactive power control method is presented below. A flow diagram of the proposed method is shown in Figure 4.

• According to the RES forcast power and RES output power, the RES power curtailment is calculated, which is the TSTTC gap ($\Delta P_m^{\max }$).
• With the data read from PMU, SCADA and the system parameter database, the method presented in Section 2, Section 3 and Section 4 is used to calculate the sensitivity between TSTTC and reactive power in Equation (16), and the reactive power devices are sorted by their sensitivities.
• The reactive power device that is capable of reactive power adjustment and with the biggest sensitivity is selected, and its reactive power adjustment is calculated as follows:

  $$\Delta Q_i^{}=\min (\Delta P_m^{\max }/S_{Q_i}^{P_m^{\max }},Q_i^{\max }-Q_i^{},\Delta Q_i^U,\Delta Q_i^{US}),$$

  (26)

  where $\Delta P_m^{\max }/S_{Q_i}^{P_m^{\max }}$ is the reactive power adjustment needed to fill the TSTTC gap, $Q_i^{\max }-Q_i^{}$ is the device’s maximum reactive power adjustment within its adjustment capability, $\Delta Q_i^U$ is the maximum available reactive power adjustment considering voltage level [13], and $\Delta Q_i^{US}$ is the maximum available reactive power adjustment considering voltage stability [15].
• Each time after the reactive power is adjusted, the TSTTC is updated and the RES output power is increased accordingly. Then, all steps are repeated until there is no RES power curtailment, or the reactive power control is not effective enough, or all the reactive power devices run out of adjustment capability.

6. Case Analysis

The Gansu Province Power Grid in China was taken as an example, and the comprehensive simulation program Power System Analysis Software Package (PSASP) was used to verify the effectiveness of the proposed reactive power control method.

6.1. Test System Description

The schematic diagram of the Gansu Province Power Grid is shown in Figure 5. The Gansu Province Power Grid is composed of the sending-end which is the Hexi area grid and the receiving-end which is the Gansu main grid, while the sending-end and receiving-end are connected by the Hexi–Wusheng 750 kV transmission lines.

In the sending-end, at the end of 2019, the total installed capacities of wind farms, photovoltaic power stations, and conventional generation plants were 12,773 MW, 7606 MW, and 4164 MW, respectively, and the maximum load was 4940 MW. The RES power needs to be delivered to the receiving-end through the transmission lines. The TSTTC of the transmission lines is around 4400 MW in the typical winter big load operation conditions, and it is far from sufficient during the peak periods of renewable primary energy, causing severe RES power curtailment.

Taking the typical winter big load operation conditions as the original operation conditions, the RES output power, the conventional generation output power, and the total load are 6073 MW, 1900 MW, and 3569 MW, respectively. The RES forcast power is 6485 MW and the original TSTTC is 4404 MW. Therefore, there is 412 MW of RES power curtailment due to the insufficiency of the TSTTC, and the TSTTC gap is 412 MW. The expected fault for the TSTTC calculation is an N − 1 fault on the Hexi–Wusheng 750-kV transmission lines. The reactive power adjustment capabilities of conventional generation plants and substations are listed in

Table 1. Reactive power adjustment capabilities of conventional generation plants and substations (sorted by the first letter of names).

Conventional Generation Plants	Reactive Power Adjustment Capabilities (MVar)	Substations	Reactive Power Adjustment Capabilities (MVar)
Baiyin	200	Baiyin	250
Balingsan	200	Dunhuang	300
Jinchang	300	Hexi	250
Jingtai	300	Jiuquan	200
Jingyuan	400	Lanzhou	250
Jiuquan	350	Pingliang	300
Lanlv	400	Wusheng	250
Pingliang	300	Yumen	250
Zhangye	350	Zhangye	300

.

6.2. Analysis of the Results of Reactive Power Control Method for Enhancing the TSTTC of Transmission Lines

Based on the original operation condition above, taking the first reactive power adjustment as an example, the sensitivity between the TSTTC and the reactive power of each conventional generation plant and substation is shown in

Table 2. Sensitivity between the transient stability total transfer capability (TSTTC) and the reactive power of each conventional generation plant and substation in the first reactive power adjustment (sorted by sensitivities).

Conventional Generation Plants	Sensitivity (MW/MVar)	Substations	Sensitivity (MW/MVar)
Baiyin	0.195	Wusheng	0.248
Jingtai	0.172	Hexi	0.223
Jingyuan	0.137	Baiyin	0.199
Jinchang	0.089	Zhangye	0.078
Zhangye	0.030	Lanzhou	0.041
Lanlv	0.023	Jiuquan	0.033
Pingliang	0.021	Pingliang	0.013
Jiuquan	0.011	Yumen	0.013
Balingsan	0.010	Dunhuang	0.012

.

As shown in Table 2, the Wusheng substation has the biggest sensitivity, and its reactive power adjustment is 250 MW, as calculated from Equation (26). The system transient stability before and after the reactive power adjustment of Wusheng substation is shown in Figure 6, and the system transient stability is represented by the power angle difference curve of the two power plants with the largest power angle difference in the system after an N − 1 fault occurs. As shown in Figure 6, the system transient stability is near critical before the adjustment, and it is improved after the adjustment.

After the first reactive power adjustment, because the system transient stability is improved, the TSTTC is enhanced by 62 MW. Therefore, more RES output power can be delivered through the transmission lines, and the RES power curtailment is reduced by 62 MW to 350 MW.

The whole process of reactive power adjustment is shown in

Table 3. Whole process of reactive power adjustment.

Adjustment Times	Adjustment Nodes	Sensitivity (MW/MVar)	Adjustment Devices	Reactive Power Adjustment (MVar)
1	Wusheng substation	0.248	Shunt reactors	250
2	Hexi substation	0.216	Shunt capacitors	250
3	Baiyin substation	0.192	Shunt capacitors	250
4	Baiyin power plant	0.190	Generators	200
5	Jingtai power plant	0.167	Generators	300
6	Jingyuan power plant	0.135	Generators	400
7	Jinchang power plant	0.087	Generators	300
8	Zhangye substation	0.077	Shunt reactors	300
9	Lanzhou substation	0.040	Shunt reactors	250
10	Jiuquan substation	0.035	Shunt reactors	200

. The detailed operation condition information after each reactive power adjustment is provided in the Supplementary Materials.

Figure 7 shows the changing curve of the TSTTC of the Hexi–Wusheng 750-kV transmission lines after each reactive power adjustment. Due to the reactive power adjustment, the TSTTC of Hexi–Wusheng 750-kV transmission lines is enhanced from 4404 MW to 4776 MW.

As shown in Figure 7, after eight reactive power adjustments, the effect of reactive power adjustment is no longer obvious, and the TSTTC is 4769 MW. This is because the adjustment capacity of the devices with a high sensitivity was used up, and the remaining devices with low sensitivities have little effect on enhancing TSTTC by adjusting their reactive power; thus, the adjustment would be stopped after the eighth time.

Thereofre, in this case, if the TSTTC gap is less than 355 MW, it can be totally filled using the proposed reactive power control method. Thus, in this case, the proposed method can help to consume 355 MW of RES power curtailment by delivering it to the load center.

6.3. Accuracy of the Sensitivity between TSTTC and Reactive Power

In this paper, in order to obtain the analytical expression of the sensitivity between TSTTC and reactive power, while deriving the relationship between TSTTC and the Thevenin equivalent voltage in Section 2, the system is considered equivalent to a single-machine system. In practical operation, for a multi-machine system, the calculation of TSTTC uses the continuous power flow method with transient stability constraints [19]; thus, the accuracy of the sensitivity between the TSTTC and reactive power calculated in this paper needs to be analyzed.

Figure 8 shows the TSTTC calculated using the sensitivity proposed in this paper and the TSTTC calculated using the method in Reference [19] using 10 reactive power adjustments described above. The original TSTTC was calculated using the method in Reference [19], giving 4404 MW. The relative average error of this method compared to the continuous power flow method is 0.23%.

Therefore, the sensitivity derived in this paper is accurate enough for reactive power control when enhancing the TSTTC in practical operation.

7. Conclusions

A reactive power control method for enhancing the TSTTC of transmission lines was proposed in this paper. The key is to obtain the sensitivity between TSTTC and reactive power, which is used as the control priority in the reactive power control method, so that the TSTTC can be effectively enhanced to a certain value. The detailed derivation and the calculation method to obtain the sensitivity between the TSTTC and reactive power were presented, followed by the reactive power control method. At last, the method was applied to the Gansu Province Power Grid. Results show that the reactive power control method can effectively enhance the TSTTC of transmission lines; therefore, more RES power can be delivered to the load center, and the RES power curtailment is reduced; furthermore, the derived sensitivity between the TSTTC and reactive power was verified to be accurate enough in practical operation.

The method proposed in this paper is meaningful for reducing RES power curtailment for systems with large-scale integration of intermittent RES to the sending-end.