Maximizing Solar PV Dissemination under Differential Subsidy Policy across Regions
Abstract
:1. Introduction
2. Analytical Model
2.1. Regional-Level Optimization: Investment Decisions
2.2. Social-Level Optimization: Maximizing the Dissemination of Solar PV Capacity with a Budget Constraint
3. Evaluations
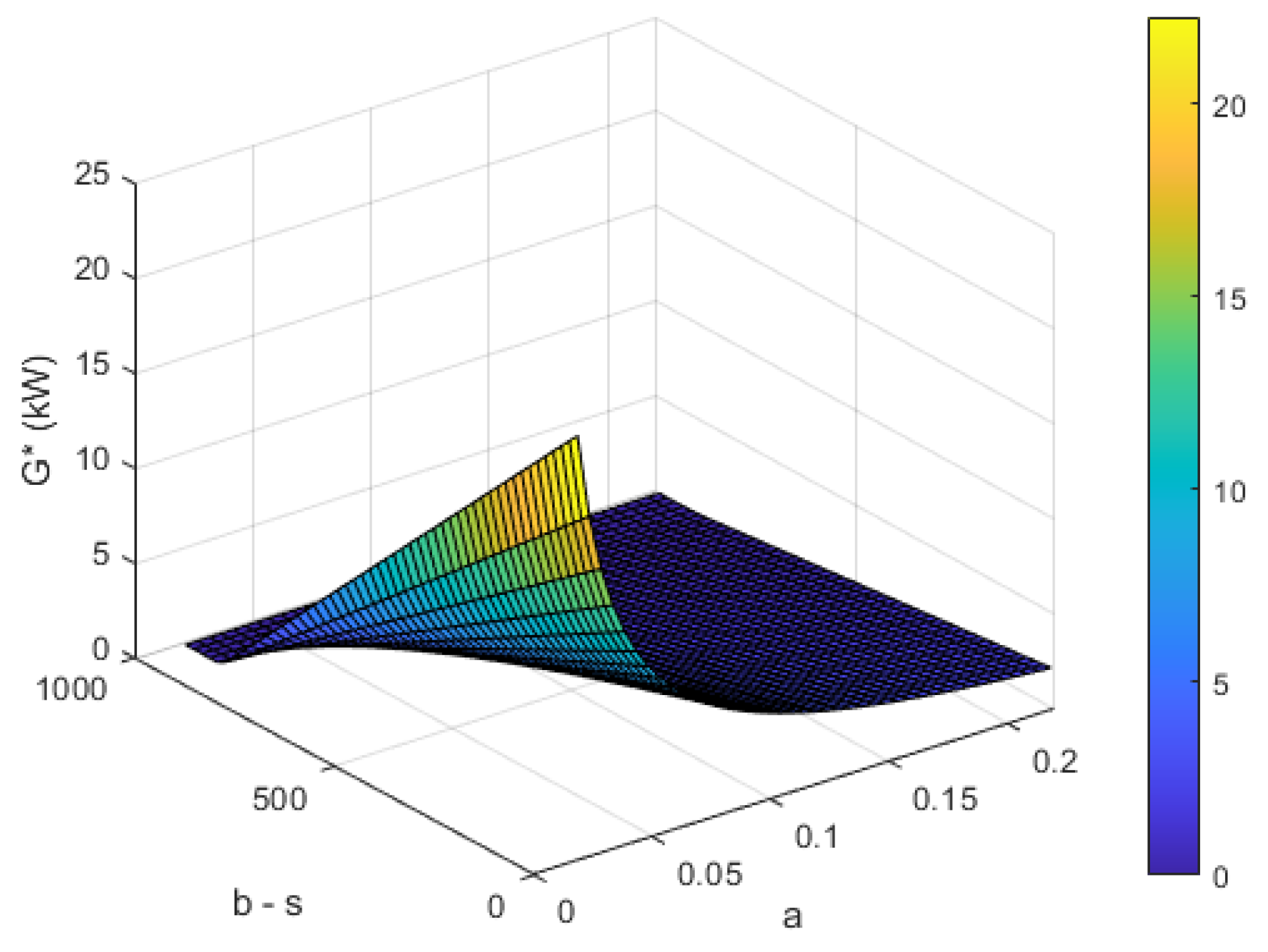
3.1. Numerical Result
3.2. Case Study 1
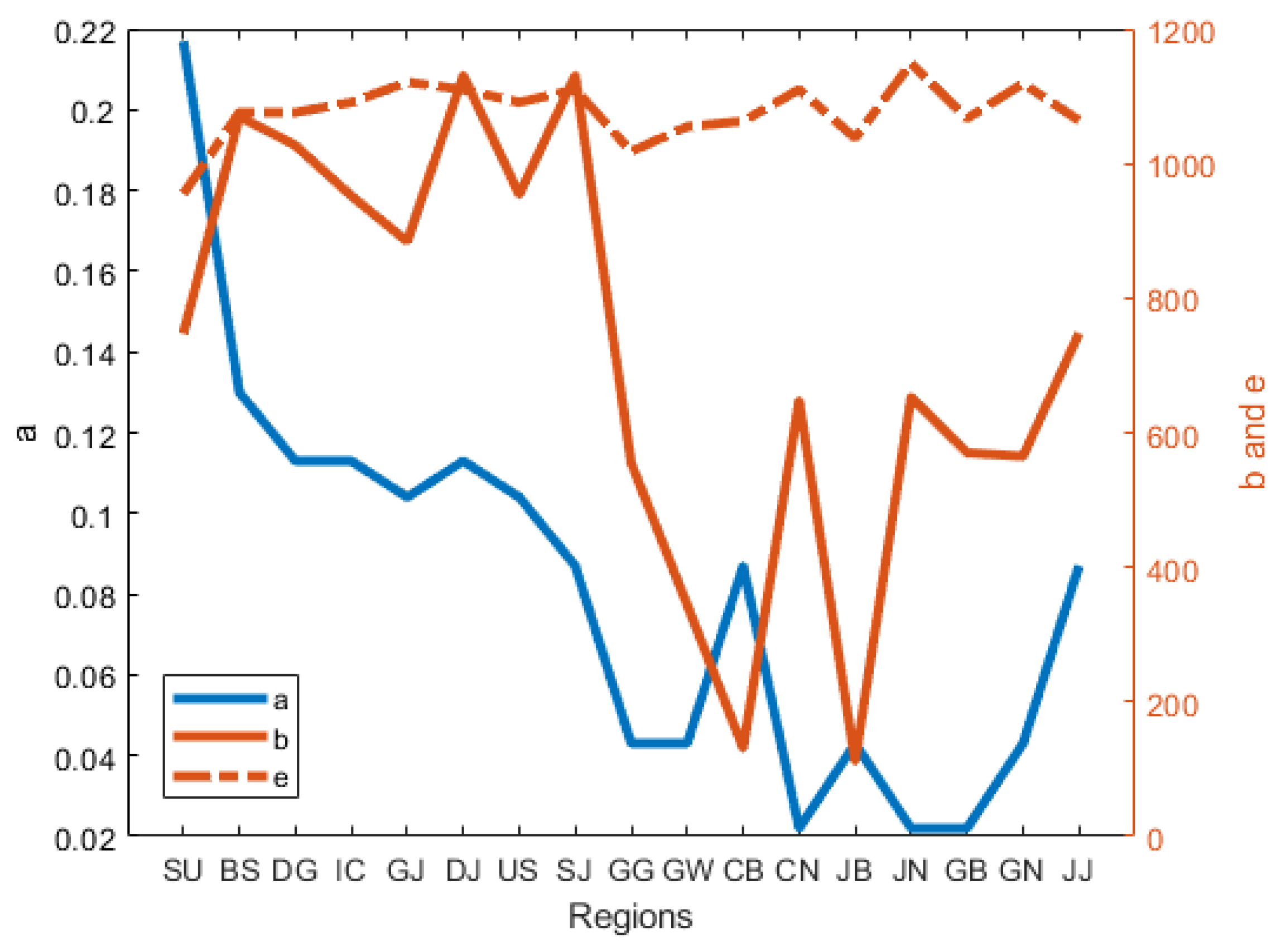
3.3. Case Study 2
3.3.1. Parameter Settings
3.3.2. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Analytic Solution for Social-Level Optimization
References
- Renewable Energy Target—An Australian Government Scheme. Available online: http://www.cleanenergyregulator.gov.au/RET/ (accessed on 6 May 2020).
- RES LEGAL 2019. EEG Feed-in Tariff in Germany. European Commission. 2019. Available online: http://www.res-legal.eu/search-by-country/germany/single/s/res-e/t/promotion/aid/feed-in-tariff-eeg-feed-in-tariff/lastp/135/ (accessed on 6 May 2020).
- Ministry of New and Renewable Energy Government of India. National Solar Mission—Gentral Financial Assistance (CFA). Available online: https://mnre.gov.in/img/documents/uploads/file_f-1585710569965.pdf (accessed on 6 May 2020).
- International Institute for Sustainable Development. India’s Energy Transition: Mapping Subsidies to Fossil Fuels and Clean Energy in India GSI Report; International Institute for Sustainable Development: Winnipeg, MB, Canada, 2017; Available online: https://www.iisd.org/sites/default/files/publications/india-energytransition.pdf (accessed on 6 May 2020).
- Tanzania’s SE4ALL Action Agenda; Ministry of Energy & Minerals: Dar es Salaam, Tanzania, 2015. Available online: https://www.seforall.org/sites/default/files/TANZANIA_AA-Final.pdf (accessed on 6 May 2020).
- Kwon, T.H. Policy Synergy or Conflict for Renewable Energy Support: Case of RPS and Auction in South Korea. Energy Policy 2018, 123, 443–449. [Google Scholar] [CrossRef]
- International Energy Agency. World Energy Outlook 2013; International Energy Agency: Paris, France, 2013; Available online: https://webstore.iea.org/world-energy-outlook-2013 (accessed on 6 May 2020).
- REN21. Renewables 2019 Global Status Report 2019; REN21 Secretariat: Paris, France. Available online: https://www.ren21.net/gsr-2019/ (accessed on 6 May 2020).
- IEA. Germany 2020; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/germany-2020 (accessed on 6 May 2020).
- Senate Bill (SB) 100. 10 September 2018. Available online: https://www.energy.ca.gov/sb100 (accessed on 6 May 2020).
- Rodrìguez, L.R.; Duminil, E.; Ramos, J.S.; Eicker, U. Assessment of the photovoltaic potential at urban level based on 3D city models: A case study and new methodological approach. Sol. Energy 2017, 146, 264–275. [Google Scholar] [CrossRef]
- Lettner, G.; Auer, H.; Fleischhacker, A.; Schwabeneder, D.; Dallinger, B.; Moisl, F.; Roman, E.; Velte, D.; Ana, H. Existing and future PV prosumer concepts. Technische Universitaet Wien, Fundacion Tecnalia Research & Innovation, with the Collaboration of PVP4Grid Consortium. Available online: https://www.pvp4grid.eu/wp-content/uploads/2018/08/D2.1_Existing-future-prosumer-concepts_PVP4Grid_FV.pdf (accessed on 6 May 2020).
- Palmintier, B.; Broderick, R.; Mather, B.; Coddington, M.; Baker, K.; Ding, F.; Reno, M.; Lave, M.; Bharatkumar, A. On the Path to SunShot: Emerging Issues and Challenges in Integrating Solar with the Distribution System; Nrel/Tp-5D00-6533, Sand2016-2524 R; U.S. Department of Energy: Washington, DC, USA, 2016.
- Appen, J.V.; Braun, M.; Stetz, T.; Diwold, K.; Geibel, D. Time in the Sun: The Challenge of High PV Penetration in the German Electric Grid. IEEE Power Energy Mag. 2013, 11, 55–64. [Google Scholar] [CrossRef]
- Olowu, T.O.; Sundararajan, A.; Moghaddami, M. Sarwat, A.I. Future Challenges and Mitigation Methods for High Photovoltaic Penetration: A Survey. Energies 2018, 11, 1782. [Google Scholar] [CrossRef] [Green Version]
- Aleem, A.A.; Hussain, S.M.S.; Ustun, T.S. A Review of Strategies to Increase PV penetration Level in Smart Grids. Energies 2020, 13, 636. [Google Scholar] [CrossRef] [Green Version]
- Martins, V.F.; Borges, C.L.T. Active distribution network integrated planning incorporating distributed generation and load response uncertainties. IEEE Trans. Power Syst. 2011, 26, 2164–2172. [Google Scholar] [CrossRef]
- Mehmood, K.K.; Khan, S.U.; Lee, S.J.; Haider, Z.M.; Rafique, M.K.; Kim, C.H. A real-time optimal coordination scheme for the voltage regulation of a distribution network including an OLTC, capacitor banks, and multiple distributed energy resources. Electr. Power Energy Syst. 2018, 94, 1–14. [Google Scholar] [CrossRef]
- Capitanescu, F.; Ochoa, L.F.; Margossian, H.; Hatziargyriou, N.D. Assessing the potential of network reconfiguration to improve distributed generation hosting capacity in active distribution systems. IEEE Trans. Power Syst. 2014, 30, 346–356. [Google Scholar] [CrossRef]
- Bläsi, A.; Requate, T. Feed-in-tariffs for electricity from renewable energy resources to move down the learning curve? Public Finan. Manag. 2010, 10, 213–250. [Google Scholar]
- Reichenbach, J.; Requate, T. Subsidies for renewable energies in the presence of learning effects and market power. Resour. Energy Econ. 2012, 34, 236–254. [Google Scholar] [CrossRef] [Green Version]
- Andora, M.; Voss, A. Optimal renewable-energy promotion: Capacity subsidies vs generation subsidies. Resour. Energy Econ. 2016, 45, 144–158. [Google Scholar] [CrossRef]
- Kalkuhl, M.; Edenhofer, O.; Lessmann, K. Renewable energy subsidies: Second-best policy or fatal aberration for mitigation? Resour. Energy Econ. 2013, 35, 217–234. [Google Scholar] [CrossRef] [Green Version]
- Mavsar, P.; Sredenšek, K.; Štumberger, B.; Hadžiselimović , M.; Seme, S. Simplified Method for Analyzing the Availability of Rooftop Photovoltaic Potential. Energies 2019, 12, 4233. [Google Scholar] [CrossRef] [Green Version]
- Melius, J.; Margolis, R.; Ong, S. Estimating Rooftop Suitability for PV: A Review of Methods, Patents, and Validation Techniques; Technical Report NREL/TP-6A20-60593; National Renewable Energy Lab.: Golden, CO, USA, 2013.
- Lee, M.; Hong, T.; Jeong, K.; Kim, J. A Bottom-up Approach for Estimating the Economic Potential of the Rooftop Solar Photovoltaic System Considering the Spatial and Temporal Diversity. Appl. Energy 2018, 232, 640–656. [Google Scholar] [CrossRef]
- Endres, A. Environmental Economics: Theory and Policy; Cambridge University Press: Cambridge, UK, 2010; ISBN 9780521173926. [Google Scholar]
- Korea Meteorological Administration. Analysis Report of Weather Resource to Fully Utilize Solar Energy in Korea, 2008 (Wrriten in Korean). Available online: http://www.kma.go.kr/download_01/climate_energy.pdf (accessed on 6 May 2020).



| a | b | e | w/o s | w/ | w/ | |||
|---|---|---|---|---|---|---|---|---|
| A | 2 | 2500 | 2500 | 0 | 76 | 19 | 632 | 158 |
| B | 1 | 5000 | 2500 | 0 | 76 | 0 | 2500 | 0 |
| C | 1 | 2500 | 5000 | 1250 | 76 | 1288 | 0 | 1250 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suh, J.; Yoon, S.-G. Maximizing Solar PV Dissemination under Differential Subsidy Policy across Regions. Energies 2020, 13, 2763. https://doi.org/10.3390/en13112763
Suh J, Yoon S-G. Maximizing Solar PV Dissemination under Differential Subsidy Policy across Regions. Energies. 2020; 13(11):2763. https://doi.org/10.3390/en13112763
Chicago/Turabian StyleSuh, Jeongmeen, and Sung-Guk Yoon. 2020. "Maximizing Solar PV Dissemination under Differential Subsidy Policy across Regions" Energies 13, no. 11: 2763. https://doi.org/10.3390/en13112763





