Analysis of the Propagation Characteristic of Subsynchronous Oscillation in Wind Integrated Power System
Abstract
:1. Introduction
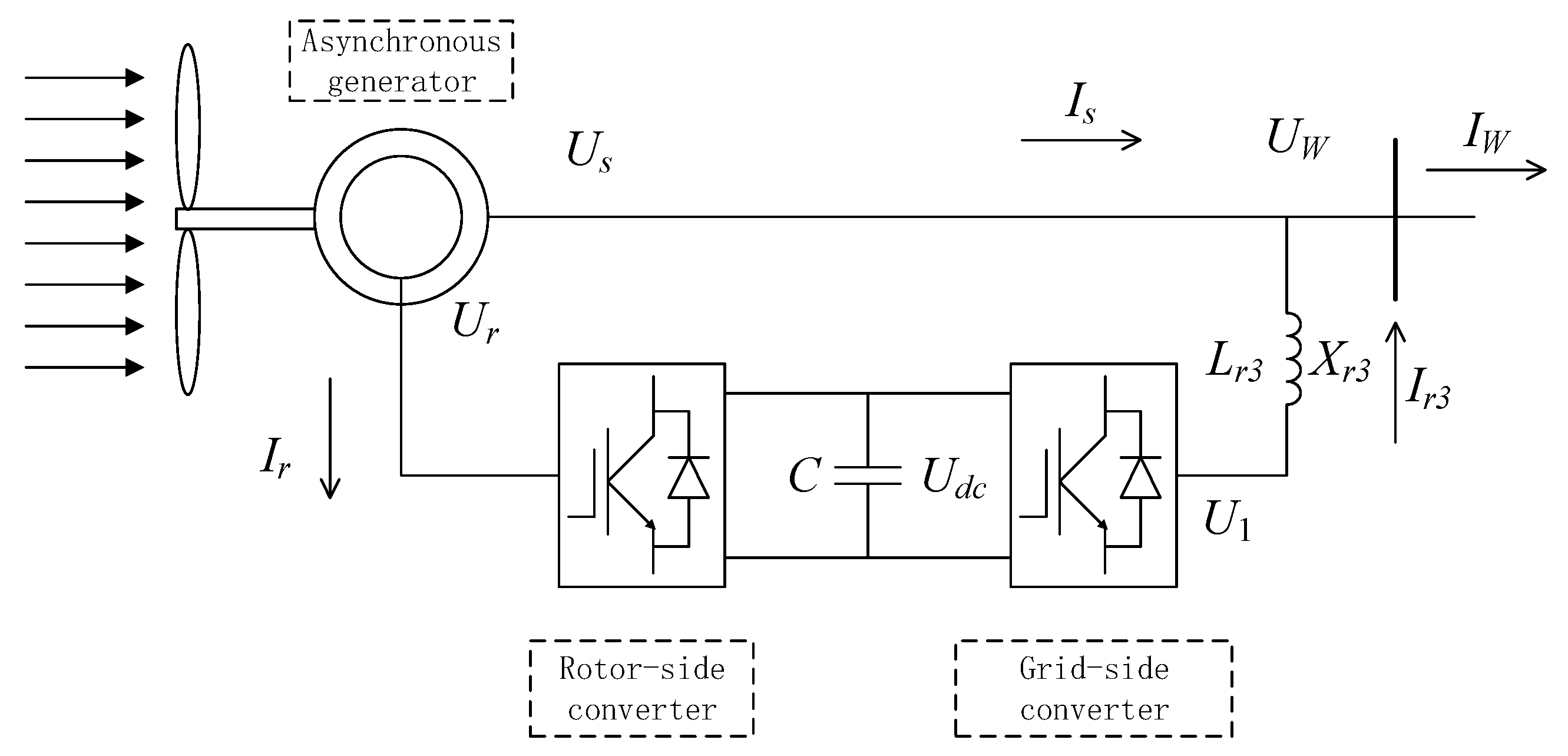
2. Dynamic Model of Wind Integrated Power System
3. Oscillation Propagation Factor
3.1. The Linearization Model
3.2. Oscillation Propagation Factor
4. Simulation Results and Analysis
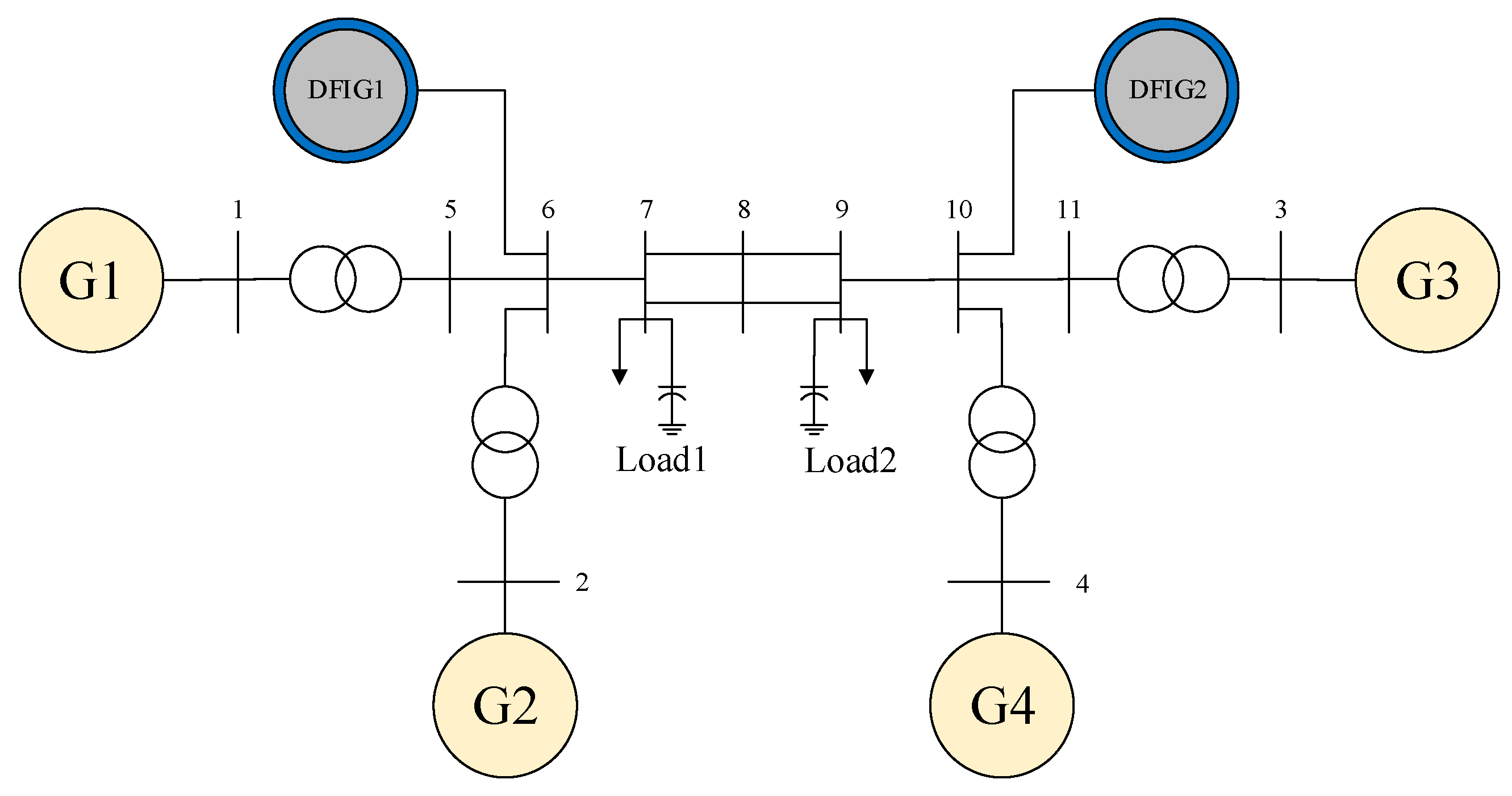
4.1. Two Area Four Machine System
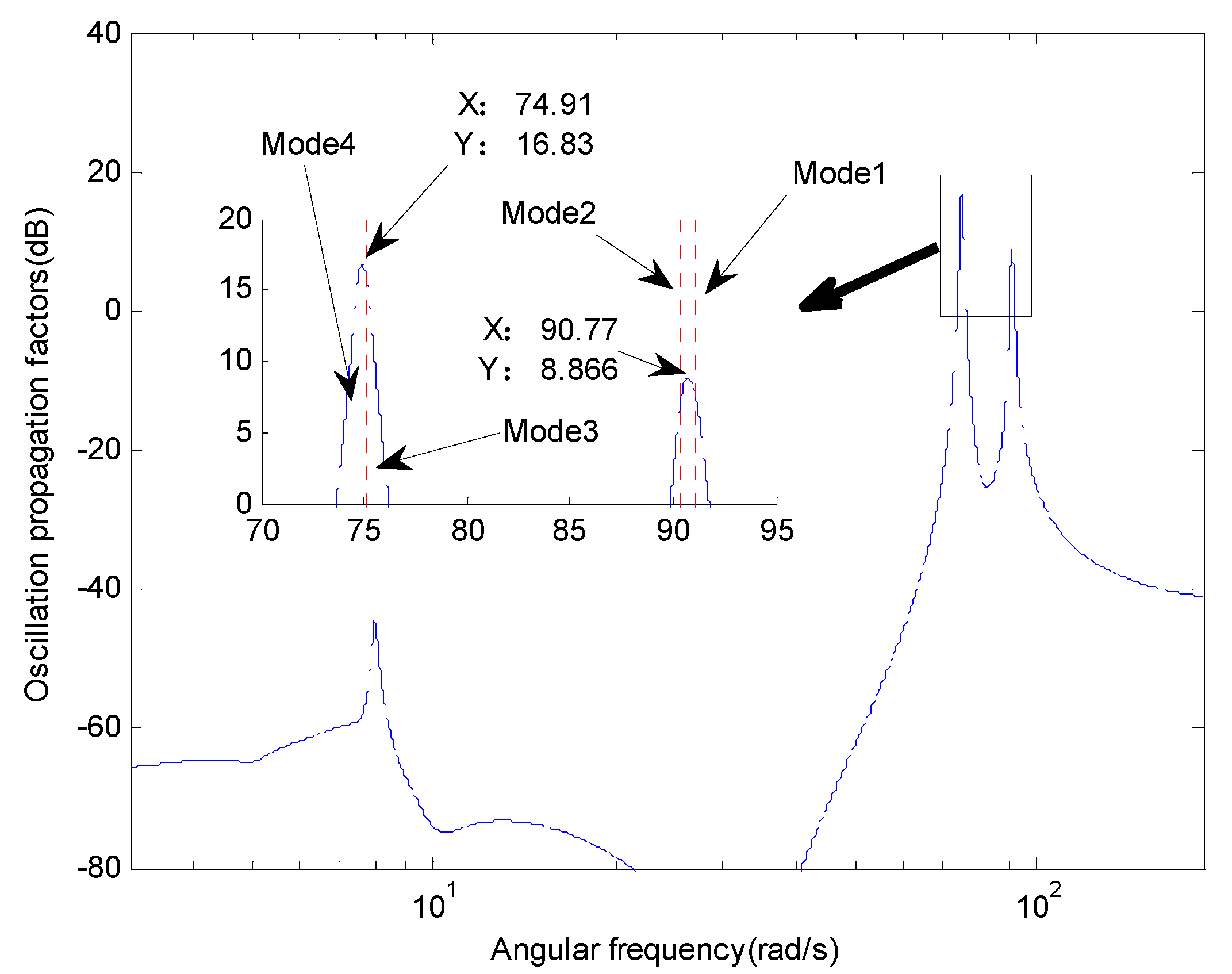
4.1.1. Frequency Domain Simulation Results
4.1.2. Time Domain Simulation Results
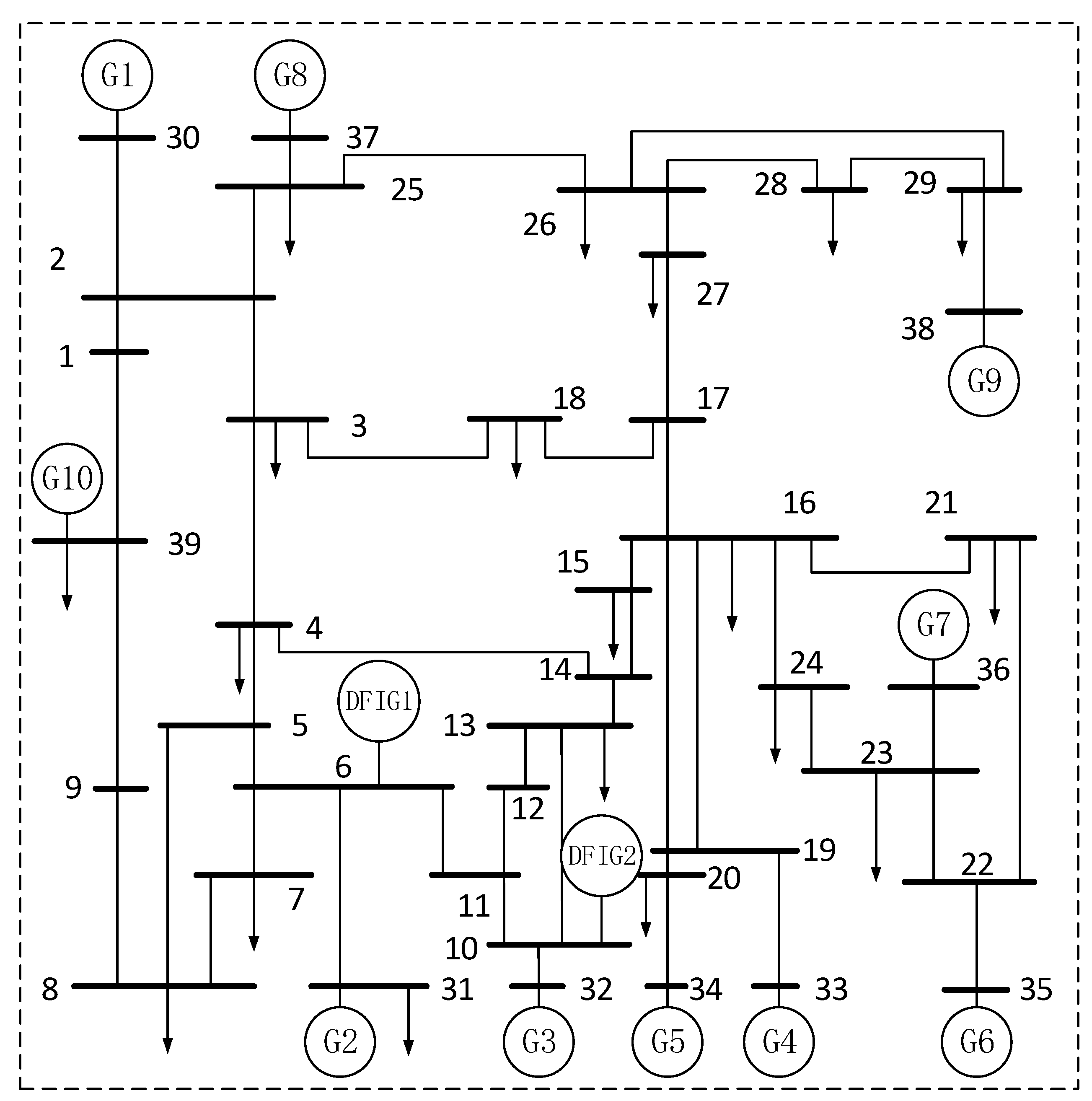
4.2. New England 39 Bus System
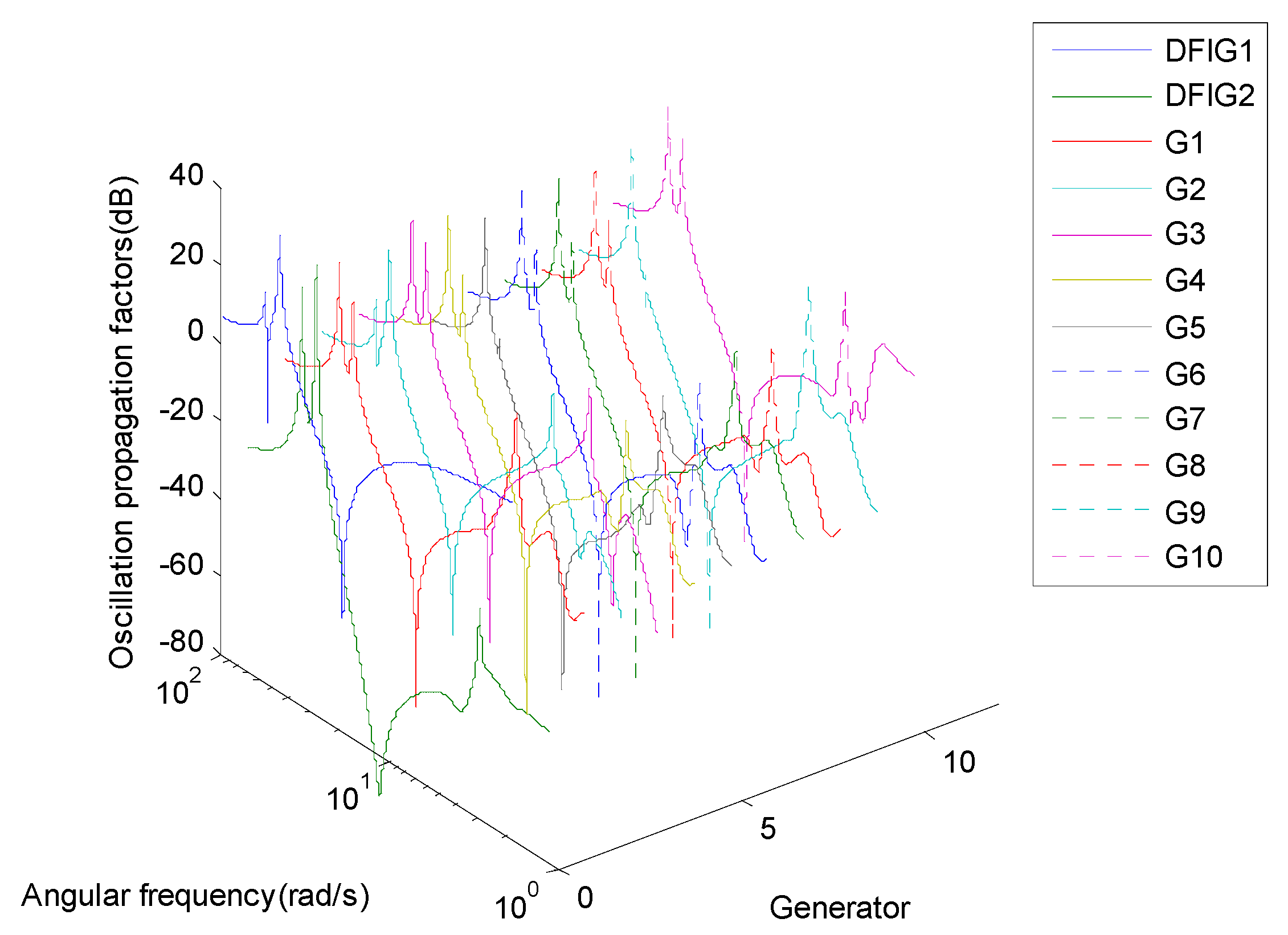
4.2.1. Frequency Domain Simulation Results
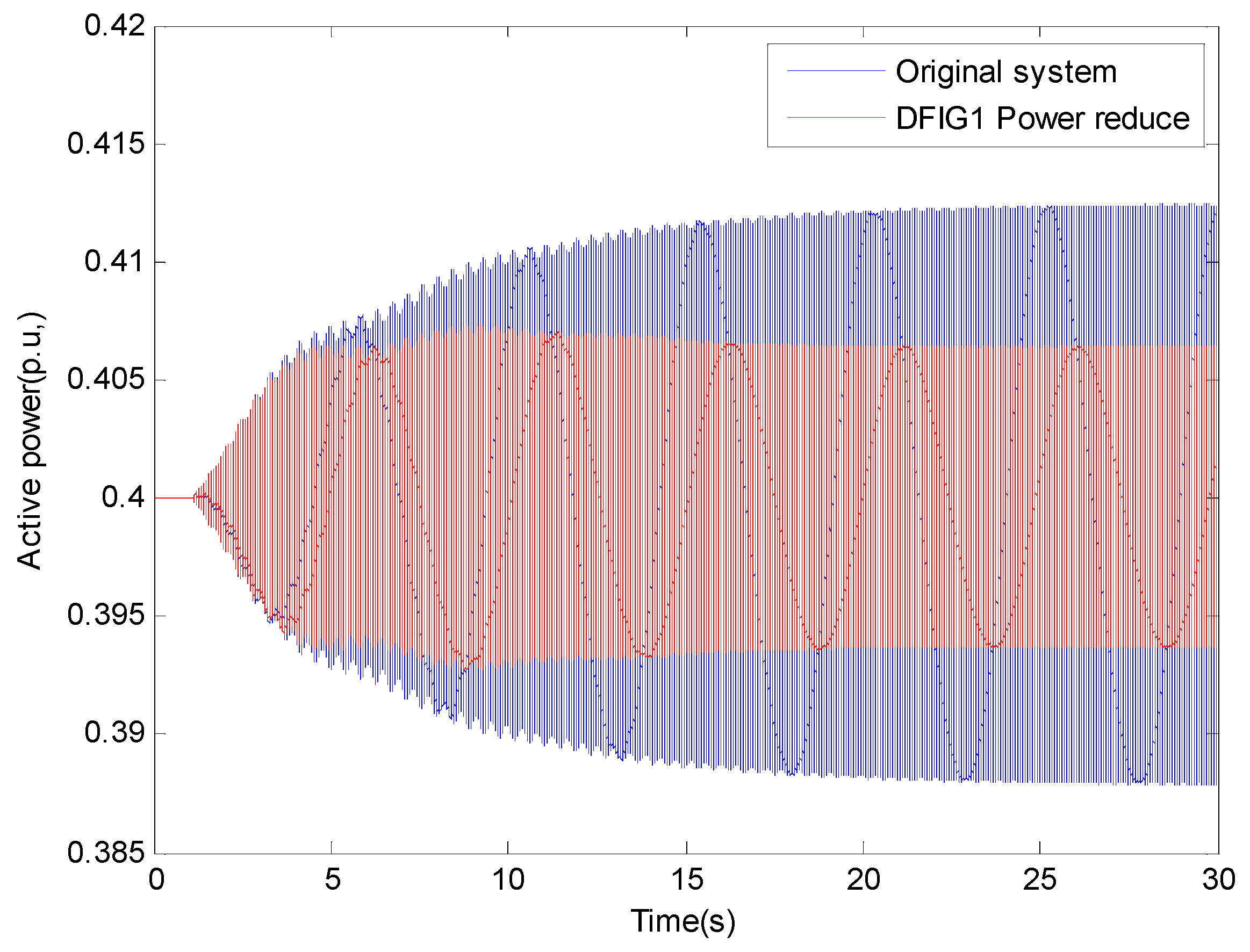
4.2.2. Time Domain Simulation Results
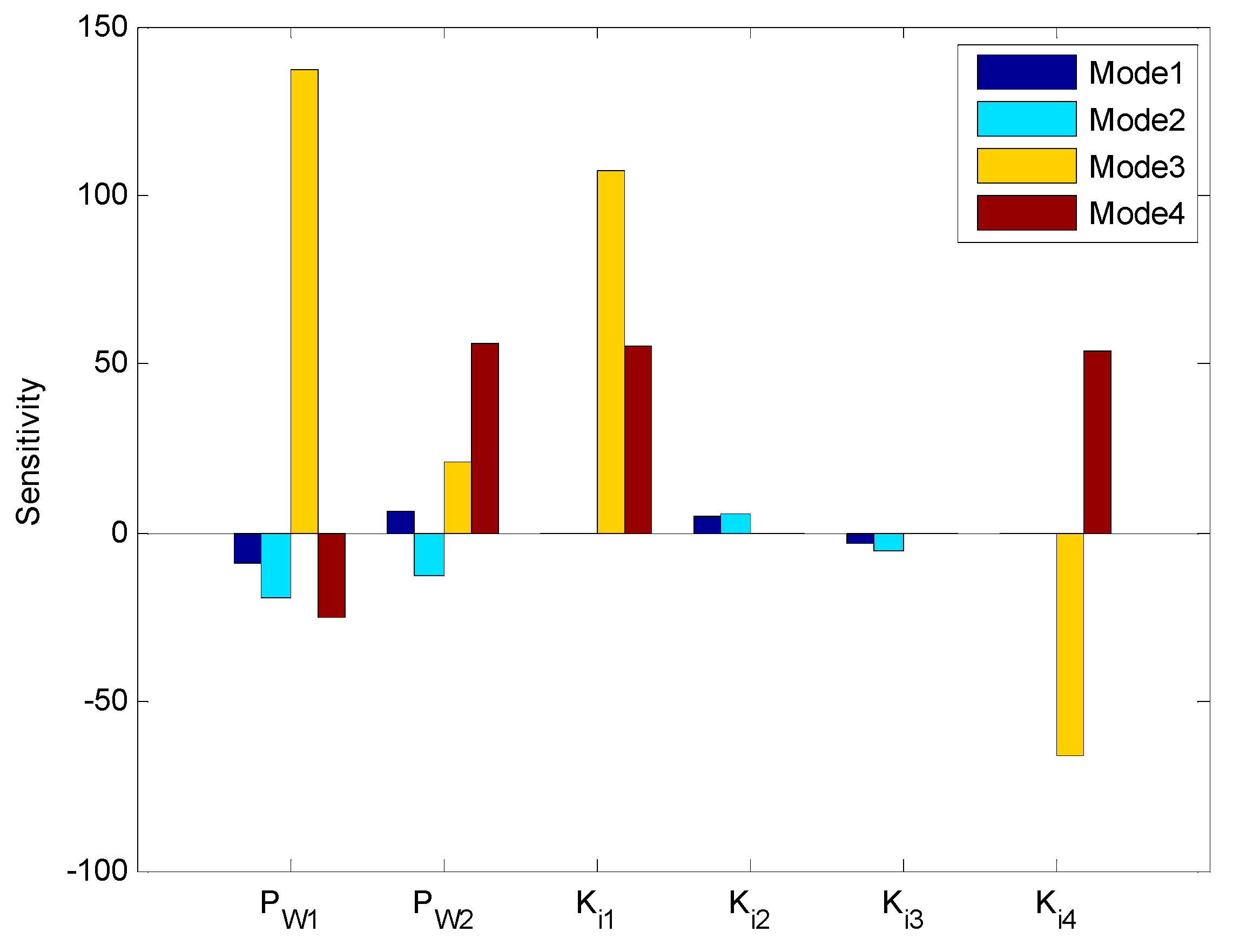
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Leon, A.E. Integration of DFIG-Based Wind Farms Into Series-Compensated Transmission Systems. IEEE Trans. Sustain. Energy 2017, 7, 451–460. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Zhang, C.; Li, Y.; Liu, H.; Hu, Y. Quantitative SSR analysis of series-compensated DFIG-based wind farms using aggregated RLC circuit model. IEEE Trans. Power Syst. 2017, 32, 474–483. [Google Scholar] [CrossRef]
- Gao, F.; He, Q.; Hao, Z.; Zhang, B. The research of subsynchronous oscillation in PMSG wind farm. In Proceedings of the IEEE PES AsiaPacificPower and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 1883–1887. [Google Scholar]
- Dincer, I. Renewable energy and sustainable development: A crucial review. Renew. Sustain. Energy Rev. 2000, 4, 157–175. [Google Scholar] [CrossRef]
- Khan, M.A.A.; Shahriar, M.M.; Islam, M.S. Power quality improvement of DFIG and PMSG based hybrid wind farm using SMES. In Proceedings of the International Conference on Electrical & Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017; pp. 1–4. [Google Scholar]
- Fan, L.; Yuvarajan, S.; Kavasseri, R. Harmonics analysis of a DFIG for a wind energy conversion system. IEEE Trans. Energy Convers. 2010, 25, 181–190. [Google Scholar] [CrossRef]
- Djurović, S.; Vilchis-Rodriguez, D.S.; Smith, A.C. Supply induced interharmonic effects in wound rotor and doubly-fed induction generators. IEEE Trans. Energy Convers. 2015, 30, 1397–1408. [Google Scholar] [CrossRef]
- Wen, T.; Huang, Y.; Zhao, D.; Zhu, L.; Wang, X. Mechanism of Sub-synchronous Interaction caused by inter-harmonics in DFIG. J. Eng. 2017, 13, 892–896. [Google Scholar] [CrossRef]
- Dong, X.; Zang, W.; Dong, C.; Xu, T. SSR characteristics study considering DFIGs at different locations in large wind farm. In Proceedings of the China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–6. [Google Scholar]
- Leon, A.E.; Solsona, J.A. Sub-synchronous interaction damping control for DFIG wind turbines. IEEE Trans. Power Syst. 2015, 30, 419–428. [Google Scholar] [CrossRef]
- Cheng, Y.; Sahni, M.; Muthumuni, D.; Badrzadeh, B. Reactance scan crossover-based approach for investigating SSCI concerns for DFIG-based wind turbines. IEEE Trans. Power Deliv. 2013, 28, 742–751. [Google Scholar] [CrossRef]
- Suriyaarachchi, D.H.R.; Annakkage, U.D.; Karawita, C.; Jacobson, D.A. A Procedure to Study Sub-Synchronous Interactions in Wind Integrated Power Systems. IEEE Trans. Power Syst. 2013, 28, 377–384. [Google Scholar] [CrossRef]
- Fan, L.; Miao, Z. Nyquist-stability-criterion-based SSR explanation for type-3 wind generators. IEEE Trans. Energy Conv. 2012, 27, 807–809. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Cespedes, M.; Sun, J. Modeling and mitigation of harmonic resonance between wind turbines and the grid. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 2109–2116. [Google Scholar]
- Wu, F.; Zhang, X.; Godfrey, K.; Ju, P. Modeling and Control of Wind Turbine with Doubly Fed Induction Generator. In Proceedings of the IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29–31 October 2006; pp. 1404–1409. [Google Scholar]
- Qiao, W. Dynamic modeling and control of doubly fed induction generators driven by wind turbines. In Proceedings of the IEEE PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–8. [Google Scholar]
- Erdogan, N.; Henao, H.; Grisel, R. A proposed Technique for Simulating the Complete Electric Drive Systems with a Complex Kinematics Chain. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; pp. 1240–1245. [Google Scholar]
- Abad, G.; Rodriguez, M.A.; Iwanski, G.; Poza, J. Direct Power Control of Doubly Fed Induction Generator based Wind Turbines under Unbalanced Grid Voltage. IEEE Trans. Power Electron. 2010, 25, 442–452. [Google Scholar] [CrossRef]
- Jiang, J.; Chao, Q.; Chen, J.; Chang, X. Simulation study on frequency response characteristic of different wind turbines. Renew. Energy Resour. 2010, 28, 24–28. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kundur, P. Power System Stability and Control; Balu, N.J., Lauby, M.G., Eds.; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Holmes, D. Pulse Width Modulation for Power Converters: Principles and Practice; JohnWiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Pai, M.A. Energy Function Analysis for Power System Stability; Kluwer Academic Publishers: Boston, MA, USA, 1989. [Google Scholar]
- Xie, X.; Liu, W.; Liu, H.; Du, Y.; Li, Y. A system-wide protection against unstable SSCI in series-compensated wind power systems. IEEE Trans. Power Deliv. 2018, 33, 3095–3104. [Google Scholar] [CrossRef]


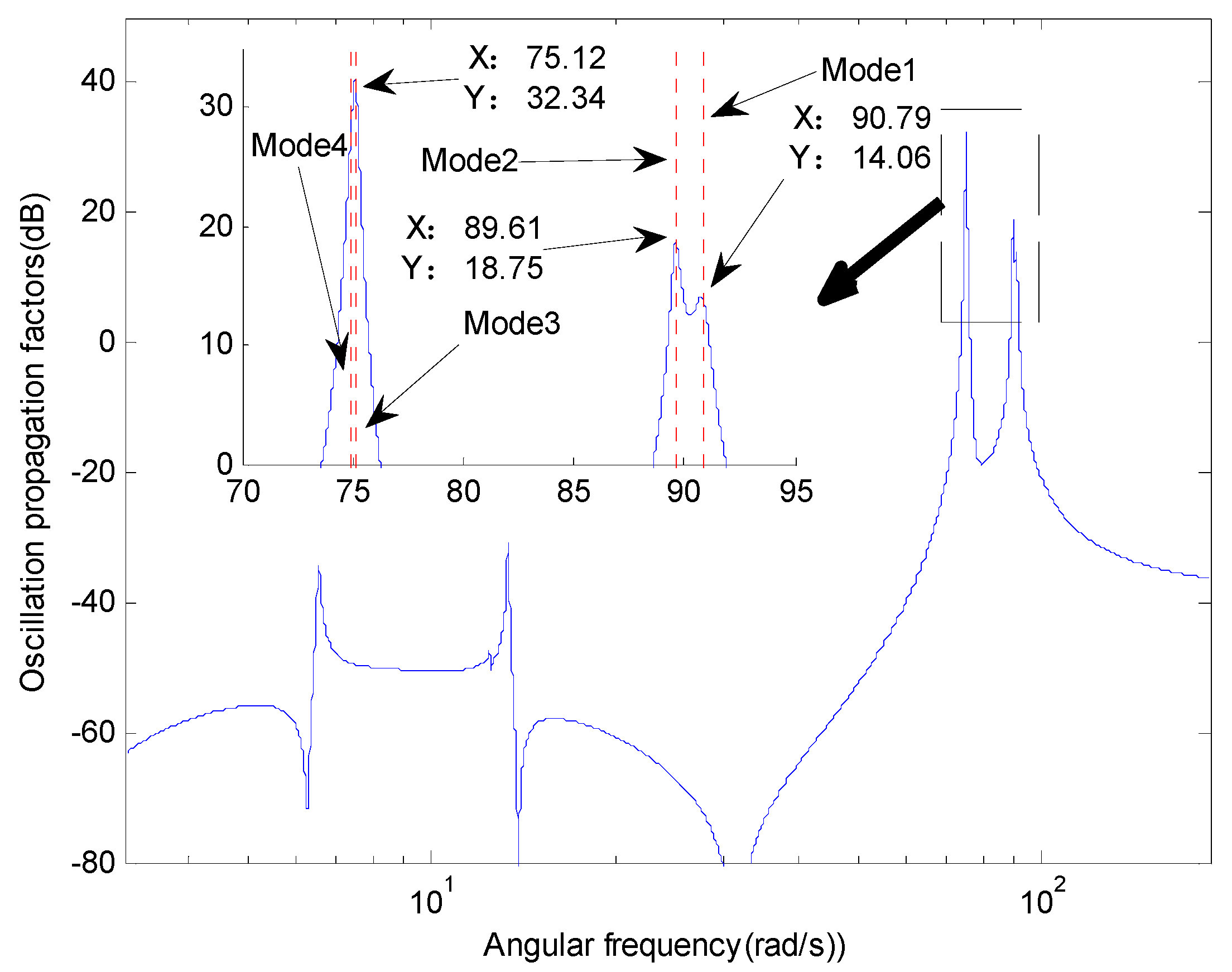



| Mode | Eigenvalue | Angular Frequency (Rad/s) | Damping Ratio |
|---|---|---|---|
| 1 | −0.3364 ± 90.8578j | 90.8578 | 0.0037 |
| 2 | −0.1806 ± 89.5917j | 89.5917 | 0.0020 |
| 3 | −0.1297 ± 75.1461j | 75.1461 | 0.0017 |
| 4 | −0.2758 ± 74.9510j | 74.9510 | 0.0037 |
| 5 | −0.0368 ± 13.3422j | 13.3422 | 0.0028 |
| 6 | −0.0403 ± 12.4648j | 12.4648 | 0.0032 |
| 7 | −0.0355 ± 6.5300j | 6.5300 | 0.0054 |
| Mode | Eigenvalue | Angular Frequency (Rad/s) | Damping Ratio |
|---|---|---|---|
| 1 | −0.2973 ± 90.9755j | 90.9755 | 0.0033 |
| 2 | −0.2285 ± 89.8449j | 89.8449 | 0.0025 |
| 3 | −0.2367 ± 75.1553j | 75.1553 | 0.0031 |
| 4 | −0.2539 ± 74.9392j | 74.9392 | 0.0034 |
| 5 | −0.0373 ± 13.3797j | 13.3797 | 0.0028 |
| 6 | −0.0403 ± 12.4733j | 12.4733 | 0.0032 |
| 7 | −0.0395 ± 6.3194j | 6.3194 | 0.0062 |
| Mode | Eigenvalue | Angular Frequency (Rad/s) | Damping Ratio |
|---|---|---|---|
| 1 | −0.5060 ± 90.4108j | 90.4108 | 0.0056 |
| 2 | −0.5494 ± 91.0655j | 91.0655 | 0.0060 |
| 3 | −0.4586 ± 74.7992j | 74.7992 | 0.0061 |
| 4 | −0.5610 ± 75.0893j | 75.0893 | 0.0075 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Z.; Peng, S.; Yang, J.; Deng, J.; He, H.; Wang, T. Analysis of the Propagation Characteristic of Subsynchronous Oscillation in Wind Integrated Power System. Energies 2019, 12, 1081. https://doi.org/10.3390/en12061081
Wen Z, Peng S, Yang J, Deng J, He H, Wang T. Analysis of the Propagation Characteristic of Subsynchronous Oscillation in Wind Integrated Power System. Energies. 2019; 12(6):1081. https://doi.org/10.3390/en12061081
Chicago/Turabian StyleWen, Zhiping, Shutao Peng, Jing Yang, Jun Deng, Hanqing He, and Tong Wang. 2019. "Analysis of the Propagation Characteristic of Subsynchronous Oscillation in Wind Integrated Power System" Energies 12, no. 6: 1081. https://doi.org/10.3390/en12061081





