Experimental and Theoretical Study on Dynamic Hydraulic Fracture
Abstract
:1. Introduction
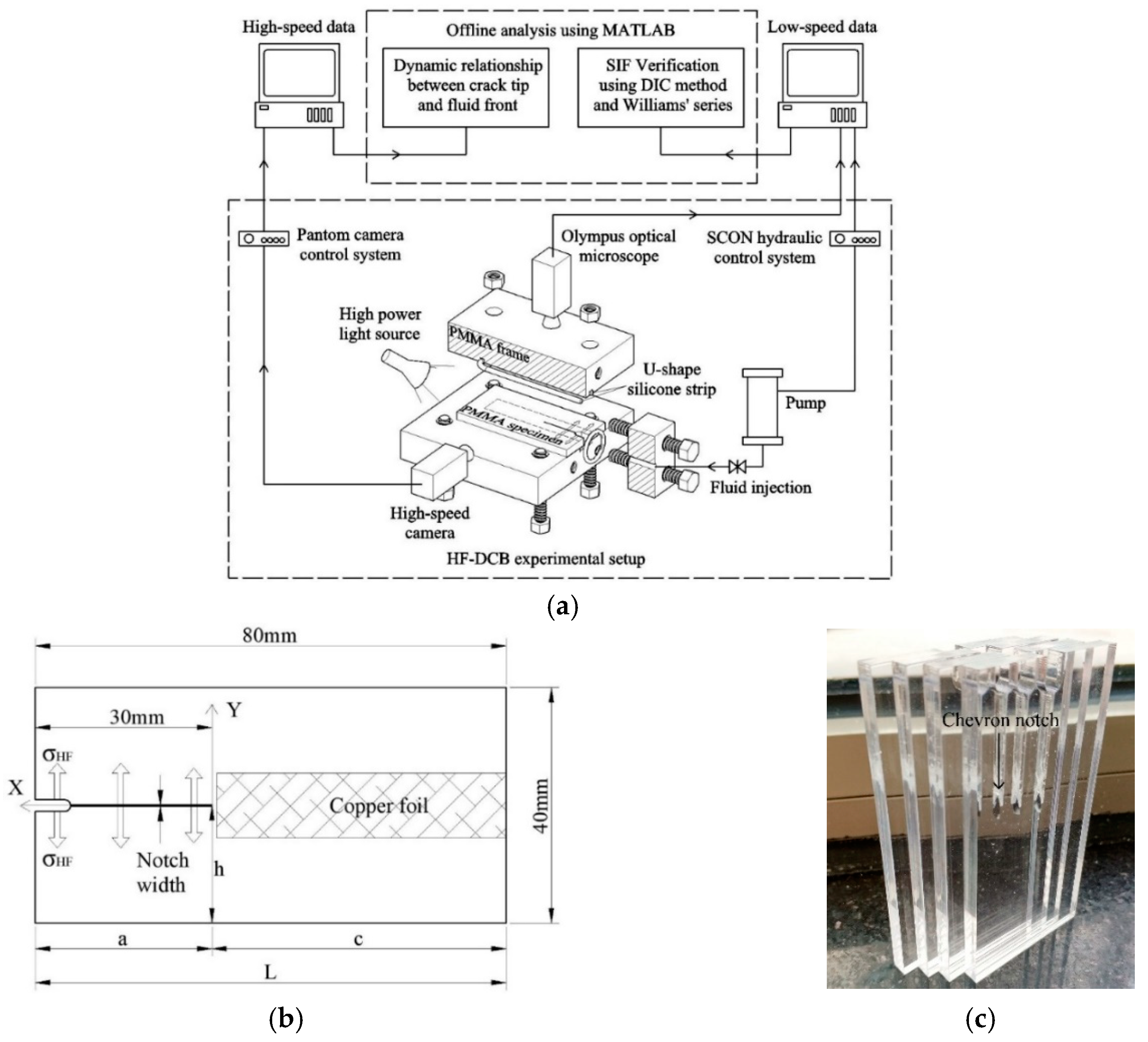
2. Experimental Setup and Verification
2.1. Experimental Setup
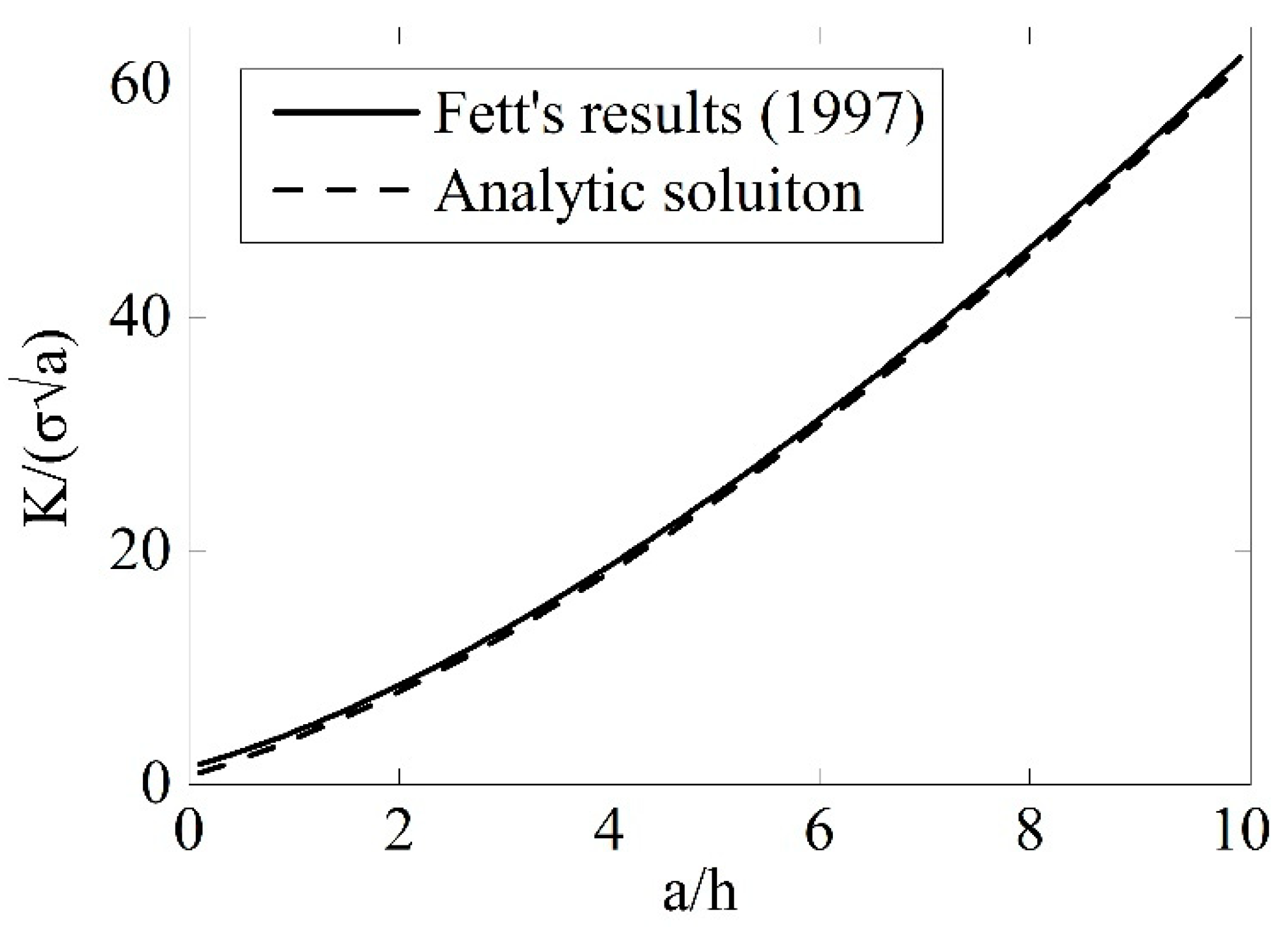
2.2. The Theoretical and Experimental Verification of Stress Intensity Factor (SIF)
2.2.1. Theoretical Verification
2.2.2. Experimental Verification
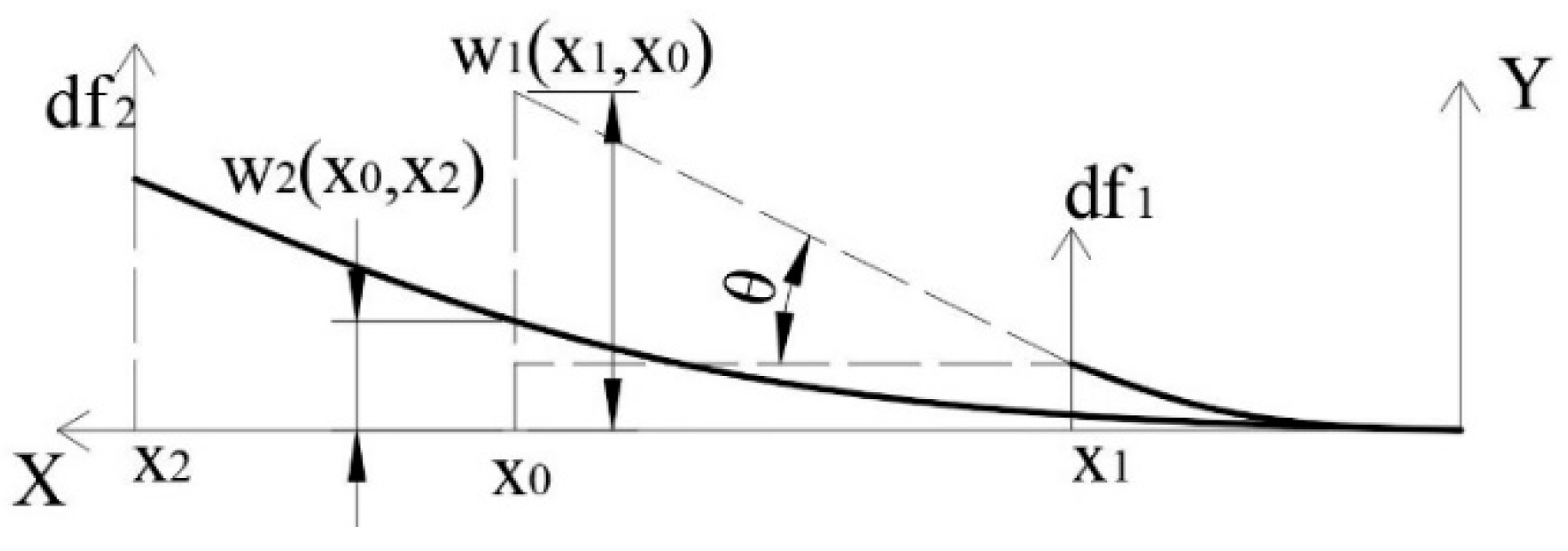
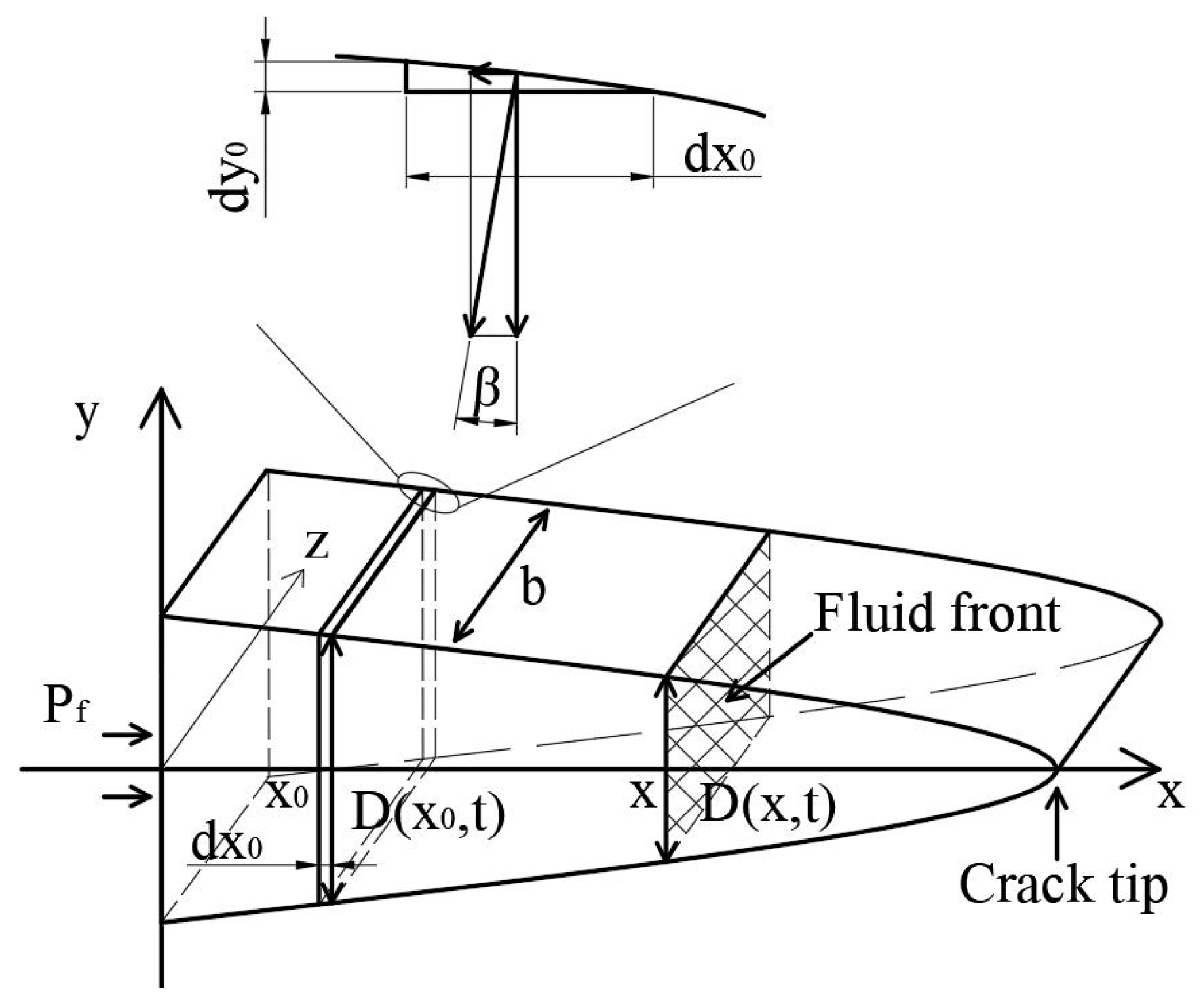
3. The Relationship Between the Crack Tip and the Fluid Front in Dynamic Hydraulic Fracture (HF)
3.1. Governing Equations
3.2. Energy Conservation in the Dynamic Process
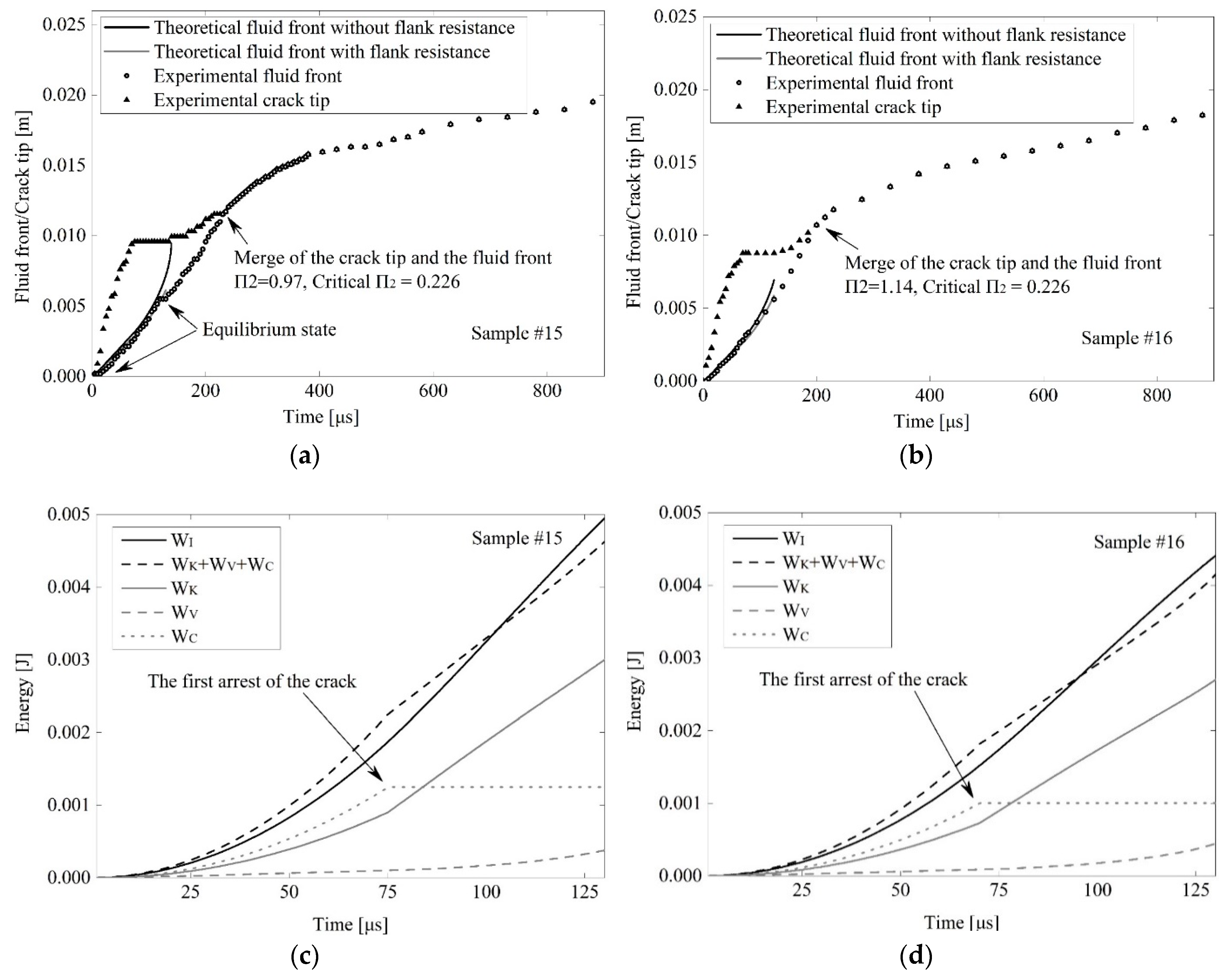
3.3. Comparison between Experimental and Theoretical Results
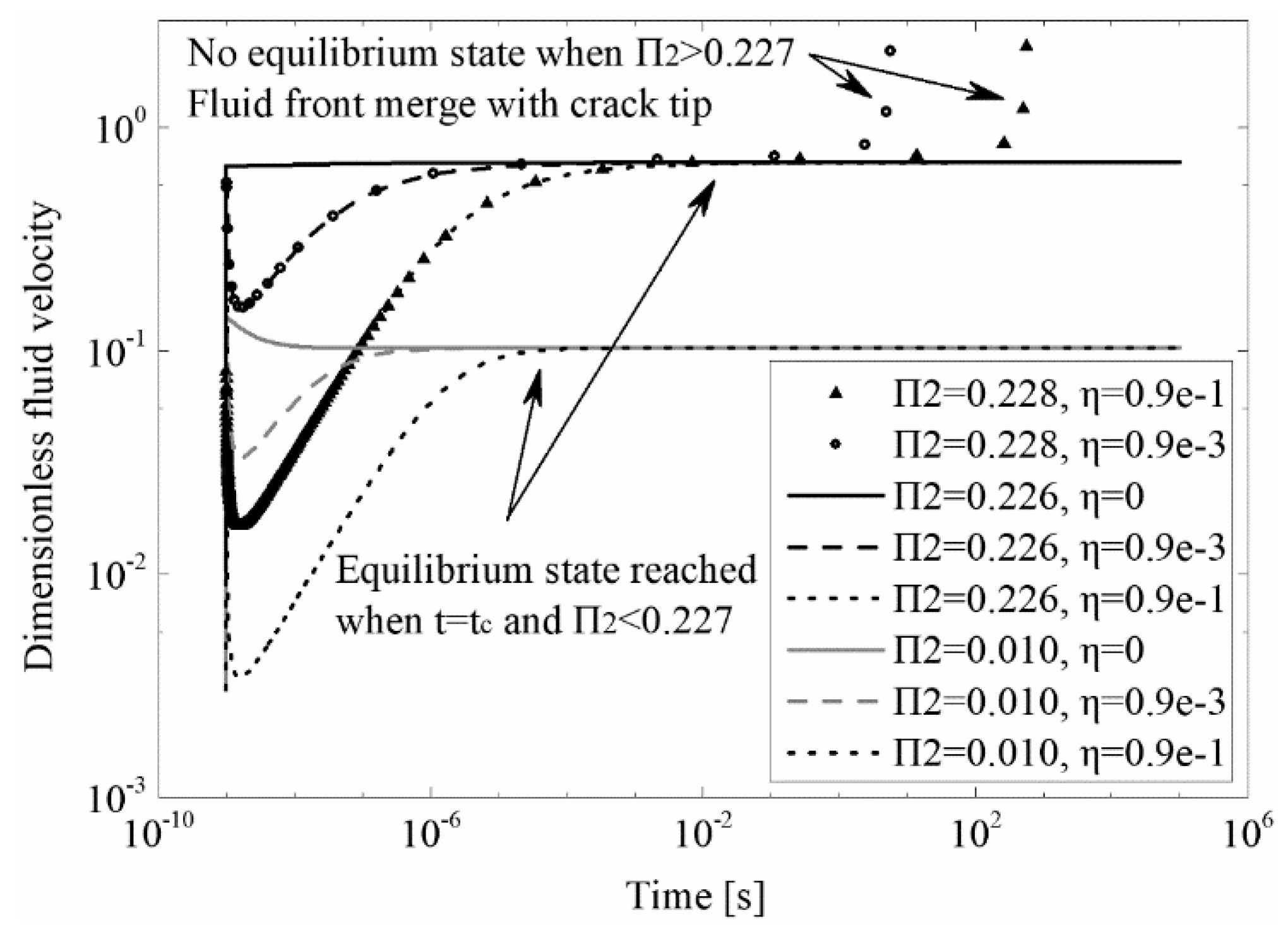
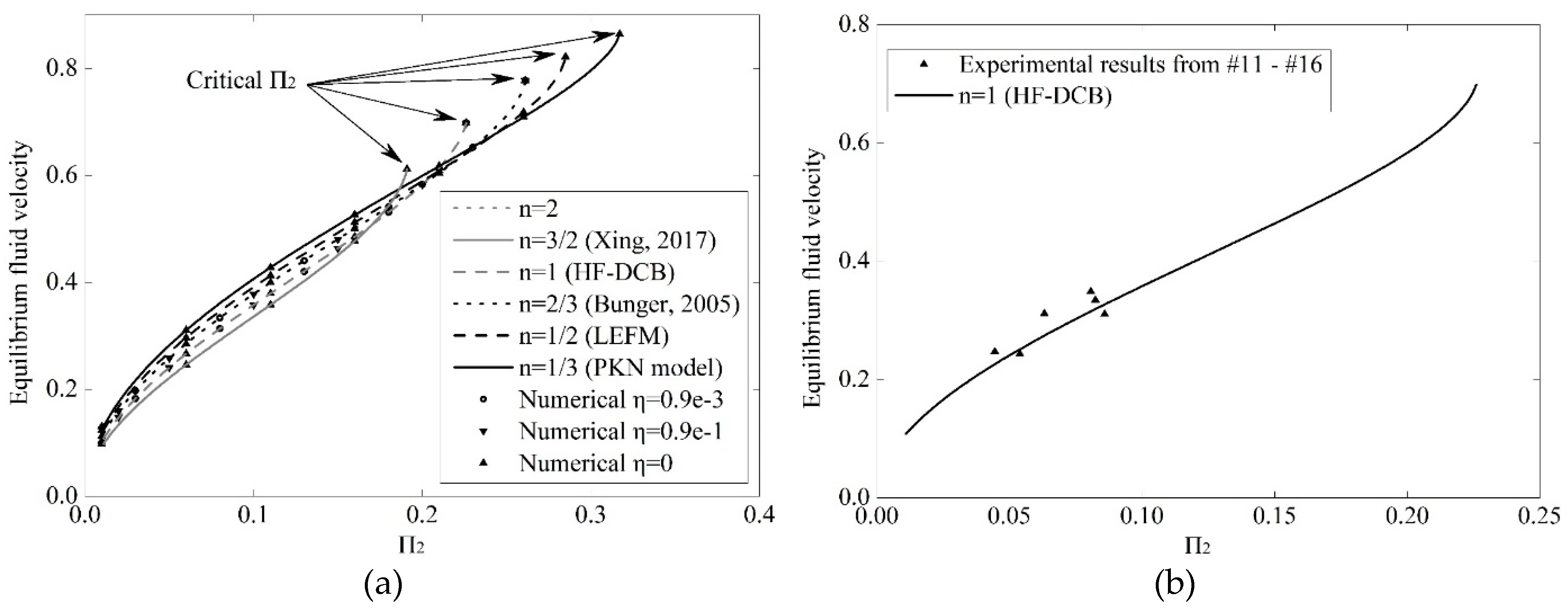
3.4. Will the Fluid Front Catch Up with a Propagating Crack?
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| , | Initial crack length, a non-dimensional value ( in this paper) characterizing the slope of the linear crack profile |
| A | A factor controlling the opening of the crack width in the general with a dimension of ( is the length dimension) |
| Thickness of the specimen | |
| , | The position of crack tip, the velocity of the crack tip |
| The crack opening width as a function of time and fluid front position x | |
| Elastic modulus of the specimen | |
| The drag force induced by viscosity | |
| The resistance induced by the slowly-varying flanks of the crack | |
| The total driving force | |
| The resistance from the fluid pressure | |
| , | Point loads in beam analysis |
| Energy release rate | |
| Stress intensity factor | |
| Half width of the specimen | |
| Length of the specimen | |
| The total momentum of the fluid | |
| Point load in beam analysis | |
| The dimensionless instantaneous velocity of the fluid front | |
| , | Input pressure, fracturing pressure |
| Equilibrium fluid velocity | |
| Stress distribution of the fracturing fluid | |
| Flow rate | |
| The distance to crack tip | |
| Time | |
| The time needed for the fluid to approach the equilibrium state | |
| Total strain energy stored in the specimen | |
| , | Velocity of the fluid front |
| Volume between the two beams | |
| The constant velocity of the crack tip | |
| , | The (rate of the) input energy |
| , | The (rate of the) kinetic energy of the fluid |
| , | The (rate of the) energy dissipated by viscosity |
| , | The (rate of the) work done by the fluid on the crack flanks |
| Beam deflection in double-cantilever-beam (DCB) specimen | |
| Beam deflection in hydraulic fracture in double-cantilever-beam (HF-DCB) specimen | |
| , , | The position of fluid front, the velocity of the fluid front, the acceleration of the fluid front, a point in the fluid |
| The dimensionless secant velocity of the fluid front | |
| Critical as a function of controlling the existence of equilibrium state | |
| Critical as a function of controlling the separation between the fluid front and the crack tip | |
| Density of the fluid | |
| , | Hydraulic pressure |
| Dynamic viscosity of the fracturing fluid (water with black ink): | |
| Beam deflection angle in beam analysis and a polar-coordinate parameter in Williams’ fitting | |
| Shear modulus of the specimen | |
| Poisson’s ratio | |
| Shear stress of the fluid |
Appendix A. Hydraulic Fracture in Double-Cantilever-Beam (HF-DCB) Solutions
References
- Germanovich, L.N.; Astakhov, D.K.; Mayerhofer, M.J.; Shlyapobersky, J.; Ring, L.M. Hydraulic fracture with multiple segments I. Observations and model formulation. Int. J. Rock Mech. Min. Sci. 1997, 34, 97.e1–97.e19. [Google Scholar] [CrossRef]
- Garagash, D.I.; Detournay, E.; Adachi, J.I. Multiscale tip asymptotics in hydraulic fracture with leak-off. J. Fluid Mech. 2011, 669, 260–297. [Google Scholar] [CrossRef]
- Sachau, T.; Bons, P.D.; Gomez-Rivas, E. Transport efficiency and dynamics of hydraulic fracture networks. Front. Phys. 2015, 3, 63. [Google Scholar] [CrossRef]
- Yew, C.H.; Weng, X. Mechanics of hydraulic fracturing. Gulf Prof. Publ. 2014, 23, 164–166. [Google Scholar]
- Cao, T.D.; Hussain, F.; Schrefler, B.A. Porous media fracturing dynamics: Stepwise crack advancement and fluid pressure oscillations. J. Mech. Phys. Solids 2018, 111, 113–133. [Google Scholar] [CrossRef]
- Abe, H.; Keer, L.M.; Mura, T. Growth rate of a penny-shaped crack in hydraulic fracturing of rocks, 2. J. Geophys. Res. 1976, 81, 6292–6298. [Google Scholar] [CrossRef]
- Garagash, D.; Detournay, E. The tip region of a fluid-driven fracture in an elastic medium. J. Appl. Mech. 2000, 67, 183–192. [Google Scholar] [CrossRef]
- Jeffrey, R.G. The combined effect of fluid lag and fracture toughness on hydraulic fracture propagation. In Low Permeability Reservoirs Symposium. Soc. Petroleum Eng. 1989. [Google Scholar] [CrossRef]
- Yew, C.H.; Liu, G.F. The fracture tip and KIc of a hydraulically induced fracture. Spe Prod. Eng. J. 1991, 171–177. [Google Scholar]
- Bunger, A.P.; Gordeliy, E.; Detournay, E. Comparison between laboratory experiments and coupled simulations of saucer-shaped hydraulic fractures in homogeneous brittle-elastic solids. J. Mech. Phys. Solids 2013, 61, 1636–1654. [Google Scholar] [CrossRef]
- Khoei, A.R.; Vahab, M.; Haghighat, E.; Moallemi, S. A mesh-independent finite element formulation for modeling crack growth in saturated porous media based on an enriched-FEM technique. Int. J. Fract. 2014, 188, 79–108. [Google Scholar] [CrossRef]
- Kostov, N.M.; Ning, J.; Gosavi, S.V.; Gupta, P.; Kulkarni, K.; Sanz, P.F. Dynamic hydraulic fracture modeling for wellbore integrity prediction in a porous medium. In Proceedings of the 2015 SIMULIA Community Conference, Berlin, Germany, 18–21 May 2015. [Google Scholar]
- Chang, H. Hydraulic Fracturing in Particulate Materials. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, Georgia, 2004. [Google Scholar]
- Frash, L.P. Laboratory-Scale Study of Hydraulic Fracturing in Heterogeneous Media for Enhanced Geothermal Systems and General Well Stimulation. Ph.D. Thesis, Colorado School of Mines, Golden, CO, USA, 2014. [Google Scholar]
- Lhomme, T.P.; De Pater, C.J.; Helfferich, P.H. Experimental study of hydraulic fracture initiation in Colton sandstone. In Proceedings of the SPE/ISRM Rock Mechanics Conference, Irving, TX, USA, 20–23 October 2002. [Google Scholar]
- Lhomme, T.P.Y. Initiation of Hydraulic Fractures in Natural Sandstones. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- Pizzocolo, F.; Huyghe, J.M.; Ito, K. Mode I crack propagation in hydrogels is step wise. Eng. Fract. Mech. 2013, 97, 72–79. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Han, K.; Hou, B.; Chen, M.; Guo, X.; Gao, J. Analysis of hydraulic fracture initiation and vertical propagation behavior in laminated shale formation. Fuel 2017, 206, 482–493. [Google Scholar] [CrossRef]
- Wu, R. Some Fundamental Mechanisms of Hydraulic Fracturing. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, Georgia, 2006. [Google Scholar]
- Wu, R.; Bunger, A.P.; Jeffrey, R.G.; Siebrits, E. A comparison of numerical and experimental results of hydraulic fracture growth into a zone of lower confining stress. In Proceedings of the 42nd US Rock Mechanics Symposium (USRMS), San Francisco, CA, USA, 29 June–2 July 2008. [Google Scholar]
- Zhang, G.Q.; Chen, M. Dynamic fracture propagation in hydraulic re-fracturing. J. Pet. Sci. Eng. 2010, 70, 266–272. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, M.; Jin, Y.; Zhang, G.Q. Analysis of fracture propagation behavior and fracture geometry using a tri-axial fracturing system in naturally fractured reservoirs. Int. J. Rock Mech. Min. Sci. 2008, 45, 1143–1152. [Google Scholar] [CrossRef]
- Fisher, M.K.; Warpinski, N.R. Hydraulic-fracture-height growth: Real data. Spe Prod. Oper. 2012, 27, 8–19. [Google Scholar] [CrossRef]
- Bosanquet, C.H. LV. on the flow of liquids into capillary tubes. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1923, 45, 525–531. [Google Scholar] [CrossRef]
- Xing, P.; Yoshioka, K.; Adachi, J.; El-Fayoumi, A.; Bunger, A.P. Laboratory measurement of tip and global behavior for zero-toughness hydraulic fractures with circular and blade-shaped (PKN) geometry. J. Mech. Phys. Solids 2017, 104, 172–186. [Google Scholar] [CrossRef]
- Bunger, A.P. Near-Surface Hydraulic Fracture. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2005. [Google Scholar]
- Bunger, A.P.; Detournay, E. Experimental validation of the tip asymptotics for a fluid-driven crack. J. Mech. Phys. Solids 2008, 56, 3101–3115. [Google Scholar] [CrossRef]
- Desroches, J.; Detournay, E.; Lenoach, B.; Papanastasiou, P.; Pearson, J.R.A.; Thiercelin, M.; Cheng, A. The crack tip region in hydraulic fracturing. Proc. R. Soc. Lond. A 1994, 447, 39–48. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. Soc. Pet. Eng. J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Perkins, T.K.; Kern, L.R. Widths of Hydraulic Fractures. J. Pet. Technol. 1961, 13, 937–949. [Google Scholar] [CrossRef]
- Kanninen, M.F. An augmented double cantilever beam model for studying crack propagation and arrest. Int. J. Fract. 1973, 9, 83–92. [Google Scholar]
- Fett, T.; Munz, D. Stress intensity factors and weight functions. Comput. Mech. 1997, 1, 112–115. [Google Scholar]
- Levenberg, K. A Method for the Solution of Certain Problems in Least-Squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D. An Algorithm for Least-squares Estimation of Nonlinear Parameters. Siam J. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Yates, J.R.; Zanganeh, M.; Tai, Y.H. Quantifying crack tip displacement fields with DIC. Eng. Fract. Mech. 2010, 77, 2063–2076. [Google Scholar] [CrossRef]
- Schechter, R.S.; Wade, W.H.; Wingrave, J.A. Sorption isotherm hysteresis and turbidity phenomena in mesoporous media. J. Colloid Interface Sci. 1977, 59, 7–23. [Google Scholar] [CrossRef]
- Ridgway, C.J.; Gane, P.A.; Schoelkopf, J. Effect of capillary element aspect ratio on the dynamic imbibition within porous networks. J. Colloid Interface Sci. 2002, 252, 373–382. [Google Scholar] [CrossRef]
- Garagash, D.I. Propagation of a plane-strain hydraulic fracture with a fluid lag: Early-time solution. Int. J. Solids Struct. 2006, 43, 5811–5835. [Google Scholar] [CrossRef] [Green Version]
- Hunsweck, M.J.; Shen, Y.; Lew, A.J. A finite element approach to the simulation of hydraulic fractures with lag. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 993–1015. [Google Scholar] [CrossRef]
- Vahab, M.; Khalili, N. Computational Algorithm for the Anticipation of the Fluid-Lag Zone in Hydraulic Fracturing Treatments. Int. J. Geomech. 2018, 18, 04018139. [Google Scholar] [CrossRef]
- Rubin, A.M. Propagation of magma-filled cracks. Annu. Rev. Earth Planet. Sci. 1995, 23, 287–336. [Google Scholar] [CrossRef]
- Xia, Y.; Jin, Y.; Chen, M.; Chen, K.P. An Enriched Approach for Modeling Multiscale Discrete-Fracture/Matrix Interaction for Unconventional-Reservoir Simulations. SPE J. 2018. [Google Scholar] [CrossRef]
- Zeng, C.; Deng, W. The Effect of Radial Cracking on the Integrity of Asperity Under Thermal Cooling Process. In Proceedings of the 52nd US Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2008. [Google Scholar]
- Dong, J.; Chen, M.; Jin, Y.; Hong, G.; Zaman, M.; Li, Y. Study on micro-scale properties of cohesive zone in shale. Int. J. Solids Struct. 2019, in press. [Google Scholar] [CrossRef]
- Li, Y.; Jia, D.; Rui, Z.; Peng, J.; Fu, C.; Zhang, J. Evaluation method of rock brittleness based on statistical constitutive relations for rock damage. J. Pet. Sci. Eng. 2017, 153, 123–132. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, L.; Yu, W.; Chen, Y. A Fully Three Dimensional Semianalytical Model for Shale Gas Reservoirs with Hydraulic Fractures. Energies 2018, 11, 436. [Google Scholar] [CrossRef]
- Li, Y.; Rui, Z.; Zhao, W.; Bo, Y.; Fu, C.; Chen, G.; Patil, S. Study on the mechanism of rupture and propagation of T-type fractures in coal fracturing. J. Nat. Gas Sci. Eng. 2018, 52, 379–389. [Google Scholar] [CrossRef]
- Li, Y.W.; Zhang, J.; Liu, Y. Effects of loading direction on failure load test results for Brazilian tests on coal rock. Rock Mech. Rock Eng. 2016, 49, 2173–2180. [Google Scholar] [CrossRef]
- Geng, Z.; Bonnelye, A.; Chen, M.; Jin, Y.; Dick, P.; David, C.; Fang, X.; Schubnel, A. Time and Temperature Dependent Creep in Tournemire Shale. J. Geophys. Res. Solid Earth 2018, 123, 9658–9675. [Google Scholar] [CrossRef]
- Geng, Z.; Bonnelye, A.; Chen, M.; Jin, Y.; Dick, P.; David, C.; Fang, X.; Schubnel, A. Elastic anisotropy reversal during brittle creep in shale. Geophys. Res. Lett. 2017, 44, 21. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, K.P.; Chen, M. An asymptotic solution for fluid production from an elliptical hydraulic fracture at early-times. Mech. Res. Commun. 2015, 63, 48–53. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Kwon, J.S.; Liu, S.; Valkó, P.P. Feedback control of proppant bank heights during hydraulic fracturing for enhanced productivity in shale formations. Aiche J. 2018, 64, 1638–1650. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Yang, S.; Kwon, J.S. Modeling of hydraulic fracturing and designing of online pumping schedules to achieve uniform proppant concentration in conventional oil reservoirs. Comput. Chem. Eng. 2018, 114, 306–317. [Google Scholar] [CrossRef]






| NO. | Crack Notch Width (mm) | Initial Crack Length (mm) | Fracturing Pressure (MPa) | Initiation Toughness * |
|---|---|---|---|---|
| #5 | Intrinsically sharp crack | 35 | 1.95 | 2.52 |
| #6 | Intrinsically sharp crack | 35 | 1.72 | 2.22 |
| #7 | Intrinsically sharp crack | 37 | 1.52 | 2.15 |
| #11 | 0.5 | 30 | 3.56 | 3.62 |
| #12 | 0.5 | 30 | 2.74 | 2.78 |
| #13 | 0.5 | 30 | 2.26 | 2.30 |
| #14 | 2.0 | 30 | 4.06 | 4.13 |
| #15 | 2.0 | 30 | 2.64 | 2.68 |
| #16 | 2.0 | 30 | 2.53 | 2.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Chen, M.; Li, Y.; Wang, S.; Zeng, C.; Zaman, M. Experimental and Theoretical Study on Dynamic Hydraulic Fracture. Energies 2019, 12, 397. https://doi.org/10.3390/en12030397
Dong J, Chen M, Li Y, Wang S, Zeng C, Zaman M. Experimental and Theoretical Study on Dynamic Hydraulic Fracture. Energies. 2019; 12(3):397. https://doi.org/10.3390/en12030397
Chicago/Turabian StyleDong, Jingnan, Mian Chen, Yuwei Li, Shiyong Wang, Chao Zeng, and Musharraf Zaman. 2019. "Experimental and Theoretical Study on Dynamic Hydraulic Fracture" Energies 12, no. 3: 397. https://doi.org/10.3390/en12030397




