Quantitative Study of the Geometrical and Hydraulic Characteristics of a Single Rock Fracture
Abstract
:1. Introduction
2. Methodology
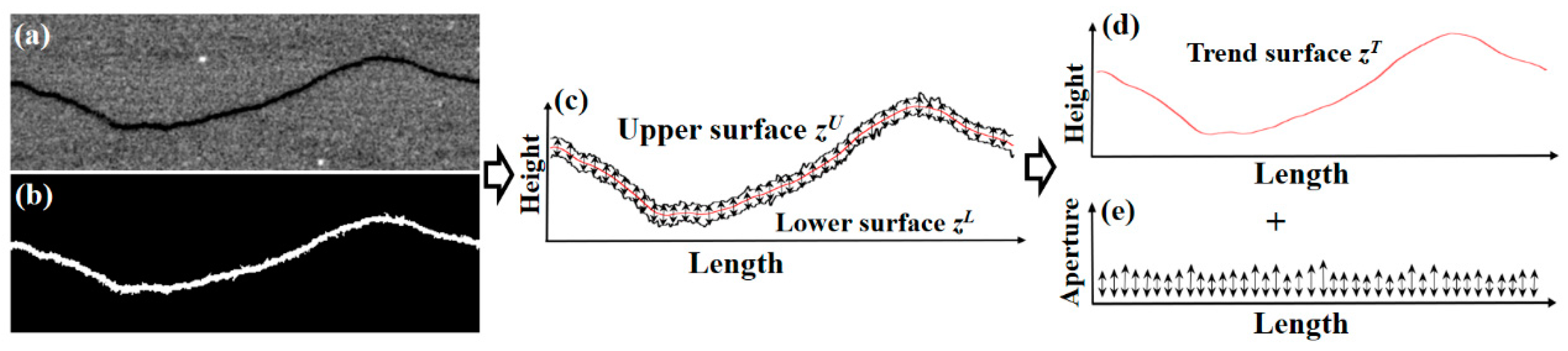
2.1. Fracture Morphology
2.1.1. Natural Fracture in CT Images
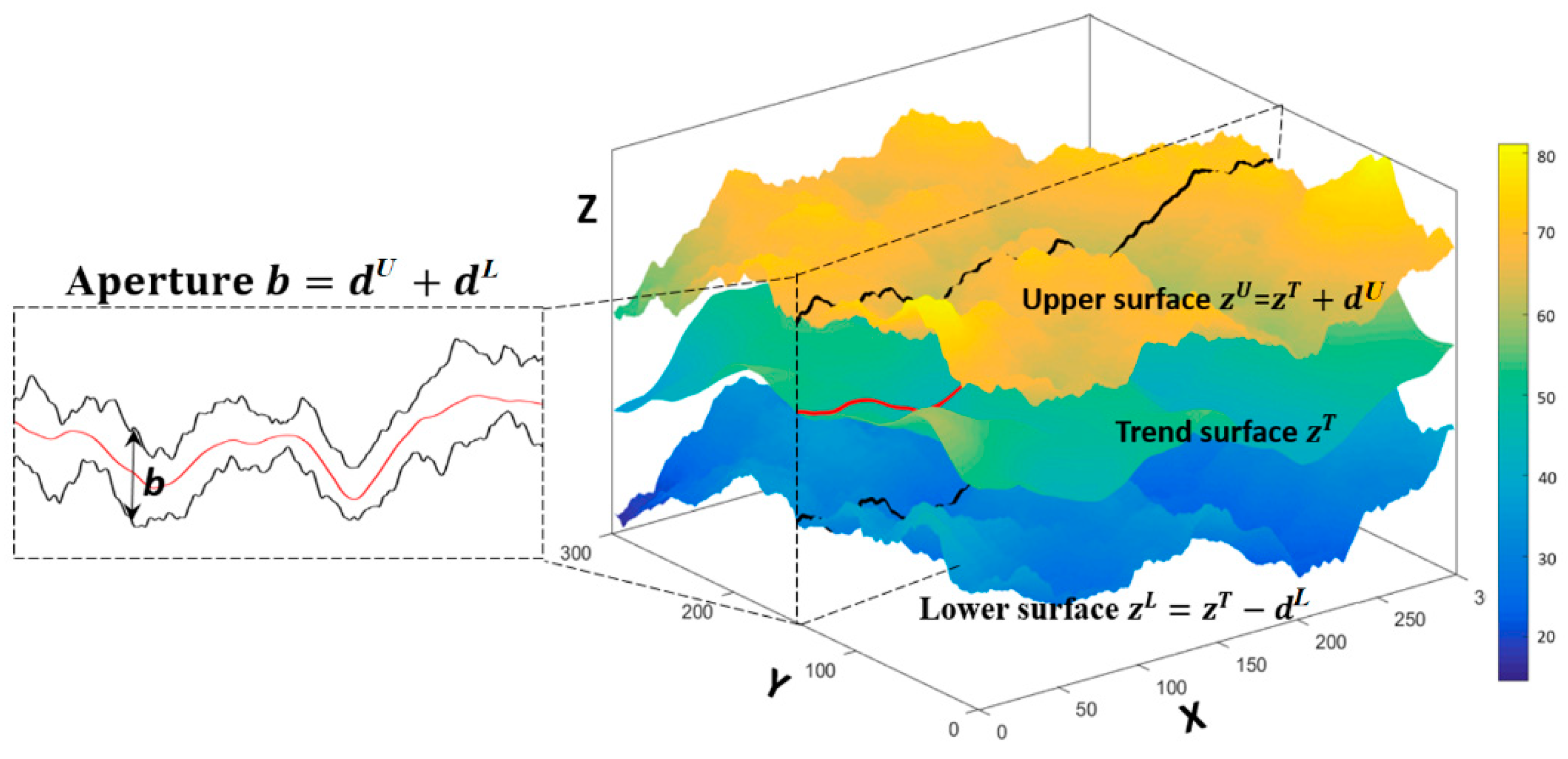
2.1.2. Fracture Characterization
2.2. Modified Cubic Law
2.3. Fracture Modelling
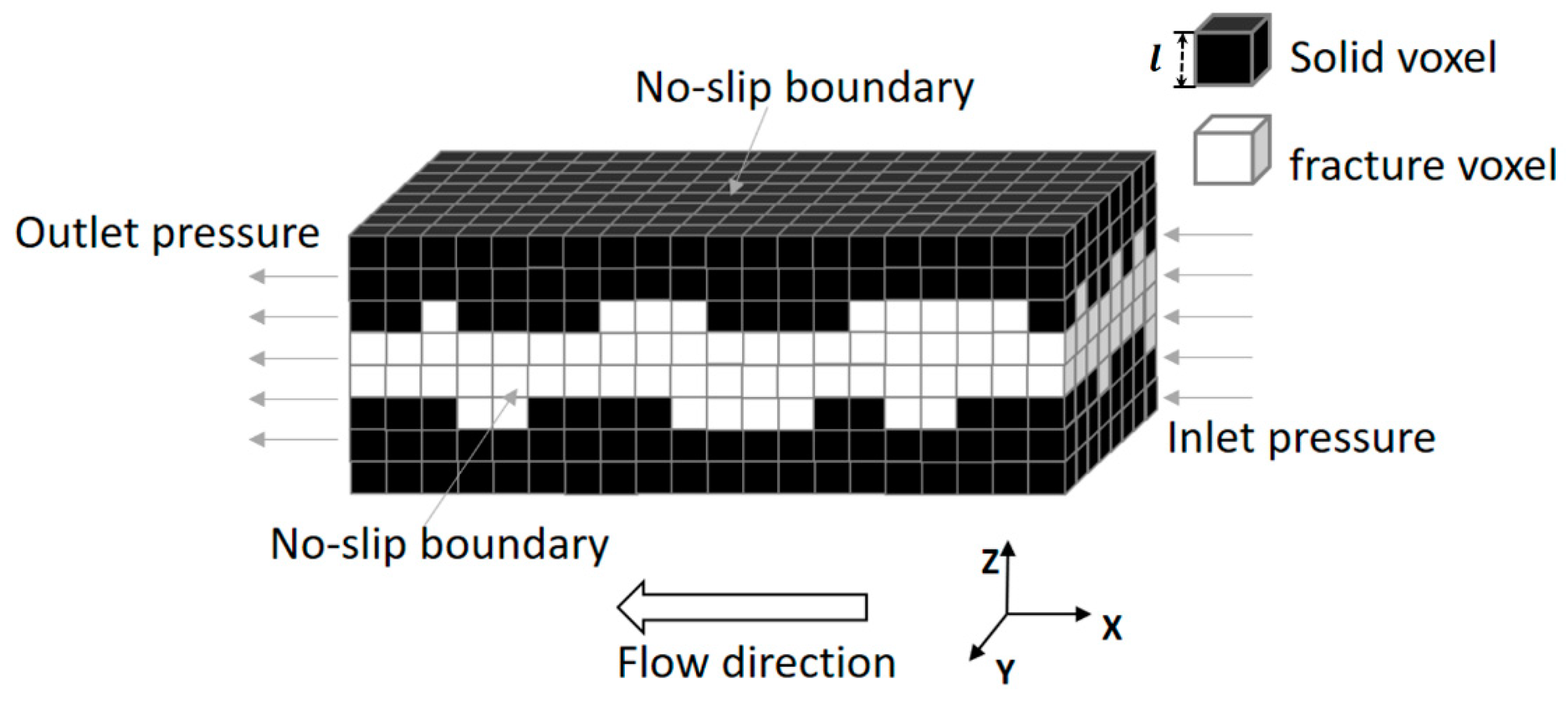
2.4. Fracture Permeability Calculation
3. Results and Discussion
3.1. Robustness of Fracture Modelling
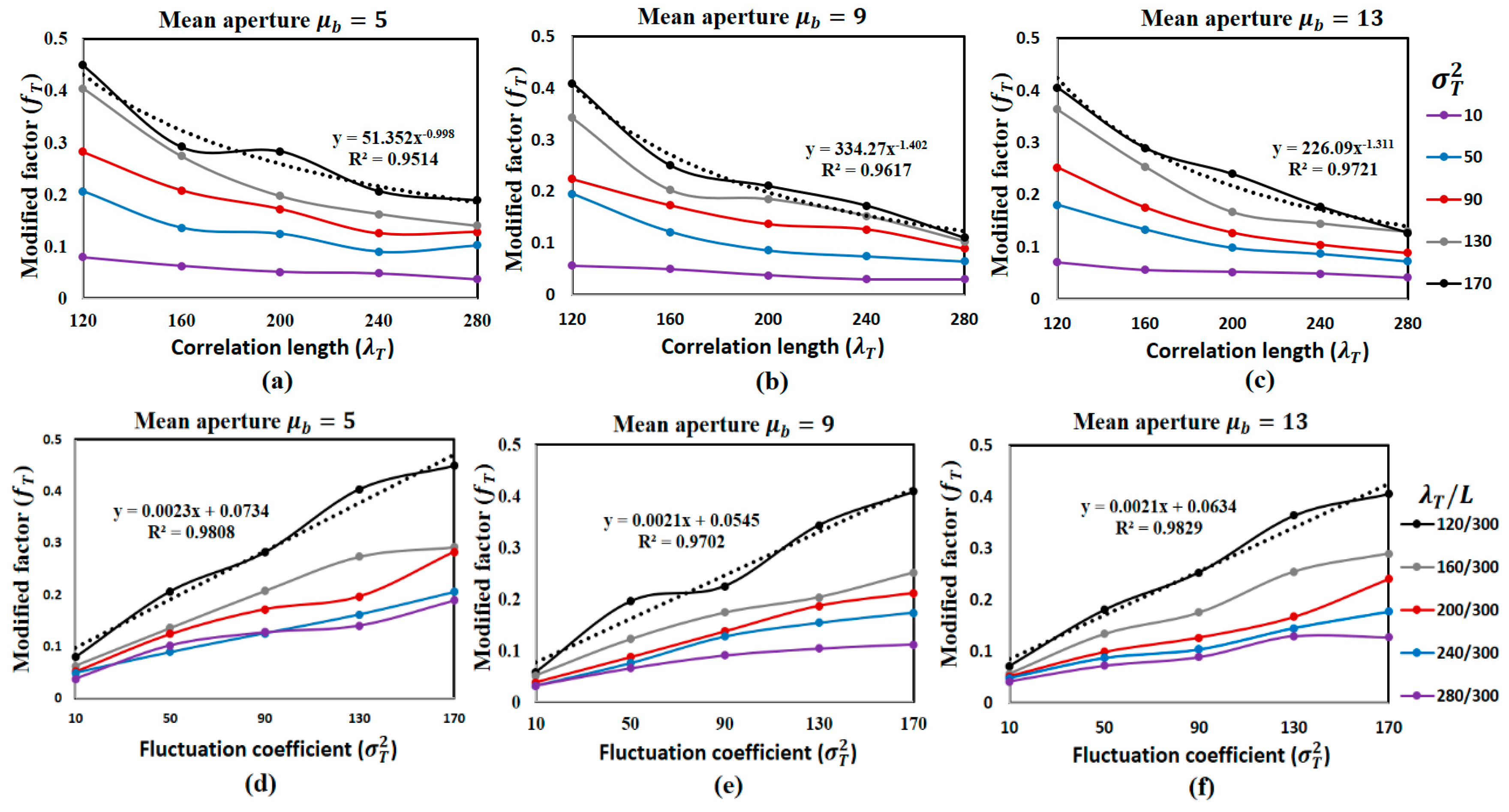
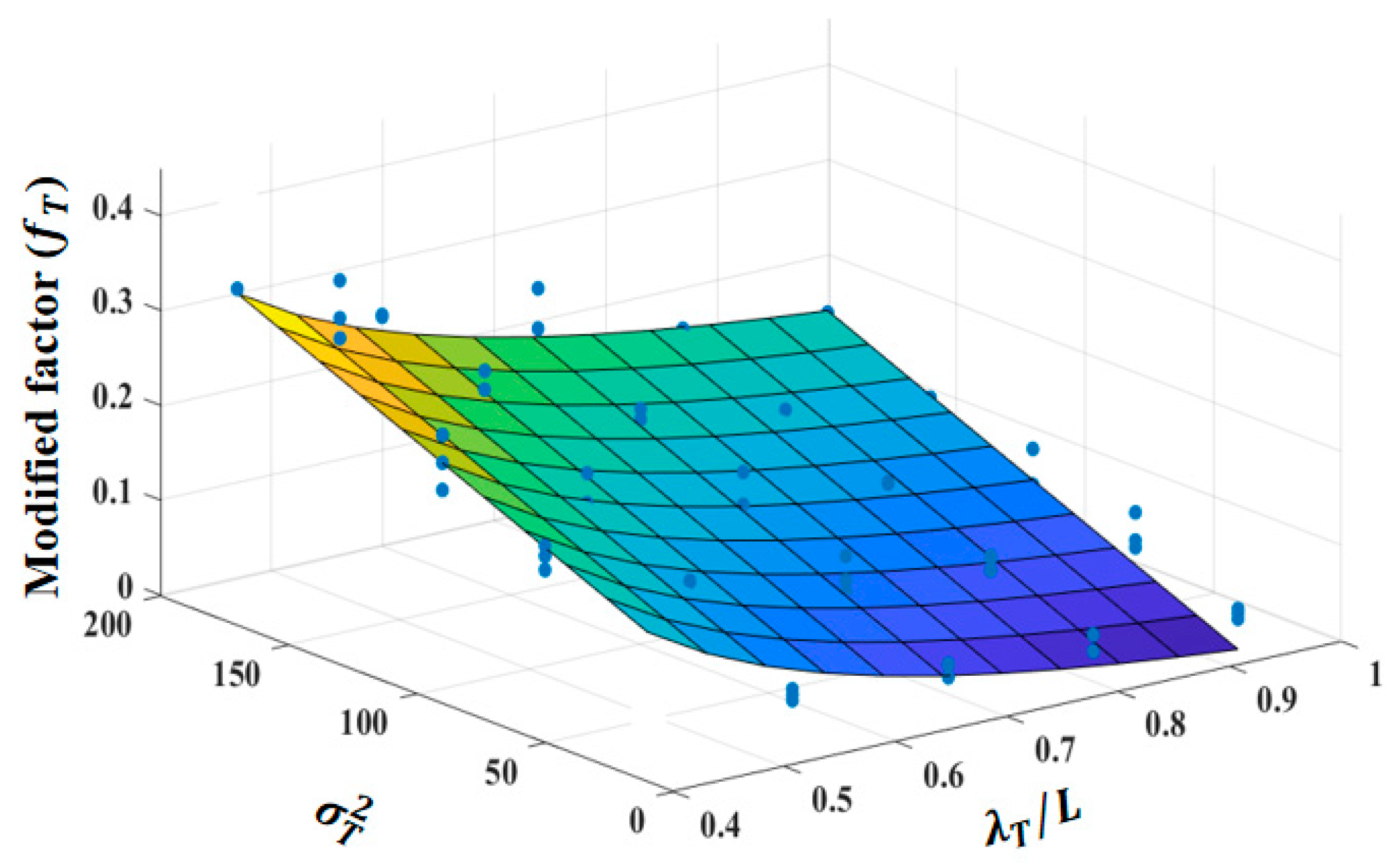
3.2. Influence of Fracture Trend Surface
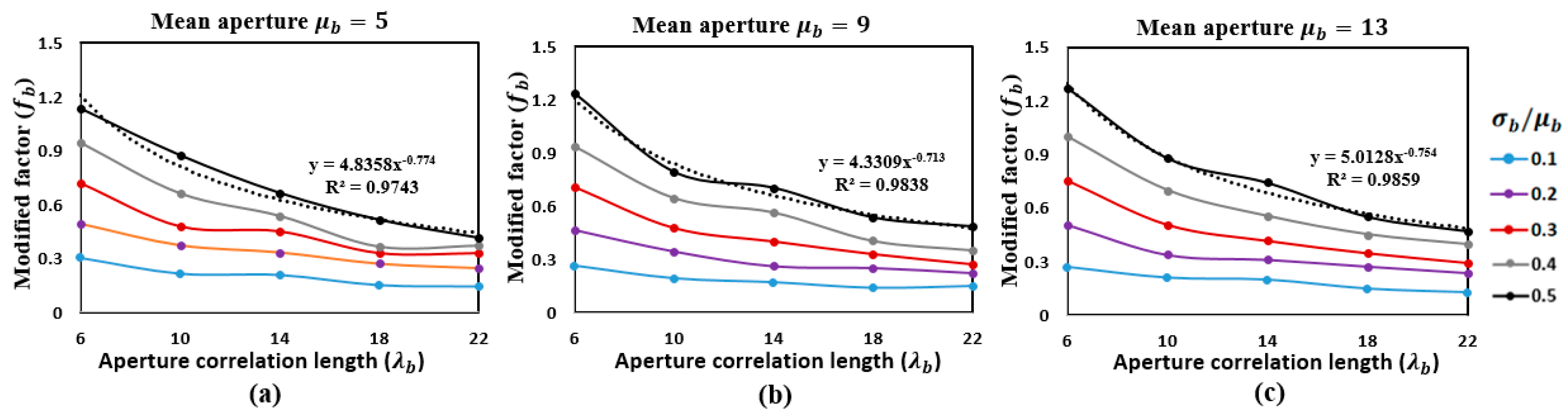
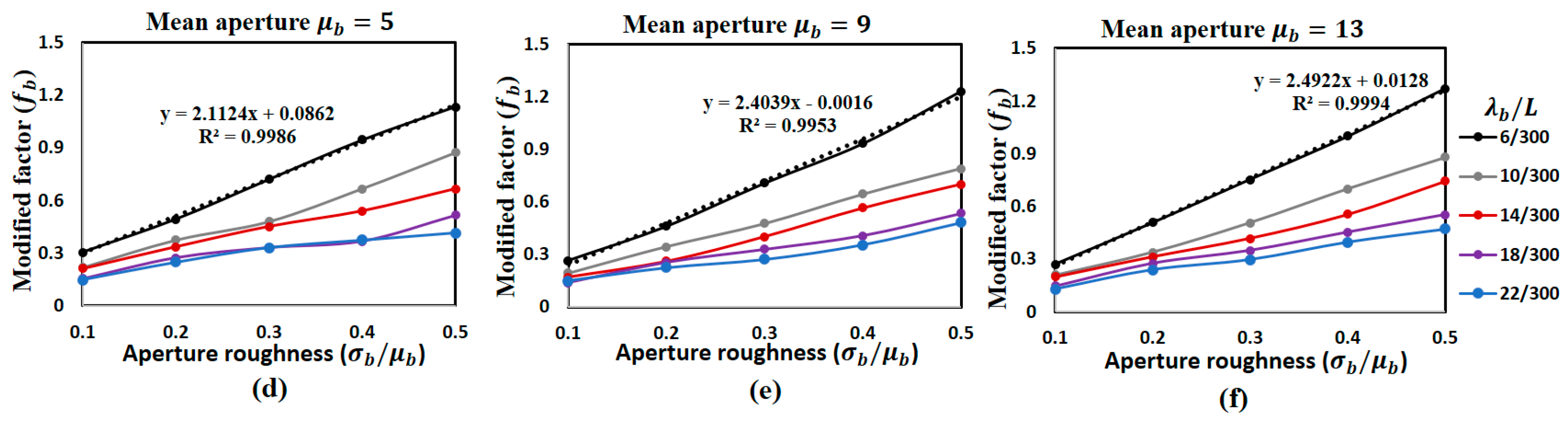
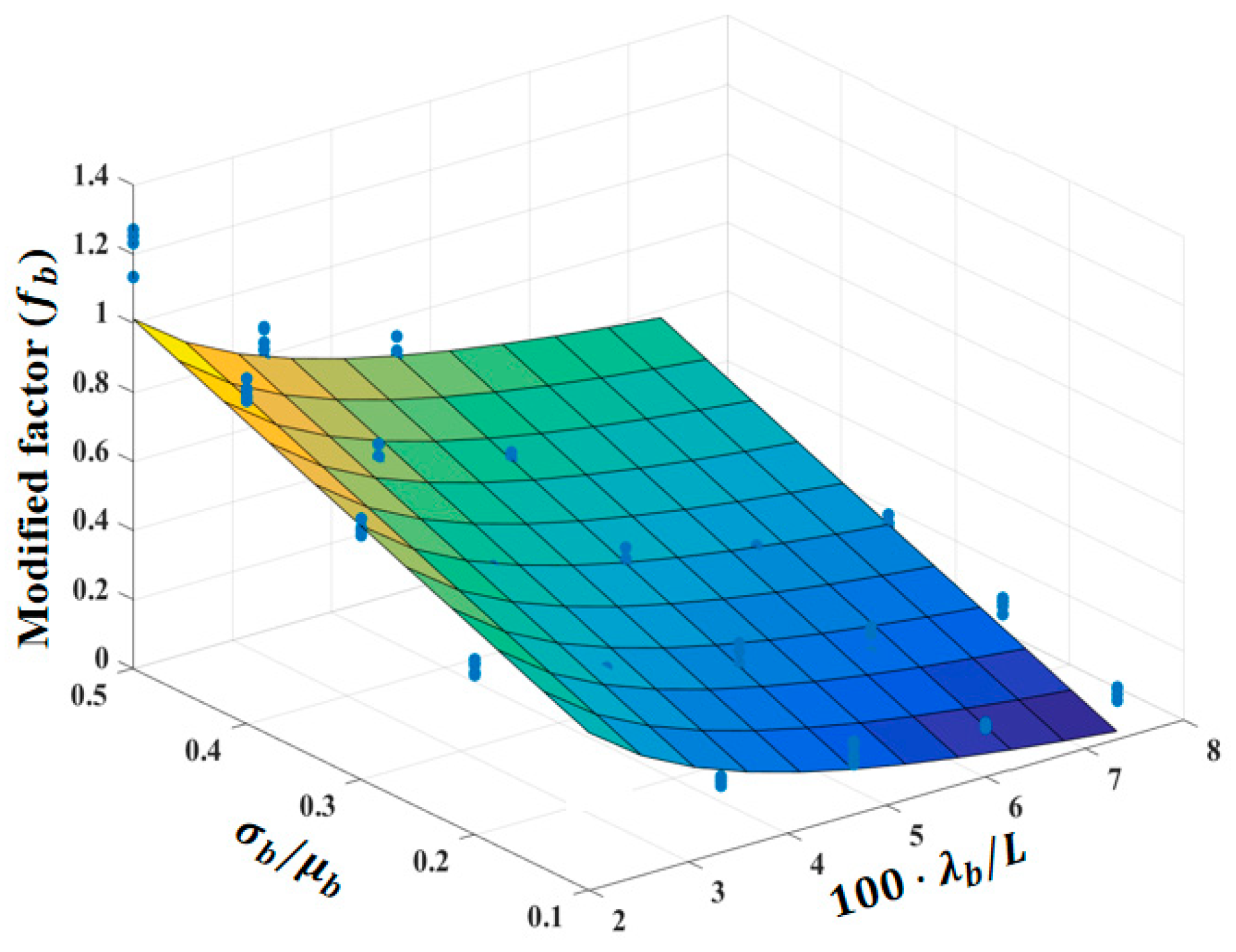
3.3. Influence of Fracture Aperture Variation
3.4. Accumulated Influence of Fracture Morphology
4. Verification with Natural Fractures
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Karpyn, Z.T.; Grader, A.S.; Halleck, P.M. Visualization of fluid occupancy in a rough fracture using micro-tomography. J. Colloid Interface Sci. 2007, 307, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Rutqvist, J.; Wu, Y.S.; Tsang, C.F.; Bodvarsson, G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Hu, R.; Liu, Q.; Xing, Y. Case study of heat transfer during artificial ground freezing with groundwater flow. Water 2018, 10, 1322. [Google Scholar] [CrossRef]
- Tsang, C.F.; Bernier, F.; Davies, C. Geohydromechanical processes in the excavation damaged zone in crystalline rock, rock salt, and indurated and plastic clays - in the context of radioactive waste disposal. Int. J. Rock Mech. Min. Sci. 2005, 42, 109–125. [Google Scholar] [CrossRef]
- Liu, S.; Sang, S.; Pan, Z.; Tian, Z.; Yang, H.; Hu, Q.; Sang, G.; Qiao, M.; Liu, H.; Jia, J. Study of characteristics and formation stages of macroscopic natural fractures in coal seam #3 for cbm development in the east qinnan block, southern quishui basin, china. J. Nat. Gas Sci. Eng. 2016, 34, 1321–1332. [Google Scholar] [CrossRef]
- Wang, L.; Cardenas, M.B. Development of an empirical model relating permeability and specific stiffness for rough fractures from numerical deformation experiments. J. Geophys. Res. Solid Earth 2016, 121, 4977–4989. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Liang, W.; Lian, H.; Yang, J.; Vinh Phu, N. Experimental study on the effect of fracture geometric characteristics on the permeability in deformable rough-walled fractures. Int. J. Rock Mech. Min. Sci. 2017, 98, 121–140. [Google Scholar] [CrossRef]
- Mourzenko, V.V.; Thovert, J.F.; Adler, P.M. Conductivity and transmissivity of a single fracture. Transp. Porous Media 2018, 123, 235–256. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Yao, J.; Zhang, L.; Ma, J.; Hejazi, S.H.; Luquot, L.; Ngarta, T.D. Flow simulation of artificially induced microfractures using digital rock and lattice boltzmann methods. Energies 2018, 11, 2145. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Abdideh, M. Application of wavelet transform to detect fractured zones using conventional well logs data (case study: Southwest of iran). Int. J. Pet. Eng. 2016, 2, 125–139. [Google Scholar] [CrossRef]
- Taherdangkoo, R.; Abdideh, M. Fracture density estimation from well logs data using regression analysis: Validation based on image logs (case study: South west iran). Int. J. Pet. Eng. 2016, 2, 289–301. [Google Scholar] [CrossRef]
- Lomize, G. Flow in Fractured Rocks; Gosenergoizdat: Moscow, Russia, 1951; Volume 127, p. 496. (In Russian) [Google Scholar]
- Wang, L.; Cardenas, M.B.; Slottke, D.T.; Ketcham, R.A.; Sharp, J.M., Jr. Modification of the local cubic law of fracture flow for weak inertia, tortuosity, and roughness. Water Resour. Res. 2015, 51, 2064–2080. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, C.; Dowd, P. A modified cubic law for single-phase saturated laminar flow in rough rock fractures. Int. J. Rock Mech. Min. Sci. 2018, 103, 107–115. [Google Scholar] [CrossRef]
- Moreno, L.; Tsang, Y.; Tsang, C.; Hale, F.; Neretnieks, I. Flow and tracer transport in a single fracture: A stochastic model and its relation to some field observations. Water Resour. Res. 1988, 24, 2033–2048. [Google Scholar] [CrossRef]
- Pyrak-Nolte, L.J.; Cook, N.G.; Nolte, D.D. Fluid percolation through single fractures. Geophys. Res. Lett. 1988, 15, 1247–1250. [Google Scholar] [CrossRef]
- Tsang, Y.; Tsang, C. Flow channeling in a single fracture as a two-dimensional strongly heterogeneous permeable medium. Water Resour. Res. 1989, 25, 2076–2080. [Google Scholar] [CrossRef]
- Murphy, J.R.; Thomson, N.R. 2-phase flow in a variable aperture fracture. Water Resour. Res. 1993, 29, 3453–3476. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Yeo, I.W. Fluid flow in rock fractures: From the navier-stokes equations to the cubic law. Geophys. Monogr. Am. Geophys. Union 2000, 122, 213–224. [Google Scholar] [CrossRef]
- Brush, D.J.; Thomson, N.R. Fluid flow in synthetic rough-walled fractures: Navier-stokes, stokes, and local cubic law simulations. Water Resour. Res. 2003, 39. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2002WR001346 (accessed on 18 July 2019).
- Tahmasebi, P.; Kamrava, S. A pore-scale mathematical modeling of fluid-particle interactions: Thermo-hydro-mechanical coupling. Int. J. Greenh. Gas Control 2019, 83, 245–255. [Google Scholar] [CrossRef]
- Zhang, X.; Tahmasebi, P. Effects of grain size on deformation in porous media. Transp. Porous Media 2019, 129, 1–21. [Google Scholar] [CrossRef]
- Zhang, Y.; Lebedev, M.; Al-Yaseri, A.; Yu, H.; Nwidee, L.N.; Sarmadivaleh, M.; Barifcani, A.; Iglauer, S. Morptiological evaluation of heterogeneous oolitic limestone under pressure and fluid flow using X-ray microtomography. J. Appl. Geophys. 2018, 150, 172–181. [Google Scholar] [CrossRef]
- Wildenschild, D.; Sheppard, A.P. X-ray imaging and analysis techniques for quantifying pore-scale structure and processes in subsurface porous medium systems. Adv. Water Resour. 2013, 51, 217–246. [Google Scholar] [CrossRef]
- Wu, Y.; Tahmasebi, P.; Lin, C.; Zahid, M.A.; Dong, C.; Golab, A.N.; Ren, L. A comprehensive study on geometric, topological and fractal characterizations of pore systems in low-permeability reservoirs based on sem, micp, nmr, and x-ray ct experiments. Mar. Pet. Geol. 2019, 103, 12–28. [Google Scholar] [CrossRef]
- Qiu, P.; Hu, R.; Hu, L.; Liu, Q.; Xing, Y.; Yang, H.; Qi, J.; Ptak, T. A numerical study on travel time based hydraulic tomography using the sirt algorithm with cimmino iteration. Water 2019, 11, 909. [Google Scholar] [CrossRef]
- Wennberg, O.P.; Rennan, L.; Basquet, R. Computed tomography scan imaging of natural open fractures in a porous rock; geometry and fluid flow. Geophys. Prospect. 2009, 57, 239–249. [Google Scholar] [CrossRef]
- Jing, Y.; Armstrong, R.T.; Ramandi, H.L.; Mostaghimi, P. Coal cleat reconstruction using micro-computed tomography imaging. Fuel 2016, 181, 286–299. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Mousavi, S.A.; Bozarjomehri, R.B.; Bakhtiari, F. Gas-liquid membrane contactors: Modeling study of non-uniform membrane wetting. J. Membr. Sci. 2018, 555, 463–472. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Piri, M. Pore-scale network modeling of three-phase flow based on thermodynamically consistent threshold capillary pressures. I. Cusp formation and collapse. Transp. Porous Media 2017, 116, 1093–1137. [Google Scholar] [CrossRef]
- Bakke, S.; Øren, P.-E. 3-d pore-scale modelling of sandstones and flow simulations in the pore networks. SPE J. 1997, 2, 136–149. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Tahmasebi, P.; Kamrava, S. Rapid multiscale modeling of flow in porous media. Phys. Rev. E 2018, 98, 052901. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Tahmasebi, P.; Lin, C.; Munawar, M.J.; Cnudde, V. Effects of micropores on geometric, topological and transport properties of pore systems for low-permeability porous media. J. Hydrol. 2019, 575, 327–342. [Google Scholar] [CrossRef]
- Fagbemi, S.; Tahmasebi, P.; Piri, M. Pore-scale modeling of multiphase flow through porous media under triaxial stress. Adv. Water Resour. 2018, 122, 206–216. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P.; Ramandi, H.L.; Mostaghimi, P.; Saadatfar, M. Stochastic modeling of coal fracture network by direct use of micro-computed tomography images. Int. J. Coal Geol. 2017, 179, 153–163. [Google Scholar] [CrossRef] [Green Version]
- Zaretskiy, Y.; Geiger, S.; Sorbie, K.; Foerster, M. Efficient flow and transport simulations in reconstructed 3d pore geometries. Adv. Water Resour. 2010, 33, 1508–1516. [Google Scholar] [CrossRef]
- Shabro, V.; Torres-Verdin, C.; Javadpour, F.; Sepehrnoori, K. Finite-difference approximation for fluid-flow simulation and calculation of permeability in porous media. Transp. Porous Media 2012, 94, 775–793. [Google Scholar] [CrossRef]
- Bijeljic, B.; Mostaghimi, P.; Blunt, M.J. Insights into non- fickian solute transport in carbonates. Water Resour. Res. 2013, 49, 2714–2728. [Google Scholar] [CrossRef]
- Guo, Z.L.; Shi, B.C.; Wang, N.C. Lattice bgk model for incompressible navier-stokes equation. J. Comput. Phys. 2000, 165, 288–306. [Google Scholar] [CrossRef]
- Succi, S.; Foti, E.; Higuera, F. Three-dimensional flows in complex geometries with the lattice boltzmann method. EPL 1989, 10, 433. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Wang, Z.M.; Ye, J.P.; Sun, H.S.; Gu, J.Y. Lattice boltzmann simulation of gas flow and permeability prediction in coal fracture networks. J. Nat. Gas Sci. Eng. 2018, 53, 153–162. [Google Scholar] [CrossRef]
- Eker, E.; Akin, S. Lattice boltzmann simulation of fluid flow in synthetic fractures. Transp. Porous Media 2006, 65, 363–384. [Google Scholar] [CrossRef]
- Dong, H.; Sun, J.; Cui, L.; Song, L.; Yan, W.; Li, Y.; Lin, Z.; Fang, H. Study on the effects of natural gas hydrate cementation mode on the physical properties of rocks. J. Geophys. Eng. 2018, 15, 1399–1406. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Vega, S.; Tao, G. Analysis of heterogeneity and permeability anisotropy in carbonate rock samples using digital rock physics. J. Pet. Sci. Eng. 2017, 156, 419–429. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Prentice Hall: New Jersey, NJ, USA, 2002. [Google Scholar]
- Jiang, Z.; van Dijke, M.I.J.; Geiger, S.; Ma, J.; Couples, G.D.; Li, X. Pore network extraction for fractured porous media. Adv. Water Resour. 2017, 107, 280–289. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Ma, J.; Wang, X. A pore-skeleton-based method for calculating permeability and capillary pressure. Transp. Porous Media 2018, 124, 767–786. [Google Scholar] [CrossRef]
- Xu, J.D.; Lin, C.; Jacobi, R.D. Characterizing fracture spatial patterns by using semivariograms. Acta Geol. Sin. Engl. Ed. 2002, 76, 89–99. [Google Scholar] [CrossRef]
- Renshaw, C.E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures. J. Geophys. Res. Solid Earth 1995, 100, 24629–24636. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Couples, G.G. A stochastic method for modelling the geometry of a single fracture: Spatially controlled distributions of aperture, roughness and anisotropy. Transp. Porous Media 2019, 128, 797–819. [Google Scholar] [CrossRef]
- Latt, J. Palabos, Parallel Lattice Boltzmann Solver; FlowKit: Lausanne, Switzerland, 2009. [Google Scholar]
- Van Golf-Racht, T.D. Fundamentals of Fractured Reservoir Engineering; Elsevier: New York, NY, USA, 1982. [Google Scholar]








| Samples | μb (μm) | σb/μb | λb (μm) | σT2 | λT (μm) | KLB (mD) | Kcl (mD) | Kmcl (mD) | εcl (%) | εmcl (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| SA1A | 5.03 | 0.26 | 6 | 160.75 | 150 | 1110.49 | 2108.41 | 982.76 | 89.86 | −11.5 |
| SA1B | 5.28 | 0.19 | 6 | 90.60 | 150 | 1443.05 | 2323.20 | 1232.62 | 60.99 | −14.58 |
| SA1C | 5.52 | 0.25 | 10 | 231.2 | 200 | 1157.60 | 2539.20 | 1297.74 | 119.35 | 12.11 |
| SA2 | 10.45 | 0.20 | 20 | 14.40 | 150 | 6166.89 | 9100.21 | 6372.08 | 47.57 | 3.33 |
| SA3 | 11.75 | 0.16 | 10 | 161.14 | 200 | 6705.99 | 11,505.21 | 7434.62 | 71.57 | 10.87 |
| SA4 | 6.74 | 0.18 | 10 | 45.99 | 150 | 2665.43 | 3785.63 | 2389.23 | 42.03 | −10.36 |
| SA5 | 11.45 | 0.14 | 10 | 18.6 | 150 | 8102.42 | 10,925.21 | 8551.35 | 34.84 | 5.54 |
| SB1 | 5.25 | 0.18 | 7 | 94.25 | 150 | 1468.85 | 2296.88 | 1271.76 | 56.37 | −13.4 |
| SB2 | 10.81 | 0.30 | 20 | 70.5 | 140 | 5689.30 | 9738.01 | 5599.80 | 71.16 | −1.57 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Jiang, Z.; Min, C. Quantitative Study of the Geometrical and Hydraulic Characteristics of a Single Rock Fracture. Energies 2019, 12, 2796. https://doi.org/10.3390/en12142796
Li X, Jiang Z, Min C. Quantitative Study of the Geometrical and Hydraulic Characteristics of a Single Rock Fracture. Energies. 2019; 12(14):2796. https://doi.org/10.3390/en12142796
Chicago/Turabian StyleLi, Xinling, Zeyun Jiang, and Chao Min. 2019. "Quantitative Study of the Geometrical and Hydraulic Characteristics of a Single Rock Fracture" Energies 12, no. 14: 2796. https://doi.org/10.3390/en12142796





