Admittance Reshaping Control Methods to Mitigate the Interactions between Inverters and Grid

Abstract

With the increasing impedance coupling between inverters and grid caused by the phase-locked loop (PLL), traditional three-phase inverters suffer from the harmonic distortion or instability problems under weak grid conditions. Therefore, the admittance reshaping control methods are proposed to mitigate the interactions between inverters and grid. Firstly, a dynamics model of traditional inverter output admittance including main circuit and PLL is developed in the direct-quadrature (dq) frame. And the qq channel impedance of the inverter presents as a negative incremental resistance with the PLL effect. Secondly, two admittance reshaping control methods are proposed to improve the system damping. The first reshaping technique uses the feedforward point of common coupling (PCC) voltage to modify the inverter output admittance. The second reshaping technique adopts the active damping controller to reconstruct the PLL equivalent admittance. The proposed control methods not only increase the system phase margin, but also ensure the system dynamic response speed. And the total harmonic distortion of steady-state grid-connected current is reduced to less than 2%. Furthermore, a specific design method of control parameters is depicted. Finally, experimental results are provided to prove the validity of the proposed control methods.

1. Introduction

With the increasing prevalence of renewable energy systems, the systems are connected to the utility grid by multiple transformers and long transmission lines because of the distributed locations of renewable energy generations [1,2]. Therefore, the utility grid shows the feature of the weak grid where the grid impedance cannot be ignored [3]. Grid-connected inverters are the important part, which transfer renewable energy to the weak grid [4,5]. Under the weak grid condition, the impedance coupling between inverters and grid may cause harmonic distortion or instability problems [6,7].

There are two impedance-based analysis methods to analyze the interaction stability between inverters and weak grid [8,9,10,11]. On the one hand, References [8,9] proposed the sequence impedance model by the harmonic linearization modeling method, which is represented by a diagonal matrix, including the positive sequence and negative sequence components. On the other hand, References [10,11] developed the dq impedance model by transforming three-phase variables into a rotating dq reference frame. The phase-locked loop (PLL) effect can be explained through linearizing the transitions between the system and the control dq frame. By the generalized Nyquist criterion, dq impedances can be utilized to analyze system stability considering the PLL effect. The following conclusions can be obtained from the above references: The negative impact of PLL on system stability is caused by the range of negative incremental resistance. It will increase the impedance coupling between inverters and grid, which reduces the system phase margin or leads to system instability.

The impedance reshaping techniques were used to mitigate the interactions between inverters and grid. References [12,13] presented the virtual impedance or active damping methods under the weak grid condition, which changes the structure of inverter output impedance or the output filter parameters. However, only the current control loop of the inverter is considered. Reference [14] proposed a special regulator replacement method with consideration of the PLL, which can effectively improve system stability by adjusting the PLL bandwidth. However, if the PLL bandwidth is small, it may weaken the dynamic performance of the system when the load changes abruptly [15]. Reference [16] used multiple resonance compensators to enhance the amplitude of the inverter output impedance at specific harmonic frequency. However, the process of selecting control parameters is unknown in this control method [17].

Motivated by the above limitations, admittance reshaping control methods are proposed in this paper. The strong points of the proposed methods are given below: On the premise of ensuring the system dynamic response speed, it can increase the system phase margin. Furthermore, a specific design method of control parameters is depicted. This paper is organized as follow: Section 2 presents the admittance model and a stability analysis of the traditional control method; Section 3 proposes two admittance reshaping control methods, designs the control parameters and comparatively analyzes system stability; Section 4 provides experimental results to prove the validity of the proposed control methods; Finally, the conclusions are summarized in Section 5.

2. Admittance Model of Three-Phase Grid-Connected System

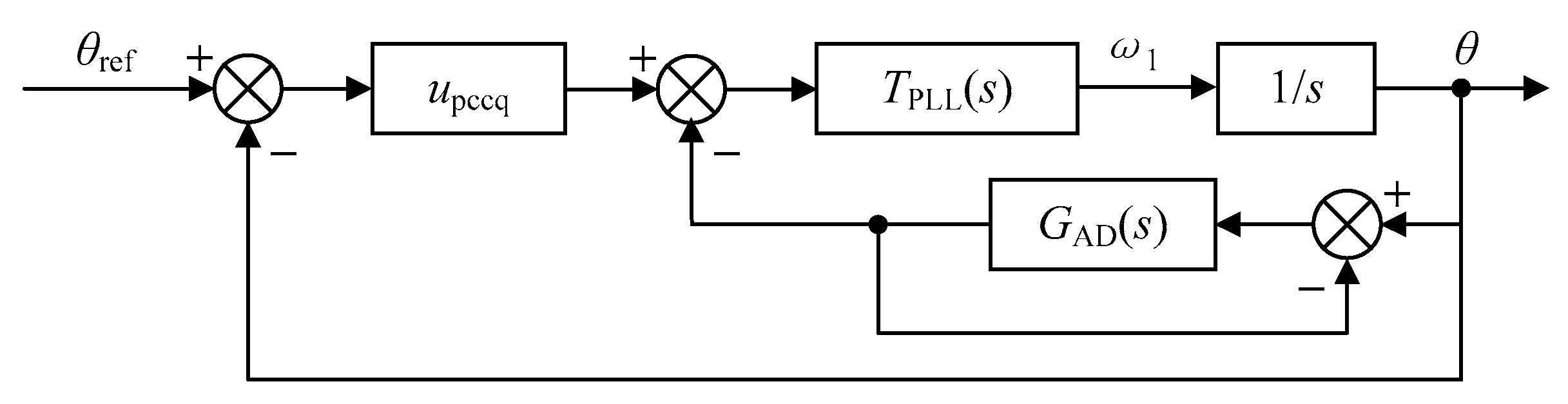
2.1. System Description

Figure 1 presents the system structure, which includes the inverter subsystem and the grid subsystem. U_dc is the DC-side voltage. u_inv, u_C1 and u_pcc are the inverter output voltage, filter capacitor voltage and point of common coupling (PCC) voltage. u_g is the grid voltage. Z_g is the grid impedance. The inductance-capacitance-inductance (LCL) filter is constituted by the inverter-side inductor L₁, grid-side inductor L₂ and filter capacitor C₁. R_L1 and R_L2 are parasitic resistances of L₁ and L₂. i_L1 is the inverter-side inductor current. i_g is the grid-connected current. i_C1 is the filter capacitor current.

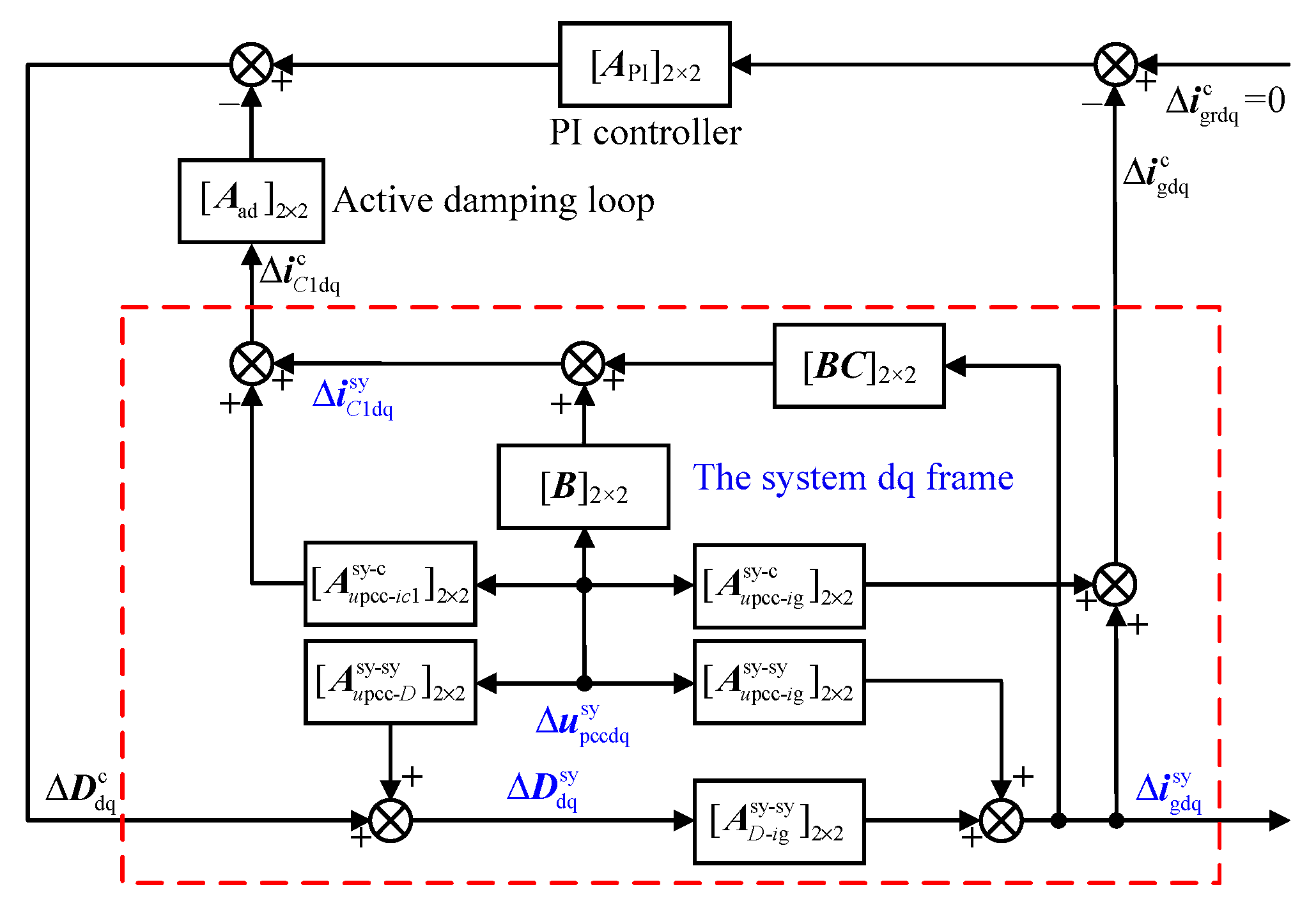
2.2. Admittance Model of Traditional Control Method

The diagram of the PLL description is shown in Figure 2, where T_PLL is the proportional integral (PI) controller of PLL, T_PLL = k_ppll + k_ipll/s, k_ppll is the proportional coefficient of PLL PI controller, and k_ipll is the integral gain of PLL PI controller. Because of the PLL dynamics, there are two dq frames in the system. The first is the system dq frame that is identified by the PCC voltage. The second is the control dq frame that is identified by PLL.

The dq admittance model of the traditional control method, considering the PLL effect, is shown in Figure 3. Outside the dotted line of Figure 3, the control diagram of the traditional control method without considering the PLL effect is pretended. The PI controller [18] is often utilized for the grid-connected current loop due to its simplicity and efficiency. The filter capacitor current feedback [19] is often introduced for the active damping loop to suppress the resonance peak of the LCL filter, which does not require additional passive components or energy loss. However, by adding the small-signal disturbance, PLL affects the grid-connected current vector and filter capacitance current vector in the control dq frame and duty cycle vector in the system dq frame. Therefore, the above vectors are converted between the system dq frame and the control dq frame, and considering the PLL effect, are shown inside the dotted line of Figure 3.

In Figure 3, the superscript variable is “sy,” which represents the variable in the system dq frame, the superscript variable is “c,” which represents the variable in the control dq frame, and the front variable is “∆,” which represents the small-signal variable. The matrices $A_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}$ = ∆$i_{\mathrm{gdq}}^{\mathrm{sy}}$/∆$D_{\mathrm{dq}}^{\mathrm{sy}}$, $A_{\mathrm{upcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}$ = ∆$i_{\mathrm{gdq}}^{\mathrm{sy}}$/∆$u_{\mathrm{pccdq}}^{\mathrm{sy}}$, $A_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}$ = ∆$D_{\mathrm{dq}}^{\mathrm{sy}}$/∆$u_{\mathrm{pccdq}}^{\mathrm{sy}}$, $A_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-c}$ = ∆$i_{\mathrm{gdq}}^{\mathrm{c}}$/∆$u_{\mathrm{pccdq}}^{\mathrm{sy}}$, $A_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}$ = ∆$i_{C1\mathrm{d}\mathrm{q}}^{\mathrm{c}}$/∆$u_{\mathrm{pccdq}}^{\mathrm{sy}}$, A_PI is the PI controller matrix of grid-connected current loop and A_ad is the active damping coefficient matrix. The derivation of the above matrices are as follows.

The vectors are converted from the system dq frame to the control dq frame via the translation matrix T_Δθ, which can be defined as

$${\mathit{T}}_{\Delta \theta }=\left[\begin{array}{cc}\cos (\Delta \theta )& \sin (\Delta \theta )\\ -\sin (\Delta \theta )& \cos (\Delta \theta )\end{array}\right].$$

(1)

The small-signal pcc voltage can be obtained as

$$\left[\begin{array}{l}{u}_{\mathrm{pccd}}^{\mathrm{c}}+\Delta u_{\mathrm{pccd}}^{\mathrm{c}}\\ u_{\mathrm{pccq}}^{\mathrm{c}}+\Delta u_{\mathrm{pccq}}^{\mathrm{c}}\end{array}\right]=\left[\begin{array}{cc}1& \Delta \theta \\ -\Delta \theta & 1\end{array}\right]\left[\begin{array}{l}{u}_{\mathrm{pccd}}^{\mathrm{sy}}+\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ u_{\mathrm{pccq}}^{\mathrm{sy}}+\Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right].$$

(2)

And (2) can be rewritten as

$$\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{c}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{c}}\end{array}\right]=\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}+u_{\mathrm{pccq}}^{\mathrm{sy}}\Delta \theta \\ -u_{\mathrm{pccd}}^{\mathrm{sy}}\Delta \theta +\Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right].$$

(3)

From Figure 2, the angle Δθ can be calculated as

$$\Delta \theta =\frac{T_{\mathrm{PLL}}(s)\Delta u_{\mathrm{pccq}}^{\mathrm{c}}}{s}.$$

(4)

Combining (3) and (4), the following equation can be obtained as

$$\Delta \theta =\frac{T_{\mathrm{PLL}}(s)\Delta u_{\mathrm{pccq}}^{\mathrm{sy}}}{s+u_{\mathrm{pccd}}^{\mathrm{sy}}{T}_{\mathrm{PLL}}(s)}=G_{\mathrm{PLL}}\Delta u_{\mathrm{pccq}}^{\mathrm{sy}},$$

(5)

where $G_{\mathrm{PLL}}=\frac{T_{\mathrm{PLL}}(s)}{s+u_{\mathrm{pccd}}^{\mathrm{sy}}{T}_{\mathrm{PLL}}(s)}$.

Substitute (5) into (3), (3) can be obtained as

$$\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{c}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{c}}\end{array}\right]=\left[\begin{array}{cc}0& u_{\mathrm{pccq}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& -u_{\mathrm{pccd}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right]\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right]+\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right].$$

(6)

Similarly, the small-signal duty ratio can be expressed as

$$\left[\begin{array}{l}\Delta D_{\mathrm{d}}^{\mathrm{sy}}\\ \Delta D_{\mathrm{q}}^{\mathrm{sy}}\end{array}\right]=\left[\begin{array}{cc}0& -D_{\mathrm{q}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& D_{\mathrm{d}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right]\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right]+\left[\begin{array}{l}\Delta D_{\mathrm{d}}^{\mathrm{c}}\\ \Delta D_{\mathrm{q}}^{\mathrm{c}}\end{array}\right].$$

(7)

And the matrix ${\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}$ can be obtained as

$${\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}=\frac{\Delta {\mathit{D}}_{\mathrm{dq}}^{\mathrm{sy}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{3\mathrm{dd}}& -A_{3\mathrm{dq}}\\ A_{3\mathrm{qd}}& A_{3\mathrm{qq}}\end{array}\right]=\left[\begin{array}{cc}0& -D_{\mathrm{q}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& D_{\mathrm{d}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right].$$

(8)

Meanwhile, the small-signal grid-connected current can be expressed as

$$\left[\begin{array}{l}\Delta i_{\mathrm{gd}}^{\mathrm{c}}\\ \Delta i_{\mathrm{gq}}^{\mathrm{c}}\end{array}\right]=\left[\begin{array}{cc}0& i_{\mathrm{gq}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& -i_{\mathrm{gd}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right]\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right]+\left[\begin{array}{l}\Delta i_{\mathrm{gd}}^{\mathrm{sy}}\\ \Delta i_{\mathrm{gq}}^{\mathrm{sy}}\end{array}\right].$$

(9)

And the matrix ${\mathit{A}}_{u\mathrm{pcc}-ig}^{\mathrm{sy}-c}$ can be obtained as

$${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}=\frac{\Delta {\mathit{i}}_{\mathrm{gdq}}^{\mathrm{c}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{4\mathrm{dd}}& A_{4\mathrm{dq}}\\ A_{4\mathrm{qd}}& -A_{4\mathrm{qq}}\end{array}\right]=\left[\begin{array}{cc}0& i_{\mathrm{gq}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& -i_{\mathrm{gd}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right].$$

(10)

At the same time, the small-signal filter capacitance current can be expressed as

$$\left[\begin{array}{l}\Delta i_{C1\mathrm{d}}^{\mathrm{c}}\\ \Delta i_{C1\mathrm{q}}^{\mathrm{c}}\end{array}\right]=\left[\begin{array}{cc}0& i_{C1\mathrm{q}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& -i_{C1\mathrm{d}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right]\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right]+\left[\begin{array}{l}\Delta i_{C1\mathrm{d}}^{\mathrm{sy}}\\ \Delta i_{C1\mathrm{q}}^{\mathrm{sy}}\end{array}\right].$$

(11)

And the matrix ${\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-c}$ can be obtained as

$${\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}=\frac{\Delta {\mathit{i}}_{C1\mathrm{dq}}^{\mathrm{c}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{5\mathrm{dd}}& A_{5\mathrm{dq}}\\ A_{5\mathrm{qd}}& -A_{5\mathrm{qq}}\end{array}\right]=\left[\begin{array}{cc}0& i_{C1\mathrm{q}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& -i_{C1\mathrm{d}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right].$$

(12)

According to the small-signal open-loop circuit model of LCL filter in the system dq frame, the following equation can be expressed as

$$\{\begin{array}{l}\left[\begin{array}{l}\Delta D_{\mathrm{d}}^{\mathrm{sy}}{U}_{\mathrm{dc}}/2\\ \Delta D_{\mathrm{q}}^{\mathrm{sy}}{U}_{\mathrm{dc}}/2\end{array}\right]-\left[\begin{array}{l}\Delta u_{C1\mathrm{d}}^{\mathrm{sy}}\\ \Delta u_{C1\mathrm{q}}^{\mathrm{sy}}\end{array}\right]=\mathit{A}\left[\begin{array}{l}\Delta i_{L1\mathrm{d}}^{\mathrm{sy}}\\ \Delta i_{L1\mathrm{q}}^{\mathrm{sy}}\end{array}\right]\\ \left[\begin{array}{l}\Delta i_{L1\mathrm{d}}^{\mathrm{sy}}\\ \Delta i_{L1\mathrm{q}}^{\mathrm{sy}}\end{array}\right]-\left[\begin{array}{l}\Delta i_{\mathrm{gd}}^{\mathrm{sy}}\\ \Delta i_{\mathrm{gq}}^{\mathrm{sy}}\end{array}\right]=\mathit{B}\left[\begin{array}{l}\Delta u_{C1\mathrm{d}}^{\mathrm{sy}}\\ \Delta u_{C1\mathrm{q}}^{\mathrm{sy}}\end{array}\right]\\ \left[\begin{array}{l}\Delta u_{C1\mathrm{d}}^{\mathrm{sy}}\\ \Delta u_{C1\mathrm{q}}^{\mathrm{sy}}\end{array}\right]-\left[\begin{array}{l}\Delta u_{\mathrm{pccd}}^{\mathrm{sy}}\\ \Delta u_{\mathrm{pccq}}^{\mathrm{sy}}\end{array}\right]=\mathit{C}\left[\begin{array}{l}\Delta i_{\mathrm{gd}}^{\mathrm{sy}}\\ \Delta i_{\mathrm{gq}}^{\mathrm{sy}}\end{array}\right]\end{array},$$

(13)

where $\mathit{A}=\left[\begin{array}{cc}s{L}_1+R_{L1}& -{\omega }_1{L}_1\\ {\omega }_1{L}_1& s{L}_1+R_{L1}\end{array}\right]$, $\mathit{B}=\left[\begin{array}{cc}s{C}_1& -{\omega }_1{C}_1\\ {\omega }_1{C}_1& s{C}_1\end{array}\right]$, $\mathit{C}=\left[\begin{array}{cc}s{L}_2+R_{L2}& -{\omega }_1{L}_2\\ {\omega }_1{L}_2& s{L}_2+R_{L2}\end{array}\right]$.

From (13), (14) can be obtained as

$$\Delta {\mathit{i}}_{C1\mathrm{dq}}^{\mathrm{sy}}=\mathit{B}\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}+\mathit{B}\mathit{C}\Delta {\mathit{i}}_{\mathrm{gdq}}^{\mathrm{sy}}.$$

(14)

By setting ∆U_dc and ∆${\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}$ to zero, the matrix ${\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}$ can be obtained as

$${\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}=\frac{\Delta {\mathit{i}}_{\mathrm{gdq}}^{\mathrm{sy}}}{\Delta {\mathit{D}}_{\mathrm{dq}}^{\mathrm{sy}}}=\mathit{E}\cdot {(\mathit{C}+\mathit{A}+\mathit{A}\mathit{B}\mathit{C})}^{-1},$$

(15)

where E = [U_dc/2, 0; 0, U_dc/2].

Similarly, by setting ∆U_dc and ∆${\mathit{D}}_{\mathrm{dq}}^{\mathrm{sy}}$ to zero, the matrix ${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}$ can be obtained as

$${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}=\frac{\Delta {\mathit{i}}_{\mathrm{gdq}}^{\mathrm{sy}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=-(\mathit{A}\mathit{B}+\mathit{I})\cdot {(\mathit{A}\mathit{B}\mathit{C}+\mathit{A}+\mathit{C})}^{-1},$$

(16)

where I is the identity matrix.

Meanwhile, the matrix A_PI can be defined as

$${\mathit{A}}_{\mathrm{PI}}=\left[\begin{array}{cc}{A}_{6\mathrm{dd}}& A_{6\mathrm{dq}}\\ A_{6\mathrm{qd}}& A_{6\mathrm{qq}}\end{array}\right]=\left[\begin{array}{cc}{G}_{\mathrm{i}}& 0\\ 0& G_{\mathrm{i}}\end{array}\right].$$

(17)

And the matrix A_ad can also be defined as

$${\mathit{A}}_{\mathrm{ad}}=\left[\begin{array}{cc}{A}_{7\mathrm{dd}}& A_{7\mathrm{dq}}\\ A_{7\mathrm{qd}}& A_{7\mathrm{qq}}\end{array}\right]=\left[\begin{array}{cc}{K}_{\mathrm{C}}& 0\\ 0& K_{\mathrm{C}}\end{array}\right].$$

(18)

From Figure 3 and Mason’s gain formula, the inverter output admittance Y_{inv_PLL} with considering the PLL effect using traditional control method can be calculated as

$${\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLL}}=\left[\begin{array}{cc}{Y}_{\mathrm{dd}}& Y_{\mathrm{dq}}\\ Y_{\mathrm{qd}}& Y_{\mathrm{qq}}\end{array}\right]=\frac{{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}-{\mathit{A}}_{\mathrm{PI}}{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}-{\mathit{A}}_{\mathrm{ad}}({\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}+\mathit{B}))}{\mathit{I}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{PI}}+{\mathit{A}}_{\mathrm{ad}}(\mathit{B}\mathit{C}))}.$$

(19)

Without considering the PLL effect, ${\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}$ = ${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}$ = ${\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}$ = 0. The inverter output admittance Y_inv using traditional control method can be calculated as

$${\mathit{Y}}_{\mathrm{inv}}=\left[\begin{array}{cc}{Y}_{\mathrm{invdd}}& Y_{\mathrm{invdq}}\\ Y_{\mathrm{invqd}}& Y_{\mathrm{invqq}}\end{array}\right]=\frac{{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}-{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}{\mathit{A}}_{\mathrm{ad}}\mathit{B}}{\mathit{I}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{PI}}+{\mathit{A}}_{\mathrm{ad}}(\mathit{B}\mathit{C}))}.$$

(20)

Meanwhile, the PLL equivalent admittance Y_PLL can be calculated as

$${\mathit{Y}}_{\mathrm{PLL}}={\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLL}}-{\mathit{Y}}_{\mathrm{inv}}=\left[\begin{array}{cc}{Y}_{\mathrm{PLLdd}}& Y_{\mathrm{PLLdq}}\\ Y_{\mathrm{PLLqd}}& Y_{\mathrm{PLLqq}}\end{array}\right]=\frac{{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}-{\mathit{A}}_{\mathrm{PI}}{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}-{\mathit{A}}_{\mathrm{ad}}{\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}})}{\mathit{I}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{PI}}+{\mathit{A}}_{\mathrm{ad}}(\mathit{B}\mathit{C}))}.$$

(21)

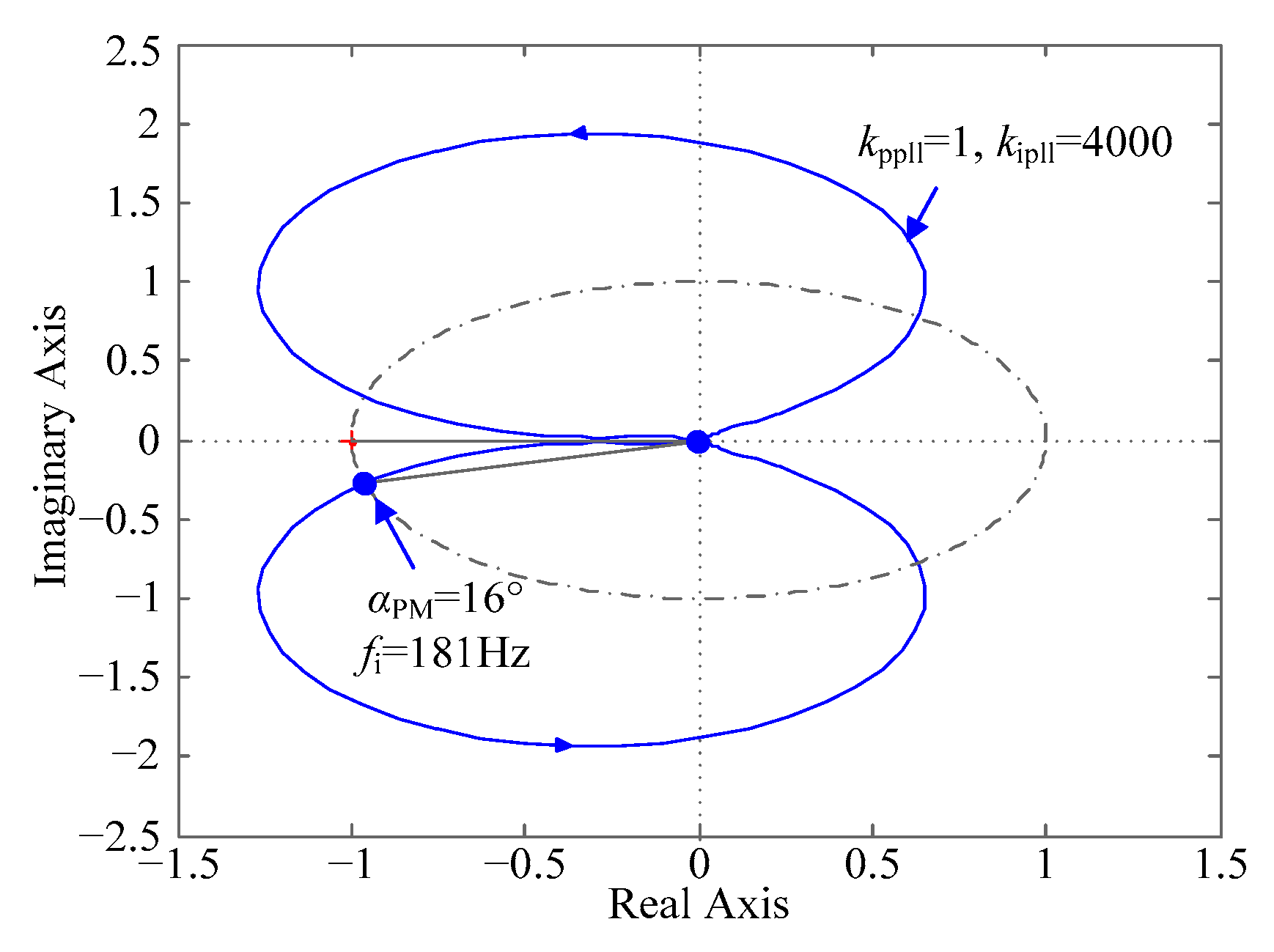
2.3. Impedance-Based Stability Criterion

Under the weak grid condition, the grid impedance can be expressed as

$${\mathit{Z}}_{\mathrm{g}}=\left[\begin{array}{cc}{Z}_{\mathrm{gdd}}& Z_{\mathrm{gdq}}\\ -Z_{\mathrm{gdq}}& Z_{\mathrm{gdd}}\end{array}\right]=\left[\begin{array}{cc}s{L}_{\mathrm{g}}& -{\omega }_1{L}_{\mathrm{g}}\\ {\omega }_1{L}_{\mathrm{g}}& s{L}_{\mathrm{g}}\end{array}\right].$$

(22)

According to the Norton theorem, the equivalent circuit of the system using the traditional control method is shown in Figure 4. The inverter subsystem is equivalent to a parallel connection between the current source and inverter output admittance Y_{inv_PLL} = (Y_inv//Y_PLL). The grid subsystem is equivalent to the grid impedance Z_g and an ideal grid in the series connection.

On the basis of the generalized Nyquist criterion [20], if the Nyquist curve for the eigenfunction of the return-ratio matrix L does not encircle (–1, j * 0), the system is in a stable state. L can be depicted as

$$\mathit{L}={\mathit{Z}}_{\mathrm{g}}\cdot {\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLL}}=\left[\begin{array}{cc}{Z}_{\mathrm{gdd}}{Y}_{\mathrm{dd}}& Z_{\mathrm{gdq}}{Y}_{\mathrm{qq}}\\ -Z_{\mathrm{gdq}}{Y}_{\mathrm{dd}}& Z_{\mathrm{gdd}}{Y}_{\mathrm{qq}}\end{array}\right].$$

(23)

Therefore, the eigenfunction of the return-ratio matrix L can be calculated as

$$\{\begin{array}{l}{l}_1=\underset{x_1}{\underbrace{Z_{\mathrm{gdd}}{Y}_{\mathrm{dd}}/2+Z_{\mathrm{gdd}}{Y}_{\mathrm{qq}}/2}}-\underset{x_2}{\underbrace{{(Z_{\mathrm{gdd}}^2{Y}_{\mathrm{dd}}^2-2Z_{\mathrm{gdd}}^2{Y}_{\mathrm{dd}}{Y}_{\mathrm{qq}}-4Z_{\mathrm{gdq}}^2{Y}_{\mathrm{dd}}{Y}_{\mathrm{qq}}+Z_{\mathrm{gdd}}^2{Y}_{\mathrm{qq}}^2)}^{1/2}/2}}\\ l_2=\underset{x_1}{\underbrace{Z_{\mathrm{gdd}}{Y}_{\mathrm{dd}}/2+Z_{\mathrm{gdd}}{Y}_{\mathrm{qq}}/2}}+\underset{x_2}{\underbrace{{(Z_{\mathrm{gdd}}^2{Y}_{\mathrm{dd}}^2-2Z_{\mathrm{gdd}}^2{Y}_{\mathrm{dd}}{Y}_{\mathrm{qq}}-4Z_{\mathrm{gdq}}^2{Y}_{\mathrm{dd}}{Y}_{\mathrm{qq}}+Z_{\mathrm{gdd}}^2{Y}_{\mathrm{qq}}^2)}^{1/2}/2}}\end{array}.$$

(24)

From (24), the retained component x₁ and secondary component x₂ can be defined as

$$\{\begin{array}{l}{x}_1=\frac{1}{2}{Z}_{\mathrm{gdd}}\cdot (Y_{\mathrm{dd}}+Y_{\mathrm{qq}})\\ x_2=\frac{1}{2}{(Z_{\mathrm{gdd}}^2{Y}_{\mathrm{dd}}^2-2Z_{\mathrm{gdd}}^2{Y}_{\mathrm{dd}}{Y}_{\mathrm{qq}}-4Z_{\mathrm{gdq}}^2{Y}_{\mathrm{dd}}{Y}_{\mathrm{qq}}+Z_{\mathrm{gdd}}^2{Y}_{\mathrm{qq}}^2)}^{1/2}\end{array}.$$

(25)

According to (25), the Bode diagrams of the retained component x₁ and secondary component x₂ are shown in Figure 5. When the distance between the two is the smallest, the magnitude of x₁ is −15.6 dB, the magnitude of x₂ is −47.2 dB. The magnitude of x₁ is 31.6 dB larger than that of x₂, which is equivalent to 38.02 times. Therefore, ignoring the secondary components x₂, (24) can be rewritten as

$$l_1=l_2=x_1=(\frac{Z_{\mathrm{gdd}}}{2})\cdot (Y_{\mathrm{dd}}+Y_{\mathrm{qq}}).$$

(26)

However, a dynamic interconnected system will be formed in the weak grid. The phase margin of the system may be insufficient. That results in increasing the distortion of grid-connected current. To guarantee enough stability and good dynamics, the range of phase margin of the system is usually required to be 30–60° under the weak grid condition.

In the Nyquist curve, the intersection point for the eigenfunction and unit circle is defined as the system cut-off frequency f_i, and the location is determined as the phase margin of the system α_PM [21]. From (26), α_PM can be expressed as

$${\alpha }_{\mathrm{PM}}={180}^{\circ }-\arg (\frac{Z_{\mathrm{gdd}}(f_{\mathrm{i}})}{2})-\arg (Y_{\mathrm{dd}}(f_{\mathrm{i}})+Y_{\mathrm{qq}}(f_{\mathrm{i}})).$$

(27)

From (27), the system phase margin is increased by decreasing arg(Z_gdd(f_i)/2) and arg(Y_dd(f_i) + Y_qq(f_i)). It is difficult to control the phase of grid impedance arg(Z_gdd(f_i)/2). Therefore, the target needs to be achieved by decreasing arg(Y_dd(f_i) + Y_qq(f_i)).

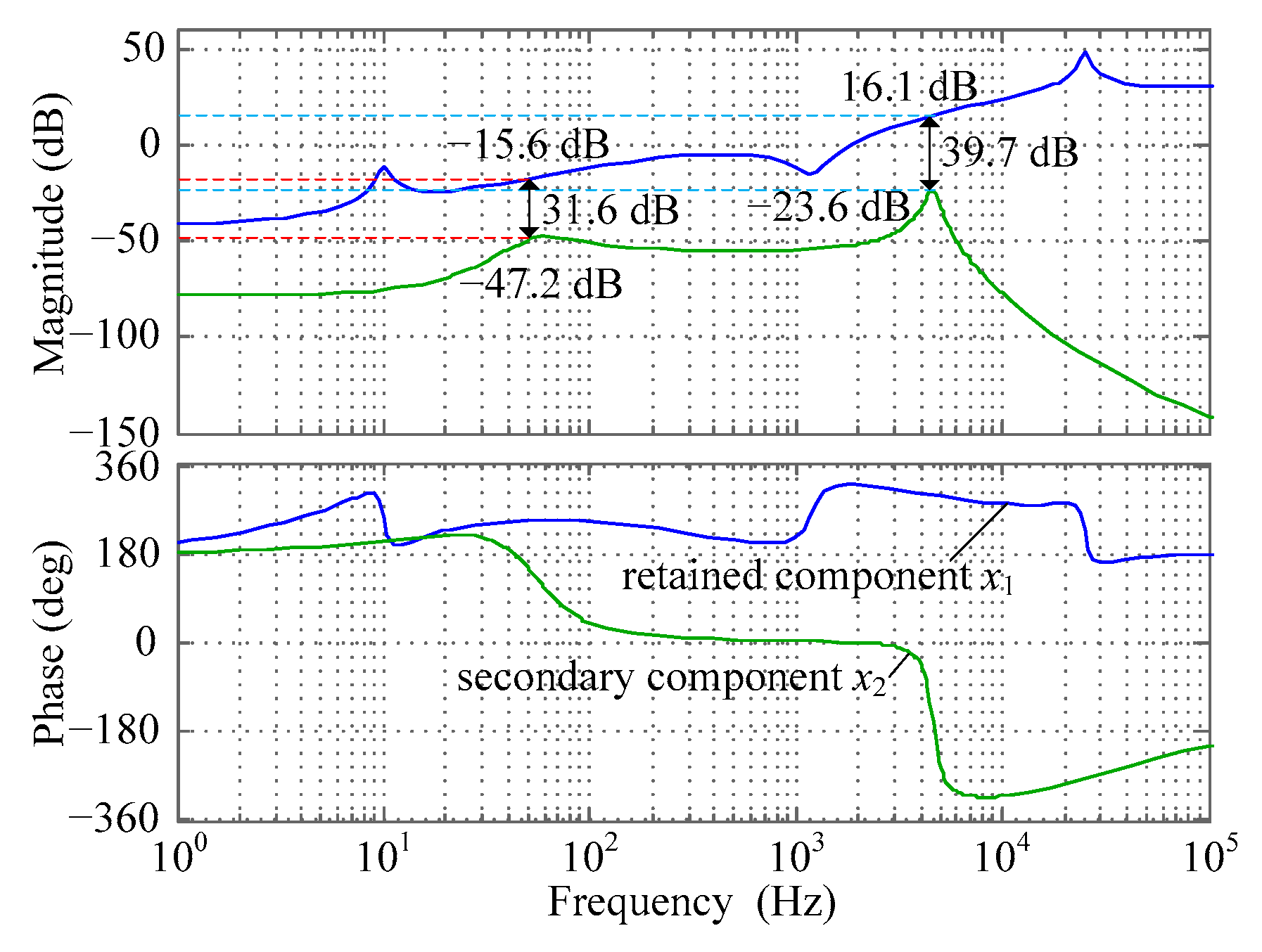
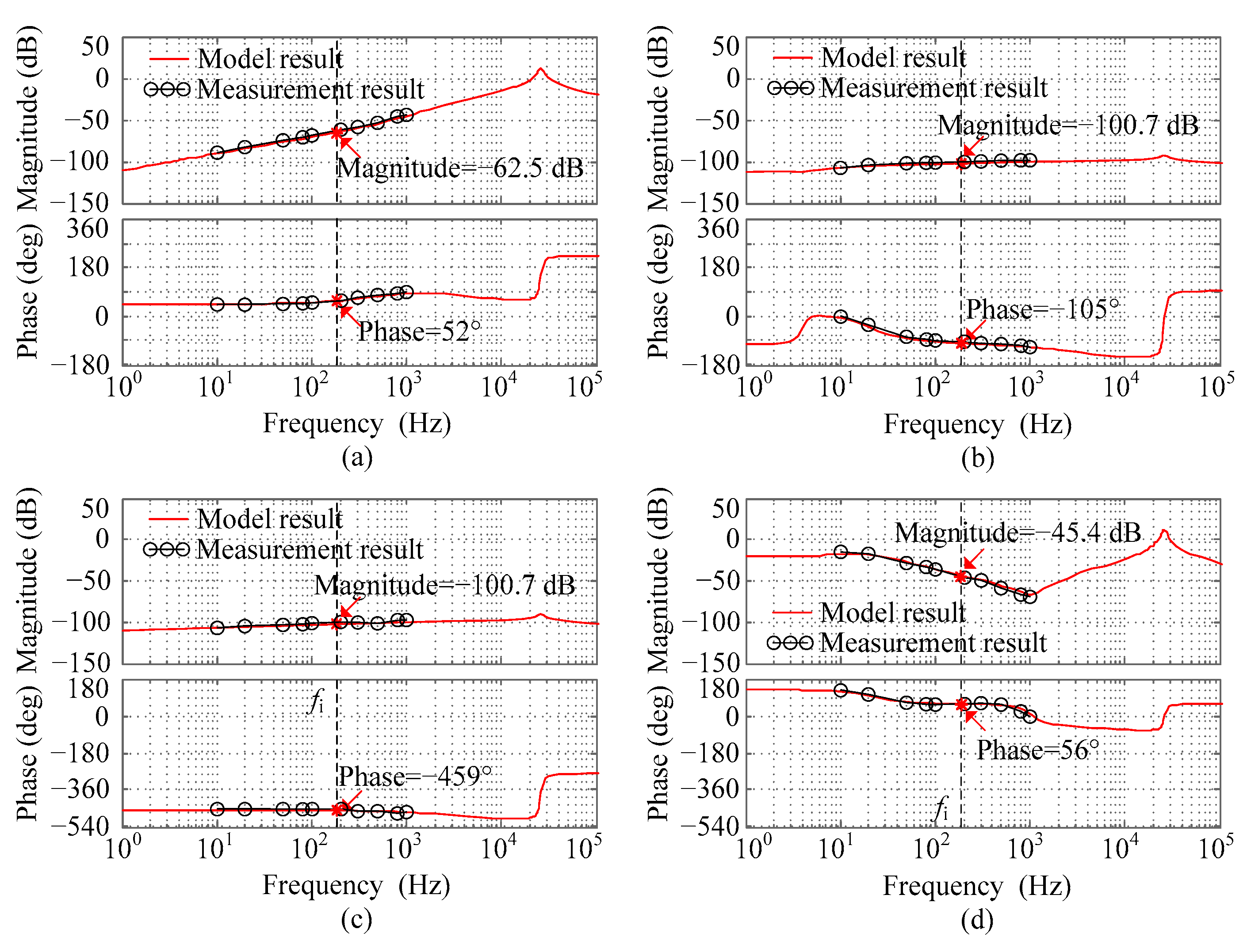
2.4. Stability Analysis of Traditional Control Method

The Nyquist diagram of the eigenfunction with the traditional control method is shown as in Figure 6. The system cut-off frequency f_i is 181 Hz and the system phase margin α_PM is 16°, which does not satisfy the requirement of sufficient stability of the system. Therefore, the system phase margin should be improved under the traditional control method.

The Bode diagrams of inverter output admittance Y_{inv_PLL} using the traditional control method are shown in Figure 7. The amplitudes and phases of Y_dd, Y_dq, Y_qd and Y_qq can be obtained at the system cut-off frequency, so arg(Y_dd(f_i) + Y_qq(f_i)) = 74°. Because the grid impedance is equivalent to the inductance, arg(Z_gdd(f_i)/2) is generally equal to 90°. According to (27), the system phase margin α_PM is 16°, which does not meet sufficient stability of the system. The results are consistent with those in Figure 6. Therefore, the system phase margin should be improved under the traditional control method. Specifically, the PLL shapes the Z_qq (1/Y_qq) as a negative incremental resistance that may destabilize the system. Meanwhile, |Y_dd| and |Y_qq| are far larger than |Y_dq| and |Y_qd|, so |Y_dq| and |Y_qd| are equal to 0, which verifies the correctness of (23). Within the range of the error, the measurement results are in agreement with the model results, which proves the correctness of the model.

3. Admittance Reshaping Control Methods for Three-Phase Grid-Connected Inverter

3.1. Admittance Reshaping Technique 1 (the Feedforward PCC Voltage)

To improve the system’s stability, the proposed admittance reshaping technique 1 uses the feedforward PCC voltage to modify the inverter output admittance Y_inv, which is equivalent to adding the virtual admittance to connect in parallel with inverter output admittance. The system diagram of the proposed admittance reshaping technique 1—considering the effect of PLL—is shown in Figure 8. Inside the left dotted line of Figure 8, the control diagram of the proposed admittance reshaping technique 1—without considering the PLL effect—is presented. The vectors are converted between the system dq frame and the control dq frame that considers the PLL effect are shown outside the left dotted line of Figure 8.

From Figure 8, the feedforward matrix A_com can be defined as

$${\mathit{A}}_{\mathrm{com}}=\left[\begin{array}{cc}{G}_{\mathrm{comdd}}& 0\\ 0& G_{\mathrm{comqq}}\end{array}\right].$$

(28)

From Figure 8, the dq admittance model of the proposed admittance reshaping technique 1 is obtained, as shown in Figure 9, where the matrix ${\mathit{A}}_{u\mathrm{pcc}-u\mathrm{pcc}}^{\mathrm{sy}-\mathrm{c}}$ can be obtained as

$${\mathit{A}}_{u\mathrm{pcc}-u\mathrm{pcc}}^{\mathrm{sy}-\mathrm{c}}=\frac{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{c}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{8\mathrm{dd}}& A_{8\mathrm{dq}}\\ A_{8\mathrm{qd}}& -A_{8\mathrm{qq}}\end{array}\right]=\left[\begin{array}{cc}0& u_{\mathrm{pccq}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\\ 0& -u_{\mathrm{pccd}}^{\mathrm{sy}}{G}_{\mathrm{PLL}}\end{array}\right].$$

(29)

Therefore, the inverter output admittance Y_{invc_PLL} with the proposed admittance reshaping technique 1 can be expressed as

$$\begin{array}{l}{\mathit{Y}}_{\mathrm{invc}\_\mathrm{PLL}}=\left[\begin{array}{cc}{Y}_{\mathrm{cdd}}& Y_{\mathrm{cdq}}\\ Y_{\mathrm{cqd}}& Y_{\mathrm{cqq}}\end{array}\right]\\ \begin{array}{ccc}& & \end{array}=\frac{{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}+{\mathit{A}}_{\mathrm{com}}{\mathit{A}}_{u\mathrm{pcc}-u\mathrm{pcc}}^{\mathrm{sy}-\mathrm{c}}-{\mathit{A}}_{\mathrm{PI}}{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}-{\mathit{A}}_{\mathrm{ad}}({\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}+\mathit{B}))}{\mathit{I}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{PI}}+{\mathit{A}}_{\mathrm{ad}}(\mathit{B}\mathit{C}))}.\end{array}$$

(30)

Without considering the PLL effect, ${\mathit{A}}_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}$ = ${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}$ = ${\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}$ = 0. The inverter output admittance Y_invc using the proposed admittance reshaping technique 1 can be calculated as

$${\mathit{Y}}_{\mathrm{invc}}=\left[\begin{array}{cc}{Y}_{\mathrm{invcdd}}& Y_{\mathrm{invcdq}}\\ Y_{\mathrm{invcqd}}& Y_{\mathrm{invcqq}}\end{array}\right]=\frac{{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{com}}{\mathit{A}}_{u\mathrm{pcc}-u\mathrm{pcc}}^{\mathrm{sy}-\mathrm{c}}-{\mathit{A}}_{\mathrm{ad}}\mathit{B})}{\mathit{I}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{PI}}+{\mathit{A}}_{\mathrm{ad}}(\mathit{B}\mathit{C}))}.$$

(31)

Next, the calculation process of the feedforward matrix A_com is introduced. The optimization function G_p(s) of the inverter output admittance phase, which can be given as

$$G_{\mathrm{p}}(s)=\frac{1+k_{\mathsf{\omega }}s}{1+k_{\mathrm{p}}{k}_{\mathsf{\omega }}s}\cdot k_{\mathrm{m}},$$

(32)

where k_p is the proportional coefficient, k_ω is the phase coefficient, and k_m is the gain coefficient. k_p and k_ω can reduce the phase at the desired frequency and k_m can compensate for the amplitude offset at the desired frequency.

The Bode diagram of the optimization function G_p(s) is shown in Figure 10. By selecting the appropriate parameters, the amplitude of G_p(s) is 0 dB at the desired frequency and the phase reaches the minimum at the desired frequency.

Meanwhile, the optimization matrix A_p can be defined as

$${\mathit{A}}_{\mathrm{p}}=\left[\begin{array}{cc}{G}_{\mathrm{p}}& 0\\ 0& G_{\mathrm{p}}\end{array}\right].$$

(33)

If the series correction between the optimization matrix A_p and inverter output admittance Y_{inv_PLL} is taken, the aim of compensating for the phase of inverter output admittance at the desired frequency will be realized. Meanwhile, the feedforward matrix A_com can also be obtained. Therefore, the inverter output admittance Y_{invc_PLL} with using the proposed admittance reshaping technique 1 can be rewritten as

$${\mathit{Y}}_{\mathrm{invc}\_\mathrm{PLL}}={\mathit{A}}_{\mathrm{p}}{\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLL}}.$$

(34)

Therefore, G_comdd in the feedforward matrix can be expressed as

$$G_{\mathrm{comdd}}=\frac{(1-k_{\mathrm{m}}{k}_{\mathrm{p}})k_{\mathsf{\omega }}s+(1-k_{\mathrm{m}})}{k_{\mathrm{m}}(k_{\mathrm{p}}{k}_{\mathsf{\omega }}s+1)}\cdot \frac{G_1-G_2}{G_{\mathrm{PWM}}{G}_{\mathrm{PLL}}{u}_{\mathrm{pccd}}^{\mathrm{sy}}},$$

(35)

where $G_1=1+\frac{(s{L}_1+R_{L1})s{C}_1}{(1+s{C}_1{R}_{C1})}$ and $G_2=L_1{C}_1{\omega }_1^2$.

Meanwhile, G_comqq in the feedforward matrix can also be expressed as

$$G_{\mathrm{comqq}}=\frac{(1-k_{\mathrm{m}}{k}_{\mathrm{p}})k_{\mathsf{\omega }}s+(1-k_{\mathrm{m}})}{k_{\mathrm{m}}(k_{\mathrm{p}}{k}_{\mathsf{\omega }}s+1)}\cdot \frac{G_1-G_2-G_3}{G_{\mathrm{PWM}}{G}_{\mathrm{PLL}}{u}_{\mathrm{pccd}}^{\mathrm{sy}}},$$

(36)

where $G_3=G_{\mathrm{PLL}}{G}_{\mathrm{PWM}}(D_{\mathrm{d}}^{\mathrm{sy}}+G_{\mathrm{i}}{i}_{\mathrm{gd}}^{\mathrm{sy}}+K_{\mathrm{C}}{i}_{C1\mathrm{d}}^{\mathrm{sy}})$.

Using the proposed admittance reshaping technique 1, Y_{invc_PLL} is equivalent to the parallel connection between Y_PLL and Y_invc. Therefore, the proposed admittance reshaping technique 1 is equivalent to adding the virtual admittance to connect in parallel with inverter output admittance Y_inv.

The Bode diagrams of inverter output admittances Y_{invc_PLL} with the proposed admittance reshaping technique 1 are shown in Figure 11, where arg(Y_cdd(f_i) + Y_cqq(f_i)) = 54°. Because the grid impedance is equivalent to the inductance, arg(Z_gdd(f_i)/2) is generally equal to 90°. According to (27), the system phase margin α_PM is 36°, which meets sufficient stability of the system. Therefore, the proposed admittance reshaping technique 1 increases the system phase margin. At the same time, the measurement results are in good agreement with the modified model, which proves the correctness of the modified model.

3.2. Admittance Reshaping Technique 2 (the Active Damping Controller)

To increase the system phase margin, the proposed admittance reshaping technique 2 adopts the active damping controller to reconstruct the PLL equivalent admittance Y_PLL. The control block diagram of the improved PLL is shown in Figure 12. The proposed admittance reshaping technique 2 reduces the phase of PLL equivalent admittance at the system cut-off frequency, which improves system stability.

From Figure 12, the closed-loop transfer function of PLL G_PLLc using the proposed admittance reshaping technique 2 can be expressed as

$$G_{\mathrm{PLLc}}=\frac{T_{\mathrm{PLL}}}{s+u_{\mathrm{pccd}}^{\mathrm{sy}}{T}_{\mathrm{PLL}}+\frac{G_{\mathrm{AD}}}{1+G_{\mathrm{AD}}}{T}_{\mathrm{PLL}}}.$$

(37)

Therefore, the matrix $A_{u\mathrm{pcc}-D}^{\mathrm{sy}-\mathrm{sy}}$ in (8) can be rewritten as

$${\mathit{A}}_{u\mathrm{pcc}-D\_\mathrm{c}}^{\mathrm{sy}-\mathrm{sy}}=\frac{\Delta {\mathit{D}}_{\mathrm{dq}}^{\mathrm{sy}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{3\mathrm{cdd}}& -A_{3\mathrm{cdq}}\\ A_{3\mathrm{cqd}}& A_{3\mathrm{cqq}}\end{array}\right]=\left[\begin{array}{cc}0& -D_{\mathrm{q}}^{\mathrm{sy}}{G}_{\mathrm{PLLc}}\\ 0& D_{\mathrm{d}}^{\mathrm{sy}}{G}_{\mathrm{PLLc}}\end{array}\right].$$

(38)

Meanwhile, the matrix ${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{c}}$ in (10) can be rewritten as

$${\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}\_\mathrm{c}}^{\mathrm{sy}-\mathrm{c}}=\frac{\Delta {\mathit{i}}_{\mathrm{gdq}}^{\mathrm{c}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{4\mathrm{cdd}}& A_{4\mathrm{cdq}}\\ A_{4\mathrm{cqd}}& -A_{4\mathrm{cqq}}\end{array}\right]=\left[\begin{array}{cc}0& i_{\mathrm{gq}}^{\mathrm{sy}}{G}_{\mathrm{PLLc}}\\ 0& -i_{\mathrm{gd}}^{\mathrm{sy}}{G}_{\mathrm{PLLc}}\end{array}\right].$$

(39)

At the same time, the matrix ${\mathit{A}}_{u\mathrm{pcc}-ic1}^{\mathrm{sy}-\mathrm{c}}$ in (12) can be rewritten as

$${\mathit{A}}_{u\mathrm{pcc}-ic1\_\mathrm{c}}^{\mathrm{sy}-\mathrm{c}}=\frac{\Delta {\mathit{i}}_{C1\mathrm{dq}}^{\mathrm{c}}}{\Delta {\mathit{u}}_{\mathrm{pccdq}}^{\mathrm{sy}}}=\left[\begin{array}{cc}{A}_{5\mathrm{cdd}}& A_{5\mathrm{cdq}}\\ A_{5\mathrm{cqd}}& -A_{5\mathrm{cqq}}\end{array}\right]=\left[\begin{array}{cc}0& i_{C1\mathrm{q}}^{\mathrm{sy}}{G}_{\mathrm{PLLc}}\\ 0& -i_{C1\mathrm{d}}^{\mathrm{sy}}{G}_{\mathrm{PLLc}}\end{array}\right].$$

(40)

Therefore, the inverter output admittance Y_{inv_PLLc} using the proposed admittance reshaping technique 2 can be expressed as

$${\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLLc}}=\left[\begin{array}{cc}{Y}_{\mathrm{cdd}}& Y_{\mathrm{cdq}}\\ Y_{\mathrm{cqd}}& Y_{\mathrm{cqq}}\end{array}\right]=\frac{{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{u\mathrm{pcc}-D\_\mathrm{c}}^{\mathrm{sy}-\mathrm{sy}}-{\mathit{A}}_{\mathrm{PI}}{\mathit{A}}_{u\mathrm{pcc}-i\mathrm{g}\_\mathrm{c}}^{\mathrm{sy}-\mathrm{c}}-{\mathit{A}}_{\mathrm{ad}}({\mathit{A}}_{u\mathrm{pcc}-i\mathrm{c}1\_\mathrm{c}}^{\mathrm{sy}-\mathrm{c}}+\mathit{B}))}{\mathit{I}+{\mathit{A}}_{D-i\mathrm{g}}^{\mathrm{sy}-\mathrm{sy}}({\mathit{A}}_{\mathrm{PI}}+{\mathit{A}}_{\mathrm{ad}}(\mathit{B}\mathit{C}))}.$$

(41)

Next, the calculation process of the active damping controller G_AD is introduced. According to (32), the closed-loop transfer function of PLL G_PLLc using the proposed admittance reshaping technique 2 can be rewritten as

$${\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLLc}}={\mathit{A}}_{\mathrm{p}}{\mathit{Y}}_{\mathrm{inv}\_\mathrm{PLL}}.$$

(42)

Therefore, the active damping controller G_AD can be obtained as

$$G_{\mathrm{AD}}=\frac{(1-G_{\mathrm{p}})s}{(G_{\mathrm{p}}-1)s+T_{\mathrm{PLL}}{G}_{\mathrm{p}}}.$$

(43)

Using proposed admittance reshaping technique 2, Y_{inv_PLLc} is equivalent to the parallel connection between Y_PLLc and Y_inv. Therefore, the proposed admittance reshaping technique 2 is equivalent to adding the virtual admittance to connect in parallel with the PLL equivalent admittance Y_PLL. Using the proposed admittance reshaping technique 2, the reconstructed inverter output admittances Y_{inv_PLLc} can achieve the same purpose as proposed admittance reshaping technique 1.

3.3. Design Method of Control Parameters

By selecting the appropriate parameters k_p and k_ω, the phase of the inverter output admittance is reduced at the system cut-off frequency, which increases the system phase margin. In addition, the amplitude of the inverter output admittance at the system cut-off frequency will be changed. Therefore, it is essential to select the appropriate parameter k_m to compensate for the amplitude offset.

The phase-frequency function of G_p(s) is expressed as

$${\varphi }_{\mathrm{p}}(\omega )=-\arctan (\frac{(k_{\mathrm{p}}-1)k_{\mathsf{\omega }}\omega }{k_{\mathrm{p}}{k}_{\mathsf{\omega }}^2{\omega }^2+1}).$$

(44)

If dϕ_p(ω)/dω = 0, the maximum compensation angular frequency ω_m can be obtained as

$${\omega }_{\mathrm{m}}=1/(\sqrt{k_{\mathrm{p}}}{k}_{\mathsf{\omega }}).$$

(45)

Combining (44) and (45), the maximum compensation phase ϕ_m can be derived as

$${\varphi }_{\mathrm{m}}=-\arctan (\frac{k_{\mathrm{p}}-1}{2\sqrt{k_{\mathrm{p}}}}).$$

(46)

To maintain the amplitude of the inverter output admittance at the system cut-off frequency, the amplitude of G_p(s) should be 0 dB at the system cut-off frequency, that is, |G_p(j2πf_i)| = 1. The gain coefficient of phase compensation k_m can be expressed as

$$k_{\mathrm{m}}=\sqrt{\frac{k_{\mathrm{p}}^2{k}_{\mathsf{\omega }}^2{\omega }_{\mathrm{m}}^2+1}{k_{\mathsf{\omega }}^2{\omega }_{\mathrm{m}}^2+1}}.$$

(47)

Using the traditional control method, the system cut-off frequency f_i is 181 Hz, and the system phase margin α_PM is 16°, which does not meet sufficient stability of the system. The parameter design process of the proposed control methods can be illustrated as follows. Firstly, the maximum compensation phase frequency ω_m should be equivalent to the system cut-off angular frequency ω_i = 2πf_i ≈ 1137rad/s. Secondly, the range of maximum compensation phase ϕ_m is −14~−44° on the basis of the required system phase margin. Then, the range of k_p is 1.6383~5.55 by (46). Next, the range of k_ω is 3.7325 × 10⁻⁴−6.8698 × 10⁻⁴ by (45). Finally, the range of k_m is 1.28–2.3558 by (47).

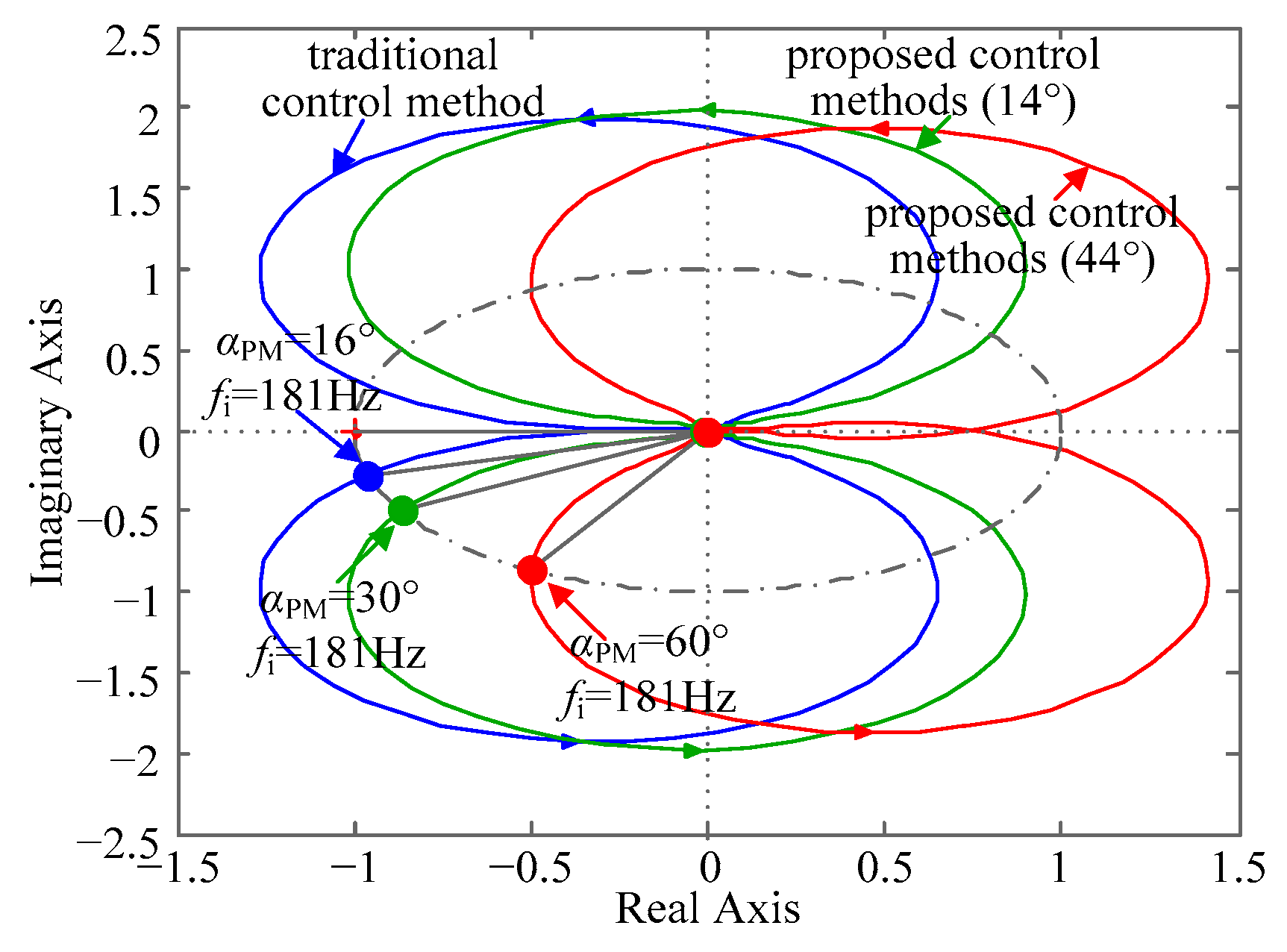
3.4. Contrast Analysis of System Stability

The Nyquist diagrams of the eigenfunction are shown in Figure 13. Using the traditional control method, the system phase margin α_PM is separately 16°. Using the proposed control methods, the system phase margins α_PM are separately 30° and 60°, which are increased by 14° and 44°, respectively. The result is the same as the designed maximum compensation phase, which meets sufficient stability and good dynamics of the system.

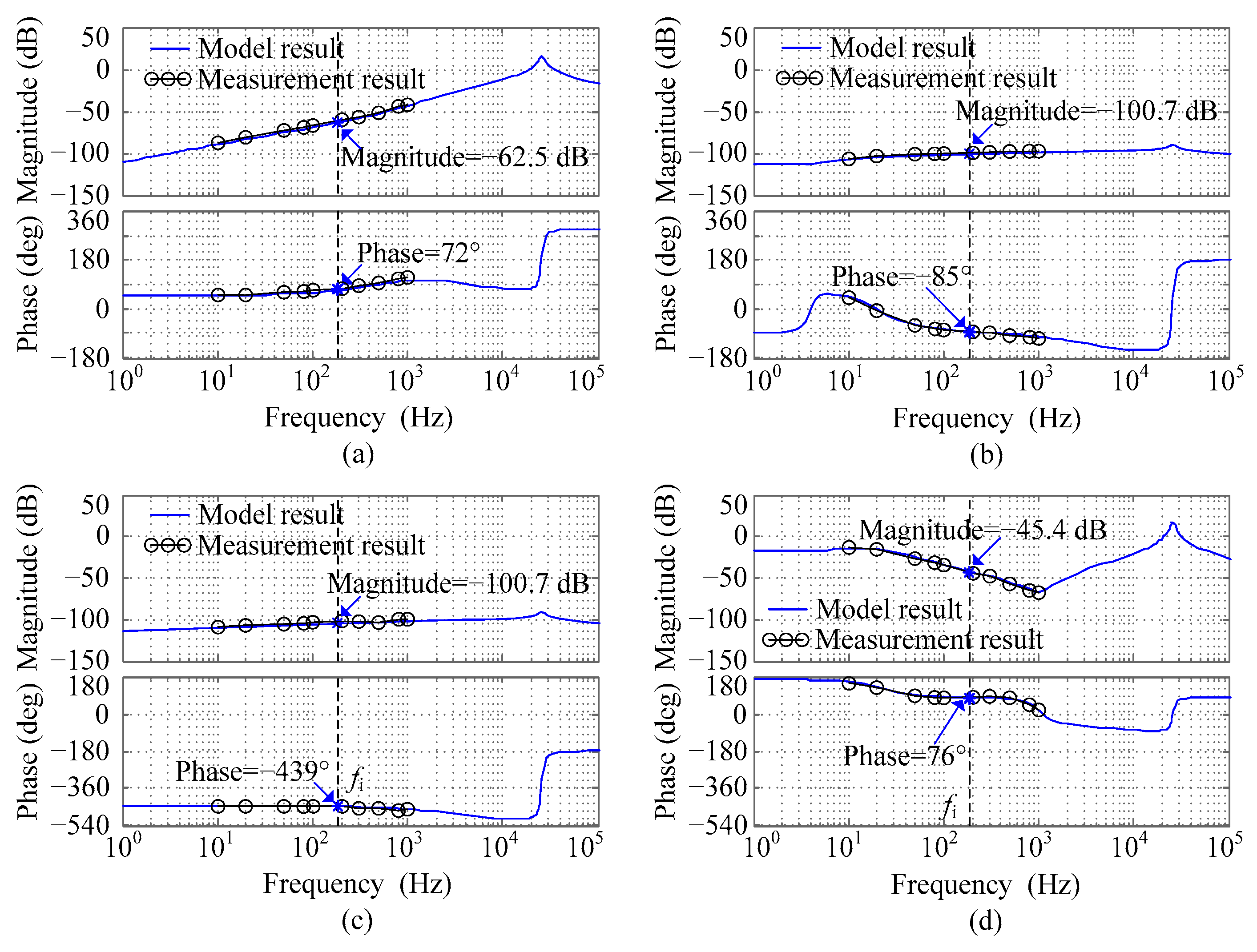
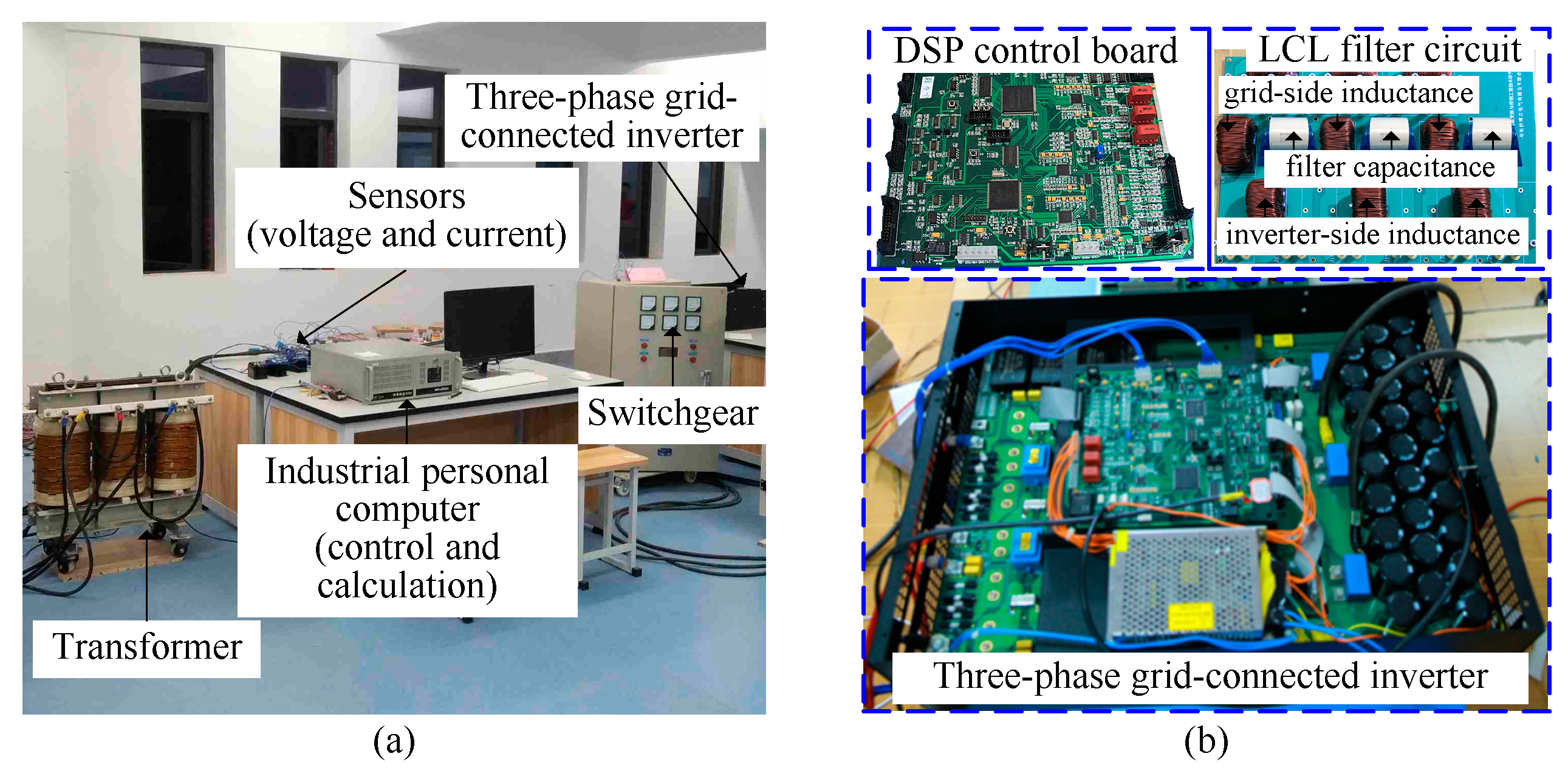
4. Experiments Verification

To prove the validity of the theoretical analysis, the experimental platform for a three-phase grid-connected system was built, as shown in Figure 14a, which included a three-phase grid-connected inverter, a detection and data acquisition circuit (voltage and current sensors), and an industrial personal computer. The three-phase grid-connected inverter in Figure 14b includes the main circuit, control board and LCL filter circuit. The system parameters are shown in

Table 1. System parameters.

Parameter/Unit	Value
DC voltage Udc/V	720
Inverter-side inductor L1/mH, RL1/Ω	0.6, 0.01
Filter capacitor C1/μF	10
Grid-side inductor L2/mH, RL2/Ω	0.15, 0.001
Grid inductor Lg/mH	0.05
Grid-connected current reference igrd, igrq/A	−73, 0
Grid-connected current $i_{\mathrm{g}\mathrm{d}}^{\mathrm{s}}$, $i_{\mathrm{g}\mathrm{q}}^{\mathrm{s}}$/A	−73, 0
PCC voltage $u_{\mathrm{p}\mathrm{c}\mathrm{c}\mathrm{d}}^{\mathrm{s}}$, $u_{\mathrm{p}\mathrm{c}\mathrm{c}\mathrm{q}}^{\mathrm{s}}$/V	311, 0
Filter capacitor current $i_{C1\mathrm{d}}^{\mathrm{s}}$, $i_{C1\mathrm{q}}^{\mathrm{s}}$/A	0.03, 0.90
Duty radio $D_{\mathrm{d}}^{\mathrm{s}}$, $D_{\mathrm{q}}^{\mathrm{s}}$	0.55, 0.01
PLL PI controller kppll, kipll	1, 4000
Grid current loop PI controller kpi, kii	0.45, 1000
Active damping coefficient KC	1.15
Fundamental frequency f1/Hz	50
Switching frequency fs/kHz	10

.

To improve the stable operation range, the stability enhancement method was proposed [14] by largely reducing the PLL bandwidth, abbreviated as the traditional control method. The traditional control method, the proposed admittance reshaping techniques 1 and 2, the experimental waveforms of PCC voltage u_pcc and the grid-connected current i_g are shown in Figure 15, Figure 16 and Figure 17. The experimental results of the grid-connected current in the three cases are shown in

Table 2. The experimental results of the grid-connected current.

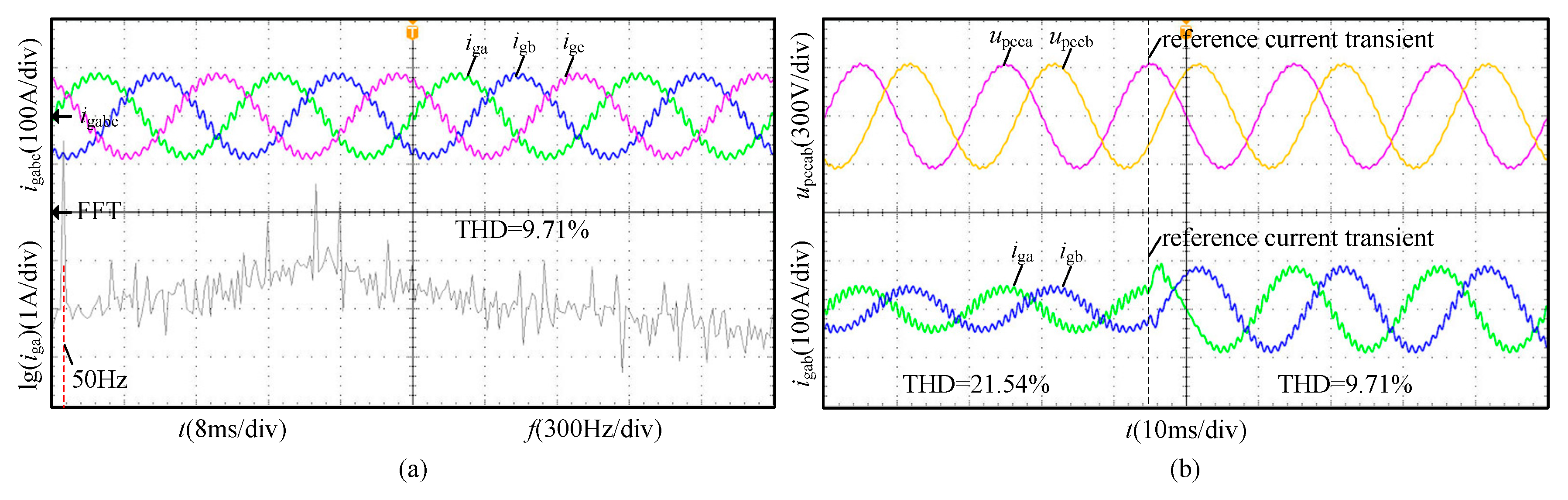
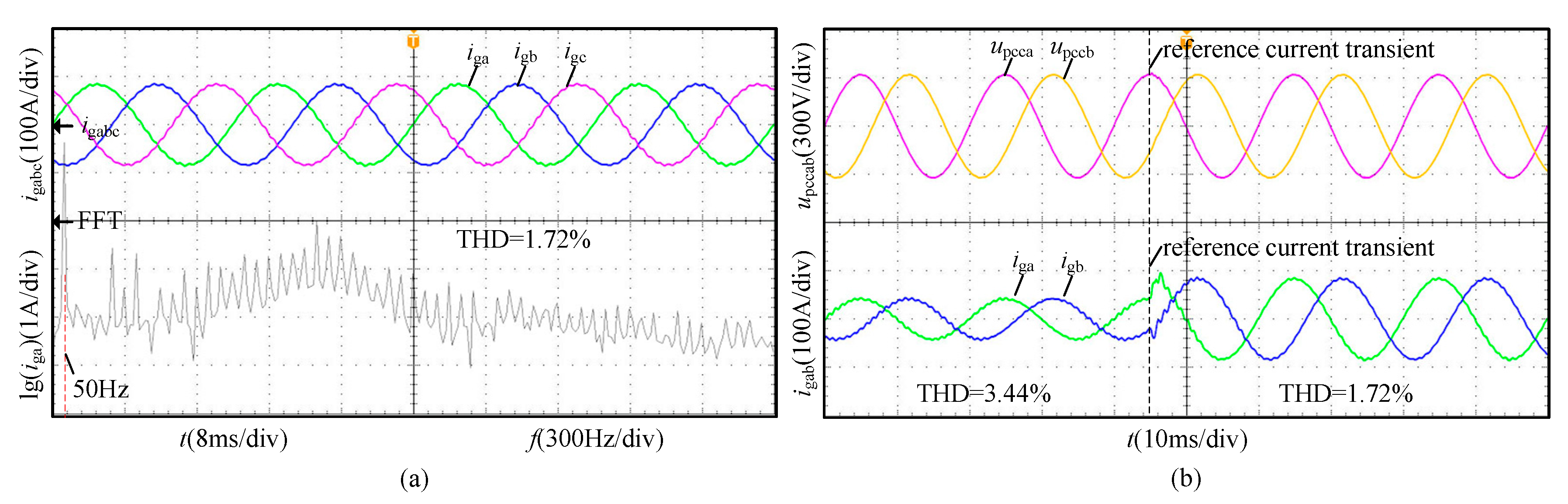
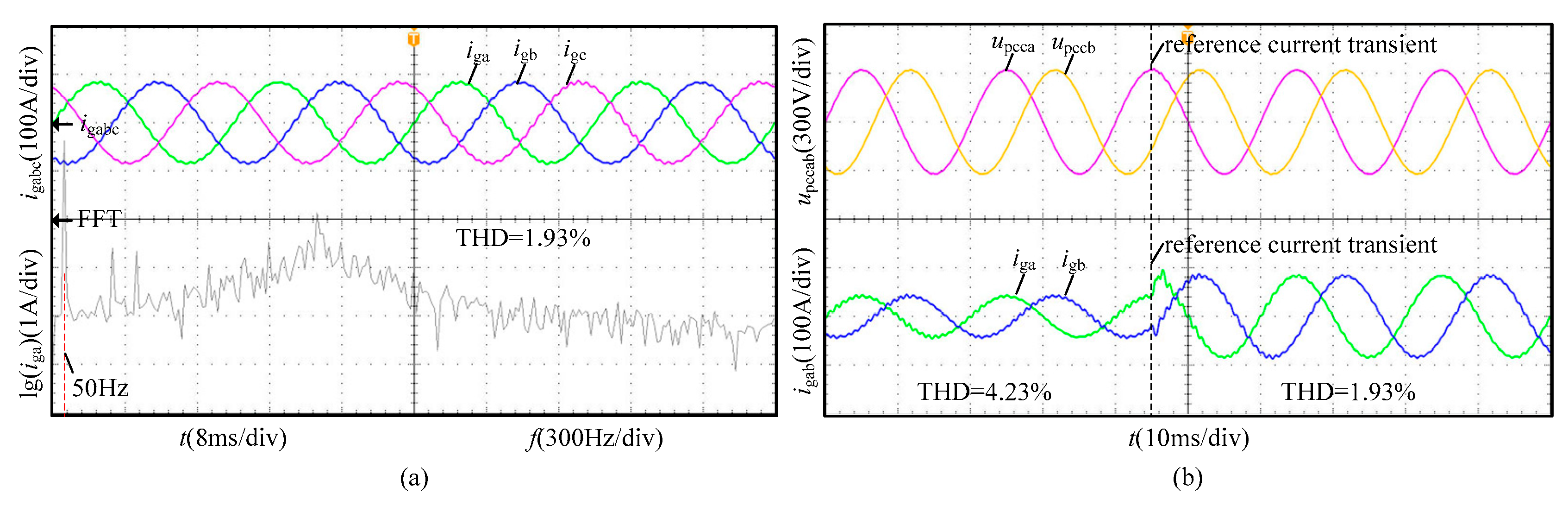
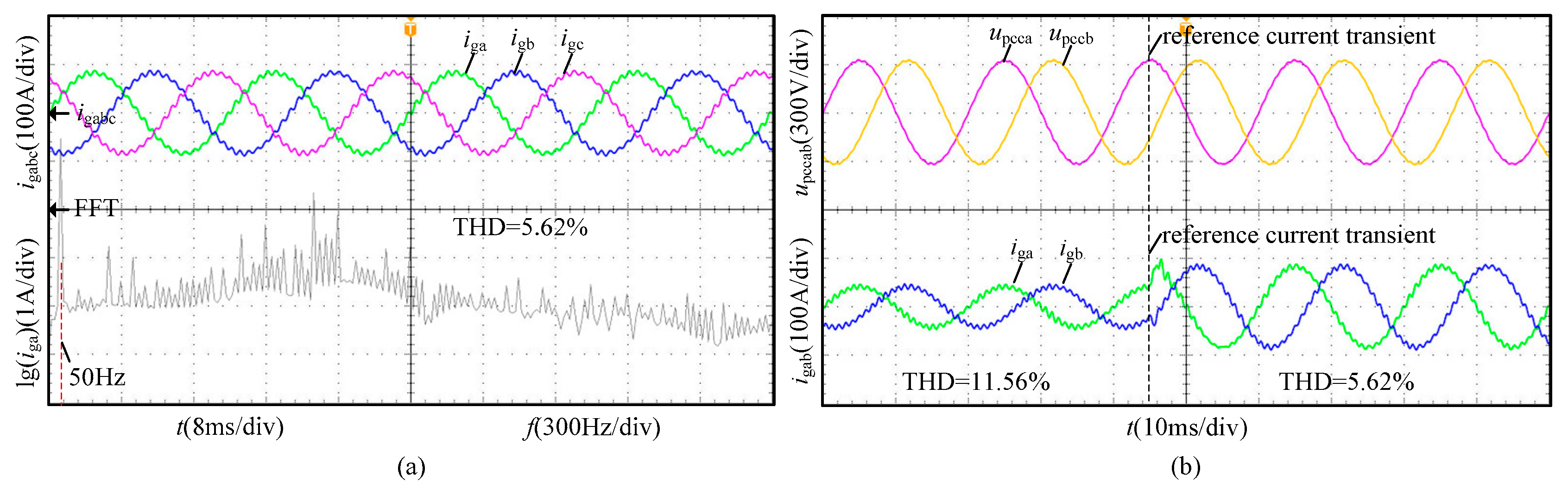
Case	THD of the Steady-State Grid-Connected Current
Traditional control method	9.71%
Admittance reshaping technique 1 (within the parameter design range)	1.72%
Admittance reshaping technique 2 (within the parameter design range)	1.93%
Admittance reshaping technique 1 (without the parameter design range)	5.62%
Admittance reshaping technique 2 (without the parameter design range)	5.84%

.

In the case of the traditional control method from Figure 15a, the total harmonic distortion (THD) of the steady-state grid-connected current is 9.71%. The harmonic contents of the grid-connected current are large. The reason is that the phase margin of the system may be insufficient using the traditional control method. Therefore, it is essential to propose the control method to increase the system phase margin.

To increase the system phase margin, admittance reshaping techniques 1 and 2 are proposed, which use a set of parameters within the design range shown in

Table 3. Different sets of parameters.

Case	ϕm	kp	kω	km
within the design range	−20°	2.04	6.16 × 10−4	1.43
without the design range	−10°	1.42	7.38 × 10−4	1.19

. In the case of the proposed admittance reshaping techniques 1 and 2 from Figure 16a and Figure 17a, the THD of the steady-state grid-connected currents are 1.72% and 1.93%. In both cases, the harmonic contents of the grid-connected current are greatly attenuated. The reason is that the proposed admittance reshaping techniques 1 and 2 increase the system damping and improve system stability. Therefore, the validity of the theoretical analysis is verified.

As can be seen in Figure 15b, Figure 16b and Figure 17b, the reference grid-connected current increases from 36.5A to 73A in the case of the traditional control method and the proposed admittance reshaping techniques 1 and 2. The transient experimental results in the three cases are similar. Therefore, compared with the traditional control method, the proposed admittance reshaping techniques 1 and 2 can ensure system dynamics.

To verify the reasonableness of the parameter design for the proposed admittance reshaping techniques 1 and 2, another set of parameters without the design range is shown in Table 3. The experimental waveforms of PCC voltage u_pcc and grid-connected current i_g in both cases are shown as Figure 18 and Figure 19. The experimental results of the grid-connected current in both cases are shown in Table 2.

From Figure 18a and Figure 19a, the THD of the steady-state grid-connected current is 5.62% and 5.84% in the case of the proposed control methods without the design range. The THD of the grid-connected current in both cases is less than that in Figure 15a with the traditional control method, but greater than that in Figure 16a and Figure 17a within the design range. The reason is that the phase margin of the system has been improved but it has not yet met sufficient stability of the system. Therefore, the reasonableness of the parameter design is verified for the proposed control methods.

As can be seen in Figure 15b, Figure 18b and Figure 19b, the reference grid-connected current increases from 36.5 A to 73 A and the transient experimental results in the three cases are similar. Therefore, compared with the traditional control method, the proposed control methods without the design range can also ensure the system dynamics.

5. Conclusions

The negative impact of PLL on system stability is caused by the range of negative incremental resistance. It will increase impedance coupling between inverters and grid, which reduces the system phase margin or leads to system instability. Therefore, two admittance reshaping control methods that consider the PLL effect are proposed to improve system damping. The first reshaping technique uses the feedforward PCC voltage to modify the inverter output admittance. The second reshaping technique adopts the active damping controller to reconstruct the PLL equivalent admittance. The proposed control methods not only increase the system phase margin but also ensure the system dynamic response speed. The total harmonic distortion of the steady-state grid-connected current is reduced to less than 2%. Furthermore, a specific design method of control parameters is depicted. Finally, experimental results are provided to prove the validity of the proposed control methods. Still, the paper does not study the effect of time delay on the proposed control methods, which is an important topic to be explored in the future.