One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials
Abstract
:1. Introduction
2. Evaluation of Logarithmic Function through Padé Polynomials
3. Initial Starting Point for the Proposed Iterative Method
- 1.
- The common approach is to choose an initial starting point from the zone of fully developed turbulent rough hydraulic flow , because in this special case of the Colebrook equation where , the equation is in explicit form with respect to ; , where is functional symbol [18,22]. Here the goal is to avoid use of logarithmic functions and therefore, this starting point is not suitable.
- 2.
- An efficient procedure for finding a sufficiently good initial starting point is proposed by Yun [35] in the integral form; Equation (8):
- 3.
- Every explicit approximation of the Colebrook equation [19,20,21,22,23,24,25,26,27,28]; , where is the functional symbol, can be used to choose an initial starting point . On the other hand, almost all available approximations contain logarithmic or/and terms with non-integer powers, which makes them unsuitable for use in the developed approach. On the other hand, having previous experience with training Artificial Neural Networks (ANN) to simulate the Colebrook equation [36], i.e., to use ability of artificial intelligence to simulate the Colebrook equation not knowing its logarithmic nature but only knowing raw input and corresponding output datasets , a computationally cheap explicit approximation of the Colebrook equation is developed through genetic programming [21,37,38,39,40]. The developed approximation is computationally efficient because of its polynomial structure; Equation (9):
- 4.
- Extensive tests over the domain of applicability of the Colebrook equation shows that one fixed value can also be used as the initial starting point for the iterative procedure in all cases. Results indicate that the proposed Padé approach works in all cases, as the argument z of ln(z) is always close to one. When Equation (9) is used, values of z are within the range 0.91–1.05. Moreover, for the most pairs of the Reynolds number and the relative roughness of inner pipe surfaces which are in the domain of applicability, the initial starting point requires the least number of iterations.
4. Proposed Iterative Method
5. Numerical Examples
| Example 1: | Example 2: | |
|---|---|---|
| , | , | |
| Iteration 0 | ||
| (9) | ||
| Iteration 1 | ||
| (11) | ||
| (12) | ||
| (10) | ||
| Iteration 2 | ||
| 0.034617535 | −0.001790646 | Padé approximant (6) |
| (14) | ||
| (13) | ||
| Iteration 3 | ||
| 0.033493733 | −0.001778995 | Padé approximant (6) |
| (16) | ||
| (15) | ||
| Final value: | ||
| = 4.22204103 | = 7.873172814 | |
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. (Lond.) 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.; White, C. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef] [Green Version]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- LaViolette, M. On the history, science, and technology included in the Moody diagram. J. Fluids Eng. 2017, 139, 030801. [Google Scholar] [CrossRef]
- Flack, K.A. Moving beyond Moody. J. Fluid Mech. 2018, 842, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Allen, J.J.; Shockling, M.A.; Kunkel, G.J.; Smits, A.J. Turbulent flow in smooth and rough pipes. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 699–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Langelandsvik, L.I.; Kunkel, G.J.; Smits, A.J. Flow in a commercial steel pipe. J. Fluid Mech. 2008, 595, 323–339. [Google Scholar] [CrossRef]
- McKeon, B.J.; Zagarola, M.V.; Smits, A.J. A new friction factor relationship for fully developed pipe flow. J. Fluid Mech. 2005, 538, 429–443. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Monte-Carlo-based reliability and vulnerability assessment of a natural gas transmission system due to random network component failures. Sustain. Resil. Infrastruct. 2017, 2, 97–107. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Giustolisi, O.; Berardi, L.; Walski, T.M. Some explicit formulations of Colebrook–White friction factor considering accuracy vs. computational speed. J. Hydroinform. 2011, 13, 401–418. [Google Scholar] [CrossRef] [Green Version]
- Danish, M.; Kumar, S.; Kumar, S. Approximate explicit analytical expressions of friction factor for flow of Bingham fluids in smooth pipes using Adomian decomposition method. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 239–251. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Constraints for using Lambert W function-based explicit Colebrook–White equation. J. Hydraul. Eng. 2004, 130, 929–931. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Brkić, D. W solutions of the CW equation for flow friction. Appl. Math. Lett. 2011, 24, 1379–1383. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. (eJSiE) 2017, 10, 2. Available online: http://epublications.bond.edu.au/ejsie/vol10/iss2/2 (accessed on 11 July 2018).
- Gregory, G.A.; Fogarasi, M. Alternate to standard friction factor equation. Oil Gas J. 1985, 83, 120–127. [Google Scholar]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef] [Green Version]
- Brkić, D.; Ćojbašić, Ž. Evolutionary optimization of Colebrook’s turbulent flow friction approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Brkić, D. Determining friction factors in turbulent pipe flow. Chem. Eng. 2012, 119, 34–39. [Google Scholar]
- Buzzelli, D. Calculating friction in one step. Mach. Des. 2008, 80, 54–55. [Google Scholar]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Serghides, T.K. Estimate friction factor accurately. Chem. Eng. 1984, 91, 63–64. [Google Scholar]
- Romeo, E.; Royo, C.; Monzón, A. Improved explicit equations for estimation of the friction factor in rough and smooth pipes. Chem. Eng. J. 2002, 86, 369–374. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion of “Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation” by Jagadeesh R. Sonnad and Chetan T. Goudar. J. Hydraul. Eng. 2008, 134, 1187. [Google Scholar] [CrossRef]
- Vatankhah, A.R.; Kouchakzadeh, S. Discussion of “Exact equations for pipe-flow problems”. J. Hydraul. Res. 2009, 47, 537–538. [Google Scholar] [CrossRef]
- Baker, G.A.; Graves-Morris, P. Padé approximants. In Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar] [CrossRef]
- Kropa, J.C. Calculator algorithms. Math. Mag. 1978, 51, 106–109. [Google Scholar] [CrossRef]
- Rising, G.R. Inside Your Calculator: From Simple Programs to Significant Insights; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Pineiro, J.A.; Ercegovac, M.D.; Bruguera, J.D. Algorithm and architecture for logarithm, exponential, and powering computation. IEEE Trans. Comput. 2004, 53, 1085–1096. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. 2017, 139, 031401. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Improved method of determining friction factor in pipes. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 941–949. [Google Scholar] [CrossRef]
- Yun, B.I. A non-iterative method for solving non-linear equations. Appl. Math. Comput. 2008, 198, 691–699. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Giustolisi, O.; Savić, D.A. A symbolic data-driven technique based on evolutionary polynomial regression. J. Hydroinform. 2006, 8, 207–222. [Google Scholar] [CrossRef]
- Petković, D.; Gocić, M.; Shamshirband, S. Adaptive Neuro-Fuzzy computing technique for precipitation estimation. Facta Univ. Ser. Mech. Eng. 2016, 14, 209–218. [Google Scholar] [CrossRef]
- Ćojbašić, Ž.; Brkić, D. Very accurate explicit approximations for calculation of the Colebrook friction factor. Int. J. Mech. Sci. 2013, 67, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Mitrev, R.; Tudjarov, B.; Todorov, T. Cloud-based expert system for synthesis and evolutionary optimization of planar linkages. Facta Univ. Ser. Mech. Eng. 2018. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef] [PubMed]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evol. Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef] [Green Version]
- Альтшуль, А.Д. Гидравлические Сопротивления; Недра: Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Lipovka, A.Y.; Lipovka, Y.L. Determining hydraulic friction factor for pipeline systems. Journal of Siberian Federal University. Eng. Technol. 2014, 7, 62–82. Available online: http://elib.sfu-kras.ru/handle/2311/10293 (accessed on 11 July 2018).
- Черникин, В.А.; Черникин, А.В. Обобщенная формула для расчета коэффициента гидравлического сопротивления магистральных трубопроводов для светлых нефтепродуктов и маловязких нефтей. Наука и Технологии Трубопроводного Транспорта Нефти и Нефтепродуктов 2012, 4, 64–66. (In Russian) [Google Scholar]
- Abbasbandy, S. Improving Newton–Raphson method for nonlinear equations by modified Adomian decomposition method. Appl. Math. Comput. 2003, 145, 887–893. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Discussion of “Approximate analytical solutions for the Colebrook equation”. J. Hydraul. Eng. 2019, 144, 06018007. [Google Scholar]
- Džunić, J.; Petković, M.S.; Petković, L.D. A family of optimal three-point methods for solving nonlinear equations using two parametric functions. Appl. Math. Comput. 2011, 217, 7612–7619. [Google Scholar] [CrossRef]
- Haaland, S.E. Simple and explicit formulas for the friction factor in turbulent pipe flow. J. Fluids Eng. 1983, 105, 89–90. [Google Scholar] [CrossRef]
- Wood, D.J.; Haaland, S.E. Discussion and closure: “Simple and explicit formulas for the friction factor in turbulent pipe flow” (Haaland, S.E., 1983, ASME J. Fluids Eng., 105, pp. 89–90). J. Fluids Eng. 1983, 105, 242–243. [Google Scholar] [CrossRef]
- Praks, P.; Kopustinskas, V.; Masera, M. Probabilistic modelling of security of supply in gas networks and evaluation of new infrastructure. Reliab. Eng. Syst. Saf. 2015, 144, 254–264. [Google Scholar] [CrossRef]
- Brkić, D. Spreadsheet-based pipe networks analysis for teaching and learning purpose. Spreadsheets Educ. (eJSiE) 2016, 9, 4. Available online: https://epublications.bond.edu.au/ejsie/vol9/iss2/4/ (accessed on 11 July 2018).
- Brkić, D. Discussion of “Economics and statistical evaluations of using Microsoft Excel solver in pipe network analysis” by I.A. Oke, A. Ismail, S. Lukman, S.O. Ojo, O.O. Adeosun, and M.O. Nwude. J. Pipeline Syst. Eng. Pract. 2018, 9, 07018002. [Google Scholar] [CrossRef]
- Brkić, D. Iterative methods for looped network pipeline calculation. Water Resour. Manag. 2011, 25, 2951–2987. [Google Scholar] [CrossRef]
- Brkić, D. A gas distribution network hydraulic problem from practice. Petrol. Sci. Technol. 2011, 29, 366–377. [Google Scholar] [CrossRef]
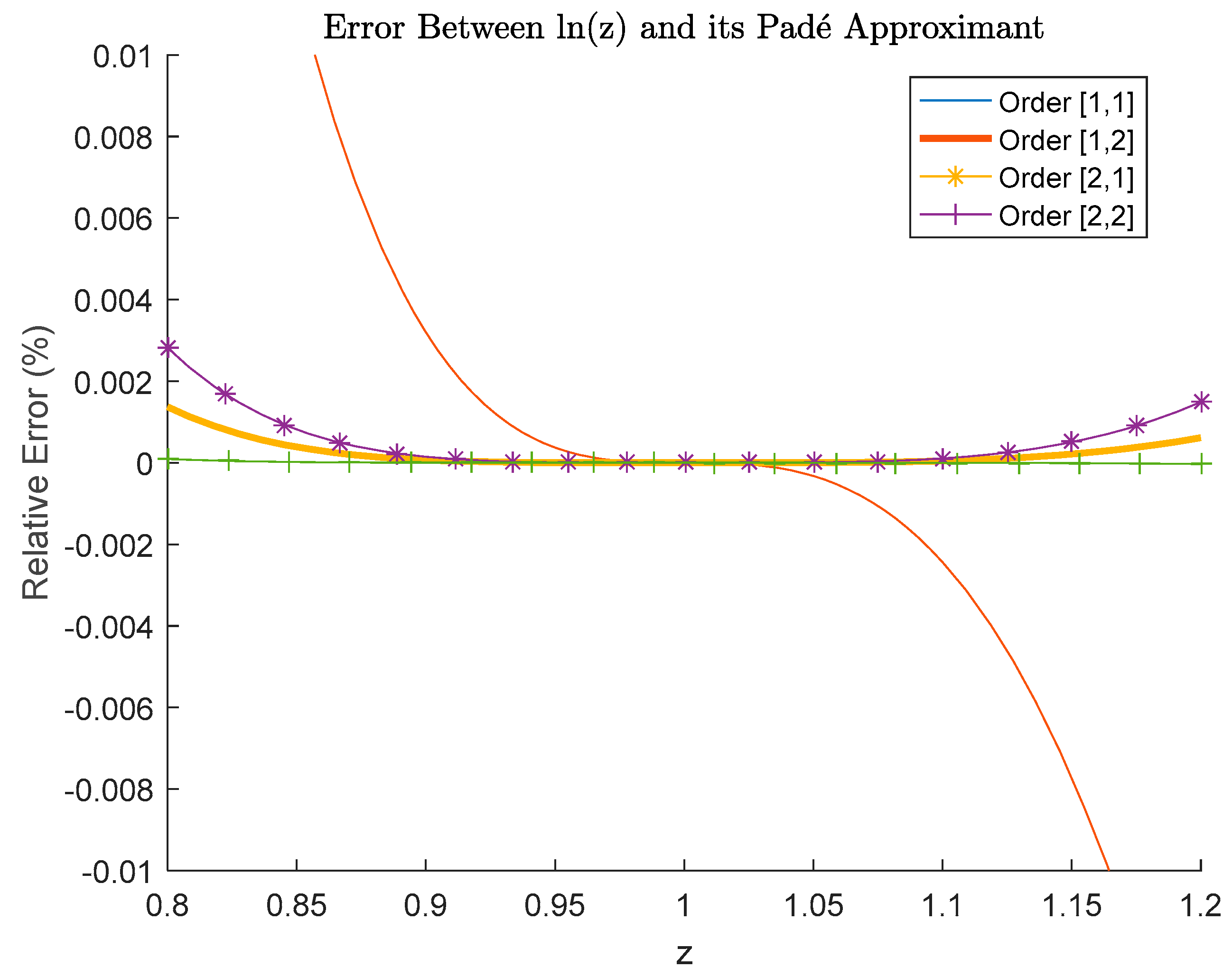

| z | Padé Approximants (2,3) | Relative Error % | |
|---|---|---|---|
| 0.6 | −0.22184875 | −0.221847398 | 6.1 × 10−4% |
| 0.65 | −0.187086643 | −0.187086228 | 2.2 × 10−4% |
| 0.7 | −0.15490196 | −0.154901848 | 7.2 × 10−5% |
| 0.75 | −0.124938737 | −0.124938712 | 2.0 × 10−5% |
| 0.8 | −0.096910013 | −0.096910009 | 4.4 × 10−6% |
| 0.85 | −0.070581074 | −0.070581074 | 6.6 × 10−7% |
| 0.9 | −0.045757491 | −0.045757491 | 4.9 × 10−8% |
| 0.95 | −0.022276395 | −0.022276395 | 6.5 × 10−10% |
| 1 | 0 | 0 | 0% |
| 1.05 | 0.021189299 | 0.021189299 | 4.8 × 10−10% |
| 1.1 | 0.041392685 | 0.041392685 | 2.7 × 10−8% |
| 1.15 | 0.06069784 | 0.06069784 | 2.7 × 10−7% |
| 1.2 | 0.079181246 | 0.079181245 | 1.3 × 10−6% |
| 1.25 | 0.096910013 | 0.096910009 | 4.4 × 10−6% |
| 1.3 | 0.113943352 | 0.113943339 | 1.2 × 10−5% |
| 1.35 | 0.130333768 | 0.130333735 | 2.6 × 10−5% |
| 1.4 | 0.146128036 | 0.146127961 | 5.1 × 10−5% |
| 1.45 | 0.161368002 | 0.161367854 | 9.2 × 10−5% |
| 1.5 | 0.176091259 | 0.176090987 | 1.5 × 10−4% |
| 1.55 | 0.190331698 | 0.190331231 | 2.5 × 10−4% |
| 1.6 | 0.204119983 | 0.204119223 | 3.7 × 10−4% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praks, P.; Brkić, D. One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials. Energies 2018, 11, 1825. https://doi.org/10.3390/en11071825
Praks P, Brkić D. One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials. Energies. 2018; 11(7):1825. https://doi.org/10.3390/en11071825
Chicago/Turabian StylePraks, Pavel, and Dejan Brkić. 2018. "One-Log Call Iterative Solution of the Colebrook Equation for Flow Friction Based on Padé Polynomials" Energies 11, no. 7: 1825. https://doi.org/10.3390/en11071825






