Optimization Scheduling Method for Power Systems Considering Optimal Wind Power Intervals
Abstract
:1. Introduction
- (1)
- A UC model considering the optimal wind power confidence intervals is established to balance the economic costs and risk of the dispatch plan for the power system with wind power integration.
- (2)
- The UC model is a mixed integer nonlinear programming (MINLP) problem with integral terms in its objective, and both the integrand function and integral upper/lower bound contain decision variables. The objective function is linearized and solved by discretizing the wind power probability density function and using auxiliary variables.
- (3)
- Based on the UC model, in addition to optimal wind power confidence intervals, the dynamic adjustment cost is introduced into intra-day rolling dispatch model to reduce the amount of adjustments among different rolling dispatch plans.
2. Overall Framework and Representation of Wind Power Uncertainty
2.1. Overall Framework
- (1)
- Day-ahead UC. It is a mixed integer nonlinear programming problem with the goal of minimizing the economic cost and risk cost. The UC for the next operating day is performed in current operation day, and it provides the UC plan of 24 h for the next day.
- (2)
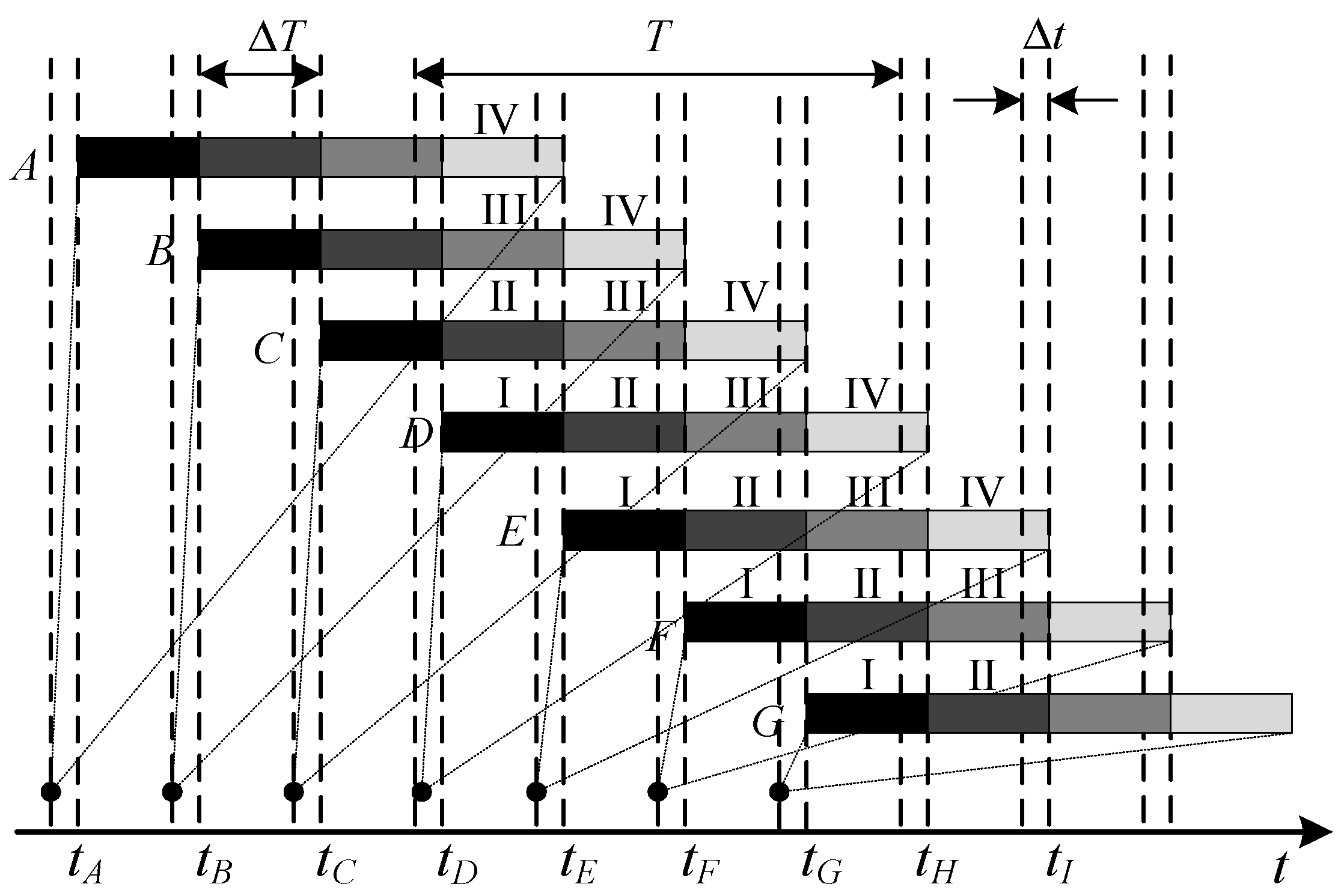
- Intra-day rolling dispatch. Based on the latest load and wind power forecasting information, it is activated every 1 h to modify the power generation output of the next 4 h in a rolling manner. In each rolling plan, only the dispatch plan of the first hour is actually executed.
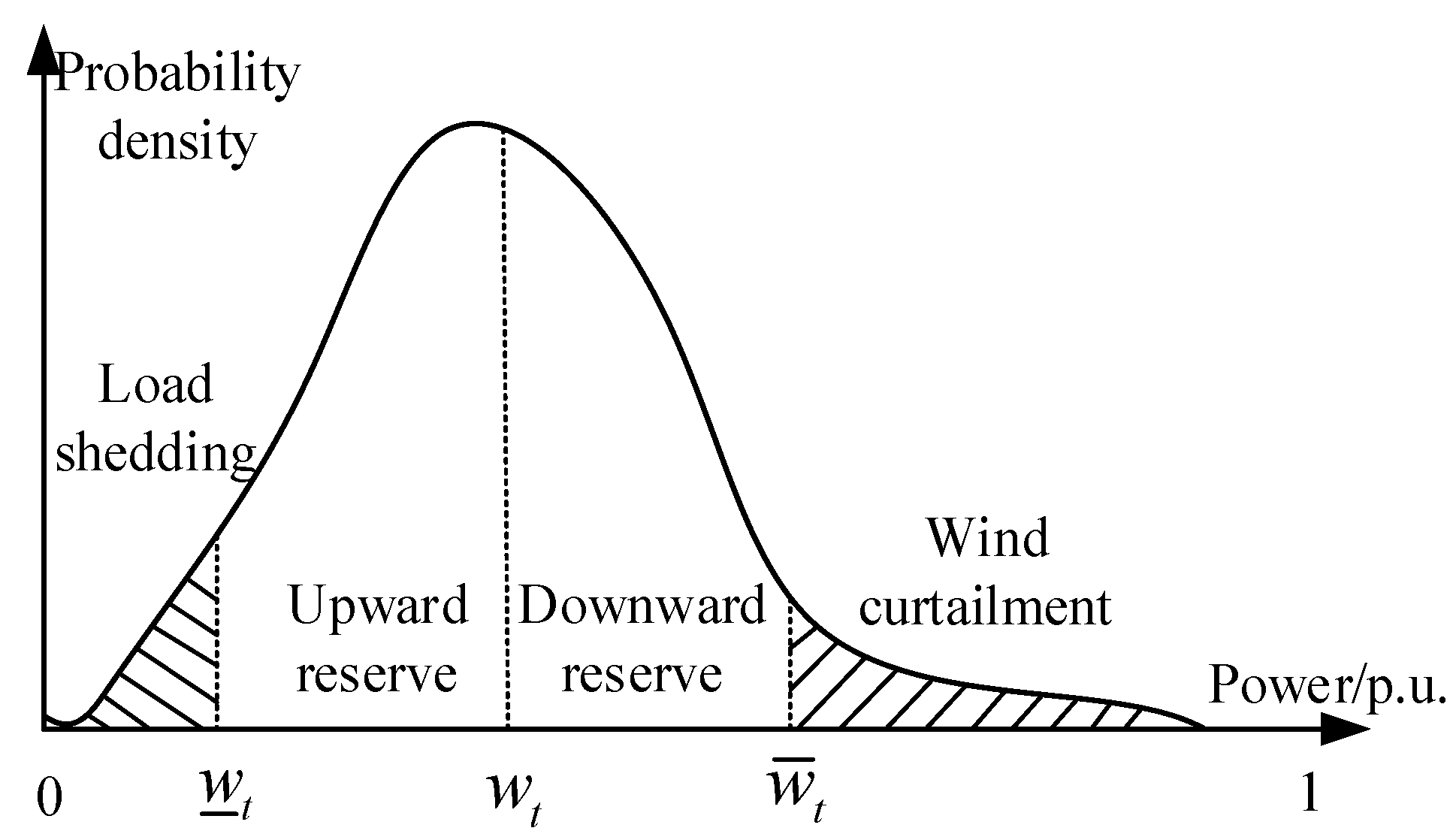
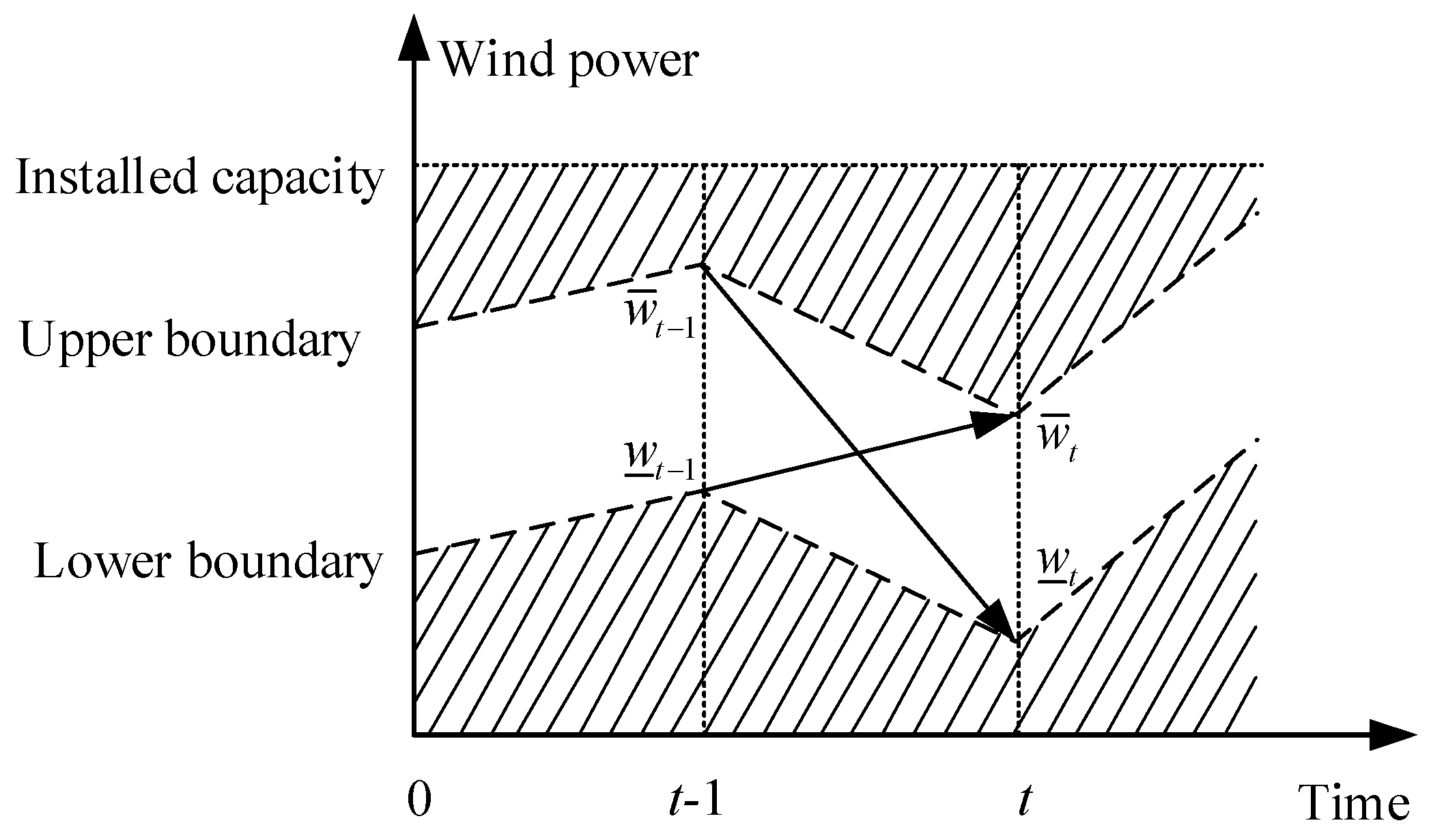
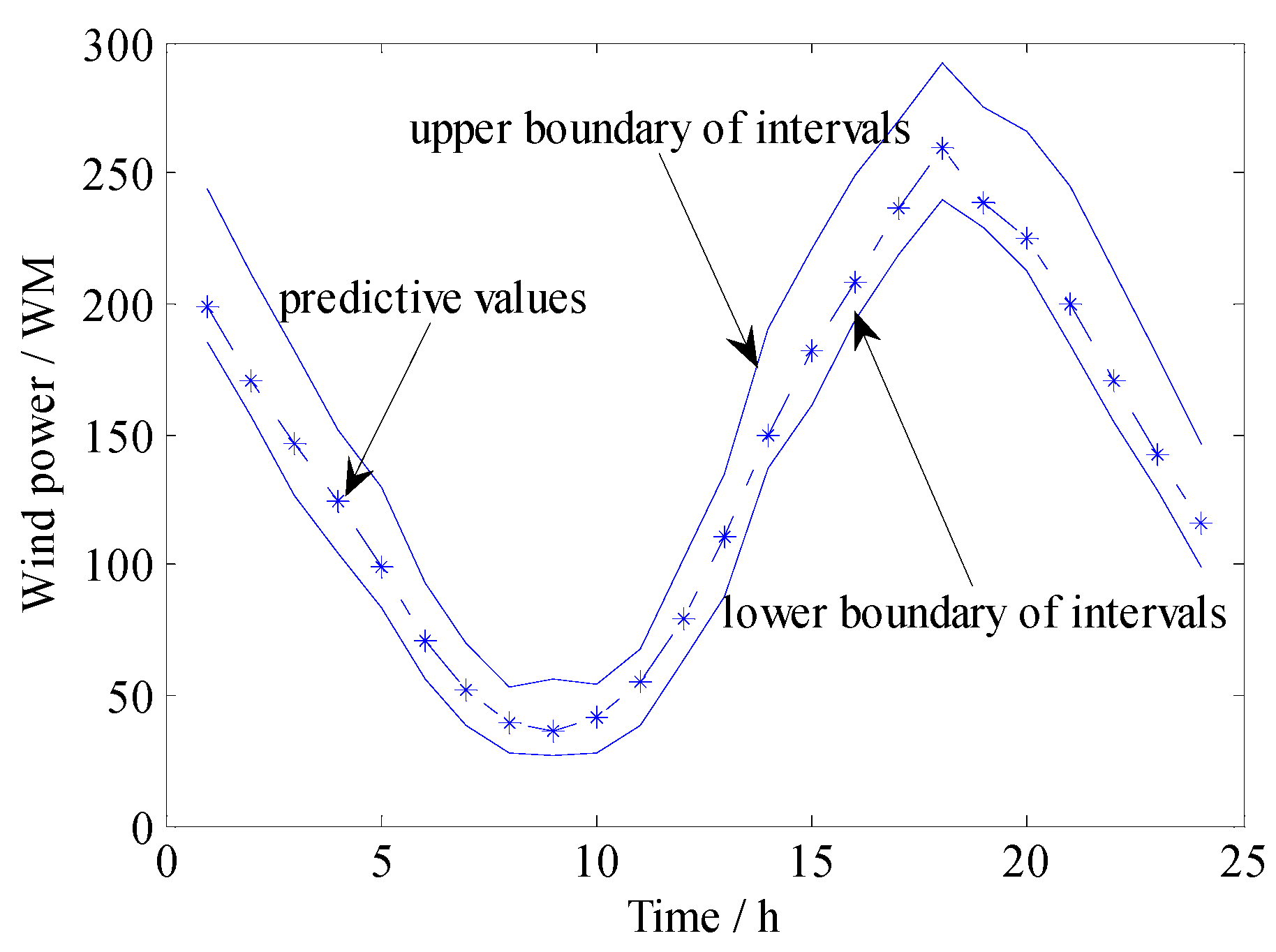
2.2. Representation of Wind Power Uncertainty
3. The Proposed Model
3.1. UC Model Based on Optimal Conficence Level
3.1.1. Objective
3.1.2. Constraints
- (1)
- Supply-demand balance constraints:where Pi,t is the active output of unit i in period t. wj,t is the schedule value of wind farm j in period t. is the load forecast value in period t.
- (2)
- Thermal power plants output constraints:where and are the upper and lower limits of the output of unit i.
- (3)
- Unit segment output constraints:where is the maximum output of unit i on segment m.
- (4)
- Unit ramping up and down constraints:where URi, DRi are the maximum up and down ramp rate of unit i.
- (5)
- Unit minimum ON and OFF time limits:where and are the minimum start-up time and shut-down time for unit i, respectively.
- (6)
- Unit upward and downward reserves constraints:
3.2. Rolling Dispatch Model
3.2.1. Objective
3.2.2. Constraints
3.3. Model Transformation and Solution
4. Simulation and Discussion
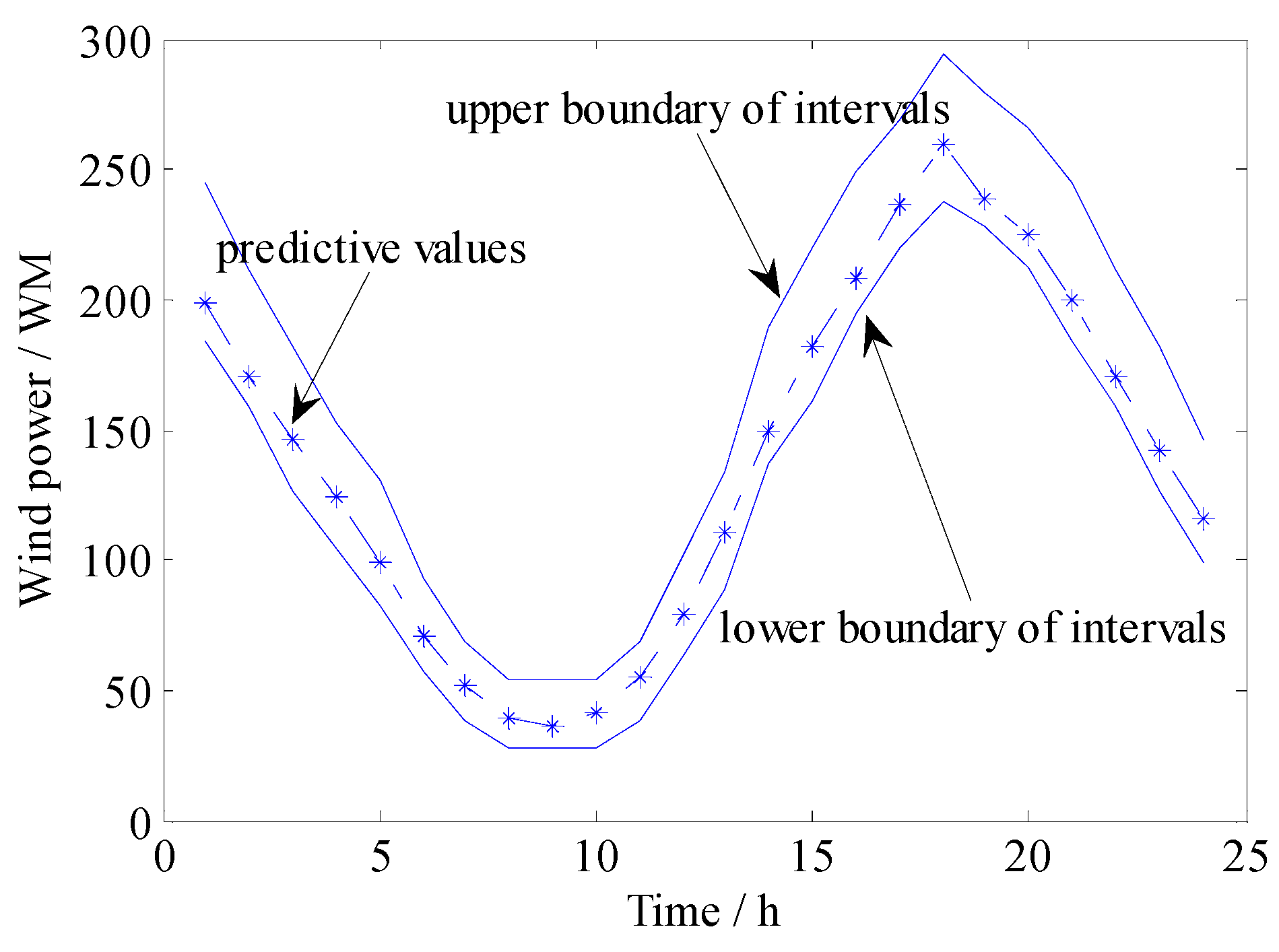
4.1. Data and Parameters Setting
4.2. Results of UC Model
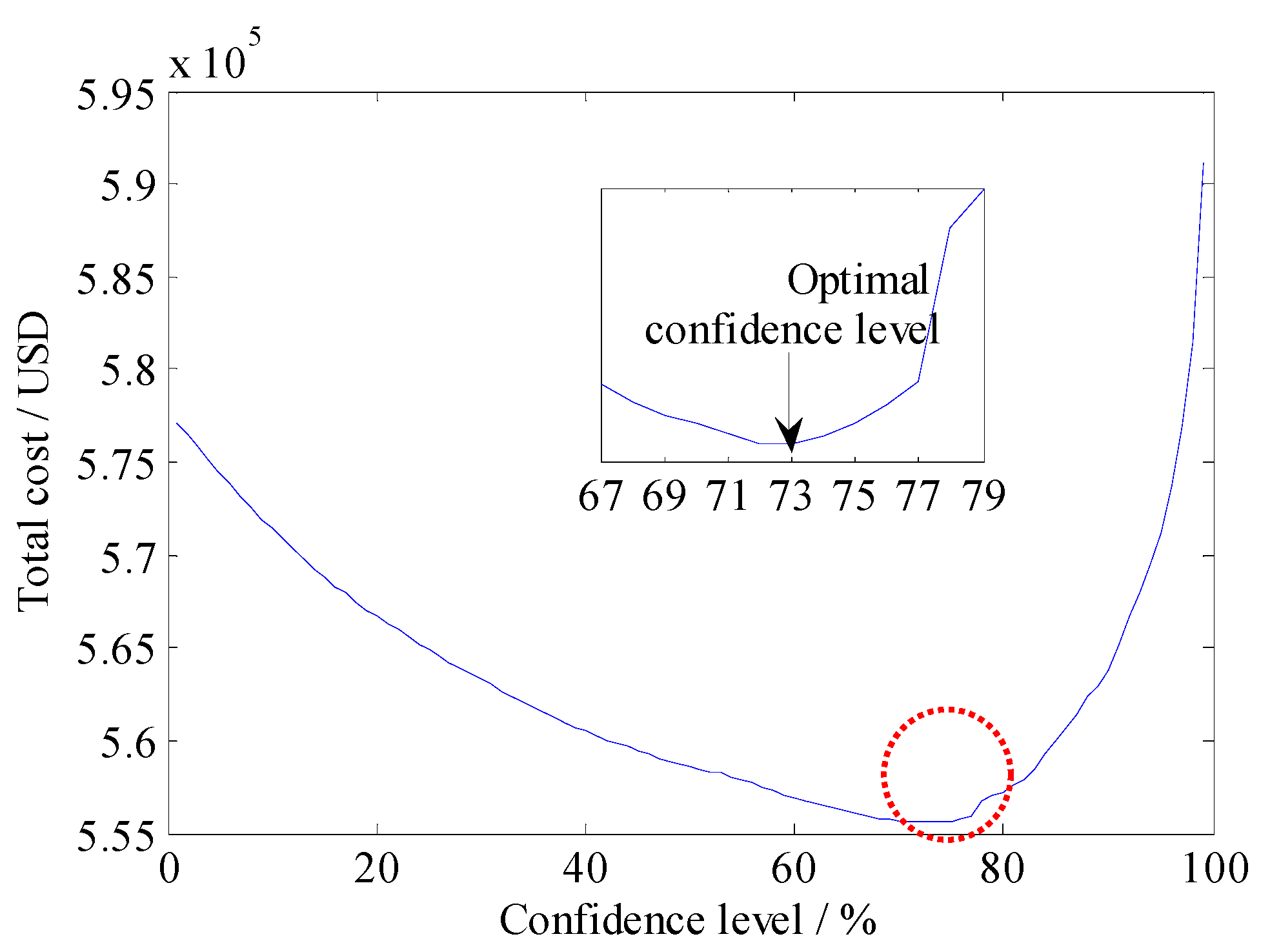
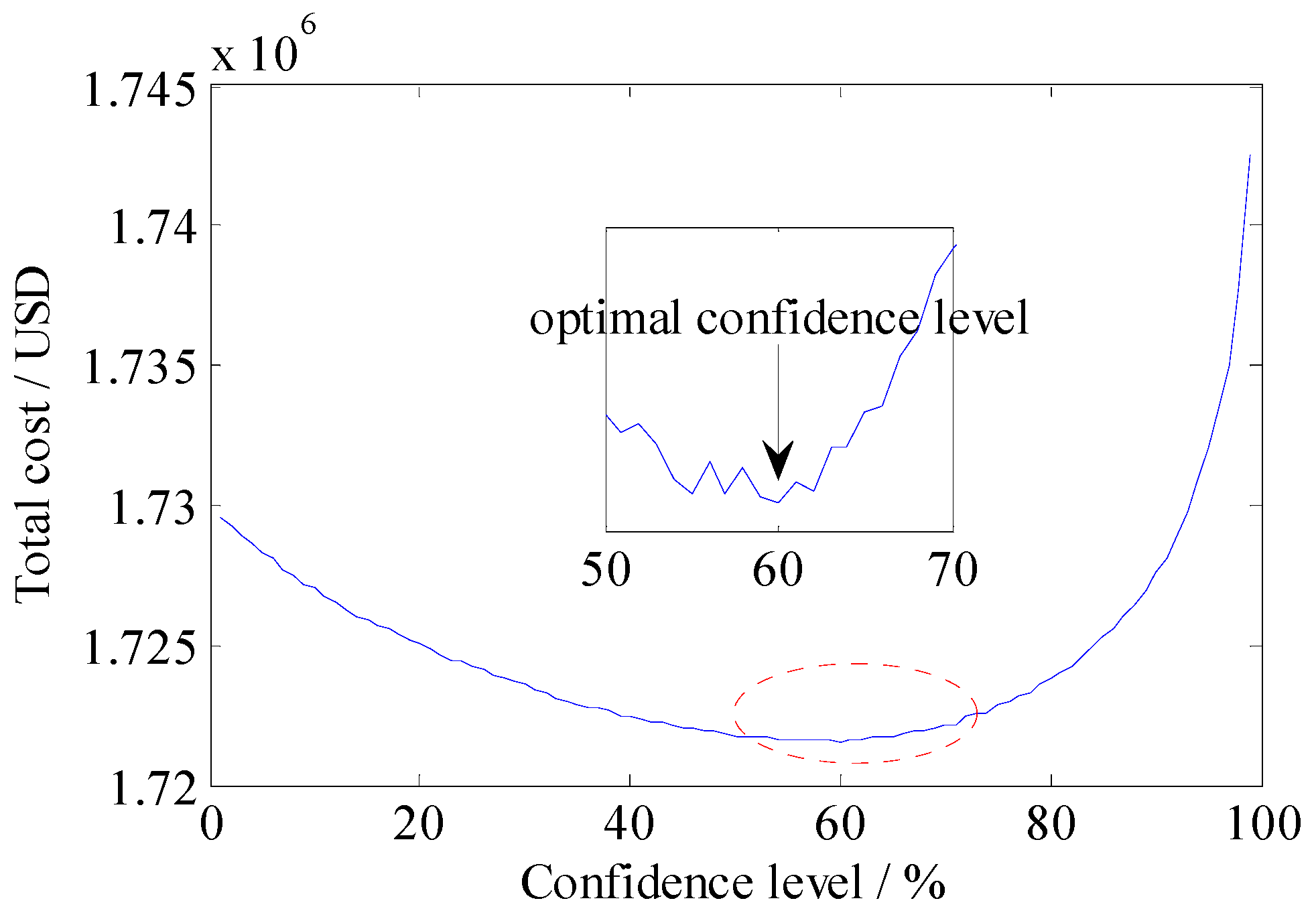
4.2.1. Case 1 and Case 2
4.2.2. Case 3 and Case 4
4.3. Rolling Dispatch Model Results
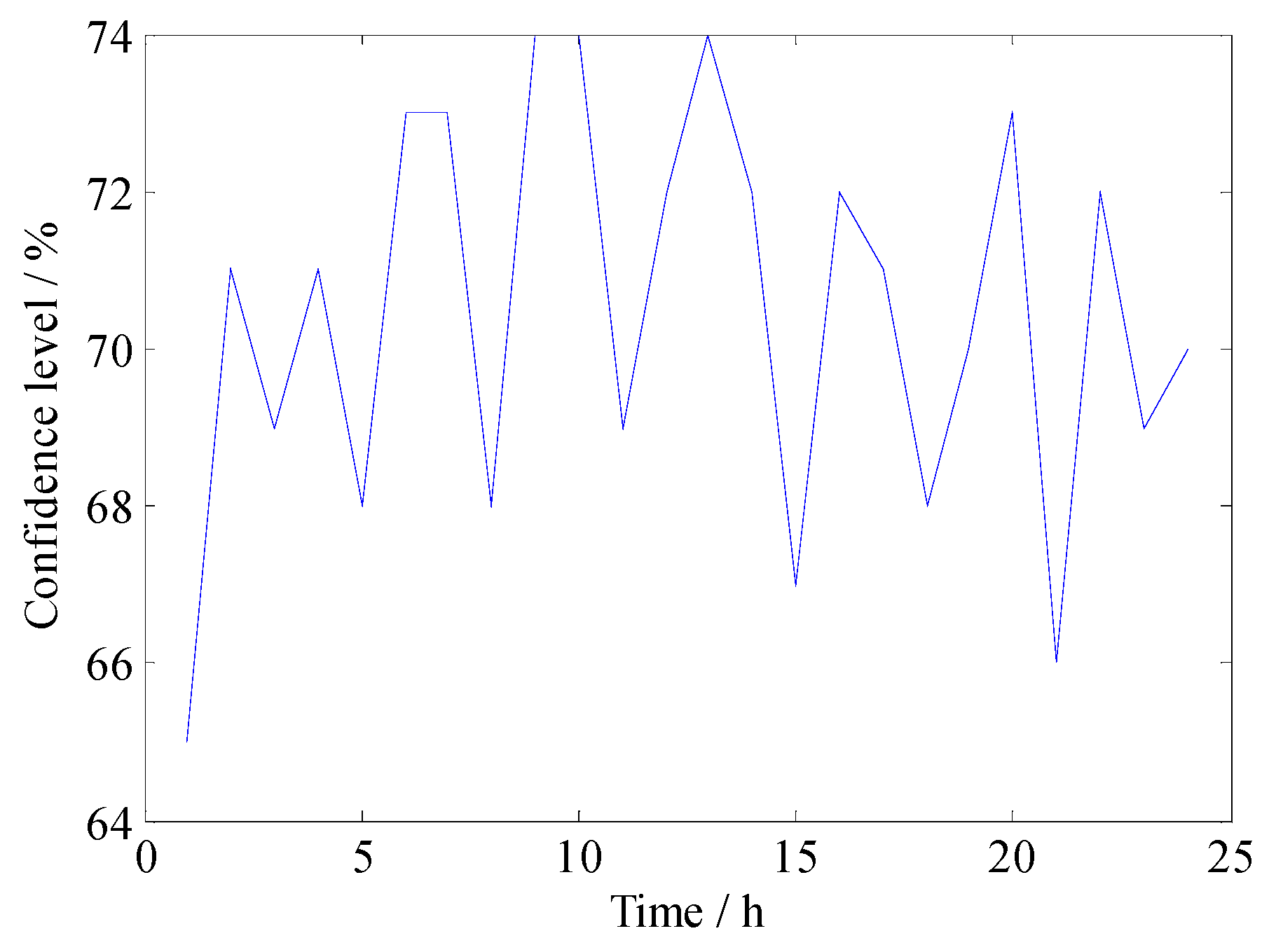
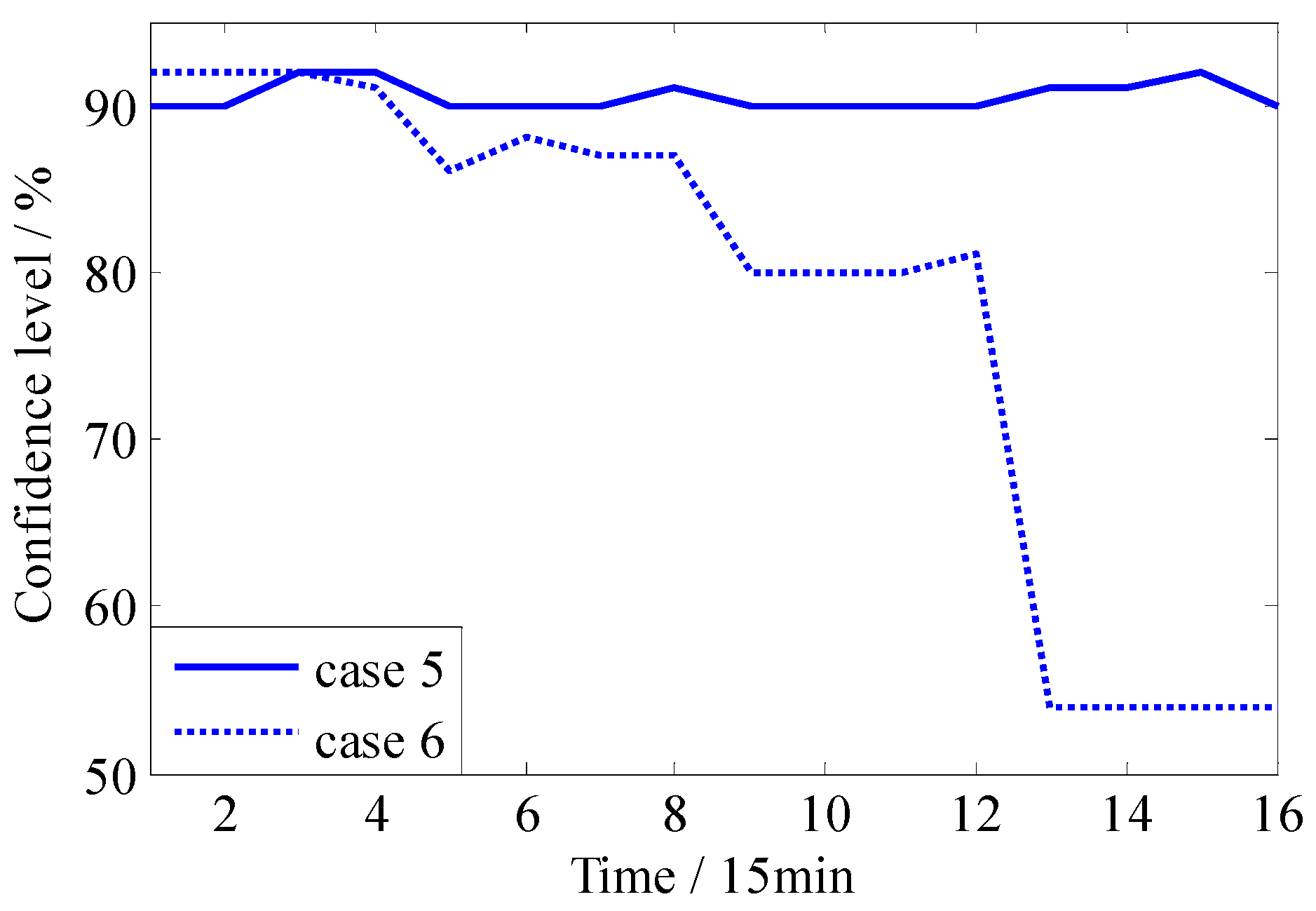
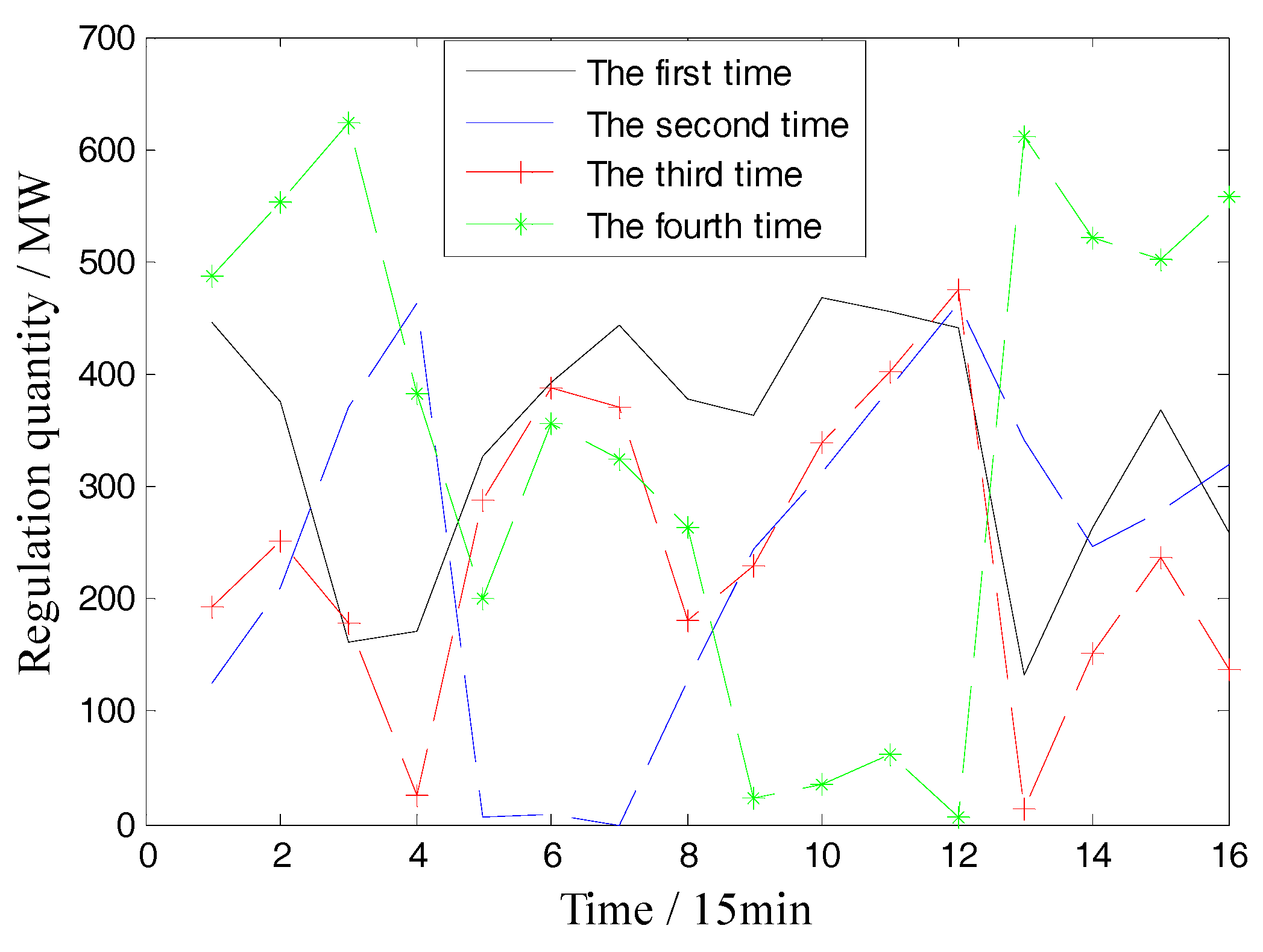
4.3.1. Comparison of Case 5 and Case 6
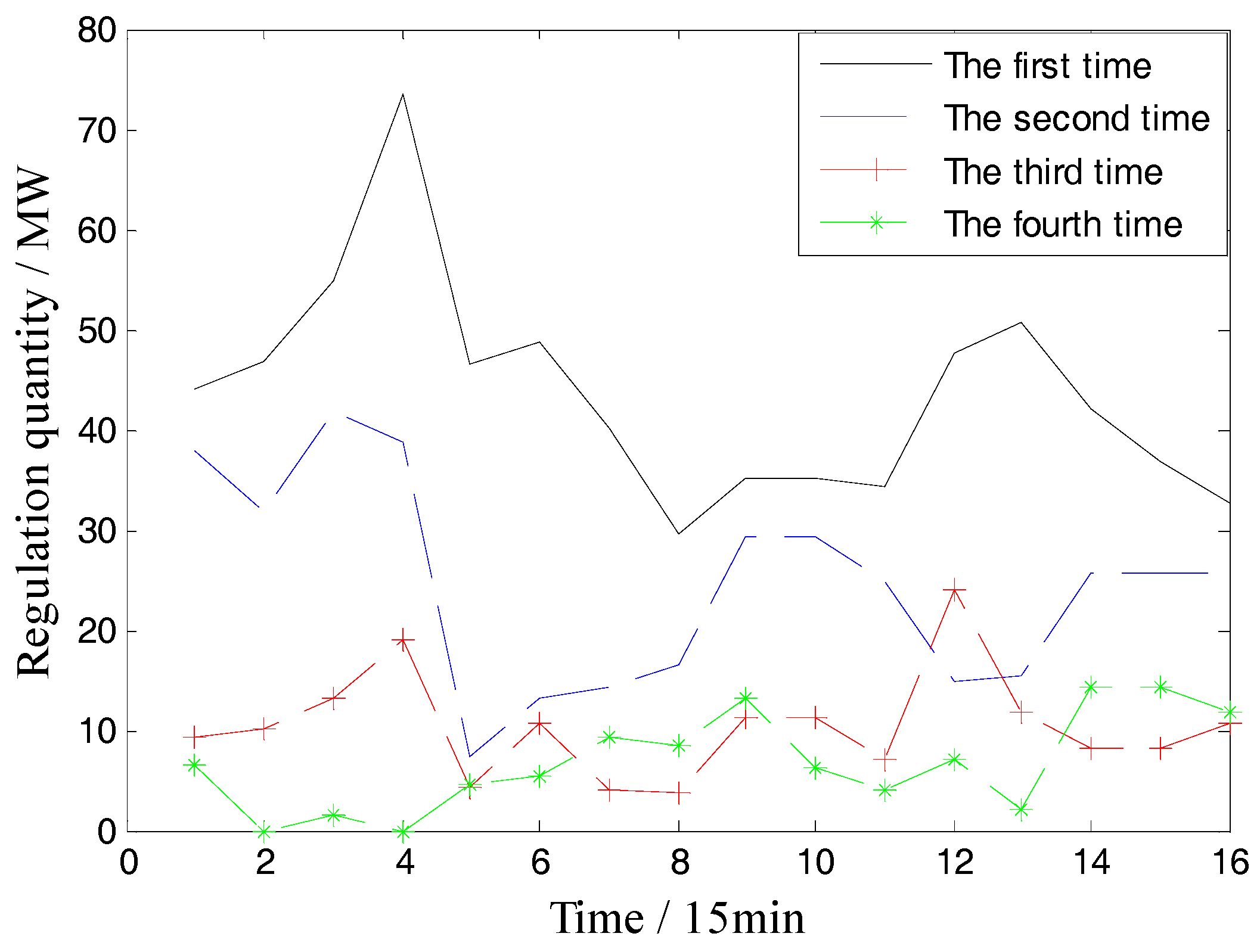
4.3.2. Comparison of Case 6 and Case 7
5. Conclusions
- (1)
- The simulation results show that as the wind power confidence level changes, there is a tradeoff between the economic cost and risk cost. The global optimal point which balance the economic cost and risk cost of the system can be effectively obtained by the proposed model.
- (2)
- The simulation results of intra-day rolling dispatch model shows that this model can help to reduce the regulation quantity and avoid repeated regulations, thereby reducing the overall cost within the scheduling periods.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Time Period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wind power | 0.57 | 0.49 | 0.42 | 0.36 | 0.28 | 0.2 | 0.15 | 0.11 | 0.1 | 0.12 | 0.16 | 0.23 |
| Time period | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Wind power | 0.32 | 0.43 | 0.52 | 0.59 | 0.68 | 0.74 | 0.68 | 0.64 | 0.57 | 0.49 | 0.41 | 0.33 |
| Number | Time Period | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 1 | 0.12 | 0.14 | 0.16 | 0.18 | 0.23 | 0.24 | 0.26 | 0.26 | 0.26 | 0.28 | 0.32 | 0.35 | 0.41 | 0.44 | 0.47 | 0.51 |
| 2 | 0.22 | 0.23 | 0.25 | 0.25 | 0.25 | 0.27 | 0.31 | 0.34 | 0.4 | 0.43 | 0.46 | 0.5 | 0.57 | 0.61 | 0.62 | 0.62 |
| 3 | 0.25 | 0.27 | 0.3 | 0.33 | 0.39 | 0.42 | 0.44 | 0.48 | 0.55 | 0.59 | 0.6 | 0.61 | 0.68 | 0.68 | 0.7 | 0.75 |
| 4 | 0.38 | 0.41 | 0.43 | 0.47 | 0.53 | 0.57 | 0.58 | 0.58 | 0.66 | 0.66 | 0.68 | 0.73 | 0.77 | 0.81 | 0.81 | 0.82 |
| 5 | 0.52 | 0.56 | 0.56 | 0.57 | 0.64 | 0.64 | 0.65 | 0.7 | 0.78 | 0.82 | 0.83 | 0.83 | 0.85 | 0.82 | 0.77 | 0.74 |
| 6 | 0.62 | 0.62 | 0.64 | 0.68 | 0.76 | 0.79 | 0.8 | 0.8 | 0.83 | 0.8 | 0.75 | 0.72 | 0.67 | 0.66 | 0.69 | 0.68 |
| 7 | 0.74 | 0.77 | 0.77 | 0.78 | 0.8 | 0.77 | 0.72 | 0.69 | 0.65 | 0.64 | 0.67 | 0.67 | 0.65 | 0.61 | 0.54 | 0.52 |
| Time Period | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Load | 700 | 750 | 850 | 950 | 1000 | 1100 | 1150 | 1200 | 1300 | 1400 | 1500 | 1550 |
| Time period | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Load | 1400 | 1300 | 1200 | 1050 | 1000 | 1100 | 1200 | 1400 | 1300 | 1100 | 900 | 800 |
| μ1 | μ2 | μ3 | μ4 | ||||
|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 5 | 1 | 0.5 | 0.1 |
| Period | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | G9 | G10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 455 | 247.1 | 130 | 130 | 162 | 50.1 | 0 | 0 | 0 | 0 |
| 2 | 455 | 210.2 | 130 | 130 | 162 | 48.8 | 0 | 0 | 0 | 0 |
| 3 | 455 | 270.2 | 60 | 107.5 | 162 | 48.1 | 0 | 0 | 0 | 0 |
| 4 | 455 | 330.2 | 20 | 70 | 144.3 | 43.2 | 0 | 0 | 0 | 0 |
| 5 | 358.4 | 455 | 0 | 0 | 162 | 41.8 | 0 | 0 | 0 | 0 |
| 6 | 314.2 | 455 | 0 | 0 | 162 | 38.1 | 0 | 0 | 0 | 0 |
| 7 | 261.2 | 455 | 0 | 0 | 162 | 44.8 | 0 | 0 | 0 | 0 |
| 8 | 222.2 | 455 | 0 | 0 | 162 | 44.8 | 0 | 0 | 0 | 0 |
| 9 | 168.3 | 455 | 0 | 0 | 162 | 43.1 | 0 | 0 | 0 | 0 |
| 10 | 150 | 451.7 | 0 | 0 | 162 | 42.7 | 0 | 0 | 0 | 0 |
| 11 | 150 | 454.7 | 0 | 0 | 133.6 | 43.1 | 0 | 0 | 0 | 0 |
| 12 | 150 | 455 | 0 | 0 | 73.6 | 74.2 | 0 | 0 | 0 | 0 |
| 13 | 150 | 455 | 0 | 0 | 93.4 | 47.7 | 0 | 0 | 0 | 0 |
| 14 | 150 | 455 | 0 | 0 | 74.4 | 80 | 0 | 0 | 0 | 0 |
| 15 | 150 | 455 | 0 | 0 | 102 | 78.4 | 0 | 0 | 0 | 0 |
| 16 | 154.5 | 455 | 0 | 0 | 162 | 42.9 | 0 | 0 | 0 | 0 |
| Period | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | G9 | G10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 455 | 455 | 130 | 20 | 43.7 | 70.5 | 0 | 0 | 0 | 0 |
| 2 | 455 | 455 | 107.4 | 20 | 25 | 73.6 | 0 | 0 | 0 | 0 |
| 3 | 455 | 455 | 78.6 | 20 | 25 | 69.2 | 0 | 0 | 0 | 0 |
| 4 | 428.1 | 395 | 70 | 70 | 25 | 74.6 | 0 | 0 | 0 | 0 |
| 5 | 358.4 | 455 | 0 | 0 | 162 | 41.8 | 0 | 0 | 0 | 0 |
| 6 | 314.2 | 455 | 0 | 0 | 162 | 38.1 | 0 | 0 | 0 | 0 |
| 7 | 261.2 | 455 | 0 | 0 | 162 | 44.8 | 0 | 0 | 0 | 0 |
| 8 | 222.2 | 455 | 0 | 0 | 162 | 44.8 | 0 | 0 | 0 | 0 |
| 9 | 168.3 | 455 | 0 | 0 | 162 | 43.1 | 0 | 0 | 0 | 0 |
| 10 | 150 | 451.7 | 0 | 0 | 162 | 42.7 | 0 | 0 | 0 | 0 |
| 11 | 150 | 427.1 | 0 | 0 | 133.6 | 70.7 | 0 | 0 | 0 | 0 |
| 12 | 150 | 455 | 0 | 0 | 73.6 | 74.2 | 0 | 0 | 0 | 0 |
| 13 | 455 | 200.7 | 0 | 0 | 25 | 65.5 | 0 | 0 | 0 | 0 |
| 14 | 455 | 199 | 0 | 0 | 25.4 | 80 | 0 | 0 | 0 | 0 |
| 15 | 455 | 225 | 0 | 0 | 25.4 | 80 | 0 | 0 | 0 | 0 |
| 16 | 455 | 254 | 0 | 0 | 25.4 | 80 | 0 | 0 | 0 | 0 |
References
- Zavala, E.M.V.M.; Rocklin, M. A computational framework for uncertainty quantification and stochastic optimization in unit commitment with wind power generation. IEEE Trans. Power Syst. 2011, 26, 431–441. [Google Scholar]
- Qianfan, W.; Yongpei, G.; Jianhui, W. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output. IEEE Trans. Power Syst. 2012, 27, 206–215. [Google Scholar]
- Lorca, Á.; Sun, X.A. Adaptive robust optimization with dynamic uncertainty sets for multi-period economic dispatch under significant wind. IEEE Trans. Power Syst. 2015, 30, 1702–1713. [Google Scholar] [CrossRef]
- Yu, Y.; Luh, P.B.; Litvinov, E. Grid integration of distributed wind generation: Hybrid markovian and interval unit commitment. IEEE Trans. Smart Grid 2015, 6, 3061–3072. [Google Scholar] [CrossRef]
- Wu, W.; Chen, J.; Zhang, B. A robust wind power optimization method for look-ahead power dispatch. IEEE Trans. Sustain. Energy 2014, 5, 507–515. [Google Scholar] [CrossRef]
- Doostizadeh, M.; Aminifar, F.; Ghasemi, H. Energy and reserve scheduling under wind power uncertainty: An adjustable interval approach. IEEE Trans. Smart Grid 2016, 7, 2943–2952. [Google Scholar] [CrossRef]
- Liu, Y.; Nair, N.C. A two-stage stochastic dynamic economic dispatch model considering wind uncertainty. IEEE Trans. Sustain. Energy 2016, 7, 819–829. [Google Scholar] [CrossRef]
- Ding, T.; Guo, Q.L.; Bo, R. Interval economic dispatch model with uncertain wind power injection and spatial branch and bound method. Proc. CSEE 2014, 34, 3707–3714. [Google Scholar]
- Mei, S.; Zhang, D.; Wang, Y. Robust optimization of static reserve planning with large-scale integration of wind power: A game theoretic approach. IEEE Trans. Sustain. Energy 2014, 5, 535–545. [Google Scholar] [CrossRef]
- Du, E.; Zhang, N.; Kang, C. Exploring the flexibility of CSP for wind power integration using interval optimization. In Proceedings of the IEEE Power and Energy Society General Meeting PESGM, Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Wang, Y.; Xia, Q.; Kang, C. Unit commitment with volatile node injections by using interval optimization. IEEE Trans. Power Syst. 2011, 26, 1705–1713. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, Z. Comparison of scenario-based and interval optimization approaches to stochastic SCUC. IEEE Trans. Power Syst. 2012, 27, 913–921. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Zhang, B. Robust look-ahead power dispatch with adjustable conservativeness accommodating significant wind power integration. IEEE Trans. Sustain. Energy 2015, 6, 781–790. [Google Scholar] [CrossRef]
- Tang, C.; Xu, J.; Sun, Y. Look-ahead economic dispatch with adjustable confidence interval based on a truncated versatile distribution model for wind power. IEEE Trans. Power Syst. 2017, 33, 1755–1767. [Google Scholar] [CrossRef]
- Xie, L.; Carvalho, P.M.S.; Ferreira, L.A.F.M. Wind integration in power systems: Operational challenges and possible solutions. Proc. IEEE 2011, 99, 214–232. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, N. Coordinated operation of concentrated solar power and wind resources for the provision of energy and reserve services. IEEE Trans. Power Syst. 2017, 32, 1260–1271. [Google Scholar] [CrossRef]
- Ma, X.Y.; Sun, Y.Z.; Fang, H.L. Scenario generation of wind power based on statistical uncertainty and variability. IEEE Trans. Sustain. Energy 2013, 4, 894–904. [Google Scholar] [CrossRef]
- Basu, M. Dynamic economic emission dispatch using nondominated sorting genetic algorithm-II. Int. J. Electr. Power Energy Syst. 2008, 30, 140–149. [Google Scholar] [CrossRef]
- EirGrid, Actual and Forecast Wind Power Data. Available online: http://www.eirgridgroup.com/ (accessed on 15 January 2017).


| Hour | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | G9 | G10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 285.7 | 150 | 0 | 0 | 0 | 57.1 | 0 | 0 | 0 | 0 |
| 2 | 316.3 | 202.7 | 0 | 0 | 0 | 49.5 | 0 | 0 | 0 | 0 |
| 3 | 385.5 | 262.7 | 0 | 0 | 0 | 53.1 | 0 | 0 | 0 | 0 |
| 4 | 455 | 322.7 | 0 | 0 | 0 | 51 | 0 | 0 | 0 | 0 |
| 5 | 446.6 | 382.4 | 0 | 20 | 0 | 49.6 | 0 | 0 | 0 | 0 |
| 6 | 455 | 442.4 | 0 | 90 | 0 | 39.9 | 0 | 0 | 0 | 0 |
| 7 | 455 | 455 | 0 | 130 | 0 | 60.8 | 0 | 0 | 0 | 0 |
| 8 | 455 | 455 | 20 | 130 | 25 | 79.2 | 0 | 0 | 0 | 0 |
| 9 | 455 | 455 | 90 | 130 | 85 | 49.2 | 0 | 0 | 0 | 0 |
| 10 | 455 | 455 | 130 | 130 | 145 | 49.2 | 0 | 0 | 0 | 0 |
| 11 | 455 | 455 | 130 | 130 | 162 | 43.8 | 25 | 0 | 0 | 0 |
| 12 | 455 | 455 | 130 | 130 | 162 | 64.4 | 75.1 | 0 | 0 | 0 |
| 13 | 455 | 455 | 90 | 90 | 130.8 | 48.3 | 25 | 0 | 0 | 0 |
| 14 | 455 | 455 | 20 | 20 | 140.4 | 53 | 0 | 0 | 0 | 0 |
| 15 | 455 | 424.6 | 0 | 0 | 80.4 | 53.1 | 0 | 0 | 0 | 0 |
| 16 | 391.5 | 364.6 | 0 | 0 | 25 | 53.3 | 0 | 0 | 0 | 0 |
| 17 | 381.3 | 304.6 | 0 | 0 | 25 | 49.9 | 0 | 0 | 0 | 0 |
| 18 | 408.8 | 335 | 0 | 0 | 42 | 55.8 | 0 | 0 | 0 | 0 |
| 19 | 403.8 | 395 | 0 | 0 | 102 | 54.4 | 0 | 0 | 0 | 0 |
| 20 | 455 | 455 | 0 | 0 | 162 | 80 | 0 | 10 | 0 | 0 |
| 21 | 455 | 455 | 0 | 0 | 115.7 | 57.1 | 0 | 10 | 0 | 0 |
| 22 | 408.2 | 395 | 0 | 0 | 65.8 | 49.5 | 0 | 0 | 0 | 0 |
| 23 | 338.2 | 335 | 0 | 0 | 25 | 53.1 | 0 | 0 | 0 | 0 |
| 24 | 358.4 | 275 | 0 | 0 | 0 | 52.3 | 0 | 0 | 0 | 0 |
| Case | Total Cost (USD) | Fuel Cost (USD) | Reserve Capacity Cost (USD) | Risk Cost (USD) |
|---|---|---|---|---|
| 1 | 555,574 | 491,300 | 19,158 | 40,516 |
| 2 | 1,721,658 | 1,664,158 | 12,275 | 44,421 |
| Hour | G1 | G2 | G3 | G4 | G5 | G6 | G7 | G8 | G9 | G10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 285.6 | 150 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| 2 | 317.1 | 199.4 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| 3 | 387 | 259.4 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| 4 | 454.9 | 319.4 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| 5 | 448.7 | 379.4 | 0 | 20 | 0 | 20 | 0 | 0 | 0 | 0 |
| 6 | 455 | 439.4 | 0 | 90 | 0 | 20 | 0 | 0 | 0 | 0 |
| 7 | 455 | 455 | 0 | 130 | 0 | 36.8 | 0 | 0 | 0 | 0 |
| 8 | 455 | 455 | 20 | 130 | 25 | 59.8 | 0 | 0 | 0 | 0 |
| 9 | 455 | 455 | 90 | 130 | 85 | 27.3 | 0 | 0 | 0 | 0 |
| 10 | 455 | 455 | 130 | 130 | 145 | 27.3 | 0 | 0 | 0 | 0 |
| 11 | 455 | 455 | 130 | 130 | 162 | 72.3 | 25 | 0 | 0 | 0 |
| 12 | 455 | 455 | 130 | 130 | 162 | 34.7 | 77 | 0 | 0 | 0 |
| 13 | 455 | 455 | 90 | 90 | 125.4 | 20 | 25 | 0 | 0 | 0 |
| 14 | 455 | 455 | 20 | 20 | 136.7 | 20 | 0 | 0 | 0 | 0 |
| 15 | 455 | 427.9 | 0 | 0 | 76.7 | 20 | 0 | 0 | 0 | 0 |
| 16 | 386.3 | 367.9 | 0 | 0 | 25 | 20 | 0 | 0 | 0 | 0 |
| 17 | 374.4 | 307.9 | 0 | 0 | 25 | 20 | 0 | 0 | 0 | 0 |
| 18 | 422.6 | 335 | 0 | 0 | 26.8 | 20 | 0 | 0 | 0 | 0 |
| 19 | 416.6 | 395 | 0 | 0 | 86.8 | 20 | 0 | 0 | 0 | 0 |
| 20 | 455 | 455 | 0 | 0 | 146.8 | 61.7 | 0 | 10 | 0 | 0 |
| 21 | 455 | 455 | 0 | 0 | 115.3 | 20 | 0 | 10 | 0 | 0 |
| 22 | 406.5 | 395 | 0 | 0 | 64.9 | 20 | 0 | 0 | 0 | 0 |
| 23 | 336.5 | 335 | 0 | 0 | 25 | 20 | 0 | 0 | 0 | 0 |
| 24 | 356.4 | 275 | 0 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| Case | Total Cost (USD) | Fuel Cost (USD) | Reserve Capacity Cost (USD) | Risk Cost (USD) |
|---|---|---|---|---|
| 3 | 541,554 | 475,488 | 21,365 | 40,101 |
| 4 | 1,720,576 | 1,663,199 | 12,461 | 44,112 |
| Case | Total Cost (USD) | Fuel Cost (USD) | Upward Reserve Cost (USD) | Downward Reserve Cost (USD) | Risk Cost (USD) |
|---|---|---|---|---|---|
| 5 | 423,525 | 364,359 | 10,749.4 | 18,800.6 | 29,616 |
| 6 | 421,114.3 | 361,927.3 | 12,713.8 | 16,836.2 | 29,637 |
| Case | Regulation 1 (MW) | Regulation 2 (MW) | Regulation 3 (MW) | Regulation 4 (MW) | Fuel Cost (USD) | Risk Cost (USD) | Reserve Cost (USD) |
|---|---|---|---|---|---|---|---|
| 6 | 6727.2 | 1574.5 | 1987.5 | 2363.3 | 361927.3 | 29637 | 29550 |
| 7 | 699.4 | 392.3 | 166.8 | 109.4 | 359407.1 | 29819 | 28739.6 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, M.; Hu, Z. Optimization Scheduling Method for Power Systems Considering Optimal Wind Power Intervals. Energies 2018, 11, 1710. https://doi.org/10.3390/en11071710
Hu M, Hu Z. Optimization Scheduling Method for Power Systems Considering Optimal Wind Power Intervals. Energies. 2018; 11(7):1710. https://doi.org/10.3390/en11071710
Chicago/Turabian StyleHu, Mengyue, and Zhijian Hu. 2018. "Optimization Scheduling Method for Power Systems Considering Optimal Wind Power Intervals" Energies 11, no. 7: 1710. https://doi.org/10.3390/en11071710





