1. Introduction
The share of renewable energy in the electric system has greatly increased worldwide in the last decade. Such a growth is mainly related to the increasing utilization of wind and solar energy sources, with hydraulic energy almost completely exploited in many countries. The use of renewable energy sources (RES) contributes significantly to the reduction of CO2 emission and to the sustainability of the overall energy system. On the other hand, the intermittency and the uncertainty in forecasting RES availability bring serious issues in the management of electric grids. The production from RES (especially from wind and sun) is inherently independent from the electric request and, therefore, to fulfil safely the load demand along the time, the production from thermo-electric and hydro plants has to be scheduled accordingly. The intermittency and the uncertainty in predicting the RES availability with a sufficient level of accuracy over time force the electric grid operators to rearrange the unit commitment by putting in operation (or switching off) other generators or by deploying the available spinning reserve. Such actions entail additional costs, which are ultimately passed on to the end consumer.
Electric energy storage (EES) can contribute to mitigating the above issues and, consequently, to further promoting the market penetration of RES. EES systems can generate additional electricity when RES availability is insufficient to meet the forecast production level or store electricity in case of an excess of availability.
Such an application calls for EES featured by suitably long charging–discharging phase durations (hours) and by an adequate storage capacity. The most suited technologies to accomplish such a task are pumped hydro storage (PHS), battery energy storage (BES) and compressed air energy storage (CAES). A comprehensive review about the state-of-the-art of the above technologies is given in [
1].
The CAES basic principle of operation is rather simple. Electricity is absorbed from the grid during low demand periods to power a compressor which fills with air a storage tank. During high electricity demand periods, the compressed air is taken from the reservoir and expanded in an air turbine to produce electric power. On the basis of such a concept, a variety of solutions have been proposed and investigated over time. Such solutions can be classified into three main categories: diabatic CAES (D-CAES), adiabatic CAES (A-CAES) and isothermal CAES (I-CAES).
In D-CAES, an external heat source (usually a fuel) is utilized to heat the compressed air before the expansion. Existing CAES plants (Huntdorf and McIntosh plants) fall into this category. During the discharge phase, the air taken from the reservoir enters a combustion chamber fed with natural gas. The combustion gas is expanded in a high-pressure turbine, reheated in a secondary combustion chamber, expanded in a low pressure turbine and finally discharged into the atmosphere. A multistage intercooled/aftercooled compression process is adopted to reduce the compression work and to keep the air temperature within the operational limits featuring the industrial compressor stages [
2].
In a scenario geared towards a progressive de-carbonization of the electric systems, the use of fossil fuels to support an ESS may be deemed inappropriate. Therefore, to achieve an emission-free, pure storage technology, the adiabatic CAES concept (A-CAES) has been proposed. In such a concept, the heat absorbed by the intercoolers during the compression phase is stored in a thermal energy storage (TES) system and utilized during the discharge phase to heat the pressurized air. A-CAES systems can be classified into high temperature (400–800 °C) [
3,
4] and low temperature (80–200 °C) systems [
5]. High temperature systems call for innovative compressors capable of operating at very high discharge temperatures. Besides this, the development of high temperature and pressure TES still requires considerable technological and economic efforts [
5]. Low temperature A-CAES systems are not affected by the above issues. However, the huge number of compression and expansion stages needed to reach a satisfactory performance level represents a major drawback [
6]. Such complex compression and expansion trains eventually entail relevant investment costs and complications in controlling plant operation.
Finally, the recently proposed isothermal CAES (I-CAES) approach removes the need for TES. Quasi-isothermal compression and expansion are accomplished by exchanging heat with the surrounding environment by using heat transfer surfaces or a liquid medium in direct contact with the air. Solutions based on the adoption of liquid pistons appear too slow for industrial uses [
7,
8]. Concepts based on the addition of a liquid to absorb, store and release the heat to accomplish near isothermal compression and expansion processes are not yet mature for industrial applications [
8].
Many countries are pursuing as a final goal a “decarbonized” electric system. Nevertheless, the traditional fossil fueled plants will still play a key role in the next decades. Taking the above into consideration, the possibility of using such plants to improve grid storage capabilities can represent an attractive option.
In the past decade, Nakhamkin introduced the so-called second-generation diabatic CAES concept [
9]. Basically, second-generation diabatic CAES plants (D-CAES2) integrate the air compression and storage system with a commercially available gas turbine (GT). According to such a concept, a GT power augmentation is achieved by injecting the stored air downstream of the GT compressor. Improvements can be attained by pre-heating the stored air by using the GT exhaust and expanding the heated air in a topping turbine prior to the injection in the GT combustion chamber. Such systems have the potential to bring relatively low investment costs, good storage efficiency, high availability and reliability levels, and a good response to quick load change requests [
9]. Such a concept has been further investigated by the author [
10,
11]. The performance of a small-size CAES plant coupled with a 4600 kW Mercury recuperated GT has been evaluated during the overall operational cycle (charging, storage and discharging phases). A 30% maximum extra power delivery (some 1500 kW) in respect to the nominal design GT output power has been assessed with a satisfactory storage efficiency values around 70%.
As previously discussed, a drawback of D-CAES2 is the need for an additional amount of fuel to heat the stored air mass flow rate injected downstream of the GT compressor. To overcome or reduce such a downside, alternative concepts integrating D-CAES systems into fossil fueled energy systems have been recently investigated by various authors.
As an example, Li et al. [
12] proposed the integration of a D-CAES system into a diesel engine to produce electricity for off-grid applications. During the CAES discharge phase, the compressed air is heated by using the otherwise wasted thermal energy content of the diesel engine exhaust gases. The same concept has been taken up in [
13]. In order to further improve the overall system performance, the engine exhaust gas, after being used to preheat the compressed air before expansion, is supplied to an ammonia-water absorption refrigeration system. Moreover, during the charging phase, the heat removed by the intercoolers is used to satisfy thermal needs.
Chen et al. [
14] take as a starting point the fact that about 50% of energy used in Chinese industry is rejected into the environment, mostly in form of low-grade heat available at temperatures lower than 200 °C. They concluded that such a low-grade heat can be regarded as a free heat source to feed CAES systems. The resulting D-CAES storage efficiency level is not completely satisfactory, due to the low expanding air temperature that can be achieved by using the low-grade waste heat. Significant improvements are attained by reducing the compression work during the charging phase. Such a reduction is achieved by lowering the temperature of the air entering the compression stages by means of a vapor compression chiller driven by electric power absorbed from the grid.
Safaei et al. [
15] carried out a techno-economic analysis of a D-CAES integrated into a complex system constituted by a wind farm, GT-based power plants and a district heating network fed by fossil-fueled large-size boilers. They introduced the concept of distributed CAES, where the air compression stations are distributed near the district heating facilities. The heat absorbed during the intercooled compression is used to feed the district heating network, thereby reducing or negating the fuel consumption of the boilers. The economic result of the distributed CAES is compared with the traditional diabatic one. They concluded that, under specific conditions related to the fuel price and to the level of the emission tax, the distributed CAES shows a better economic performance.
Meng et al. [
16] investigated the integration of a D-CAES system with an organic rankine cycle (ORC) to recover the waste heat from intercoolers in the charging process and from the exhaust air in the discharging process. The additional ORC electricity generation, obtained without using additional fuel, leads to a storage efficiency improvement of about 6%.
In the aim of achieving a fuel free energy storage system, the author proposed a novel concept integrating a D-CAES into a Gas-Steam combined cycle (GSCC) plant [
17].
In a GSCC, the otherwise wasted thermal content of GT exhaust gas is used to generate steam in a heat recovery steam generator (HRSG). Steam is expanded in a steam turbine (ST) to produce power in addition to that produced by the GT without using supplementary fuel. At the present time, such plants allow the large scale conversion of the fuel energy into electricity in the most efficient way. In GSCC plants, the electricity production per kilogram of exhaust gas fed to HRSG ranges from 100 to 250 kJ/kg, depending on the gas temperature and on the steam section arrangement (dual or triple pressure steam production, steam reheating and so on) [
18]. Higher values are typical of large size plants based on advanced heavy duty GTs. Such GTs are featured by high exhaust gas temperatures (about 600 °C), which allow the production of high temperature/high pressure steam. In order to maximize the conversion efficiency, such plants are equipped with rather complex steam sections where superheated steam is produced at high, medium and low pressure. Small/medium-size GSCC plants (i.e., 50–200 MW) are featured by a lower electricity production per kilogram of exhaust gas (100–180 kJ/kg). Usually, small/medium size GSCC plants are arranged with a dual pressure HRSG and no steam reheating before the expansion in the low pressure ST.
The here proposed integrated plant concept stems from the following considerations. In a D-CAES, the compressed air is heated before the expansion in order to increase the output power. The idea is to take a fraction of the GT exhaust gas flow rate fed to HRSG to heat the stored compressed air: if the electricity produced per kilogram of GT exhaust gas is higher than that obtained during normal GSCC operation, such an electricity surplus can be deemed as being achieved without using additional fuel.
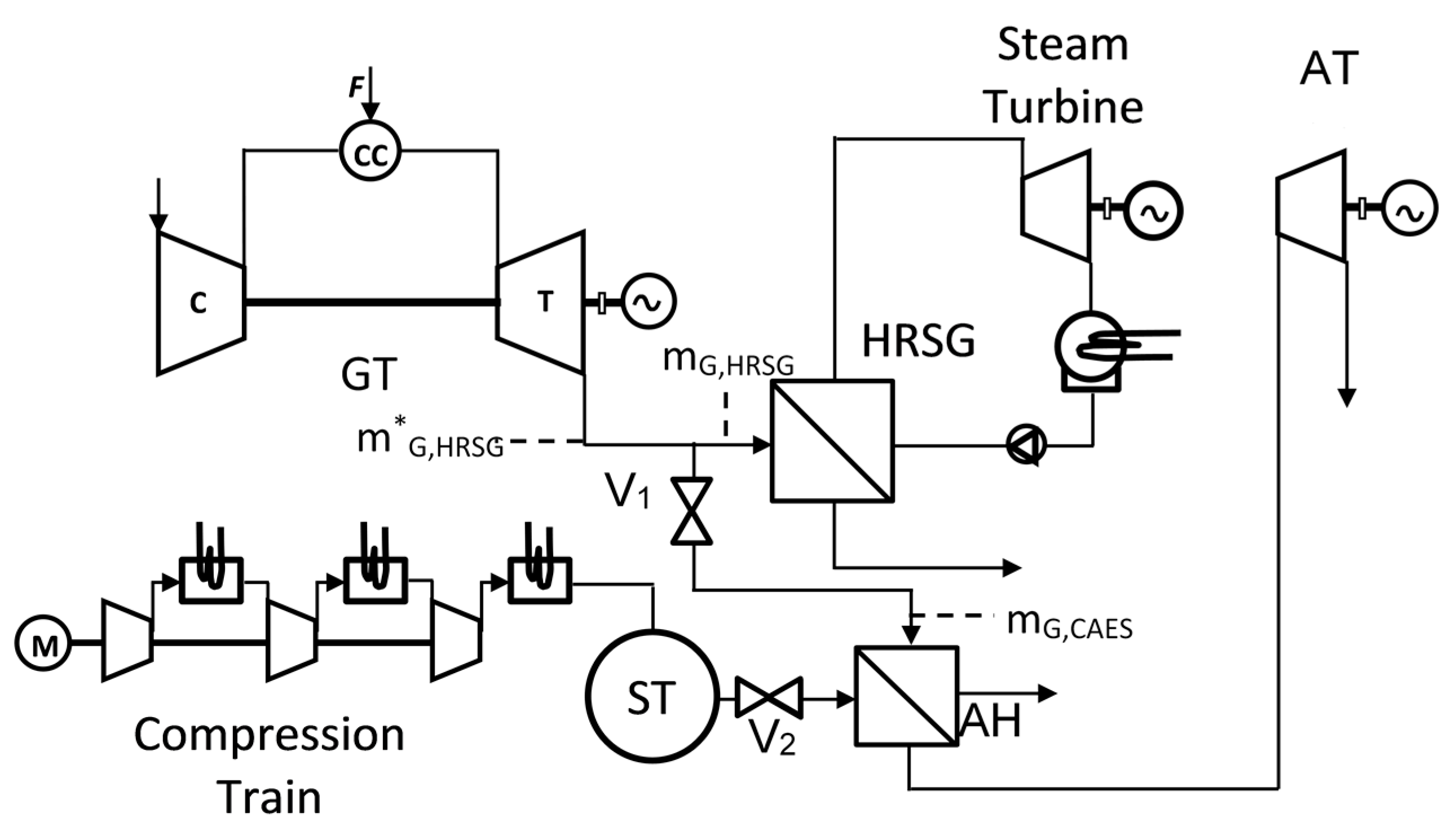
The plant reference layout is given in
Figure 1. During the charging phase, a certain amount of electric power is absorbed from the grid to drive an electric motor M connected to a multi-stage intercooled/aftercooled compressor. As the charging phase takes place, both valves V1 and V2 are closed. Therefore, the compressed air is stored into the reservoir while all the GT exhaust gas flow
During the discharge phase, conversely, both valves V1 and V2 are opened. As a result, a fraction of GT exhaust gas is diverted to the air heater (AH) to heat the stored compressed air prior to its expansion in an air turbine (AT). The integrated system can give rise to a surplus of power production in respect to that produced by the sole GSCC plant, provided that a sufficient amount of air is fed to the AT at an appropriate level of pressure and temperature. Preliminary investigation addressed to CAES systems integrated into medium/small-size GSCC have shown that the CAES production per kilogram of GT exhaust gas, by varying the expanding air pressure in the range 60–100 bar, is 3–4 times greater than that actually achieved by using the kilogram of gas for steam production in the HRSG.
Such an augmentation can give rise to an electricity surplus production with respect to normal GSCC operation in the order of 300–350 kJ per kilogram of exhaust gas without any additional use of fuel. As a result, the storage system can be regarded as a “fuel free” one as BES, PHS or adiabatic CAES.
In order to explore the practical feasibility of the proposed system, a techno-economic analysis aimed at assessing plant performance and investment costs has been carried out [
17]. Results have shown that, despite the relatively high investment costs and the storage efficiency being less than those featuring alternative storage approaches, the proposed system may be considered of interest due to the long life duration and to the proven technologies available for the key plant components.
It has to be pointed out that such a preliminary investigation was addressed to a first assessment of the potentialities of the proposed concept. As reported in [
17], evaluations had been performed by adopting conservative assumptions and, for sake of simplification, by neglecting some aspects related to GSCC plant operations expected to give a positive contribution to the performance of the whole integrated system.
A more accurate and realistic performance assessment has been discussed in a paper [
19] presented at the 4th International Conference on Energy and Environmental Research (ICEER 2017): taking as reference a commercially available GSCC plant, various design options featured by different CAES power outputs are analyzed and evaluated taking the above aspects into consideration. In the present work, which is an extension of the ICEER 2017 conference paper, further CAES design options are analyzed and discussed.
2. Technical Considerations
In the previously cited author’s paper [
17], the integrated system storage efficiency was evaluated according to the following formula:
where
is the electric production attained by expanding the stored air,
the loss of electric production from GSCC due to the lowering of the gas mass flow rate entering the HRSG and
the electricity absorbed from the grid during the charging phase to compress the mass of air fed to the gas expander.
The term
can be expressed as
where
represents the mass of gas taken to feed the air heater and which, therefore, does not contribute to the steam generation in the HRSG and
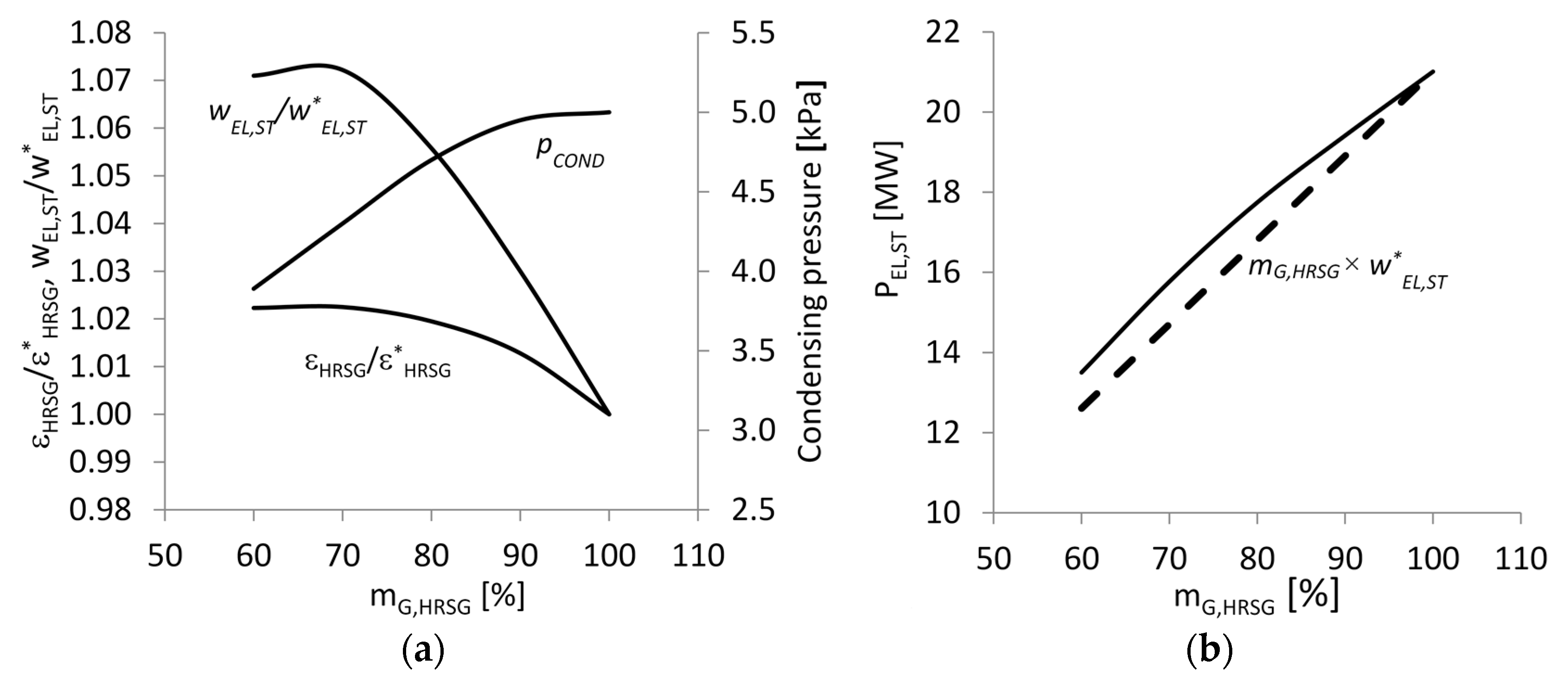
the electricity generated per kilogram of gas in the GSCC steam section at reference (design) condition. Nevertheless, the storage efficiency given by Equation (1) takes no account of two significant aspects characterizing the part load behavior of the GSCC steam section:
The first outcome stems from the fact that when the gas mass flow rate reduces, the steam production is reduced too. As a consequence, the ratio between the actual heat transfer surface and gas (or steam) mass flow rate increases. Conversely, the mass flow reduction on both sides leads to a decrease of the overall heat transfer coefficient. If the gas flow rate reduction is not too high, the first effect prevails on the second one and the ratio between steam production and gas mass flow rate shows an increasingly trend. The heat transfer enhancement leads to a reduction of the HRSG exhaust temperature
and, consequently, to an improved HRSG effectiveness
defined as:
being
the gas mass flow rate entering the HRSG,
the gas specific heat,
and
the gas inlet and outlet temperatures respectively and, finally,
the ambient temperature.
Such a situation is typically encountered in GSCC plant part load operations when the power output is reduced by closing the compressor variable inlet guide vanes (VIGVs) and variable stator vanes (VSVs): the GT exhaust flow decreases linearly with the GT power output while the turbine exhaust temperature is kept constant at its design value [
20]. The resulting part load HRSG performance is analyzed and widely discussed in [
21,
22].
The second aspect under consideration is related to the condenser heat duty reduction occurring when the GSCC steam section operates at part load. If the coolant mass flow is kept constant at its design value, condensing temperature and pressure decrease with decreasing the steam mass flow rate entering the condenser. Such a pressure reduction can bring to small but not negligible specific work improvements. In fact, due to really high steam specific volume at the last turbine stage exit (around 25 kg/m
3), a condensing pressure drop of 1 kPa leads to a work augmentation of about 25 kJ per kilogram of steam. Taking into account that typical values for steam specific work are within the range of 1000 to 1500 kJ/kg [
18], improvements ranging from 1.5 to 2.5% can be achieved.
To take into account benefits arising from the previously discussed aspects, the actual electricity surplus generated during the discharge phase
is evaluated as follows:
where
is the electric production from the stored air,
is the electricity actually produced by the GSCC steam section fed with a reduced gas mass flow and
the electric production at reference design condition (i.e., when the CAES plant is not in operation). Equation (4) can be rewritten as
where
is the mass of gas fed to the HRSG and
the steam section electric production per kilogram of gas. Superscript “*” designates the reference design condition. Taking into consideration that during CAES operations
(
Figure 1), Equation (5) can be rearranged as follows:
The last term represents the loss of electric production
already defined in Equation (2) and the positive term in square brackets accounts for the increase in electricity production due to steam section improved part load operations. Thus, a formulation that best expresses the storage efficiency of the integrated system has been introduced:
4. Integrated Plant Performance Analysis
In order to assess the integrated plant performance at design point, analyses have been carried out by varying relevant design quantities such as , and the gas mass flow rate derived to fed the AH .
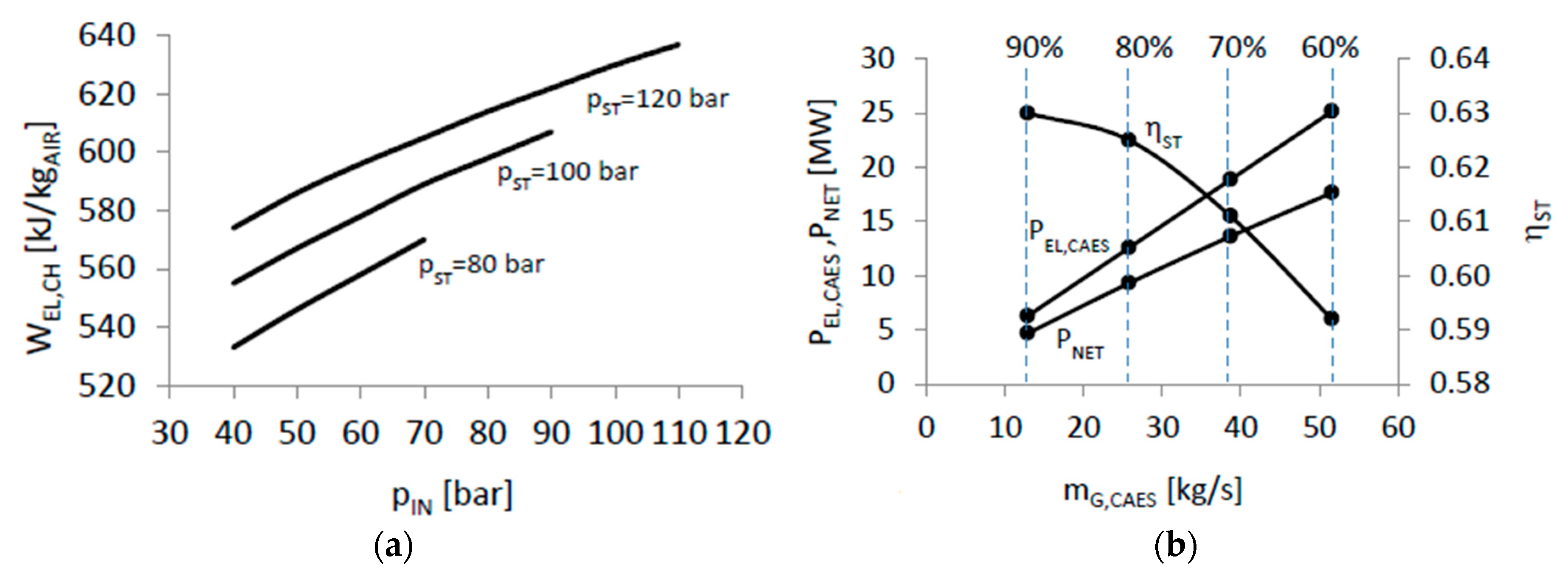
At first, CAES systems featured by different design values of have been taken into consideration. In each case, a storage pressure of 100 bar has been assumed while the pressure at the end of the discharge phase is fixed at 60 bar. According to Equation (16), an electric absorption of 578 kJ per kilogram of stored air is required to accomplish the charging phase.
Results achieved by varying
from 13 to about 52 kg/s (corresponding to
ranging from 90 to 60%) are shown in
Figure 3b. The AT electric power output
varies linearly with
, as a consequence of assumptions reported in
Section 3.3. The net power production
—defined according to Equation (4)—ranges from 5 to about 18 MW. Storage efficiency—valuated according to Equation (7)—decreases by increasing the CAES size, i.e., the GT exhaust gas mass flow rate. Values higher than 60% are achieved for
values ranging from 5 to 10 MW.
Equation (1) gives a constant storage efficiency value of 0.56, irrespective of the size of the system. It has to be pointed out that the use of Equation (1) leads to a noticeable 10% underestimation in respect to the actual performance of the integrated system. Such a performance reassessment reinforces the conclusions drawn in [
19] about the potential of the proposed system to emerge as an economically viable storage alternative.
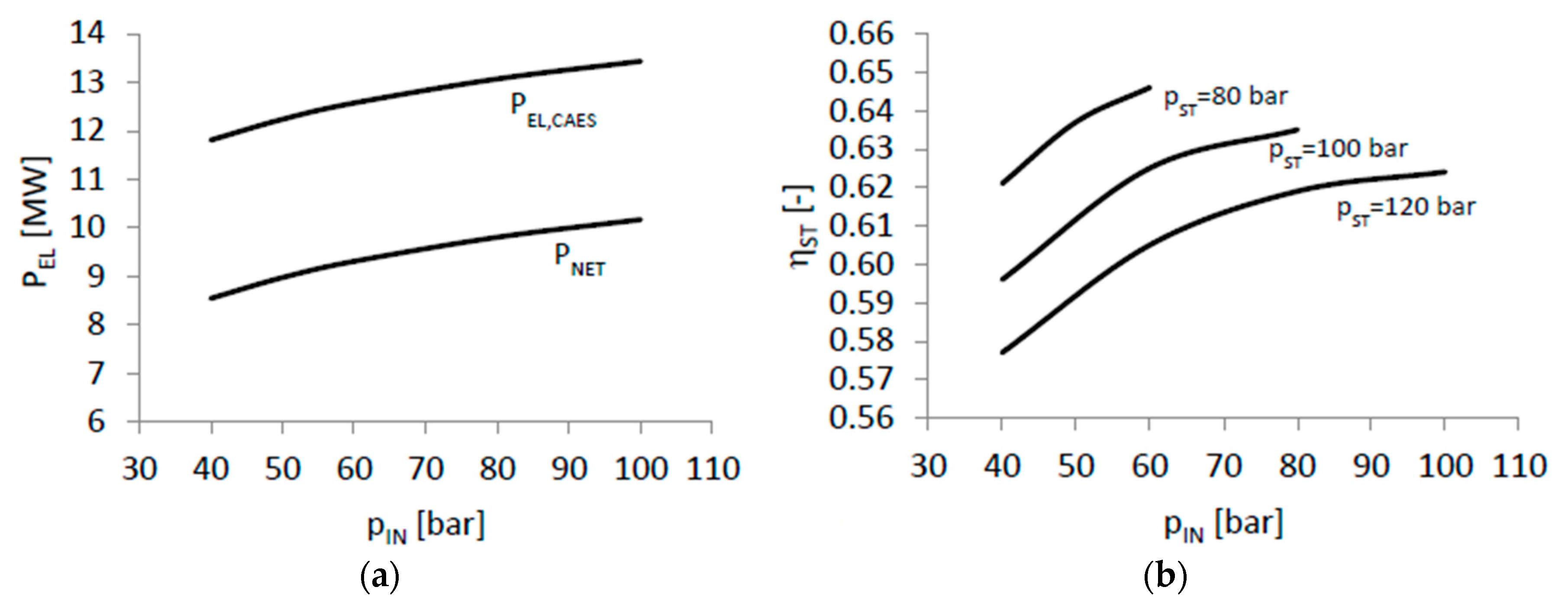
Plant design point performance has been investigated by varying both the storage pressure
and the pressure at the beginning of the charging phase
. In carrying out the analysis, design gas mass flow rate
has been kept constant at 25.6 kg/s, corresponding to a 80%
reduction.
Section 3.3 assumptions lead to an air mass flow rate fed to the AT exactly equal to
On the basis of
Figure 2b data, an 80%
reduction leads to an actual steam power production of some 17.8 MW.
The power delivered by the AT does not depend on
.
Figure 4a shows both the power output actually produced by the AT and the CAES net power output
as a function of
. It can be observed that by increasing
from 40 to 100 bar,
shows an increase from 8.5 to some 10 MW.
Results concerning the storage efficiency are given in
Figure 4b. It can be noticed that the higher the storage pressure is, the lower the storage efficiency is. By assuming
equal to 80 bar, the storage efficiency ranges from 62 to some 65%.
For a given storage pressure,
increases with increasing
. Recalling the comments provided at the end of
Section 3.2, the adoption of high
values leads to large storage volumes. Such a consequence is of key importance, since the artificial storage system constitutes the major investment cost item, as reported in [
19].
Finally, it can be noticed that by increasing , storage efficiency curves tend to assume a flat trend. On the basis of the above consideration, the adoption of design values not particularly high may be beneficial in terms of plant costs.
All the above aspects, and their consequences in terms of storage efficiency and plant cost, are investigated in the next section.
5. Case Study
A techno-economic analysis aimed at estimating the CAES plant cost has been carried out. Taking as a reference the GSCC plant introduced in
Section 3.1, three different CAES design options have been investigated under the following design assumptions:
Storage pressure: 100 bar;
Net power production: 6000 kW;
Discharge phase duration: 3 h at the maximum rated power;
Charge phase duration at constant power: 5 h.
The three design options are featured by different values of the pressure at the beginning of the charging phase
: 40, 60 and 80 bar respectively. By assuming the discharge phase occurring at maximum rated power, an electric production of 18,000 kWh is expected.Main CAES plant design data are reported in
Table 2. All the CAES plants under consideration operate with the same AT inlet temperature (495 °C). As a consequence of
Section 3.3 assumptions, the heating of the air mass flow rate fed to the AT requires exactly the same amount of GT exhaust mass flow rate. Since the AT specific work increases by increasing
=
, the higher
is, the lower the air mass flow rate required to produce the rated power is, and, consequently, the lower the GT exhaust mass flow rate
fed to the AH is. As reported in
Table 2, by increasing
from 40 to 80 bar, an almost constant AT power output (around 8000 kW) is requested to achieve the rated net power output, while both the GT exhaust and the air mass flow rates decrease significantly (from 18.1 to 15.8 kg/s). The mass of stored air
can be evaluated by multiplying the design AT air mass flow rate by the duration of the discharge phase. Therefore, by increasing
, lower amounts of stored air are required to match the design targets.
The storage volume
is calculated according to the following equation:
It strongly depends on the difference between maximum and minimum pressure inside the reservoir. Therefore, even though high design values imply the storage of lesser amounts of air, the storage volumes show significant increases.
On the basis of
Table 2 data,
values of 60 and 80 bar leads to a storage volume 40 % and 160% larger than the storage volume evaluated for
= 40 bar.
Once the mass of stored air is defined, the electricity absorbed during the charging phase
can be evaluated according to
Figure 3a data. Finally, the compressor train rated power is established by dividing
by the duration of the charging phase. It can be noticed as the storage efficiency increases by increasing
, as reported in
Figure 4a.
Table 2 data are used to estimate the investment costs of the main plant items.
It can be noticed that the major difference among the design options under consideration concerns the storage volume requirement. Additional data necessary to estimate the artificial storage cost have been found by applying a sizing procedure based on an ANSI standard. Main sizing assumptions and results are given in
Table 3. Pipe sections of 30”
OD and 12 m length, made of ANSI b.125.1 carbon steel, have been selected to arrange the reservoir. The sizing procedure led to a tube wall thickness of about 40 mm. As a result, 5300, 7200 and 13,700 ton (metric) of steel are required in case of
equal to 40, 60 and 80 bar respectively.
The last line of
Table 3 gives the tube’s overall length. It can be noticed that length figures are in the order of thousands of meters. The storage reservoir can be assembled by connecting pipe runs in a parallel arrangement obtained by welding ten 12 m pipe sections. A distance between pipe runs of 1.2 m (about twice the tube
OD) is considered adequate to accomplish operations required to build, maintain and inspect the reservoir. With reference to the
= 40 bar case, a land surface of 120 × 80 m is required, corresponding to a football field (soccer for US and Canadian Readers). By assuming
= 60 bar and
= 80 bar, the required land surface increases by a factor of 1.4 and 2.6, respectively. Significant land savings can be achieved by adopting alternative (and slightly more expensive) arrangements. As an example, the tube runs can be stacked by using suitable supports, as reported in [
33].
The artificial storage system investment cost has been evaluated taking the following items into consideration:
The overall investment cost (given in 2016 €) is estimated by adding indirect costs (20% of the direct cost) [
31] and shipping costs, assumed equal to 30% of the steel pipe purchase cost on the basis of vendors information.
The compressor train is constituted by four centrifugal stages. The compressor packaged system cost has been evaluated according to [
35]. The compressor base cost (including auxiliary equipment such as filtering system and heat transfer devices for intercooling and after-cooling) is given as a function of the power delivered to the compressed air (gas horsepower). Direct costs (foundations, piping, instruments, electric equipment, painting, insulation and labor) and indirect costs (engineering, contractor’s fee, etc.) are evaluated by applying suitable factors equal to 1.64 and 1.35 [
35]. Finally, the overall cost is obtained by adding the cost of the electric motor, given as a function of the brake horsepower. In the proposed layout, compression and expansion trains are connected by a synchronous electric machine operating as motor during the charging phase and as generator during discharge. Costs are given in 2001 USD.
The air heater (AH) technology is the same for HRSGs commonly used in GSCC plants, the sole difference being the tube side fluid (pressurized air instead of water/steam). Hence, to determine the AH investment cost, the approach proposed by Foster–Pegg in 1989 [
36] suitably modified by the author [
37] has been adopted. The base cost (given in 2004 thousands of €) is expressed as the sum of three terms accounting for (i) the heat transfer surface area, (ii) the devices required for the proper air management (valves, headers, etc.), (iii) the enclosure, insulation and stack. To estimate the AH installed cost, a cumulative additional cost factor equal to 1.5 accounting for direct and indirect installation cost has been adopted on the basis of vendor information.
The air turbine (AT) is assumed derivate from a steam turbine, according to what reported in [
2,
23]. Therefore, the AT investment cost has been estimated by adopting a correlation developed for steam turbines given in [
38]. Such a correlation provides the turbine base cost (in 1994 USD) as a function of the rated power, the inlet temperature and the efficiency. An installation factor of 1.25 has been assumed.
The investment cost of the main plant components is reported in
Table 4. All costs have been updated by using the Marshall & Swift index and converted into 2016 €.
As expected, in all cases, the artificial storage system represents the main cost item. Moreover, such a cost increases significantly by increasing
, while the other cost items do not show relevant changes. Such an increase greatly influences the overall plant cost: with reference to
Table 4 data, the overall plant cost evaluated by assuming
= 80 bar is roughly doubled in respect to that estimated for
= 40 bar. Therefore, the choice of high
values—which involves benefits in term of storage efficiency—leads to high and hardly bearable plant costs. In fact, in a context like the present one featured by low electricity prices, high plant costs are unlikely to be compensated by the reduced operational costs stemming from the adoption of high efficiency solutions.
Finally, a qualitative comparison with battery energy storage (BES) systems is attempted on the basis of cost information provided in [
39]. The
= 40 bar CAES system performance is compared with Na-S battery and Li-ion battery storage systems characterized by the same power and storage capacity. As reported in
Table 5, the CAES cost is approximately twice the cost estimated for the Na-S batteries and significantly lower than that of LI-ion based storage system.
However, it has to be pointed out that CAES life duration is considerably longer than those commonly estimated for BES systems taken into consideration (15 years for both Na-S and Li-ion batteries [
39]).
Such a high life duration is expected to bring to a significantly lower levelized cost of storage (LCOS), as reported in [
40]. Moreover, other CAES features which positively affect the life cycle analysis are related to the absence of emissions during operations and to the easy plant dismantling at the end of the useful life. In this respect, the CAES storage system salvage value is estimated (on the basis of prices provided by the steel recycle manufacturers) as some 25% of the steel pipe purchase cost, as reported in [
31].
Moreover, BES technologies (including those presently commercially available) show some drawbacks and need further R&D efforts to improve relevant aspects related to emissions, loss of performance, dismantling and so on. Instead, the key components of the proposed CAES concept (compression train, artificial reservoir, air heater and air turbine) are based on proven and consolidated technologies.