Numerical Modelling of Ice-Covered Insulator Flashover: The Influence of Arc Velocity and Arc Propagation Criteria
Abstract
:1. Introduction
2. Presentation of the Mono-Arc Numerical FEM Model
2.1. Assumptions Used for Numerical Modelling
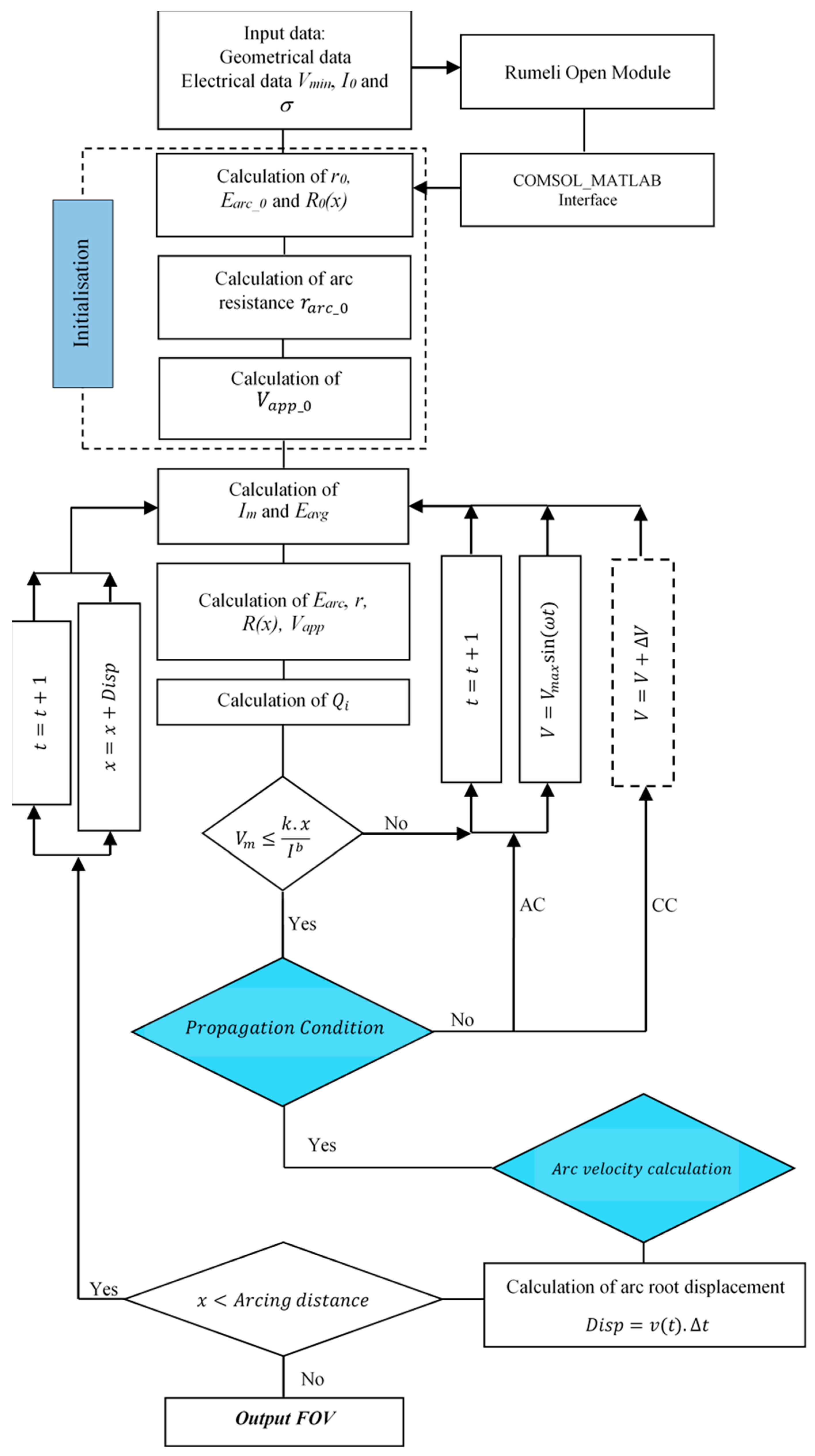
2.2. Subsection Presentation of the Calculation Algorithm
3. Study of the Influence of Arc Velocity Criteria
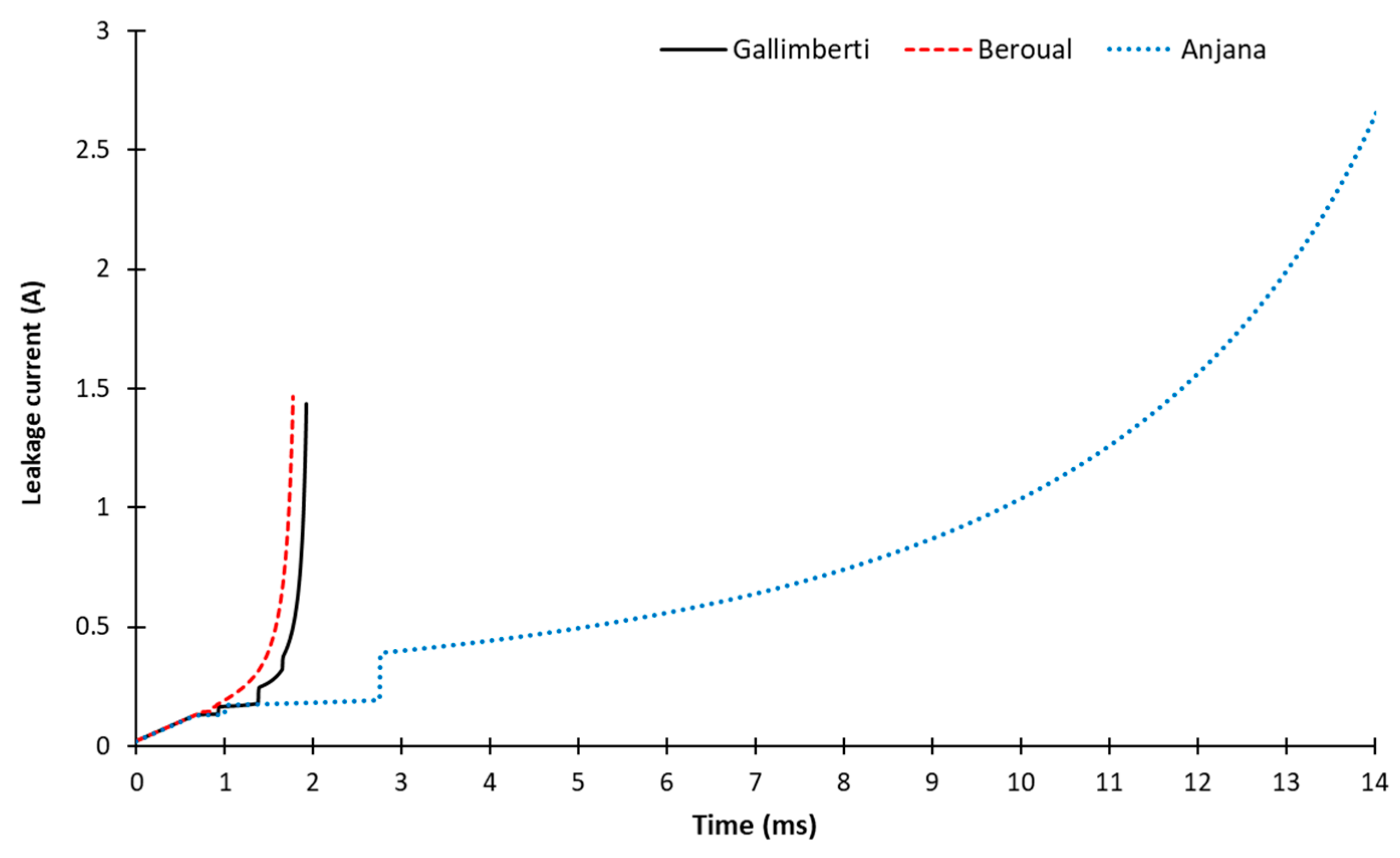
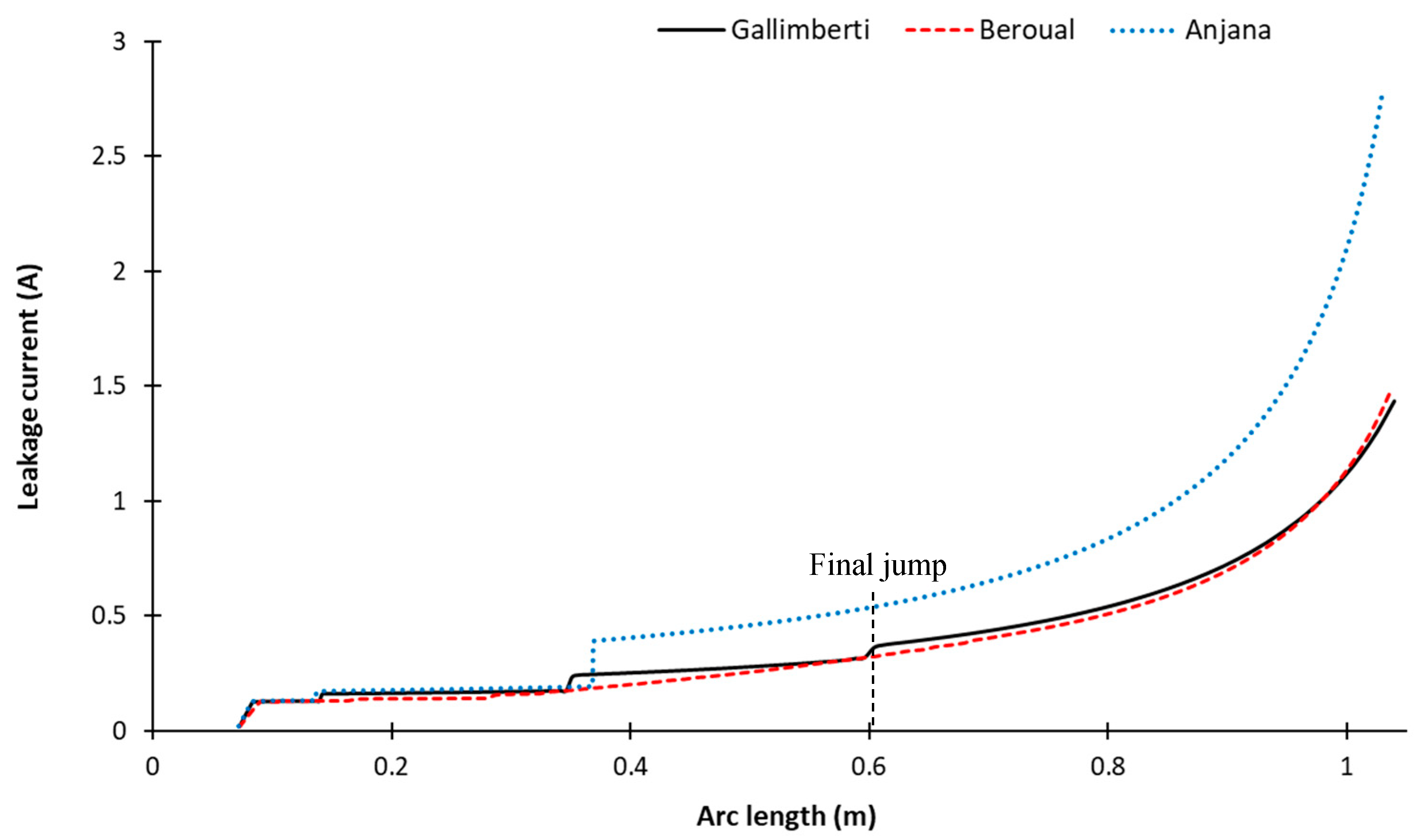
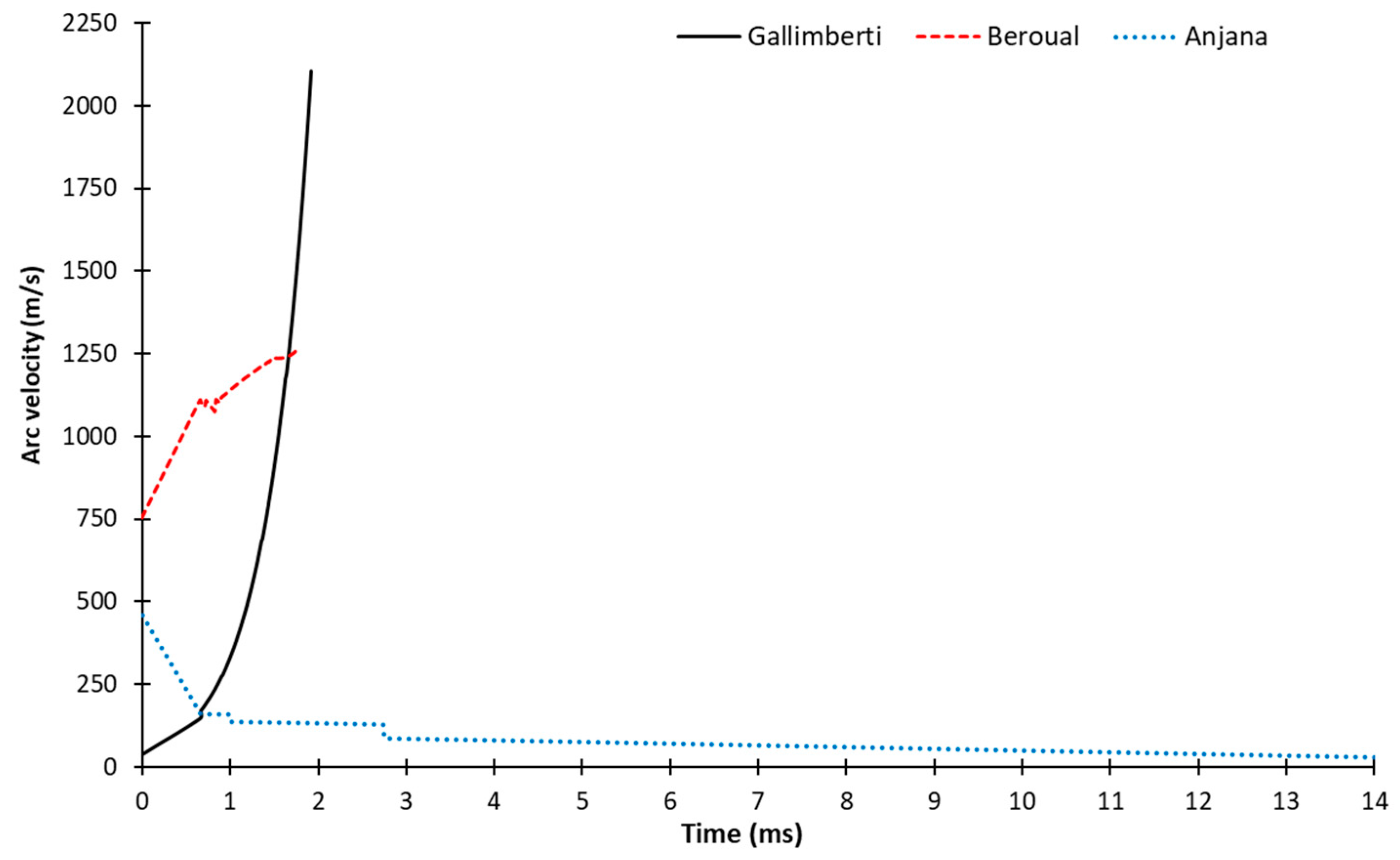
3.1. Arc Velocity Criteria
3.1.1. Gallimberti Criterion
3.1.2. Beroual Criterion
3.1.3. Anjan and Lakshminarassimh Criterion
3.2. Experimental Set-Up and Simulation Parameters
3.3. Influence of the Arc Velocity Criteria on the FOV Results
4. Study of the Influence of Arc Propagation Criteria
4.1. Arc Propagation Criteria
4.1.1. Hampton Criterion
4.1.2. Hesketh Criterion
4.1.3. Billings and Wilkins Criterion
4.1.4. Gosh Criterion
4.1.5. Dhahbi and Beroual Criterion
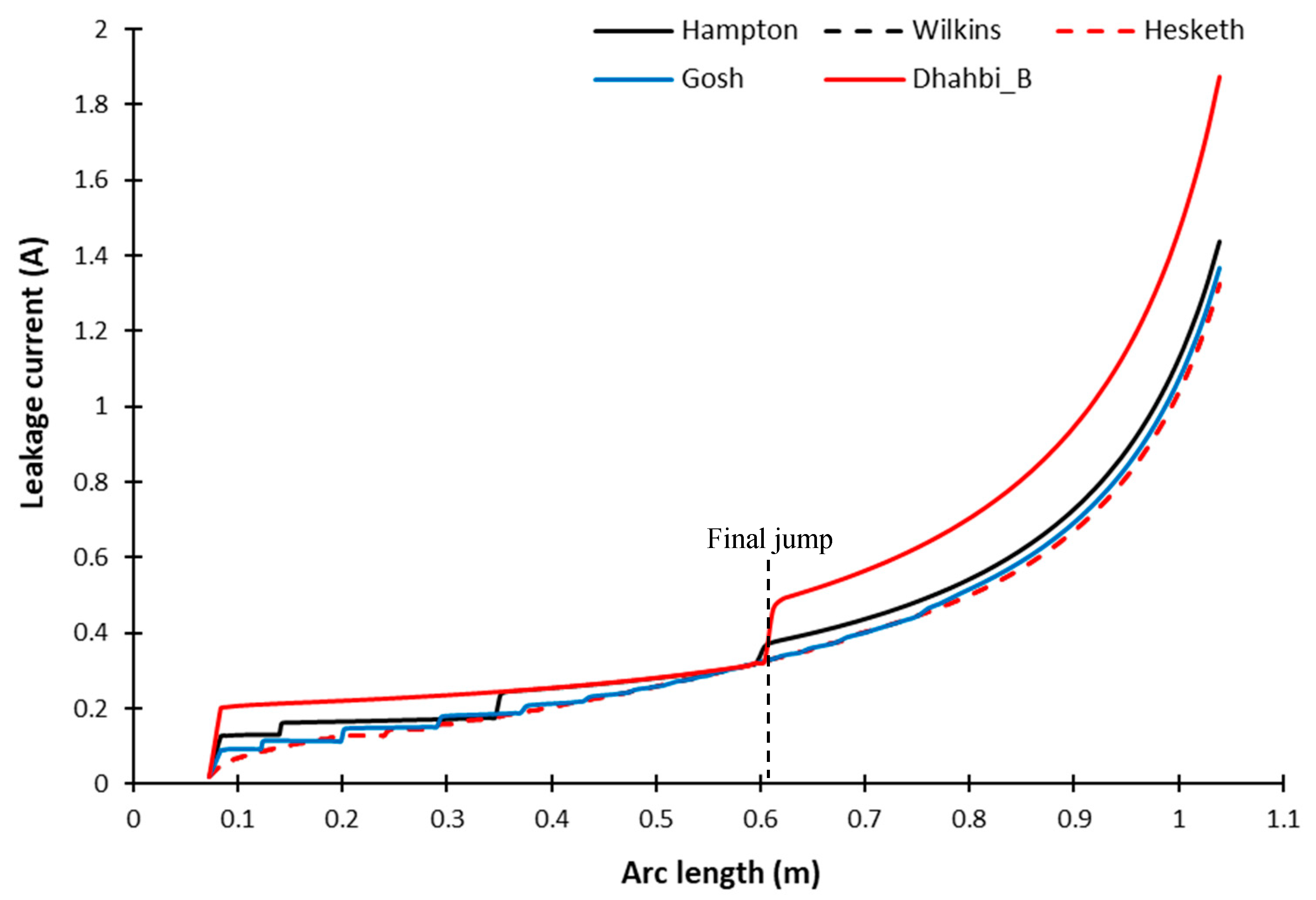
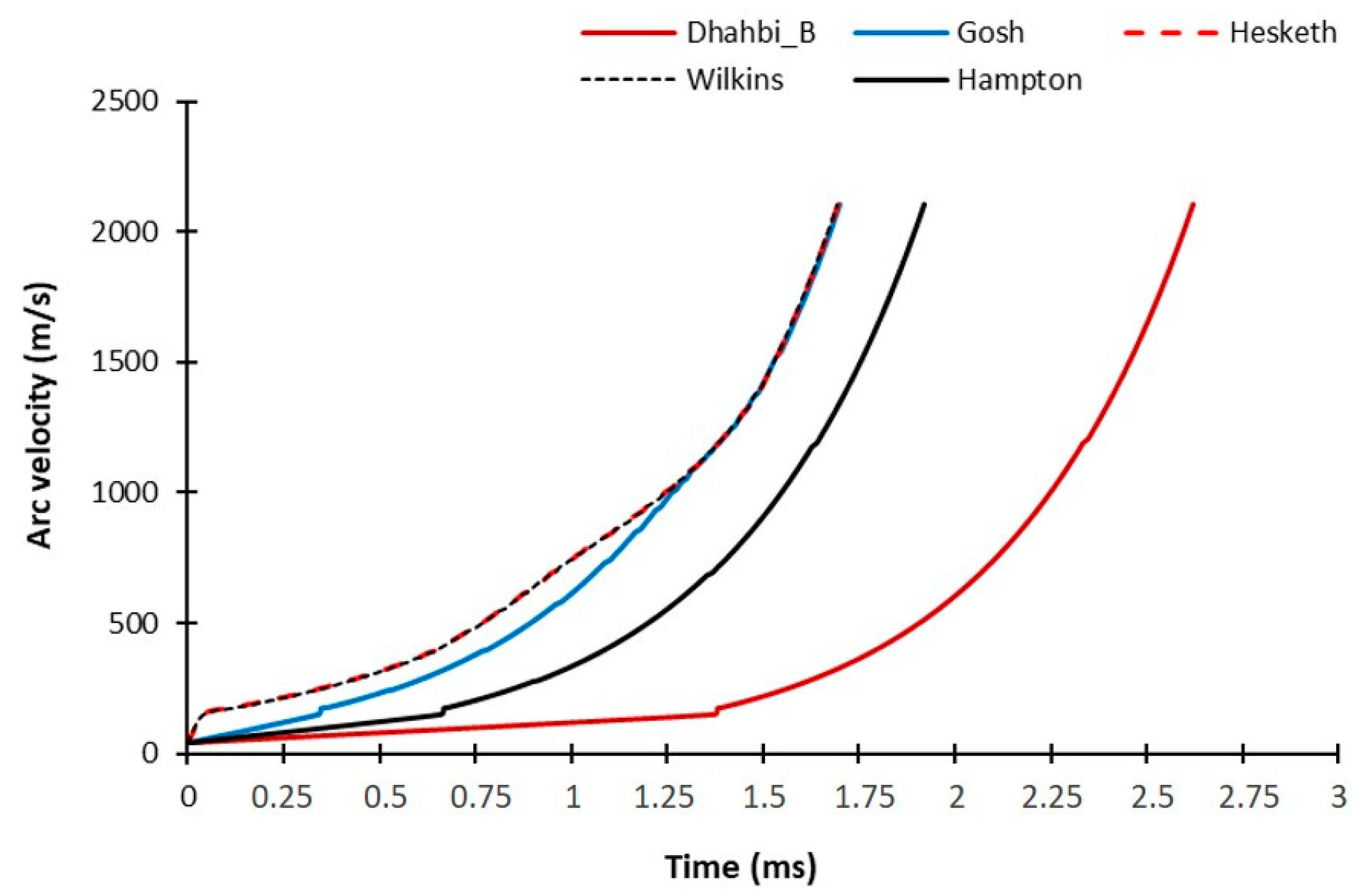
4.2. Influence of the Arc Propagation Criteria on the FOV Results
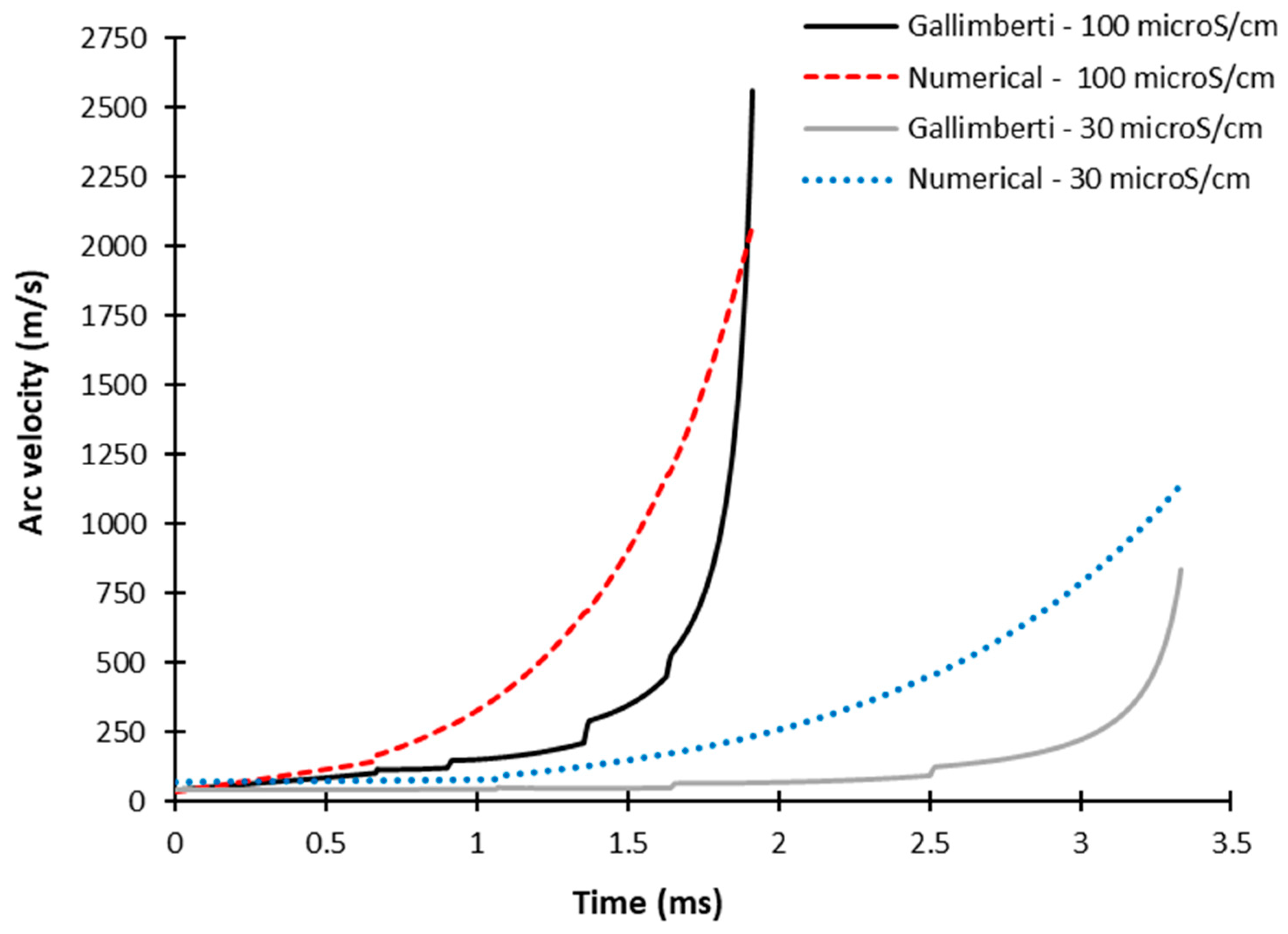
5. Improvement of Gallimberti Arc Velocity Criterion
6. Discussion
6.1. Influence of the Arc Velocity Criteria
6.2. Influence of the Arc Propagation Criteria
6.3. Improvement of Gallimberti Arc Velocity Criterion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khalifa, M.M.; Morris, R.M. Performance of line insulators under rime ice. IEEE Trans. Power Appar. Syst. 1967, PAS-86, 692–698. [Google Scholar] [CrossRef]
- Meier, A.; Niggli, W.M. The influence of snow and ice deposits on supertension transmission line insulator strings with special reference to high altitude operation. In Proceedings of the IEEE Conference Publication 44, London, UK, September 1968; pp. 386–395. [Google Scholar]
- Kawai, M. AC flashover tests at project UHV on ice-coated insulators. IEEE Trans. Power Appar. Syst. 1970, 80, 1800–1804. [Google Scholar] [CrossRef]
- Farzaneh, M.; Chisholm, W.A. 50 Years of icing performance of outdoor insulators. IEEE Electr. Insul. Mag. 2014, 30, 14–24. [Google Scholar] [CrossRef]
- Farzaneh, M.; Chisholm, W.A. Insulators for Icing and Polluted Environments; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Fikke, S.M. Possible effects of contaminated ice on insulator strength. In Proceedings of the 5th International Workshop on Atmospheric Icing of Structures (IWAIS), Tokyo, Japan, 29 October–1 November 1990. [Google Scholar]
- Makkonen, H.; Komuro, H.; Takasu, K. Withstand voltage characteristics of insulator string covered with snow and ice. IEEE Trans. Power Deliv. 1991, 6, 1243–1250. [Google Scholar]
- Farzaneh, M.; Kiernicki, J. Flashover problems caused by ice build-up on insulators. IEEE Electr. Insul. Mag. 1995, 11, 5–17. [Google Scholar] [CrossRef]
- Chisholm, W.; Kuffel, J. Performance of insulation coating under contamination and icing conditions. In Proceedings of the CEA Spring Meeting, Vancouver, BC, Canada, 2–4 June 1995. [Google Scholar]
- Farzaneh, M.; Drapeau, J.F. AC flashover performance of insulators covered with artificial ice. IEEE Trans. Power Deliv. 1995, 10, 1038–1051. [Google Scholar] [CrossRef]
- Farzaneh, M. Ice accretion on high voltage conductors and insulators and related phenomena. Philos. Trans. R. Soc. A 2000, 358, 2971–3005. [Google Scholar] [CrossRef]
- Volat, C.; Farzaneh, M. 3-D modeling of potential and electric field distributions along an EHV ceramic post insulator covered with ice—Part I: Simulations during a melting period. IEEE Trans. Power Deliv. 2005, 20, 2006–2013. [Google Scholar] [CrossRef]
- Volat, C.; Farzaneh, M. 3-D modeling of potential and electric field distributions along an EHV ceramic post insulator covered with ice—Part II: Influence of air gaps and partial arcs. IEEE Trans. Power Deliv. 2005, 20, 2014–2021. [Google Scholar] [CrossRef]
- Farzaneh, M.; Zhang, J.; Chen, X. Modeling of the AC arc discharge on ice surfaces. IEEE Trans. Power Deliv. 1997, 12, 325–338. [Google Scholar] [CrossRef]
- Farzaneh, M.; Zhang, J. Modeling of DC arc discharge on ice surfaces. IEE Proc. Gener. Trans. Distrib. 2000, 147, 86–94. [Google Scholar] [CrossRef]
- Farzaneh, M.; Zhang, J. A multi-arc model for predicting AC critical flashover voltage of ice-covered insulators. IEEE Trans. Dielectr. Electr. Insul. 2007, 14, 1401–1409. [Google Scholar] [CrossRef]
- Farzaneh, M.; Fofana, I.; Tavakoli, C.; Chen, X. Dynamic modeling of DC arc discharge on ice surfaces. IEEE Trans. Dielectr. Electr. Insul. 2003, 10, 463–474. [Google Scholar] [CrossRef]
- Tavakoli, C.; Farzaneh, M.; Fofana, I.; Beroual, A. Dynamics and modeling of AC arc on ice surfaces. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1278–1285. [Google Scholar] [CrossRef]
- Taheri, S.; Farzaneh, M.; Fofana, I. Improved dynamic model of DC arc discharge on ice-covered post insulator surfaces. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 729–739. [Google Scholar] [CrossRef]
- Taheri, S.; Farzaneh, M.; Fofana, I. Dynamic modeling of AC multiple arcs of EHV post station insulators covered with ice. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 2214–2223. [Google Scholar] [CrossRef]
- Mercure, H.P.; Drouet, M.G. Dynamic measurement of the current distribution in the foot of an arc propagating along the surface of an electrolyte. IEEE Trans. Power Appl. Syst. 1982, 101, 725–736. [Google Scholar] [CrossRef]
- Farokhi, S.; Nekahi, A.; Farzaneh, M. Mechanisms and processes of arc propagation over an ice-covered surface. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 2634–2641. [Google Scholar] [CrossRef]
- Nasser, E. Contamination flashover of outdoor insulation. ETZ-A 1982, 93, 321–325. [Google Scholar]
- Rahal, E.H.A.M. Sur les Mécanismes Physiques du Contournement des Isolateurs Haute Tension. Ph.D. Thesis, University Paul Sabatier, Toulouse, France, 1979. [Google Scholar]
- Jolly, D.C. Physical Process in the Flashover of Insulators with Contamination Surfaces. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1971. [Google Scholar]
- Wilkins, R. Flashover voltage of high-voltage insulators with uniform surface-pollution films. Proc. Inst. Electr. Eng. 1969, 116, 457–465. [Google Scholar] [CrossRef]
- Flazi, F. Étude du Contournement Électrique des Isolateurs HT Pollués. Critères D’élongation de la Décharge Dynamique du Phénomène. Ph.D. Thesis, Université Paul Sabatier, Toulouse, France, 1987. (In French). [Google Scholar]
- Slama, M.E.-A. Étude Expérimentale et Modélisation de L’influence de la Constitution Chimique et de la Répartition de la Pollution Sur le Contournement des Isolateurs HT. Ph.D. Thesis, École Centrale de Lyon, Lyon, France, 2011. (In French). [Google Scholar]
- Water, R.T.; Haddah, A.; Griffiths, H.; Harid, N.; Sarkar, P. Partial arc and spark models of the flashover of lightly polluted insulators. IEEE Trans. Dielectr. Electr. Insul. 2010, 17, 417–424. [Google Scholar] [CrossRef]
- Rizk, F.A.M.; Rezazada, A.Q. Modeling of altitude effects on AC flashover of polluted HV insulators. IEEE Trans. Power Deliv. 1997, 12, 810–822. [Google Scholar] [CrossRef]
- Matsumoto, T.; Ishi, M.; Kawamura, T. Optoelectronic measurement of partial arcs on contaminated surface. IEEE Trans. Electr. Insul. 1984, 19, 531–548. [Google Scholar] [CrossRef]
- Hadi, H. Mécanismes de Contournement et sa Modélisation Dynamique Appliquée Aux Isolateurs Réels. Ph.D. Thesis, Université des Sciences et Technologies d’Oran, Bir El Djir, Algeria, 2002. (In French). [Google Scholar]
- Volat, C.; Farzaneh, M.; Mhaguen, N. Improved FEM models of one-and two- arcs to predict AC critical flashover voltage of ice covered insulators. IEEE Trans. Dielectr. Electr. Insul. 2011, 18, 393–400. [Google Scholar] [CrossRef]
- Jabbari, M.; Volat, C.; Farzaneh, M. A new single-arc AC dynamic fem model of arc propagation on ice surfaces. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Ottawa, ON, Canada, 3–7 June 2013; pp. 360–364. [Google Scholar]
- Jabbari, M.; Volat, C.; Fofana, I. Application of a new dynamic numerical model to predict polluted insulator flashover voltage. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Philadephia, PA, USA, 8–11 June 2014; pp. 102–106. [Google Scholar]
- Hampton, B.F. Flashover mechanism of polluted insulation. Inst. Electr. Eng. IEE 1964, 111, 985–990. [Google Scholar] [CrossRef]
- Rumeli, A. Computation of Pollution Flashover Voltages of High Voltage Insulators; Technical Report; Tubitak Engineering Research Group: Ankara, Turkey, 1973. [Google Scholar]
- Bessedik, S.A.; Hadi, H.; Volat, C.; Jabbari, M. refinement of residual resistance calculation dedicated to polluted insulator flashover models. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1207–1215. [Google Scholar] [CrossRef]
- Bondiou-Clergerie, A.; Gallimberti, I. Theoretical modelling of the development of the positive spark in long gaps. J. Phys. D. Appl. Phys. 1994, 27, 1252–1266. [Google Scholar] [CrossRef]
- Beroual, A. Electronic gaseous process in the breakdown phenomena of dielectric liquids. J. Appl. Phys. 1993, 73, 4528–4533. [Google Scholar] [CrossRef]
- Beroual, A.; Dhahbi-Megriche, N. Model for calculation of flashover characteristics on polluted insulating surfaces under DC stress. In Proceedings of the 1998 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (Cat. No.98CH36257), Atlanta, GA, USA, 25–28 October 1998; pp. 80–83. [Google Scholar]
- Anjana, S.; Lakshminarasmha, C.S. Computed of flashover voltages of polluted insulators using dynamic arc model. In Proceedings of the 6th International Symposium on High Voltage Engineering, New Orleans, LA, USA, 28 August–1 September 1989. [Google Scholar]
- Hesketh, S. General criterion for the prediction of pollution flashover. Proc. Inst. Electr. Eng. 1967, 114, 531–540. [Google Scholar] [CrossRef]
- Billings, M.J.; Wilkins, R. Considerations of the suppression of insulator flashover by resistive surface films. Proc. Inst. Electr. Eng. 1966, 113, 1649–1653. [Google Scholar] [CrossRef]
- Ghosh, P.S.; Chatterjee, N. Polluted insulator flashover model. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 128–136. [Google Scholar] [CrossRef]
- Mayr, O. Beitrag zur Theorie des statischen und des dynamischen Lichtbogens. Arch. Elektrotech. 1943, 37, 588–608. (In Germany) [Google Scholar] [CrossRef]
- Dhahbi-Megriche, N.; Beroual, A.; Krähenbühl, L. A new proposal model for flashover of polluted insulators. J. Phys. D. Appl. Phys. 1997, 30, 889–894. [Google Scholar] [CrossRef]
- Dhahbi-Megriche, N.; Beroul, A. Flashover Dynamic Model of Polluted Insulators under AC Voltage. IEEE Trans. Electr. Insul. 2000, 7, 283–289. [Google Scholar] [CrossRef]
- Fofana, I.; Beroual, A. A new proposal for calculation of the leader velocity based on energy consideration. J. Phys. D Appl. Phys. 1996, 29, 691–696. [Google Scholar] [CrossRef]
- Sundararajan, R.; Sadhureddy, N.; Gorur, R. Computer-aided Design of Porcelain Insulators under Polluted Conditions. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 121–127. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| A | 204.7 |
| n | 0.5607 |
| k | 1118 |
| b | 0.5277 |
| α | 0.0675 |
| β | 2.45 |
| B | 0.875 |
| Water Conductivity (µS/cm) | Experimental FOV [18] (kVrms) | FOV Obtained with Gallimberti (kVrms) | FOV Obtained with Beroual (kVrms) | FOV Obtained with Anjana and Lakshminarasimha (kVrms) |
|---|---|---|---|---|
| Arcing distance of 40 cm | ||||
| 30 | 48 | 49.6 | 53.5 | 51.4 |
| 65 | 43 | 42.4 | 50.6 | 49.1 |
| 100 | 40 | 37.5 | 50.6 | 41.8 |
| Arcing distance of 80 cm | ||||
| 30 | 86 | 92.3 | 90.7 | 91.7 |
| 65 | 78 | 78.9 | 88.3 | 84.5 |
| 100 | 74 | 69.6 | 89.4 | 89.3 |
| Arcing distance of 103 cm | ||||
| 30 | 106 | 112.6 | 102.6 | 123 |
| 65 | 97 | 97.0 | 92.2 | 101.8 |
| 100 | 92 | 86.5 | 94.1 | 115.7 |
| Water Conductivity (µS/cm) | Gallimberti (%) | Beroual (%) | Anjana and Lakshminarasimha (%) |
|---|---|---|---|
| Arcing distance of 40 cm | |||
| 30 | 3.3 | 11.4 | 7.0 |
| 65 | 1.4 | 17.6 | 4.5 |
| 100 | 6.2 | 26.5 | 9.0 |
| Arcing distance of 80 cm | |||
| 30 | 7.3 | 5.4 | 6.6 |
| 65 | 1.1 | 15.8 | 8.3 |
| 100 | 5.0 | 20.8 | 20.6 |
| Arcing distance of 103 cm | |||
| 30 | 6.2 | 3.2 | 16.0 |
| 65 | 0.0 | 4.9 | 4.9 |
| 100 | 6.0 | 2.2 | 25.7 |
| Average discrepancy (%) | 4.1 | 12.0 | 11.4 |
| Water Conductivity (µS/cm) | Experimental (kVrms) | Hampton (kVrms) | Billings and Wilkins (kVrms) | Hesketh (kVrms) | Ghosh (kVrms) | Dhahbi and Beroual (kVrms) |
|---|---|---|---|---|---|---|
| Arcing distance of 80 cm | ||||||
| 30 | 86 | 92.3 | 84.7 | 92.5 | 92.6 | 92.5 |
| 100 | 74 | 69.6 | 69.4 | 71.6 | 71.6 | 71.6 |
| Arcing distance of 103 cm | ||||||
| 30 | 106 | 112.6 | 112.2 | 112.4 | 112.4 | 112.4 |
| 100 | 92 | 86.5 | 86.5 | 88 | 88 | 88 |
| Water Conductivity (µS/cm) | Hampton (%) | Billings and Wilkins (%) | Hesketh (%) | Ghosh (%) | Dhahbi and Beroual (%) |
|---|---|---|---|---|---|
| Arcing distance of 80 cm | |||||
| 30 | 7.3 | 1.5 | 7.6 | 7.7 | 7.6 |
| 100 | 5.0 | 6.2 | 3.2 | 3.2 | 3.2 |
| Arcing distance of 103 cm | |||||
| 30 | 6.2 | 6.2 | 5.8 | 6.0 | 6.0 |
| 100 | 6.0 | 6.0 | 5.8 | 4.3 | 4.3 |
| Average discrepancy (%) | 6.1 | 4.8 | 5.3 | 5.3 | 5.3 |
| Water Conductivity (µS/cm) | Experimental FOV [8] (kVrms) | FOV with Numerical Criterion (kVrms) | FOV with Gallimberti Criterion (kVrms) |
|---|---|---|---|
| Arcing distance of 40 cm | |||
| 30 | 48 | 50.1 | 49.6 |
| 65 | 43 | 42.9 | 42.4 |
| 100 | 40 | 38.7 | 37.5 |
| Arcing distance of 80 cm | |||
| 30 | 86 | 92.6 | 93.3 |
| 65 | 78 | 79.8 | 78.9 |
| 100 | 74 | 71.6 | 68.6 |
| Arcing distance of 103 cm | |||
| 30 | 106 | 113.4 | 114.8 |
| 65 | 97 | 97.4 | 97.0 |
| 100 | 92 | 87.8 | 86.5 |
| Water Conductivity (µS/cm) | Discrepancy Obtained with Numerical Criterion (%) | Discrepancy Obtained with Gallimberti Criterion (%) |
|---|---|---|
| Arcing distance of 40 cm | ||
| 30 | 4.3 | 3.3 |
| 65 | 0.2 | 1.3 |
| 100 | 3.2 | 6.2 |
| Arcing distance of 80 cm | ||
| 30 | 7.6 | 8.4 |
| 65 | 2.3 | 1.5 |
| 100 | 3.2 | 7.2 |
| Arcing distance of 103 cm | ||
| 30 | 6.9 | 8.3 |
| 65 | 0.4 | 0 |
| 100 | 4.5 | 5.9 |
| Average discrepancy (%) | 3.6 | 4.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabbari, M.; Volat, C.; Fofana, I. Numerical Modelling of Ice-Covered Insulator Flashover: The Influence of Arc Velocity and Arc Propagation Criteria. Energies 2018, 11, 2807. https://doi.org/10.3390/en11102807
Jabbari M, Volat C, Fofana I. Numerical Modelling of Ice-Covered Insulator Flashover: The Influence of Arc Velocity and Arc Propagation Criteria. Energies. 2018; 11(10):2807. https://doi.org/10.3390/en11102807
Chicago/Turabian StyleJabbari, Marouane, Christophe Volat, and Issouf Fofana. 2018. "Numerical Modelling of Ice-Covered Insulator Flashover: The Influence of Arc Velocity and Arc Propagation Criteria" Energies 11, no. 10: 2807. https://doi.org/10.3390/en11102807
APA StyleJabbari, M., Volat, C., & Fofana, I. (2018). Numerical Modelling of Ice-Covered Insulator Flashover: The Influence of Arc Velocity and Arc Propagation Criteria. Energies, 11(10), 2807. https://doi.org/10.3390/en11102807







