Determining Switched Reluctance Motor Current Waveforms Exploiting the Transformation from the Time to the Position Domain
Abstract
:1. Introduction
2. Switched Reluctance Motor Expressed in the Position Domain
3. Discrete Representation
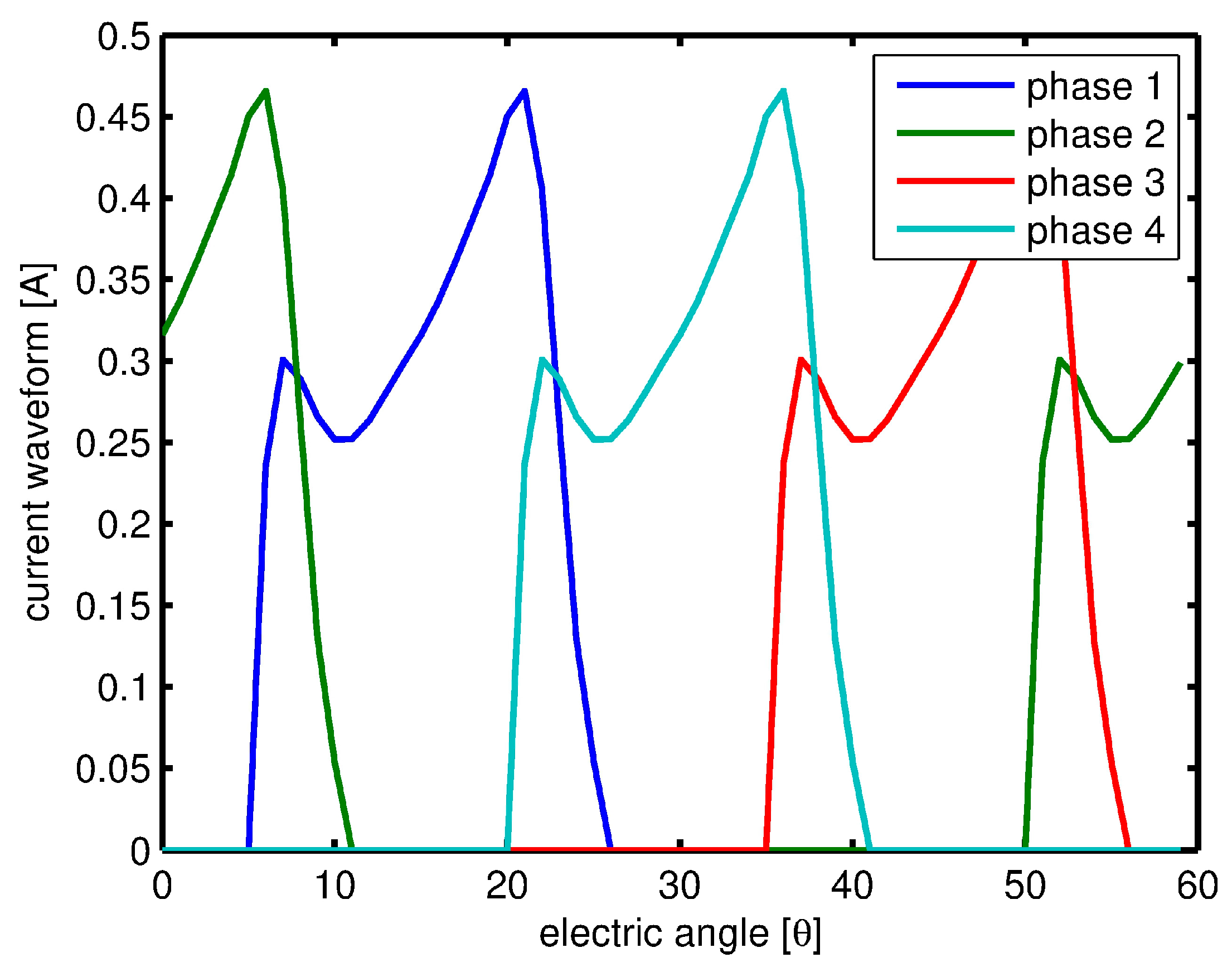
4. Searching for Current Waveforms
5. Constrained Voltage
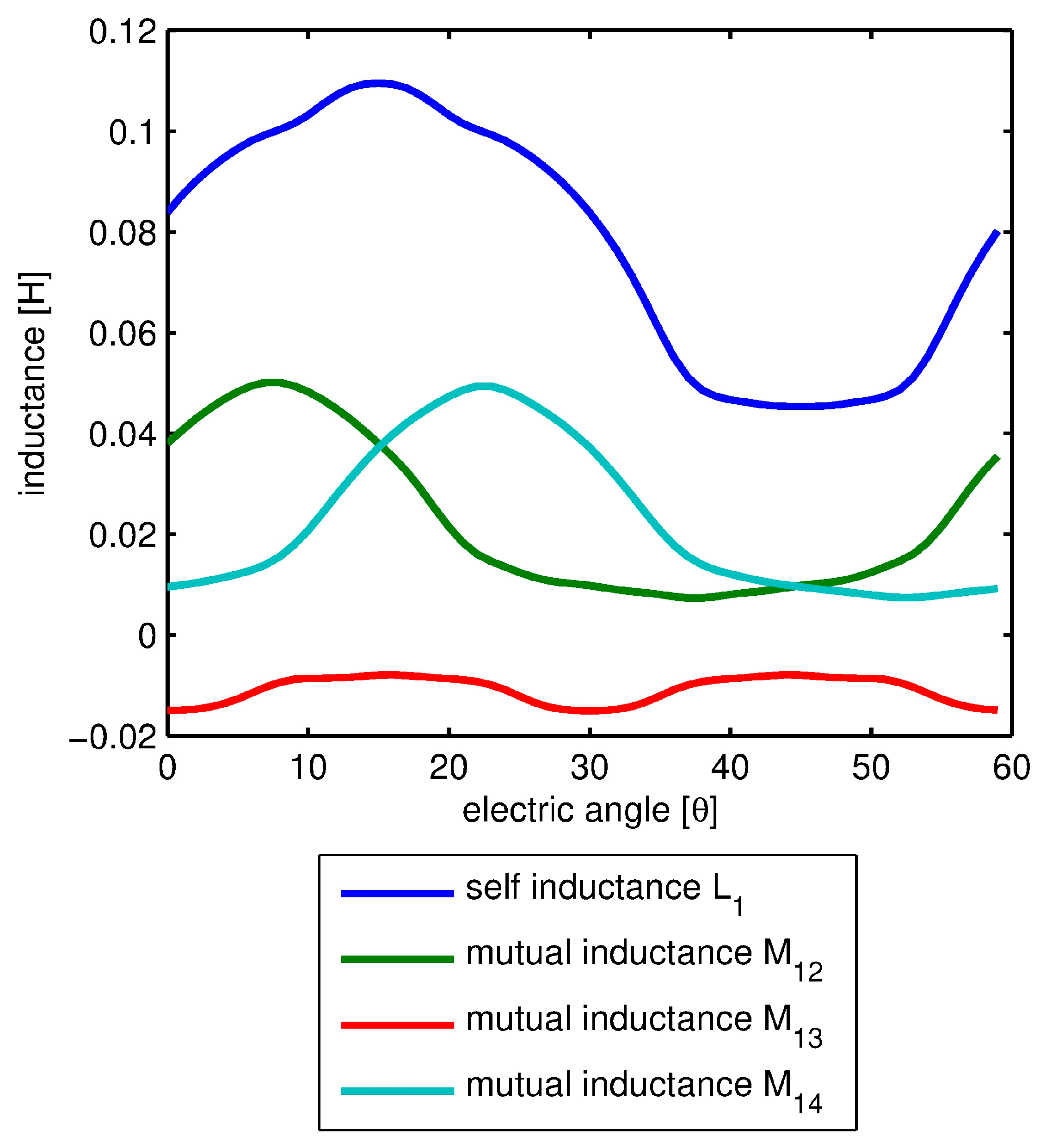
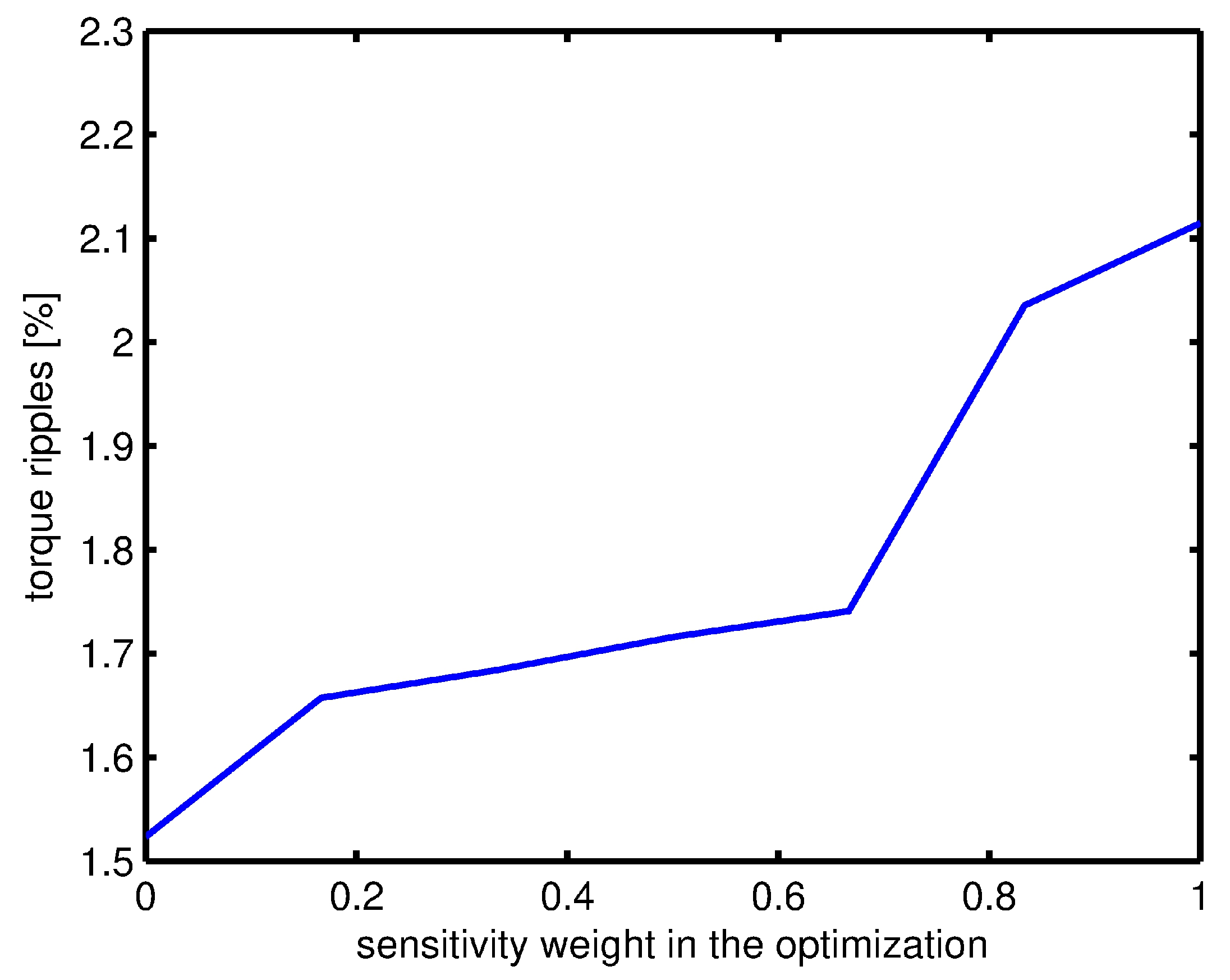
6. Sensitivity Analysis
7. The Optimisation Problem
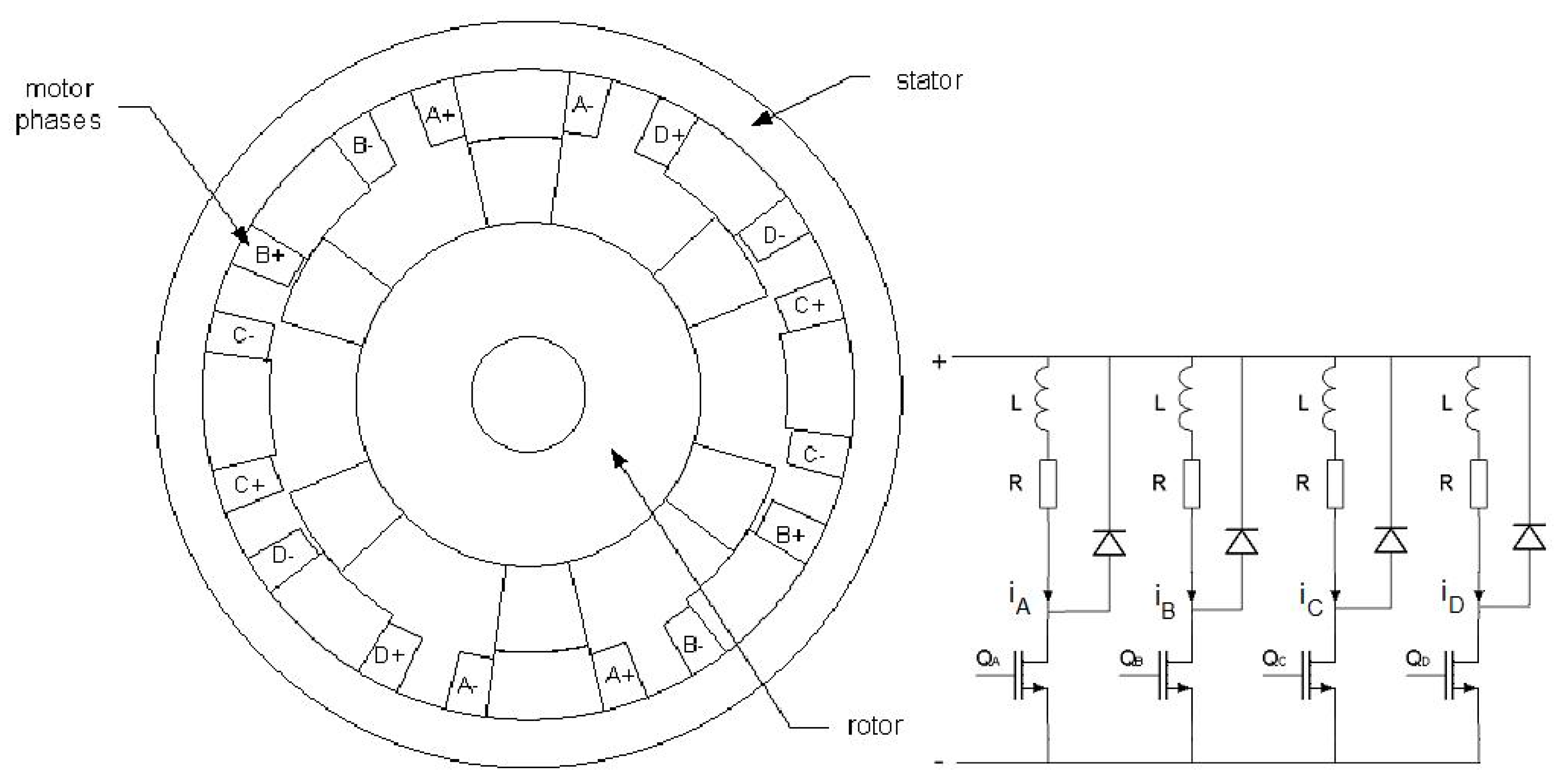
8. The Experimental Setup
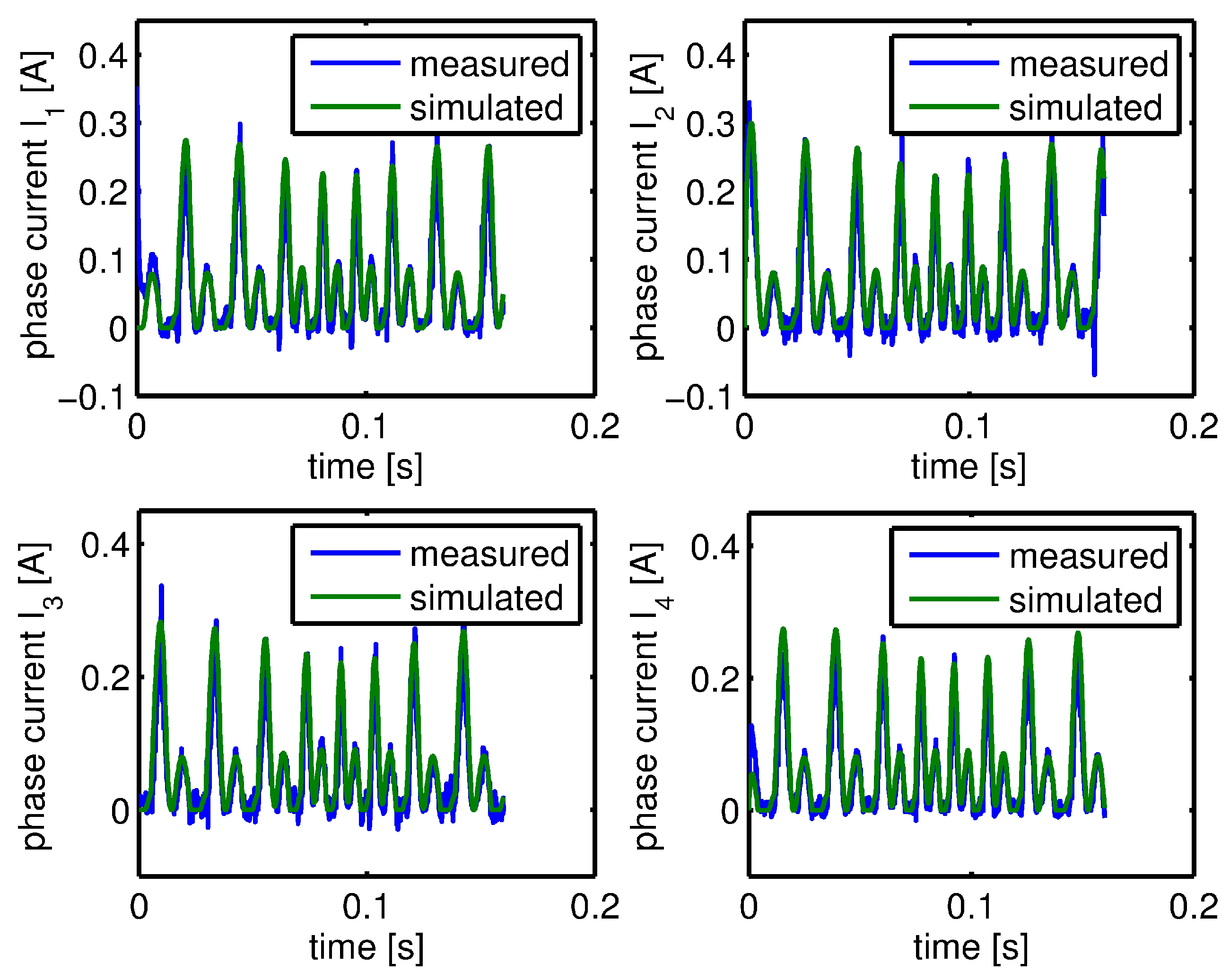
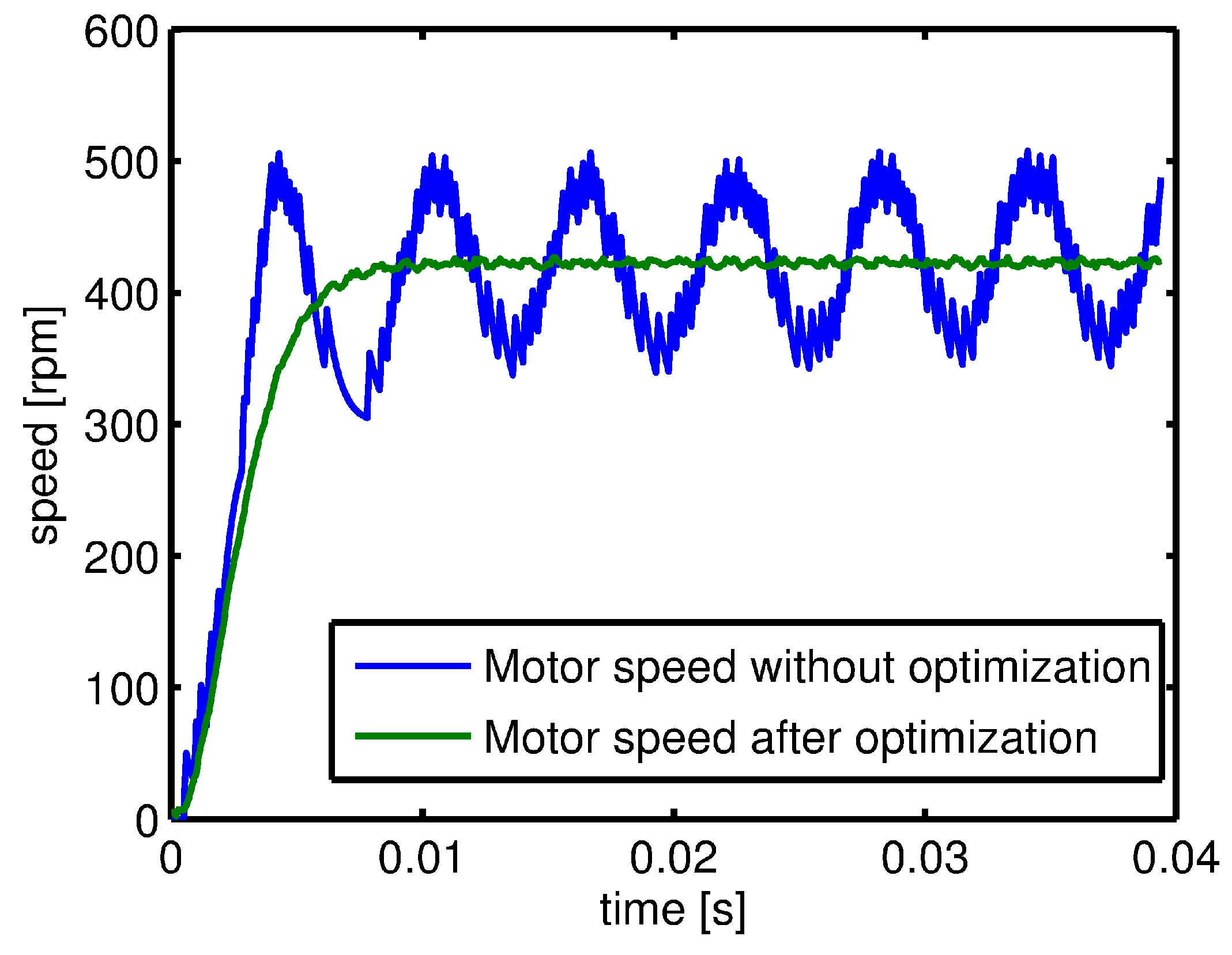
9. The Optimization Process
10. The Closed Loop Control Algorithm
11. Conclusions
Author Contributions
Conflicts of Interest
References
- Vijayakumar, K.; Karthikeyan, R.; Paramasivam, S.; Arumugam, R.; Srinivas, K.N. Switched Reluctance Motor Modeling, Design, Simulation, and Analysis: A Comprehensive Review. IEEE Trans. Magn. 2008, 44, 4605–4617. [Google Scholar] [CrossRef]
- Stępień, S.; Bernat, J. Modeling and optimal control of variable reluctance stepper motor. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2011, 30, 726–740. [Google Scholar] [CrossRef]
- Ilic-Spong, M.; Marino, R.; Peresada, S.M.; Taylor, D.G. Feedback linearizing control of switched reluctance motors. IEEE Trans. Autom. Control 1987, 32, 371–379. [Google Scholar] [CrossRef]
- Wallace, R.S.; Taylor, D.G. A balanced commutator for Switched Reluctance Motors to Reduce Torque Ripple. IEEE Trans. Power Electron. 1992, 7, 617–626. [Google Scholar] [CrossRef]
- Filicori, F.; Guarino, C.; Bianco, L.; Tonielli, A. Modeling and Control Strategies for a Variable Reluctance Direct-Drive Motor. IEEE Trans. Ind. Electron. 1993, 40, 105–115. [Google Scholar] [CrossRef]
- Buja, G.S.; Menis, R.; Valla, M.I. Variable Structure Control of an SRM Drive. IEEE Trans. Ind. Electron. 1993, 40, 56–63. [Google Scholar] [CrossRef]
- Illic-Spong, M.; Miller, T.J.E.; MacMinn, S.R.; Thorp, J.S. Instantaneous torque control of electric motor drives. IEEE Trans. Power Electron. 1987, 2, 55–61. [Google Scholar] [CrossRef]
- Xue, X.D.; Cheng, W.E.; Ho, S.L. Optimization and Evaluation of Torque-Sharing Functions for Torque Ripples Minimization in Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2009, 24, 2076–2090. [Google Scholar] [CrossRef]
- Moron, C.; Garcia, A.; Tremps, E.; Somolinos, J.A. Torque Control of Switched Reluctance Motors. IEEE Trans. Magn. 2012, 48, 1661–1664. [Google Scholar] [CrossRef]
- Cheok, A.D.; Fukuda, Y. A New Torque and Flux Control Method for Switched Reluctance Motor Drives. IEEE Trans. Power Electron. 2002, 17, 543–557. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Dasgupta, S.; Panda, S.K.; Xu, J.X. A Lyapunov Function-Based Robust Direct Torque Controller for a Switched Reluctance Motor Drive System. IEEE Trans. Power Electron. 2012, 27, 555–564. [Google Scholar] [CrossRef]
- Bernat, J.; Kołota, J.; Stępień, S.; Sykulski, J. A steady state solver for modelling rotating electromechanical devices exploiting the transformation from time to position domain. Int. J. Numer. Model. Electron. Netw. Devices Fields 2014, 27, 213–228. [Google Scholar] [CrossRef]


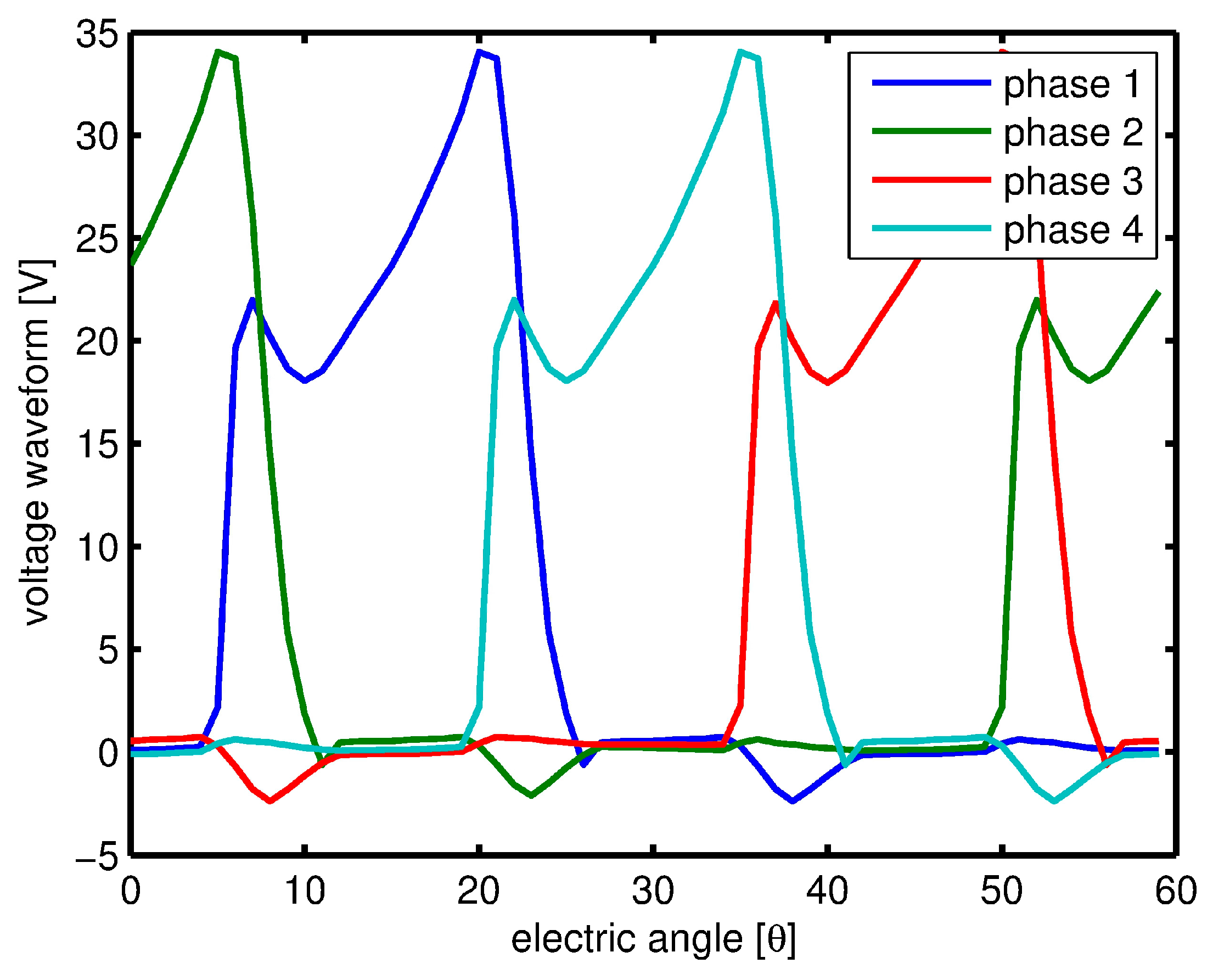
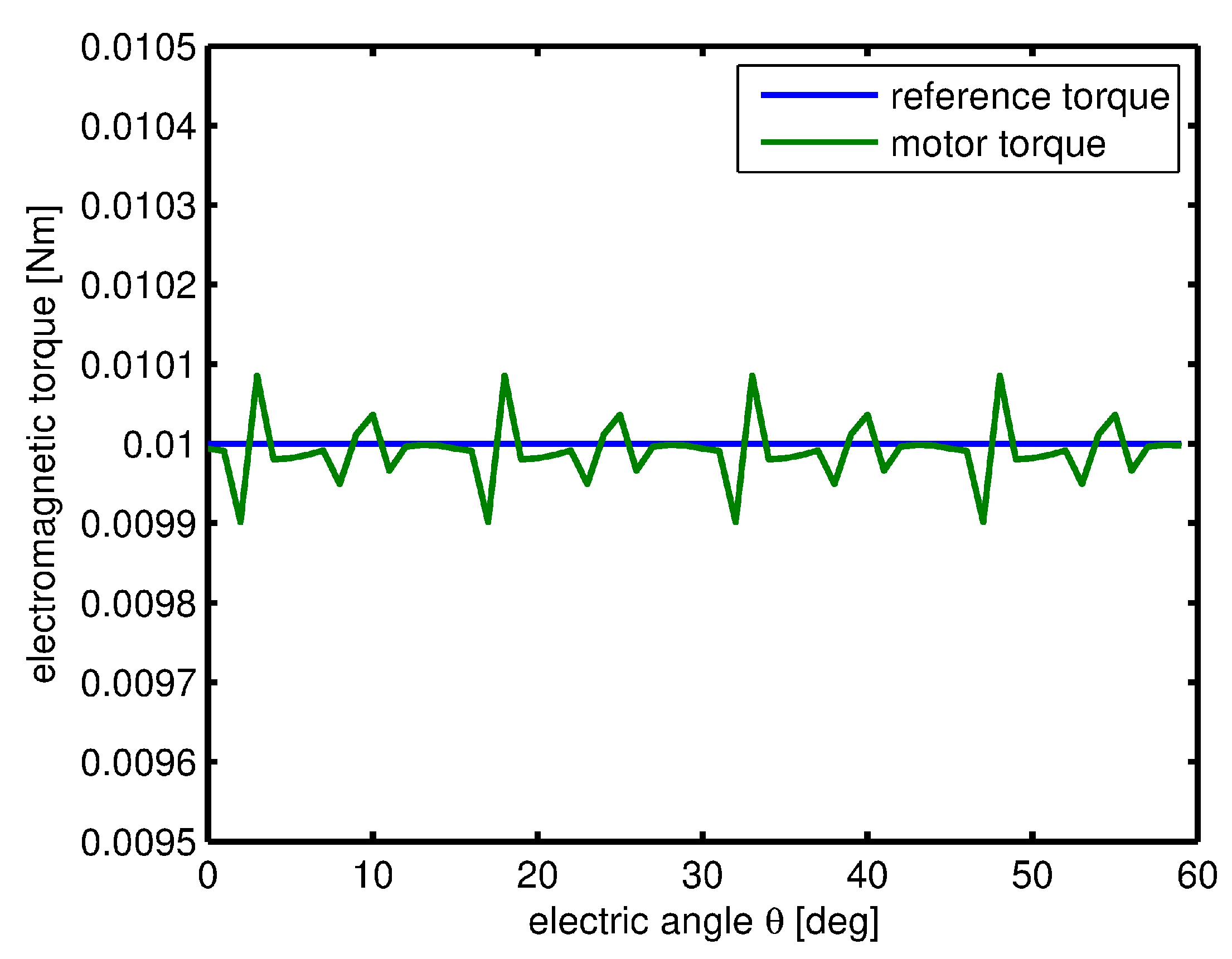
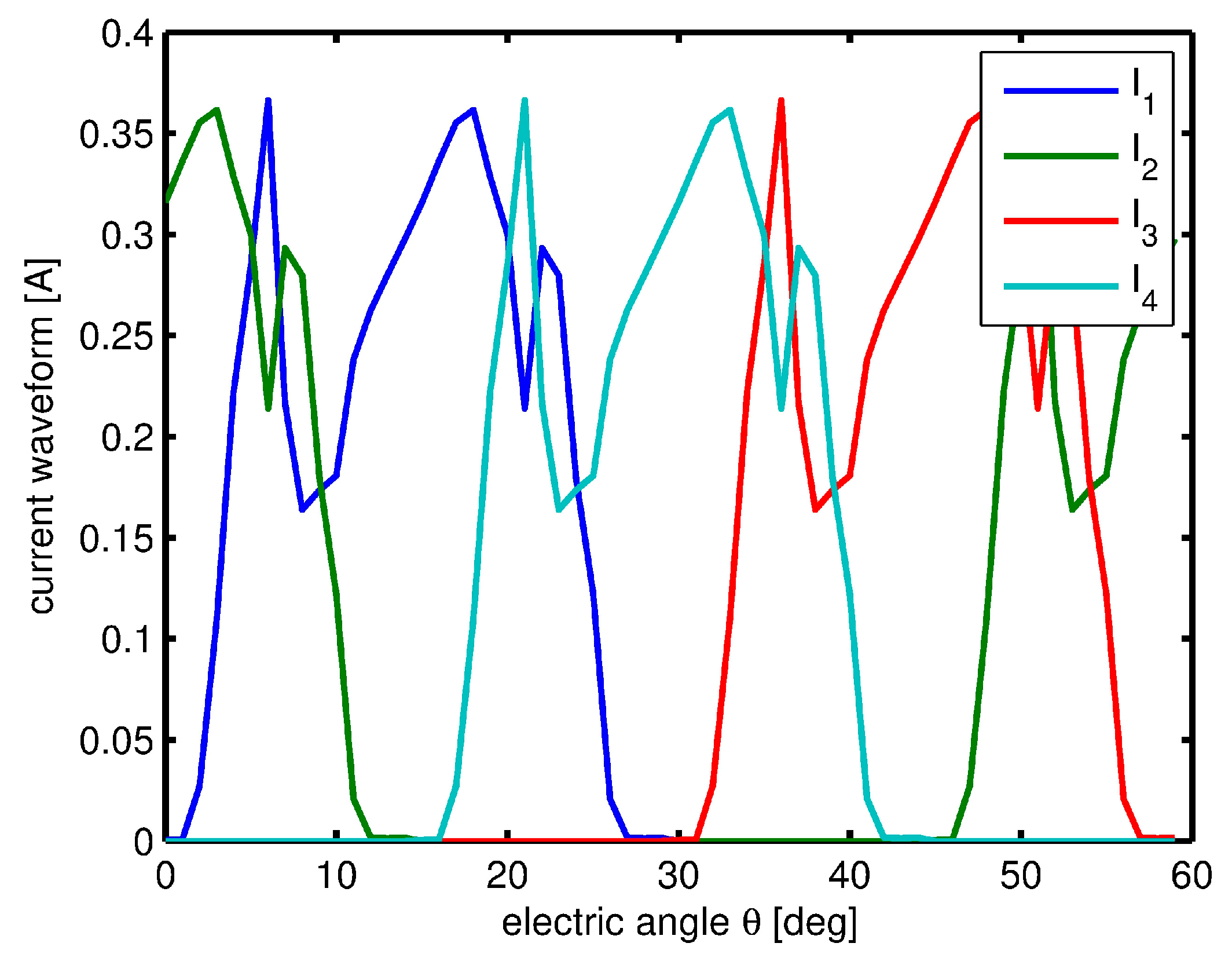

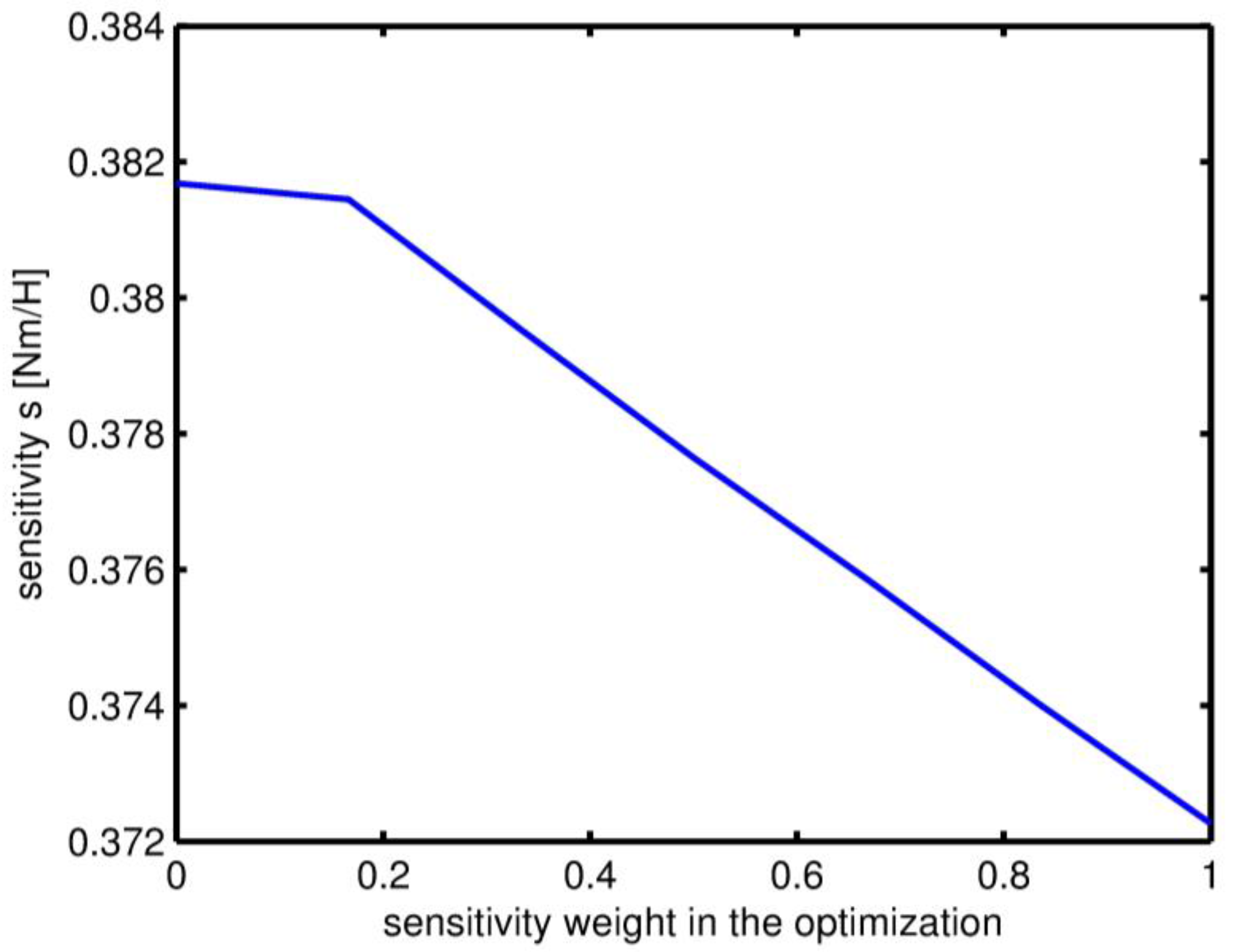

| Outer diameter of stator | 39 mm |
| Inter diameter of stator | 34 mm |
| Outer diameter of rotor | 26.96 mm |
| Inter diameter of rotor | 5 mm |
| Air gap length | 0.02 mm |
| Motor length | 30 mm |
| Resistance/phase | 75 Ω |
| Rotor inertia | 0.13 g∙cm2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bernat, J.; Stępień, S.; Sykulski, J.K. Determining Switched Reluctance Motor Current Waveforms Exploiting the Transformation from the Time to the Position Domain. Energies 2017, 10, 799. https://doi.org/10.3390/en10060799
Bernat J, Stępień S, Sykulski JK. Determining Switched Reluctance Motor Current Waveforms Exploiting the Transformation from the Time to the Position Domain. Energies. 2017; 10(6):799. https://doi.org/10.3390/en10060799
Chicago/Turabian StyleBernat, Jakub, Sławomir Stępień, and Jan K. Sykulski. 2017. "Determining Switched Reluctance Motor Current Waveforms Exploiting the Transformation from the Time to the Position Domain" Energies 10, no. 6: 799. https://doi.org/10.3390/en10060799







