Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review
Abstract
:1. Introduction
2. State of The Art of The Technology
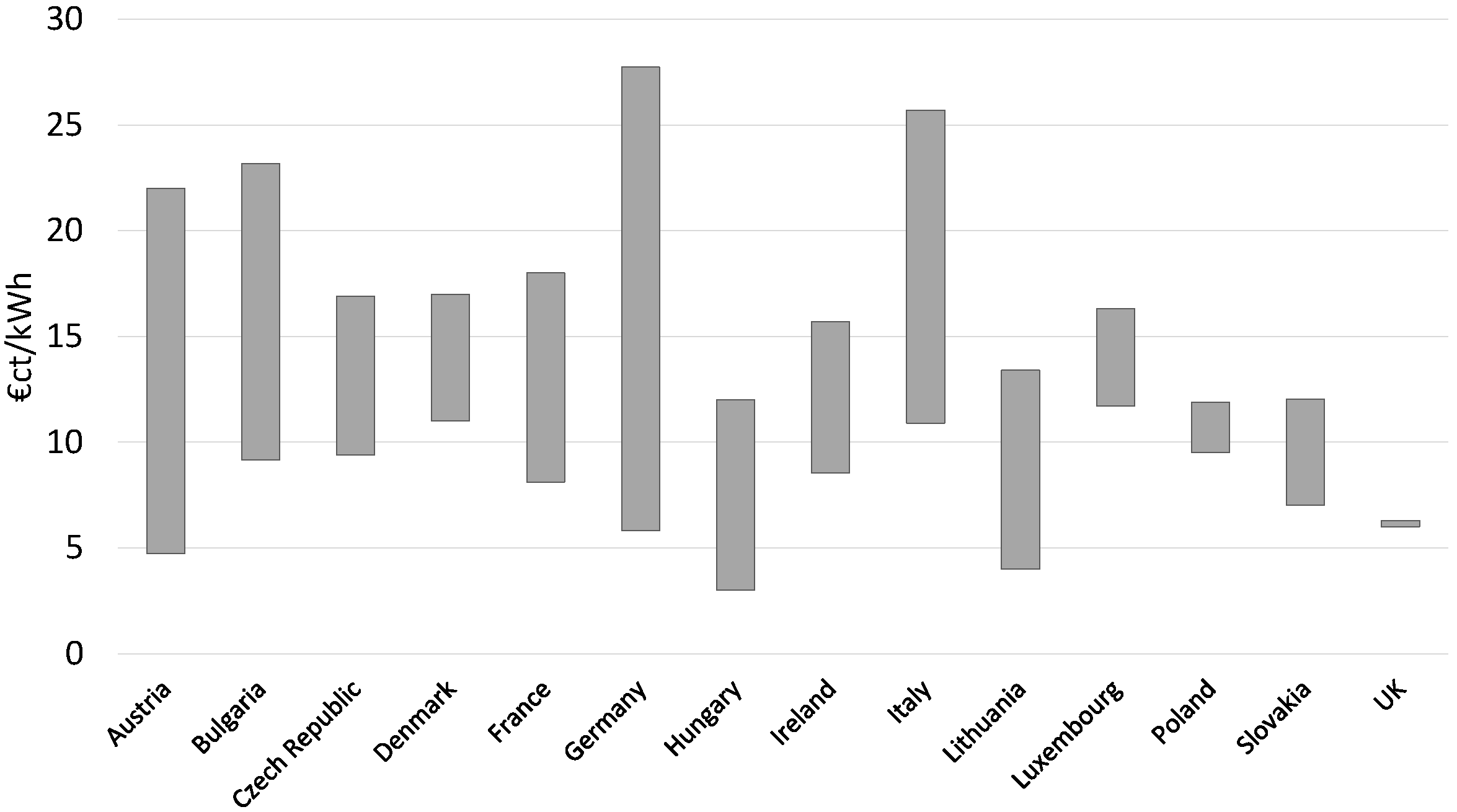
2.1. European Incentives Scenario
- Feed-in Tariffs (FiTs)
- Premium Tariffs (FiP)
- Green certificates/quota obligations
- Investment incentives
- Auctions/tenders
- Net metering
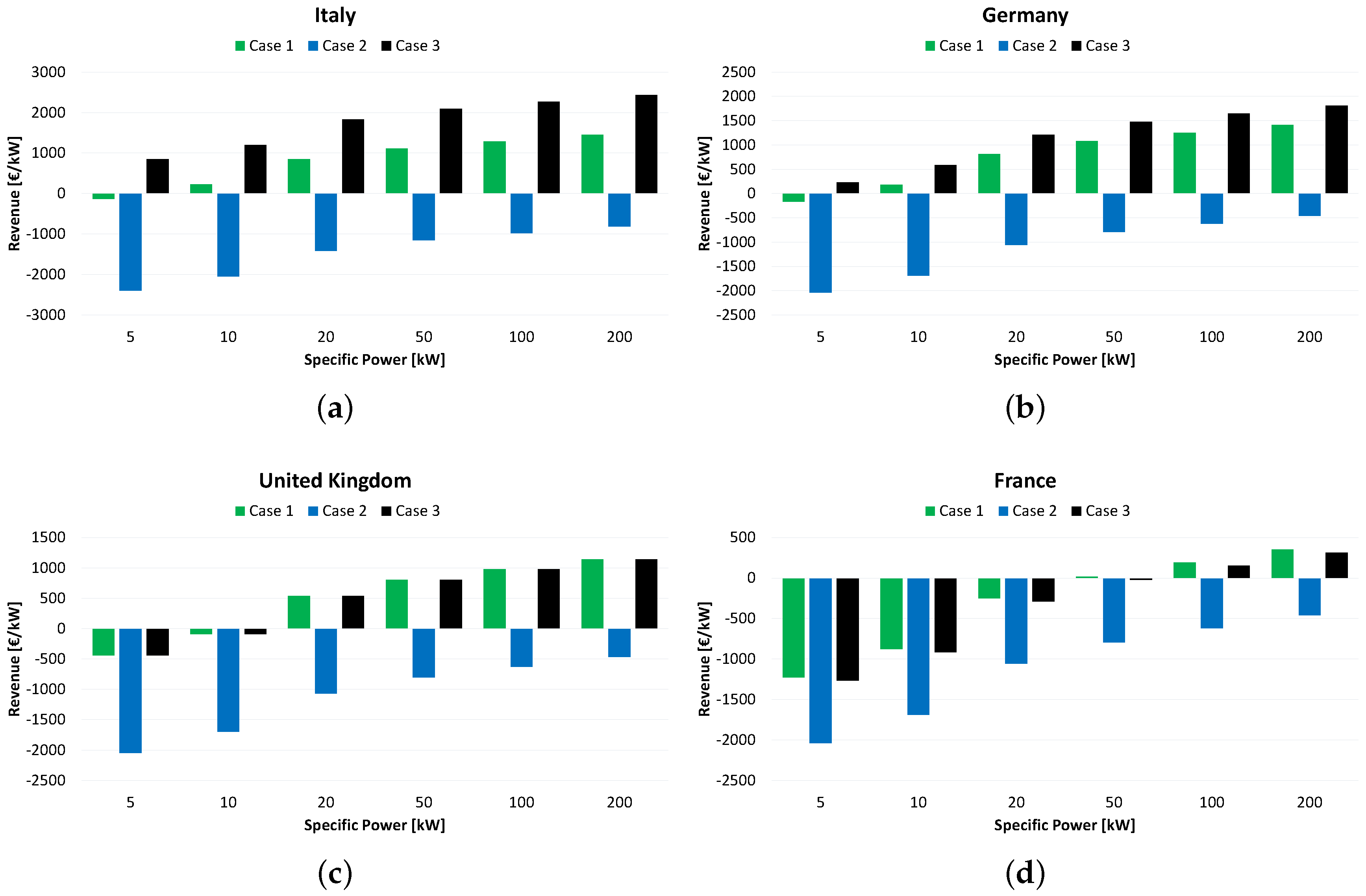
- Case 1: An industrial company invests in the installation of an ORC system to produce the electrical energy demand of its factory. The ORC plant is coupled to process waste heat. The investment is paid back from the savings on the energy bill since the electricity is not purchased any more at the market price from the grid.
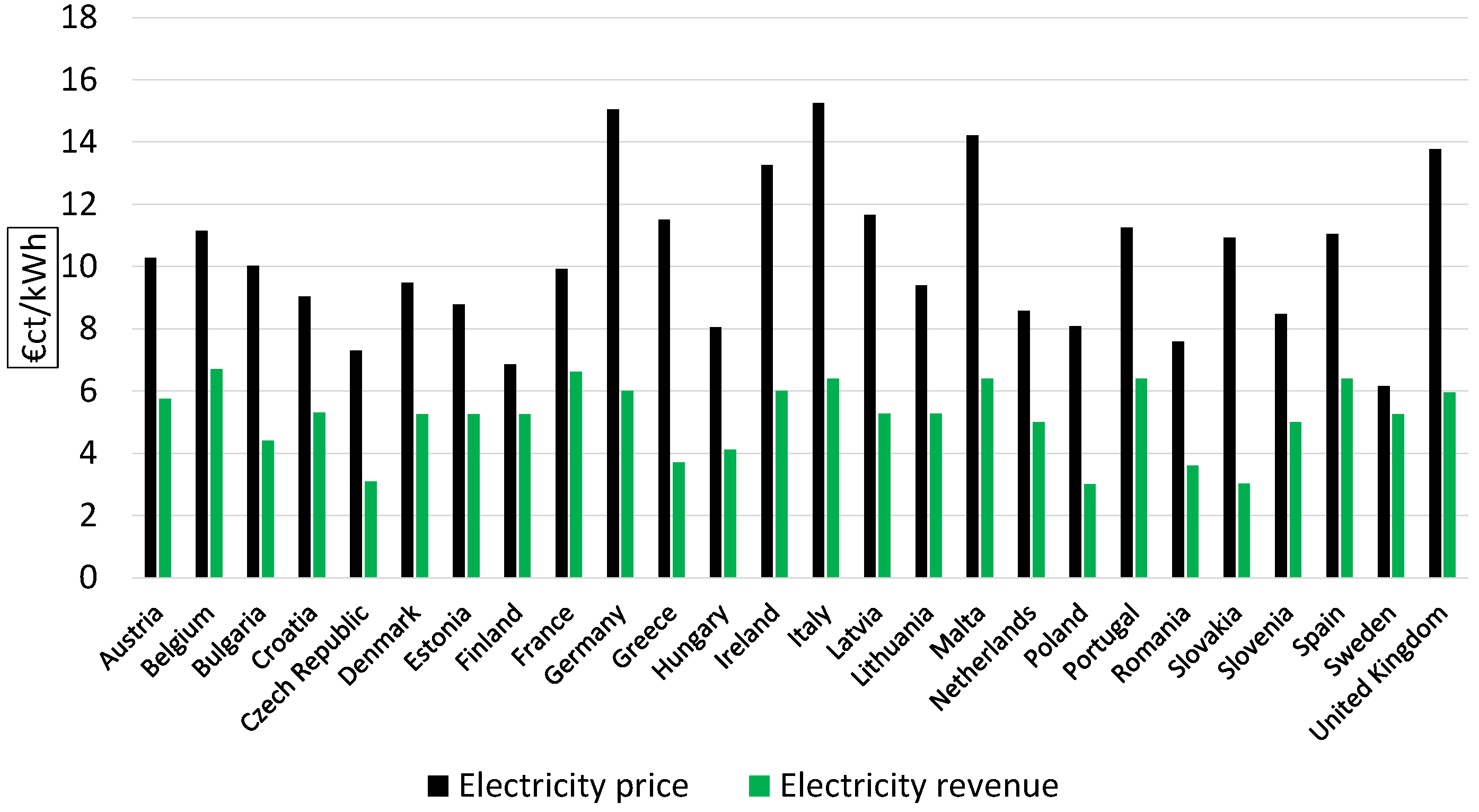
- Case 2: A stationary engine operator installs an ORC unit to generate additional power by recovering the thermal energy in the exhaust gasses to sell it to the grid at the actual market price. In this case, the income depends on the price at which the grid purchases the energy produced by the ORC plant (see Figure 4).
- Case 3: An ORC plant is installed to produce electrical energy from a renewable energy source, such as biomass, solar or geothermal energy. Such a plant is eligible for the feed-in tariff.
2.2. ORC Market Analysis
3. Working Fluid Selection
- Price: Since organic fluids are expensive (20–30 €/kg), it is important to find the correct trade-off between cost and performance [71]. Generally, fluids used in operating ORC plants are extensively used in other fields, which lowers their price.
- Density: Chen et al. [84] underline that low density leads to a high volumetric flow rate of the working fluid. This has an impact on different components of the system. The higher the volumetric flow rate, the bigger the size of the components and, in turn, their cost. However, a high volumetric flow rate allows for the reduction of the rotational speed of the expander, which has a positive impact on the reliability of turbo-expanders.
- Condensation pressure: Ideally, the condensation pressure should be as close as possible to atmospheric. In fact, a high condensing pressure leads to an increase in the overall system pressure, which requires more resistant and therefore more expensive materials. Condensing pressures below 0.5 bar leads to an increase in the sealing costs to prevent air from entering the system. Moreover, lower pressures increase the size of the condenser. [14].
- Freezing point: The freezing point needs to be well below the minimum ambient temperature in the site in which the system is installed, to avoid solidification of the working fluid during periods of inactivity of the ORC plant [85].
- Cycle top pressure: It is important to keep the cycle top pressure well below the fluid critical pressure [86]. This is necessary to prevent the formation of liquid droplets during the expansion process and to overcome instability during vaporization. Low pressure allows for the use of less expensive materials, which has a positive impact on system costs. High pressure implies high fluid density, which in turns lowers the system size. A trade-off has to be found through a techno-economic analysis.
- Heat transfer coefficient: The heat transfer coefficient plays a crucial role in the definition of the size and cost of the heat exchangers [87]. The selection of an organic compound with good heat transfer properties would lead to the reduction of the heat transfer surface, which, in turn, lowers the overall size, weight and cost of the ORC system [88].
- Fluid decomposition temperature: Organic fluids suffer from chemical decomposition at high temperature [89]. For this reason, it is important that the temperature of the heat source in the evaporator does not overcome the decomposition temperature of the working fluid.
- Molecular weight: Fluids with high molecular weight allow for a smaller rotational speed of the expander [90], which in turn affects positively its efficiency and typically diminishes the cost of the generator.
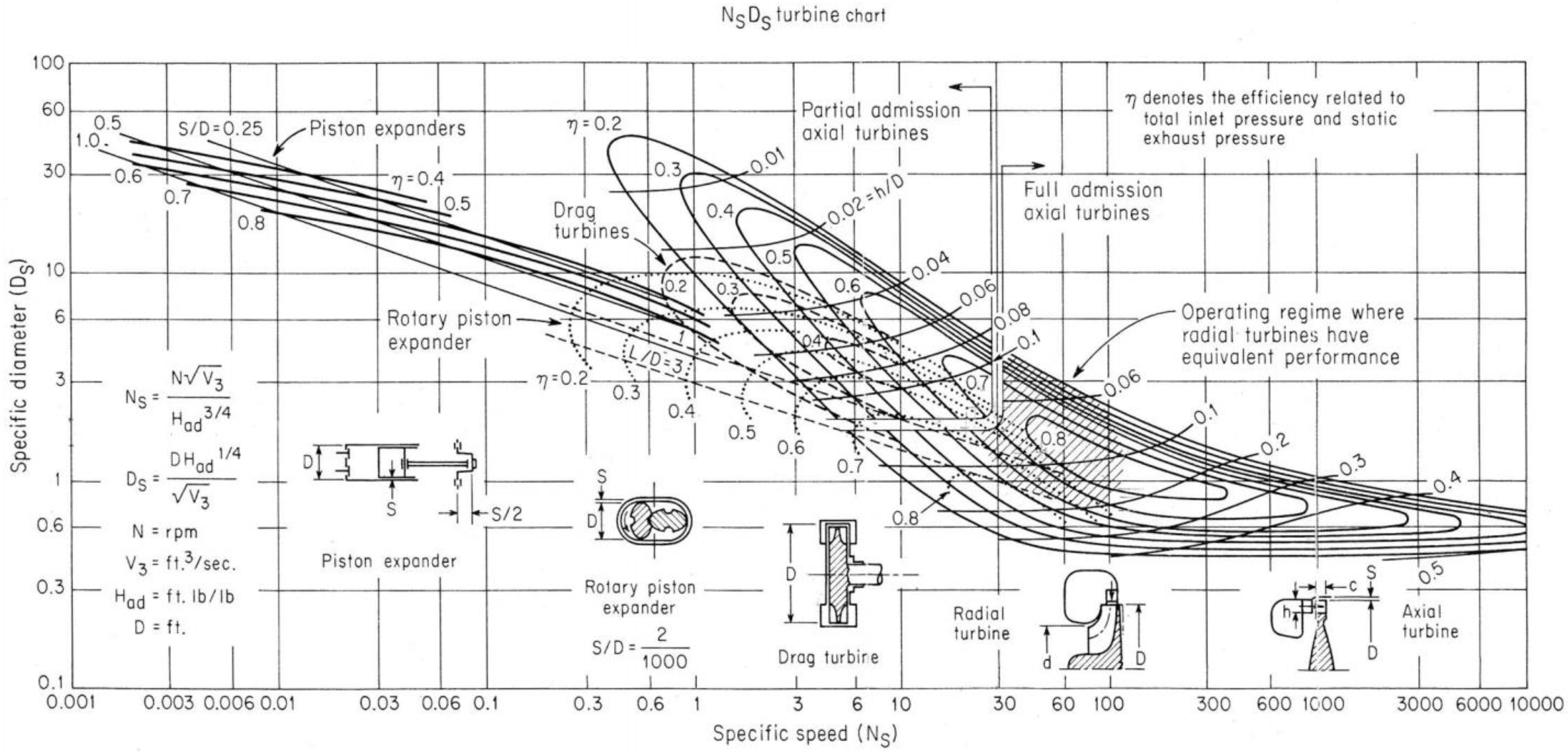
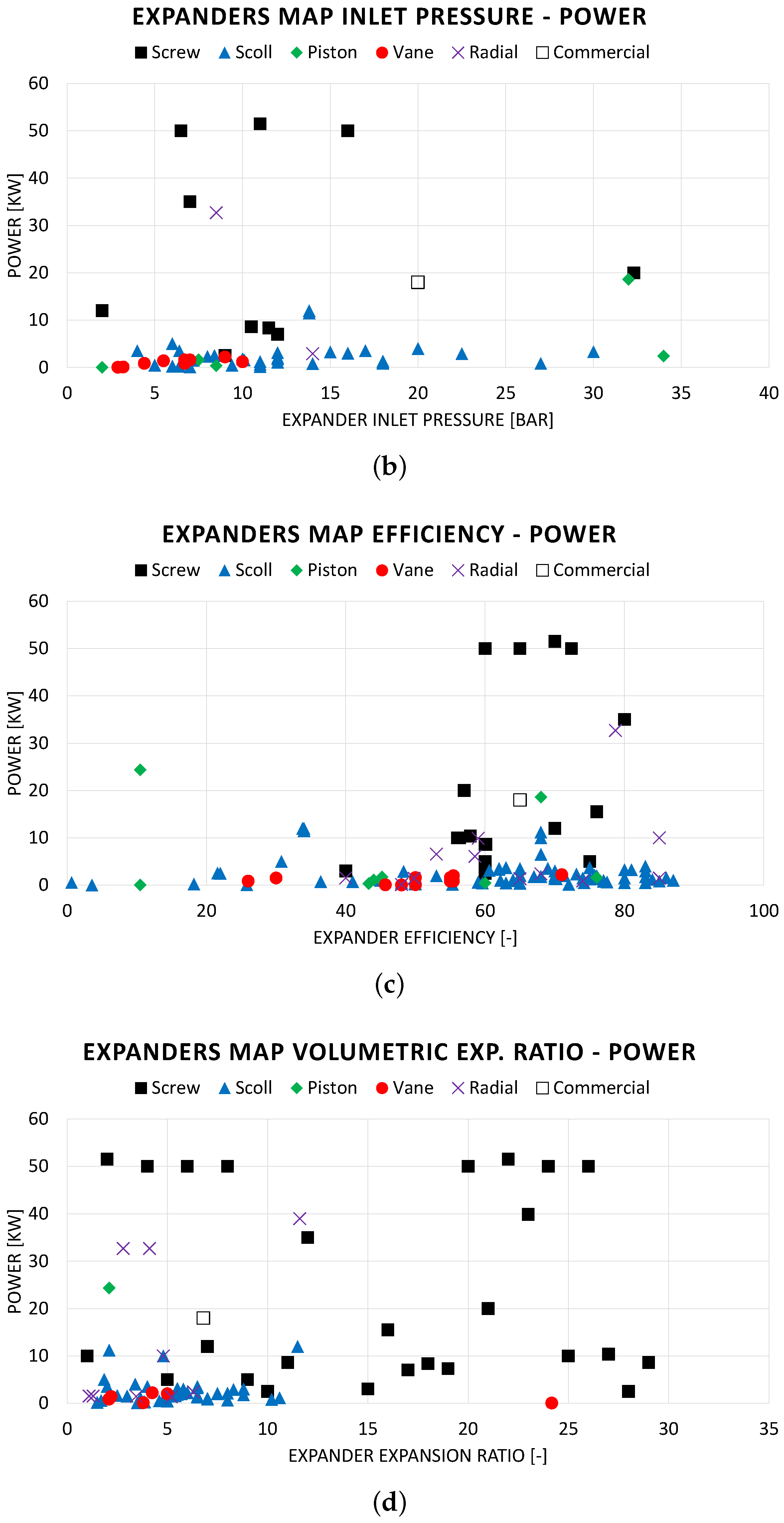
4. Expander Selection
4.1. ORC Plants of 1–20 kW
4.2. ORC Plants of 20–70 kW
4.3. ORC Plants of 70–100 kW
4.4. Comparative Analysis
5. Conclusions
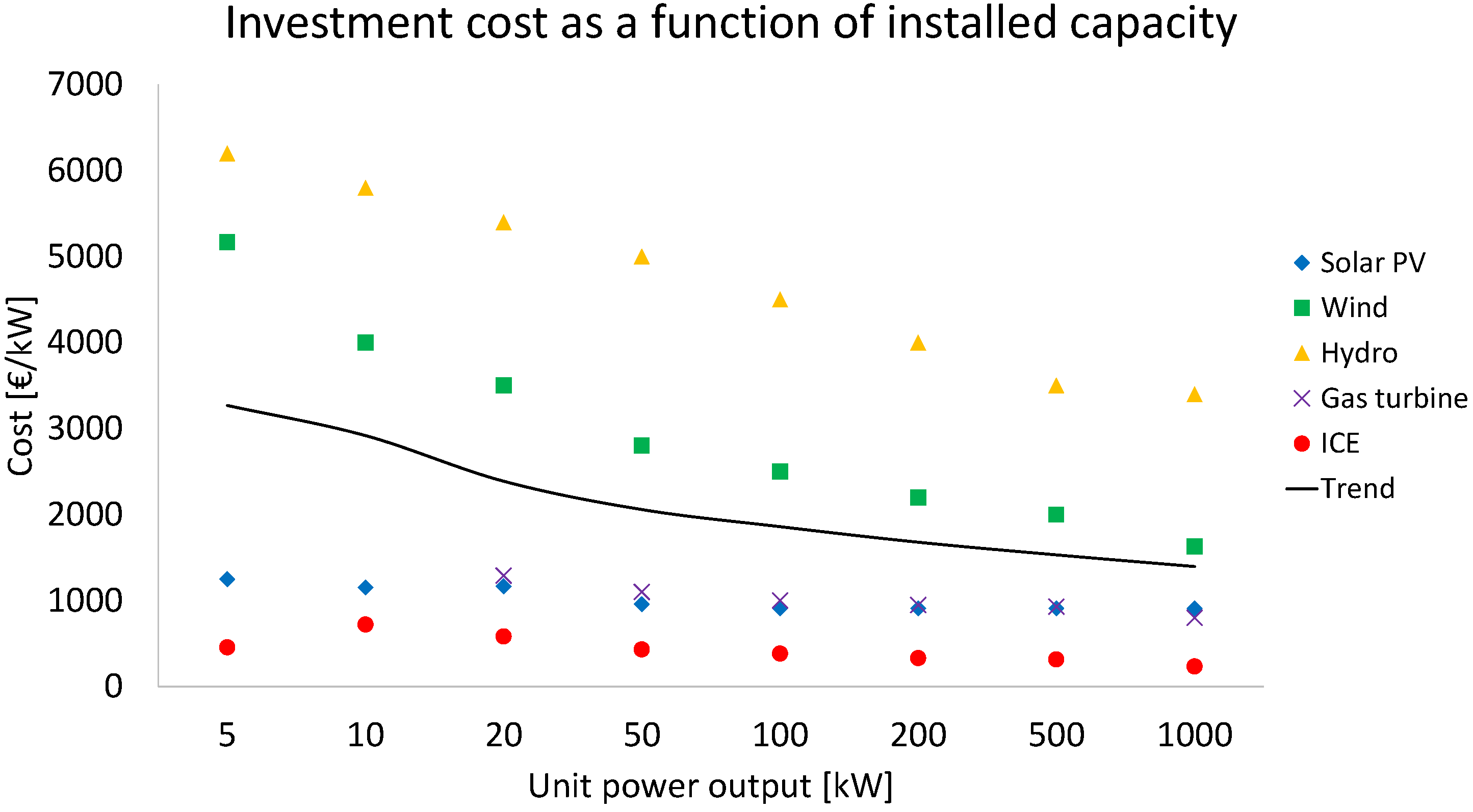
- The specific cost of ORC units should not exceed the value of 3500 €/kW and 2500 €/kW in the power range of 5–10 kW and 10–100 kW, respectively.
- The main reason why ORC technology is not widely available at a commercial level in small-scale power production is its high specific cost. Therefore, efforts should tend towards the optimization of the system to reduce the specific cost, which in turn lowers the payback period.
- With the objective of reducing the specific cost of the technology for small-scale applications, it is important that research pursues the goal of performing a more holistic analysis, in which all indicators that influence the specific costs are optimized at the same time. Thermodynamic, economic and technical aspects should be optimized together to guarantee the dissemination of small-scale ORC plants.
- The literature lacks experimental data of ORC systems in the power range of 10–100 kW, which are required to facilitate the diffusion of the ORC technology in the small-scale power range.
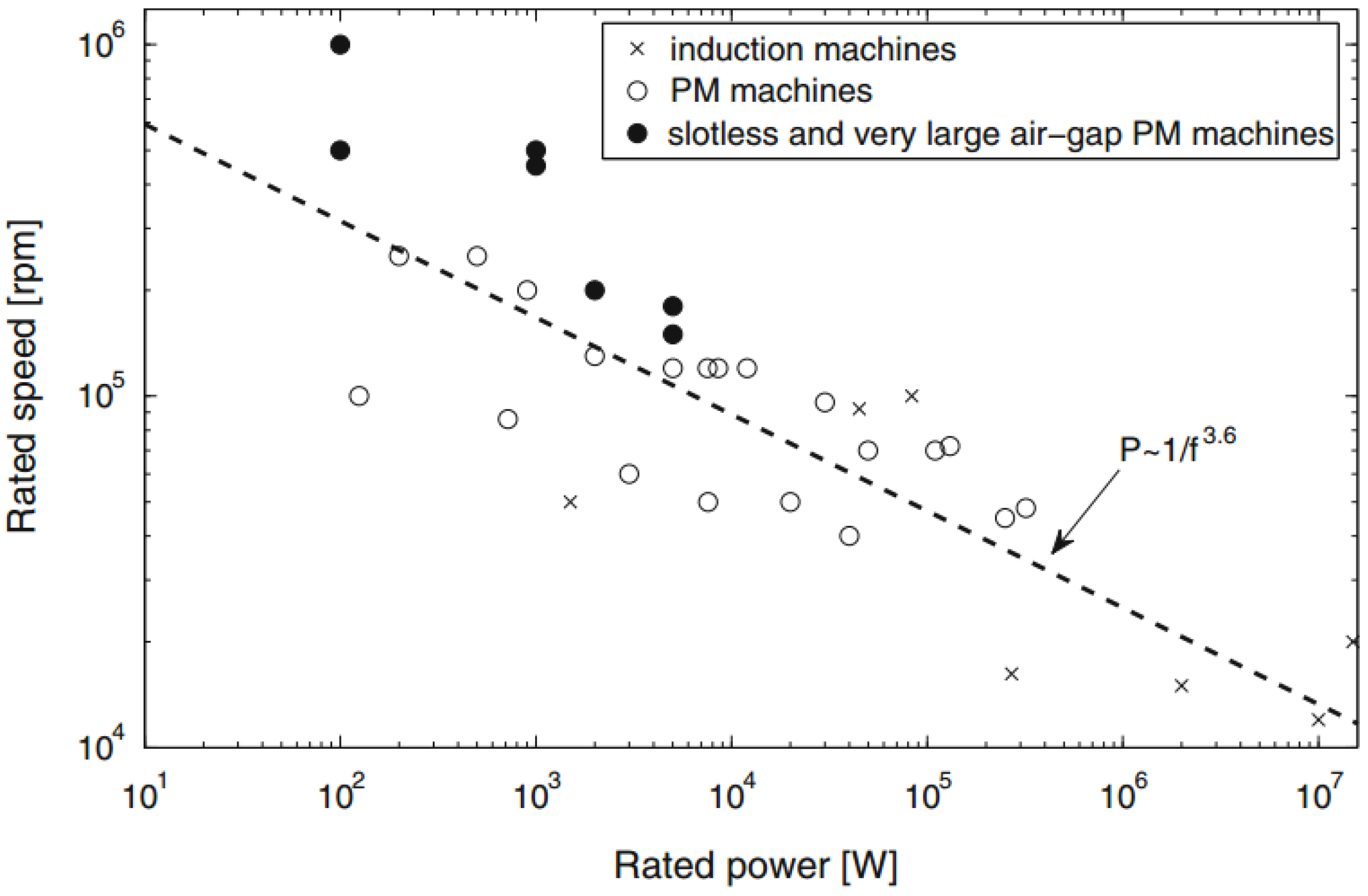
- The expander plays a crucial role in the definition of the system’s performance. Much effort has been put into the investigation of volumetric expanders. However, it is important to highlight that the efficiency, compactness and power-to-weight ratio of turbo expanders overcome those of volumetric machines, particularly when the power output is above 10 kW. The reduction in cost of high speed electric generators together with the use of working fluids that do not require an unreasonably high turbine rotational speed could rapidly make small-scale ORC units cost-effective.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ORC | Organic Rankine Cycle |
| SME | Small Medium Enterprise |
| BPHE | Brazed Plate Heat Exchanger |
| PV | Photovoltaics |
| ICE | Internal Combustion Engine |
| FiT | Feed-in Tariff |
| FiP | Feed-in Premium |
| PBP | Payback Period |
| PFC | Perfluorocarbon |
| HFO | Hydrofluoroolefin |
| HFC | Hydrofluorocarbon |
| ODP | Ozone Depleting Potential |
| GWP | Global Warming Potential |
| NFPA | National Fire Protection Association |
| ASHRAE | American Society of Heating, Refrigerating and Air-Conditioning Engineers |
| CAMD | Computer Aided Molecular Design |
| CHP | Combined Heat and Power |
| PM | Permanent Magnet |
References
- European Commission. The Paris Protocol—A Blueprint for Tackling Global Climate Change Beyond 2020; COM(2015)81 Final/2; Communication from the Commission to the European Parliament and the Council: Brussels, Belgium, 2015. [Google Scholar]
- Alanne, K.; Saari, A. Distributed energy generation and sustainable development. Renew. Sustain. Energy Rev. 2006, 10, 539–558. [Google Scholar] [CrossRef]
- Spigarelli, F.; Curran, L.; Arteconi, A. China and Europe’s Partnership for a More Sustainable World: Challenges and Opportunities; Emerald Group Publishing Limited: Bingley, UK, 2016. [Google Scholar]
- Quoilin, S.; Lemort, V. Technological and economical survey of organic Rankine cycle systems. In Proceedings of the 5th European Conference on Economics and Management of Energy in Industry, Vilamoura, Portugal, 14–17 April 2009. [Google Scholar]
- ORC World Map Website. Available online: http://orc-world-map.org/ (accessed on 15 March 2017).
- Lemmens, S. Cost engineering techniques and their applicability for cost estimation of organic rankine cycle systems. Energies 2016, 9, 485. [Google Scholar] [CrossRef]
- Lecompte, S.; Lemmens, S.; Huisseune, H.; van den Broek, M.; de Paepe, M. Multi-objective thermo-economic optimization strategy for ORCs applied to subcritical and transcritical cycles for waste heat recovery. Energies 2015, 8, 2714–2741. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef]
- Cavazzini, G.; Dal Toso, P. Techno-economic feasibility study of the integration of a commercial small-scale ORC in a real case study. Energy Convers. Manag. 2015, 99, 161–175. [Google Scholar] [CrossRef]
- White, M.; Sayma, A.I. Improving the economy-of-scale of small organic rankine cycle systems through appropriate working fluid selection. Appl. Energy 2016, 183, 1227–1239. [Google Scholar] [CrossRef]
- Lazova, M.; Huisseune, H.; Kaya, A.; Lecompte, S.; Kosmadakis, G.; de Paepe, M. Performance Evaluation of a Helical Coil Heat Exchanger Working under Supercritical Conditions in a Solar Organic Rankine Cycle Installation. Energies 2016, 9, 432. [Google Scholar] [CrossRef]
- Bari, S.; Hossain, S.N. Waste heat recovery from a diesel engine using shell and tube heat exchanger. Appl. Therm. Eng. 2013, 61, 355–363. [Google Scholar] [CrossRef]
- Longo, G.A. Refrigerant R134a condensation heat transfer and pressure drop inside a small brazed plate heat exchanger. Int. J. Refrig. 2008, 31, 780–789. [Google Scholar] [CrossRef]
- Quoilin, S.; van den Broek, M.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic survey of Organic Rankine Cycle (ORC) systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Drescher, U.; Brüggemann, D. Fluid selection for the Organic Rankine Cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar]
- Tchanche, B.F.; Papadakis, G.; Lambrinos, G.; Frangoudakis, A. Fluid selection for a low-temperature solar organic Rankine cycle. Appl. Therm. Eng. 2009, 29, 2468–2476. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.S.; Lee, D.H. Volumetric expanders for low grade heat and waste heat recovery applications. Renew. Sustain. Energy Rev. 2016, 57, 1090–1109. [Google Scholar] [CrossRef]
- Manfrida, G.; Fiaschi, D. Expander technologies for thermal distributed power generation: A review. In Proceedings of the 4th International Conference on Contemporary Problems of Thermal Engineering CPOTE 2016, Katowice, Poland, 14–16 September 2016. [Google Scholar]
- Energy Saving Trust Website. Available online: http://www.energysavingtrust.org.uk/renewable-energy/electricity/wind-turbines (accessed on 15 March 2017).
- National Renewable Energy Laboratory (NREL). U.S. Solar Photovoltaic System Cost Benchmark: Q1 2016. Available online: http://www.nrel.gov/docs/fy16osti/66532.pdf (accessed on 15 March 2017).
- US Department of Energy. Available online: http://www.nrel.gov/docs/fy04osti/34783.pdf (accessed on 15 March 2017).
- Honda, Power Equipment. Available online: http://powerequipment.honda.com/generators/models/eb5000 (accessed on 15 March 2017).
- WBDG Website. Available online: https://www.wbdg.org/resources/microturbines (accessed on 15 March 2017).
- International Renewable Energy Agency (IRENA). Renew Able Energy Technologies: Cost Analysis Series. Available online: http://www.irena.org/documentdownloads/publications/re_technologies_cost_analysis-hydropower.pdf (accessed on 15 March 2017).
- Eurostat. Available online: http://ec.europa.eu/eurostat/statistics-explained/index.php/Electricity_price_statistics (accessed on 15 March 2017).
- European Commission. Questions and Answers: EU Commission: Guidance for State Intervention in Electricity; MEMO/13/948; European Commission: Brussels, Belgium, 2013. [Google Scholar]
- Res Legal Europe. Legal Sources on Renewable Energy. 2016. Available online: http://www.res-legal.eu/ (accessed on 15 March 2017).
- Odyssee-Mure. Policies by Topics. 2016. Available online: http://www.measures-odyssee-mure.eu/topics-energy-efficiency-policy.asp (accessed on 15 March 2017).
- European Commission. Commission Staff Working Document; SWD/2015/0141; European Commission: Brussels, Belgium, 2015. [Google Scholar]
- Guide to Cost-Benefit Analysis of Investment Projects. Available online: http://ec.europa.eu/regional_policy/sources/docgener/studies/pdf/cba_guide.pdf (accessed on 15 March 2017).
- Tabor, H.; Bronicki, L. Establishing Criteria for Fluids for Small Vapor Turbines; Technical Report; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1964. [Google Scholar]
- Angelino, G.; Gaia, M.; Macchi, E. A review of Italian activity in the field of organic Rankine cycles. VDI-Berichte 1984, 465–482. [Google Scholar]
- Exergy Website. Available online: http://exergy-orc.com/ (accessed on 15 March 2017).
- Triogen Website. Available online: http://www.triogen.nl/ (accessed on 15 March 2017).
- Enogia Website. Available online: http://www.enogia.com/ (accessed on 15 March 2017).
- Enertime-Rainbow Website. Available online: http://www.enertime.com/ (accessed on 15 March 2017).
- Entropea Labs Website. Available online: http://entropea.com/ (accessed on 15 March 2017).
- ElectraTherm Website. Available online: https://electratherm.com/ (accessed on 15 March 2017).
- Zuccato Energia Website. Available online: http://www.zuccatoenergia.it/index.php/en/ (accessed on 15 March 2017).
- General Electric Website. Heat Recovery Solutions. Available online: https://powergen.gepower.com/ (accessed on 15 March 2017).
- Infinity Turbine Website. Available online: http://www.infinityturbine.com/ (accessed on 15 March 2017).
- Pratt and Whitney Website. Available online: www.pw.utc.com#sthash.eXRMnLuY.dpuf (accessed on 15 March 2017).
- Termo 2 Power Website. Available online: http://termo2power.com/ (accessed on 15 March 2017).
- Calnetix Website. Available online: www.calnetix.com (accessed on 15 March 2017).
- Mattei Group Website. Available online: www.matteigroup.com (accessed on 15 March 2017).
- Rank Website. Available online: www.rankweb.es (accessed on 15 March 2017).
- EXAy Website. Available online: www.exaenergie.com (accessed on 15 March 2017).
- New Comen Website. Available online: http://www.solarexpo.com/files/convegni/convegni-e-seminari/2010/102/Zampieri.pdf (accessed on 15 March 2017).
- Orcan Website. Available online: http://www.orcan-energy.com/en (accessed on 15 March 2017).
- ConPower Website. Available online: http://www.conpower.de/index.html (accessed on 15 March 2017).
- Clean Power. Clear Power Turbo Expander Generators. Available online: http://www.clearpowersystems.com/wp-content/uploads/2016/01/ClearPower-Systems-Inc.-Brochure-Updated-January-28th-2016-1.9MB-File-Size-.pdf (accessed on 15 March 2017).
- Zero Emissions Website. Available online: http://www.zeintlplc.com/wp-content/uploads/2015/09/ZE-ORC-Spec-Sheet.pdf (accessed on 15 March 2017).
- Icenova Engineering. Available online: https://tis.bz.it/doc-bereiche/ren_doc/pdf/rossetti-technologyday-20110722.pdf (accessed on 15 March 2017).
- Clime on Website. Available online: http://climeon.com/ (accessed on 15 March 2017).
- Exoes Website. Available online: http://www.exoes.com/EN/ (accessed on 15 March 2017).
- E-Rational Website. Available online: http://e-rational.net/ (accessed on 15 March 2017).
- Opcon Website. Available online: http://opconenergysystem.com/en/home/ (accessed on 15 March 2017).
- Wang, D.; Ling, X.; Peng, H.; Liu, L.; Tao, L. Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation. Energy 2013, 50, 343–352. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Council Regulation 1005/2009 on Substances That Deplete the Ozone Layer, 31.10.2009 OJ L 286. Available online: http://www.legislation.gov.uk/uksi/2015/168/pdfs/uksi_20150168_en.pdf (accessed on 15 March 2017).
- National Fire Proteciont Association (NFPA). NFPA 329: Recommended Practice for Handling Releases of Flammable and Combustible Liquids and Gases; National Fire Protection Association: Quincy, MA, USA, 2015. [Google Scholar]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. 2009 ASHRAE Handbook: Fundamentals; American Society of Heating, Refrigeration and Air-Conditioning Engineers: Atlanta, GA, USA, 2009. [Google Scholar]
- Erhart, T.G.; Gölz, J.; Eicker, U.; van den Broek, M. Working Fluid Stability in Large-Scale Organic Rankine Cycle-Units Using Siloxanes—Long-Term Experiences and Fluid Recycling. Energies 2016, 9, 422. [Google Scholar] [CrossRef]
- Papadopoulos, A.I.; Stijepovic, M.; Linke, P. On the systematic design and selection of optimal working fluids for Organic Rankine Cycles. Appl. Therm. Eng. 2010, 30, 760–769. [Google Scholar] [CrossRef]
- Ziviani, D.; Beyene, A.; Venturini, M. Advances and challenges in ORC systems modeling for low grade thermal energy recovery. Appl. Energy 2014, 121, 79–95. [Google Scholar] [CrossRef]
- Linke, P.; Papadopoulos, A.I.; Seferlis, P. Systematic methods for working fluid selection and the design, integration and control of organic Rankine cycles—A review. Energies 2015, 8, 4755–4801. [Google Scholar] [CrossRef]
- Mago, P.J.; Chamra, L.M.; Srinivasan, K.; Somayaji, C. An examination of regenerative organic Rankine cycles using dry fluids. Appl. Therm. Eng. 2008, 28, 998–1007. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Rayegan, R.; Tao, Y. A procedure to select working fluids for Solar Organic Rankine Cycles (ORCs). Renew. Energy 2011, 36, 659–670. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, J.; Gao, L. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery. Energy Convers. Manag. 2009, 50, 576–582. [Google Scholar] [CrossRef]
- Qiu, G. Selection of working fluids for micro-CHP systems with ORC. Renew. Energy 2012, 48, 565–570. [Google Scholar] [CrossRef]
- Angelino, G.; Di Paliano, P.C. Multicomponent working fluids for organic Rankine cycles (ORCs). Energy 1998, 23, 449–463. [Google Scholar] [CrossRef]
- Quoilin, S.; Aumann, R.; Grill, A.; Schuster, A.; Lemort, V.; Spliethoff, H. Dynamic modeling and optimal control strategy of waste heat recovery Organic Rankine Cycles. Appl. Energy 2011, 88, 2183–2190. [Google Scholar] [CrossRef]
- Desideri, A.; Dechesne, B.; Wronski, J.; van den Broek, M.; Gusev, S.; Lemort, V.; Quoilin, S. Comparison of Moving Boundary and Finite-Volume heat exchanger models in the modelica language. Energies 2016, 9, 339. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, W.; Hou, G.; Fang, F. Dynamic modeling and multivariable control of organic Rankine cycles in waste heat utilizing processes. Comput. Math. Appl. 2012, 64, 908–921. [Google Scholar] [CrossRef]
- Maizza, V.; Maizza, A. Unconventional working fluids in organic Rankine-cycles for waste energy recovery systems. Appl. Therm. Eng. 2001, 21, 381–390. [Google Scholar] [CrossRef]
- Sciubba, E.; Tocci, L.; Toro, C. Thermodynamic analysis of a Rankine dual loop waste thermal energy recovery system. Energy Convers. Manag. 2016, 122, 109–118. [Google Scholar] [CrossRef]
- Da Lio, L.; Manente, G.; Lazzaretto, A. Predicting the optimum design of single stage axial expanders in ORC systems: Is there a single efficiency map for different working fluids? Appl. Energy 2016, 167, 44–58. [Google Scholar] [CrossRef]
- La Seta, A.; Andreasen, J.G.; Pierobon, L.; Persico, G.; Haglind, F. Design of organic Rankine cycle power systems accounting for expander performance. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015. [Google Scholar]
- Baral, S.; Kim, D.; Yun, E.; Kim, K.C. Experimental and thermoeconomic analysis of small-scale solar organic Rankine cycle (SORC) system. Entropy 2015, 17, 2039–2061. [Google Scholar] [CrossRef]
- Nusiaputra, Y.Y.; Wiemer, H.J.; Kuhn, D. Thermal-Economic modularization of small, organic Rankine cycle power plants for mid-enthalpy geothermal fields. Energies 2014, 7, 4221–4240. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Legros, A.; Guillaume, L.; Lemort, V. Working fluid selection and operating maps for Organic Rankine Cycle expansion machines. In Proceedings of the 21st International Compressor Conference, West Lafayette, IN, USA, 16–19 July 2012; p. 10. [Google Scholar]
- Franchetti, B.; Pesiridis, A.; Pesmazoglou, I.; Sciubba, E.; Tocci, L. Thermodynamic and technical criteria for the optimal selection of the working fluid in a mini-ORC. In Proceedings of the 29th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Portorož, Slovenia, 19–23 June 2016. [Google Scholar]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar]
- Vélez, F.; Segovia, J.J.; Martín, M.C.; Antolín, G.; Chejne, F.; Quijano, A. A technical, economical and market review of organic Rankine cycles for the conversion of low-grade heat for power generation. Renew. Sustain. Energy Rev. 2012, 16, 4175–4189. [Google Scholar] [CrossRef]
- Qiu, G.; Liu, H.; Riffat, S. Expanders for micro-CHP systems with organic Rankine cycle. Appl. Therm. Eng. 2011, 31, 3301–3307. [Google Scholar] [CrossRef]
- Karellas, S.; Schuster, A.; Leontaritis, A.D. Influence of supercritical ORC parameters on plate heat exchanger design. Appl. Therm. Eng. 2012, 33, 70–76. [Google Scholar] [CrossRef]
- Oyewunmi, O.A.; Markides, C.N. Thermo-Economic and Heat Transfer Optimization of Working-Fluid Mixtures in a Low-Temperature Organic Rankine Cycle System. Energies 2016, 9, 448. [Google Scholar] [CrossRef]
- Hung, T.C.; Shai, T.; Wang, S. A review of organic Rankine cycles (ORCs) for the recovery of low-grade waste heat. Energy 1997, 22, 661–667. [Google Scholar]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (Organic Rankine Cycles) power plants for the exploitation of medium–low temperature geothermal sources–Part B: Techno-economic optimization. Energy 2014, 66, 435–446. [Google Scholar] [CrossRef]
- Kosmadakis, G.; Manolakos, D.; Papadakis, G. Developments on Small-Scale Organic Rankine Cycle (ORC) Systems. J. Fundam. Renew. Energy Appl. 2016, 2016. [Google Scholar] [CrossRef]
- Ziviani, D.; Gusev, S.; Lecompte, S.; Groll, E.; Braun, J.; Horton, W.T.; van den Broek, M.; de Paepe, M. Characterizing the performance of a single-screw expander in a small-scale organic Rankine cycle for waste heat recovery. Appl. Energy 2016, 181, 155–170. [Google Scholar] [CrossRef]
- Helvaci, H.; Khan, Z.A. Experimental study of thermodynamic assessment of a small scale solar thermal system. Energy Convers. Manag. 2016, 117, 567–576. [Google Scholar] [CrossRef]
- Li, G.; Zhang, H.; Yang, F.; Song, S.; Chang, Y.; Yu, F.; Wang, J.; Yao, B. Preliminary Development of a Free Piston Expander–Linear Generator for Small-Scale Organic Rankine Cycle (ORC) Waste Heat Recovery System. Energies 2016, 9, 300. [Google Scholar] [CrossRef]
- Pu, W.; Yue, C.; Han, D.; He, W.; Liu, X.; Zhang, Q.; Chen, Y. Experimental study on Organic Rankine cycle for low grade thermal energy recovery. Appl. Therm. Eng. 2016, 94, 221–227. [Google Scholar] [CrossRef]
- Kang, S.H. Design and preliminary tests of ORC (organic Rankine cycle) with two-stage radial turbine. Energy 2016, 96, 142–154. [Google Scholar] [CrossRef]
- Pini, M.; Persico, G.; Casati, E.; Dossena, V. Preliminary design of a centrifugal turbine for organic rankine cycle applications. J. Eng. Gas Turbines Power 2013, 135, 042312. [Google Scholar] [CrossRef]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N. Modelling and optimization of organic Rankine cycle based on a small-scale radial inflow turbine. Energy Convers. Manag. 2015, 91, 186–198. [Google Scholar]
- Fiaschi, D.; Manfrida, G.; Maraschiello, F. Thermo-fluid dynamics preliminary design of turbo-expanders for ORC cycles. Appl. Energy 2012, 97, 601–608. [Google Scholar] [CrossRef]
- Palumbo, C.F.; Barnabei, V.F.; Preziuso, E.; Coronetta, U. Design and CFD analysis of a Ljungstrom turbine for an ORC cycle in a waste heat recovery application. In Proceedings of the the 29th International Conferenceon Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Portorož, Slovenia, 19–23 June 2016. [Google Scholar]
- Al Jubori, A.; Al-Dadah, R.K.; Mahmoud, S.; Ennil, A.B.; Rahbar, K. Three dimensional optimization of small-scale axial turbine for low temperature heat source driven organic Rankine cycle. Energy Convers. Manag. 2017, 133, 411–426. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Manente, G. A new criterion to optimize ORC design performance using efficiency correlations for axial and radial turbines. Int. J. Thermodyn. 2014, 17, 192–200. [Google Scholar] [CrossRef]
- Kang, S.H. Design and experimental study of ORC (organic Rankine cycle) and radial turbine using R245fa working fluid. Energy 2012, 41, 514–524. [Google Scholar] [CrossRef]
- Leibowitz, H.; Smith, I.; Stosic, N. Cost effective small scale ORC systems for power recovery from low grade heat sources. In Proceedings of the ASME 2006 International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; American Society of Mechanical Engineers: New York, NY, USA, 2006; pp. 521–527. [Google Scholar]
- Kenneth, E.; Nichols, P. How to Select Turbomachinery for Your Application; Barber-Nichols Inc.: Arvada, CO, USA, 2012; pp. 5–6. [Google Scholar]
- Hsieh, J.C.; Fu, B.R.; Wang, T.W.; Cheng, Y.; Lee, Y.R.; Chang, J.C. Design and preliminary results of a 20-kW transcritical organic Rankine cycle with a screw expander for low-grade waste heat recovery. Appl. Therm. Eng. 2017, 110, 1120–1127. [Google Scholar] [CrossRef]
- Capata, R.; Toro, C. Feasibility analysis of a small-scale ORC energy recovery system for vehicular application. Energy Convers. Manag. 2014, 86, 1078–1090. [Google Scholar] [CrossRef]
- Freeman, J.; Hellgardt, K.; Markides, C.N. Working fluid selection and electrical performance optimisation of a domestic solar-ORC combined heat and power system for year-round operation in the UK. Appl. Energy 2016. [Google Scholar] [CrossRef]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an Organic Rankine Cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef]
- Yun, E.; Kim, D.; Yoon, S.Y.; Kim, K.C. Experimental investigation of an organic Rankine cycle with multiple expanders used in parallel. Appl. Energy 2015, 145, 246–254. [Google Scholar]
- Chang, J.C.; Hung, T.C.; He, Y.L.; Zhang, W. Experimental study on low-temperature organic Rankine cycle utilizing scroll type expander. Appl. Energy 2015, 155, 150–159. [Google Scholar]
- Vodicka, V.; Guillaume, L.; Mascuch, J.; Lemort, V. Testing and modeling a vane expander used in an ORC working with hexamethyldisiloxane (MM). In Proceedings of the ASME ORC 2015: International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015. [Google Scholar]
- Di Battista, D.; Mauriello, M.; Cipollone, R. Waste heat recovery of an ORC-based power unit in a turbocharged diesel engine propelling a light duty vehicle. Appl. Energy 2015, 152, 109–120. [Google Scholar]
- Badr, O.; O’Callaghan, P.; Probert, S. Multi-vane expanders: Geometry and vane kinematics. Appl. Energy 1985, 19, 159–182. [Google Scholar] [CrossRef]
- Badr, O.; O’Callaghan, P.; Probert, S. Multi-vane expander performance: Breathing characteristics. Appl. Energy 1985, 19, 241–271. [Google Scholar]
- Badr, O.; Probert, S.; O’Callaghan, P. Multi-vane expanders: Internal-leakage losses. Appl. Energy 1985, 20, 1–46. [Google Scholar] [CrossRef]
- Lemort, V.; Guillaume, L.; Legros, A.; Declaye, S.; Quoilin, S. A comparison of piston, screw and scroll expanders for small scale Rankine cycle systems. In Proceedings of the 3rd International Conference on Microgeneration and Related Technologies, Naples, Italy, 15–17 April 2013. [Google Scholar]
- Peterson, R.; Wang, H.; Herron, T. Performance of a small-scale regenerative Rankine power cycle employing a scroll expander. Proc. Inst. Mech. Eng. A J. Power Energy 2008, 222, 271–282. [Google Scholar] [CrossRef]
- Fiaschi, D.; Manfrida, G.; Maraschiello, F. Design and performance prediction of radial ORC turboexpanders. Appl. Energy 2015, 138, 517–532. [Google Scholar]
- Fu, B.R.; Lee, Y.R.; Hsieh, J.C. Experimental investigation of a 250-kW turbine organic Rankine cycle system for low-grade waste heat recovery. Int. J. Green Energy 2016, 13, 1442–1450. [Google Scholar]
- Macchi, E.; Astolfi, M. Organic Rankine Cycle (ORC) Power Systems; Woodhead Publishing: Sawston, UK, 2017. [Google Scholar]
- Borisavljevic, A. High-speed PM machines: Applications, trends and limits. In Limits, Modeling and Design of High-Speed Permanent Magnet Machines; Springer: Berlin/Heidelberg, Germany, 2013; pp. 13–27. [Google Scholar]



| Country | Cost Covered (%) | Amount Awarded (k€) | Note |
|---|---|---|---|
| Belgium | 5–50 | 80–1500 | Min invest. 7.5–25 k€ |
| Bulgaria | 15–70 | 57 | - |
| Czech Republic | 50–70 | 3600 | - |
| Finland | 30–40 | - | - |
| France | 20–40 | 1000–5000 | - |
| Germany | 30 | - | Min invest. 30 k€ |
| Italy | 25 | - | - |
| Latvia | - | 2000 | - |
| Lithuania | 80 | 200–1500 | - |
| Luxembourg | 40–45 | - | - |
| Poland | 100 | - | Min invest. 45.53–113.826 k€, 40 kW |
| Romania | 50 | 2000 | Own consumption only |
| Slovenia | 50 | 200 | - |
| Company Name | Country | Power (kW) | Expander Type | Heat source T (°C) | Notes |
|---|---|---|---|---|---|
| Exergy [33] | IT | 100–240,000 | Radial | - | Commercial |
| Triogen [34] | NLD | 160 | Axial | 200–300 | Patent on expander coupled with the pump |
| Enogia [35] | FR | 10–20–40–100 | Radial | 90–160–400 | Commercial, turbine coupled with high speed generator |
| Rainbow [36] | FR | 100 | Axial | - | Expander 12–15 krpm, efficiency > 80% |
| Entropea Labs [37] | UK | 20–300 | Radial | 400–500 | Prototype |
| ElectraTherm [38] | USA | 35–65–110 | Screw | 77–122 | Commercial, induction asynchronous generator brushless |
| Zuccato Energia [39] | IT | 30–40–50 | Radial | Water T > 94 | Commercial, synchronous generator 15 krpm, ceramic bearings |
| GE clean energy [40] | USA | 125 | Radial | 143 | Commercial, R 245fa, rotational speed 26.5 krpm, magnetic bearings |
| Infinity turbine [41] | USA | 5–50–100 | Radial | <110 | fluid R 245fa, magnetic bearings |
| Pratt and Whitney [42] | USA | 80–260 | Radial | 91–149 | Fluid R 245fa, 2 pole induction machine |
| Termo 2 Power [43] | PL | <300 | Rotary lobe | - | Prototype, 1.5–3 krpm, self exciting synchronous generator |
| Calnetix [44] | USA | 125 | Axial | Low | 24.5 krpm, magnetic bearings |
| Mattei [45] | IT | 3 | Vane | 80–150 | - |
| Rank [46] | SP | 50–100 | Radial | 85–140 | 2–5 years payback period |
| EXA [47] | IT | 15–150 | Piston/screw | 70–350 | Fluids R 134, R 245fa, Toluene, Induction generator |
| NewComen [48] | IT | 3–120 | - | - | - |
| Orcan [49] | GER | 20 | Radial | 550 | - |
| ConPower [50] | GER | 13–75 | - | - | Prototype |
| Clean power [51] | USA | 77 | Scroll | 270 | Expander speed 1.5–1.8 krpm, fluid R 245fa |
| ZE [52] | UK | 95–130 | Multi stage radial | - | Permanent magnet generator |
| ICENOVA [53] | IT | 10–30 | Eneftech scroll | 150 | R 245fa, Regenerated cycle |
| Climeon [54] | SWE | 150 | Turbine | 70–120 | - |
| Exoes [55] | FR | 15 | Piston swashplate | - | Transport applications |
| E-rational [56] | BEL | <500 | Single screw | 105–150 | Asynchronous generator |
| Opcon [57] | SWE | <800 | SRM Turbine | 250 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tocci, L.; Pal, T.; Pesmazoglou, I.; Franchetti, B. Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review. Energies 2017, 10, 413. https://doi.org/10.3390/en10040413
Tocci L, Pal T, Pesmazoglou I, Franchetti B. Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review. Energies. 2017; 10(4):413. https://doi.org/10.3390/en10040413
Chicago/Turabian StyleTocci, Lorenzo, Tamas Pal, Ioannis Pesmazoglou, and Benjamin Franchetti. 2017. "Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review" Energies 10, no. 4: 413. https://doi.org/10.3390/en10040413
APA StyleTocci, L., Pal, T., Pesmazoglou, I., & Franchetti, B. (2017). Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review. Energies, 10(4), 413. https://doi.org/10.3390/en10040413






