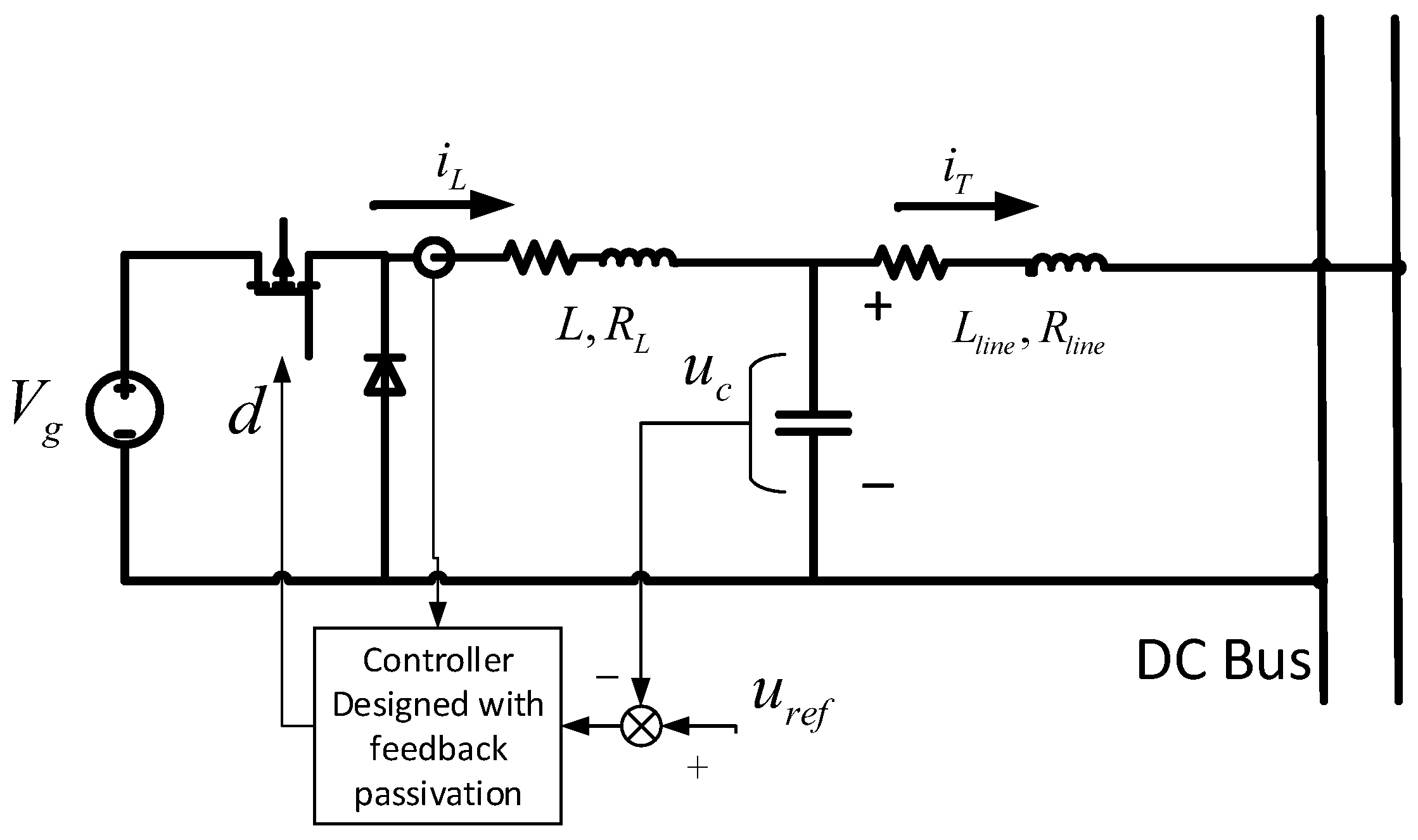
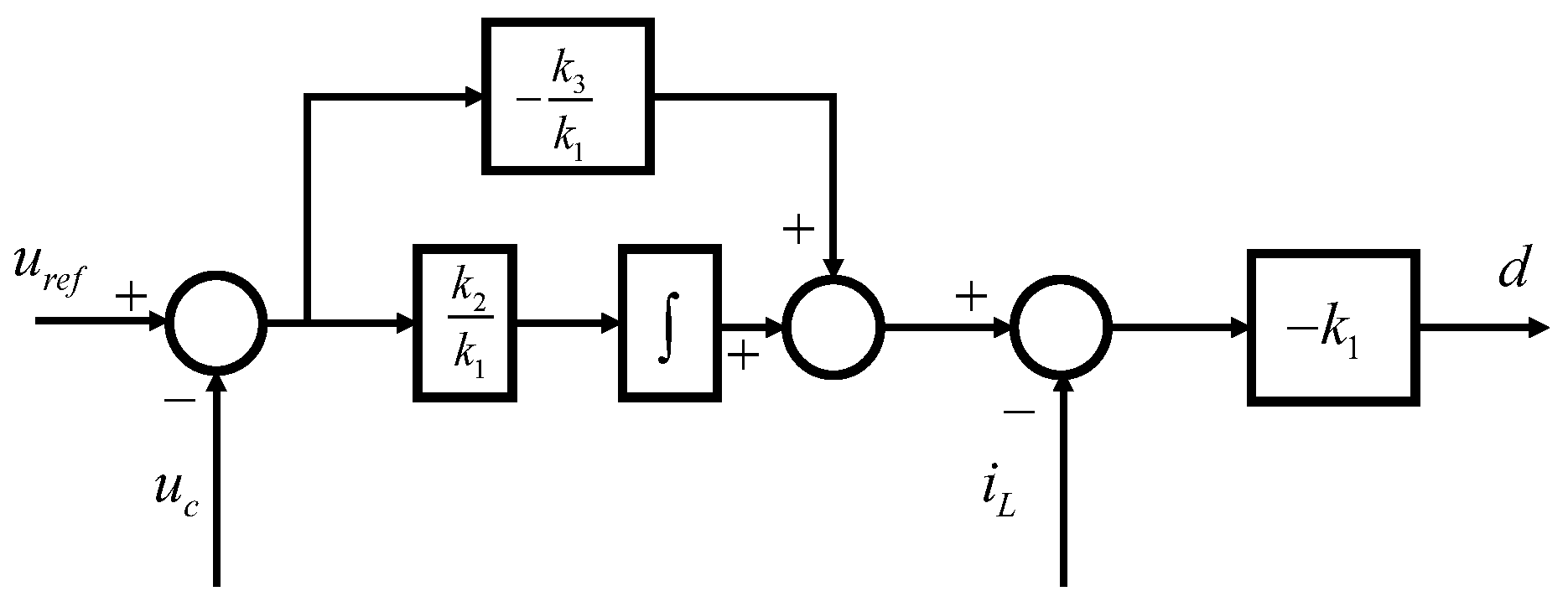
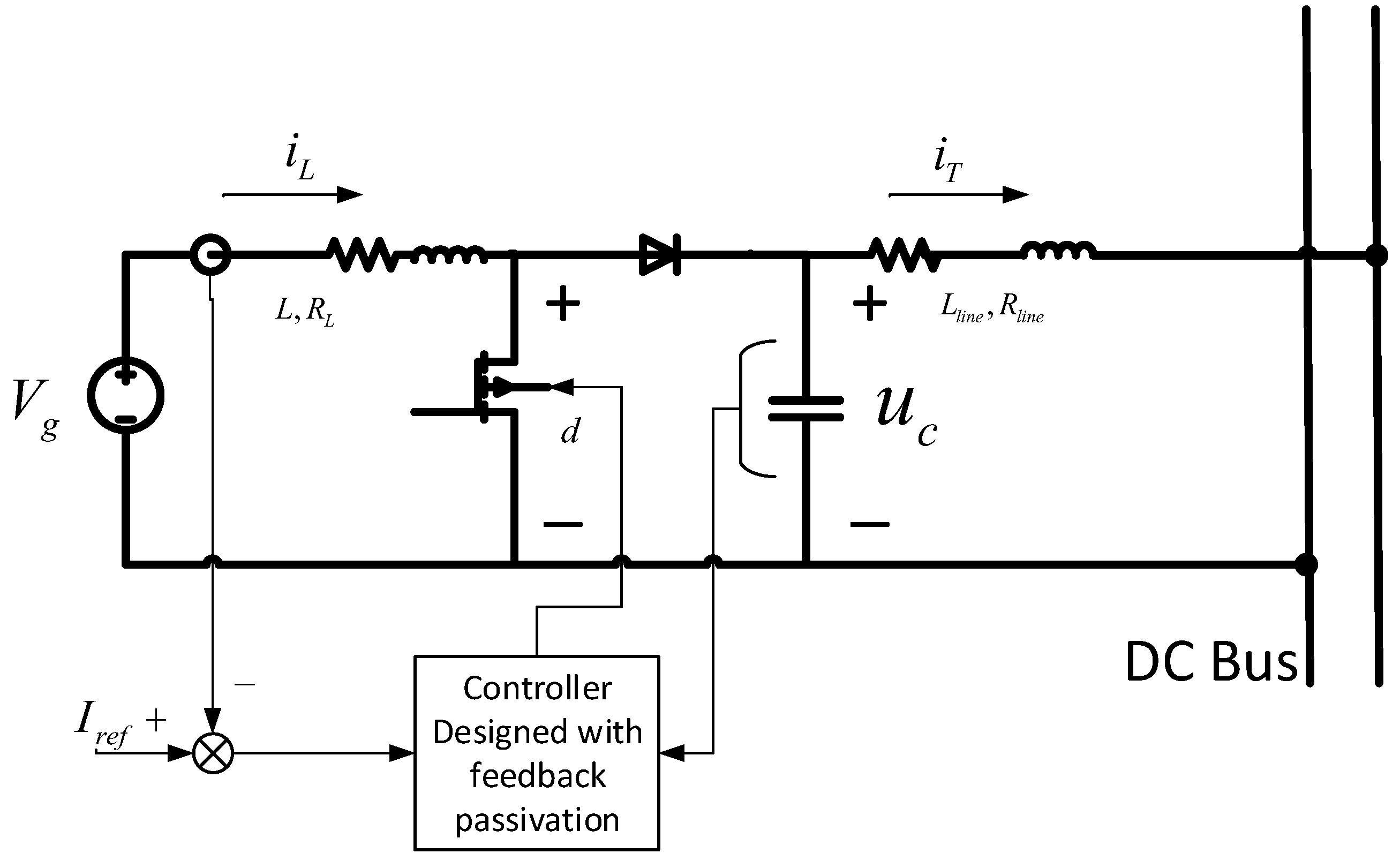
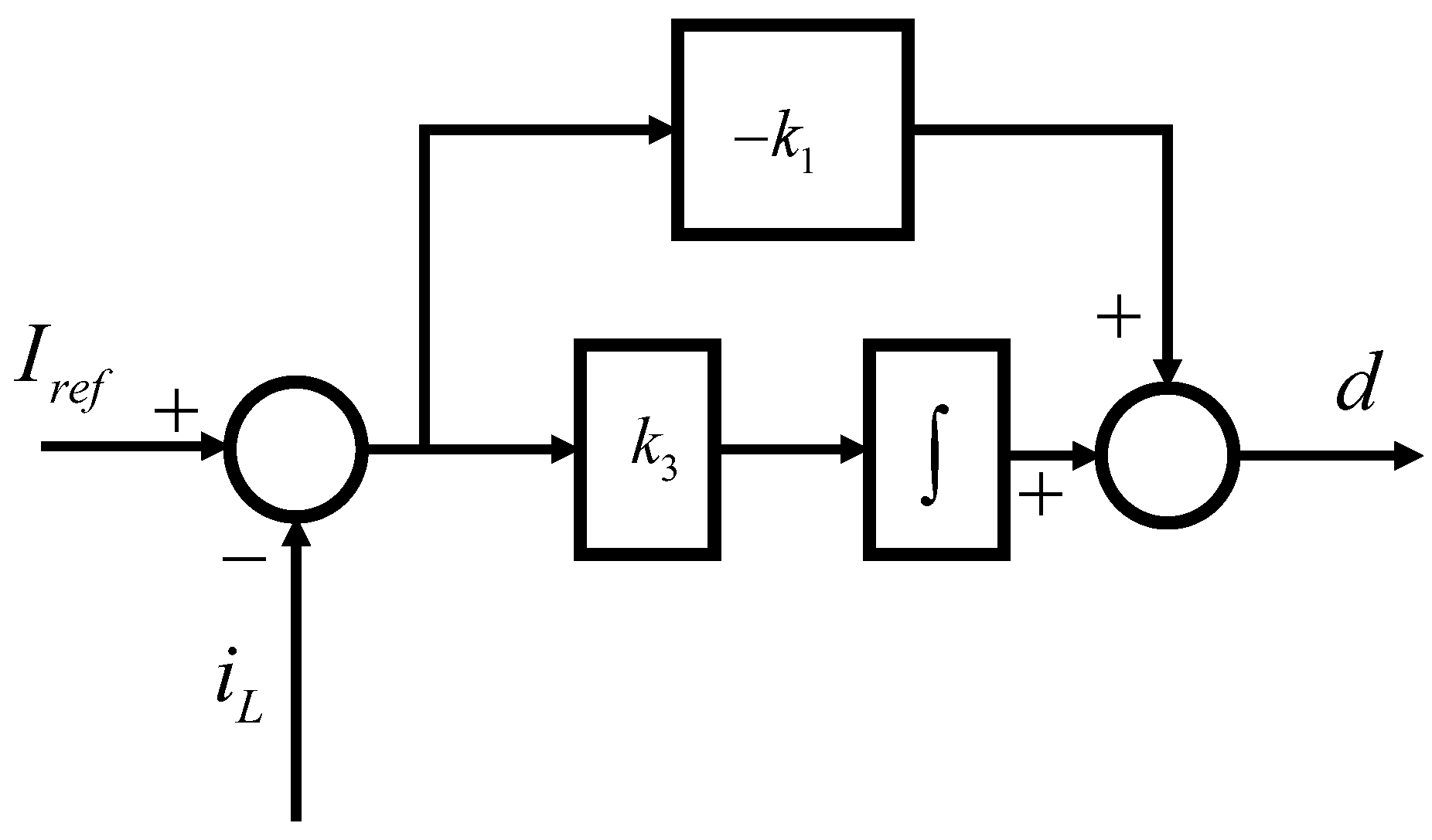
1. Introduction
With the deterioration of the environment and the reduction of fossil reserves, applications of renewable energy and energy storage systems (ESSs) are rapidly increasing.Most of these new components have a DC feature in essence, which may pose technical and operational challenges for the integration into the existing AC systems. Meanwhile, significant advances in power electronics technology have produced a number of power converters for DC voltage transformation into various levels for different applications. In this context, DC microgrids are emerging as an attractive solution for the integration of renewable-based distributed generators (DGs) and ESSs [
1].
The stability of DC microgrids is a critical problem. Its studies have been performed by small or large signal analysis [
1,
2,
3,
4,
5,
6,
7,
8,
9], in which the DC microgrid is analyzed collectively, based on a comprehensive model of the whole microgrid. The comprehensive model is sensitive to the change of every unit, particularly to the fluctuation of the microgrids’ network. The results based on such a high entropy model may have limited effectiveness in providing valuable information for stable design [
10]. This paper follows a decomposition approach in which the DC microgrid is analyzed as a network with two parts: a node system consisting of converters and a dynamical edge system consisting of loads and transmission lines to connect the converters and loads. The nodes and edges division is compared to results of a work on a multi-agent systems [
11]. According to [
11], the outputs of the edge dynamic systems form the external inputs of the node dynamic systems, which are termed “neighboring inputs” representing the coupling actions between nodes. The outputs of the node dynamic systems are the inputs of the edge dynamic systems. As explored in [
12], an edge system consisting of resistor-lnductor-capacitor (RLC) components is positive real (PR), or weakly strictly positive real (WSPR) if there exists at least one resistance inside. As it is well-known that the passivity is preserved when two passivity systems are connected properly, this paper makes a passivity design for the converters in a DC microgrid. When each converter has a passive interface, then the DC microgrid with a WSPR (weakly strictly positive real) edge system is guaranteed to be stable.
The passivity-based control (PBC), as a kind of passivation design, has been extensively utilized on the control of converters. In [
13], passivity-based feedback controllers are derived for the indirect stabilization of the average output voltage in pulse-width-modulation (PWM) controlled DC–DC power converters of the ”boost“, “buck-boost“, and “buck“ types. In [
14], the authors present an overview of passivity-based stability assessment, including techniques for space-vector modeling of VSCs (voltage source converters) whereby expressions for the input admittance can be derived. In [
15], the author investigate the DC-bus voltage regulation problem for a three-phase boost type PWM AC–DC converter using PBC theory. The models are shown to be Euler–Lagrange (EL) systems corresponding to a suitable set of average EL parameters.The PBC aims to make the controllers themselves be passive, which together with a passive plant stabilizes the closed-loop system. In contrast, the passivity design made by this paper focuses on the interface passivity instead of the passivity of controllers. The interface passivity is a kind of passivity equivalent to the PRness of transfer functions from injecting currents of microgrid
to output voltages of converters
.
and
are the output and the input of edge systems, respectively.
In passivity theory, the Kalman–Yakubovich–Popov (KYP) Lemma establishes an equivalence between the conditions in the frequency domain for a system to be positive real, an input–output relationship of the system in the time domain, and conditions on the matrices describing the state-space representation of the system. With the KYP Lemma, many significant results in the control field have been presented for the direct passivation regulating the input–output relationship [
16,
17], while a few results exist for the indirect passivation regulating the relationship between external input and output [
18,
19]. The interface passivity addressed in this paper is a kind of indirect passivation that is more difficult than direct passivation since external input can not be controlled. On the contrary, the PBC control is a kind of direct passivation. In [
19], necessary and sufficient conditions for the feasibility of indirect passivation of strictly positive real (SPR) was presented for a class of single-input and single-output systems. It should be pointed out that typical DC–DC converters, including “buck” and “boost”, do not satisfy the necessary and sufficient condition. This paper proposes a feedback passivation design for DC–DC converters to make them have interface passivity. The resulted transfer functions are PR rather than SPR in the penalty of requiring edge systems to be WSPR rather than PR.
Making a converter’s interface be passive is not new. Gu et al. [
18] have addressed this subject recently by using a feedforward control method of SISO (single input single output) systems in the frequency domain. In this paper, the interface passivity is discussed in the time domain.In contrast to the frequency domain analysis, the time domain analysis utilizing state-space representation is possible to confirm the state of the system parameters and not merely input–output relations. Moreover, it fits with in the multiple-input and multiple-output essence of two parts of DC microgrids, while the SISO method of frequency domain omitting the off-diagonal coupling term is not rigorous for microgrids. The main contributions of this paper are: (1) a decoupling viewpoint of DC microgrids by which the stability is guaranteed by the interface passivity of node system and the WSPR of the edge system, independent of the network structure; and (2) a feedback passivation method is proposed for controlling typical converters to be of the interface passivity.
The remainder of this manuscript is organized as follows.
Section 2 relates the stability of the DC microgrid to the interface passivity.
Section 3 details the feedback passivation design of typical DC converters.
Section 4 makes a hardware-in-loop real-time laboratory (RTLab) (version 10.7, OPAL-RT Technologies Inc., Montréal, QC, Canada) simulation to verify the analytic results, followed by conclusions in
Section 5.
2. Passivity Criterion of Converters in DC Microgrids
In this section, the DC microgrid is analyzed as a network with two parts: dynamical edges and nodes. The structure is shown in
Figure 1. The first part is composed of transmission lines and loads, and another part is composed of converters. According to [
11], a multi-agent system is often described by a graph, where nodes represent the dynamic subsystems and edges the interactions between these subsystems. One benefit of the division is that we can take advantage of the the passivity of transmission lines more intuitively. That is, the feedback interconnected system of two passive subsystems is passive then stable. From the viewpoint of power electronics, the division of the nodes and dynamical edges makes it easy to depict the requirement of the interfaces, due to the fact that, in a microgrid system, the nodes (converters) under control are connected via dynamical edges (transmission lines and loads). For a certain structure of the dynamical edges, a common requirement can be put forward to every interface. As a result, it is convenient for applying distributed control law for the nodes.
Denote the vectors that collect the current injections and output voltages of converters and loads by
and
, respectively. We then have:
where
is a diagonal transfer function matrix between
and
, in which the controller going to be designed is included.
Meanwhile, denote
Y as the admittance transfer function matrix between the output voltage
and the injecting current
of the network composed by transmission lines, that is:
The system composed of Equation (
1) and Equation (
2) admits the compact block-diagram representation in
Figure 2. The converters, loads and the transmission lines are connected via a feedback interconnection. Stable conditions are given based on the feedback interconnection.
Theorem 1. If all elements in are PR, when Y is weakly SPR, the microgrid is asymptotically stable.
Proof. When
and
Y are PR and weakly SPR, respectively, from [
20] (Lemma 3.37), the feedback interconnection in
Figure 2 is asymptotically stable. ☐
Remark 1. The theorem that a system composed of two PR subsystems via feedback interconnection is PR is well-known in passsivity theory. However, it should be mentioned here that passivity yields Lyapunov stability but not asymptotical stability. For instance, is passive but not stable. In [18,21,22], etc., the authors assert the stability only based on the interconnection of PR systems. Even though similar assertions are always true in circuits’ analysis, it is essential to explain the fact theoretically. From Definition 2.53 of [20], a PR system is weakly SPR when it is Hurwitz. The assumption of Y is reasonable for when the transmission lines contain resistive elements. Then, Y is Hurwitz, while the edge system consisting of RLC components is passive itself according to [12]. In fact, acts like an “interface impedance” of the nodes in a sense. The nodes can also be expressed in an “admittance” form, that is, a transfer function matrix (denote as ) with the input and the output . Similarly, the dynamical edges also have the form of an impedance matrix (denoted as Z). To construct the interconnection feedback structure according to the passivity theory, we have two ways to describe the whole system, using shown in Figure 2 or shown in Figure 3. and are not proposed for the reason that, in these cases, we may encounter the problem as follows: firstly, or may not exist. Secondly, when Z or Y is WSPR, the inverse of them may not be WSPR. For example, is WSPR while is not. In several past works, the analysis are based on admittances or impedances only, and risks will be taken. Without loss of generality, the following analysis is based on the structure shown in
Figure 2. As
Figure 2 shows, in fact,
and
Y represent the influence on the stability from converters, loads and electrical network, respectively. Due to the feedback interconnection and the weak SPRness of
Y, making every transfer function in
be PR is a convenient way to stabilize the closed loop. It should be mentioned that the loads are passive according to Definition 2.1 in [
20]. Ths is to make the grid-connected interfaces of converters be passive and then
is passive.
By the way, the result in Theorem 1 is always true, regardless of the structure changing—for example, the plug and play of distributed generators (DGs) or ESSs and the fluctuations of loads and transmission lines. The remainder of the paper is focused on the interfaces’ passivation problem for converters.
4. Real-Time Laboratory Experimental Results
In order to verify the proposed feedback passivation method, a DC microgrid test system is built in the RTLab 10.7.
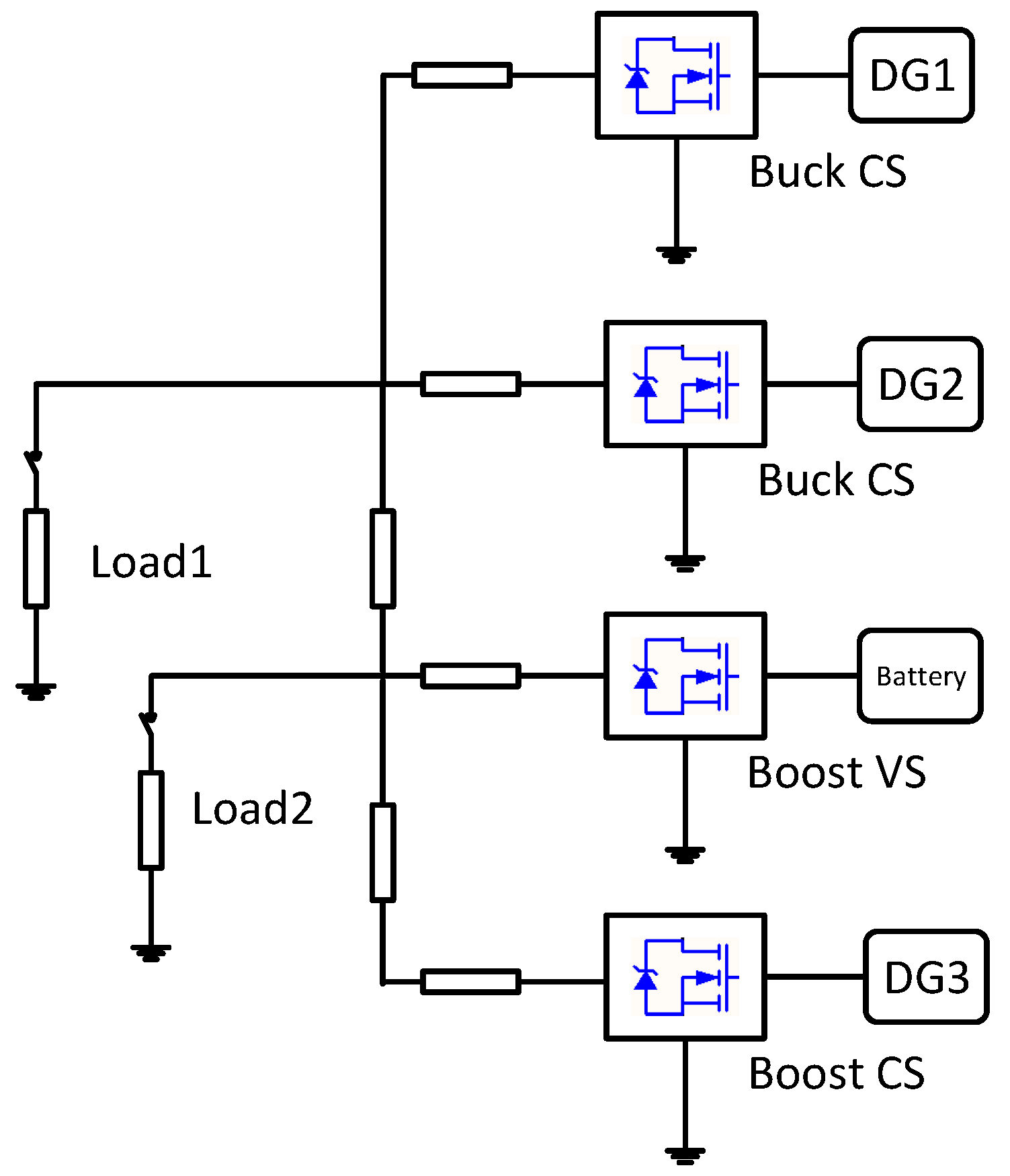
Figure 8 shows the structure of the hardware in loop platform.The system consists of DGs, battery ESSs, local loads and transmission lines.
Three DGs work in current source mode, and the ESS operates in the voltage source mode to maintain the bus voltage at 560
V. Buck and boost circuits are adopted for DC–DC conversion. The detailed converter configurations are listed in
Table 1.
In this paper, through the direct code generation method using Matlab (2013b, Mathworks Inc. Natick, MA, USA) and code composer studio (CCS), the proposed passive control algorithm is compiled and downloaded to digital signal processor (DSP) (TMS28335). The control loop in the experiment is realized by external DSP chips, and only the main circuits are simulated in software.
4.1. Test on Feedback Passivation
Firstly, the original passivity criterion is validated. According to the methods proposed in
Section 3, based on the control diagrams in
Figure 5 and
Figure 7, if all converters are controlled under the feedback passivation method to achieve passivity, then the system is stable. As
Figure 9a shows, when DG1 and DG2 converters are switched to the conventional dual-loop control to become non-passive, the system experiences a transition first, and then becomes stable with more seriously fluctuating waveforms. In
Figure 9b, the two converters are switched back to controllers with feedback passivation and the waveforms restored to be smooth. When three DG converters are controlled to be non-passive, then the system is unstable, as
Figure 9c shows. The results above prove the effectiveness of the feedback passivation.
4.2. Test on Stability in Varying Microgrid Structures
The most obvious advantage of the feedback passivation method is that the stability is always guaranteed no matter to what structure the microgrid changes—for instance, the plug-and-play issue of distributed resources.
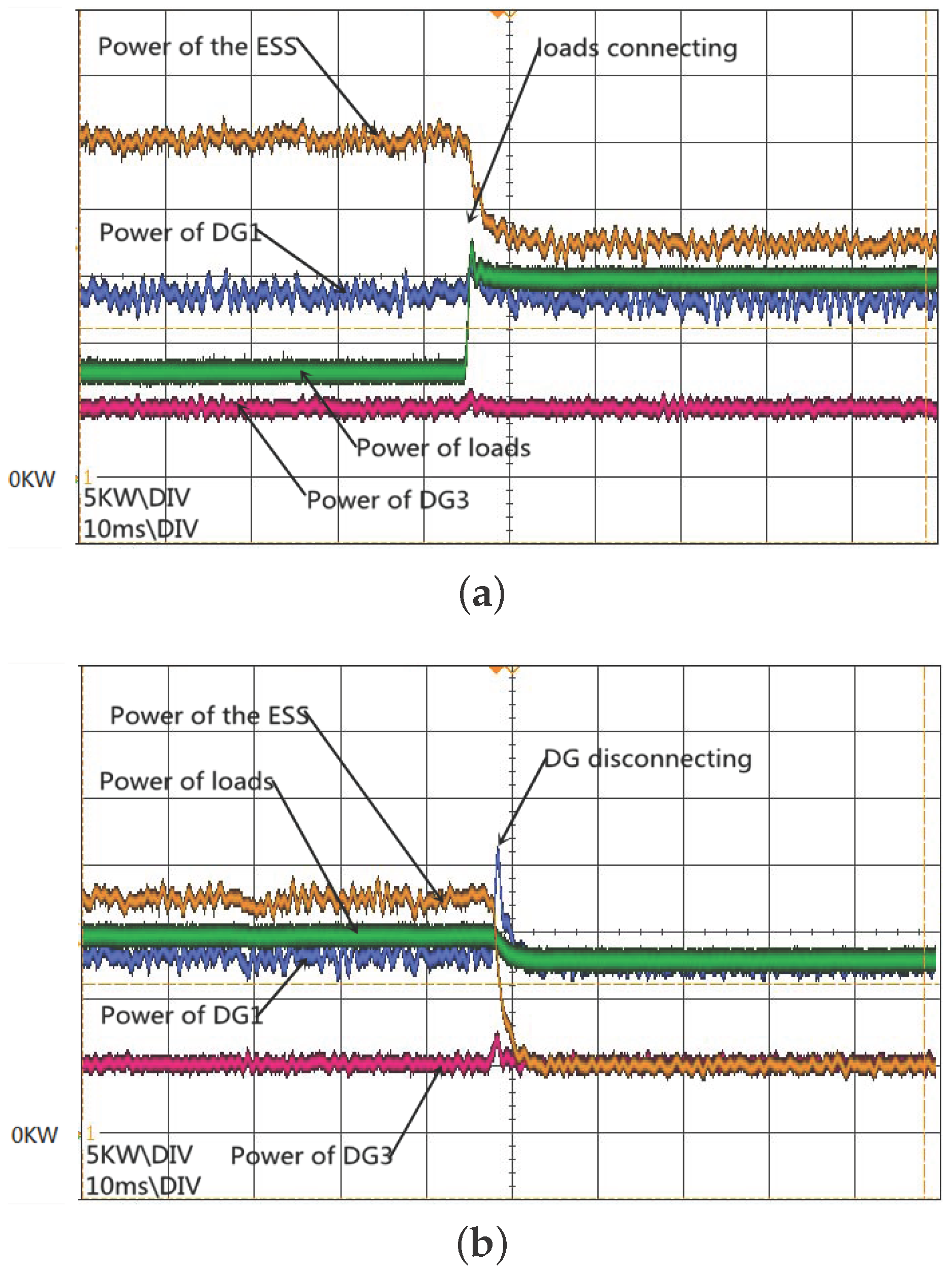
To verify this benefit, DGs and loads are switching in this experiment. Three DGs, ESSs and one load (50 Ω, 0.1 mH) are connected to the microgrid initially.
Figure 10a shows the transition of the connecting of another load (50 Ω, 0.1 mH). Then, as
Figure 10b shows, DG2s are disconnected from the system.
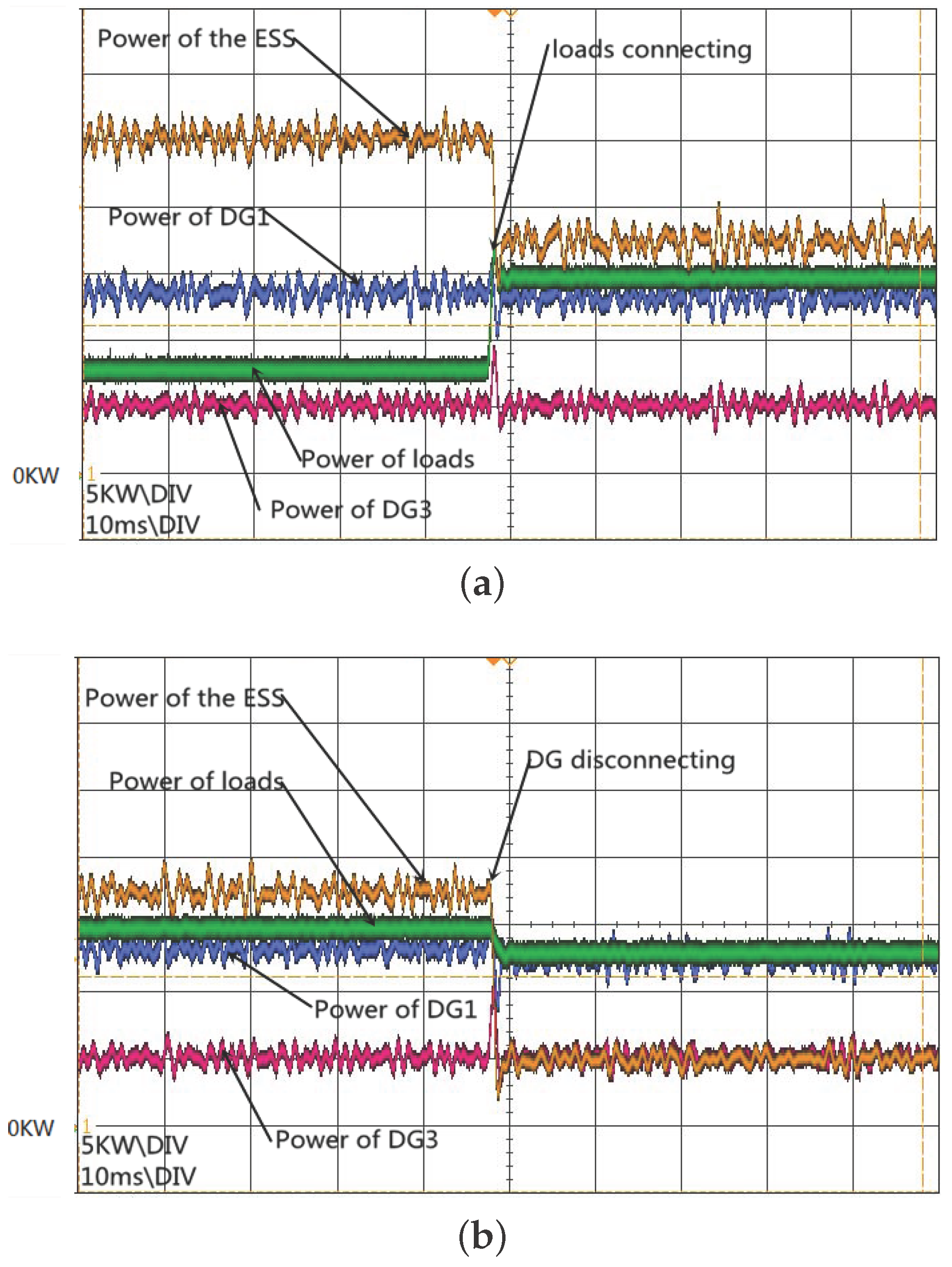
As a comparison, the same procedure is implemented in the scenario while converters of DG1 and DG2 are controlled to be non-passive by the conventional dual-loop controllers and the system is stable.
Figure 11a,b show the load connection and DG2 disconnection, respectively.
From the figures above, one can find that the overshoot of the control group is obviously more serious than the group with feedback passivation. For instance, in
Figure 10a, no overshoot exists in the power waveform of the ESS, while for the control group, the overshoot is about 2 KW, as
Figure 11a shows. The comparison of
Figure 10b and
Figure 11b confirms the same phenomenon. It should be mentioned that, in
Figure 11b, the waveforms’ fluctuation becomes smoother after DG2 disconnection. It is reasonable that the removal of a non-passive part from the system is benefit to stability.
5. Conclusions
Due to the various network structures of DC microgrids, the conventional methods for the stability analysis, by which the microgrids are treated as a whole system, do not seem suitable enough. Because the electrical network often consists of passive elements, the passivity theory is applied to the interface passivity in this paper.
A decoupling viewpoint of DC microgrids is proposed in this paper, by which the microgrid is divided into two parts, including a WSPR electrical network called an edge system and a node system consisting of converters under control. The decoupling method brings convenience to stability analysis due to the fact that when every converter’s interface passivity is achieved, the microgrid is stable. In this paper, the feedback passivation method for typical DC–DC converters is proposed in the time domain, and the proposed method is used in practical applications.
The major contributions of this paper are verified through an RTlab experiment, compared with the typical dual-loop control method, which proves the effectiveness, applicability and robustness of the proposed feedback passivation method.