An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Response Surface Method for Optimizing Biodiesel
3. Experiments Design
4. Using Response Surface Methodology to Optimize Biodiesel Variables
5. Results
5.1. Experimental Results
5.2. Analysis of Variance
5.3. Multi-Response Optimization
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meka, P.K.; Tripathi, V.; Singh, R.P. Synthesis of biodiesel fuel from safflower oil using various reaction parameters. J. Oleo Sci. 2007, 56, 9–12. [Google Scholar] [CrossRef]
- Yan, J.; Zheng, X.; Li, S. A novel and robust recombinant Pichia pastoris yeast whole cell biocatalyst with intracellular over expression of a Thermomyces lanuginosus lipase: Preparation, characterization and application in biodiesel production. Bioresour. Technol. 2014, 151, 43–48. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.N.; Phan, T.M. Biodiesel production from waste cooking oils. Fuel 2008, 87, 3490–3496. [Google Scholar] [CrossRef]
- Ministerio de Agricultura, Alimentación y Medio Ambiente. Gobierno de España. Available online: http://www.mapama.gob.es/es (accessed on 16 June 2016).
- Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas. Available online: http://www.ciemat.es (accessed on 16 June 2016).
- Atabani, A.; Silitonga, A.; Badruddin, I.A.; Mahlia, T.; Masjuki, H.; Mekhilef, S. A comprehensive review on biodiesel as an alternative energy resource and its characteristics. Renew. Sustain. Energy Rev. 2012, 16, 2070–2093. [Google Scholar] [CrossRef]
- Balakrishnan, K.; Olutoye, M.A.; Hameed, B.H. Synthesis of methyl esters from waste cooking oil using construction waste material as solid base catalyst. Bioresour. Technol. 2013, 128, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Shahid, E.M.; Jamal, Y. Production of biodiesel: A technical review. Renew. Sustain. Energy Rev. 2011, 15, 4732–4745. [Google Scholar] [CrossRef]
- Borges, M.E.; Díaz, L. Recent developments on heterogeneous catalysts for biodiesel production by oil esterification and transesterification reactions: A review. Renew. Sustain. Energy Rev. 2012, 16, 2839–2849. [Google Scholar] [CrossRef]
- Yaakob, Z.; Mohammad, M.; Alherbawi, M.; Alam, Z.; Sopian, K. Overview of the production of biodiesel from Waste cooking oil. Renew. Sustain. Energy Rev. 2013, 18, 184–193. [Google Scholar] [CrossRef]
- Kulkarni, M.G.; Dalai, A.K. Waste cooking oil an economical source for biodiesel: A review. Ind. Eng. Chem. Res. 2006, 45, 2901–2913. [Google Scholar] [CrossRef]
- Ghadge, S.V.; Raheman, H. Process optimization for biodiesel production from mahua (Madhuca indica) oil using response surface methodology. Bioresour. Technol. 2006, 97, 379–384. [Google Scholar] [CrossRef] [PubMed]
- Enweremadu, C.C.; Barawa, M.M. Technical aspects of production and analysis of biodiesel from used cooking oil—A review. Renew. Sustain. Energy Rev. 2009, 13, 2205–2224. [Google Scholar] [CrossRef]
- Myers, R.H. Response Surfaces Methodology, 1st ed.; Allyn and Bacan Inc.: Boston, MA, USA, 1971. [Google Scholar]
- Harrington, E.C. The desirability function. Ind. Qual. Control 1965, 21, 494–498. [Google Scholar]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B (Methodological) 1951, 13, 1–45. [Google Scholar]
- Lostado, R.; García, R.E.; Martinez, R.F. Optimization of operating conditions for a double-row tapered roller bearing. Int. J. Mech. Mater. Des. 2016, 12, 353–373. [Google Scholar] [CrossRef]
- Lostado, R.; Escribano, R.; Martínez, M.A.; Múgica, R. Improvement in the design of welded joints of EN 235JR low carbon steel by multiple response surface methodology. Metals 2016, 6, 205–226. [Google Scholar] [CrossRef]
- Moussaoui, K.; Mousseigne, M.; Senatore, J.; Chieragatti, R.; Lamesle, P. Influence of milling on the fatigue lifetime of a Ti6Al4V titanium alloy. Metals 2015, 5, 1148–1162. [Google Scholar] [CrossRef]
- Gopalsamy, B.M.; Mondal, B.; Ghosh, S. Taguchi method and ANOVA: An approach for process parameters optimization of hard machining while machining hardened steel. J. Sci. Ind. Res. India 2009, 68, 686–695. [Google Scholar]
- Derringer, G.; Suich, R. Simultaneous optimization of several response variables. J. Qual. Technol. 1980, 12, 214–219. [Google Scholar]
- Kuhn, M. Desirability: Desirabiliy Function Optimization and Ranking. Available online: http://CRAN.R-project.org/package=desirability (accessed on 25 August 2016).
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Box, G.E.; Behnken, D.W. Some new three level designs for the study of quantitative variables. Technometrics 1960, 2, 455–475. [Google Scholar] [CrossRef]
- Atapour, M.; Kariminia, H.R.; Moslehabadi, P.M. Optimization of biodiesel production by alkali-catalyzed transesterification of used frying oil. Process Saf. Environ. Prot. 2014, 92, 179–185. [Google Scholar] [CrossRef]
- Farag, H.; El-Maghraby, A.; Taha, N.A. Optimization of factors affecting esterification of mixed oil with high percentage of free fatty acid. Fuel Process. Technol. 2011, 92, 507–510. [Google Scholar] [CrossRef]
- Silva, G.F.; Camargo, F.L.; Ferreira, A.L. Application of response surface methodology for optimization of biodiesel production by transesterification of soybean oil with ethanol. Fuel Process. Technol. 2011, 92, 407–413. [Google Scholar] [CrossRef]
- Hamze, H.; Akia, M.; Yazdani, F. Optimization of biodiesel production from the waste cooking oil using response surface methodology. Process Saf. Environ. Prot. 2015, 94, 1–10. [Google Scholar] [CrossRef]
- El-Gendy, N.S.; El-Gharabawy, A.A.; Amr, S.S.; Ashour, F.H. Response surface optimization of an alkaline transesterification of waste cooking oil. Int.J. ChemTech Res. 2015, 8, 385–398. [Google Scholar]
- R: The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 25 July 2016).
- Leung, D.Y.C.; Guo, Y. Transesterification of neat and used frying oil: Optimization for biodiesel production. Fuel Process. Technol. 2006, 87, 883–890. [Google Scholar] [CrossRef]
- ASTM D445. Standard Test Method for Kinematic Viscosity of Transparent and Opaque Liquids. Available online: http://www.astm.org/Standards/D445 (accessed on 25 March 2016).
- ASTM D941. Standard Test Method for Density and Relative Density of Liquids by Lipkin Bicapillary Pycnometer. Available online: http://www.astm.org/Standards/D941 (accessed on 25 March 2016).
- ASTM D2015-00 Test Method for Gross Calorific Value of Coal and Coke by the Adiabatic Bomb Calorimeter. Available online: http://www.astm.org/Standards/D2015 (accessed on 12 April 2016).
- Mumtaz, M.W.; Adnan, A.; Anwar, F.; Mukhtar, H.; Raza, M.A.; Ahmad, F. Response surface methodology: An emphatic tool for optimized biodiesel production using rice bran and sunflower oils. Energies 2012, 5, 3307–3328. [Google Scholar] [CrossRef]
- Mansourpoor, M.; Shariati, A. Optimization of biodiesel production from sunflower oil using response surface methodology. Chem. Eng. Process Technol. 2012, 3. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, J.; Zeng, G.; Shi, J.; Tong, J.; Huang, G. Optimization of conversion of waste rapeseed oil with high FFA to biodiesel using response surface methodology. Renew. Energy 2008, 33, 1678–1684. [Google Scholar] [CrossRef]
- Dhingra, S.; Bhushan, G.; Dubey, K.K. Development of a combined approach for improvement and optimization of Karanja biodiesel using response surface methodology and genetic algorithm. Energy 2013, 7, 495–505. [Google Scholar] [CrossRef]
- Aworanti, O.A.; Agarry, S.E.; Ajani, A.O. Statistical optimization of process variables for biodiesel production from waste cooking oil using heterogeneous base catalyst. Br. Biotechnol. 2013, 3, 116–132. [Google Scholar] [CrossRef]
- Omar, W.N.; Amin, N.A. Optimization of heterogeneous biodiesel production from waste cooking palm oil via response surface methodology. Biomass Bioenergy 2011, 35, 1329–1338. [Google Scholar] [CrossRef]
- Noshadi, I.; Amin, N.A.S.; Parnas, R.S. Continuous production of biodiesel from waste cooking oil in a reactive distillation column catalyzed by solid heteropoly acid: Optimization using response surface methodology (RSM). Fuel 2012, 94, 156–164. [Google Scholar] [CrossRef]
- Rashid, U.; Anwar, F.; Ashraf, M.; Saleem, M.; Yusup, S. Application of response surface methodology for optimizing transesterification of Moringa oleifera oil: Biodiesel production. Energy Convers. Manag. 2011, 52, 3034–3042. [Google Scholar] [CrossRef]
- Hameed, B.H.; Lai, L.F.; Chin, L.H. Production of biodiesel from palm oil (Elaeis guineensis) using heterogeneous catalyst: An optimized process. Fuel Process. Technol. 2009, 90, 606–610. [Google Scholar] [CrossRef]
- Ghoreishi, S.M.; Moein, P. Biodiesel synthesis from waste vegetable oil via transesterification reaction in supercritical methanol. J. Supercrit. Fluids 2013, 76, 24–31. [Google Scholar] [CrossRef]
- Azócar, L.; Heipieper, H.J.; Muñoz, R.; Navia, R. Improving fatty acid methyl ester production yield in a lipase-catalyzed process using waste frying oils as feedstock. J. Biosci. Bioeng. 2010, 109, 609–614. [Google Scholar] [CrossRef] [PubMed]
- Pullen, J.; Saeed, K. Investigation of the factors affecting the progress of base catalyzed transesterification of rapeseed oil to biodiesel FAME. Fuel Process. Technol. 2015, 130, 127–135. [Google Scholar] [CrossRef]
- De Paola, M.; Ricca, E.; Calabrò, V.; Curcio, S.; Iorio, G. Factor analysis of transesterification reaction of waste oil for biodiesel production. Bioresour. Technol. 2009, 100, 5126–5131. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.T.; Park, Y.T. Application of Taguchi experimental design for the optimization of effective parameters on the rapeseed methyl ester production. Environ. Eng. Res. 2010, 15, 129–134. [Google Scholar] [CrossRef]
- Dwivedi, G.; Sharma, M.P. Application of Box-Behnken design in optimization of biodiesel yield from Pongamia oil and its stability analysis. Fuel 2015, 147, 279. [Google Scholar] [CrossRef]
- Lenth, R.V. Response-surface methods in R, using rsm. J. Stat. Softw. 2009, 32, 1–17. [Google Scholar] [CrossRef]
- Max, K. Desirability Function Optimization and Ranking. Available online: https://CRAN.R-project.org/package=desirability (accessed on 28 March 2016).
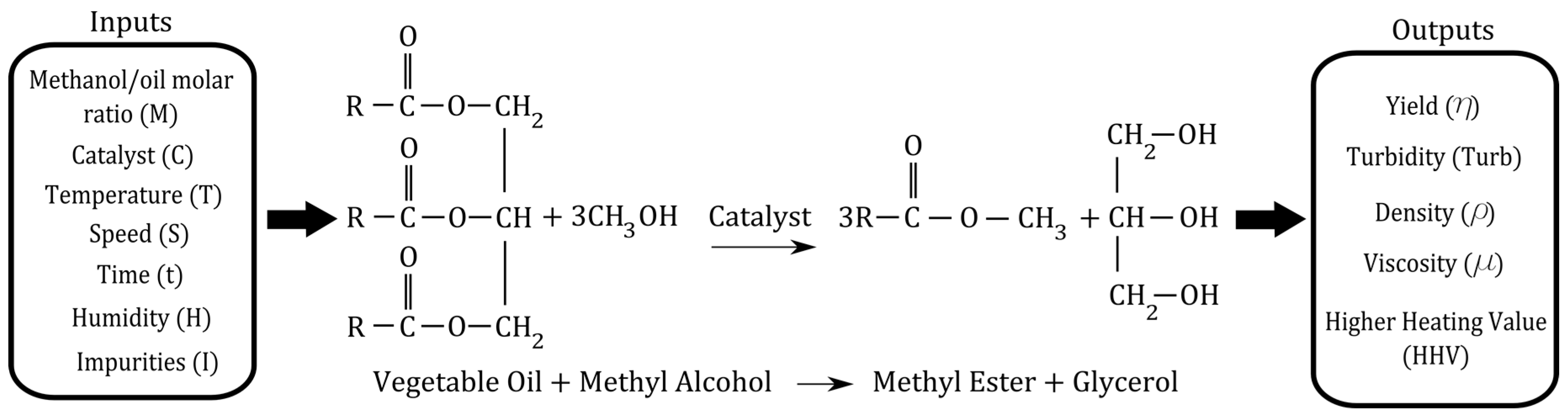

| Inputs | Notation | Magnitude | Levels | ||
|---|---|---|---|---|---|
| −1 | 0 | +1 | |||
| Ratio oil | M | 6/1 | 7.5/1 | 9/1 | |
| Catalyst | C | wt. % | 1 | 1.5 | 2 |
| Time | t | min | 20 | 30 | 40 |
| Speed | S | rpm | 500 | 750 | 1000 |
| Temp | T | °C | 20 | 30 | 40 |
| Humidity | H | wt. % | 0 | 1.5 | 3 |
| Impurity | I | wt. % | 0 | 1.5 | 3 |
| Sample | Inputs | ||||||
|---|---|---|---|---|---|---|---|
| Molar Ratio | Catalyst (wt. %) | Time (min) | Speed (rpm) | Temp (°C) | Humidity (wt. %) | Impurity (wt. %) | |
| 25 | 6 | 1 | 30 | 500 | 30 | 1.5 | 1.5 |
| 29 | 6 | 1 | 30 | 1000 | 30 | 1.5 | 1.5 |
| 27 | 6 | 2 | 30 | 500 | 30 | 1.5 | 1.5 |
| 31 | 6 | 2 | 30 | 1000 | 30 | 1.5 | 1.5 |
| 41 | 6 | 1.5 | 20 | 750 | 20 | 1.5 | 1.5 |
| 45 | 6 | 1.5 | 20 | 750 | 40 | 1.5 | 1.5 |
| 9 | 6 | 1.5 | 30 | 750 | 30 | 0 | 0 |
| 13 | 6 | 1.5 | 30 | 750 | 30 | 0 | 3 |
| 11 | 6 | 1.5 | 30 | 750 | 30 | 3 | 0 |
| 15 | 6 | 1.5 | 30 | 750 | 30 | 3 | 3 |
| 43 | 6 | 1.5 | 40 | 750 | 20 | 1.5 | 1.5 |
| 47 | 6 | 1.5 | 40 | 750 | 40 | 1.5 | 1.5 |
| 26 | 9 | 1 | 30 | 500 | 30 | 1.5 | 1.5 |
| 30 | 9 | 1 | 30 | 1000 | 30 | 1.5 | 1.5 |
| 28 | 9 | 2 | 30 | 500 | 30 | 1.5 | 1.5 |
| 32 | 9 | 2 | 30 | 1000 | 30 | 1.5 | 1.5 |
| 42 | 9 | 1.5 | 20 | 750 | 20 | 1.5 | 1.5 |
| 46 | 9 | 1.5 | 20 | 750 | 40 | 1.5 | 1.5 |
| 10 | 9 | 1.5 | 30 | 750 | 30 | 0 | 0 |
| 14 | 9 | 1.5 | 30 | 750 | 30 | 0 | 3 |
| 12 | 9 | 1.5 | 30 | 750 | 30 | 3 | 0 |
| 16 | 9 | 1.5 | 30 | 750 | 30 | 3 | 3 |
| 44 | 9 | 1.5 | 40 | 750 | 20 | 1.5 | 1.5 |
| 48 | 9 | 1.5 | 40 | 750 | 40 | 1.5 | 1.5 |
| 49 | 7.5 | 1 | 20 | 750 | 30 | 0 | 1.5 |
| 53 | 7.5 | 1 | 20 | 750 | 30 | 3 | 1.5 |
| 17 | 7.5 | 1 | 30 | 750 | 20 | 1.5 | 0 |
| 21 | 7.5 | 1 | 30 | 750 | 20 | 1.5 | 3 |
| 19 | 7.5 | 1 | 30 | 750 | 40 | 1.5 | 0 |
| 23 | 7.5 | 1 | 30 | 750 | 40 | 1.5 | 3 |
| 51 | 7.5 | 1 | 40 | 750 | 30 | 0 | 1.5 |
| 55 | 7.5 | 1 | 40 | 750 | 30 | 3 | 1.5 |
| 50 | 7.5 | 2 | 20 | 750 | 30 | 0 | 1.5 |
| 54 | 7.5 | 2 | 20 | 750 | 30 | 3 | 1.5 |
| 18 | 7.5 | 2 | 30 | 750 | 20 | 1.5 | 0 |
| 22 | 7.5 | 2 | 30 | 750 | 20 | 1.5 | 3 |
| 20 | 7.5 | 2 | 30 | 750 | 40 | 1.5 | 0 |
| 24 | 7.5 | 2 | 30 | 750 | 40 | 1.5 | 3 |
| 52 | 7.5 | 2 | 40 | 750 | 30 | 0 | 1.5 |
| 56 | 7.5 | 2 | 40 | 750 | 30 | 3 | 1.5 |
| 33 | 7.5 | 1.5 | 20 | 500 | 30 | 1.5 | 0 |
| 37 | 7.5 | 1.5 | 20 | 500 | 30 | 1.5 | 3 |
| 35 | 7.5 | 1.5 | 20 | 1000 | 30 | 1.5 | 0 |
| 39 | 7.5 | 1.5 | 20 | 1000 | 30 | 1.5 | 3 |
| 1 | 7.5 | 1.5 | 30 | 500 | 20 | 0 | 1.5 |
| 5 | 7.5 | 1.5 | 30 | 500 | 20 | 3 | 1.5 |
| 3 | 7.5 | 1.5 | 30 | 500 | 40 | 0 | 1.5 |
| 7 | 7.5 | 1.5 | 30 | 500 | 40 | 3 | 1.5 |
| 2 | 7.5 | 1.5 | 30 | 1000 | 20 | 0 | 1.5 |
| 6 | 7.5 | 1.5 | 30 | 1000 | 20 | 3 | 1.5 |
| 4 | 7.5 | 1.5 | 30 | 1000 | 40 | 0 | 1.5 |
| 8 | 7.5 | 1.5 | 30 | 1000 | 40 | 3 | 1.5 |
| 34 | 7.5 | 1.5 | 40 | 500 | 30 | 1.5 | 0 |
| 38 | 7.5 | 1.5 | 40 | 500 | 30 | 1.5 | 3 |
| 36 | 7.5 | 1.5 | 40 | 1000 | 30 | 1.5 | 0 |
| 40 | 7.5 | 1.5 | 40 | 1000 | 30 | 1.5 | 3 |
| Sample | Outputs | ||||
|---|---|---|---|---|---|
| η | Turb (NTU) | ρ (g/mL) | µ (mm2/s) | HHV (MJ/Kg) | |
| 25 | 93 | 0.65 | 0.83 | 7.03 | 42.70 |
| 29 | 93 | 1.05 | 0.85 | 5.15 | 41.83 |
| 27 | 40 | 1.78 | 0.822 | 5.65 | 42.06 |
| 31 | 9.5 | 58.5 | 0.83 | 5.05 | 41.78 |
| 41 | 29 | 8.48 | 0.84 | 5.40 | 41.94 |
| 45 | 29 | 0.21 | 0.85 | 5.93 | 42.19 |
| 9 | 87 | 86 | 0.83 | 6.00 | 42.22 |
| 13 | 76 | 1 | 0.86 | 5.40 | 41.94 |
| 11 | 75 | 1.89 | 0.85 | 8.05 | 43.17 |
| 15 | 77 | 1.18 | 0.83 | 5.39 | 41.94 |
| 43 | 31 | 2.44 | 0.85 | 4.67 | 41.61 |
| 47 | 57 | 2.94 | 0.79 | 7.40 | 42.87 |
| 26 | 88 | 6 | 0.83 | 9.83 | 43.99 |
| 30 | 55 | 3.52 | 0.80 | 6.07 | 42.26 |
| 28 | 50 | 3.81 | 0.79 | 9.24 | 43.72 |
| 32 | 23 | 1.66 | 0.79 | 6.38 | 42.40 |
| 42 | 59 | 1.09 | 0.81 | 6.16 | 42.30 |
| 46 | 91 | 2.45 | 0.83 | 7.97 | 43.13 |
| 10 | 83 | 6.29 | 0.82 | 5.67 | 42.07 |
| 14 | 90 | 1.42 | 0.80 | 5.65 | 42.06 |
| 12 | 90 | 1.01 | 0.82 | 7.81 | 43.06 |
| 16 | 71 | 10.14 | 0.85 | 10.15 | 44.14 |
| 44 | 85 | 0.67 | 0.84 | 6.15 | 42.29 |
| 48 | 82 | 1.01 | 0.81 | 6.17 | 42.30 |
| 49 | 93 | 1.47 | 0.80 | 8.96 | 43.59 |
| 53 | 89 | 1.62 | 0.82 | 8.20 | 43.24 |
| 17 | 92 | 1.06 | 0.81 | 6.47 | 42.44 |
| 21 | 95 | 0.69 | 0.82 | 9.40 | 43.79 |
| 19 | 91 | 1.53 | 0.83 | 9.43 | 43.81 |
| 23 | 86 | 1.61 | 0.81 | 7.24 | 42.80 |
| 51 | 94 | 0.22 | 0.84 | 6.13 | 42.28 |
| 55 | 89 | 0.42 | 0.83 | 11.99 | 44.99 |
| 50 | 63 | 0.34 | 0.82 | 0 | 39.45 |
| 54 | 87 | 0.36 | 0.81 | 4.48 | 41.52 |
| 18 | 45.5 | 53 | 0.82 | 5.97 | 42.21 |
| 22 | 23 | 1.09 | 0.82 | 5.32 | 41.91 |
| 20 | 24.6 | 0.64 | 0.80 | 6.07 | 42.25 |
| 24 | 22 | 18.03 | 0.81 | 4.67 | 41.61 |
| 52 | 66 | 0.31 | 0.81 | 4.08 | 41.33 |
| 56 | 90 | 1.01 | 0.84 | 5.77 | 42.12 |
| 33 | 93 | 1.18 | 0.82 | 5.65 | 42.06 |
| 37 | 83 | 1.34 | 0.84 | 8.22 | 43.25 |
| 35 | 100 | 0.56 | 0.81 | 6.10 | 42.27 |
| 39 | 93 | 0.72 | 0.73 | 6.36 | 42.39 |
| 1 | 98 | 0.48 | 0.84 | 3.78 | 41.20 |
| 5 | 75 | 1.85 | 0.79 | 11.98 | 44.99 |
| 3 | 86 | 2 | 0.81 | 4.82 | 41.68 |
| 7 | 86 | 1.59 | 0.77 | 7.15 | 42.75 |
| 2 | 83 | 2.71 | 0.79 | 12.14 | 45.06 |
| 6 | 82 | 0.9 | 0.82 | 8.16 | 43.22 |
| 4 | 88 | 0.63 | 0.83 | 6.03 | 42.23 |
| 8 | 95 | 0.94 | 0.81 | 6.35 | 42.38 |
| 34 | 78 | 0.74 | 0.81 | 5.83 | 42.14 |
| 38 | 77 | 7.42 | 0.82 | 8.59 | 43.42 |
| 36 | 93 | 0.78 | 0.83 | 5.54 | 42.01 |
| 40 | 85 | 1.96 | 0.82 | 7.81 | 43.06 |
| Variable | Degrees of freedom | Sum of Square | Mean Square | F Value | p-Value | Significance Code |
|---|---|---|---|---|---|---|
| M | 1 | 1211.3 | 1211.3 | 6.0928 | 0.017267 | * |
| M2 | 1 | 2992.5 | 2992.5 | 15.0525 | 0.000325 | *** |
| M × C | 1 | 10,324.9 | 10,324.9 | 51.9357 | 3.98 × 10-9 | *** |
| C2 | 1 | 4004.9 | 4004.9 | 20.1451 | 4.63 × 10-5 | *** |
| T | 1 | 67 | 67 | 0.337 | 0.564327 | |
| T2 | 1 | 2819 | 2819 | 14.1802 | 0.000462 | *** |
| H | 1 | 0 | 0 | 0.0002 | 0.988511 | |
| C × H | 1 | 498.1 | 498.1 | 2.5057 | 0.120145 | |
| H2 | 1 | 1610.2 | 1610.2 | 8.0996 | 0.006541 | * |
| Residuals | 47 | 9343.7 | 198.8 | |||
| R2 | 0.846 | - | - | - | - |
| Variable | Degrees of freedom | Sum of Square | Mean Square | F Value | p-Value | Significance Codes |
|---|---|---|---|---|---|---|
| M | 1 | 672.6 | 672.57 | 6.8629 | 1.24 × 10-2 | * |
| M2 | 1 | 379.6 | 379.58 | 3.8733 | 5.60 × 10-2 | . |
| M·C | 1 | 481.1 | 481.06 | 4.9088 | 3.25 × 10-2 | * |
| C2 | 1 | 601.6 | 601.62 | 6.1389 | 1.75 × 10-2 | * |
| t | 1 | 0 | 0 | 0 | 9.98 × 10-1 | |
| t2 | 1 | 366.4 | 366.44 | 3.7392 | 6.02 × 10-2 | . |
| M·S | 1 | 44.1 | 44.08 | 0.4497 | 5.06 × 10-1 | |
| C·S | 1 | 1011.1 | 1011.13 | 10.3175 | 2.60 × 10-3 | ** |
| T | 1 | 108.6 | 108.56 | 1.1077 | 2.99 × 10-1 | |
| C·T | 1 | 266.4 | 266.4 | 2.7183 | 1.07 × 10-1 | |
| H | 1 | 954.2 | 954.19 | 9.7365 | 3.35 × 10-1 | ** |
| M·H | 1 | 486.7 | 486.72 | 4.9665 | 3.15 × 10-2 | * |
| I | 1 | 1011.8 | 1011.83 | 10.3246 | 2.60 × 10-3 | ** |
| M·I | 1 | 691.1 | 691.14 | 7.0524 | 1.13 × 10-2 | * |
| T·I | 1 | 1207.6 | 1207.62 | 12.3225 | 1.12 × 10-3 | ** |
| H·I | 1 | 425.6 | 425.63 | 4.3431 | 4.36 × 10-2 | * |
| I2 | 1 | 672.6 | 672.57 | 6.8629 | 1.24 × 10-2 | * |
| Residuals | 1 | 379.6 | 379.58 | 3.8733 | 5.60 × 10-2 | . |
| R2 | 0.8304 | - | - | - | - | - |
| Variable | Degrees of freedom | Sum of Square | Mean Square | F Value | p-Value | Significance Codes |
|---|---|---|---|---|---|---|
| M | 1 | 0.002408 | 0.002408 | 11.0961 | 1.87 × 10-3 | ** |
| M2 | 1 | 0.002043 | 0.002043 | 9.4134 | 3.86 × 10-3 | ** |
| t | 1 | 0.000626 | 0.000625 | 2.8818 | 9.74 × 10-2 | . |
| M·t | 1 | 0.000535 | 0.000535 | 2.4668 | 1.24 × 10-1 | |
| M·S | 1 | 0.000229 | 0.000229 | 1.0563 | 3.10 × 10-1 | |
| t·S | 1 | 0.002631 | 0.002631 | 12.1215 | 1.22 × 10-3 | ** |
| S2 | 1 | 0.001614 | 0.001614 | 7.4355 | 9.45 × 10-3 | ** |
| M·T | 1 | 0.000399 | 0.000399 | 1.8386 | 1.83 × 10-1 | |
| C·T | 1 | 0.000831 | 0.000831 | 3.8272 | 5.74 × 10-2 | . |
| t·T | 1 | 0.002083 | 0.002083 | 9.5978 | 3.56 × 10-3 | ** |
| S·T | 1 | 0.001085 | 0.001085 | 4.9986 | 3.10 × 10-2 | * |
| H | 1 | 1.6E-06 | 1.62E-06 | 0.0075 | 9.32 × 10-1 | |
| M·H | 1 | 0.000379 | 0.000379 | 1.7466 | 1.94 × 10-1 | |
| S·H | 1 | 0.001178 | 0.001178 | 5.4282 | 2.49 × 10-2 | * |
| t·I | 1 | 1.63E-05 | 1.63E-05 | 0.075 | 7.86 × 10-1 | |
| S·I | 1 | 0.002431 | 0.002431 | 11.203 | 1.79 × 10-3 | ** |
| Residuals | 40 | 0.008681 | 0.000217 | |||
| R2 | 0.8249 | - | - | - | - | - |
| Variable | Degrees of freedom | Sum of Square | Mean Square | F Value | p-Value | Significance Codes |
|---|---|---|---|---|---|---|
| M·t | 1 | 2.524 | 2.524 | 1.3462 | 2.52 × 10-1 | |
| S2 | 1 | 1.383 | 1.383 | 0.7375 | 3.95 × 10-1 | |
| T2 | 1 | 1.613 | 1.613 | 0.8601 | 3.59 × 10-1 | |
| M·H | 1 | 21.914 | 21.914 | 11.6874 | 1.33 × 10-3 | ** |
| C·H | 1 | 37.86 | 37.86 | 20.1916 | 4.70 × 10-5 | *** |
| T·H | 1 | 5.704 | 5.704 | 3.0419 | 8.78 × 10-2 | . |
| S·H | 1 | 32.831 | 32.831 | 17.5093 | 1.27 × 10-4 | *** |
| H2 | 1 | 3.889 | 3.889 | 2.074 | 1.57 × 10-1 | |
| M·I | 1 | 2.316 | 2.316 | 1.2353 | 2.72 × 10-1 | |
| T·I | 1 | 10.54 | 10.54 | 5.6212 | 2.20 × 10-2 | * |
| Residuals | 46 | 86.252 | 1.875 | |||
| R2 | 0.7635 | - | - | - | - | - |
| Variable | Degrees of freedom | Sum of Square | Mean Square | F Value | p-Value | Significance Codes |
|---|---|---|---|---|---|---|
| M | 1 | 1.3244 | 1.3244 | 10.9006 | 2.00 × 10-3 | ** |
| C | 1 | 1.912 | 1.91204 | 15.7373 | 2.86 × 10-4 | *** |
| C2 | 1 | 0.0526 | 0.05259 | 0.4329 | 5.14 × 10-1 | |
| M·t | 1 | 0.002 | 0.00199 | 0.0164 | 8.99 × 10-1 | |
| S2 | 1 | 0.1591 | 0.15914 | 1.3098 | 2.59 × 10-1 | |
| M·T | 1 | 0.1132 | 0.11318 | 0.9315 | 3.40 × 10-1 | |
| S·T | 1 | 0.1062 | 0.10621 | 0.8741 | 3.55 × 10-1 | |
| T2 | 1 | 0.6665 | 0.66652 | 5.4859 | 2.41 × 10-2 | * |
| H | 1 | 0.517 | 0.51699 | 4.2551 | 4.55 × 10-2 | * |
| C·H | 1 | 0.5179 | 0.51788 | 4.2625 | 4.53 × 10-2 | * |
| t·H | 1 | 0.4687 | 0.46874 | 3.858 | 5.63 × 10-2 | . |
| S·H | 1 | 1.6756 | 1.67561 | 13.7913 | 6.09 × 10-4 | *** |
| H2 | 1 | 0.5589 | 0.55887 | 4.5999 | 3.79 × 10-2 | * |
| M·I | 1 | 0.0383 | 0.03825 | 0.3148 | 5.78 × 10-1 | |
| T·I | 1 | 0.6052 | 0.60519 | 4.9811 | 3.12 × 10-2 | * |
| Residuals | 41 | 4.9814 | 0.1215 | |||
| R2 | 0.7977 | - | - | - | - | - |
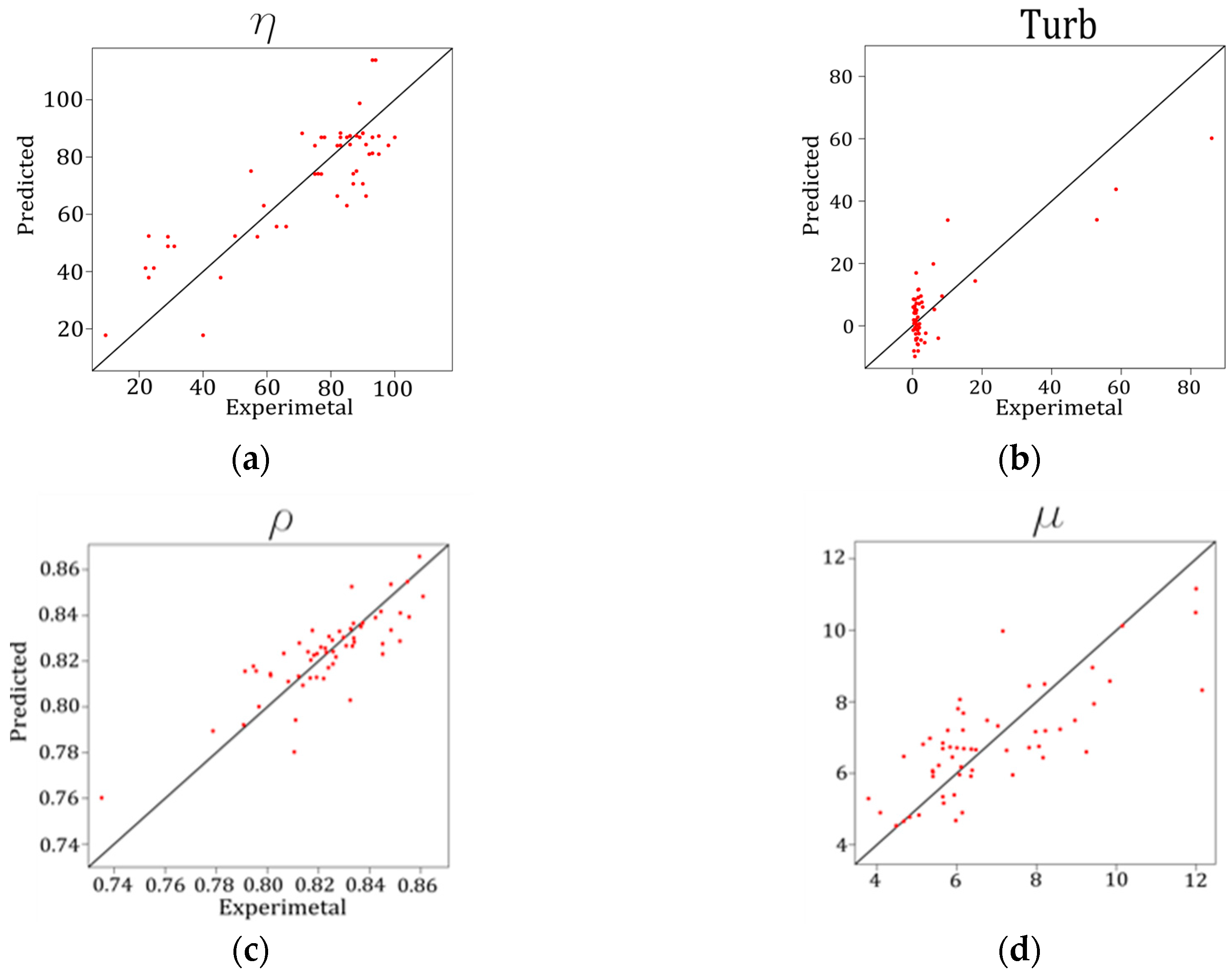
| Errors | η | Turb (NTU) | ρ (g/mL) | µ (mm2/s) | HHV (MJ/Kg) |
|---|---|---|---|---|---|
| MAE | 10.445 | 6.305 | 0.009 | 0.980 | 0.231 |
| RMSE | 12.803 | 8.293 | 0.012 | 1.230 | 0.296 |
| Sample | Inputs | ||||||
|---|---|---|---|---|---|---|---|
| Molar Ratio | Catalyst (wt. %) | Time (min) | Speed (rpm) | T (°C) | Humidity (wt. %) | Impurity (wt. %) | |
| 1 | 6.35 | 1.16 | 21.79 | 531.17 | 38.04 | 1.37 | 2.66 |
| 2 | 8.77 | 1.49 | 39.99 | 804.66 | 26.08 | 2.07 | 1.84 |
| 3 | 6.98 | 1.7 | 22.05 | 587.12 | 27.44 | 2.98 | 1.8 |
| 4 | 7.48 | 1.57 | 21.41 | 881.61 | 37.85 | 2.86 | 0.6 |
| 5 | 6.3 | 1.57 | 23.74 | 531.29 | 36.59 | 1.77 | 0.9 |
| 6 | 6.2 | 1.56 | 25.97 | 808.46 | 20.3 | 0.58 | 1.39 |
| 7 | 6.64 | 1.27 | 32.54 | 747.92 | 38.14 | 1.58 | 1.54 |
| 8 | 7.95 | 1.91 | 25.67 | 772.08 | 29.35 | 1.51 | 0.12 |
| 9 | 7.36 | 1.03 | 37.08 | 526.82 | 39.83 | 2.39 | 2.32 |
| 10 | 7.31 | 1.71 | 32.93 | 528.27 | 34.67 | 1.02 | 1.98 |
| 11 | 6.75 | 1.2 | 29.07 | 711.16 | 34.27 | 2.57 | 2.17 |
| 12 | 8.76 | 1.35 | 25.69 | 929.16 | 26.92 | 0.33 | 1.34 |
| 13 | 7.9 | 1.69 | 24.33 | 855.05 | 34.23 | 0.3 | 0.94 |
| 14 | 8.49 | 1.86 | 28.35 | 830.26 | 31.21 | 2.17 | 0.11 |
| 15 | 7.31 | 1.71 | 32.93 | 528.27 | 34.67 | 1.02 | 1.98 |
| Errors | η | Turb (NTU) | ρ (g/mL) | µ (mm2/s) | HHV (MJ/Kg) |
|---|---|---|---|---|---|
| MAE | 15.081 | 9.130 | 0.063 | 1.941 | 0.449 |
| RMSE | 22.853 | 14.648 | 0.066 | 2.202 | 0.556 |
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.24 | 0.921 |
| C | Minimize → 1 | 1.0 | 0.75 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.99 | 1.000 |
| T | In range → 30 | 1.0 | 20.40 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.20 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.15 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 99.99 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.232 |
| µ | Minimize → 3.79 | 1.0 | 8.00 | 0.496 |
| HHV | Maximize → 20.52 | 1.0 | 21.55 | 0.431 |
| Overall Desirability | 0.710 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.52 | 0.827 |
| C | Minimize → 1 | 1.0 | 0.78 | 1.000 |
| t | Minimize → 20 | 1.0 | 19.99 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.67 | 1.000 |
| T | In range → 30 | 1.0 | 24.44 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.21 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.17 | 1.000 |
| η | Maximize → 9.50 | 3.0 | 100.00 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.247 |
| µ | Minimize → 3.79 | 1.0 | 7.78 | 0.523 |
| HHV | Maximize → 20.52 | 1.0 | 21.53 | 0.422 |
| Overall Desirability | 0.709 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.24 | 0.921 |
| C | Minimize → 1 | 1.0 | 0.75 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.99 | 1.000 |
| T | In range → 30 | 1.0 | 20.40 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.20 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.15 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 99.99 | 1.000 |
| Turb | Minimize → 0.21 | 3.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.232 |
| µ | Minimize → 3.79 | 1.0 | 8.00 | 0.496 |
| HHV | Maximize → 20.52 | 1.0 | 21.55 | 0.431 |
| Overall Desirability | 0.710 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 7.35 | 0.551 |
| C | Minimize → 1 | 1.0 | 1.00 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 1.0 | 500.01 | 1.000 |
| T | In range → 30 | 1.0 | 26.79 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.00 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.10 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 94.35 | 0.938 |
| Turb | Minimize → 0.21 | 1.0 | 3.23 | 0.965 |
| ρ | Minimize → 0.74 | 3.0 | 0.82 | 0.025 |
| µ | Minimize → 3.79 | 3.0 | 7.04 | 0.228 |
| HHV | Maximize → 20.52 | 1.0 | 21.43 | 0.378 |
| Overall Desirability | 0.467 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.40 | 0.868 |
| C | Minimize → 1 | 1.0 | 1.00 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.60 | 1.000 |
| T | In range → 30 | 1.0 | 33.70 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.21 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.16 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 136.97 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.241 |
| µ | Minimize → 3.79 | 1.0 | 9.86 | 0.274 |
| HHV | Maximize → 20.52 | 3.0 | 22.04 | 0.256 |
| Overall Desirability | 0.626 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.09 | 0.972 |
| C | Minimize → 1 | 3.0 | 0.73 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.96 | 1.000 |
| T | In range → 30 | 1.0 | 29.78 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.20 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.17 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 100.00 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.224 |
| µ | Minimize → 3.79 | 1.0 | 8.03 | 0.493 |
| HHV | Maximize → 20.52 | 1.0 | 21.55 | 0.430 |
| Overall Desirability | 0.710 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.24 | 0.921 |
| C | Minimize → 1 | 1.0 | 0.75 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 3.0 | 499.99 | 1.000 |
| T | In range → 30 | 1.0 | 20.40 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.21 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.15 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 99.99 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.232 |
| µ | Minimize → 3.79 | 1.0 | 8.00 | 0.496 |
| HHV | Maximize → 20.52 | 1.0 | 21.55 | 0.431 |
| Overall Desirability | 0.710 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 1.0 | 6.09 | 0.972 |
| C | Minimize → 1 | 1.0 | 0.73 | 1.000 |
| t | Minimize → 20 | 3.0 | 19.98 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.96 | 1.000 |
| T | In range → 30 | 1.0 | 29.78 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.20 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.16 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 100.00 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.224 |
| µ | Minimize → 3.79 | 1.0 | 8.03 | 0.493 |
| HHV | Maximize → 20.52 | 1.0 | 21.55 | 0.430 |
| Overall Desirability | 0.710 | |||
| Goal | Importance | Value | Desirability | |
|---|---|---|---|---|
| M | Minimize → 6 | 3.0 | 6.00 | 1.000 |
| C | Minimize → 1 | 1.0 | 0.72 | 1.000 |
| t | Minimize → 20 | 1.0 | 20.00 | 1.000 |
| S | Minimize → 500 | 1.0 | 499.96 | 1.000 |
| T | In range → 30 | 1.0 | 29.78 | 1.000 |
| H | In range → 1.5 | 1.0 | 0.19 | 1.000 |
| I | In range → 1.5 | 1.0 | 0.17 | 1.000 |
| η | Maximize → 9.50 | 1.0 | 100.00 | 1.000 |
| Turb | Minimize → 0.21 | 1.0 | 0.00 | 1.000 |
| ρ | Minimize → 0.74 | 1.0 | 0.83 | 0.219 |
| µ | Minimize → 3.79 | 1.0 | 8.07 | 0.488 |
| HHV | Maximize → 20.52 | 1.0 | 21.55 | 0.431 |
| Overall Desirability | 0.710 | |||
| Optimization Scenarios | Experimental Values Obtained | ||||||
|---|---|---|---|---|---|---|---|
| η | Turb (NTU) | ρ (g/mL) | µ (mm2/s) | HHV (MJ/Kg) | MAE | RMSE | |
| 1st Scenario | 0.98 | 0.03 | 0.89 | 0.34 | 0.20 | 0.05 | 0.03 |
| 2nd Scenario | 0.99 | 0.02 | 0.63 | 0.27 | 0.16 | 0.09 | 0.05 |
| 3rd Scenario | 0.98 | 0.01 | 0.89 | 0.34 | 0.21 | 0.04 | 0.02 |
| 4th Scenario | 0.00 | 0.92 | 0.00 | 0.00 | 0.00 | 0.12 | 0.08 |
| 5th Scenario | 0.98 | 0.02 | 0.77 | 1.00 | 0.99 | 0.06 | 0.03 |
| 6th Scenario | 0.98 | 0.02 | 0.98 | 0.35 | 0.20 | 0.07 | 0.04 |
| 7th Scenario | 0.97 | 0.01 | 0.89 | 0.34 | 0.20 | 0.04 | 0.03 |
| 8th Scenario | 0.98 | 0.03 | 0.94 | 0.35 | 0.20 | 0.10 | 0.07 |
| 9th Scenario | 0.98 | 0.02 | 0.99 | 0.37 | 0.20 | 0.05 | 0.03 |
| MAE | 0.02 | 0.03 | 0.02 | 0.00 | 0.01 | 0.07 | 0.04 |
| RMSE | 0.06 | 0.09 | 0.08 | 0.01 | 0.02 | 0.25 | 0.14 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corral Bobadilla, M.; Lostado Lorza, R.; Escribano García, R.; Somovilla Gómez, F.; Vergara González, E.P. An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions. Energies 2017, 10, 130. https://doi.org/10.3390/en10010130
Corral Bobadilla M, Lostado Lorza R, Escribano García R, Somovilla Gómez F, Vergara González EP. An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions. Energies. 2017; 10(1):130. https://doi.org/10.3390/en10010130
Chicago/Turabian StyleCorral Bobadilla, Marina, Rubén Lostado Lorza, Rubén Escribano García, Fátima Somovilla Gómez, and Eliseo P. Vergara González. 2017. "An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions" Energies 10, no. 1: 130. https://doi.org/10.3390/en10010130
APA StyleCorral Bobadilla, M., Lostado Lorza, R., Escribano García, R., Somovilla Gómez, F., & Vergara González, E. P. (2017). An Improvement in Biodiesel Production from Waste Cooking Oil by Applying Thought Multi-Response Surface Methodology Using Desirability Functions. Energies, 10(1), 130. https://doi.org/10.3390/en10010130










