The Interplay between COVID-19 and the Economy in Canada
Abstract
:1. Introduction
- An epidemiological model that accounts for spatial spread, time-dependent parameters, different levels of disease severity, vaccination, age-range dependency, and labor status of those of working age.
- Model parameters that are calibrated from the daily Canadian provincial reports on COVID-19 infections, hospitalizations, admissions to ICU, deaths, and monthly labor status.
- An explicit connection between the pandemic and the economy through labor market dynamics.
2. The Model
3. Estimation Procedure
4. Numerical Results
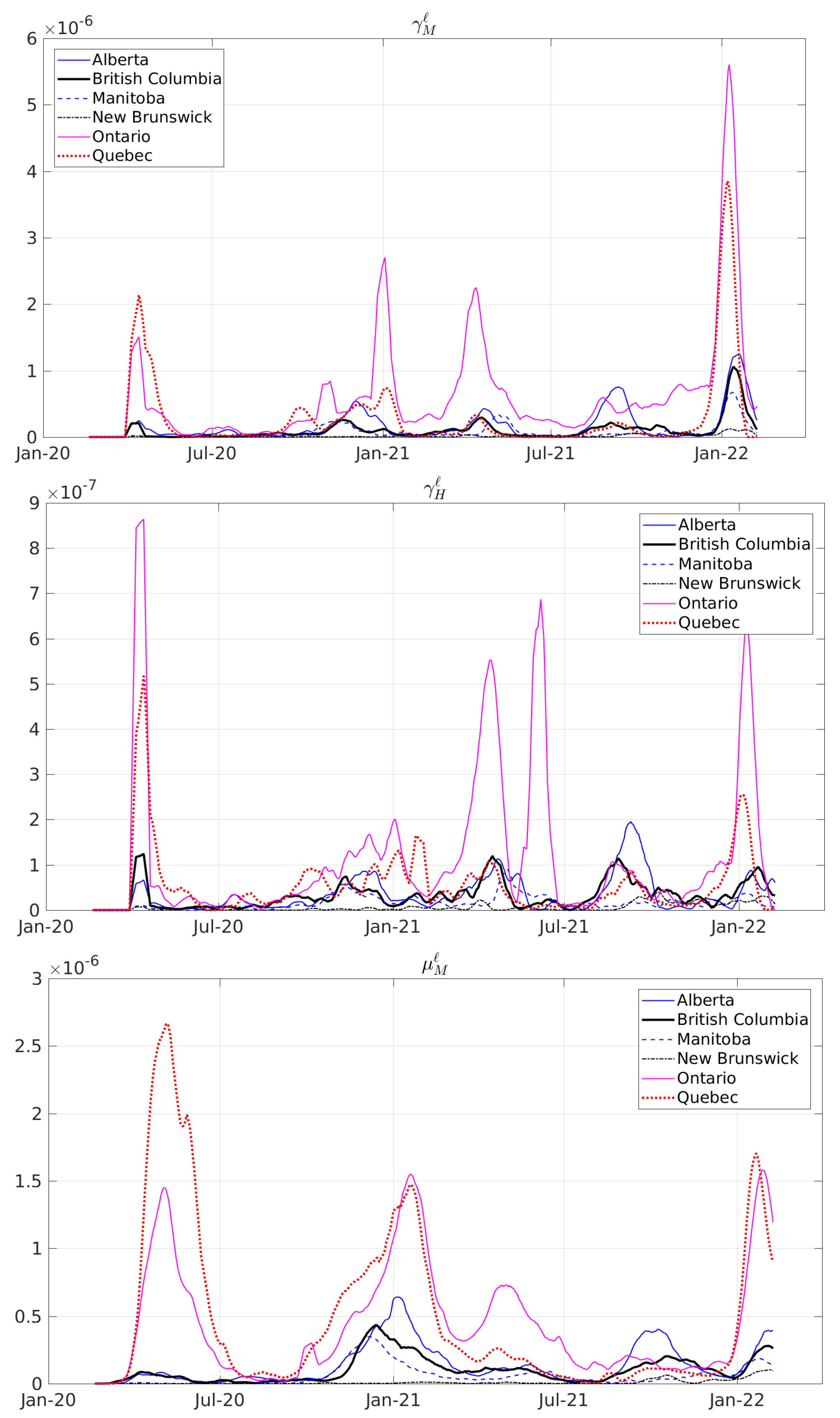
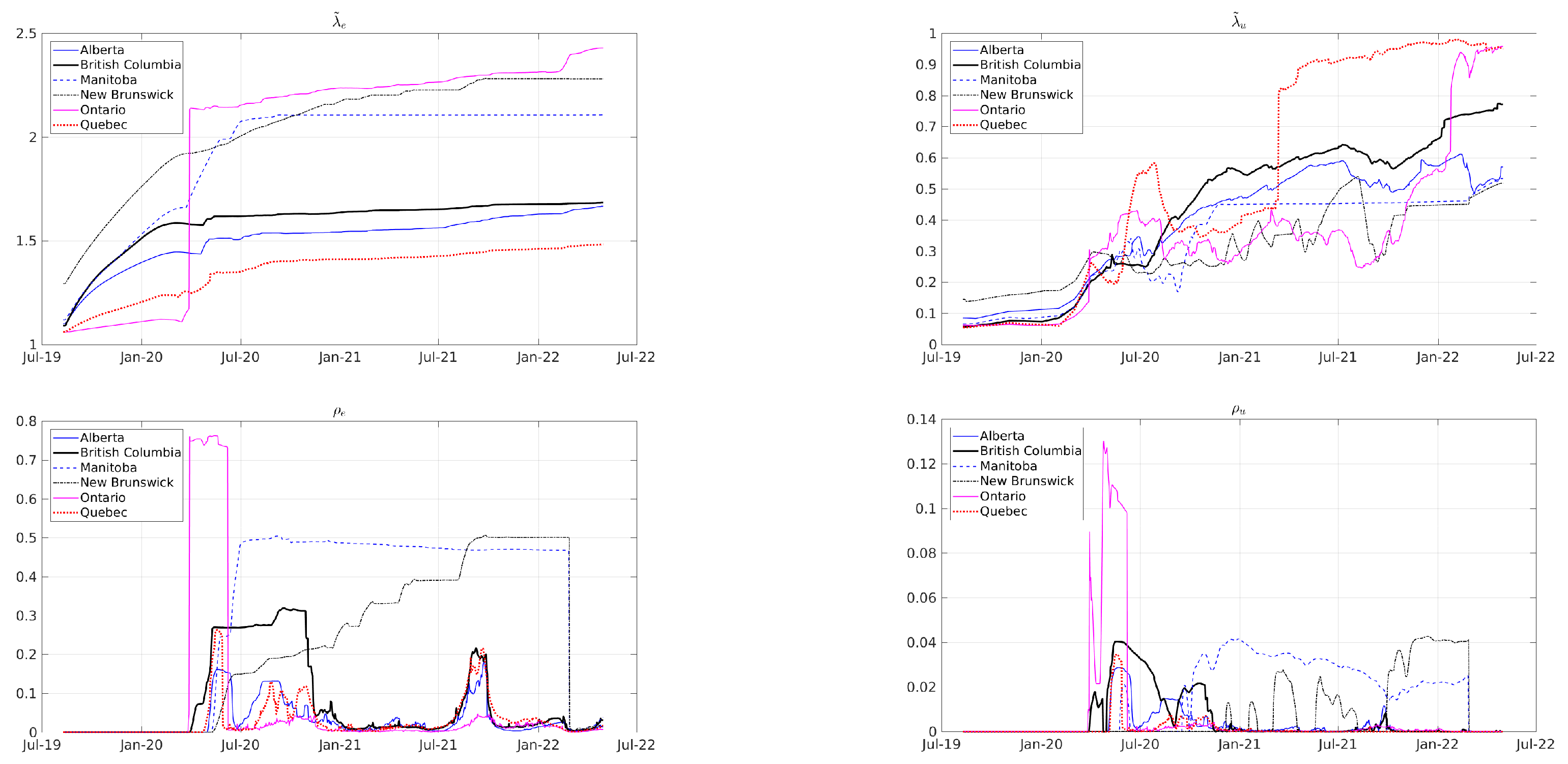
4.1. Model Calibration
4.2. Backtesting
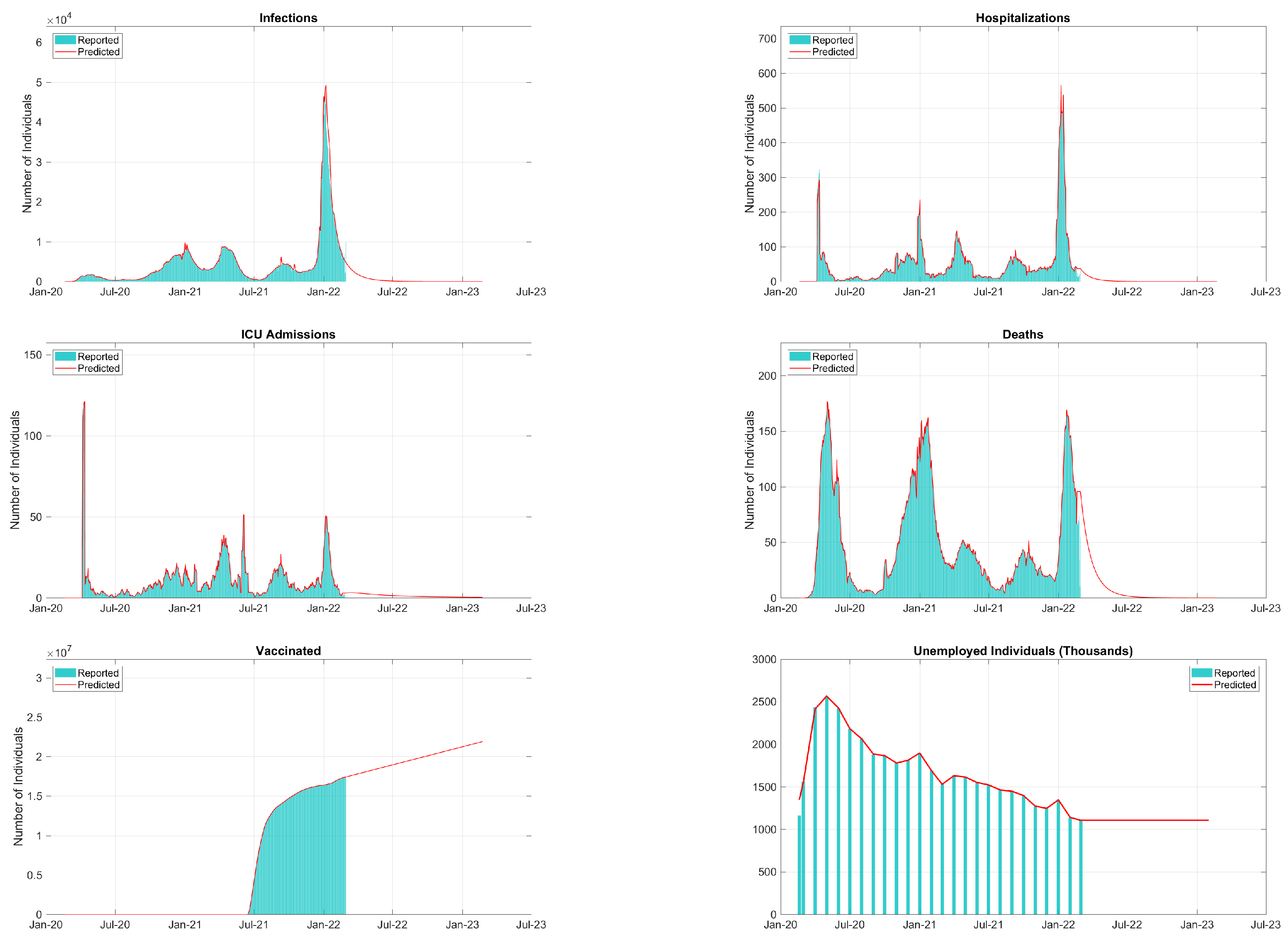
4.3. Long-Term Predictions
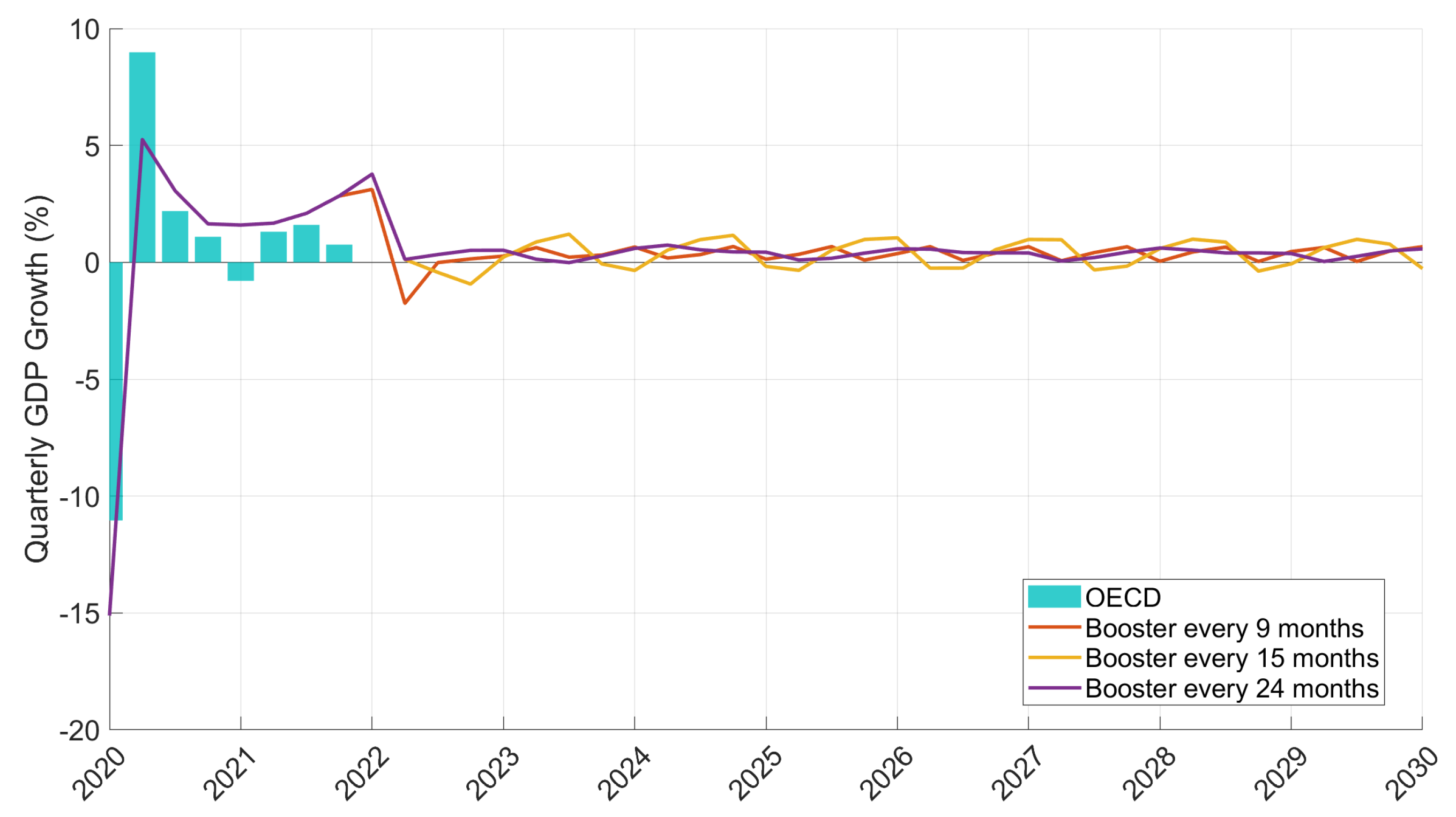
5. Economic Effect
6. Conclusions and Further Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
| 1 | See, for example, covid19.who.int (accessed on 5 October 2022). |
| 2 | Data on air travel distance downloaded 20 November 2020 from https://www.distancefromto.net/ (accessed on 20 November 2020). |
| 3 | For clarity, consider provinces and suppose that the distance between the centers of 1 and 2 is in the same range as the distance between the centers of 2 and 3, say 3000 to 4000 K. We then impose the constraint and estimate using data for both pairs of provinces. This reduces the original 78 parameters , , to the five parameters . |
| 4 | The term 1 inside the argument for the logarithms is added to avoid indefinite values when the number of reported infections is zero. |
| 5 | Notice that, to find the values for j = 1,2,3, we just have to consider the series values for previous dates. |
| 6 | Data downloaded on 15 March 2022 from https://resources-covid19canada.hub.arcgis.com/datasets/provincial-daily-totals/explore (accessed on 15 March 2022). |
| 7 | Data downloaded on 20 Novemver 2020 from https://www.statcan.gc.ca/eng/subjects-start/population_and_demography (accessed on 20 Novemver 2020). |
| 8 | Data downloaded on 1 July 2022 from https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1410028703 (accessed on 1 July 2022). |
| 9 | In accordance with data in https://www.cdc.gov/coronavirus/2019-ncov/variants/omicron-variant.html (accessed on 20 May 2022). |
| 10 | |
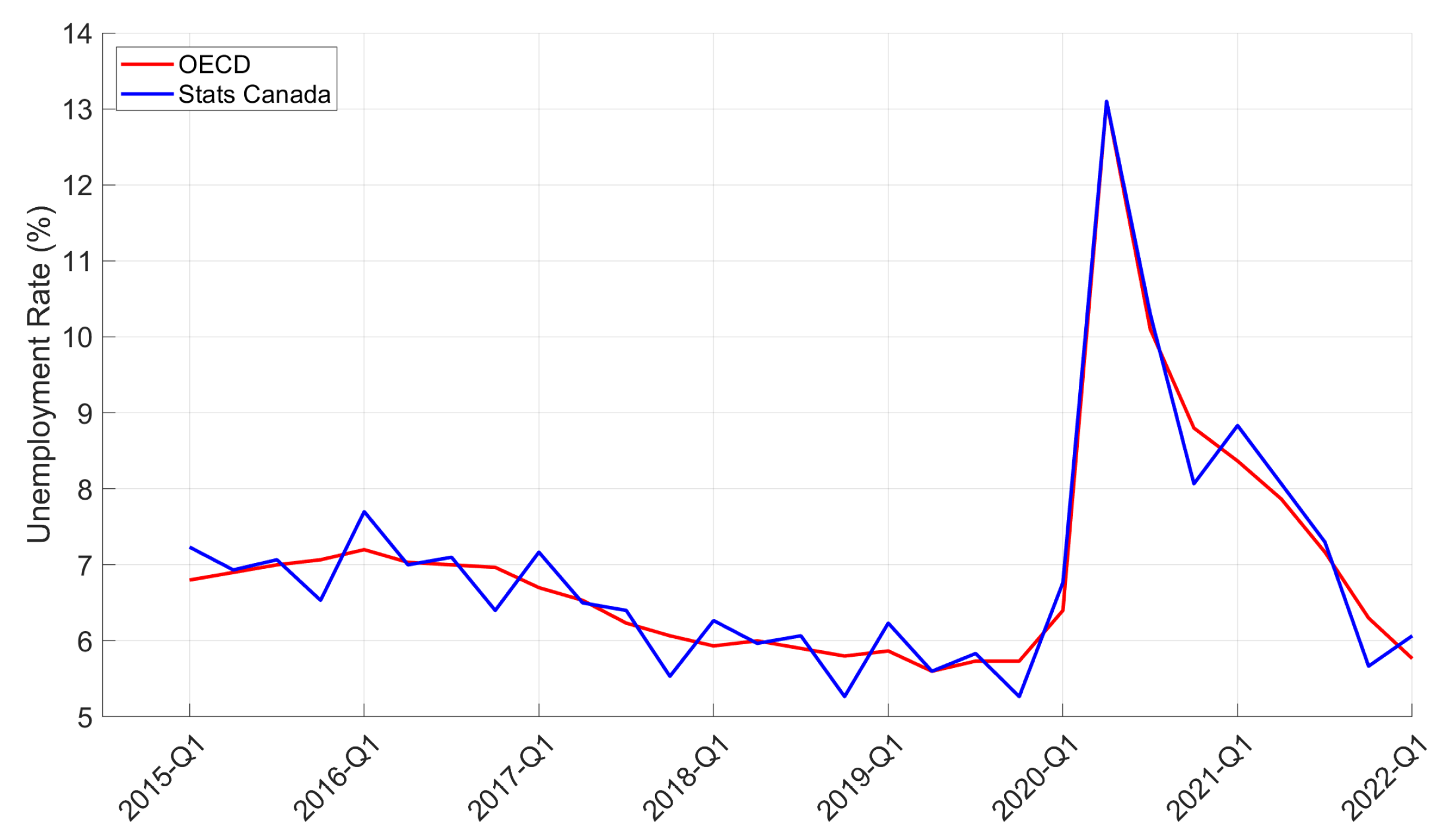
| 11 | Data downloaded on 20 July 2022 from https://data.oecd.org/unemp/unemployment-rate.htm (accessed on 20 July 2022). |
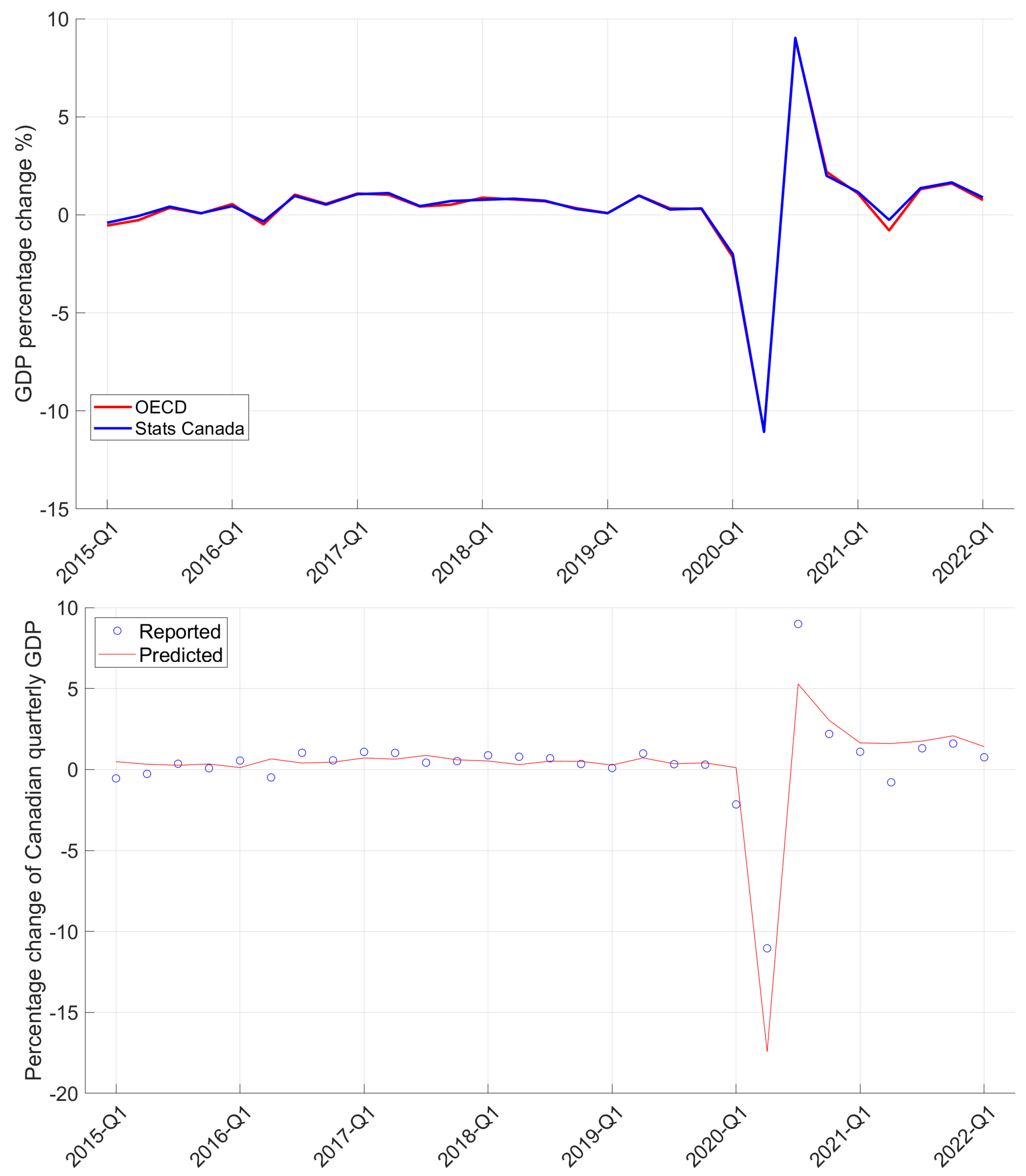
| 12 | Data downloaded on 20 July 2022 from https://data.oecd.org/gdp/quarterly-gdp.htm (accessed on 20 July 2022). |
| 13 | Downloaded on 20 July 2022 from https://www150.statcan.gc.ca/t1/tbl1/en/cv.action?pid=3610043401 (accessed on 20 July 2022). |
| 14 | We use a 12-month average of the time-varying parameters in Okun’s law for these simulations. |
References
- Abate, Semagn Mekonnen, Siraj Ahmed Ali, Bahiru Mantfardo, and Bivash Basu. 2020. Rate of Intensive Care Unit admission and outcomes among patients with coronavirus: A systematic review and Meta-analysis. PLoS ONE 15: e0235653. [Google Scholar] [CrossRef] [PubMed]
- Acemoglu, Daron, Victor Chernozhukov, Iván Werning, and Michael D. Whinston. 2021. Optimal targeted lockdowns in a multigroup sir model. American Economic Review: Insights 3: 487–502. [Google Scholar] [CrossRef]
- Albani, Vinicius V. L., Roseane A. S. Albani, Nara Bobko, Eduardo Massad, and Jorge P. Zubelli. 2021. On the Role of Financial Support Programs in Mitigating the Sars-CoV-2 Spread in Brazil. BMC Public Health 22: 1781. [Google Scholar] [CrossRef] [PubMed]
- Albani, V., R. Albani, E. Massad, and J. Zubelli. 2022. Nowcasting and forecasting COVID-19 waves: The recursive and stochastic nature of transmission. Royal Society Open Science 9: 220489. [Google Scholar] [CrossRef] [PubMed]
- Albani, Vinicius, Jennifer Loria, Eduardo Massad, and Jorge Zubelli. 2021a. COVID-19 Underreporting and its Impact on Vaccination Strategies. BMC Infectious Diseases 21: 1111. [Google Scholar] [CrossRef] [PubMed]
- Albani, Vinicius V. L., Jennifer Loria, Eduardo Massad, and Jorge P. Zubelli. 2021b. The Impact of COVID-19 Vaccination Delay: A Data-Driven Modelling Analysis for Chicago and New York City. Vaccine 39: 6088–6094. [Google Scholar] [CrossRef] [PubMed]
- Albani, Vinicius V. L., Roberto M. Velho, and Jorge P. Zubelli. 2021. Estimating, monitoring, and forecasting COVID-19 epidemics: A spatiotemporal approach applied to NYC data. Scientific Reports 11: 1–15. [Google Scholar] [CrossRef]
- Alleman, Tijs, Jenna Vergeynst, Lander De Visscher, Michiel Rollier, Elena Torfs, Ingmar Nopens, and Jan Baetens. 2021. Assessing the effects of non-pharmaceutical interventions on SARS-CoV-2 transmission in Belgium by means of an extended SEIQRD model and public mobility data. Epidemics 37: 100505. [Google Scholar] [CrossRef]
- Alvarez, Fernando, David Argente, and Francesco Lippi. 2021. A simple planning problem for COVID-19 lock-down, testing, and tracing. American Economic Review: Insights 3: 367–82. [Google Scholar] [CrossRef]
- Amaku, Marcos, Dimas Tadeu Covas, Francisco Antonio Bezerra Coutinho, Raymundo Soares Azevedo, and Eduardo Massad. 2021. Modelling the impact of delaying vaccination against SARS-CoV-2 assuming unlimited vaccine supply. Theoretical Biology and Medical Modelling 18: 1–11. [Google Scholar] [CrossRef]
- Amaku, Marcos, Dimas Tadeu Covas, Francisco Antonio Bezerra Coutinho, Raymundo Soares Azevedo Neto, Claudio Struchiner, Annelies Wilder-Smith, and Eduardo Massad. 2021. Modelling the test, trace and quarantine strategy to control the COVID-19 epidemic in the state of São Paulo, Brazil. Infectious Disease Modelling 6: 46–55. [Google Scholar] [CrossRef] [PubMed]
- Aronna, M., R. Guglielmi, and L. Moschen. 2022. Estimate of the rate of unreported COVID-19 cases during the first outbreak in rio de janeiro. Infectious Disease Modelling 7: 317–32. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, Badar Nadeem. 2020. Economic impact of government interventions during the COVID-19 pandemic: International evidence from financial markets. Journal of Behavioral and Experimental Finance 27: 100371. [Google Scholar] [CrossRef] [PubMed]
- Balmford, Ben, James D. Annan, Julia C. Hargreaves, Marina Altoè, and Ian J. Bateman. 2020. Cross-country comparisons of COVID-19: Policy, politics and the price of life. Environmental and Resource Economics 76: 525–51. [Google Scholar] [CrossRef] [PubMed]
- Bayraktar, Erhan, Asaf Cohen, and April Nellis. 2021. A macroeconomic SIR model for COVID-19. Mathematics 9: 1901. [Google Scholar] [CrossRef]
- Bhopal, Sunil, and Raj Bhopal. 2020. Sex differential in COVID-19 mortality varies markedly by age. The Lancet 396: 532–33. [Google Scholar] [CrossRef]
- Calvetti, Daniela, Alexander Hoover, Johnie Rose, and Erkki Somersalo. 2020a. Bayesian dynamical estimation of the parameters of an SE(A)IR COVID-19 spread model. arXiv arXiv:2005.04365. [Google Scholar]
- Calvetti, Daniela, Alexander Hoover, Johnie Rose, and Erkki Somersalo. 2020b. Metapopulation Network Models for Understanding, Predicting, and Managing the Coronavirus Disease COVID-19. Frontiers in Physics 8: 261. [Google Scholar] [CrossRef]
- Campos, Eduardo Lima, Rubens Penha Cysne, Alexandre L. Madureira, and Gélcio L.Q. Mendes. 2021. Multi-generational SIR modeling: Determination of parameters, epidemiological forecasting and age-dependent vaccination policies. Infectious Disease Modelling 6: 751–65. [Google Scholar] [CrossRef]
- Candido, Darlan, Ingra Claro, Jaqueline De Jesus, William Souza, Filipe Moreira, Simon Dellicour, Thomas Mellan, Louis Du Plessis, Rafael Pereira, and Flavia Sales. 2020. Evolution and epidemic spread of SARS-CoV-2 in Brazil. Science 369: 1255–60. [Google Scholar] [CrossRef]
- Cartocci, Alessandra, Gabriele Cevenini, and Paolo Barbini. 2021. A compartment modeling approach to reconstruct and analyze gender and age-grouped COVID-19 Italian data for decision-making strategies. Journal of Biomedical Informatics 118: 103793. [Google Scholar] [CrossRef] [PubMed]
- CDC, COVID-19 Response Team. 2020. Severe outcomes among patients with coronavirus disease 2019 (COVID-19)—United States, February 12–March 16, 2020. Morbidity and Mortality Weekly Report 69: 343–46. [Google Scholar] [CrossRef] [PubMed]
- Chen, Ziren, Lin Feng, Harold Lay Jr., Khaled Furati, and Abdul Khaliq. 2022. SEIR model with unreported infected population and dynamic parameters for the spread of COVID-19. Mathematics and Computers in Simulation 198: 31–46. [Google Scholar] [CrossRef] [PubMed]
- CIHI. 2022. COVID-19 Intervention Timeline in Canada. Ottawa: CIHI. [Google Scholar]
- Coelho, Flávio, Raquel Lana, Oswaldo Cruz, Daniel Villela, Leonardo Bastos, Ana Pastore y Piontti, Jessica Davis, Alessandro Vespignani, Claudia Codeço, and Marcelo Gomes. 2020. Assessing the spread of COVID-19 in Brazil: Mobility, morbidity and social vulnerability. PLoS ONE 15: e0238214. [Google Scholar] [CrossRef] [PubMed]
- CP24. 2020. A Timeline of Events in Canada’s Fight against COVID-19. Available online: https://www.cp24.com/news/a-timeline-of-events-in-canada-s-fight-against-covid-19-1.5231865?cache=noluapbixfwukoj%3FclipId%3D89563 (accessed on 5 August 2022).
- Cruz-Aponte, Mayteé, and José Caraballo-Cueto. 2021. Balancing fiscal and mortality impact of COVID-19 mitigation measurements. Letters in Biomathematics 8: 255–66. [Google Scholar] [CrossRef]
- Eichenbaum, Martin S., Sergio Rebelo, and Mathias Trabandt. 2021. The Macroeconomics of Epidemics. The Review of Financial Studies 34: 5149–87. [Google Scholar] [CrossRef]
- Eikenberry, Steffen, Marina Mancuso, Enahoro Iboi, Tin Phan, Keenan Eikenberry, Yang Kuang, Eric Kostelich, and Abba Gumel. 2020. To mask or not to mask: Modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infectious Disease Modelling 5: 293–308. [Google Scholar] [CrossRef]
- Engl, H., M. Hanke, and A. Neubauer. 1996. Regularization of Inverse Problems, Volume 375 of Mathematics and Its Applications. Dordrecht: Kluwer Academic Publishers Group. [Google Scholar]
- Farboodi, Maryam, Gregor Jarosch, and Robert Shimer. 2021. Internal and external effects of social distancing in a pandemic. Journal of Economic Theory 196: 105293. [Google Scholar] [CrossRef]
- Fernández-Villaverde, Jesús, and Charles I. Jones. 2020. Macroeconomic Outcomes and COVID-19: A Progress Report. NBER Working Papers 28004. Cambridge, MA: National Bureau of Economic Research, Inc. [Google Scholar]
- Gamerman, Dani, and Hedibert F. Lopes. 2006. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference. Boca Raton: CRC Press. [Google Scholar]
- Gatto, Marino, Enrico Bertuzzo, Lorenzo Mari, Stefano Miccoli, Luca Carraro, Renato Casagrandi, and Andrea Rinaldo. 2020. Spread and dynamics of the COVID-19 epidemic in italy: Effects of emergency containment measures. Proceedings of the National Academy of Sciences 117: 10484–91. [Google Scholar] [CrossRef] [Green Version]
- Gianfelice, Paulo Roberto de Lima, Ricardo Sovek Oyarzabal, Americo Cunha Jr., Jose Mario Vicensi Grzybowski, Fernando da Conceição Batista, and Elbert E. N. Macau. 2022. The starting dates of COVID-19 multiple waves. Chaos: An Interdisciplinary Journal of Nonlinear Science 32: 031101. [Google Scholar] [CrossRef]
- Góes, Maria Cristina Barbieri, and Ettore Gallo. 2021. Infection is the cycle: Unemployment, output and economic policies in the COVID-19 pandemic. Review of Political Economy 33: 377–93. [Google Scholar] [CrossRef]
- Goldberg, Yair, Micha Mandel, Yinon Bar-On, Omri Bodenheimer, Laurence Freedman, Eric Haas, Ron Milo, Sharon Alroy-Preis, Nachman Ash, and Amit Huppert. 2021. Waning immunity after the BNT162b2 vaccine in Israel. New England Journal of Medicine 385: e85. [Google Scholar] [CrossRef] [PubMed]
- Grasselli, Giacomo, Alberto Zangrillo, Alberto Zanella, Massimo Antonelli, Luca Cabrini, Antonio Castelli, Danilo Cereda, Antonio Coluccello, Giuseppe Foti, and Roberto Fumagalli. 2020. Baseline characteristics and outcomes of 1591 patients infected with SARS-CoV-2 admitted to ICUs of the Lombardy region, Italy. JAMA 323: 1574–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimm, Veronika, Friederike Mengel, and Martin Schmidt. 2021. Extensions of the SEIR model for the analysis of tailored social distancing and tracing approaches to cope with COVID-19. Scientific Reports 11: 1–16. [Google Scholar] [CrossRef] [PubMed]
- Guan, Wei-jie, Zheng-yi Ni, Yu Hu, Wen-hua Liang, Chun-quan Ou, Jian-xing He, Lei Liu, Hong Shan, Chun-liang Lei, and David SC Hui. 2020. Clinical characteristics of coronavirus disease 2019 in China. New England Journal of Medicine 382: 1708–20. [Google Scholar] [CrossRef]
- He, Shaobo, Yuexi Peng, and Kehui Sun. 2020. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dynamics 101: 1667–80. [Google Scholar] [CrossRef]
- IHME COVID-19 Forecasting Team. 2020. Modeling COVID-19 scenarios for the united states. Nature Medicine 27: 94–105. [Google Scholar]
- Ioannidis, John, Sally Cripps, and Martin Tanner. 2020. Forecasting for COVID-19 has failed. International Journal of Forecasting 38: 423–38. [Google Scholar] [CrossRef]
- Jin, Jian-Min, Peng Bai, Wei He, Fei Wu, Xiao-Fang Liu, De-Min Han, Shi Liu, and Jin-Kui Yang. 2020. Gender Differences in Patients with COVID-19: Focus on Severity and Mortality. Frontiers in Public Health 2020: 152. [Google Scholar] [CrossRef]
- Keeling, M. J., and R. Rohani. 2008. Modeling Infectious Diseases in Humans and Animals. Princeton: Princeton University Press. [Google Scholar]
- Kemp-Benedict, Eric. 2020. Macroeconomic Impacts of the Public Health Response to COVID-19. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3593294 (accessed on 20 May 2022).
- Kermack, William, and Anderson McKendrick. 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London A 115: 700–21. [Google Scholar] [CrossRef] [Green Version]
- Kishore, Nishant, Rebecca Kahn, Pamela P. Martinez, Pablo M. De Salazar, Ayesha S. Mahmud, and Caroline O. Buckee. 2021. Lockdowns result in changes in human mobility which may impact the epidemiologic dynamics of sars-cov-2. Scientific Reports 11: 6995. [Google Scholar] [CrossRef] [PubMed]
- Kupek, Emil. 2021. How many more? Under-reporting of the COVID-19 deaths in Brazil in 2020. Tropical Medicine & International Health 26: 1019–28. [Google Scholar]
- Lauer, Stephen, Kyra Grantz, Qifang Bi, Forrest Jones, Qulu Zheng, Hannah Meredith, Andrew Azman, Nicholas Reich, and Justin Lessler. 2020. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Annals of Internal Medicine 172: 577–83. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A., O. Nagornov, and S. Tyuflin. 2021. Inverse problem for coefficients of equations describing propagation of COVID-19 epidemic. Journal of Physics: Conference Series 2036: 012028. [Google Scholar] [CrossRef]
- Levin, Einav, Yaniv Lustig, Carmit Cohen, Ronen Fluss, Victoria Indenbaum, Sharon Amit, Ram Doolman, Keren Asraf, Ella Mendelson, and Arnona Ziv. 2021. Waning immune humoral response to BNT162b2 COVID-19 vaccine over 6 months. New England Journal of Medicine 385: e84. [Google Scholar] [CrossRef] [PubMed]
- Libotte, Gustavo Barbosa, Fran Sérgio Lobato, Gustavo Mendes Platt, and Antônio J. Silva Neto. 2020. Determination of an optimal control strategy for vaccine administration in COVID-19 pandemic treatment. Computer Methods and Programs in Biomedicine 196: 105664. [Google Scholar] [CrossRef] [PubMed]
- Lyra, Wladimir, José-Dias do Nascimento Jr., Jaber Belkhiria, Leandro de Almeida, Pedro Paulo M Chrispim, and Ion de Andrade. 2020. COVID-19 pandemics modeling with modified determinist SEIR, social distancing, and age stratification. The effect of vertical confinement and release in Brazil. PLoS ONE 15: e0237627. [Google Scholar] [CrossRef]
- Maliszewska, Maryla, Aaditya Mattoo, and Dominique Van Der Mensbrugghe. 2020. The Potential Impact of COVID-19 on GDP and Trade: A Preliminary Assessment. Policy Research Working Paper Series 9211. Washington: The World Bank, April. [Google Scholar]
- McMahan, Christopher S., Stella Self, Lior Rennert, Corey Kalbaugh, David Kriebel, Duane Graves, Cameron Colby, Jessica A. Deaver, Sudeep C. Popat, Tanju Karanfil, and et al. 2021. COVID-19 wastewater epidemiology: A model to estimate infected populations. The Lancet Planetary Health 5: e874–e881. [Google Scholar] [CrossRef]
- Helio S. Migon, Dani Gamerman, and Francisco Louzada. 2014. Statistical Inference: An Integrated Approach. Boca Raton: CRC Press. [Google Scholar]
- Monod, M., A. Blenkinsop, X. Xi, D. Hebert, S. Bershan, S. Tietze, M. Baguelin, V. Bradley, Y. Chen, and H. Coupland. 2021. Age groups that sustain resurging COVID-19 epidemics in the United States. Science 371: eabe8372. [Google Scholar] [CrossRef]
- OECD. 2020. OECD Economic Outlook. Number 107. Paris: OECD Publishing. [Google Scholar]
- Okun, Arthur M. 1963. Potential GNP: Its Measurement and Significance. New Haven: Cowles Foundation for Research in Economics at Yale University. [Google Scholar]
- Ramadijanti, Nana, and Achmad Basuki. 2020. Comparison of COVID-19 Cases in Indonesia and Other Countries for Prediction Models in Indonesia Using Optimization in SEIR Epidemic Models. Paper presented at 2020 International Conference on ICT for Smart Society (ICISS), Bandung, Indonesia, 19–20 November; pp. 1–6. [Google Scholar]
- Saberi, Meead, Homayoun Hamedmoghadam, Kaveh Madani, Helen M. Dolk, Andrei S. Morgan, Joan K. Morris, Kaveh Khoshnood, and Babak Khoshnood. 2020. Accounting for underreporting in mathematical modeling of transmission and control of COVID-19 in Iran. Frontiers in Physics 8: 289. [Google Scholar] [CrossRef]
- Scherzer, Otmar, Markus Grasmair, Harald Grossauer, Markus Haltmeier, and Frank Lenzen. 2008. Variational Methods in Imaging, Volume 167 of Applied Mathematical Sciences. New York: Springer. [Google Scholar]
- Somersalo, Erkki, and Jari Kapio. 2004. Statistical and Computational Inverse Problems, Volume 160 of Applied Mathematical Sciences. New York: Springer. [Google Scholar]
- Spellberg, Brad, Travis B. Nielsen, and Arturo Casadevall. 2021. Antibodies, immunity, and COVID-19. JAMA Internal Medicine 181: 460–62. [Google Scholar] [CrossRef] [PubMed]
- Storm, Servaas. 2021. Lessons for the age of consequences: COVID-19 and the macroeconomy. Review of Political Economy 2021: 1–40. [Google Scholar] [CrossRef]
- Unwin, H. Juliette T., Swapnil Mishra, Valerie C. Bradley, Axel Gandy, Thomas A. Mellan, Helen Coupland, Jonathan Ish-Horowicz, Michaela A. C. Vollmer, Charles Whittaker, Sarah L. Filippi, and et al. 2020. State-level tracking of COVID-19 in the united states. Nature Communications 11: 1–9. [Google Scholar] [CrossRef] [PubMed]
- Verity, Robert, Lucy C. Okell, Ilaria Dorigatti, Peter Winskill, Charles Whittaker, Natsuko Imai, Gina Cuomo-Dannenburg, Hayley Thompson, Patrick G. T. Walker, and Han Fu. 2020. Estimates of the severity of coronavirus disease 2019: A model-based analysis. The Lancet Infectious Diseases 20: 669–77. [Google Scholar] [CrossRef]
- Lauren Vogel and Laura Eggertson. 2020. COVID-19: A Timeline of Canada’s First-Wave Response. Available online: https://cmajnews.com/2020/06/12/coronavirus-1095847/ (accessed on 5 August 2022).
- WHO. 2020. Report of the Who-China Joint Mission on Coronavirus Disease 2019 (COVID-19). Geneva: WHO. [Google Scholar]
- Wu, Joseph, Kathy Leung, Mary Bushman, Nishant Kishore, Rene Niehus, Pablo de Salazar, Benjamin Cowling, Marc Lipsitch, and Gabriel Leung. 2020. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nature Medicine 26: 506–10. [Google Scholar] [CrossRef]

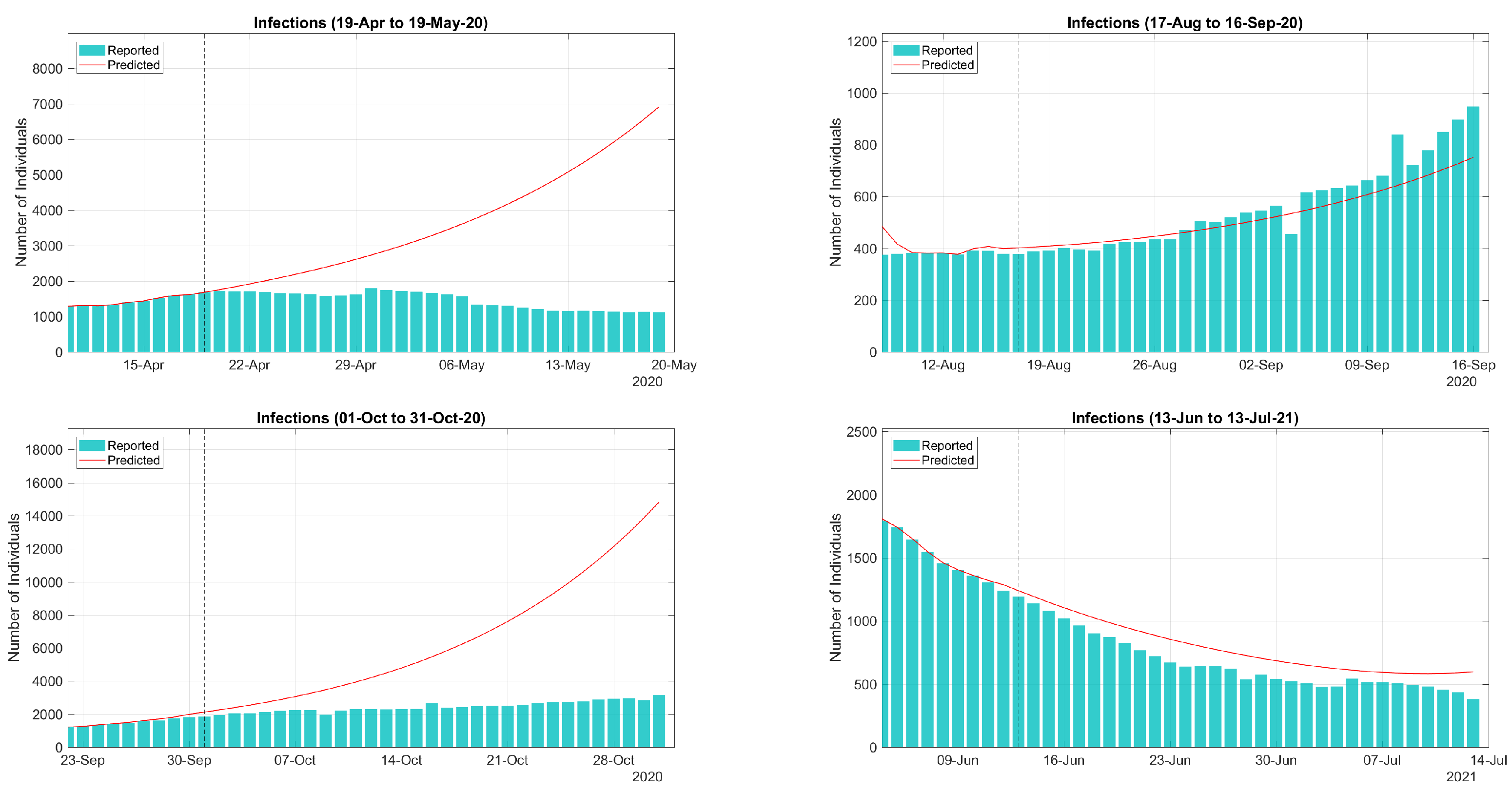


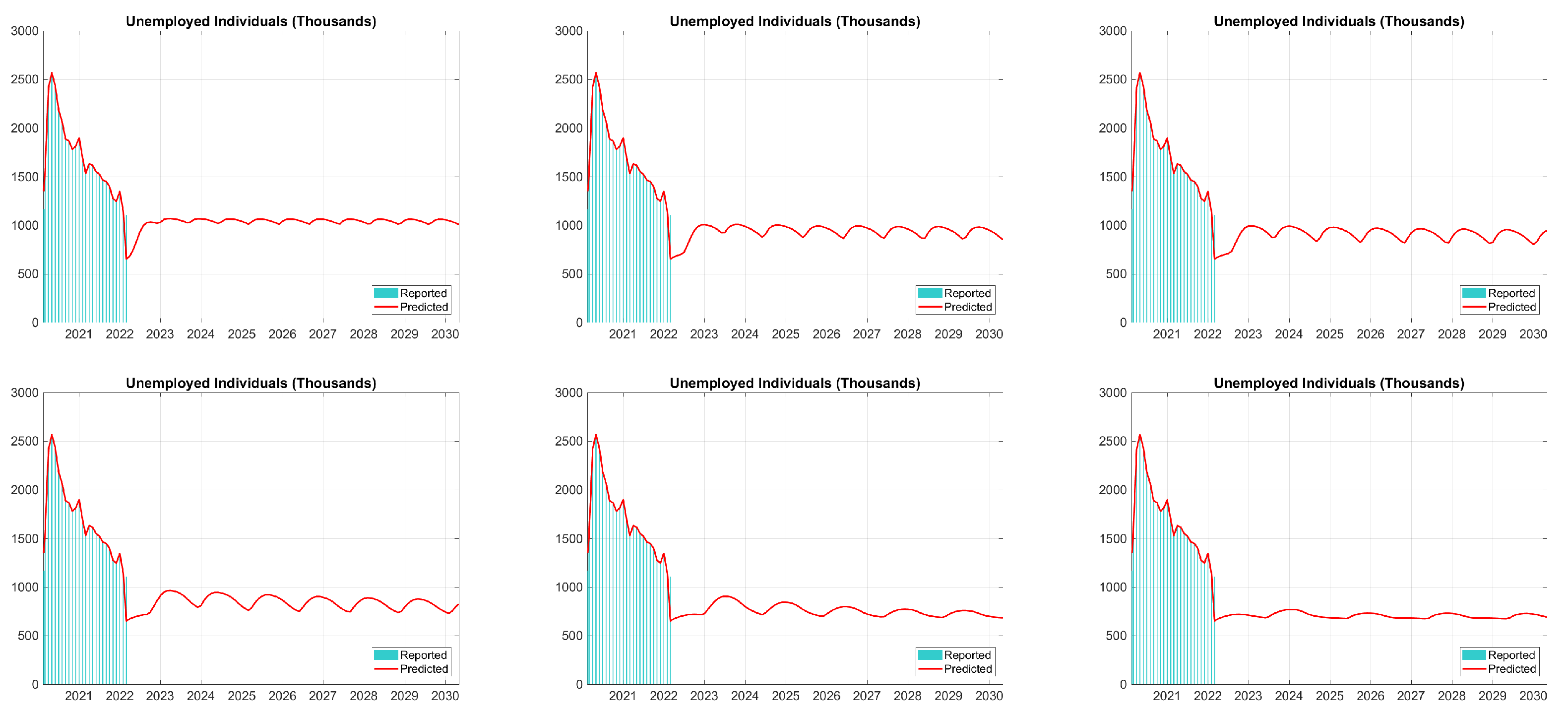

| Period | Cases | Hosp. | ICU Adm. | Deaths | Predic. Error | Calib. Error |
|---|---|---|---|---|---|---|
| 18 April to 24 April 2020 | 13,154 | 571 | 550 | 568 | 0.75% | 0.96% |
| 13,253 | 596 | 104 | 1084 | |||
| 28 May to 3 June 2020 | 6427 | 707 | 20 | 707 | 4.70% | 0.47% |
| 6744 | 33 | 30 | 868 | |||
| 17 June to 23 June 2020 | 2429 | 375 | 11 | 375 | 16.3% | 0.70% |
| 2902 | 36 | 12 | 304 | |||
| 27 July to 2 August 2020 | 3265 | 55 | 27 | 54 | 3.87% | 4.39% |
| 3397 | 63 | 26 | 57 | |||
| 5 September to 11 September 2020 | 4436 | 40 | 19 | 40 | 9.16% | 8.16% |
| 4883 | 57 | 19 | 28 | |||
| 15 October to 21 October 2020 | 18,846 | 166 | 50 | 166 | 2.89% | 1.50% |
| 19,407 | 238 | 71 | 172 | |||
| 24 November to 30 November 2020 | 38,963 | 494 | 107 | 494 | 13.4% | 6.02% |
| 45,013 | 548 | 100 | 655 | |||
| 3 January to 9 January 2021 | 84,386 | 841 | 83 | 840 | 29.8% | 13.85% |
| 65,000 | 1142 | 132 | 1140 | |||
| 12 February to 18 February 2021 | 22,904 | 700 | 43 | 700 | 2.25% | 1.90% |
| 23,431 | 131 | 43 | 525 | |||
| 24 March to 30 March 2021 | 32,367 | 214 | 88 | 213 | 12.82% | 0.82% |
| 37,127 | 417 | 141 | 230 | |||
| 3 May to 9 May 2021 | 55,040 | 350 | 175 | 349 | 9.03% | 1.43% |
| 60,503 | 477 | 73 | 372 | |||
| 12 June to 18 June 2021 | 8080 | 222 | 227 | 221 | 13.2% | 7.01% |
| 9304 | 104 | 110 | 185 | |||
| 2 July to 8 July 2021 | 3347 | 148 | 23 | 147 | 18.6% | 0.00% |
| 4110 | 108 | 12 | 123 | |||
| 20 September to 26 September 2021 | 31,751 | 197 | 135 | 196 | 7.53% | 1.24% |
| 34,335 | 482 | 117 | 287 | |||
| 30 October to 5 November 2021 | 15,023 | 243 | 38 | 243 | 16.8% | 1.11% |
| 18,065 | 240 | 34 | 227 | |||
| 19 November to 25 November 2021 | 18,165 | 177 | 40 | 176 | 13.7% | 0.32% |
| 21,037 | 300 | 48 | 170 | |||
| 9 December to 15 December 2021 | 28,110 | 137 | 59 | 137 | 19.1% | 0.57% |
| 34,767 | 324 | 69 | 162 | |||
| 29 December to 4 January 2021 | 443,096 | 122 | 70 | 122 | 56.4% | 9.83% |
| 283,268 | 1992 | 181 | 241 | |||
| 7 February to 13 February 2022 | 74,125 | 1044 | 58 | 1044 | 7.04% | 3.98% |
| 79,735 | 278 | 47 | 918 |
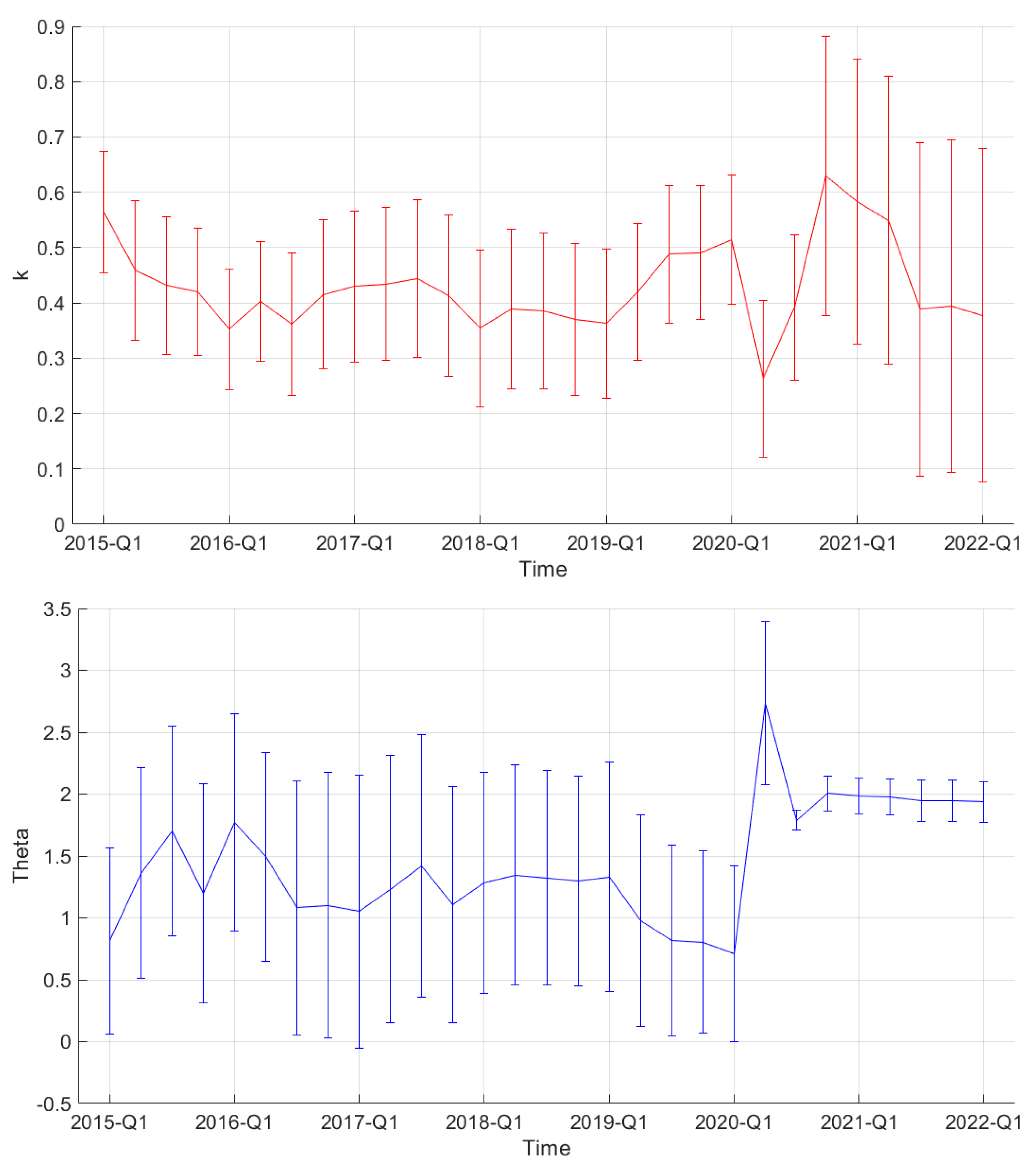
| Period | k | |
|---|---|---|
| 2019-Q4 | 0.49 (0.12) | 0.81 (0.74) |
| 2020-Q1 | 0.51 (0.12) | 0.71 (0.71) |
| 2020-Q2 | 0.26 (0.14) | 2.74 (0.66) |
| 2020-Q3 | 0.39 (0.13) | 1.79 (0.08) |
| 2020-Q4 | 0.63 (0.25) | 2.00 (0.14) |
| 2021-Q1 | 0.58 (0.26) | 1.98 (0.14) |
| 2021-Q2 | 0.55 (0.26) | 1.98 (0.14) |
| 2021-Q3 | 0.39 (0.30) | 1.95 (0.17) |
| 2021-Q4 | 0.39 (0.30) | 1.94 (0.17) |
| 2022-Q1 | 0.38 (0.30) | 1.94 (0.17) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albani, V.; Grasselli, M.; Pang, W.; Zubelli, J.P. The Interplay between COVID-19 and the Economy in Canada. J. Risk Financial Manag. 2022, 15, 476. https://doi.org/10.3390/jrfm15100476
Albani V, Grasselli M, Pang W, Zubelli JP. The Interplay between COVID-19 and the Economy in Canada. Journal of Risk and Financial Management. 2022; 15(10):476. https://doi.org/10.3390/jrfm15100476
Chicago/Turabian StyleAlbani, Vinicius, Matheus Grasselli, Weijie Pang, and Jorge P. Zubelli. 2022. "The Interplay between COVID-19 and the Economy in Canada" Journal of Risk and Financial Management 15, no. 10: 476. https://doi.org/10.3390/jrfm15100476






