Regime-Dependent Good and Bad Volatility of Bitcoin
Abstract
:1. Introduction
2. Data and Methodology
2.1. Realized Volatility, Continuous and Signed Jump Processes
2.2. Econometric Modelling
3. Estimation Results
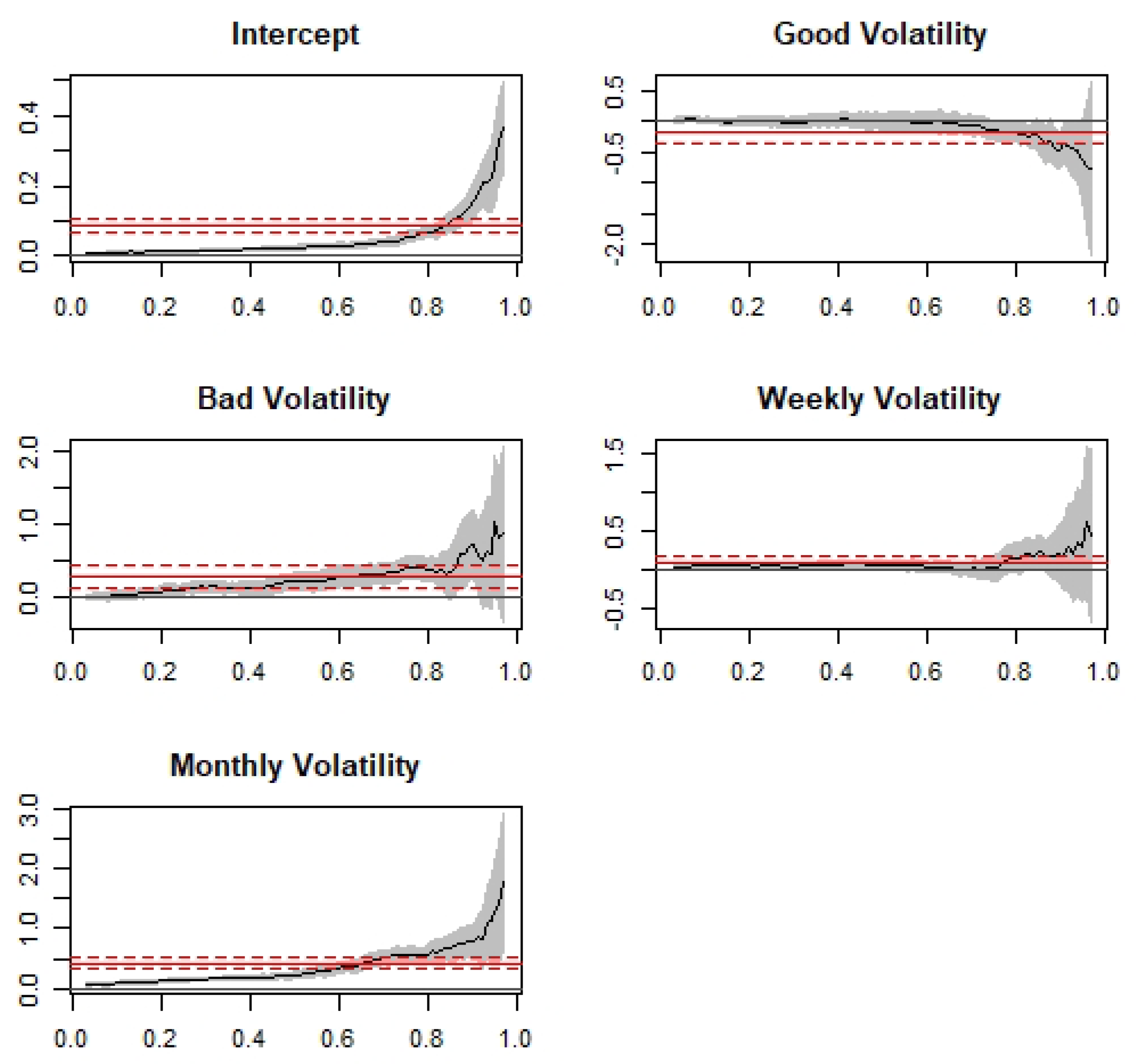
3.1. Heterogeneous Autoregressive (HAR) Model
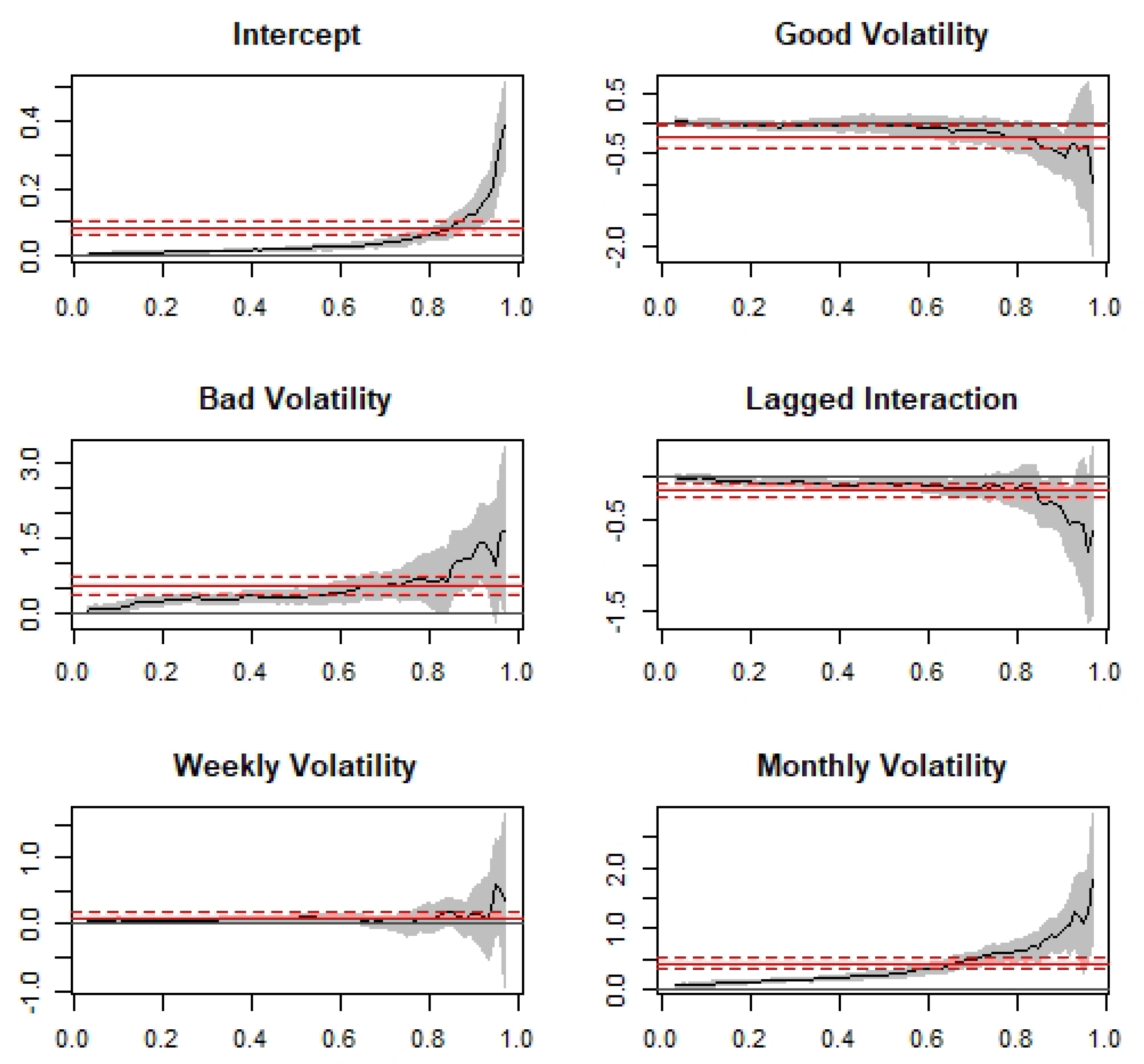
3.2. HAR–QR Model
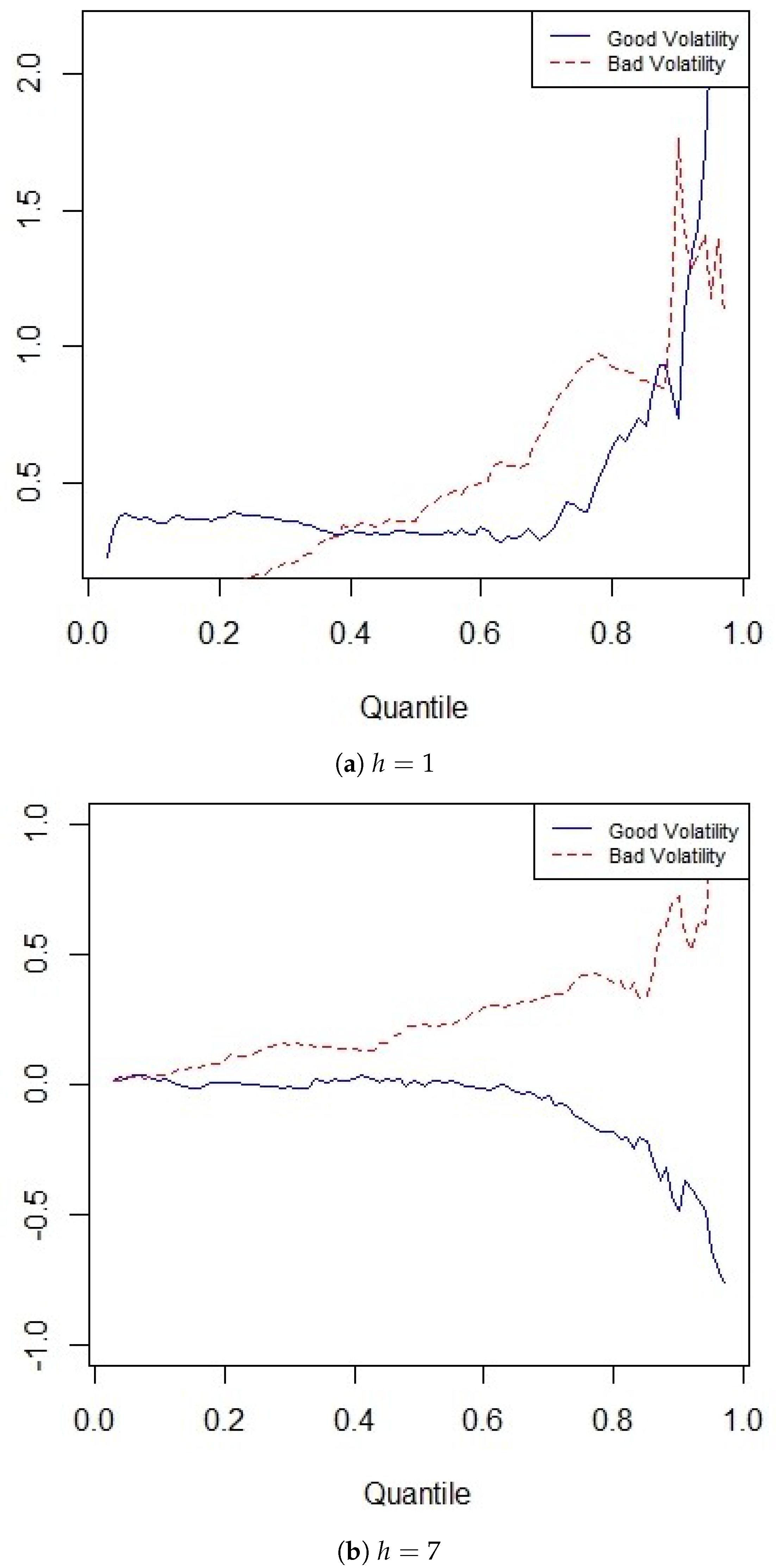
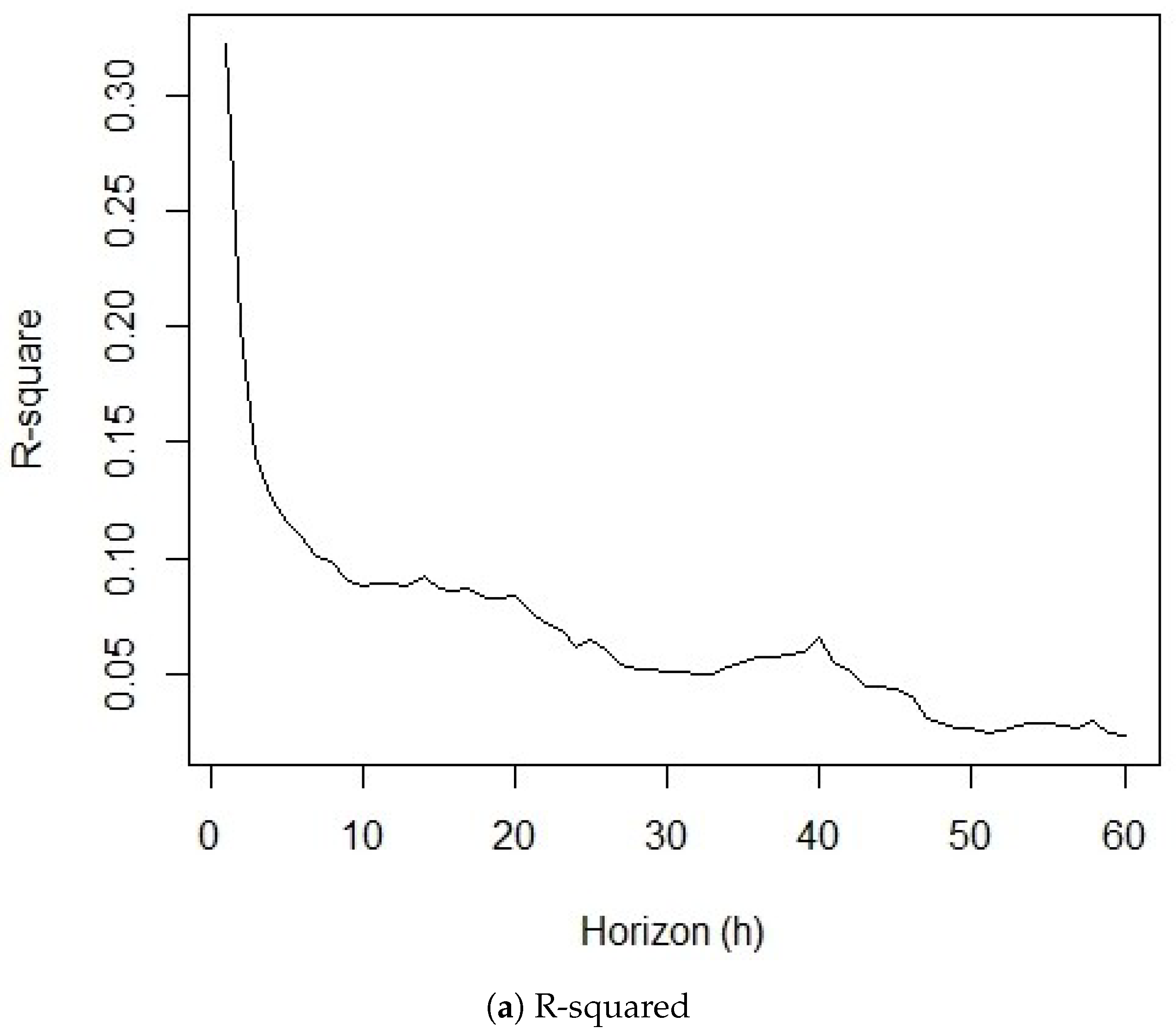
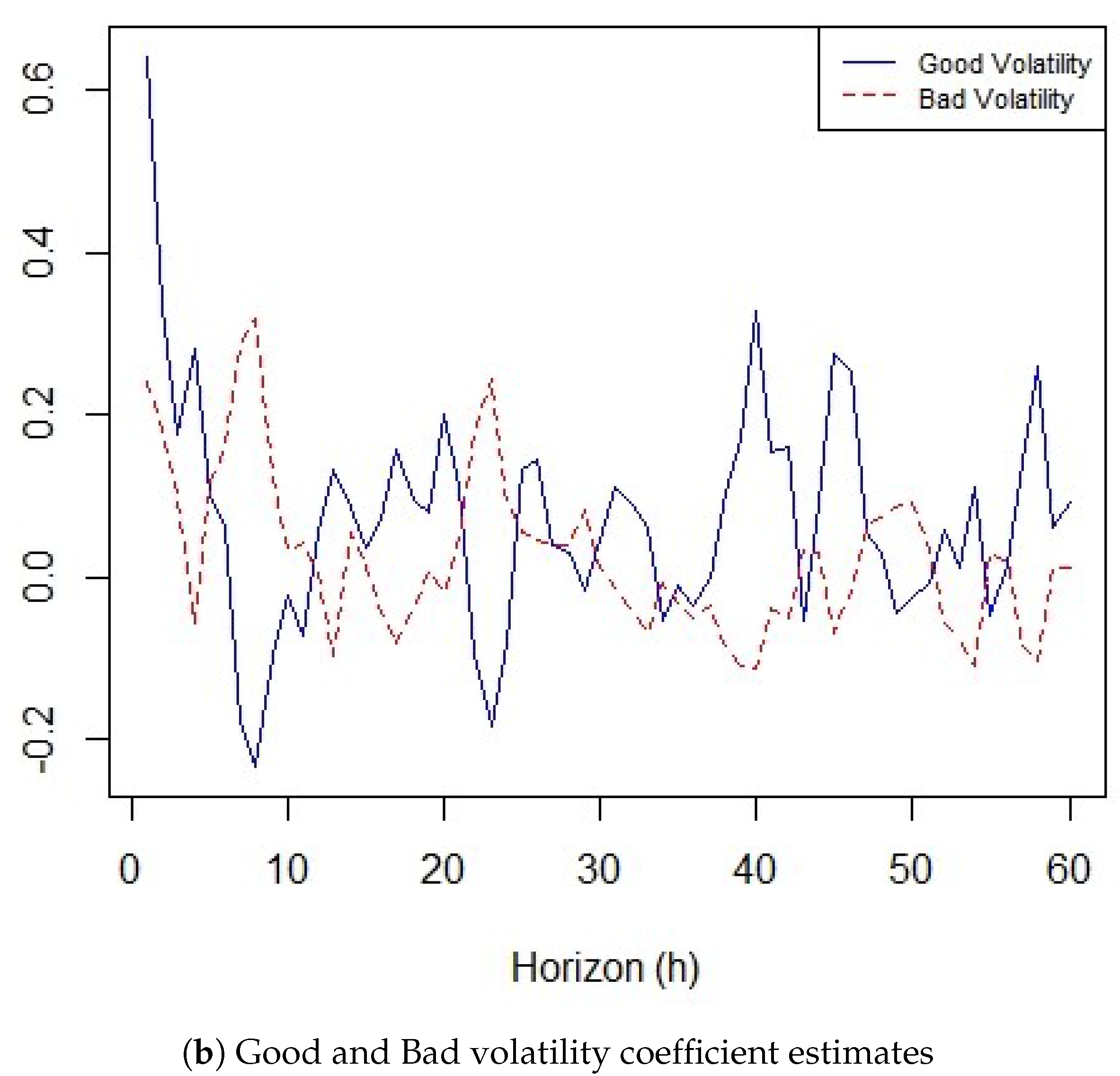
3.3. Long-Horizon Forecasts and Predictive Power
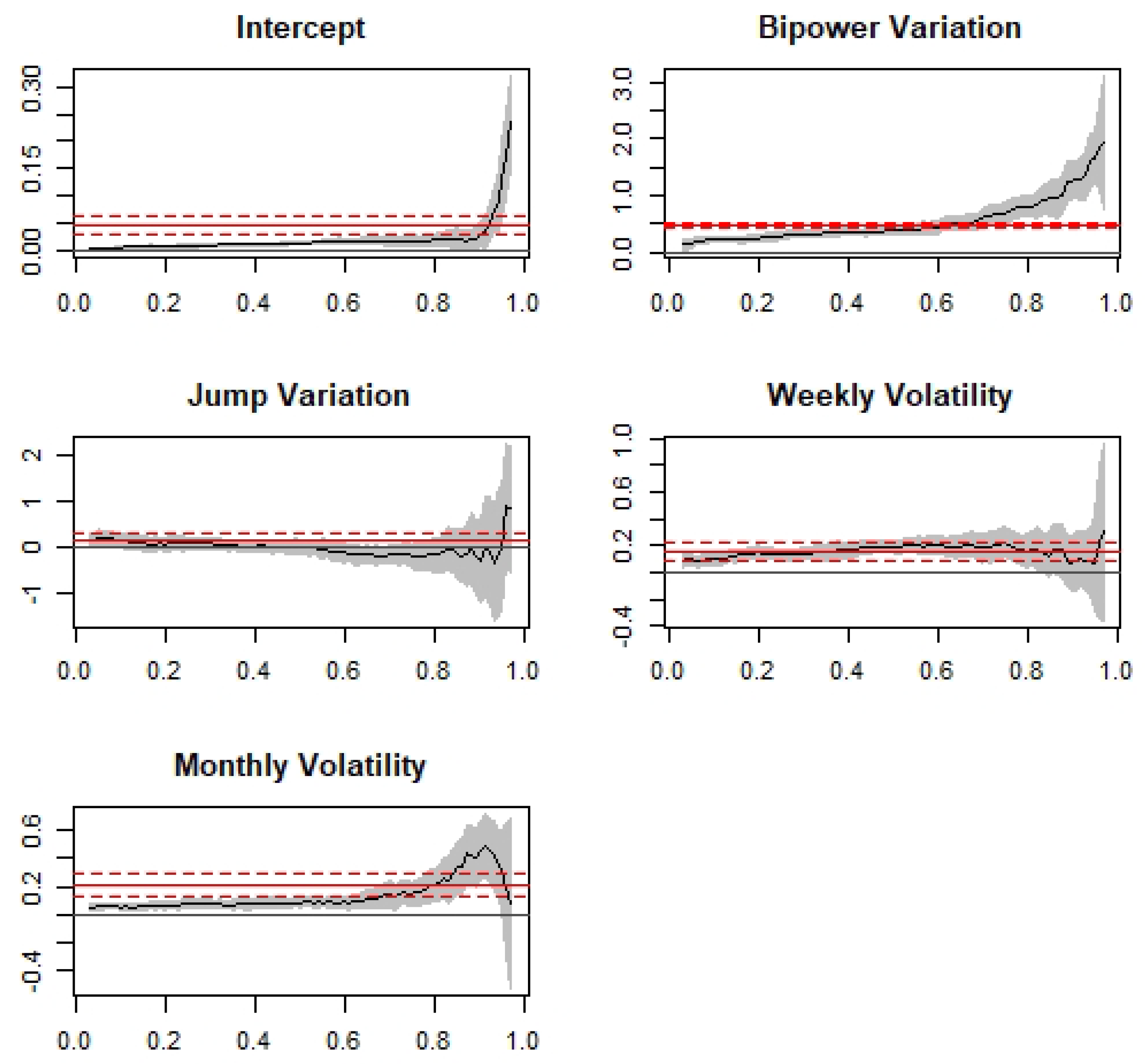
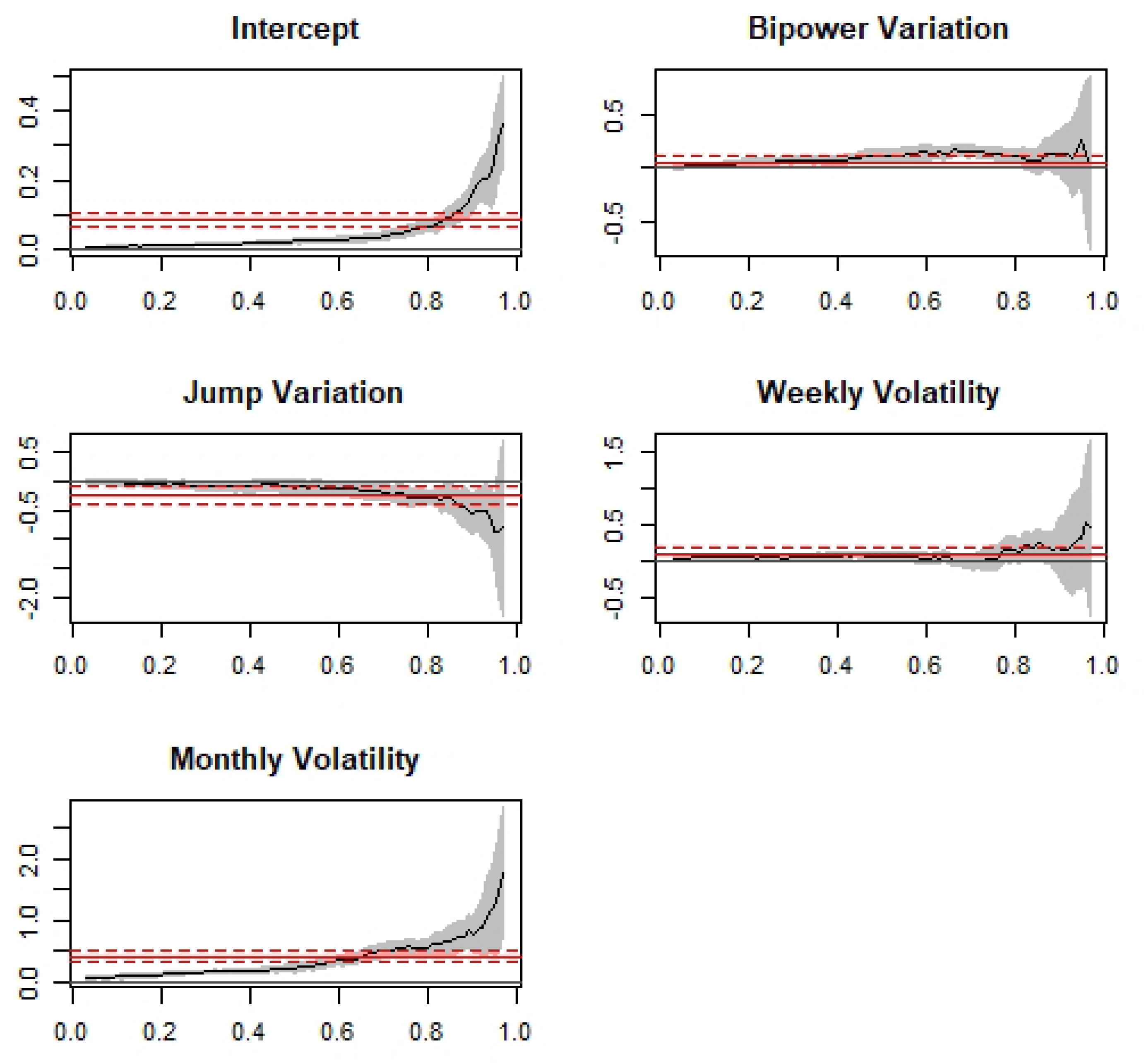
3.4. Robustness
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2001. The distribution of realized exchange rate volatility. Journal of the American Statistical Association 96: 42–55. [Google Scholar] [CrossRef]
- Avramov, Doron, Tarun Chordia, and Amit Goyal. 2006. The impact of trades on daily volatility. Review of Financial Studies 19: 1241–77. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Silja Kinnebrock, and Neil Shephard. 2008. Measuring Downside Risk-Realised Semivariance. In Volatility and Time Series Econometrics: Essays in Honor of Robert Engle. Edited by Tim Bollerslev, Jeffrey Russell and Mark Watson. Oxford: Oxford Scholarship Online. [Google Scholar]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2004. Power and bipower variation with stochastic volatility and jumps. Journal of Financial Econometrics 2: 1–37. [Google Scholar] [CrossRef] [Green Version]
- Baur, Dirk G., and Thomas Dimpfl. 2018a. Asymmetric volatility in cryptocurrencies. Economics Letters 173: 148–51. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas Dimpfl. 2018b. Think again: Volatility asymmetry and volatility persistence. Studies in Nonlinear Dynamics & Econometrics 23: 1–19. [Google Scholar]
- Baur, Dirk G., KiHoon Hong, and Adrian D. Lee. 2018. Bitcoin: Medium of exchange or speculative assets? Journal of International Financial Markets, Institutions and Money 54: 177–89. [Google Scholar] [CrossRef]
- Bekaert, Geert, and Guojun Wu. 2000. Asymmetric volatility and risk in equity markets. Review of Financial Studies 13: 1–42. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Georges Azzi, and Anne H. Dyhrberg. 2017. On the return-volatility relationship in the bitcoin market around the price crash of 2013. Economics: The Open-Access, Open-Assessment E-Journal, 11. [Google Scholar] [CrossRef] [Green Version]
- Bouri, Elie, Rangan Gupta, and David Roubaud. 2019. Herding behaviour in cryptocurrencies. Finance Research Letters 29: 216–221. [Google Scholar] [CrossRef]
- Cheikh, Nidhaleddine B., Younes. B. Zaied, and Julien Chevallier. 2020. Asymmetric volatility in cryptocurrency markets: New evidence from smooth transition GARCH models. Finance Research Letters 35: 101293. [Google Scholar] [CrossRef]
- Christie, Andrew A. 1982. The stochastic behavior of common stock variances: Value, leverage and interest rate effects. Journal of Financial Economics 10: 407–32. [Google Scholar] [CrossRef]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 174–96. [Google Scholar] [CrossRef]
- French, Kenneth R., G. William Schwert, and Robert F. Stambaugh. 1987. Expected stock returns and volatility. Journal of Financial Economics 19: 3–29. [Google Scholar] [CrossRef] [Green Version]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2017. Volatility estimation for bitcoin: A comparison of garch models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef] [Green Version]
- Katsiampa, Paraskevi, Shaen Corbet, and Brian Lucey. 2019. High frequency volatility co-movements in cryptocurrency markets. Journal of International Financial Markets, Institutions and Money 62: 35–52. [Google Scholar] [CrossRef]
- Klein, Tony, Hien P. Thu, and Thomas Walther. 2018. Bitcoin is not the new gold—A comparison of volatility, correlation, and portfolio performance. International Review of Financial Analysis 59: 105–16. [Google Scholar] [CrossRef]
- Koenker, Roger W., and Gilbert J. Bassett. 1978. Regression Quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Kyriazis, Nikolaos, Stephanos Papadamou, and Shaen Corbet. 2020. A systematic review of the bubble dynamics of cryptocurrency prices. Research in International Business and Finance 54: 101254. [Google Scholar] [CrossRef]
- Mensi, Walid, Ahmet Sensoy, Aylin Aslan, and Sang H. Kang. 2019. High-frequency asymmetric volatility connectedness between bitcoin and major precious metals markets. The North American Journal of Economics and Finance 50: 101031. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 5 December 2020).
- Patton, Andrew J., and Kevin Sheppard. 2015. Good Volatility, Bad Volatility: Signed Jumps and The Persistence of Volatility. The Review of Economics and Statistics 97: 683–97. [Google Scholar] [CrossRef] [Green Version]
- Shen, Dehua, Andrew Urquhart, and Pengfei Wang. 2020. Forecasting the volatility of bitcoin: The importance of jumps and structural breaks. European Financial Management 26: 1294–1323. [Google Scholar] [CrossRef]
- Smales, Lee. 2019. Bitcoin as a safe haven: Is it even worth considering? Finance Research Letters. [Google Scholar] [CrossRef]
- Todorova, Neda. 2017. The asymmetric volatility in the gold market revisited. Economics Letters 150: 138–41. [Google Scholar] [CrossRef]
- Yermack, David. 2013. Is Bitcoin a Real Currency? An Economic Appraisal. NBER Working Paper 19747. Available online: http://www.nber.org/papers/w19747 (accessed on 5 December 2020).
| 1. | Patton and Sheppard (2015) do not use QR but a weighted least squares (WLS). |
| 2. | The full estimation results are available upon request. |
| 3. | The full results for sub-sample is available upon request. |



| RV | RS | RS | BV | J | |
|---|---|---|---|---|---|
| Minimum | 0.003 | 0.001 | 0.002 | 0.003 | −4.205 |
| Q | 0.022 | 0.010 | 0.011 | 0.020 | −0.109 |
| Median | 0.097 | 0.045 | 0.048 | 0.085 | −0.001 |
| Mean | 0.225 | 0.106 | 0.119 | 0.204 | −0.012 |
| Q | 0.754 | 0.364 | 0.393 | 0.703 | 0.060 |
| Maximum | 11.360 | 3.578 | 7.782 | 8.452 | 1.104 |
| Correlation Matrix | |||||
| RV | 1.000 | ||||
| RS | 0.960 | 1.000 | |||
| RS | 0.979 | 0.883 | 1.000 | ||
| BV | 0.987 | 0.962 | 0.955 | 1.000 | |
| J | −0.570 | −0.318 | −0.725 | −0.518 | 1.000 |
| Dependent Variable: | |||||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
| (1) | (2) | (3) | (4) | (5) | |
| 0.040 *** | 0.041 *** | 0.044 *** | 0.044 *** | 0.039 *** | |
| (0.011) | (0.011) | (0.011) | (0.011) | (0.011) | |
| 0.417 *** | |||||
| (0.082) | |||||
| 0.173 *** | 0.162 *** | 0.164 ** | 0.157 ** | 0.158 *** | |
| (0.063) | (0.054) | (0.065) | (0.060) | (0.053) | |
| 0.211 *** | 0.205 ** | 0.209 *** | 0.204 ** | 0.210 *** | |
| (0.081) | (0.080) | (0.079) | (0.077) | (0.081) | |
| 0.239 | 0.345 | ||||
| (0.291) | (0.310) | ||||
| 0.642 ** | 0.625 ** | ||||
| (0.286) | (0.278) | ||||
| 0.450 *** | 0.469 *** | ||||
| (0.092) | (0.084) | ||||
| 0.165 | |||||
| (0.261) | |||||
| −0.073 | |||||
| (0.108) | |||||
| R | 0.321 | 0.323 | 0.327 | 0.328 | 0.324 |
| Dependent Variable: | |||||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
| (1) | (2) | (3) | (4) | (5) | |
| 0.086 *** | 0.085 *** | 0.086 *** | 0.085 *** | 0.081 *** | |
| (0.022) | (0.022) | (0.022) | (0.022) | (0.022) | |
| 0.081 ** | |||||
| (0.038) | |||||
| 0.084 | 0.097 | 0.085 | 0.096 | 0.088 | |
| (0.095) | (0.098) | (0.095) | (0.096) | (0.094) | |
| 0.096 *** | 0.097 *** | 0.096 *** | 0.097 *** | 0.428 *** | |
| (0.032) | (0.033) | (0.032) | (0.032) | (0.141) | |
| 0.287 *** | 0.512 *** | ||||
| (0.093) | (0.124) | ||||
| −0.179 | −0.215 * | ||||
| (0.112) | (0.111) | ||||
| 0.085 ** | 0.058 | ||||
| (0.041) | (0.042) | ||||
| −0.237 *** | |||||
| (0.092) | |||||
| −0.156 *** | |||||
| (0.056) | |||||
| R | 0.098 | 0.100 | 0.097 | 0.100 | 0.106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jha, K.K.; Baur, D.G. Regime-Dependent Good and Bad Volatility of Bitcoin. J. Risk Financial Manag. 2020, 13, 312. https://doi.org/10.3390/jrfm13120312
Jha KK, Baur DG. Regime-Dependent Good and Bad Volatility of Bitcoin. Journal of Risk and Financial Management. 2020; 13(12):312. https://doi.org/10.3390/jrfm13120312
Chicago/Turabian StyleJha, Kislay Kumar, and Dirk G. Baur. 2020. "Regime-Dependent Good and Bad Volatility of Bitcoin" Journal of Risk and Financial Management 13, no. 12: 312. https://doi.org/10.3390/jrfm13120312





