Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence
Abstract
:1. Introduction
2. The Model
2.1. Some Necessary Notations
2.2. The Insurance Risk Process
2.3. Description of Financial Market
2.4. Problem Formulation
3. The Closed-Form Solution to HJB Equation
4. Efficient Strategy and Efficient Frontier
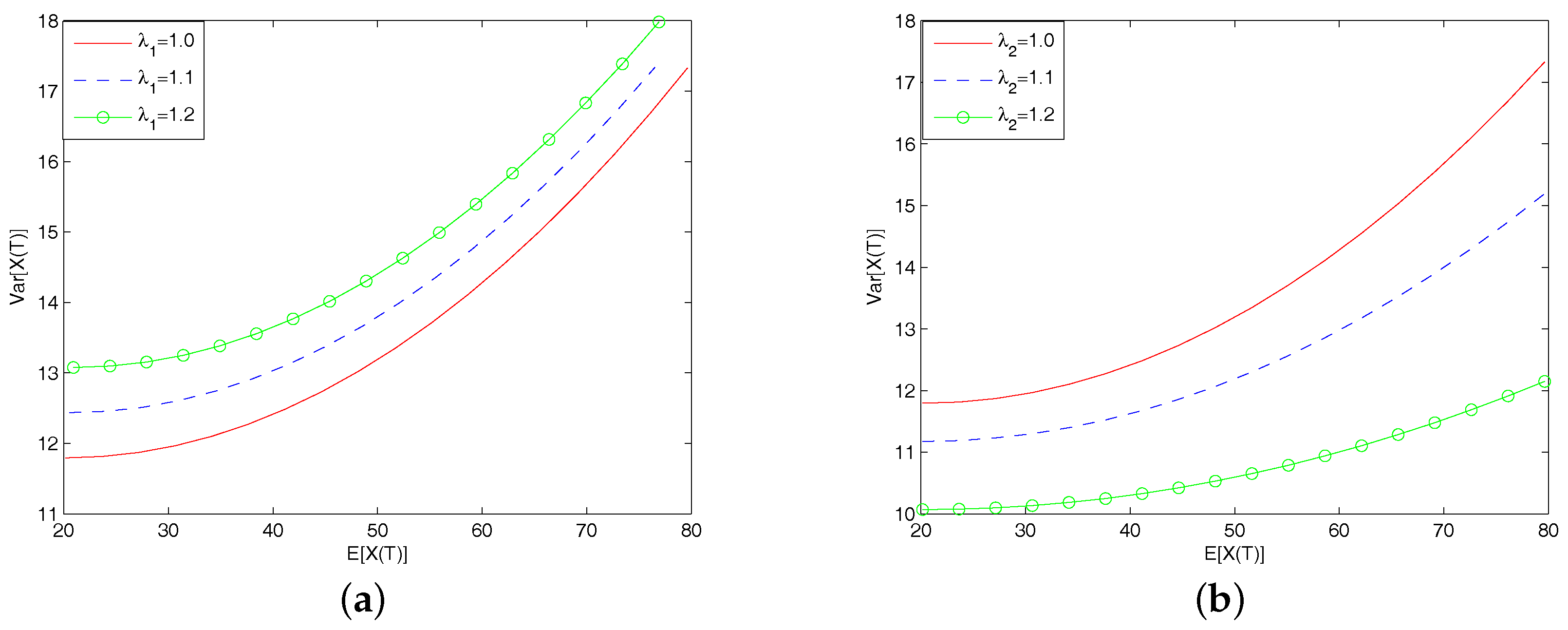
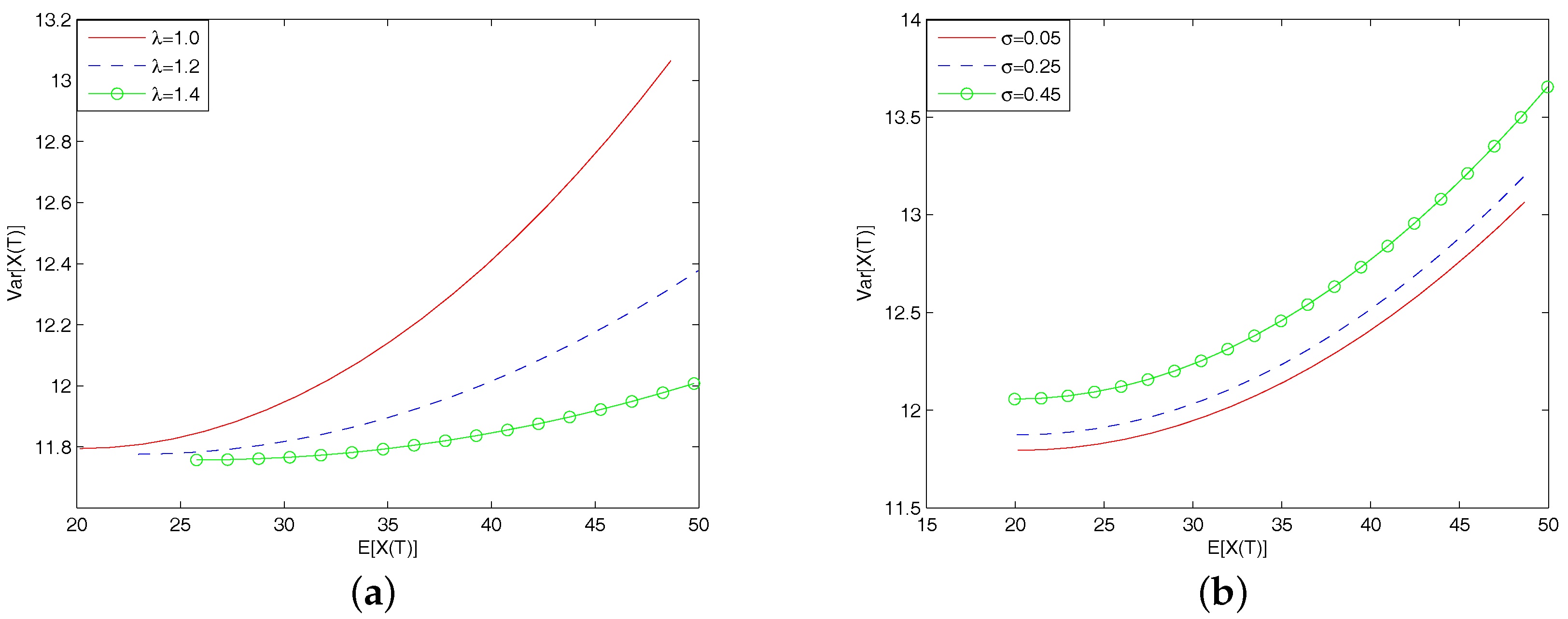
5. Sensitive Analysis
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Asmussen, Søren, Bjarne Højgaard, and Michael Taksar. 2000. Optimal risk control and dividend distribution policies. Example of excess-of loss reinsurance for an insurance corporation. Finance and Stochastics 4: 299–324. [Google Scholar] [CrossRef]
- Azcue, Pablo, and Nora Muler. 2005. Optimal reinsurance and dividend distribution policies in the Cramér-lundberg model. Mathematical Finance 15: 261–308. [Google Scholar] [CrossRef]
- Bäuerle, Nicole. 2005. Benchmark and mean-variance problems for insurers. Mathematical Methods of Operations Research 62: 159–65. [Google Scholar] [CrossRef]
- Bai, Lihua, and Huayue Zhang. 2008. Dynamic mean-variance problem with constranit risk control for the insurers. Mathematical Methods of Operations Research 68: 181–205. [Google Scholar] [CrossRef]
- Bai, Lihua, and Junyi Guo. 2010. Optimal dividend payments in the classical risk model when payments are subject to both transaction costs and taxes. Scandinavian Actuarial Journal 1: 36–55. [Google Scholar] [CrossRef]
- Bai, Lihua, Jun Cai, and Ming Zhou. 2013. Optimal reinsurance policies for an insurer with a bivariate reserve risk process in a dynamic setting. Insurance: Mathematics and Economics 53: 664–70. [Google Scholar] [CrossRef]
- Bi, Junna, and Junyi Guo. 2013. Optimal mean-variance problem with constrained controls in a jump-diffusion financial market for an insurer. Journal of Optimization Theory and Applications 157: 252–75. [Google Scholar] [CrossRef]
- Bi, Junna, Zhibin Liang, and Fangjun Xu. 2016. Optimal mean-variance investment and reinsurance problems for the risk model with common shock dependence. Insurance: Mathematics and Economics 70: 245–58. [Google Scholar] [CrossRef]
- Bielecki, T. R., H. Jin, S. R. Pliska, and X. Y. Zhou. 2005. Dynamic mean-variance with portfolio selection with bankruptcy prohibition. Mathematical Finance 15: 213–44. [Google Scholar] [CrossRef]
- Bouchard, Bruno, and Huyên Pham. 2004. Wealth-path dependent utility maximization in incomplete financial markets. Finance and Stochastics 8: 579–603. [Google Scholar] [CrossRef]
- Browne, Sid. 1995. Optimal investment policies for a firm with a random risk process: Exponentional utility and minimizing the probability of ruin. Mathematics of Operations Research 20: 937–58. [Google Scholar] [CrossRef]
- Cojocaru, Ionica. 2017. Ruin probabilities in multivariate risk models with periodic common shock. Scandinavian Actuarial Journal 2: 159–74. [Google Scholar] [CrossRef]
- Cossette, Hélene, and Etienne Marceau. 2000. The discrete-time risk model with correlated classes of business. Insurance: Mathematics and Economics 26: 133–49. [Google Scholar] [CrossRef]
- Delong, Łukasz. 2005. Optimal investment strategy for a non-life insurance company: Quadratic loss. Applications of Mathematics 32: 263–77. [Google Scholar] [CrossRef]
- Delong, Łukasz, and Russell Gerrard. 2007. Mean-variance portfolio selection for a non-life insurance company. Mathematical Methods of Operations Research 66: 339–67. [Google Scholar] [CrossRef]
- Fleming, Wendell H., and Halil Mete Soner. 2006. Controled Markov Processes and Viscosity Solutions. New York: Springer. [Google Scholar]
- Liang, Zhibin, and Kam Chuen Yuen. 2016. Optimal dynamic reinsurance with dependent risks: Variance premium principle. Scandinavian Actuarial Journal 1: 18–36. [Google Scholar] [CrossRef] [Green Version]
- Liang, Zhibin, Kam Chuen Yuen, and Caibin Zhang. 2017. Optimal reinsurance and investment in a jump-diffusion financial market with common shock dependence. Journal of Applied Mathematics and Computing 56: 637–64. [Google Scholar] [CrossRef]
- Liang, Zhibin, Junna Bi, Kam Chuen Yuen, and Caibin Zhang. 2016. Optimal mean-variance reinsurance and investment in a jump-diffusion financial market with common shock dependence. Mathematical Methods of Operations Research 84: 155–81. [Google Scholar] [CrossRef]
- Lim, Andrew EB. 2004. Quadratic hedging and mean-variance portfolio selection with random parameters in an incomplete market. Mathematics of Operations Research 29: 132–61. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio selection. Journal of Finance 7: 77–91. [Google Scholar]
- Merton, Robert C. 1972. An analytical derivation of the efficient portfolio frontier. Journal of Financial and Quatative Analysis 7: 1851–72. [Google Scholar] [CrossRef]
- Ming, Zhiqin, Zhibin Liang, and Caibin Zhang. 2016. Optimal mean-variance reinsurance with common shock dependence. Anziam Journal 58: 162–81. [Google Scholar] [CrossRef]
- Protter, Philip E. 2004. Stochastic Integration and Differential Equations, 2nd ed. Berlin: Springer. [Google Scholar]
- Schmidli, Hanspeter. 2002. On minimizing the ruin probability by investment and reinsurance. Annals of Applied Probability 12: 890–907. [Google Scholar] [CrossRef]
- Yang, Hailiang, and Lihong Zhang. 2005. Optimal investment for an insurer with jump-diffusion risk process. Insurance: Mathematics and Economics 37: 615–34. [Google Scholar] [CrossRef]
- Yong, Jiongmin, and Xun Yu Zhou. 1999. Stochastic Controls: Hamilton Systems and HJB Equations. New York: Springer. [Google Scholar]
- Yuen, Kam Chuen, Zhibin Liang, and Ming Zhou. 2015. Optimal proportional reinsurance with common shock dependence. Insurance: Mathematics and Economics 64: 1–13. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Caibin, and Zhibin Liang. 2017. Portfolio optimization for jump-diffusion risky asset with common shock dependence and state dependent risk aversion. Optimal Control Applications and Methods 38: 229–46. [Google Scholar] [CrossRef]
- Zhou, Xun Yu, and Duan Li. 2000. Continuous-time mean-variance portfolio selection: A stochastic LQ framework. Applied Mathematics and Optimization 42: 19–33. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Sun, Z. Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence. J. Risk Financial Manag. 2018, 11, 25. https://doi.org/10.3390/jrfm11020025
Tian Y, Sun Z. Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence. Journal of Risk and Financial Management. 2018; 11(2):25. https://doi.org/10.3390/jrfm11020025
Chicago/Turabian StyleTian, Yingxu, and Zhongyang Sun. 2018. "Mean-Variance Portfolio Selection in a Jump-Diffusion Financial Market with Common Shock Dependence" Journal of Risk and Financial Management 11, no. 2: 25. https://doi.org/10.3390/jrfm11020025




