Effect of the Duration Time of a Nuclear Accident on Radiological Health Consequences
Abstract
:1. Introduction
2. Material and Methods
2.1. The Gaussian Model
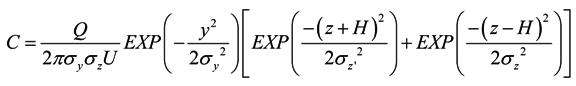
2.2. Estimation of Radiation Dose
| Isotope | Inhalation | Air Submersion | Surface Submersion |
|---|---|---|---|
| (mSv Bq−1) | (mSv/Bqsm−3) | (mSv/Bqsm−2) | |
| 137Cs | 3.90 × 10−5 | 9.28 × 10−14 | 2.99 × 10−15 |
| 131I | 7.40 × 10−6 | 1.69 × 10−11 | 3.64 × 10−13 |
3. Results and Discussion
3.1. Atmospheric Dispersion Characteristics of Radioactive Substances
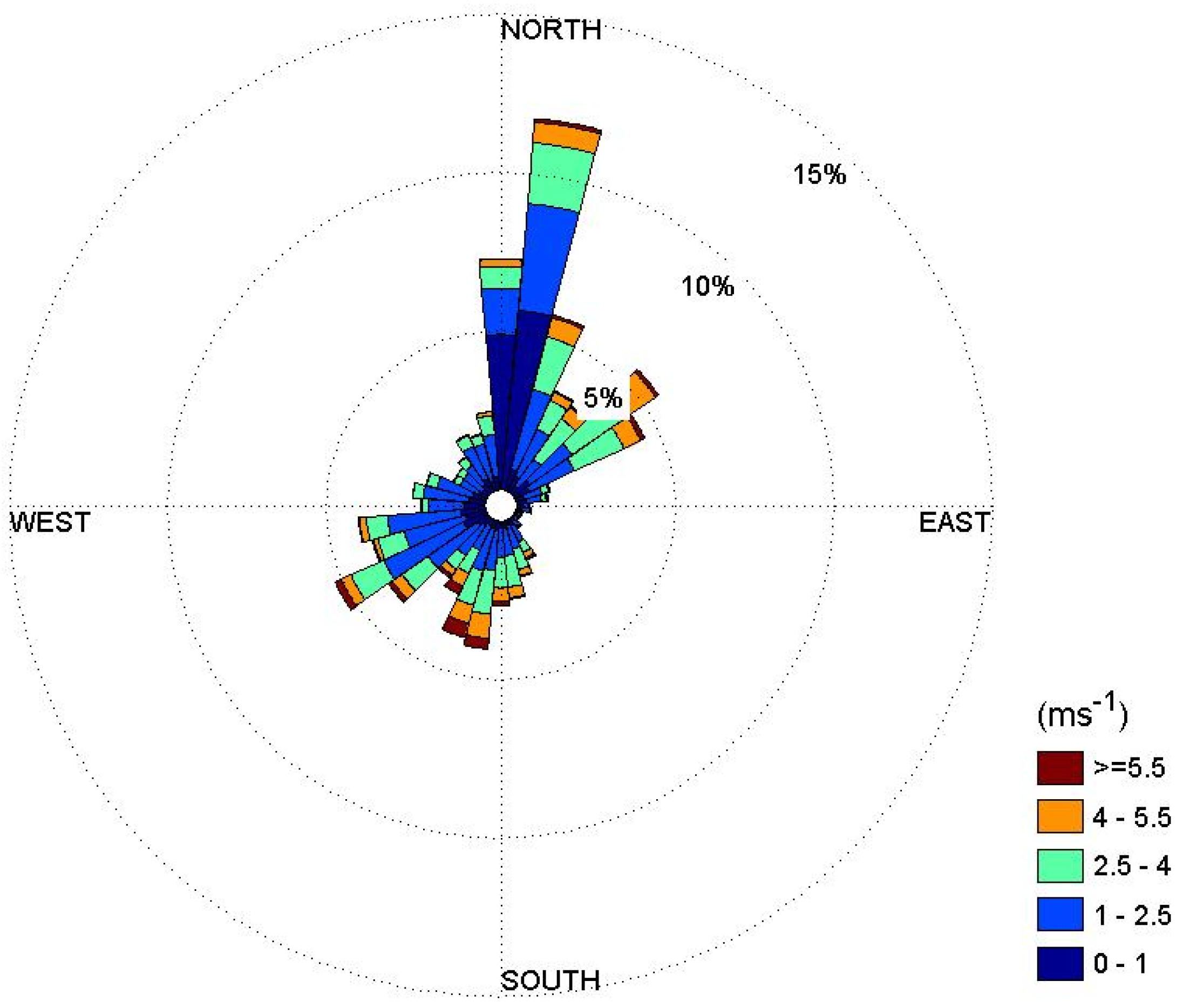
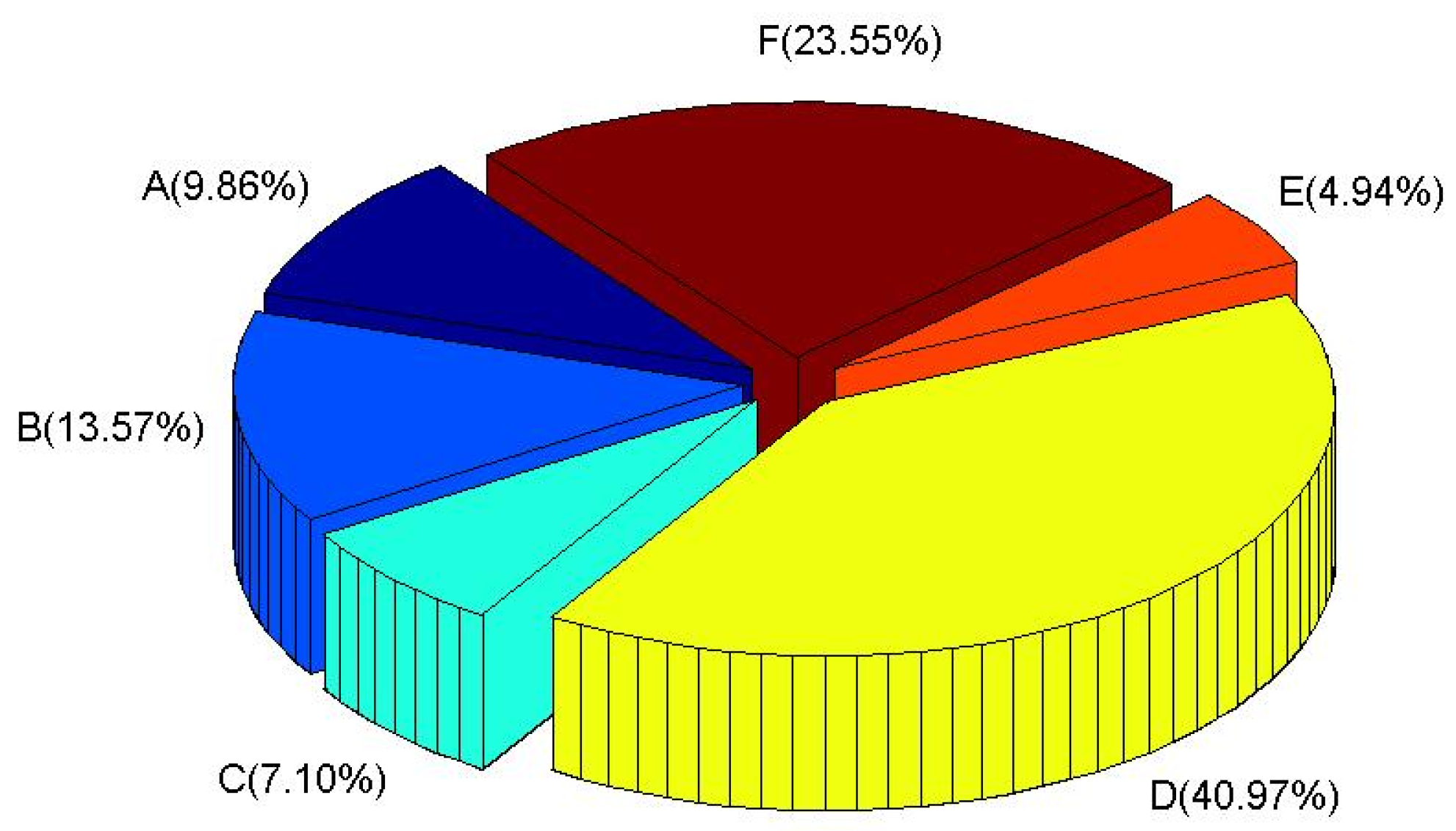

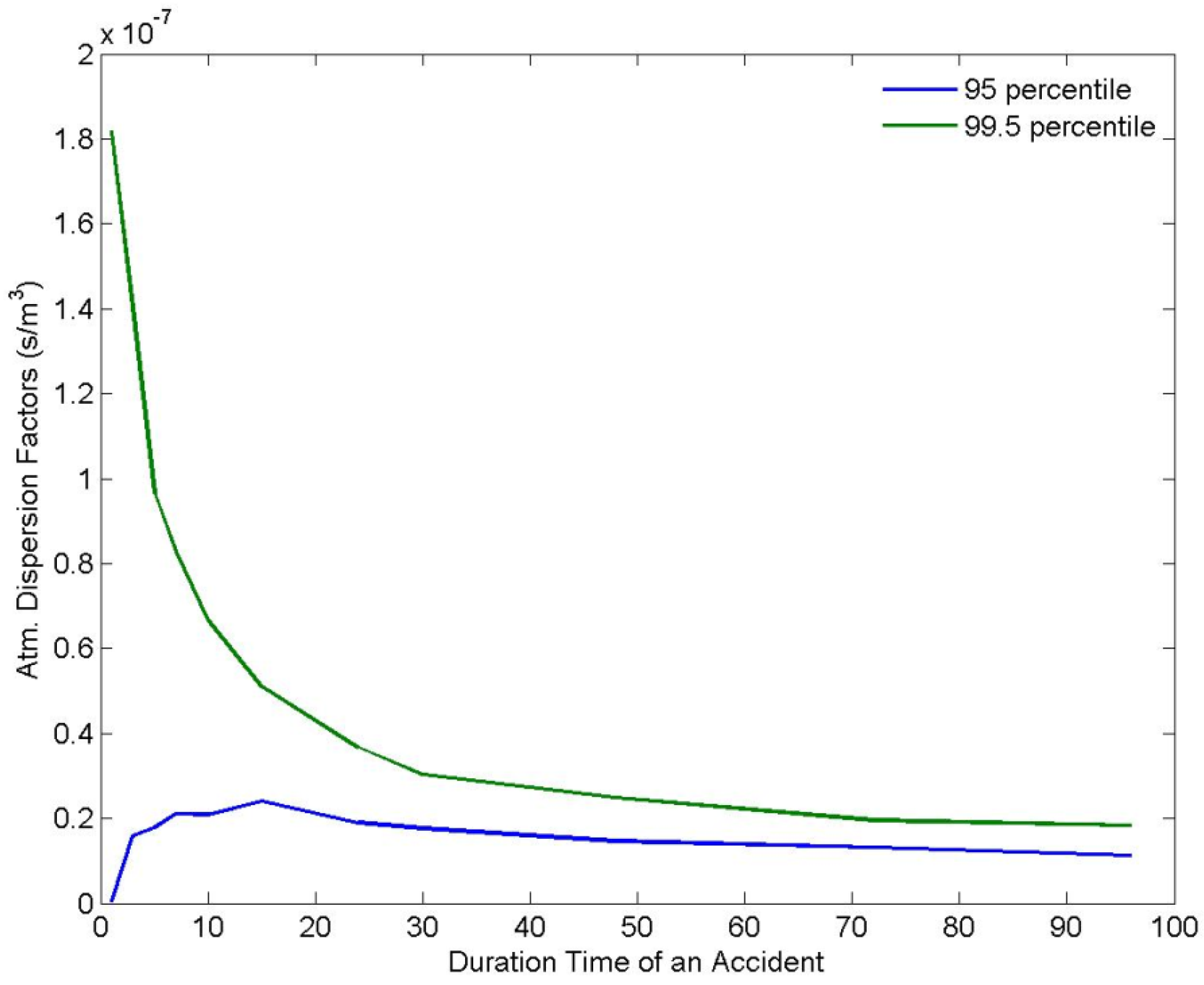
3.2. Radiation Dose and Acute Health Effects on the Residents.
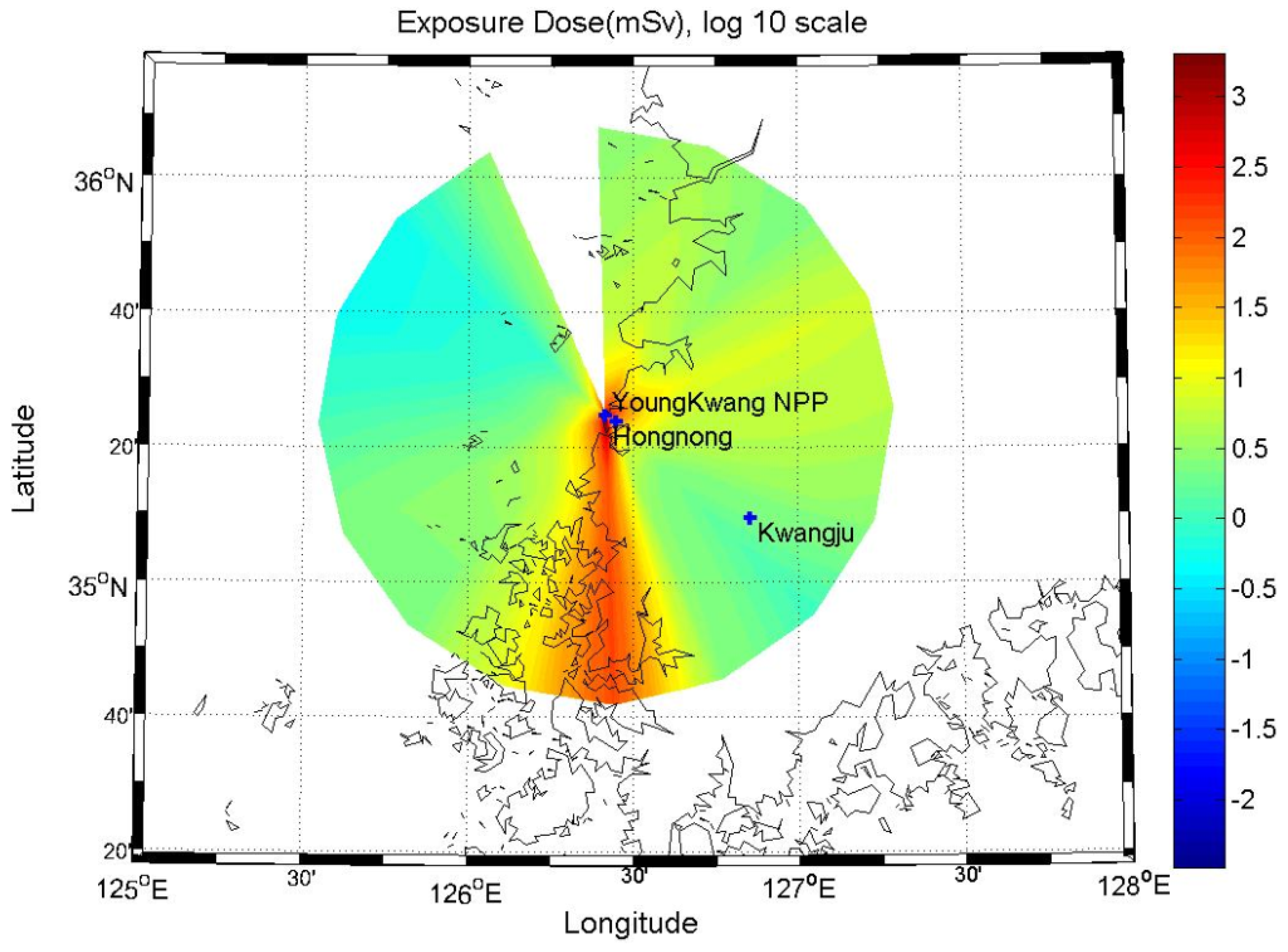
| Inhalation | Air submersion | Ground surface | Total | |
|---|---|---|---|---|
| 137Cs | 5.70 × 10 −1 | 4.06 × 10−6 | 1.31 × 10−1 | 5.70 × 10−1 |
| 131I | 1.29 × 10+0 | 8.81 × 10−3 | 1.90 × 10−7 | 1.30 × 10+0 |
| Total | 1.86 × 10+0 | 8.81 × 10−3 | 1.90 × 10−7 | 1.87 × 10+0 |

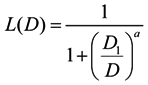
| Time | 95 Percentile Dose (mSv) | 99.5 Percentile dose (mSv) | Light Acute Disorder (/Person) | Serious Acute Disorder (/Person) | Acute Death (/Person) |
|---|---|---|---|---|---|
| 1 h | 2.24 × 10−1 | 9.77 × 10+1 | 1.74 × 10−7 | 1.23 × 10−13 | 1.84 × 10−9 |
| 3 h | 8.48 × 10+0 | 7.55 × 10+1 | 2.42 × 10−8 | 9.71 × 10−15 | 4.54 × 10−10 |
| 5 h | 8.48 × 10+0 | 5.20 × 10+1 | 1.40 × 10−9 | 2.47 × 10−16 | 6.02 × 10−11 |
| 7 h | 1.13 × 10+1 | 4.45 × 10+1 | 4.27 × 10−1 | 5.33 × 10−17 | 2.59 × 10−11 |
| 10 h | 1.12 × 10+1 | 3.58 × 10+1 | 8.11 × 10−11 | 6.26 × 10−18 | 7.96 × 10−12 |
| 15 h | 1.30 × 10+1 | 2.74 × 10+1 | 1.05 × 10−11 | 4.50 × 10−19 | 1.87 × 10−12 |
| 24 h | 1.02 × 10+1 | 1.97 × 10+1 | 8.47 × 10−13 | 1.75 × 10−2 | 3.13 × 10−13 |
| 30 h | 9.49 × 10+0 | 1.63 × 10+1 | 1.99 × 10−13 | 2.70 × 10−21 | 1.12 × 10−13 |
| 48 h | 7.85 × 10+0 | 1.34 × 10+1 | 4.46 × 10−14 | 3.93 × 10−22 | 3.87 × 10−14 |
| 72 h | 7.05 × 10+0 | 1.05 × 10+1 | 6.93 × 10−15 | 3.56 × 10−23 | 1.03 × 10−14 |
| 96 h | 6.02 × 10+0 | 9.84 × 10+0 | 4.22 × 10−15 | 1.88 × 10−23 | 7.27 × 10−15 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Murakami, M.; Oki, T. Estimation of thyroid doses and health risks resulting from the intake of radioactive iodine in foods and drinking water by the citizens of Tokyo after the Fukushima nuclear accident. Chemosphere 2012, 87, 1355–1360. [Google Scholar] [CrossRef]
- Priest, N.D. Radiation doses received by adult Japanese populations living outside Fukushima Prefecture during March 2011, following the Fukushima 1 nuclear power plant failures. J. Environ. Radioactiv. 2012, 114, 162–170. [Google Scholar] [CrossRef]
- Lozano, R.L.; Hernández-Ceballos, M.A.; Adame, J.A.; Casas-Ruíz, M.; Sorribas, M.; San Miguel, E.G.; Bolívar, J.P. Radioactive impact of Fukushima accident on the Iberian Peninsula: Evolution and plume previous pathway. Environ. Int. 2011, 37, 1259–1264. [Google Scholar] [CrossRef]
- Schöppner, M.; Plastino, W.; Povinec, P.P.; Wotaw, G.; Bella, F.; Budano, A.; Vincenzi, M.; Ruggieri, F. Estimation of the time-dependent radioactive source-term from the Fukushima nuclear power plant accident using atmospheric transport modeling. J. Environ. Radioactiv. 2012, 114, 10–14. [Google Scholar]
- Steinhauser, G.; Merz, S.; Hainz, D.; Sterba, J.H. Artificial radioactivity in environmental media (air, rainwater, soil, vegetation) in Austria after the Fukushima nuclear accident. Environ. Sci. Pollut. Res. 2013, 20, 2527–2534. [Google Scholar] [CrossRef]
- MELCOR Accident Consequence Code System (MACCS) Model Description. Available online: http://pbadupws.nrc.gov/docs/ML0635/ML063560409.pdf (accessed on 10 January 2014).
- Ballyk, C.R.; Khaloo, R.; Moffeltt, R. ADDAM version 1.0 theory manual; CW-111090–225–002, revision 03; Natus Medical Inc.: San Carlos, CA, USA, 2003. [Google Scholar]
- Jeong, H.J.; Han, M.H.; Hwang, W.T.; Kim, E.H. Application of data assimilation to improve the forecasting capability of an atmospheric dispersion model for a radioactive plume. Ann. Nucl. Energy 2008, 35, 838–844. [Google Scholar] [CrossRef]
- Beychok, M.R. Fundamentals of Stack Gas Dispersion; Milton R Beychok: New Beach, CA, USA, 2005. [Google Scholar]
- Till, J.E.; Grogan, H.A. Radiological risk assessment and environmental analysis; Oxford University Press, Inc.: New York, NY, USA, 2008. [Google Scholar]
- International Atomic Energy Agency (IAEA). Available online: http://iaea.org/newscenter/news/tsunamiupdate01.html (accessed on 25 May 2013).
- Lujaniene, G.; Bycenkiene, S.; Povinec, P.P.; Gera, M. Radionuclides from the Fukushima accident in the air over Lithuania: Measurement and modeling approaches. J. Environ. Radioactiv. 2012, 114, 71–80. [Google Scholar] [CrossRef]
- Steinhauser, G.; Brandl, A.; Johnson, T.E. Comparison of the Chernobyl and Fukushima nuclear accidents: A review of the environmental impacts. Sci. Total Environ. 2014, 470–471, 800–817. [Google Scholar] [CrossRef]
- Park, S.J.; Yang, W.Y.; Lim, S.H. Damage Simulations of Nuclear Accidents at YeoungKwang andKori in Korea; The Korea Federation for Environmental Movement: Seoul, Korea, 2012. (in Korean) [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Jeong, H.; Park, M.; Jeong, H.; Hwang, W.; Kim, E.; Han, M. Effect of the Duration Time of a Nuclear Accident on Radiological Health Consequences. Int. J. Environ. Res. Public Health 2014, 11, 2865-2875. https://doi.org/10.3390/ijerph110302865
Jeong H, Park M, Jeong H, Hwang W, Kim E, Han M. Effect of the Duration Time of a Nuclear Accident on Radiological Health Consequences. International Journal of Environmental Research and Public Health. 2014; 11(3):2865-2875. https://doi.org/10.3390/ijerph110302865
Chicago/Turabian StyleJeong, Hyojoon, Misun Park, Haesun Jeong, Wontae Hwang, Eunhan Kim, and Moonhee Han. 2014. "Effect of the Duration Time of a Nuclear Accident on Radiological Health Consequences" International Journal of Environmental Research and Public Health 11, no. 3: 2865-2875. https://doi.org/10.3390/ijerph110302865




