Analysis of the Spatial Variation of Hospitalization Admissions for Hypertension Disease in Shenzhen, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
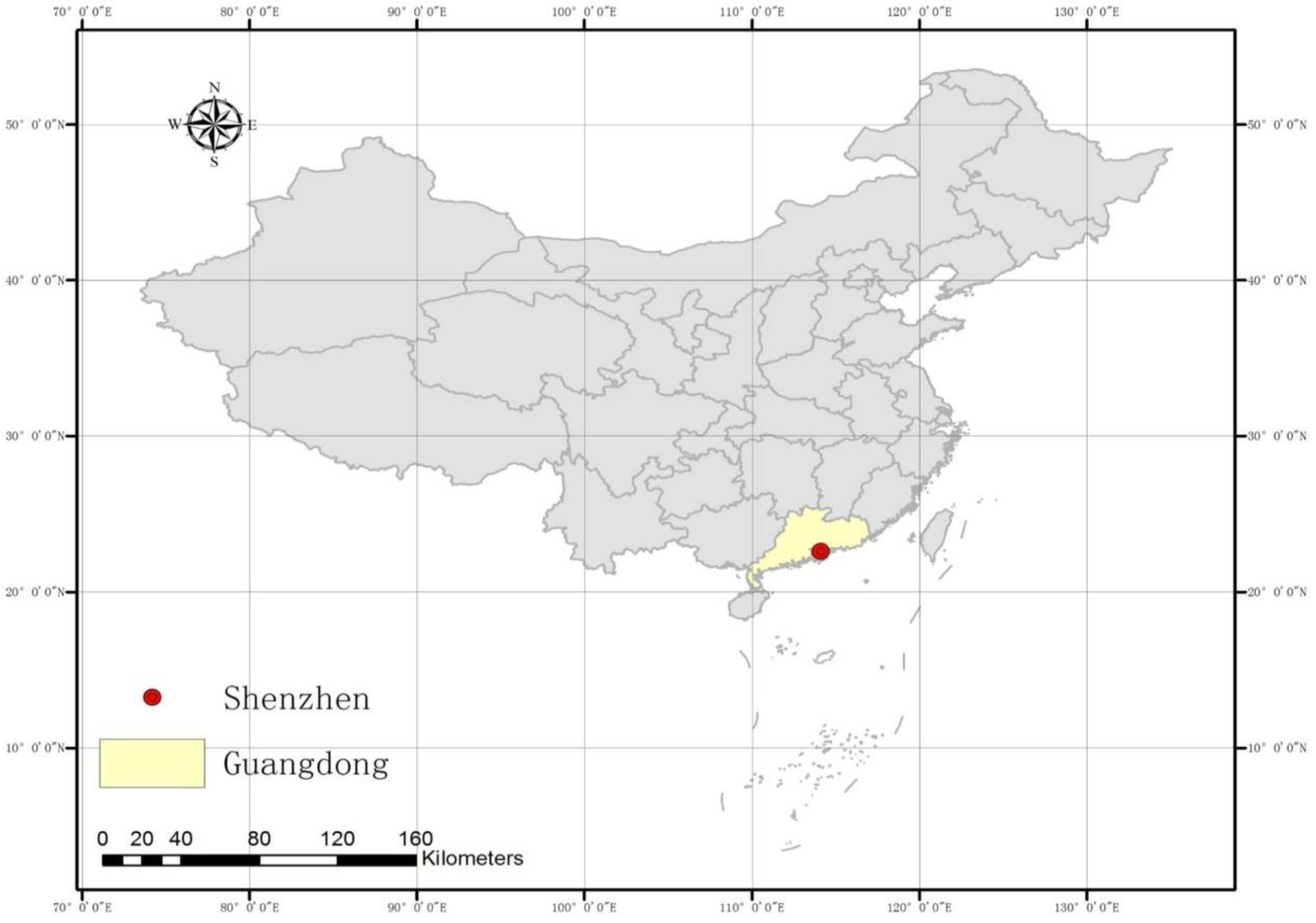
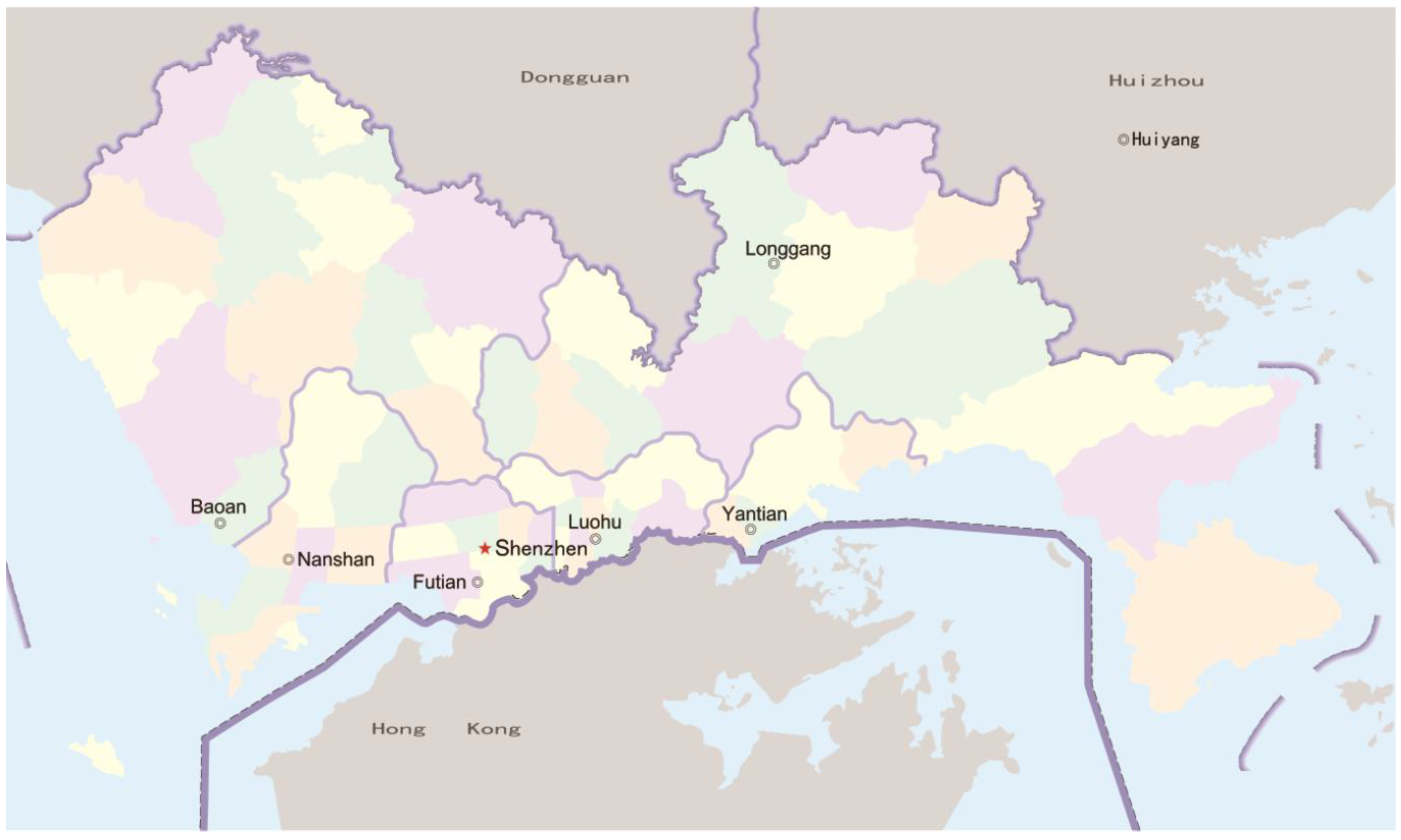
2.2. Data
2.3. Standardized Ratio Calculation
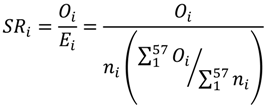
2.4. Bayesian Model-Based Disease Mapping
3. Results
3.1. The Spatial Variations of the Observed Admission Cases at Multiple Levels
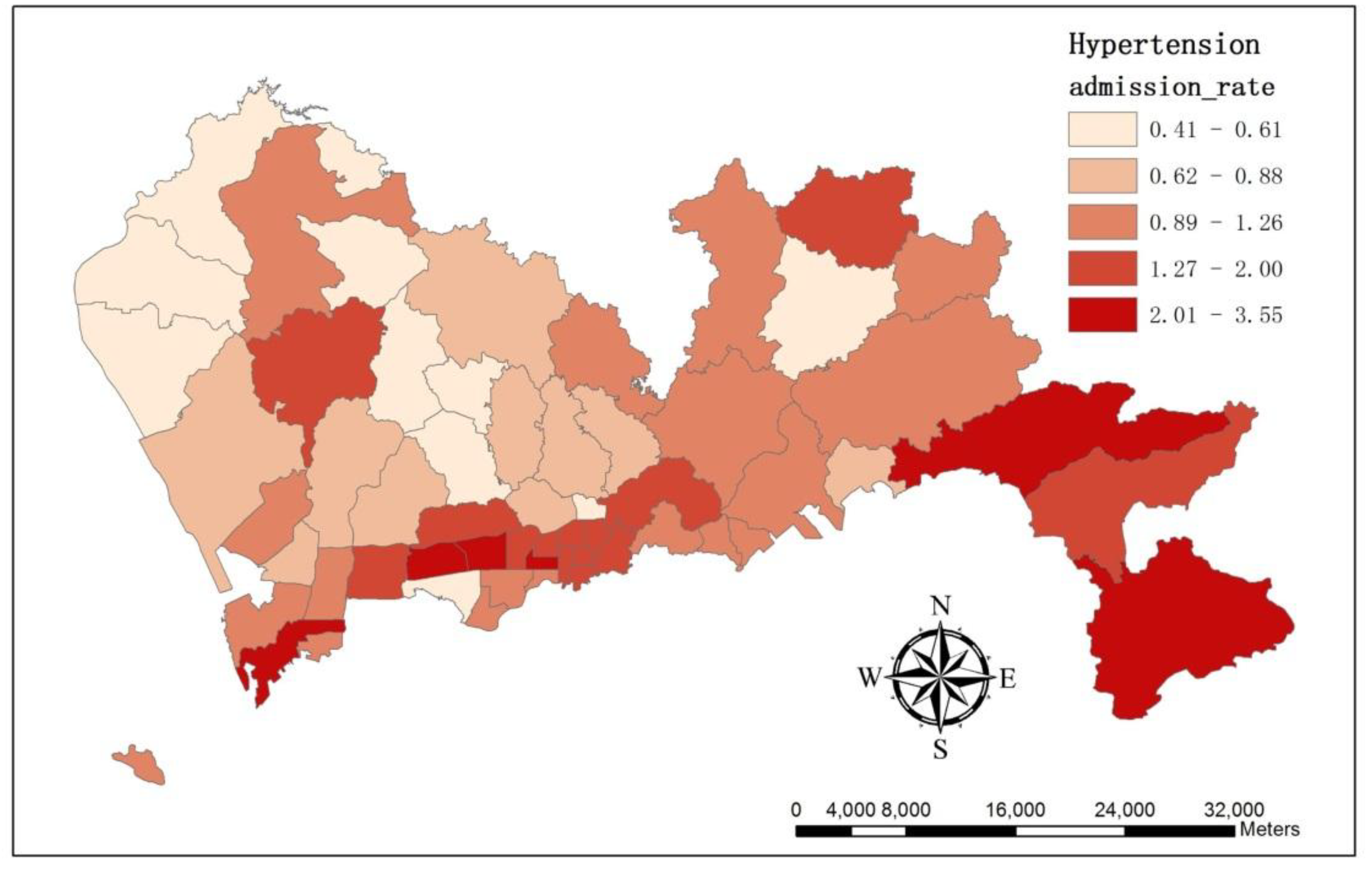
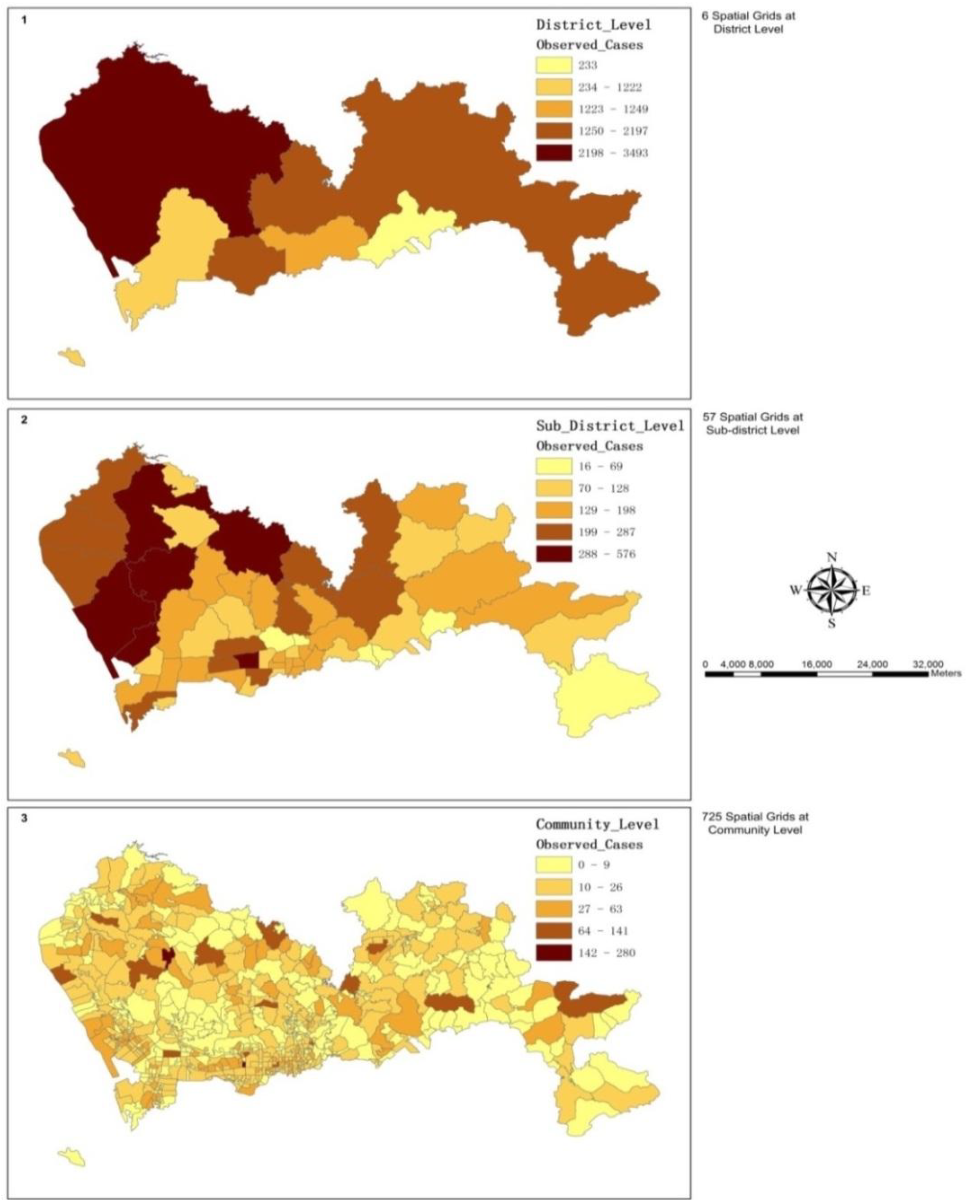
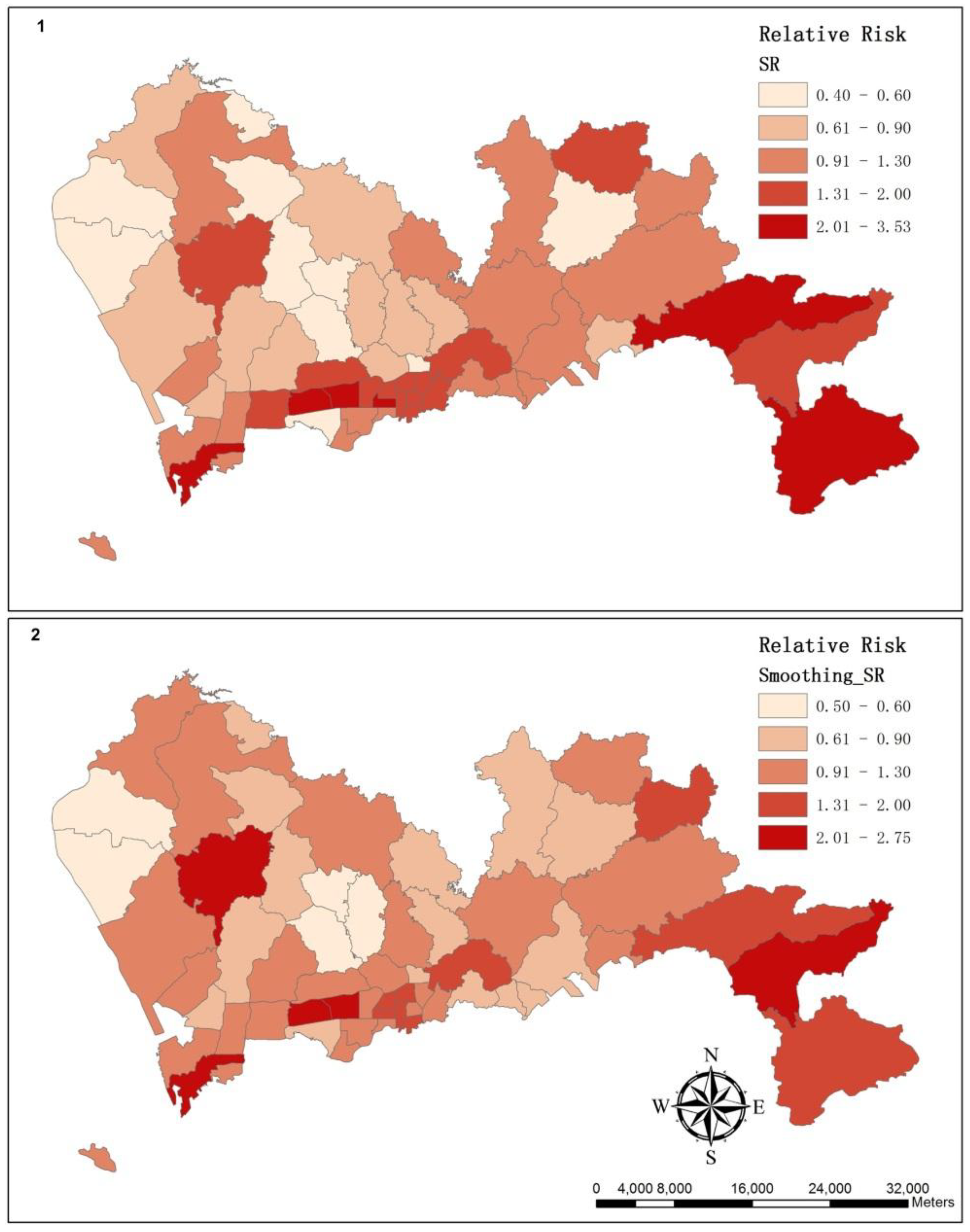
3.2. The Spatial Variation of the Relative Risk of Hospital Admissions for Hypertension
| Cluster Type | Sub-district | Observed Cases | Expected Cases | SR | GiPValue | GiZscore |
|---|---|---|---|---|---|---|
| Hot spot | Fubao | 107 | 107.21 | 1.00 | 0.01 | 2.55 |
| Futian | 248 | 247.83 | 1.00 | 0.08 | 1.74 | |
| Nanyuan | 109 | 113.97 | 0.96 | 0.08 | 1.77 | |
| Shatou | 134 | 226.66 | 0.59 | 0.06 | 1.90 | |
| Guiyuan | 152 | 82.59 | 1.84 | 0.07 | 1.82 | |
| Kuiyong | 176 | 61.34 | 2.87 | 0.02 | 2.34 | |
| Nanao | 51 | 19.05 | 2.68 | 0.03 | 2.14 | |
| Dapeng | 87 | 46.44 | 1.87 | <0.01 | 3.15 | |
| Cold spot | Guannan | 370 | 453.96 | 0.82 | 0.08 | −1.77 |
| Shajing | 287 | 531.41 | 0.54 | 0.09 | −1.72 | |
| Dalang | 147 | 279.45 | 0.53 | 0.05 | −1.94 | |
| Longhua | 148 | 366.27 | 0.40 | 0.02 | −2.39 | |
| Pinghu | 219 | 229.34 | 0.95 | 0.06 | −1.91 |

| Cluster Type | Sub-district | Observed Cases | Expected Cases | Relative Risk | p-value |
|---|---|---|---|---|---|
| Primary | Meilin | 212 | 152.13 | 2.69 | <0.0001 |
| Lianhua | 576 | 163.28 | 2.69 | <0.0001 | |
| Xiangmihu | 216 | 82.43 | 2.69 | <0.0001 | |
| Secondary | Dapeng | 87 | 46.44 | 2.52 | <0.0001 |
| Kuiyong | 176 | 61.34 | 2.52 | <0.0001 | |
| Nanao | 51 | 19.05 | 2.52 | <0.0001 | |
| Zhaoshang | 224 | 80.12 | 2.84 | <0.0001 | |
| Liantang | 82 | 84.40 | 1.44 | <0.0001 | |
| Donghu | 166 | 83.55 | 1.44 | <0.0001 | |
| Huangbei | 170 | 112.03 | 1.44 | <0.0001 | |
| Cuizhu | 160 | 115.91 | 1.44 | <0.0001 | |
| Dongxiao | 46 | 103.72 | 1.44 | <0.0001 | |
| Dongmen | 153 | 91.46 | 1.44 | <0.0001 | |
| Sungang | 94 | 63.47 | 1.44 | <0.0001 | |
| Nanhu | 157 | 90.83 | 1.44 | <0.0001 | |
| Guiyuan | 152 | 82.59 | 1.44 | <0.0001 | |
| Shiyan | 444 | 248.76 | 1.82 | <0.0001 | |
| Pingdi | 142 | 95.70 | 1.49 | 0.0014 | |
| Gongming | 400 | 320.10 | 1.26 | 0.0018 |
3.3. Summary of the Hierarchical Bayesian Models
| # of Model | Description | Dbar | Dhat | pD | DIC |
|---|---|---|---|---|---|
| 1 | Intercept & road density with coefficient | 3,015.580 | 3,013.600 | 1.985 | 3,017.570 |
| 2 | Intercept & road density without coefficient | 3,283.520 | 3,282.530 | 0.995 | 3,284.520 |
| 3 | Intercept & unstructured component | 328.936 | 283.227 | 45.709 | 374.646 |
| 4 | Intercept & structured component | 334.725 | 291.671 | 43.054 | 377.779 |
| 5 | Intercept & unstructured & structured component | 316.465 | 273.777 | 42.688 | 359.153 |
| 6 | Intercept & road density with coefficient & structured & unstructured component | 356.994 | 306.799 | 50.195 | 407.189 |
| # of Model | Explanation Variables | Mean | SD | MC Error | Credible Interval | |
|---|---|---|---|---|---|---|
| 2.5% | 97.5% | |||||
| 1 | Intercept | −0.2729 | 0.02323 | 2.873E-4 | −0.3187 | −0.228 |
| Coefficient | 0.4525 | 0.03394 | 4.168E-4 | 0.3862 | 0.519 | |
| 2 | Intercept | −0.6257 | 0.009773 | 3.893E-5 | −0.6449 | −0.6066 |
| 3 | Intercept | 0.05549 | 0.07219 | 0.001014 | −0.08567 | 0.197 |
| Variance of unstructured component | 4.373 | 1.032 | 0.006073 | 2.633 | 6.666 | |
| 4 | Intercept | 0.06246 | 0.03228 | 1.39E-4 | −0.001213 | 0.1252 |
| Variance of structured component | 1.015 | 0.1706 | 0.001032 | 0.7188 | 1.386 | |
| 5 | Intercept | 0.07391 | 0.05503 | 5.591E-4 | −0.03969 | 0.1805 |
| Variance of unstructured component | 819.7 | 13,800.0 | 435.8 | 3.965 | 1,710.0 | |
| Variance of structured component | 2.207 | 2.364 | 0.08871 | 0.9082 | 6.592 | |
| 6 | Intercept | −0.03228 | 0.2274 | 0.01064 | −0.4436 | 0.4754 |
| Coefficient | 0.1787 | 0.3556 | 0.0167 | −0.6419 | 0.8033 | |
| Variance of structured component | 17.75 | 203.0 | 7.739 | 0.8435 | 48.67 | |
| Variance of unstructured component | 26.78 | 188.6 | 6.437 | 3.147 | 122.8 | |
4. Discussion and Conclusions
| Sub-district | SR | Smoothing SR | Rank of Expected Cases | Rank of Area |
|---|---|---|---|---|
| Kuiyong | 2.87 | 1.36 | 53 | 5 |
| Huaqiangbei | 2.73 | 1.78 | 51 | 54 |
| Nanao | 2.68 | 1.82 | 56 | 2 |
| Lianhua | 3.53 | 2.75 | 25 | 43 |
| Shahe | 1.62 | 0.94 | 30 | 34 |
| Pingdi | 1.48 | 0.91 | 39 | 16 |
| Yantian | 1.19 | 0.69 | 47 | 18 |
| Donghu | 1.99 | 1.51 | 44 | 25 |
| Dongmen | 1.67 | 1.20 | 40 | 57 |
| Shatoujiao | 1.14 | 0.71 | 54 | 45 |
Acknowledgments
Conflicts of Interest
References
- Carretero, O.A.; Oparil, S. Essential hypertension. Part I: Definition and etiology. Circulation 2000, 101, 329–335. [Google Scholar] [CrossRef]
- Go, A.S.; Mozaffarian, D.; Roger, V.L.; Benjamin, E.J.; Berry, J.D.; Borden, W.B.; Bravata, D.M.; Dai, S.; Ford, E.S.; Fox, C.S.; et al. Heart disease and stroke statistics—2013 update a report from the American Heart Association. Circulation 2013, 127, 6–245. [Google Scholar]
- Cohen, L.; Curhan, G.C.; Forman, J.P. Influence of age on the association between lifestyle factors and risk of hypertension. J. Am. Soc. Hypertens. 2012, 4, 284–290. [Google Scholar] [CrossRef]
- Wang, L.; Manson, J.E.; Gaziano, J.M.; Buring, J.E.; Sesso, H.D. Fruit and vegetable intake and the risk of hypertension in middle-ages and older women. Amer. J. Hypertens. 2012, 2, 180–189. [Google Scholar]
- Islam, M.R.; Khan, I.; Attia, J.; Hassan, S.M.N.; McEvoy, M.; D’Este, C.; Azim, S.; Akhter, A.; Akter, S.; Shahidullah, S.M.; et al. Association between hypertension and chronic arsenic exposure in drinking water: A cross-sectional study in Bangladesh. Int. J. Environ. Res. Public Health 2012, 9, 4522–4536. [Google Scholar] [CrossRef]
- Miyaki, K.; Song, Y.; Taneichi, S.; Tsutsumi, A.; Hashimoto, H.; Kawakami, N.; Takahashi, M.; Shimazu, A.; Inoue, A.; Kurioka, S.; et al. Socioeconomic status is significantly associated with dietary salt intakes and blood pressure in Japanese workers (J-HOPE Study). Int. J. Environ. Res. Public Health 2013, 10, 980–993. [Google Scholar]
- Liu, L.S. 2010 Chinese guidelines for the management of hypertension. Chin. J. Hypertens. 2011, 19, 701–743. [Google Scholar]
- Gu, D.; Reynolds, K.; Wu, X.; Chen, J.; Duan, X.; Muntner, P.; Huang, G.; Reynolds, R.F.; Su, S.; Whelton, P.K.; et al. Prevalence, awareness, treatment, and control of hypertension in China. Hypertension 2002, 40, 920–927. [Google Scholar] [CrossRef]
- Luo, L.; Luan, R.S.; Yuan, P. Meta-analysis of risk factor on hypertension in China. Chin. J. Epidemiol. 2003, 24, 50–53. [Google Scholar]
- Wang, R.; Zhao, Y.; He, X.; Ma, X.; Yan, X.; Sun, Y.; Liu, W.; Gu, Z.; Zhao, J.; He, J. Impact of hypertension on health-related quality of life in a population-based study in Shanghai, China. Public Health 2009, 123, 534–539. [Google Scholar] [CrossRef]
- Ahn, S.; Zhao, H.; Smith, M.L.; Ory, M.G.; Phillips, C.D. BMI and lifestyle changes as correlates to changes in self-reported diagnosis of hypertension among older Chinese adults. J. Am. Soc. Hypertens. 2011, 5, 21–30. [Google Scholar] [CrossRef]
- Mujahid, M.S.; Roux, A.V.D.; Morenoff, J.D.; Raghunathan, T.E.; Cooper, R.S.; Ni, H.; Shea, S. Neighborhood characteristics and hypertension. Epidemiology 2008, 19, 590–598. [Google Scholar] [CrossRef]
- Elliott, P.; Wartenberg, D. Spatial epidemiology: Current approaches and future challenges. Environ. Health Perspect. 2004, 112, 998–1006. [Google Scholar] [CrossRef]
- Pfeiffer, D.; Robinson, T.; Stevenson, M.; Stevens, K.B.; Rogers, D.J.; Clements, A.C. Spatial Analysis in Epidemiology; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Lawson, A.B.; Browne, W.J.; Rodeiro, C.L.V. Disease Mapping with WinBUGS and MLwiN; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Haining, R.P. Spatial Data Analysis: Theory and Practice; Cambridge University Press: Oxford, UK, 2003. [Google Scholar]
- Black, R.J.; Sharp, L.; Finlayson, A.R.; Harkness, E.F. Cancer incidence in a population potentially exposed to radium-226 at Dalgety Bay, Scotland. Br. J. Cancer 1994, 69, 140–143. [Google Scholar] [CrossRef]
- Clarke, K.C.; Gaydos, L.J. Loose-coupling a cellular automaton model and GIS: Long-term urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inf. Sci. 1998, 12, 699–714. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based land-use suitability analysis: A critical overview. Prog. Plan. 2004, 62, 3–65. [Google Scholar] [CrossRef]
- Congdon, P. A model for spatially disaggregated trends and forecasts of diabetes prevalence. J. Data Sci. 2012, 10, 579–595. [Google Scholar]
- Gebreab, S.Y.; Roux, A.V.D. Exploring racial disparities in CHD mortality between blacks and whites across the United States: A geographically weighted regression approach. Health Place 2012, 18, 1006–1014. [Google Scholar] [CrossRef]
- Faes, C.; van der Stede, Y.; Guis, H.; Staubach, C.; Ducheyne, E.; Hendrickx, G.; Mintiens, K. Factors affecting Bluetongue serotype 8 spread in northern Europe in 2006: The geographical epidemiology. Prev. Vet. Med. 2013, 110, 149–158. [Google Scholar] [CrossRef]
- Congdon, P.; Lloyd, P. Estimating small area diabetes prevalence in the US using the behavioral risk factor surveillance system. J. Data Sci. 2010, 8, 235–252. [Google Scholar]
- Banerjee, S.; Carlin, B.; Gelfand, A. Hierarchical Modeling and Analysis for Spatial Data; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Congdon, P. Applied Bayesian Hierarchical Methods; Chapman and Hall/CRC: Boca Raton, FL, USA, 2010. [Google Scholar]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Gelman, A. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 2006, 1, 515–534. [Google Scholar]
- Páez, A.; Scott, D.M. Spatial statistics for urban analysis: A review of techniques with examples. GeoJournal 2005, 61, 53–67. [Google Scholar] [CrossRef]
- Anselin, L.; Getis, A. Spatial statistical analysis and geographic information systems. Ann. Reg. Sci. 1992, 26, 19–33. [Google Scholar] [CrossRef]
- Montello, D.R. Spatial Information Theory a Theoretical Basis for Gis; Frank, A.U., Campari, I., Eds.; Springer-Verlag: Berlin, Germany, 1993; pp. 312–321. [Google Scholar]
- Montello, D.R. International Encyclopedia of Social & Behavioral Sciences; Smelser, N.J., Baltes, P.B., Eds.; Pergamon Press: Oxford, UK, 2001; pp. 13501–13504. [Google Scholar]
- Costanza, R.; Maxwell, T. Resolution and predictability: An approach to the scaling problem. Landscape Ecol. 1994, 9, 47–57. [Google Scholar] [CrossRef]
- Dungan, J.L.; Perry, J.N.; Dale, M.R.T.; Legendre, P.; Citron Pousty, S.; Fortin, M.J.; Jakomulska, A.; Miriti, M.; Rosenberg, M.S. A balanced view of scale in spatial statistical analysis. Ecography 2002, 25, 626–640. [Google Scholar] [CrossRef]
- Shenzhen Statistics and Information Bureau. Shenzhen Statistical Yearbook; China Statistics Press: Beijing, China, 2012.
- Zhang, D.; Mou, J.; Cheng, J.Q.; Griffiths, S.M. Public health services in Shenzhen: A case study. Public Health 2011, 125, 15–19. [Google Scholar] [CrossRef]
- Li, H.; Bell, A.C. Overweight and obesity in children from Shenzhen, Peoples Republic of China. Health Place 2003, 9, 371–376. [Google Scholar] [CrossRef]
- Soljak, M.; Calderon-Larrañaga, A.; Sharma, P.; Cecil, E.; Bell, D.; Abi-Aad, G.; Majeed, A. Does higher quality primary health care reduce stroke admissions? A national cross-sectional study. Br. J. Gen. Pract. 2011, 61, 801–807. [Google Scholar] [CrossRef]
- ICD-10: International Statistical Classification of Diseases and Related Health Problems; World Health Organization: Geneva, Switzerland, 2004.
- Van de Poel, E.; O’Donnell, O.; van Doorslaer, E. Urbanization and the spread of diseases of affluence in China. Econ. Hum. Biol. 2009, 7, 200–216. [Google Scholar] [CrossRef]
- Allender, S.; Foster, C.; Hutchinson, L.; Arambepola, C. Quantification of urbanization in relation to chronic diseases in developing countries: A systematic review. J. Urban Health 2008, 85, 938–951. [Google Scholar] [CrossRef]
- Lee, D. A comparison of conditional autoregressive models used in Bayesian disease mapping. Spat. Spatiotemporal Epidemiol. 2011, 2, 79–89. [Google Scholar] [CrossRef]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Richardson, S.; Abellan, J.J.; Best, N. Bayesian spatio-temporal analysis of joint patterns of male and female lung cancer risks in Yorkshire (UK). Stat. Methods Med. Res. 2006, 15, 385–407. [Google Scholar] [CrossRef]
- Thomas, A.; Best, N.; Lunn, D.; Arnold, R.; Spiegelhalter, D. GeoBUGS User Manual. Available online: http://www.mrc-bsu.cam.ac.uk/bugs/winbugs/geobugs12manual.pdf (accessed on 1 July 2013).
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS-a Bayesian modelling framework: Concepts, structure, and extensibility. Stat. Comput. 2000, 10, 325–337. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. B 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Kulldorf, M. SatScan User Guide. Available online: http://www.satscan.org/techdoc.html (accessed on 2 June 2013).
- Soljak, M.; Samarasundera, E.; Indulkar, T.; Walford, H.; Majeed, A. Variations in cardiovascular disease under-diagnosis in England: National cross-sectional spatial analysis. BMC Cardiovasc. Disord. 2011, 11, 12. [Google Scholar] [CrossRef]
- Weycker, D.; Nichols, G.A.; O’Keeffe-Rosetti, M.; Edelsberg, J.; Khan, Z.M.; Kaura, S.; Oster, G. Risk-factor clustering and cardiovascular disease risk in hypertensive patients. Amer. J. Hypertens. 2007, 20, 599–607. [Google Scholar] [CrossRef]
- Zhou, J.; Lurie, M.N.; Bärnighausen, T.; McGarvey, S.T.; Newell, M.L.; Tanser, F. Determinants and spatial patterns of adult overweight and hypertension in a high HIV prevalence rural South African population. Health Place 2012, 18, 1300–1306. [Google Scholar]
- Mitchel, A. Spatial Measurements and Statistics. In The ESRI Guide to GIS Analysis; ESRI Press: Redlands, CA, USA, 2005; Volume 2. [Google Scholar]
- Kulldorff, M. Scan Statistics and Application; Glaz, J., Balakrishnan, N., Eds.; Birkhäuser: Boston, MA, USA, 1999; pp. 303–322. [Google Scholar]
- Zhang, T.; Zhang, Z.; Lin, G. Spatial scan statistics with overdispersion. Stat. Med. 2012, 31, 762–774. [Google Scholar] [CrossRef]
- Levine, N. CrimeStat III User Workbook and Data. Available online: http://www.icpsr.umich.edu/CrimeStat/workbook.html (accessed on 20 July 2013).
- Bluhm, G.L.; Berglind, N.; Nordling, E.; Rosenlund, M. Road traffic noise and hypertension. Occup. Environ. Med. 2007, 64, 122–126. [Google Scholar]
- Hansell, A.L.; Blangiardo, M.; Fortunato, L.; Floud, S.; de Hoogh, K.; Fecht, D.; Ghosh, R.E.; Laszlo, H.E.; Pearson, C.; Beale, L.; et al. Aircraft noise and cardiovascular disease near Heathrow airport in London: Small area study. BMJ 2013, 347. [Google Scholar] [CrossRef]
- Correia, A.W.; Peters, J.L.; Levy, J.I.; Melly, S.; Dominici, F. Residual exposure to aircraft noise and hospital admissions for cardiovascular diseases: Multi-airport retrospective study. BMJ 2013, 347. [Google Scholar] [CrossRef]
- Soljak, M.; Majeed, A.; Eliahoo, J.; Dornhorst, A. Ethnic inequalities in the treatment and outcome of diabetes in three English Primary Care Trusts. Int. J. Equity Health 2007, 6. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wang, Z.; Du, Q.; Liang, S.; Nie, K.; Lin, D.-n.; Chen, Y.; Li, J.-j. Analysis of the Spatial Variation of Hospitalization Admissions for Hypertension Disease in Shenzhen, China. Int. J. Environ. Res. Public Health 2014, 11, 713-733. https://doi.org/10.3390/ijerph110100713
Wang Z, Du Q, Liang S, Nie K, Lin D-n, Chen Y, Li J-j. Analysis of the Spatial Variation of Hospitalization Admissions for Hypertension Disease in Shenzhen, China. International Journal of Environmental Research and Public Health. 2014; 11(1):713-733. https://doi.org/10.3390/ijerph110100713
Chicago/Turabian StyleWang, Zhensheng, Qingyun Du, Shi Liang, Ke Nie, De-nan Lin, Yan Chen, and Jia-jia Li. 2014. "Analysis of the Spatial Variation of Hospitalization Admissions for Hypertension Disease in Shenzhen, China" International Journal of Environmental Research and Public Health 11, no. 1: 713-733. https://doi.org/10.3390/ijerph110100713
APA StyleWang, Z., Du, Q., Liang, S., Nie, K., Lin, D.-n., Chen, Y., & Li, J.-j. (2014). Analysis of the Spatial Variation of Hospitalization Admissions for Hypertension Disease in Shenzhen, China. International Journal of Environmental Research and Public Health, 11(1), 713-733. https://doi.org/10.3390/ijerph110100713






