Quantitative Structure–Toxicity Relationship in Bioactive Molecules from a Conceptual DFT Perspective
Abstract
:1. Introduction
2. Theoretical Background
3. Methodology
3.1. Multiple Linear Regression (MLR)
3.2. Neural Networks (NNs)
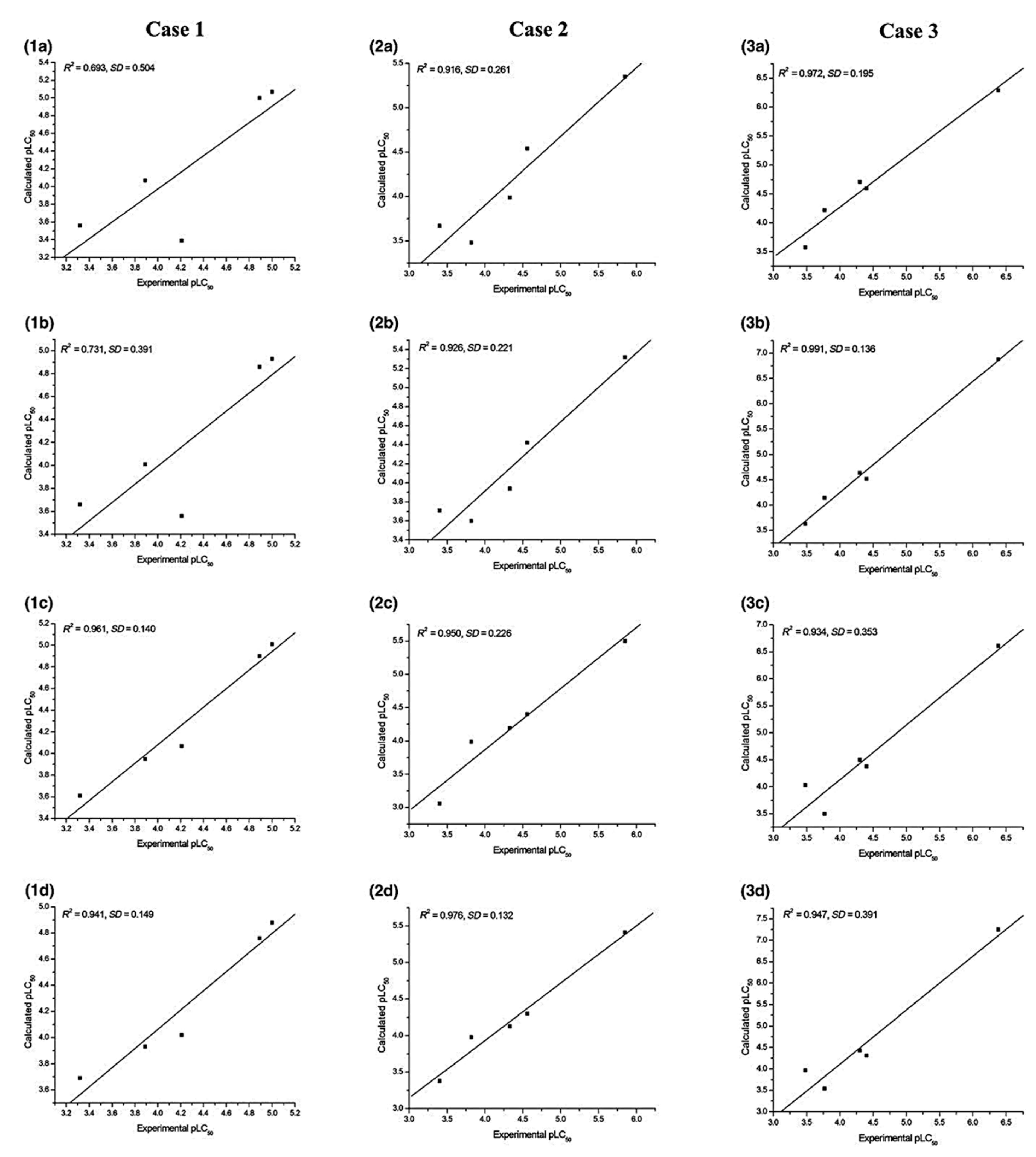
4. Case Studies
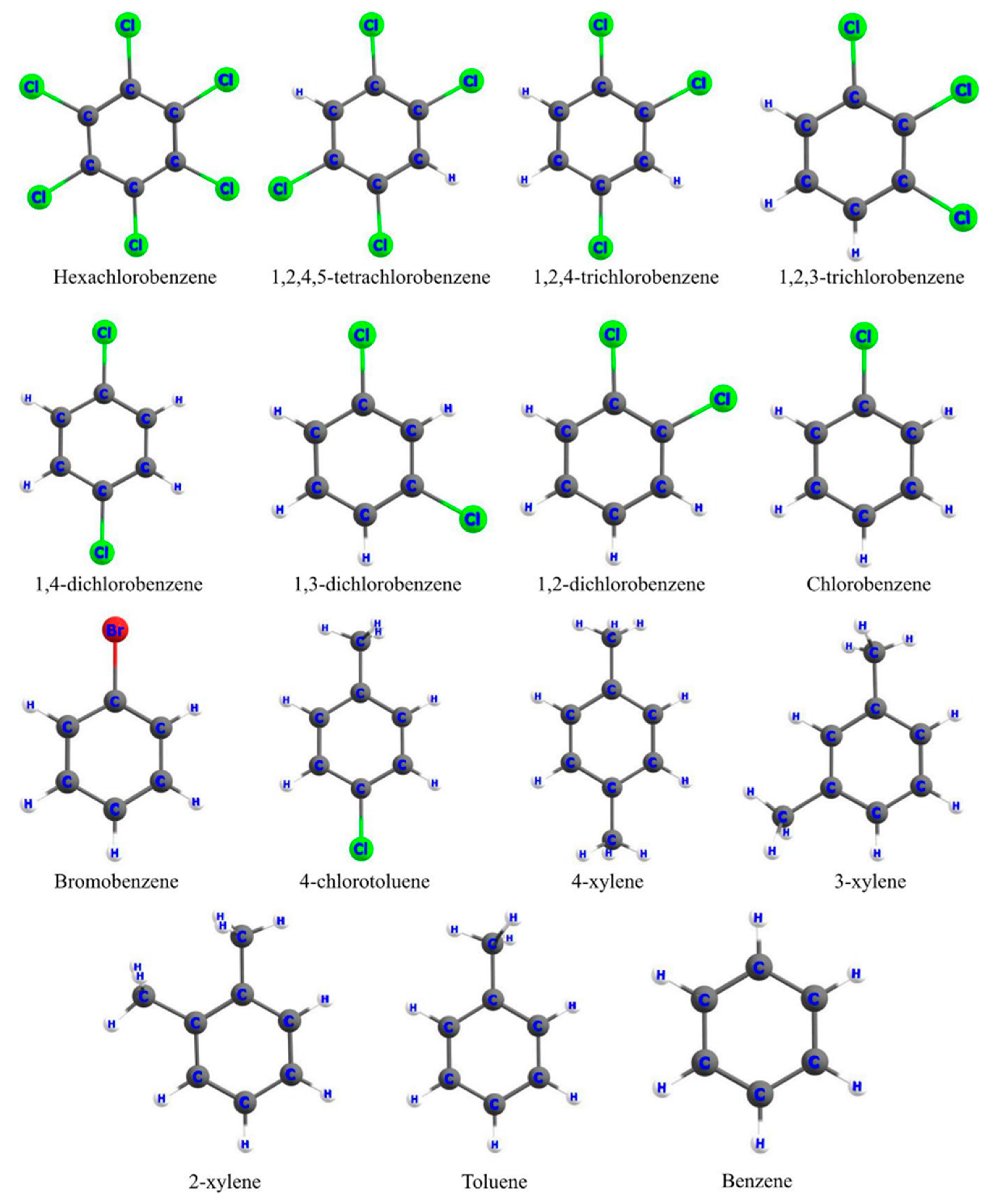
4.1. Pimephales Promelas
4.2. Tetrahymena Pyriformis
4.3. Trypanosoma Brucei
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karcher, W.; Devillers, J. SAR and QSAR in environmental chemistry and toxicology: Scientific tool or wishful thinking? In Practical Applications of Quantitative Structure–Activity Relationships (QSAR) in Environmental Chemistry and Toxicology; Karcher, W., Devillers, J., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1990; pp. 1–12. [Google Scholar]
- Selassie, C.; Mekapati, S.; Verma, R. QSAR: Then and Now. Curr. Top. Med. Chem. 2002, 2, 1357–1379. [Google Scholar] [CrossRef]
- Roy, K.; Mitra, I. Advances in quantitative structure–activity relationship models of antioxidants. Expert Opin. Drug Discov. 2009, 4, 1157–1175. [Google Scholar] [CrossRef]
- Schultz, T.W.; Cronin, M.T.D.; Walker, J.D.; Aptula, A.O. Quantitative structure–activity relationships (QSARs) in toxicology: A historical perspective. J. Mol. Struct. THEOCHEM 2003, 622, 1–22. [Google Scholar] [CrossRef]
- Schultz, T.W.; Cronin, M.T.D.; Netzeva, T.I. The present status of QSAR in toxicology. J. Mol. Struct. THEOCHEM 2003, 622, 23–38. [Google Scholar] [CrossRef]
- Gombar, V.K.; Mattioni, B.E.; Zwickl, C.; Deahl, J.T. Computational Approaches for Assessment of Toxicity: A Historical Perspective and Current Status. In Computational Toxicology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 183–215. [Google Scholar]
- Hansch, C.; Maloney, P.P.; Fujita, T.; Muir, R.M. Correlation of Biological Activity of Phenoxyacetic Acids with Hammett Substituent Constants and Partition Coefficients. Nature 1962, 194, 178–180. [Google Scholar] [CrossRef]
- Hansch, C.; Hoekman, D.; Leo, A.; Weininger, D.; Selassie, C.D. Chem-bioinformatics: Comparative QSAR at the interface between chemistry and biology. Chem. Rev. 2002, 102, 783–812. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Kuanar, M.; Slavov, S.; Hall, C.D.; Karelson, M.; Kahn, I.; Dobchev, D.A. ChemInform Abstract: Quantitative Correlation of Physical and Chemical Properties with Chemical Structure: Utility for Prediction. ChemInform 2011, 42. [Google Scholar] [CrossRef]
- Fujita, T.; Winkler, D.A. Understanding the Roles of the “two QSARs”. J. Chem. Inf. Model. 2016, 56, 269–274. [Google Scholar] [CrossRef]
- Wang, L.; Ding, J.; Pan, L.; Cao, D.; Jiang, H.; Ding, X. Quantum chemical descriptors in quantitative structure–activity relationship models and their applications. Chemom. Intell. Lab. Syst. 2021, 217, 104384. [Google Scholar] [CrossRef]
- Tropsha, A. Best practices for QSAR model development, validation, and exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef]
- Verina, J.; Malde, A.; Khedkar, S.; Iyer, R.; Coutinho, E. Local indices for similarity analysis (LISA)-A 3D-QSAR formalism based on local molecular similarity. J. Chem. Inf. Model. 2009, 49, 2695–2707. [Google Scholar] [CrossRef]
- Verma, R.P.; Hansch, C. Use of 13C NMR chemical shift as QSAR/QSPR descriptor. Chem. Rev. 2011, 111, 2865–2899. [Google Scholar] [CrossRef]
- McFarland, J.W. On the parabolic relationship between drug potency and hydrophobicity. J. Med. Chem. 1970, 13, 1192–1196. [Google Scholar] [CrossRef]
- Itskowitz, P.; Tropsha, A. K nearest neighbors QSAR modeling as a variational problem: Theory and applications. J. Chem. Inf. Model. 2005, 45, 777–785. [Google Scholar] [CrossRef]
- Ruggiu, F.; Gizzi, P.; Galzi, J.L.; Hibert, M.; Haiech, J.; Baskin, I.; Horvath, D.; Marcou, G.; Varnek, A. Quantitative structure-property relationship modeling: A valuable support in high-throughput screening quality control. Anal. Chem. 2014, 86, 2510–2520. [Google Scholar] [CrossRef] [Green Version]
- Nieto-Draghi, C.; Fayet, G.; Creton, B.; Rozanska, X.; Rotureau, P.; De Hemptinne, J.C.; Ungerer, P.; Rousseau, B.; Adamo, C. A General Guidebook for the Theoretical Prediction of Physicochemical Properties of Chemicals for Regulatory Purposes. Chem. Rev. 2015, 115, 13093–13164. [Google Scholar] [CrossRef]
- Shahlaei, M.; Fassihi, A. QSAR analysis of some 1-(3,3-diphenylpropyl)-piperidinyl amides and ureas as CCR5 inhibitors using genetic algorithm-least square support vector machine. Med. Chem. Res. 2013, 22, 4384–4400. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Maran, U.; Lobanov, V.S.; Karelson, M. Structurally Diverse Quantitative Structure-Property Relationship Correlations of Technologically Relevant Physical Properties. J. Chem. Inf. Comput. Sci. 2000, 40, 1–18. [Google Scholar] [CrossRef]
- Shahlaei, M.; Madadkar-Sobhani, A.; Fassihi, A.; Saghaie, L.; Shamshirian, D.; Sakhi, H. Comparative quantitative structure-activity relationship study of some 1-aminocyclopentyl-3-carboxyamides as CCR2 inhibitors using stepwise MLR, FA-MLR, and GA-PLS. Med. Chem. Res. 2012, 21, 100–115. [Google Scholar] [CrossRef]
- Simarro, P.P.; Franco, J.; Diarra, A.; Postigo, J.A.R.; Jannin, J. Update on field use of the available drugs for the chemotherapy of human African trypanosomiasis. Parasitology 2012, 139, 842–846. [Google Scholar] [CrossRef]
- Vigneresse, J.L. Revisiting immiscibility through DFT chemical descriptors. Theor. Chem. Acc. 2020, 139, 1–15. [Google Scholar] [CrossRef]
- Gupta, S.P. Quantitative Structure–Activity Relationship Studies on Na+, K+-ATPase Inhibitors. Chem. Rev. 2012, 112, 3171–3192. [Google Scholar] [CrossRef] [PubMed]
- Gholivand, K.; Ebrahimi Valmoozi, A.A.; Mahzouni, H.R.; Ghadimi, S.; Rahimi, R. Molecular docking and QSAR studies: Noncovalent interaction between acephate analogous and the receptor site of human acetylcholinesterase. J. Agric. Food Chem. 2013, 61, 6776–6785. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Sandler, S.I. Physicochemical properties of hazardous energetic compounds from molecular simulation. J. Chem. Theory Comput. 2013, 9, 2389–2397. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.P. QSAR Studies on Hydroxamic Acids: A Fascinating Family of Chemicals with a Wide Spectrum of Activities. Chem. Rev. 2015, 115, 6427–6490. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, X.; Wang, Z. A review on progress in QSPR studies for surfactants. Int. J. Mol. Sci. 2010, 11, 1020–1047. [Google Scholar] [CrossRef] [Green Version]
- Bo, W.; Chen, L.; Qin, D.; Geng, S.; Li, J.; Mei, H.; Li, B.; Liang, G. Application of quantitative structure-activity relationship to food-derived peptides: Methods, situations, challenges and prospects. Trends Food Sci. Technol. 2021, 114, 176–188. [Google Scholar] [CrossRef]
- Belfield, S.J.; Enoch, S.J.; Firman, J.W.; Madden, J.C.; Schultz, T.W.; Cronin, M.T.D. Determination of “fitness-for-purpose” of quantitative structure-activity relationship (QSAR) models to predict (eco-)toxicological endpoints for regulatory use. Regul. Toxicol. Pharmacol. 2021, 123, 104956. [Google Scholar] [CrossRef]
- Cherkasov, A.; Muratov, E.N.; Fourches, D.; Varnek, A.; Baskin, I.I.; Cronin, M.; Dearden, J.; Gramatica, P.; Martin, Y.C.; Todeschini, R.; et al. QSAR modeling: Where have you been? Where are you going to? J. Med. Chem. 2014, 57, 4977–5010. [Google Scholar] [CrossRef] [Green Version]
- Bruce, C.L.; Melville, J.L.; Pickett, S.D.; Hirst, J.D. Contemporary QSAR Classifiers Compared. J. Chem. Inf. Model. 2007, 47, 219–227. [Google Scholar] [CrossRef]
- Ferrins, L.; Gazdik, M.; Rahmani, R.; Varghese, S.; Sykes, M.L.; Jones, A.J.; Avery, V.M.; White, K.L.; Ryan, E.; Charman, S.A.; et al. Pyridyl benzamides as a novel class of potent inhibitors for the kinetoplastid Trypanosoma brucei. J. Med. Chem. 2014, 57, 6393–6402. [Google Scholar] [CrossRef] [PubMed]
- Escuder-Gilabert, L.; Sagrado, S.; Villanueva-Camañas, R.M.; Medina-Hernández, M.J. Quantitative Retention-Structure and Retention-Activity Relationship Studies of Local Anesthetics by Micellar Liquid Chromatography. Anal. Chem. 1998, 70, 28–34. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.D.; Zhang, L.J.; Qian, Y. Systematic Multiscale Method for Studying the Structure–Performance Relationship of Drug-Delivery Systems. Ind. Eng. Chem. Res. 2012, 51, 4719–4730. [Google Scholar] [CrossRef]
- Burden, F.R. Quantitative Structure-Activity Relationship Studies Using Gaussian Processes. J. Chem. Inf. Comput. Sci. 2001, 41, 830–835. [Google Scholar] [CrossRef] [PubMed]
- Khadikar, P.V.; Mather, K.C.; Singh, S.; Phadnis, A.; Shrivastava, A.; Mandaloi, M. Study on quantitative structure–toxicity relationships of benzene derivatives acting by narcosis. Bioorg. Med. Chem. 2002, 10, 1761–1766. [Google Scholar] [CrossRef]
- Padmanabhan, J.; Parthasarathi, R.; Subramanian, V.; Chattaraj, P.K. Group Philicity and Electrophilicity as Possible Descriptors for Modeling Ecotoxicity Applied to Chlorophenols. Chem. Res. Toxicol. 2006, 19, 356–364. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Padmanabhan, J.; Subramanian, V.; Maiti, B.; Chattaraj, P.K. Chemical Reactivity Profiles of Two Selected Polychlorinated Biphenyls. J. Phys. Chem. A 2003, 107, 10346–10352. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Subramanian, V.; Roy, D.R.; Chattaraj, P.K. Electrophilicity index as a possible descriptor of biological activity. Bioorg. Med. Chem. 2004, 12, 5533–5543. [Google Scholar] [CrossRef]
- Russom, C.L.; Bradbury, S.P.; Broderius, S.J.; Hammermeister, D.E.; Drummond, R.A. Predicting modes of toxic action from chemical structure: Acute toxicity in the fathead minnow (Pimephales Promelas). Environ. Toxicol. Chem. 1997, 16, 948–967. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Cronin, M.T.D.; Dearden, J.C. Quantitative Structure-Activity Relationships of Chemicals Acting by Non-polar Narcosis—Theoretical Considerations. Quant. Struct. Relatsh. 1998, 17, 131–138. [Google Scholar] [CrossRef]
- Karelson, M.; Lobanov, V.S.; Katritzky, A.R. Quantum-Chemical Descriptors in QSAR/QSPR Studies. Chem. Rev. 1996, 96, 1027–1044. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, A.; Giri, S.; Duley, S.; Anoop, A.; Bultinck, P.; Chattaraj, P.K. Aromaticity in all-metal annular systems: The counter-ion effect. Phys. Chem. Chem. Phys. 2011, 13, 14865–14878. [Google Scholar] [CrossRef] [PubMed]
- Chattaraj, P.K.; Roy, D.R. Update 1 of: Electrophilicity Index. Chem. Rev. 2007, 107, PR46–PR74. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Sarkar, U.; Roy, D.R. Electrophilicity Index. Chem. Rev. 2006, 106, 2065–2091. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1874. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA; Oxford, UK, 1989. [Google Scholar]
- Geerlings, P.; Chamorro, E.; Chattaraj, P.K.; De Proft, F.; Gázquez, J.L.; Liu, S.; Morell, C.; Toro-Labbé, A.; Vela, A.; Ayers, P. Conceptual density functional theory: Status, prospects, issues. Theor. Chem. Acc. 2020, 139, 36. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Padmanabhan, J.; Elango, M.; Chitra, K.; Subramanian, V.; Chattaraj, P.K. p K a Prediction Using Group Philicity. J. Phys. Chem. A 2006, 110, 6540–6544. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Padmanabhan, J.; Sarkar, U.; Maiti, B.; Subramanian, V.; Chattaraj, P.K. Toxicity analysis of benzidine through chemical reactivity and selectivity profiles: A DFT approach. Internet Electron. J. Mol. Des. 2003, 2, 798–813. [Google Scholar]
- Bansal, S.; Dixit, R. Performance enhancement of the pattern recalling efficiency of Hopfield neural network using genetic algorithm for cursive handwritten character recognition. Int. J. Appl. Pattern Recognit. 2016, 3, 59. [Google Scholar] [CrossRef]
- Gridach, M. Character-level neural network for biomedical named entity recognition. J. Biomed. Inform. 2017, 70, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Hertz, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computation; CRC Press: Boca Raton, FL, USA, 2018; Volume 44, ISBN 9780429968211. [Google Scholar]
- Pal, R.; Jana, G.; Sural, S.; Chattaraj, P.K. Hydrophobicity versus electrophilicity: A new protocol toward quantitative structure–toxicity relationship. Chem. Biol. Drug Des. 2019, 93, 1083–1095. [Google Scholar] [CrossRef] [PubMed]
- Bianucci, A.M.; Micheli, A.; Sperduti, A.; Starita, A. A Novel Approach to QSPR/QSAR Based on Neural Networks for Structures. In Soft Computing Approaches in Chemistry; Springer: Berlin/Heidelberg, Germany, 2003; pp. 265–296. [Google Scholar]
- Hansch, C.; Fujita, T. p-σ-π Analysis. A Method for the Correlation of Biological Activity and Chemical Structure. J. Am. Chem. Soc. 1964, 86, 1616–1626. [Google Scholar] [CrossRef]
- Kubinyi, H. Methods and Principles in Medicinal Chemistry. In QSAR: Hansch Analysis and Related Approaches; Wiley-VCH: Weinheim, Germany; New York, NY, USA, 1993; p. 438. ISBN 352730035X. [Google Scholar]
- Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithica, NY, USA, 1960. [Google Scholar]
- Sen, K.; Jorgenson, C. Electronegativity. In Structure and Bonding Bonding; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Pearson, R.G. Chemical Hardness; WileyVCH: Weinheim, Germany, 1997. [Google Scholar]
- Chattaraj, P.K. (Ed.) Chemical Reactivity Theory; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9780429137228. [Google Scholar]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The density functional viewpoint. J. Chem. Phys. 1977, 68, 3801–3807. [Google Scholar] [CrossRef]
- Pauling, L. The nature of the chemical bond. IV. the energy of single bonds and the relative electronegativity of atoms. J. Am. Chem. Soc. 1932, 54, 3570–3582. [Google Scholar] [CrossRef]
- Mulliken, R.S. A New Electroaffinity Scale; Together with Data on Valence States and on Valence Ionization Potentials and Electron Affinities. J. Chem. Phys. 1934, 2, 782–793. [Google Scholar] [CrossRef]
- Allred, A.L.; Rochow, E.G. A scale of electronegativity based on electrostatic force. J. Inorg. Nucl. Chem. 1958, 5, 264–268. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Ingold, C.K. 266. Significance of tautomerism and of the reactions of aromatic compounds in the electronic theory of organic reactions. J. Chem. Soc. 1933, 1120–1127. [Google Scholar] [CrossRef]
- Ingold, C.K. Principles of an Electronic Theory of Organic Reactions. Chem. Rev. 1934, 15, 225–274. [Google Scholar] [CrossRef]
- Maynard, A.T.; Huang, M.; Rice, W.G.; Covell, D.G. Reactivity of the HIV-1 nucleocapsid protein p7 zinc finger domains from the perspective of density-functional theory. Proc. Natl. Acad. Sci. USA 1998, 95, 11578–11583. [Google Scholar] [CrossRef] [Green Version]
- Atoms, D.T.; Parr, M.R.G.; Yang, W. Book Review. Density Funct. Theory Atoms Mol. 1989, 47, 10101. [Google Scholar]
- Koopmans, T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
- Mačernis, M. Nonlinear correlations between ν 1 Raman band and global scalar properties for different length carotenoids. Lith. J. Phys. 2019, 58, 358–378. [Google Scholar] [CrossRef] [Green Version]
- Flores-Holguín, N.; Frau, J.; Glossman-Mitnik, D. Conceptual DFT-Based Computational Peptidology of Marine Natural Compounds: Discodermins A–H. Molecules 2020, 25, 4158. [Google Scholar] [CrossRef]
- Roy, D.R.; Sarkar, U.; Chattaraj, P.K.; Mitra, A.; Padmanabhan, J.; Parthasarathi, R.; Subramanian, V.; Van Damme, S.; Bultinck, P. Analyzing toxicity through electrophilicity. Mol. Divers. 2006, 10, 119–131. [Google Scholar] [CrossRef]
- Roy, D.R.; Parthasarathi, R.; Maiti, B.; Subramanian, V.; Chattaraj, P.K. Electrophilicity as a possible descriptor for toxicity prediction. Bioorg. Med. Chem. 2005, 13, 3405–3412. [Google Scholar] [CrossRef]
- Pal, R.; Pal, G.; Jana, G.; Chattaraj, P.K. An In Silico QSAR Model Study Using Electrophilicity as a Possible Descriptor Against T. Brucei. Int. J. Chemoinform. Chem. Eng. 2019, 8, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Gaussian Inc.: Wallingford, UK, 2016. [Google Scholar]
- Duchowicz, P. Linear Regression QSAR Models for Polo-Like Kinase-1 Inhibitors. Cells 2018, 7, 13. [Google Scholar] [CrossRef] [Green Version]
- Peter, S.C.; Dhanjal, J.K.; Malik, V.; Radhakrishnan, N.; Jayakanthan, M.; Sundar, D. Quantitative Structure-Activity Relationship (QSAR): Modeling Approaches to Biological Applications. In Encyclopedia of Bioinformatics and Computational Biology; Elsevier: Amsterdam, The Netherlands, 2019; pp. 661–676. [Google Scholar]
- Liu, P.; Long, W. Current mathematical methods used in QSAR/QSPR studies. Int. J. Mol. Sci. 2009, 10, 1978–1998. [Google Scholar] [CrossRef] [PubMed]
- Luco, J.M.; Ferretti, F.H. QSAR Based on Multiple Linear Regression and PLS Methods for the Anti-HIV Activity of a Large Group of HEPT Derivatives. J. Chem. Inf. Comput. Sci. 1997, 37, 392–401. [Google Scholar] [CrossRef]
- Liman, W.; Oubahmane, M.; Hdoufane, I.; Bjij, I.; Villemin, D.; Daoud, R.; Cherqaoui, D.; El Allali, A. Monte Carlo Method and GA-MLR-Based QSAR Modeling of NS5A Inhibitors against the Hepatitis C Virus. Molecules 2022, 27, 2729. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.S.; Yin, C.S.; Wang, L.S. Combined MEDV-GA-MLR method for QSAR of three panels of steroids, dipeptides, and COX-2 inhibitors. J. Chem. Inf. Comput. Sci. 2002, 42, 749–756. [Google Scholar] [CrossRef] [PubMed]
- Ambure, P.; Gajewicz-Skretna, A.; Cordeiro, M.N.D.S.; Roy, K. New workflow for QSAR model development from small data sets: Small dataset curator and small dataset modeler. Integration of data curation, exhaustive double cross-validation, and a set of optimal model selection techniques. J. Chem. Inf. Model. 2019, 59, 4070–4076. [Google Scholar] [CrossRef] [PubMed]
- Tsou, L.K.; Yeh, S.H.; Ueng, S.H.; Chang, C.P.; Song, J.S.; Wu, M.H.; Chang, H.F.; Chen, S.R.; Shih, C.; Chen, C.T.; et al. Comparative study between deep learning and QSAR classifications for TNBC inhibitors and novel GPCR agonist discovery. Sci. Rep. 2020, 10, 16771. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Akhtar, J.; Zhang, X.; Sun, L.; Guan, S.; Li, X.; Chen, G.; Liu, J.; Jeon, H.N.; Kim, M.S.; et al. Comprehensive strategies of machine-learning-based quantitative structure-activity relationship models. iScience 2021, 24, 103052. [Google Scholar] [CrossRef]
- Chakravarti, S.K.; Alla, S.R.M. Descriptor Free QSAR Modeling Using Deep Learning with Long Short-Term Memory Neural Networks. Front. Artif. Intell. 2019, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- Stitou, M.; Toufik, H.; Bouachrine, M.; Bih, H.; Lamchouri, F. Machine learning algorithms used in Quantitative structure—Activity relationships studies as new approaches in drug discovery. In Proceedings of the 2019 International Conference on Intelligent Systems and Advanced Computing Sciences (ISACS), Taza, Morocco, 26–27 December 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Ancuceanu, R.; Dinu, M.; Neaga, I.; Laszlo, F.G.; Boda, D. Development of QSAR machine learning-based models to forecast the effect of substances on malignant melanoma cells. Oncol. Lett. 2019, 17, 4188–4196. [Google Scholar] [CrossRef]
- Keyvanpour, M.R.; Shirzad, M.B. An Analysis of QSAR Research Based on Machine Learning Concepts. Curr. Drug Discov. Technol. 2021, 18, 17–30. [Google Scholar] [CrossRef]
- Mosier, P.D.; Jurs, P.C. QSAR/QSPR studies using probabilistic neural networks and generalized regression neural networks. J. Chem. Inf. Comput. Sci. 2002, 42, 1460–1470. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Mussa, H.Y.; Mitchell, J.B.O.; Glen, R.C. Classifying molecules using a sparse probabilistic kernel binary classifier. J. Chem. Inf. Model. 2011, 51, 1539–1544. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, J.; Saaidpour, S. Artificial neural network-based quantitative structural property relationship for predicting boiling points of refrigerants. QSAR Comb. Sci. 2009, 28, 1245–1254. [Google Scholar] [CrossRef]
- Shahlaei, M.; Fassihi, A.; Saghaie, L. Application of PC-ANN and PC-LS-SVM in QSAR of CCR1 antagonist compounds: A comparative study. Eur. J. Med. Chem. 2010, 45, 1572–1582. [Google Scholar] [CrossRef]
- Ajmani, S.; Jadhav, K.; Kulkarni, S.A. Three-dimensional QSAR using the k-nearest neighbor method and its interpretation. J. Chem. Inf. Model. 2006, 46, 24–31. [Google Scholar] [CrossRef]
- Myint, K.Z.; Wang, L.; Tong, Q.; Xie, X.Q. Molecular fingerprint-based artificial neural networks QSAR for ligand biological activity predictions. Mol. Pharm. 2012, 9, 2912–2923. [Google Scholar] [CrossRef]
- Yaffe, D.; Cohen, Y. Neural network based temperature-dependent quantitative structure property relations (QSPRs) for predicting vapor pressure of hydrocarbons. J. Chem. Inf. Comput. Sci. 2001, 41, 463–477. [Google Scholar] [CrossRef]
- Burden, F.R.; Ford, M.G.; Whitley, D.C.; Winkler, D.A. Use of Automatic Relevance Determination in QSAR Studies Using Bayesian Neural Networks. J. Chem. Inf. Comput. Sci. 2000, 40, 1423–1430. [Google Scholar] [CrossRef]
- Espinosa, G.; Yaffe, D.; Arenas, A.; Cohen, Y.; Giralt, F. A fuzzy ARTMAP-based Quantitative Structure-Property Relationship (QSPR) for predicting physical properties of organic compounds. Ind. Eng. Chem. Res. 2001, 40, 2757–2766. [Google Scholar] [CrossRef]
- Burden, F.R.; Winkler, D.A. Robust QSAR models using bayesian regularized neural networks. J. Med. Chem. 1999, 42, 3183–3187. [Google Scholar] [CrossRef]
- Koutsoukas, A.; Lowe, R.; Kalantarmotamedi, Y.; Mussa, H.Y.; Klaffke, W.; Mitchell, J.B.O.; Glen, R.C.; Bender, A. Erratum: “in silico target predictions: Defining a benchmarking data set and comparison of performance of the multiclass naïve bayes and parzen-rosenblatt window”. J. Chem. Inf. Model. 2014, 54, 2180–2182. [Google Scholar] [CrossRef]
- Ghasemi, F.; Mehridehnavi, A.; Fassihi, A.; Pérez-Sánchez, H. Deep neural network in QSAR studies using deep belief network. Appl. Soft Comput. J. 2018, 62, 251–258. [Google Scholar] [CrossRef]
- Netzeva, T.I.; Schultz, T.W.; Aptula, A.O.; Cronin, M.T.D. Partial Least Squares modelling of the acute toxicity of aliphatic compounds to Tetrahymena pyriformis. SAR QSAR Environ. Res. 2003, 14, 265–283. [Google Scholar] [CrossRef] [PubMed]
- Schultz, T.W.; Cronin, M.T.D.; Netzeva, T.I.; Aptula, A.O. Structure-toxicity relationships for aliphatic chemicals evaluated with Tetrahymena pyriformis. Chem. Res. Toxicol. 2002, 15, 1602–1609. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Benfenati, E. QSAR modelling of aldehyde toxicity against a protozoan, Tetrahymena pyriformis by optimization of correlation weights of nearest neighboring codes. J. Mol. Struct. THEOCHEM 2004, 679, 225–228. [Google Scholar] [CrossRef]
- Castro, E.A.; Toropov, A.A.; Nesterova, A.I.; Nazarov, A.U. QSAR study of the toxic action of aliphatic compounds to the bacteria Vibrio fisheri based on correlation weighting of local graph invariants. J. Mol. Struct. THEOCHEM 2003, 639, 129–135. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Roy, D.R.; Giri, S.; Mukherjee, S.; Subramanian, V.; Parthasarathi, R.; Bultinck, P.; Van Damme, S. An atom counting and electrophilicity based QSTR approach. J. Chem. Sci. 2007, 119, 475–488. [Google Scholar] [CrossRef]
- Pecka, J.; Ponec, R. Simple analytical method for evaluation of statistical importance of correlations in QSAR studies. J. Math. Chem. 2000, 27, 13–22. [Google Scholar] [CrossRef]
- Parthasarathi, R.; Padmanabhan, J.; Subramanian, V.; Maiti, B.; Chattaraj, P.K. Toxicity analysis of 33′44′5-pentachloro biphenyl through chemical reactivity and selectivity profiles. Curr. Sci. 2004, 86, 535–542. [Google Scholar]
- Russell, R.C.G.; Williams, N.S.; Bulstrode, C.J.K. (Eds.) Bailey & Love’s Short Practice of Surgery, 23rd ed.; Arnold: London, UK, 2000. [Google Scholar]
- Jana, G.; Pal, R.; Sural, S.; Chattaraj, P.K. Quantitative structure-toxicity relationship: An “in silico study” using electrophilicity and hydrophobicity as descriptors. Int. J. Quantum Chem. 2020, 120, e26097. [Google Scholar] [CrossRef]
- Masand, V.H.; Mahajan, D.T.; Maldhure, A.K.; Rastija, V. Quantitative structure–activity relationships (QSARs) and pharmacophore modeling for human African trypanosomiasis (HAT) activity of pyridyl benzamides and 3-(oxazolo [4,5-b]pyridin-2-yl)anilides. Med. Chem. Res. 2016, 25, 2324–2334. [Google Scholar] [CrossRef]
- Héberger, K. Sum of ranking differences compares methods or models fairly. TrAC Trends Anal. Chem. 2010, 29, 101–109. [Google Scholar] [CrossRef]
- Kollár-Hunek, K.; Héberger, K. Method and model comparison by sum of ranking differences in cases of repeated observations (ties). Chemom. Intell. Lab. Syst. 2013, 127, 139–146. [Google Scholar] [CrossRef]
- Roy, D.R.; Giri, S.; Chattaraj, P.K. Arsenic toxicity: An atom counting and electrophilicity-based protocol. Mol. Divers. 2009, 13, 551–556. [Google Scholar] [CrossRef] [PubMed]
- Thanikaivelan, P.; Subramanian, V.; Raghava Rao, J.; Unni Nair, B. Application of quantum chemical descriptor in quantitative structure activity and structure property relationship. Chem. Phys. Lett. 2000, 323, 59–70. [Google Scholar] [CrossRef]



| GATS8c | Geary autocorrelation of lag-8/weighted by atomic charges |
| RDF40p | Radial distribution function-040/weighted by relative polarizabilities |
| RDF55s | Radial distribution function-055/weighted by relative I-state |
| E1 | 1st component accessibility directional WHIM index/weighted by relative I-state |
| RDF40m | Radial distribution function-040/weighted by relative mass |
| Model No. | Generalized Regression Equations | Undivided | Case 1 | Case 2 | Case 3 | ||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | SD | R2 | SD | R2 | SD | R2 | SD | ||
| 1 | pIC50 = a + b*GATS8c + c*RDF40p + d*RDF55s | 0.8284 | 0.1960 | 0.9182 | 0.1320 | 0.8216 | 0.1877 | 0.6971 | 0.2213 |
| 2 | pIC50 = a + b*GATS8c + c*RDF40p + d*ω | 0.3743 | 0.3742 | 0.4839 | 0.1872 | 0.3764 | 0.1546 | 0.2351 | 0.4378 |
| 3 | pIC50 = a + b*GATS8c + c*ω + d*RDF55s | 0.7599 | 0.2318 | 0.8325 | 0.1768 | 0.7829 | 0.2063 | 0.5114 | 0.2415 |
| 4 | pIC50 = a + b*ω + c*RDF40p + d*RDF55s | 0.7113 | 0.2542 | 0.7644 | 0.1983 | 0.7098 | 0.2283 | 0.4961 | 0.2529 |
| 5 | pIC50 = a + b*GATS8c + c*RDF40p + d*ω2 | 0.3650 | 0.3770 | 0.4825 | 0.1827 | 0.3901 | 0.1447 | 0.2211 | 0.4098 |
| 6 | pIC50 = a + b*GATS8c + c*ω2 + d*RDF55s | 0.7592 | 0.2322 | 0.8323 | 0.1762 | 0.7853 | 0.2058 | 0.5817 | 0.2299 |
| 7 | pIC50 = a + b*ω2 + c*RDF40p + d*RDF55s | 0.7068 | 0.2562 | 0.7620 | 0.1977 | 0.7101 | 0.2301 | 0.4645 | 0.2575 |
| 8 | pIC50 = a + b*GATS8c + c*ω + d*ω2 | 0.3285 | 0.3877 | 0.4334 | 0.1888 | 0.2506 | 0.1882 | 0.1725 | 0.4421 |
| 9 | pIC50 = a + b*ω + c*RDF40p + d*ω2 | 0.3660 | 0.3767 | 0.4746 | 0.1781 | 0.2911 | 0.1800 | 0.1810 | 0.4594 |
| 10 | pIC50 = a + b*ω + c*ω2 + d*RDF55s | 0.6836 | 0.2661 | 0.7637 | 0.2014 | 0.6962 | 0.2212 | 0.5163 | 0.2364 |
| 11 | pIC50 = a + b*E1s + c*RDF40m + d*GATS6m | 0.3056 | 0.3942 | 0.3991 | 0.1983 | 0.3199 | 0.2404 | 0.1159 | 0.2055 |
| 12 | pIC50 = a + b*E1s + c*RDF40m + d*ω | 0.3647 | 0.3771 | 0.4949 | 0.1839 | 0.3196 | 0.1784 | 0.2793 | 0.3939 |
| 13 | pIC50 = a + b*E1s + c*ω + d*GATS6m | 0.4847 | 0.3396 | 0.5936 | 0.2275 | 0.5415 | 0.2138 | 0.3369 | 0.3171 |
| 14 | pIC50 = a + b*ω + c*RDF40m + d*GATS6m | 0.4758 | 0.3425 | 0.5824 | 0.2177 | 0.5019 | 0.2127 | 0.3263 | 0.3134 |
| 15 | pIC50 = a + b*E1s + c*RDF40m + d*ω2 | 0.3571 | 0.3793 | 0.4997 | 0.1769 | 0.3241 | 0.1706 | 0.2135 | 0.4273 |
| 16 | pIC50 = a + b*E1s + c*ω2 + d*GATS6m | 0.4763 | 0.3424 | 0.5839 | 0.2266 | 0.5473 | 0.2083 | 0.2648 | 0.3481 |
| 17 | pIC50 = a + b*ω2 + c*RDF40m + d*GATS6m | 0.4666 | 0.3455 | 0.5708 | 0.2181 | 0.5105 | 0.2030 | 0.2518 | 0.3441 |
| 18 | pIC50 = a + b*E1s + c*ω + d*ω2 | 0.3421 | 0.3421 | 0.4673 | 0.1865 | 0.2898 | 0.1777 | 0.1339 | 0.4681 |
| 19 | pIC50 = a + b*ω + c*ω2 + d*GATS6m | 0.4784 | 0.3417 | 0.5861 | 0.2301 | 0.4044 | 0.2680 | 0.1784 | 0.3648 |
| 20 | pIC50 = a + b*ω + c*RDF40m + d*ω2 | 0.3583 | 0.3790 | 0.4822 | 0.1844 | 0.2185 | 0.2091 | 0.1454 | 0.4405 |
| 21 | pIC50 = a + b*ω + c*ω2 | 0.3272 | 0.3813 | 0.4540 | 0.1813 | 0.2922 | 0.1765 | 0.1288 | 0.4612 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pal, R.; Patra, S.G.; Chattaraj, P.K. Quantitative Structure–Toxicity Relationship in Bioactive Molecules from a Conceptual DFT Perspective. Pharmaceuticals 2022, 15, 1383. https://doi.org/10.3390/ph15111383
Pal R, Patra SG, Chattaraj PK. Quantitative Structure–Toxicity Relationship in Bioactive Molecules from a Conceptual DFT Perspective. Pharmaceuticals. 2022; 15(11):1383. https://doi.org/10.3390/ph15111383
Chicago/Turabian StylePal, Ranita, Shanti Gopal Patra, and Pratim Kumar Chattaraj. 2022. "Quantitative Structure–Toxicity Relationship in Bioactive Molecules from a Conceptual DFT Perspective" Pharmaceuticals 15, no. 11: 1383. https://doi.org/10.3390/ph15111383





