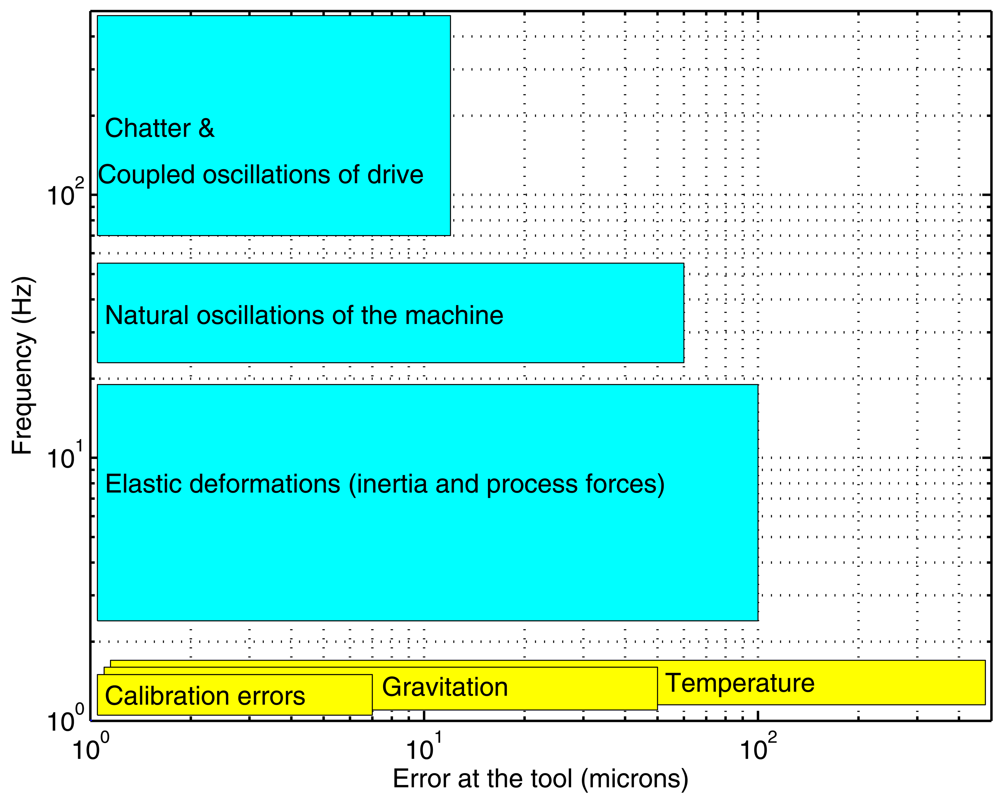
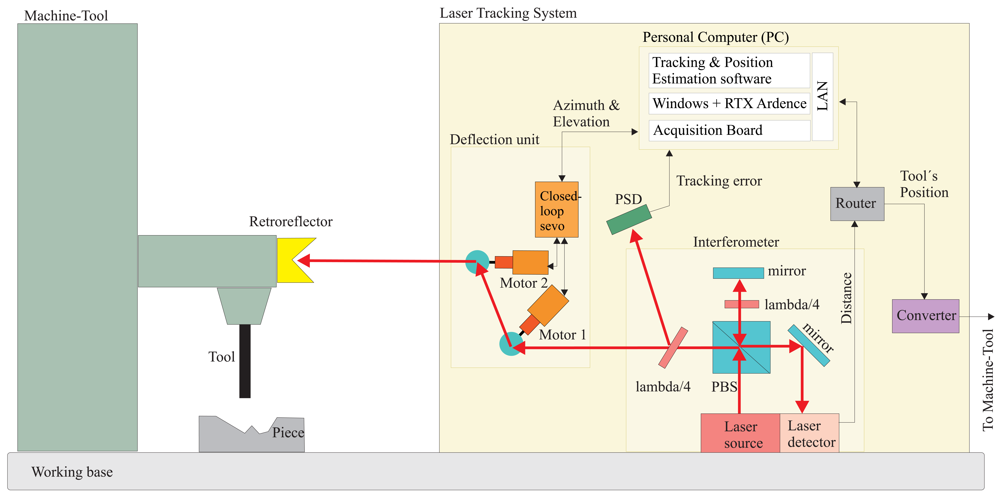
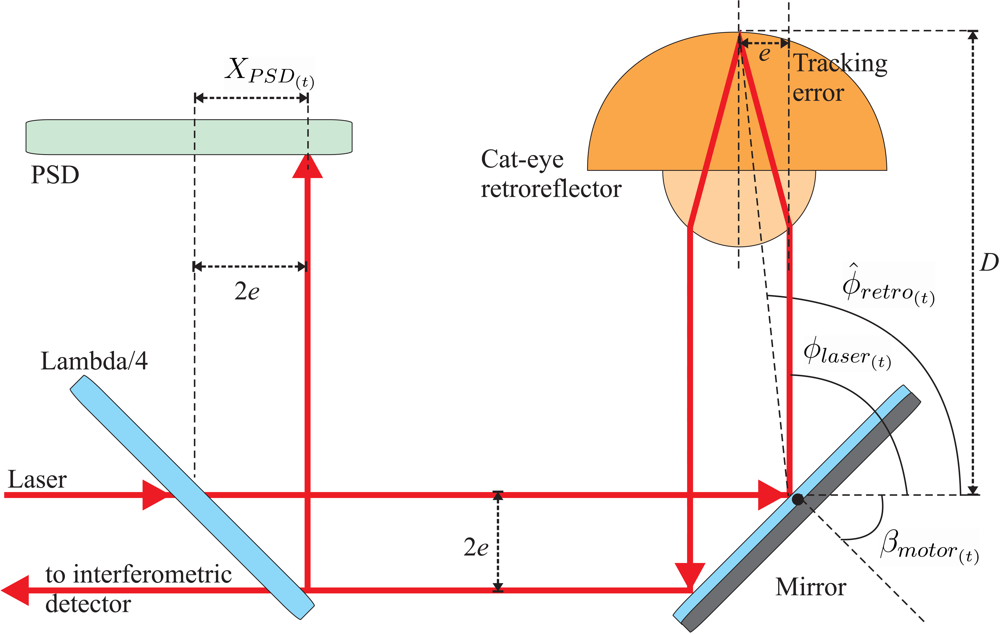
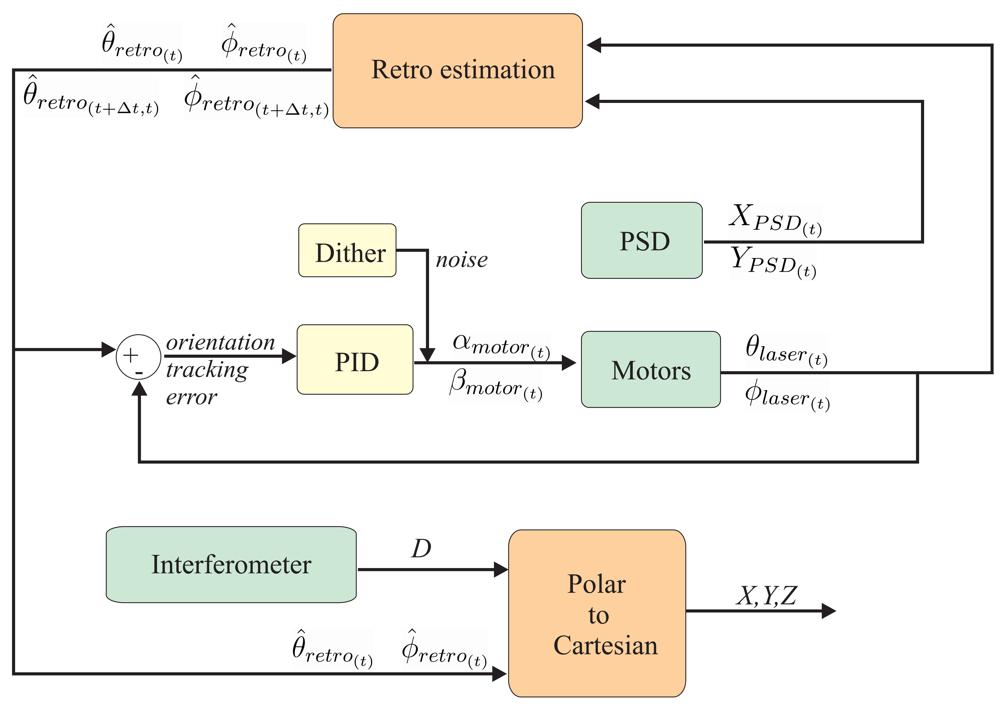
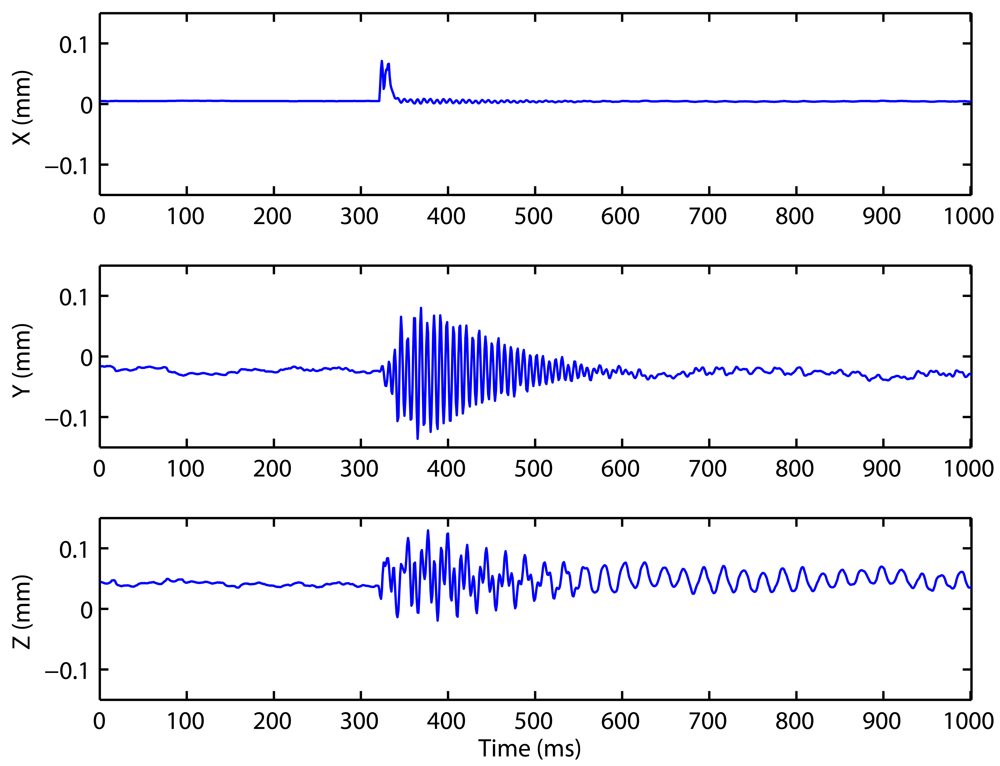
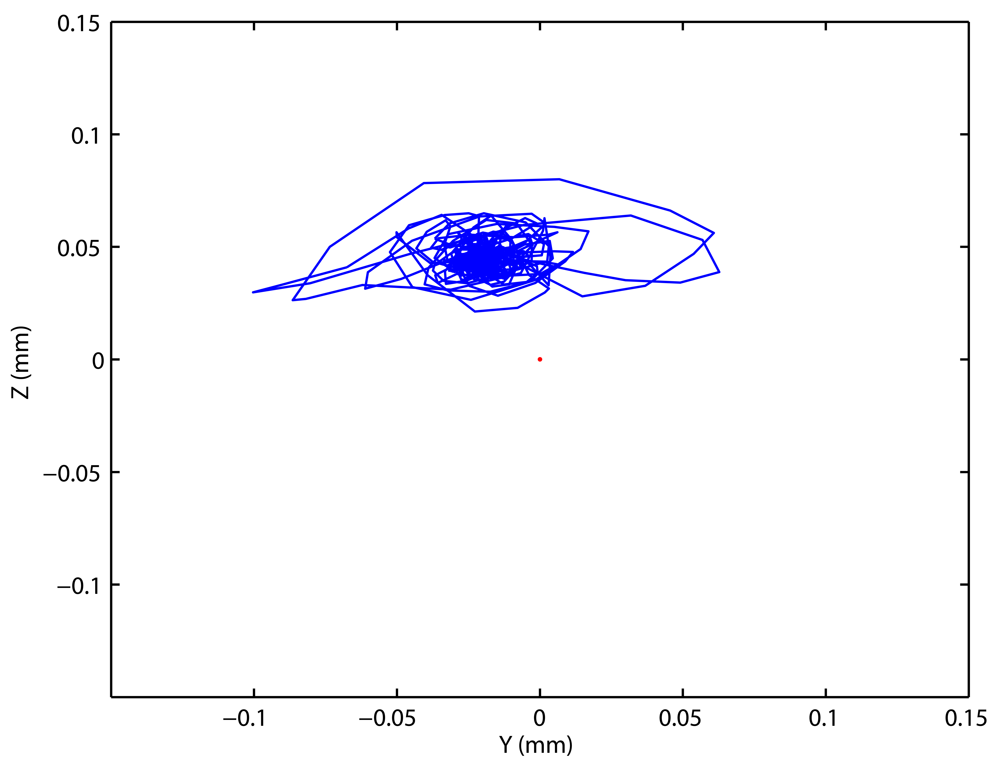
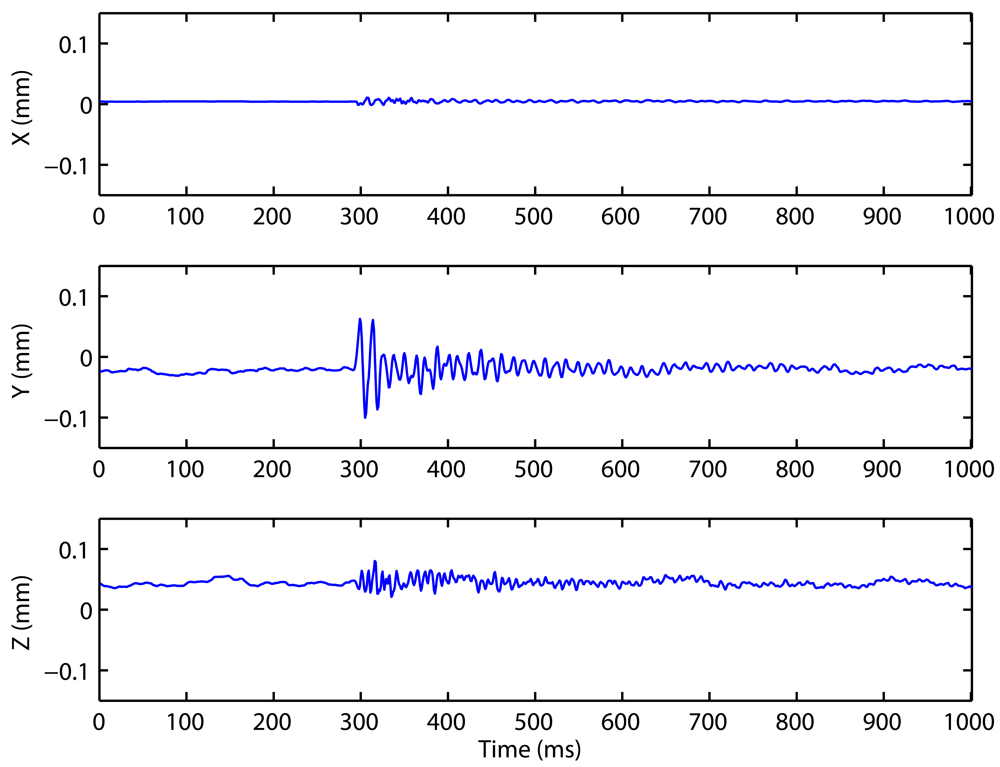
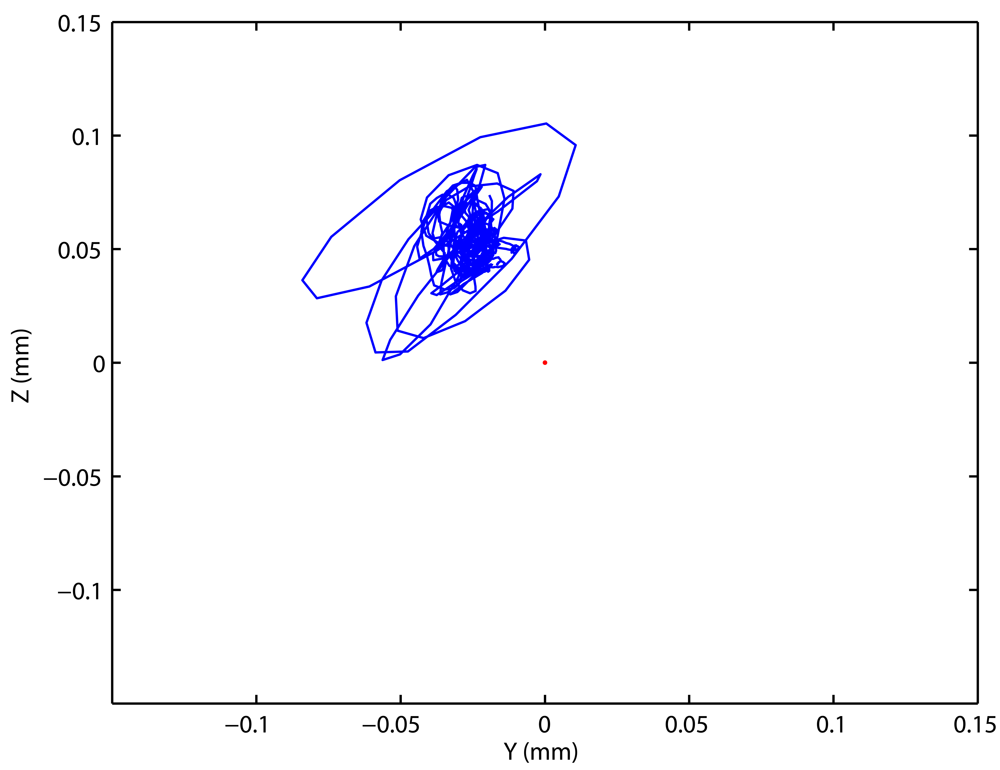
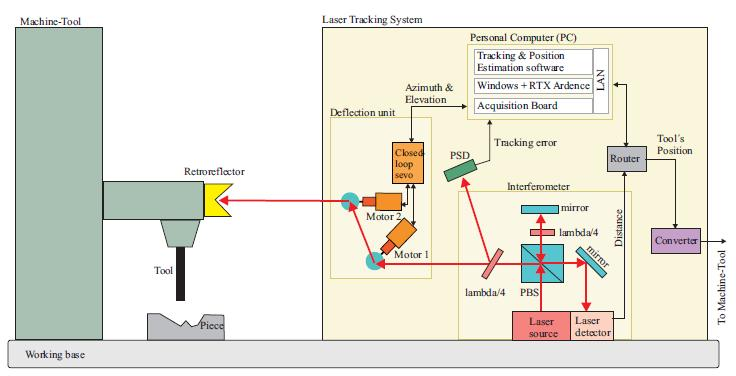
2.1. Measurement Principle and Main Components
Our laser tracking system, named LaserTrack, measures the three-dimensional (3D) position of a reference close to the tool in a machine-tool (see
Figure 2 for a conceptual scheme of the LaserTrack system). The reference is a retroreflector-like passive element. An active laser pointing device, positioned on a working base close to the piece and the machine-tool, continuously tracks the reference. The active tracking system estimates the range to the reference, by interferometry, and the azimuth and elevation angles with rotational encoders. A Positioning Sensing Device (PSD) is used to measure the tracking error (offset between the laser spot on the retro and its geometric center). Assuming that a perfect tracking of the reference is achieved, then a polar to cartesian transformation gives an estimation of the reflector's 3D position.
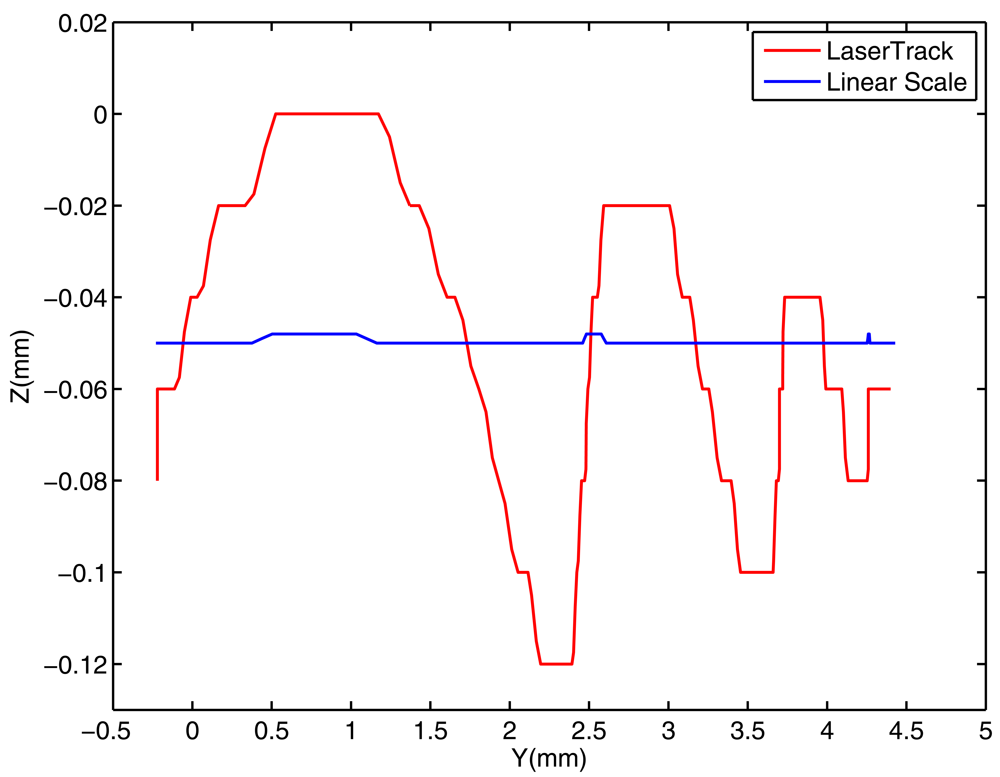
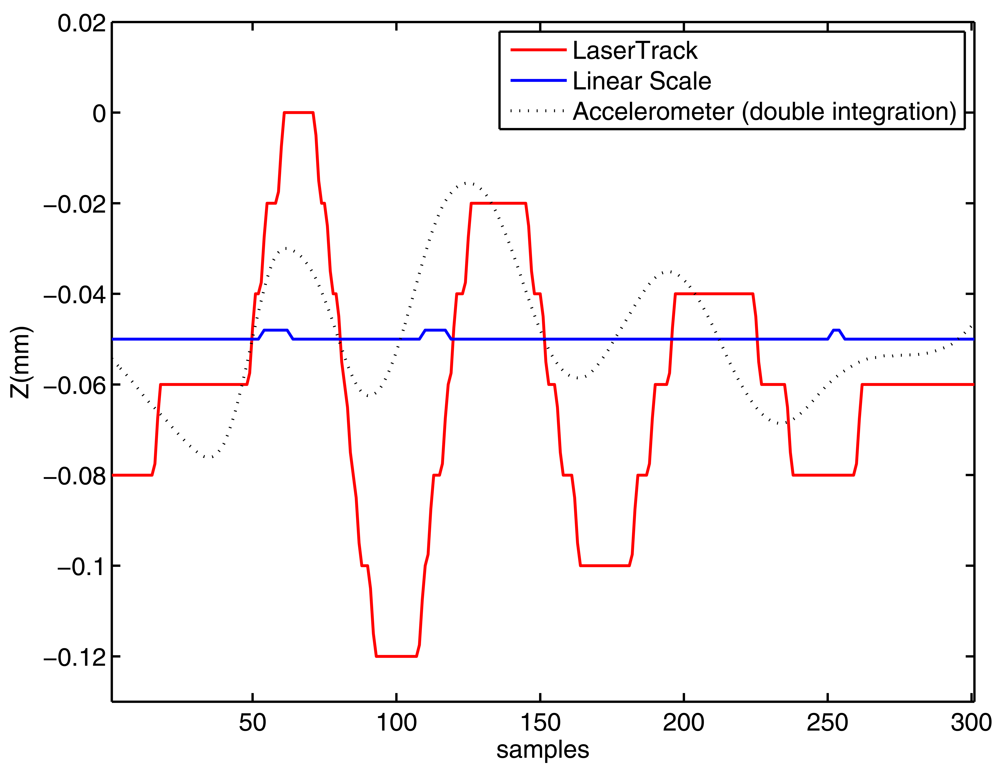
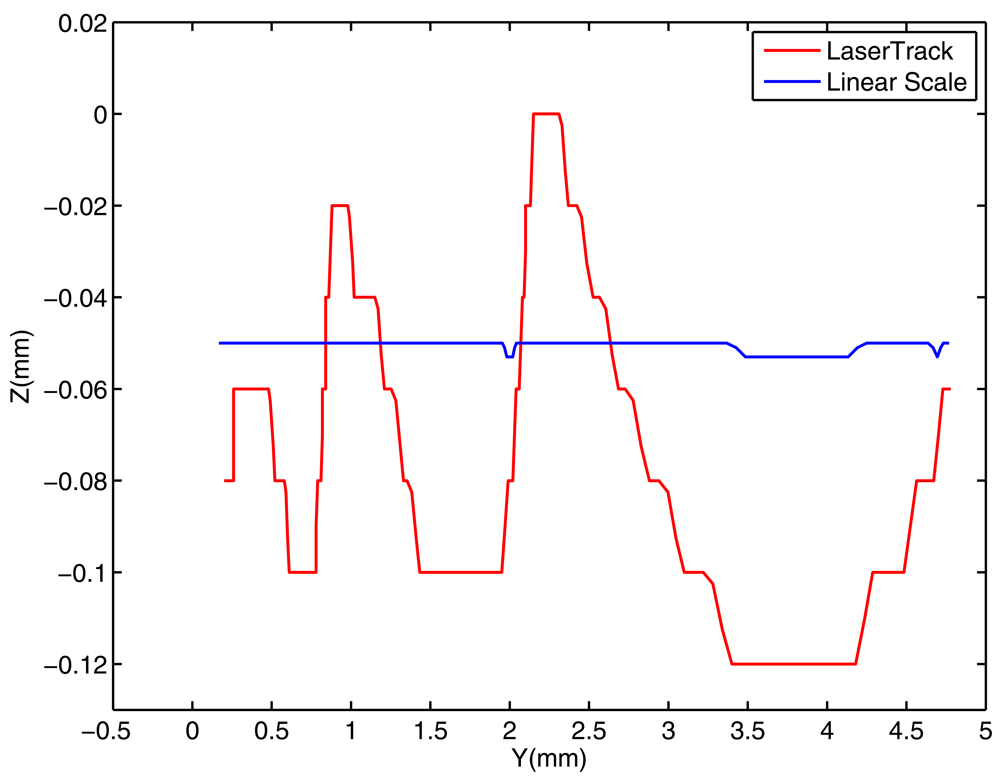
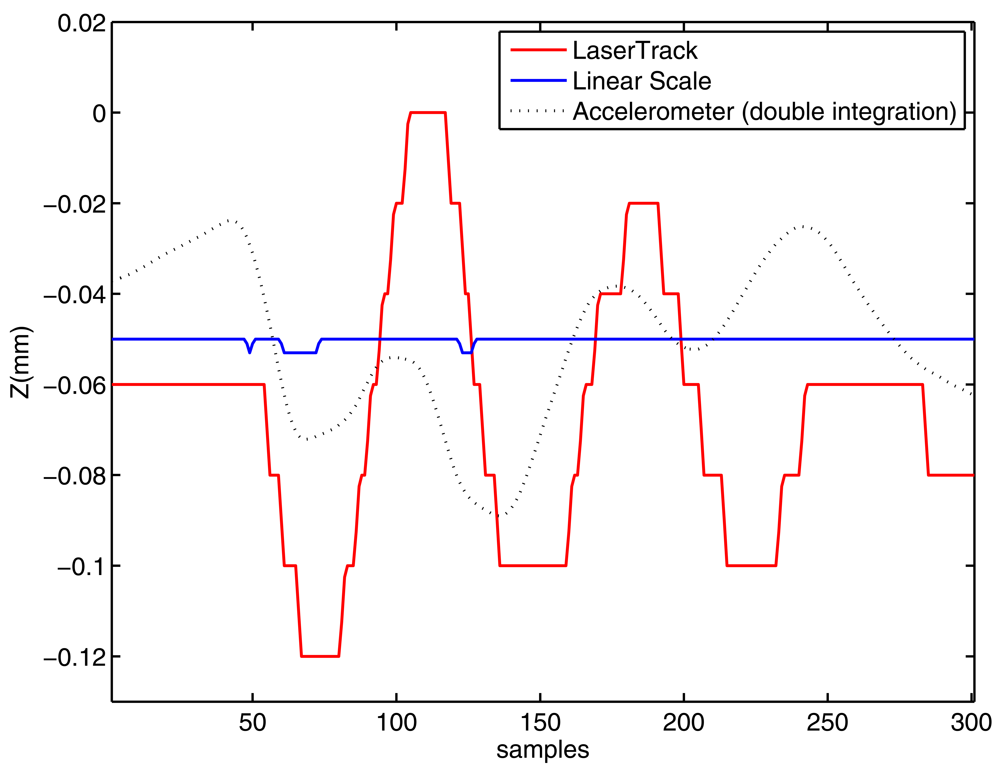
Note that the system estimates the position of the retroreflector, and not the one of the tool itself. However, if the reference is close enough to the tool, then it is expected to obtain good estimations of the actual position, oscillations and deformations on the tool; better than those deduced from the machine-tool's linear scales, at least.
The principal components of our laser tracking system are:
The optical reference to be fixed close to the tool of the machine-tool.
A laser interferometer to measure the distance to the reference reflector.
A deflection unit with two motorized mirrors to bend the laser beam towards the reference.
A Position Sensitive Detector (PSD) for estimating the tracking error.
A Personal Computer (PC) for commanding the mirrors to track the reference and to estimate its position.
A converter for translating in real-time the position estimations into a format that the Machine-Tool can understand.
2.2. The Optical Reference
The optical reference used to track the machine-tool position is a retroreflector. It returns back the incoming laser beam through a path that must be coaxial or parallel to the incident one. This reference is a totally passive component, i.e., it does not need any cabling for power supply.
Solid-glass and hollow corner cube retro-reflectors were initially used, but their performance was not ideal. Considering we operate at vertex incidence, i.e., the system tries to keep the laser beam pointing on the vertex or center of the retro-reflector, then after a reflection it generates undesirable star-like laser beam cross-sections. In addition, solid-glass reflectors suffered from a secondary reflection on the first facet of the glass. We finally used a cat-eye reflector, which has a smooth spherical reflection surface and therefore provides an unaltered laser beam cross-section which results beneficial for the interferometer measurements.
2.3. The Interferometer with Vertex Incidence for Range Estimation
The ranging measurement system is based on the interferometric Michelson-Morley principle. The design and components have been selected to operate with vertex incidence on the retro-reflector. This is necessary to unambiguously determine the position of the retro-reflector. As a consequence the optical arrangement considers a coaxial beam propagation.
Figure 3 shows the implemented optical arrangement. An helium-neon (632.8 nm) laser source (1) with a long coherent length (Limtek LS 10.3) is used as emitter having a 45-degrees polarized beam directed to a polarizing cube (2) which splits the beam in two orthogonally polarized beams: the transmission beam in the reference arm with a vertical state of polarization, and the reflected beam in the measurement arm with a horizontal state of polarization. As it is known, a reflecting element for each arm is necessary in a Michelson-Morley interferometer. Our system uses a first-surface mirror (4) for reference arm and the above mentioned cat-eye retroreflector (9) for the measurement arm [
9].
The reference wing (2-3-4) is needed to feed the interferometer detector (12) with a stable reference laser beam. The transmitted beam in (2) reaches mirror (4) after passing through a quarter wave plate (3) whose transmission axis is oriented 45 degrees from the vertical. Mirror (4) returns the beam back towards the polarizing cube (2) passing again through the quarter wave (3) plate. As the quarter wave plate (3) is crossed twice in the reference arm, the polarizing state of the incoming beam in the polarizing cube is rotated 90 degrees and a reflection in (2) is achieved.
The measurement wing (2-5-6-7-8-9) provides the capacity to measure the linear displacement along the beam axis. The reflected beam in (2) is sent to a pair of galvanometric mirrors (7, 8) after a single pass through another quarter wave plate (5) and a 90° bending mirror (6). The galvanometric mirrors (7,8) redirect the beam towards the retro-reflector attached to the machining head (9). After that, the beam travels along the same path in the opposite direction, thus having a new incidence in the quarter wave plate (5). Then, the measurement beam reaches the polarizing cube (2) with a vertical polarization state. Due to the double pass through the quarter wave plate (5), a transmission is achieved on the polarization cube (2).
Both beams, reference and measurement, travel together from the polarizing cube (2) to a final mirror (11) that redirects them to the interferometric detector (12) to evaluate the relative linear displacement of the retro-reflector along the laser beam axis.
2.4. The Deflection Unit with Motorized Mirrors
The
deflection unit, inserted along the measurement arm of the interferometer (7-8 in
Figure 3), pursues the steering of the laser beam in order to keep track of the retro-reflector. A good tracking is achieved when the laser beam points to the center of the retro-reflector within an error of ±1 mm. Therefore, for most machine-tool dynamics, it must have a fast response time (
<1 ms), a high positioning accuracy (below 3 micro-radians) and a sufficient bending range (above ±10°).
We studied several bending technologies for beam deflection. Acousto-optical and electro-optical refractive solutions have very fast response times, but they have a poor resolution (above 100 micro-radians), as well as a limited bending range. The limited bending range (below ±3°) is also the main restriction of mirrors driven by piezoelectric motors. Gimballed mirrors have a good excursion range and accuracy but they have a low angular acceleration. The best performance compromise is probably found with galvanometric motors, which mainly fulfil all the requirements but with a limited angular position accuracy (about 10 micro-radians).
We use in our system two independent light-weight and small size mirrors (15 mm of diameter), each of them commanded by one galvanometric motor (VM2015S from GSI-Lumonics). The cylindrical body of both motors can be seen inserted in the black mounting frame (7-8) in
Figure 3. Both mirrors are inside this mounting frame. The first reflecting mirror (7) changes the azimuth of the laser beam and the second mirror (8) controls its elevation.
Each motor is controlled with an stand-alone closed-loop servo (Mini-SAX controller from GSI Lumonics), which was tuned for accurate positioning. This controller has a built-in heating module to keep the motors at a constant temperature. An analog ±3 volt reference is used to command the absolute position of each motor; this signal is generated from the D/A card (14 bits) at the PC. The actual orientation of each mirror is available throughout an analog signal outputted by an absolute capacitive encoder, which is read by the A/D card (16 bits) at the PC. The acquisition board used is the model APCI-3120fromAddi-Data.
We modelled the galvanometric motors for a better knowledge of their actual deflection when a voltage,
V, is applied to them. A second-order transfer function is fitted to several amplitude step responses. The discrete state-space representation for a sampling interval, Δ
T, of 200 microseconds is:
We used this model to filter out the original angular readings, as provided from the capacitive encoder, which resulted quite noisy (3σ = 52 micro-radians). After this refinement, the noise was reduced to less than 1 micro-radian (3σ), without adding any time delay.
2.5. The Position Sensitive Detector (PSD)
A Position Sensitive Detector measures the location of a light spot in one or two-dimensions. We use a two-dimensional PSD to check whether the laser beam is pointing to the center of the retro-reflector. Any deviation of the laser from retro-reflector's center is known as the tracking error (e).
In our implementation (see
Figure 3), we use a bidimensional PSD (10) from On-TRACK Inc (model PSM2-10). It is a 3-layered P-I-N-doped photodiode with a uniform resistivity and four anodes in the first layer. The incident light creates charges on this layer that flow to the anodes. Current intensities at each anode are used to estimate the spot's position in two dimensions. This PSD has a 10 by 10 mm active area and a spectral response from 400 to 1,100 nanometers. The response time is 0.4 microseconds, it has a sub-micron resolution, but a limited all-range accuracy of ±30 microns. We tested the device in our lab and we found that the accuracy was about ±3microns if the laser spot does not separate more than 100 microns from its center.
Inserted in the measurement arm of the interferometric system, our PSD (10 in
Figure 3) collects part of the returned beam after a reflection on the air-glass interface of the quarter wave plate (5). During the initial calibration stage, the quarter wave plate (5) is oriented using a tilt-positioning mount, in order to achieve a perfect incidence at the center of the PSD sensitive area (10) meanwhile the beam hits the retro-reflector (9) at its vertex.
2.6. Retro-reflector Tracking
As already mentioned, the
tracking error (
e) is the lateral deviation of the incident laser with respect to the center of the retro-reflector. If a tracking error occurs, then the incident and return laser beams separate each other by 2 times
e. This inter-beam separation is the one sensed by the PSD (see
Figure 4). We admit a maximum beam separation of about 2 mm, i.e., a maximum
tracking error of about 1 mm. Larger beam separations can cause the loss of the retro-reflector, because of insufficient overlapping between the reference and measuring beams at the interferometric detector (12 in
Figure 3), or due to a blockage of the returned laser beam by some of the mounting frames.
Tracking errors of a millimeter does not mean a poor retro-reflector positioning accuracy. There is a correspondence between the X-Y offset in the PSD (XPSD(t), YPSD(t)) and the azimuth and elevation tracking errors, at a given time t. So, combining laser beam's azimuth and elevation angles (ϕlaser(t), θlaser(t)) with the PSD readings and the distance to the retro-reflector, D, we can estimate the angular position of the center of the retro-reflector (ϕretro(t), ϕretro(t)):
Even though the retro-reflector position can be estimated from the PSD and the laser angles, it is preferred to keep the PSD offset as low as possible in other to operate in the most accurate range of the PSD (+100 microns). This can be achieved by a tight track of the optical reference.
The tracking error can be minimized by steering the laser beam towards the center of the retro-reflector. As the retro-reflector is expected to move along a predictable trajectory, it is possible to anticipate the laser movement towards the position where the retro is expected to be at next time interval. Some predictive control algorithms for tracking, use the information gathered in its present and previous states to estimate the future velocity and acceleration in Cartesian coordinates (X,Y,Z) [
3,
10]. Shirinzadeh proposes a controller that is based on Taylor series to calculate the future position [
10]. Whereas, Vinczce minimizes a tracking-error cost function to estimate the future target position [
3]. Both algorithms present the disadvantage of being highly sensitive to noise, so a Kalman filters has to be used [
11,
12].
Our target-tracking algorithm uses the orientation of the laser beam at time
t (
ϕlaser(t) and
θlaser(t)) and the offset readings at the PSD (
XPSD(t) and
YPSD(t)) to predict (an interval Δ
T ahead) the future position in polar coordinates of the retro-reflector (
ϕ̂retro(t+Δt;t),
θ̂ retro(t+Δt;t)) and its velocity (
ϕ̂retro(t+Δt;t),
θ̂ retro(t+Δt;t)) based on states and measurements in time t. The discrepancies between the predicted retro-reflector's orientation and the actual orientation of the laser beam is used by a PID controller (
Kp = 0.5,
Ki = 0.006) to command the motors in order to keep the reference on track. The correspondence between the angles in the motors (
αlaser(t),
βlaser(t)) and the laser beam orientation (
αlaser(t),
βlaser(t)) is a non-linear function that depends on the actual positioning and orientation of mirrors in the deflection unit. The layout of the tracking loop is illustrated in
Figure 5.
Note that a dither noisy signal is added to the PID output. This strategy is used to avoid some motor oscillations that could be generated by the limited resolution of the D/A card (14 bits). This angular quantization (47 microradians; 14 microns at 30 cm distance) could cause, otherwise, a continuous oscillation from one angular state to another neighboring state whenever the PID integral error component reaches a given value. The inserted dither noise, in amplitude, is half of the actual angular quantization, and it has a probability distribution proportional to the relative closeness to the two neighboring quantization states.
For a proper prediction of retro-reflector estimates with a reduced measurement noise impact, a g-h algorithm [
11] is used for estimating the position and velocity of the retro-reflector, assuming a constant velocity model:
where
x̂(t) can be the estimated angles in azimuth (
θ̂ retro(t)) or the elevation (
ϕ̂ retro(t)), and
x̂ (t) their rates of change. The predictions in time (
t + Δ
T) based on measurements and states in time (
t) are
x̂(t+Δt, t) and
x̂ (
t+Δ
t,t).
The selection of the g-h parameters depends on the dynamics of the target to be tracked, the desired accuracy and the sampling interval Δ
T [
11]. In our implementation, Δ
T is 200 microseconds, i.e., the tracking control loop is closed at a 5 kHz frequency. The chosen g-h parameters, as a compromise between filtering and response-time, were
g = 0.062 and
h = 0.002.
2.7. Position Estimation in Cartesian Coordinates
The retro-reflector spatial position (
X,Y,Z) is calculated by using the distance
D retrieved from the interferometer, the estimated azimuth and elevation angles of the retro-reflector (now denoted for simplicity as:
θretro and
ϕretro), and several parameters that depends on the mirror mounting on the deflection unit:
This calculation (
Equation 6) is just a polar to Cartesian coordinate transformation. The Cartesian coordinate system has the origin at the center of the first mirror. This polar-to-Cartesian transformation is offset by a translation
p = (
px,py,pz) which represents the point where the laser reflects at the second mirror (8 in
Figure 3). Point
p changes when the first mirror reorients for new azimuth angles. It also depends on the physical relative arrangement between both mirrors in the deflection unit. The position and orientation of mirror #2 (8 in
Figure 3) with respect to mirror #1 (7 in
Figure 3), is defined by a translation matrix,
T21, and a rotation matrix,
R21, which include static terms defined by the mounting dimensions, and dynamic parameters dictated by the orientation of motors (
αmotor and
βmotor). So,
p, and consequently
ϕlaser and
θlaser, are non-linear functions of:
αmotor, βmotor, T21 and
R21.
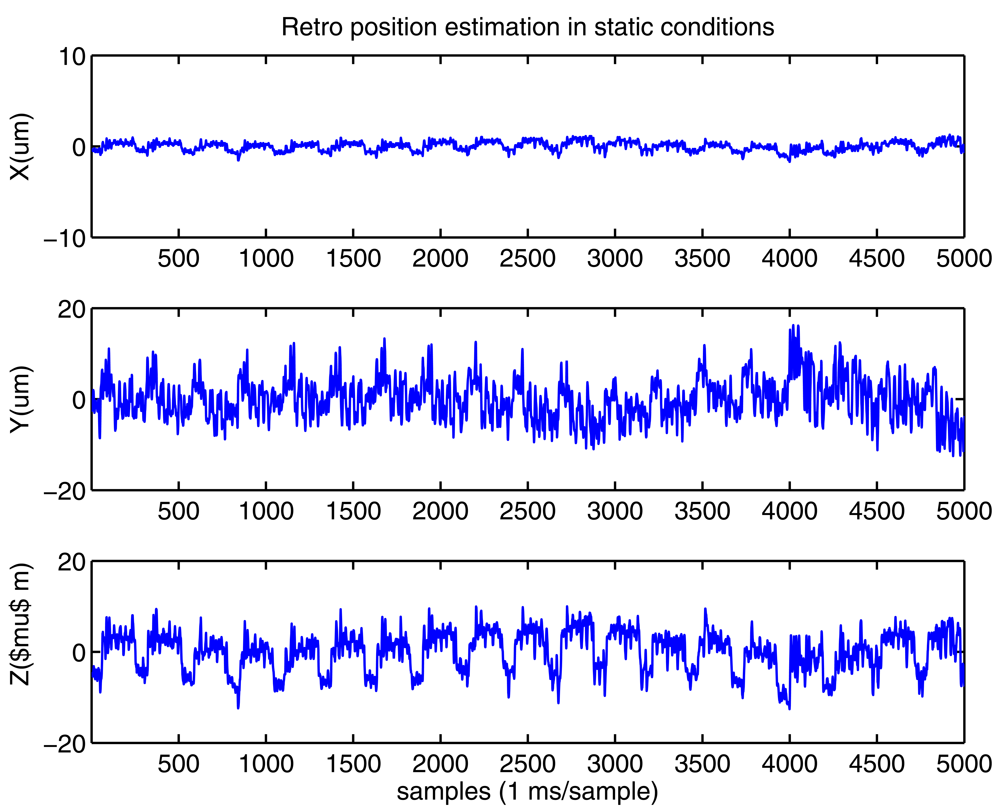
A final Kalman filter, assuming a constant velocity model, is used on each of the Cartesian coordinates to minimize some of the measurement errors propagated to this final estimation. A 3 milliseconds delay is introduced by this stage, and a 6.2 microns standard deviation (σ) is obtained for a constant retro-reflector position.
2.8. Calibration Methodology
As the 3D coordinates generated by the laser system must be coherent with the machine-tool coordinates, we assume that the machine tool has been calibrated for orthogonality, and therefore we calibrate our laser system with respect to the machine-tool coordinates in ideal or static conditions. The calibration is performed in two separate steps:
First, we determine the translational and rotational transformation between the machine-tool (M) and laser (L) coordinate reference systems. The obtained homogeneous matrix TM–L transforms coordinates in the machine system to the laser one (M⇒L). The inverse,
, does the opposite operation (L⇒M).
Second, we sequentially move the retro to a regular 3D-mesh of spatial points, and both the machine-tool and the laser retro-reflector coordinates are captured. This mesh is used for a fine correction of new position estimations based on a bilinear interpolation among the 8 closest points in the mesh. This type of calibration eliminates all non-modelled parameters in the laser system such as alignment and mounting errors.
The procedure to obtain the TM–L matrix consists in positioning the Machine-tool head in three different points [p0,p1,p2]. The first point p0 is arbitrary, the second is just a relative displacement d along X axis, i.e., p1=[p0x+d,p0y,p0z]. The last point, is just a displacement d along Z axis, so p2 = [ p0x,p0y,p0z+d]. Atypical value used by us for d is 20 cm. With the positions of these three points captured from the laser system, we can easily obtain the unitary vectors, along the M coordinate axes, seen from the L coordinate frame. And finally, we get the homogeneous matrix TM–L that allows us to translate any (X, Y, Z) position from the laser to the Machine-tool coordinate system, and viceversa.
The mesh of 3D spatial points must cover the expected working volume. The effectiveness of the double bilinear interpolations depends on the separation between points. We are not going to give the details of the implemented bilinear interpolation; however, we will illustrate its performance with a simulation.
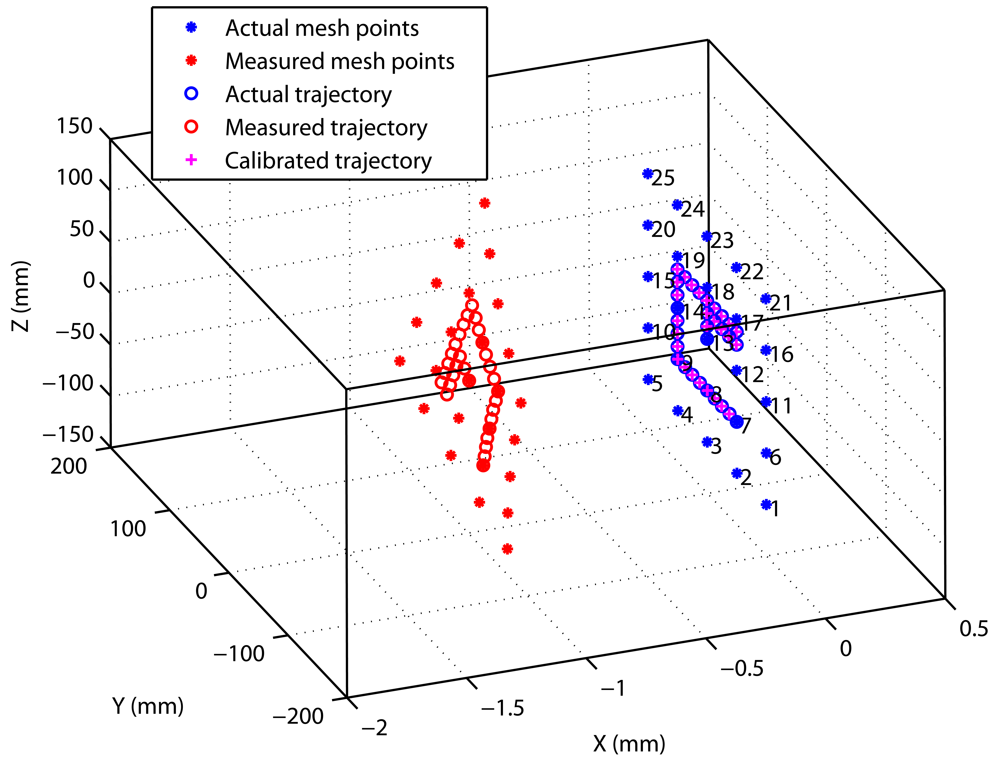
Figure 6 shows a 5
× 5 mesh grid, with points separated by 50 mm. Each of the 25 measured mesh points (red asterisks) corresponds to an ideal position (blue asterisks). Note that there is a significant error of several millimeters. In
Figure 6 a simulated trajectory close to the mesh is executed; we show the real trajectory (blue circles), as well as the measured estimations (red circles),and the trajectory points after the bilinear calibration (magenta pluses).
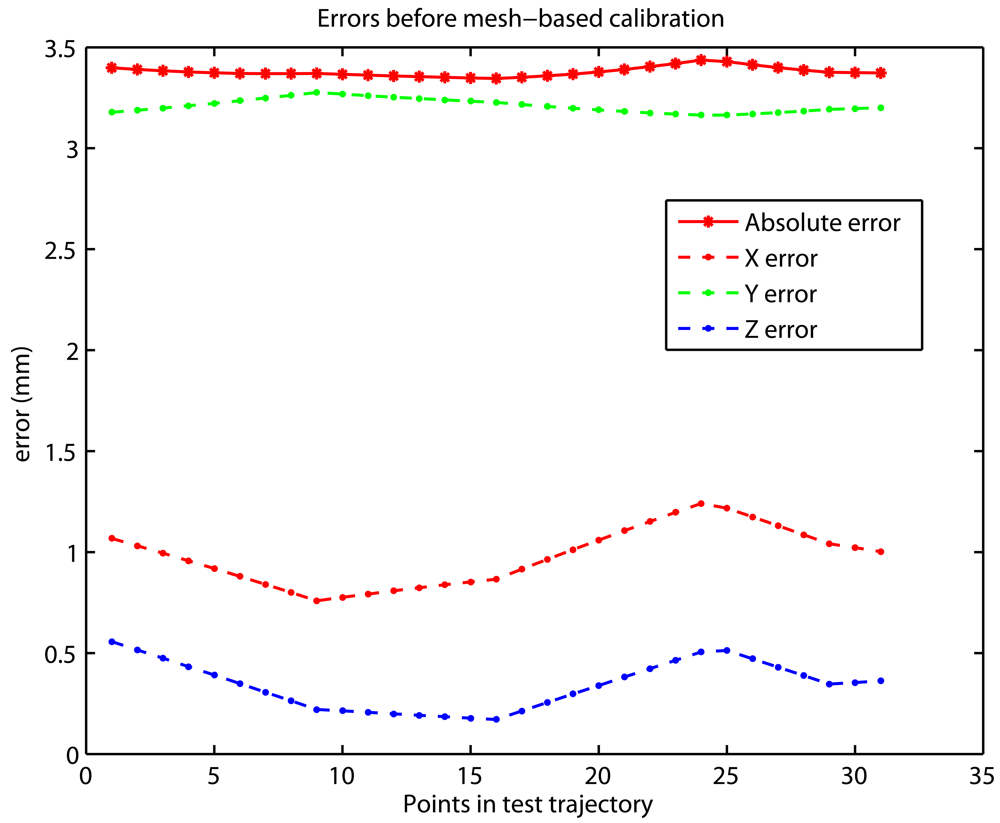
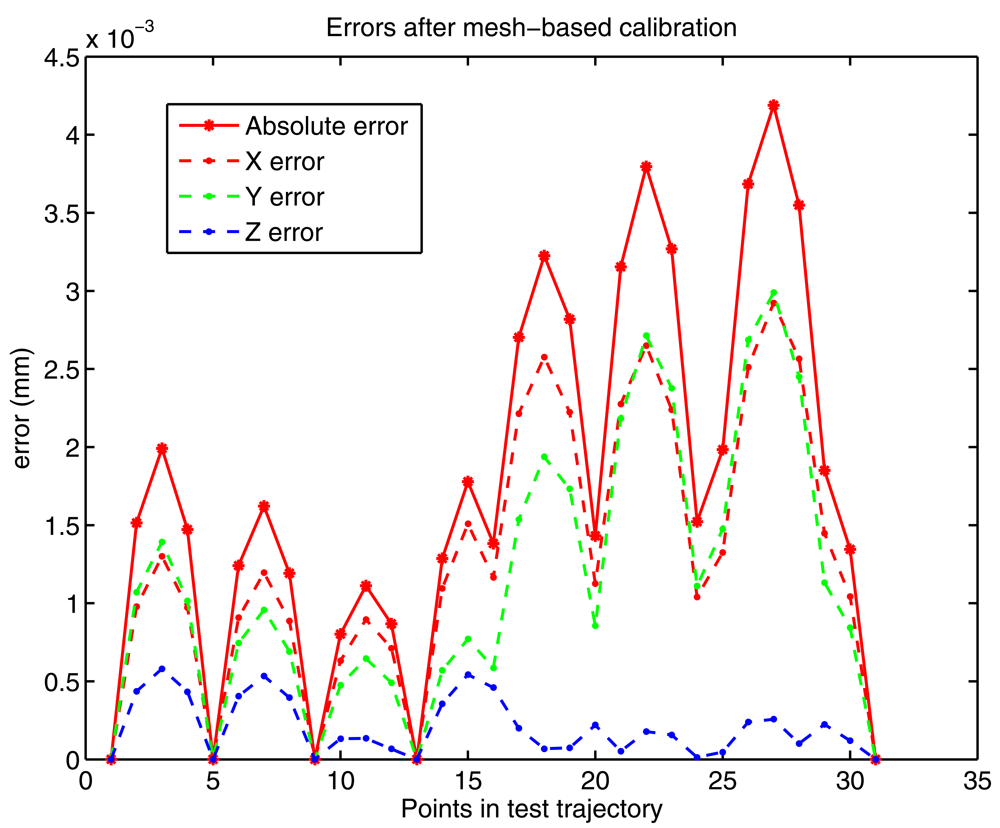
Figure 7a,b shows the errors before and after the calibration, respectively. Note that errors after calibration are null when revisiting points in the calibration mesh (points 1, 5, 9, 13 and 31). Between these revisited points, the error grows when the distance from current position to any of the mesh points in the grid increases. From these results, it is clear that the calibration procedure is effective, since a reduction of almost 3 orders of magnitude has been achieved (from 3.5 mm to 4.5 micrometers). These results were obtained with the points in the mesh separated by 50 mm. As stated before if a lower error is required then a shorter mesh-point separation must be used. For example in most of the tests performed in the next section, the mesh grid distance was only 5 mm. This guarantees that the positioning results are not affected by the performance of the calibration stage.