Surface Energy Balance Based Evapotranspiration Mapping in the Texas High Plains
Abstract
:1. Introduction
2. Materials and Methods
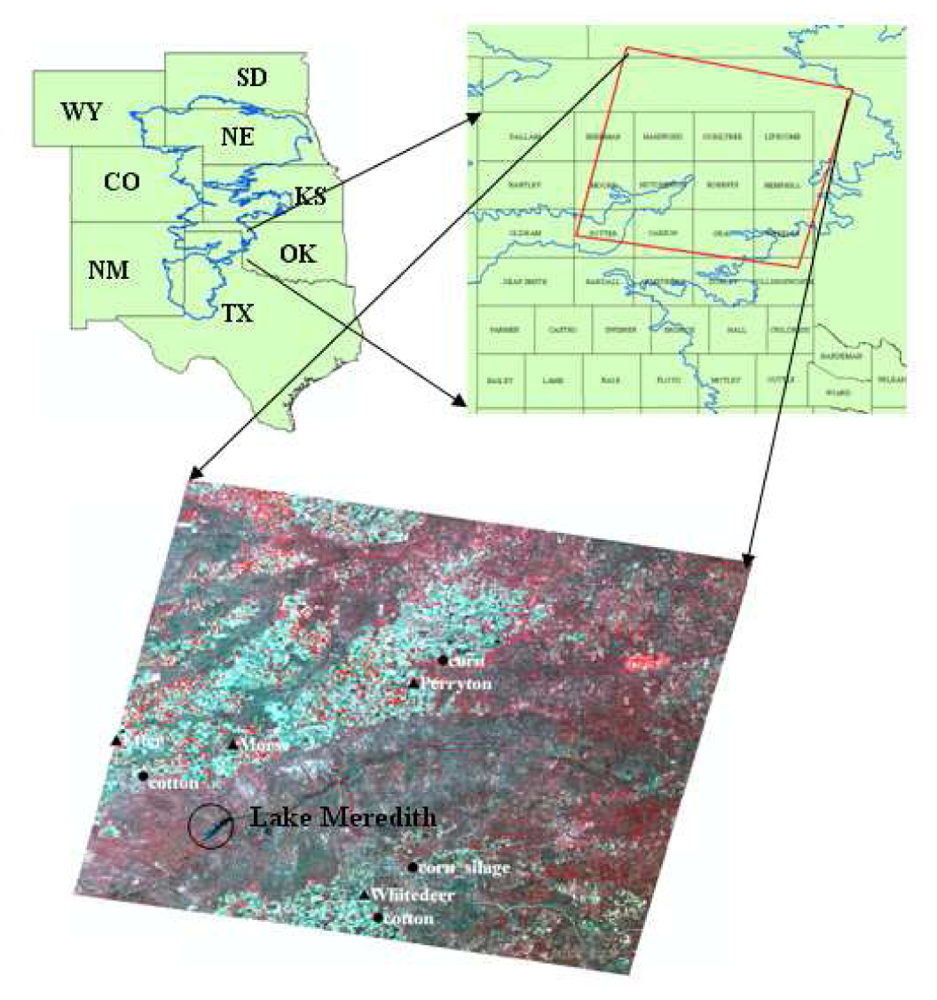
2.1. Study Area
2.1. METRIC
2.2. Data
2.3. Radiometric and Atmospheric Calibration of Satellite Images
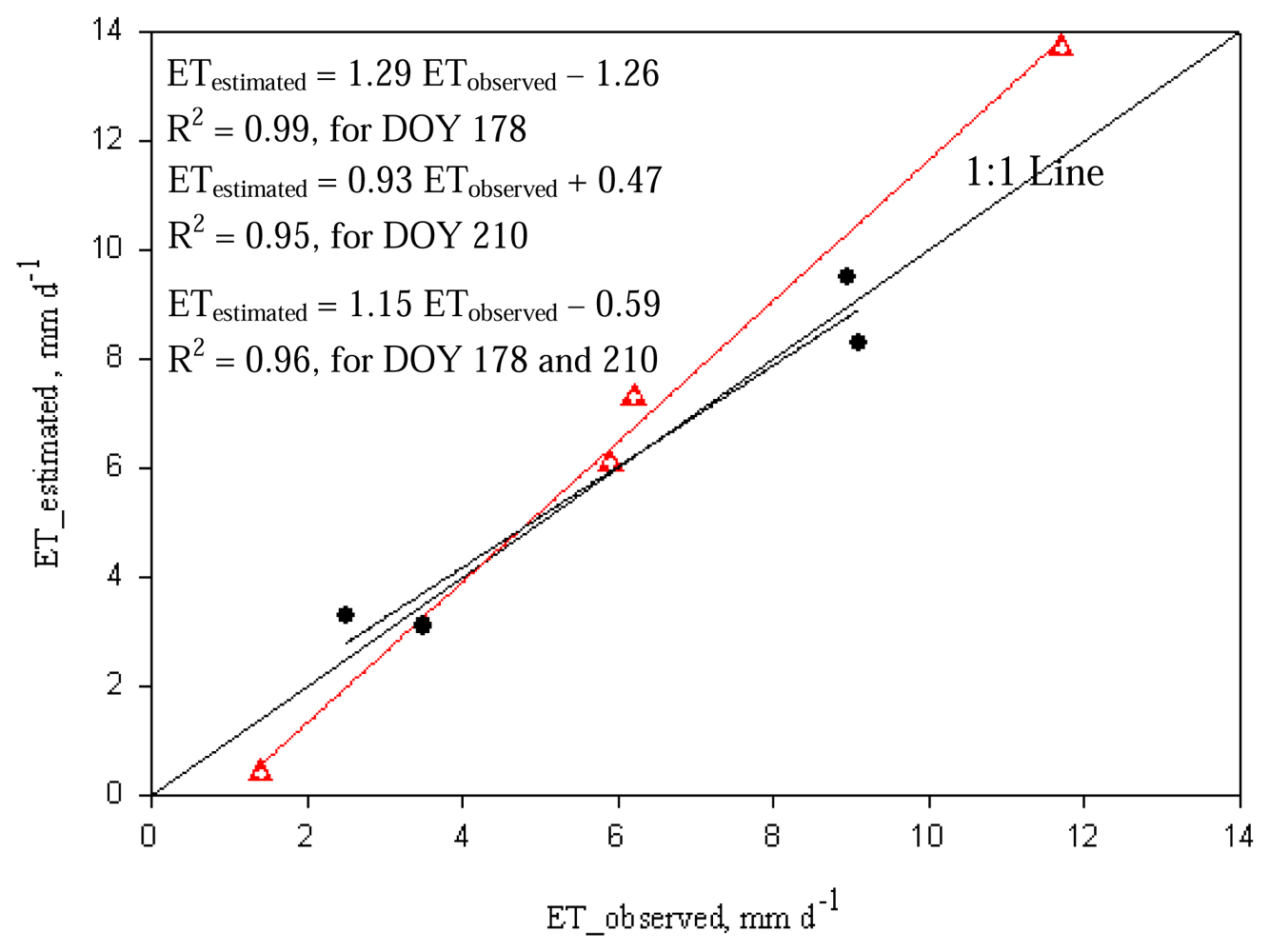
2.4. METRIC ET Verification
3. Results and Discussion
3.1. Surface Temperature
3.2. Net Radiation
3.3. Soil Heat Flux
3.4. Sensible Heat Flux
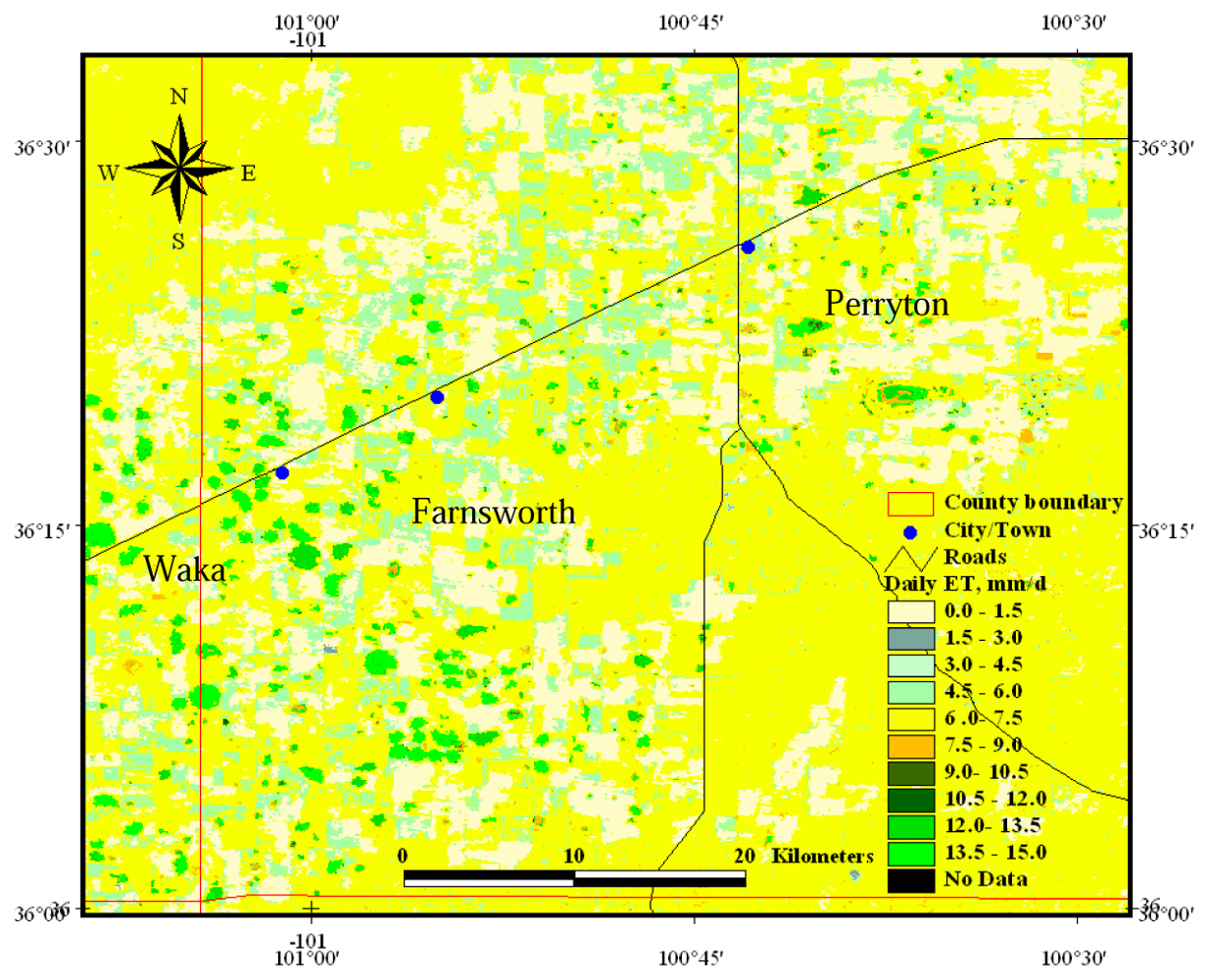
3.5. Daily ET
3. Conclusions
Appendix A
Gypsum Block Soil Moisture Readings
Appendix B
Root Zone Soil Water Content Computation
References and Notes
- Axtell, S. Ogallala Initiative. 2006. Ogallala Initiative Home Page: http://ogallala.tamu.edu/ (accessed on Aug 23, 2008).
- McGuire, V.L. Water-level changes in the high plains aquifer, predevelopment to 2003 and 2002 to 2003. U.S. Geological Survey Fact Sheet FS-2004-3097, 2004. available online: http://pubs.usgs.gov/fs/2004/3097.
- McGuire, V.L.; Johnson, M.R.; Schieffer, R.L.; Stanton, J.S.; Sebree, S.K.; Verstraeten, I.M. Water in storage and approaches to ground water management, high plains aquifer, 2000.; U.S. Geological Survey Circular 1243, 2000. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for Mapping evapotranspiration with internalized calibration (METRIC)-Model. ASCE J. Irrig. Drain. Eng. 2007, 133, 80–394. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. METRIC™: Mapping evapotranspiration at high resolution – application manual (version 2) for Landsat satellite imagery; University of Idaho, 2002; p. 59. [Google Scholar]
- Bastiaanssen, W.G.M. Regionalization of surface flux densities and moisture indicators in composite terrain: A remote sensing approach under clear skies in Mediterranean climates. Ph.D. Dissertation, CIP Data Koninklijke Blibliotheek, Den Haag, The Netherlands, 1995. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslang, A.A. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212-213, 198–212. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar]
- Gowda, P.H.; Chavez, J.L; Colaizzi, P.D; Evett, S.R.; Howell, T.A.; Tolk, J.A. ET mapping for agricultural water management: Present status and Challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar]
- Gowda, P.H.; Chavez, J.L.; Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Remote sensing based energy balance algorithms for mapping ET: Current status and future challenges. Trans. ASABE 2007, 50, 1639–1644. [Google Scholar]
- Tolk, J.A.; Evett, S.R.; Howell, T.A. Advection influences on evapotranspiration of alfalfa in a semiarid climate. Agro. J. 2006, 98, 1646–1654. [Google Scholar]
- NCSS Web Soil Survey. National Cooperative Soil Survey. Natural Resources Conservation Service, United States Department of Agriculture, 2006. available online: http://websoilsurvey.nrcs.usda.gov/app/ (accessed on Aug 23, 2008).
- Frye, R.G.; Brown, K.L.; McMahan, C.A. Vegetation/cover types of Texas. Bureau of Economic Geology, University of Texas at Austin, 2000. available online: http://www.beg.utexas.edu/Utopia/images/pagesizemaps/vegetation.pdf (accessed on Aug 23, 2008).
- New, L. Agri-Partner irrigation result demonstrations, 2005. Texas Cooperative Extension, Texas A&M System, 2005. available online: http://amarillo.tamu.edu/programs/agripartners/irrigation2005.htm (accessed on Aug 23, 2008).
- Tasumi, M. Progress in operational estimation of regional evapotranspiration using satellite imagery. Ph.D. Dissertation, University of Idaho, Moscow, ID, 2003. [Google Scholar]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar]
- Foken, F. 50 Years of the Monin-Obukhov similarity theory. Boundary-Layer Meteorol. 2006, 119, 431–447. [Google Scholar]
- Brutsaert. Evaporation into the atmosphere.; D. Reidel Publishing Company: Dordrecht, Holland, 1982; p. 299. [Google Scholar]
- ASCE-EWRI. Task Committee on Standardization of Reference Evapotranspiration, Principal. Report by the American Soc. Civil Engineers (ASCE), Report 0-7844-0805-X; In The ASCE Standardized Reference Evapotranspiration Equation; Allen, R.G., Walter, I.A., Elliott, R.L., Howell, T.A., Itenfisu, D., Jensen, M.E., Snyder, R.L., Eds.; 2005. [Google Scholar]
- TXHPET. Texas High Plains Evapotranspiration Network. 2006. TXHPET Home Page. http://txhighplainset.tamu.edu/index.jsp (accessed on Aug 23, 2008).
- TNPET. Texas North Plains ET Network. 2006. TNPET Home Page. http://amarillo2.tamu.edu/nppet/petnet1.htm (accessed on Aug 23, 2008).
- Gardner, W.H. Water content. In Methods of soil analysis, Part 1, 2nd Edition; Klute, A., Ed.; American Society of Agronomy Monograph, Soil Science Society of America: Madison, WI, 1986; No. 9. [Google Scholar]
- Yoder, R.E.; Johnson, D.L.; Wilkerson, J.B.; Yoder, D.C. Soil water sensor performance. Appl. Eng. Agric. 1998, 14, 121–133. [Google Scholar]
- Evans, R.; Cassel, D.K.; Sneed, R.E. Measuring soil water for irrigation scheduling: Monitoring methods and devices; North Carolina Cooperative Extension Service, 1996. available online: http://www.bae.ncsu.edu/programs/extension/evans/ag452-2.html (accessed on Aug 23, 2008).
- Chander, G.; Markham, M. Revised Landsat-5 TM radiometric calibration procedures and postcalibration dynamic ranges. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 2674–2677. [Google Scholar]
- Tasumi, M.; Trezza, R.; Allen, R.G.; Wright, J.L. Operational aspects of satellite-based energy balance models for irrigated crops in the semi-arid. U.S. J. Irrig. Drain. Sys. 2005, 19, 355–376. [Google Scholar]
- New, L.; Fipps, G. Center Pivot Irrigation; Bulletin B-6096; Texas Agricultural Extension Service-Texas A&M University System, 2000; p. 20. [Google Scholar]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. MODTRAN: a moderate resolution model for LOWTRAN 7; Report GL-TR-89-0122; Geophysics Laboratory: Bedford, Maryland, USA, 1989. [Google Scholar]
- Chávez, J.L.; Neale, C.M.U; Hipps, L.E.; Prueger, J.H.; Kustas, W.P. Comparing aircraft-based remotely sensed energy balance fluxes with eddy covariance tower data using heat flux source area functions. J. Hydromet. 2005, 6, 923–940. [Google Scholar]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Comparison of five models to scale daily evapotranspiration from one-time-of-day measurements. Trans. ASABE 2006, 49, 1409–1417. [Google Scholar]
- Howell, T.A.; Evett, S.R.; Tolk, J.A.; Schneider, A.D.; Steiner, J.L. Evaporation of Corn– Southern High Plains. In Evapotranspiration and Irrigation Scheduling, Proceedings of the International Conference in C.R. Camp, San Antonio, TX, Nov. 3-6, 1996; Sadler, E.J., Yoder, R.E., Eds.; American Society of Agricultural Engineers: St. Josepth, MI; pp. 158–166.
- Howell, T.A.; Tolk, J.A.; Schneider, A.D.; Evett, S.R. Evapotranspiration, yield, and water use efficiency of corn hybrids differing in maturity. Agron. J. 1998, 90, 3–9. [Google Scholar]
- Wright, J.L.; Jensen, M.E. Development and evaluation of evapotranspiration models for irrigation scheduling. Trans. ASAE 1978, 21, 88–96. [Google Scholar]
- Evett, S.R.; Howell, T.A.; Todd, R.W.; Schneider, A.D.; Tolk, J.A. Alfalfa reference ET measurement and prediction. Proc. 4th Decennial Symp., National Irrigation Symp. ASAE; Evans, R.G., Benham, B.L., Trooien, T.P., Eds.; ASAE: St. Joseph, MI, 2000; pp. 266–272. [Google Scholar]
| Variable | Units | Cold Pixel178 | Hot Pixel178 | Cold Pixel210 | Hot Pixel210 |
|---|---|---|---|---|---|
| Elevation | M | 907 | 907 | 907 | 907 |
| ETrF | - | 1.05 | 0 | 1.05 | 0 |
| Ts | K | 291.7 | 308.0 | 291.6 | 315.1 |
| Rn | W m-2 | 695.0 | 532.0 | 692.4 | 577.0 |
| G | W m-2 | 61.1 | 106.4 | 27.8 | 139.5 |
| Zom | m | 0.13 | 0.01 | 0.125 | 0.007 |
| U(200 m) | m s-1 | 14.4 | 14.4 | 5.9 | 5.9 |
| Atmospheric stability corrected values | |||||
| rah | s m-1 | 9.5 | 10.7 | 22.8 | 14.6 |
| u* | m s-1 | 0.78 | 0.62 | 0.33 | 0.35 |
| L_MO | m | 241.2 | -44.2 | 162.4 | -7.4 |
| dT | K | -1.36 | 4.43 | -0.36 | 6.55 |
| LE | W m-2 | 788.4 | 0.0 | 680.9 | 0.0 |
| H | W m-2 | -154.5 | 425.6 | -16.3 | 437.5 |
| Soil water balance | METRIC | ETd Difference (DOY 178) | ETd Difference (DOY 210) | |||||
|---|---|---|---|---|---|---|---|---|
| Crop | ETobserved (DOY 178) | ETobserved (DOY 210) | ETestimated (DOY 178) | ETestimated (DOY 210) | error | error | error | error |
| mm d-1 | mm d-1 | mm d-1 | mm d-1 | mm d-1 | % | mm d-1 | % | |
| Fully irrigated corn | 11.7 | 9.0 | 13.7 | 9.5 | 2.0 | 17.1 | 0.5 | 6.0 |
| Irrigated silage corn | 6.2 | 9.1 | 7.3 | 8.3 | 1.1 | 17.7 | -0.8 | -8.8 |
| Limited irrigated cotton | 1.4 | 2.5 | 0.4 | 3.3 | -1.0 | -71.4 | 0.8 | 32.0 |
| Irrigated cotton | 5.9 | 3.5 | 6.1 | 3.1 | 0.2 | 3.4 | -0.4 | -11.4 |
| MBE = | 0.6 | -8.3 | 0.0 | 4.5 | ||||
| RMSE = | 1.3 | 42.6 | 0.8 | 19.9 | ||||
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gowda, P.H.; Chávez, J.L.; Howell, T.A.; Marek, T.H.; New, L.L. Surface Energy Balance Based Evapotranspiration Mapping in the Texas High Plains. Sensors 2008, 8, 5186-5201. https://doi.org/10.3390/s8085186
Gowda PH, Chávez JL, Howell TA, Marek TH, New LL. Surface Energy Balance Based Evapotranspiration Mapping in the Texas High Plains. Sensors. 2008; 8(8):5186-5201. https://doi.org/10.3390/s8085186
Chicago/Turabian StyleGowda, Prasanna H., José L. Chávez, Terry A. Howell, Thomas H. Marek, and Leon L. New. 2008. "Surface Energy Balance Based Evapotranspiration Mapping in the Texas High Plains" Sensors 8, no. 8: 5186-5201. https://doi.org/10.3390/s8085186
APA StyleGowda, P. H., Chávez, J. L., Howell, T. A., Marek, T. H., & New, L. L. (2008). Surface Energy Balance Based Evapotranspiration Mapping in the Texas High Plains. Sensors, 8(8), 5186-5201. https://doi.org/10.3390/s8085186




