The Statistical Meaning of Kurtosis and Its New Application to Identification of Persons Based on Seismic Signals
Abstract
:1. Introduction
2. The statistical meaning of kurtosis
- 1)
- Cum4 (ax+ b) = a4Cum4 (x), so ks(x) is invariant by any linear transformation ks(ax+b)=ks(x)
- 2)
- Let p(x) = pe (x) + po (x), where pe (x) is even and po (x) is odd. It is easy to prove that ks(x) only depends on pe (x) and that pe (x) can be considered as a pdf.
3. The new application of kurtosis
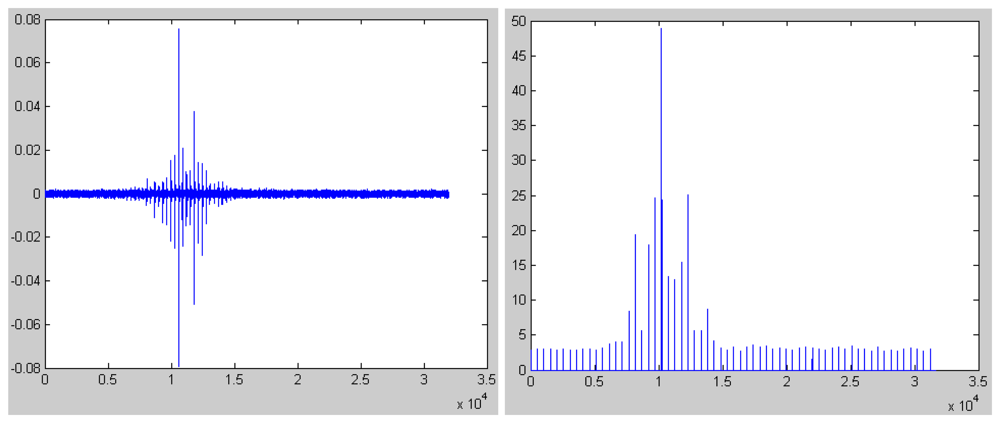
3.1. Simulation results
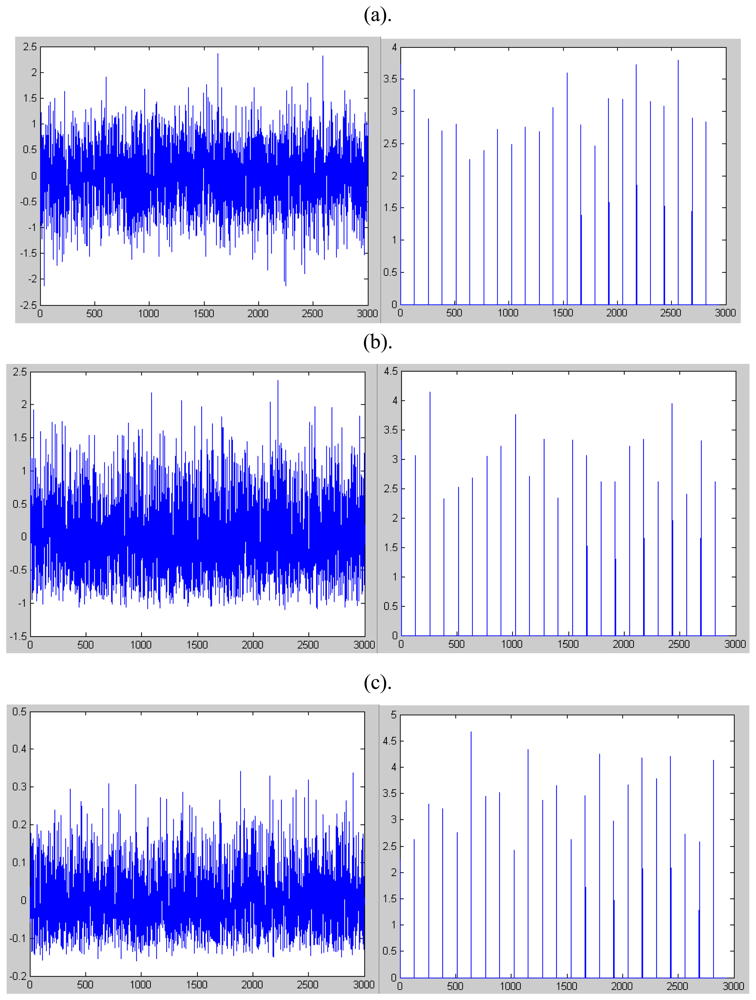
3.2. Kurtosis for background noise, tracklayer and truck
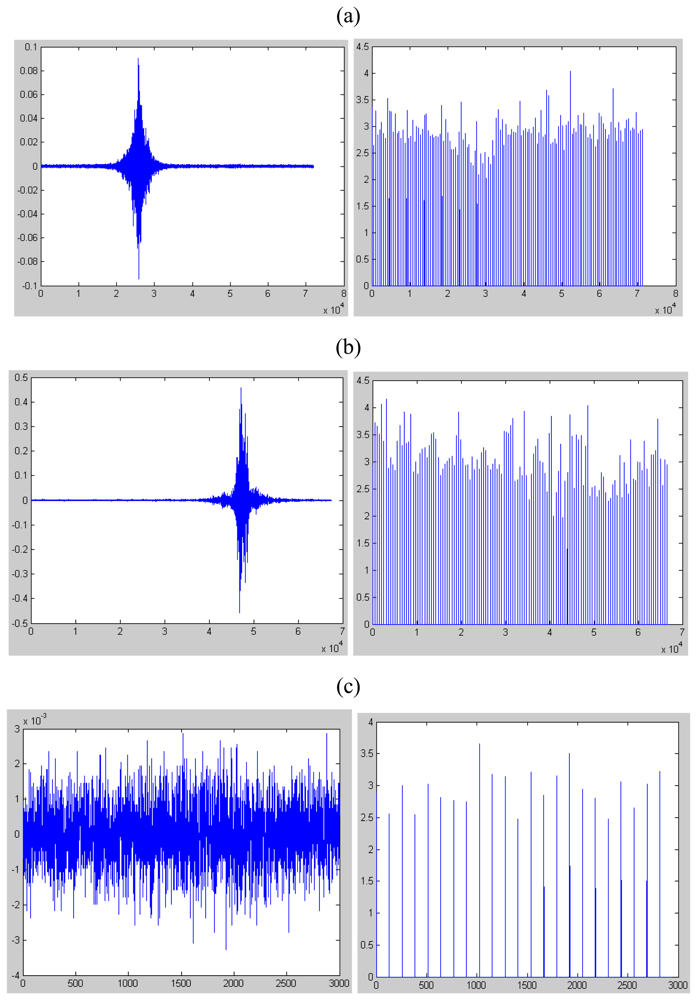
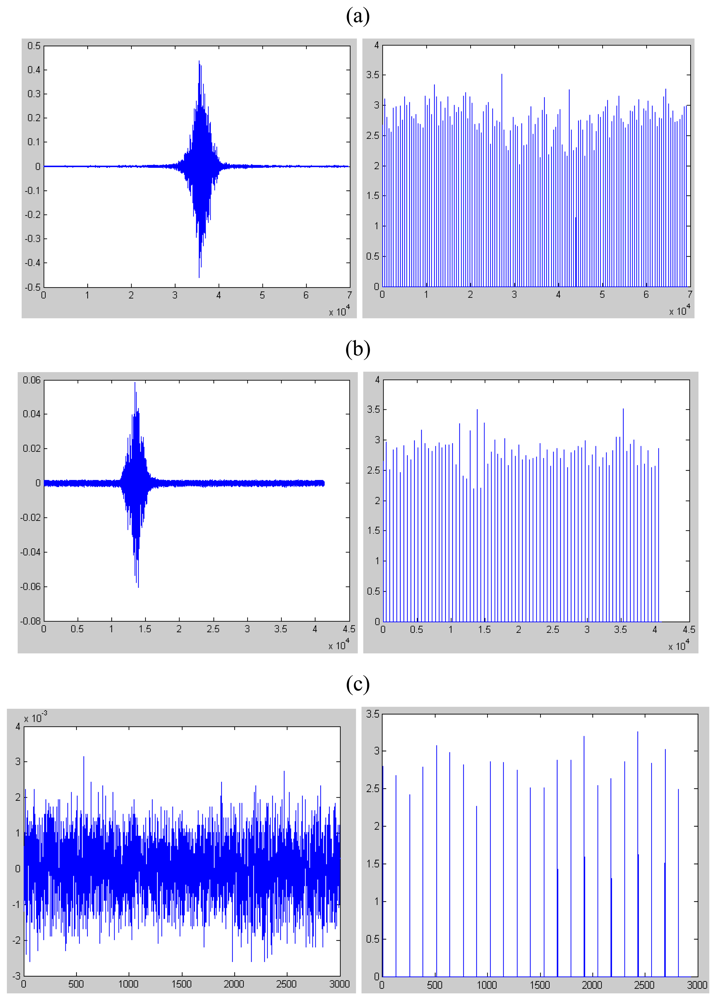
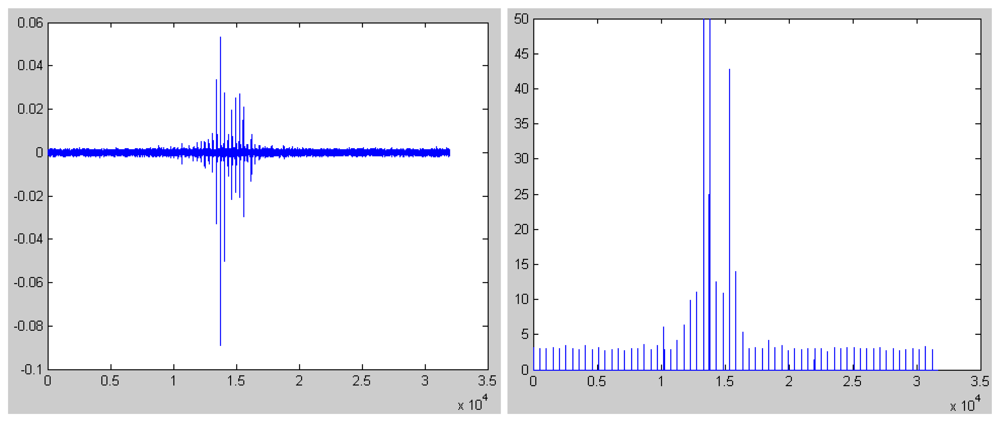
3.3. Kurtosis for person
- 1)
- The kurtosis of impulsive signals is far beyond 5;
- 2)
- The kurtosis of non-impulsive signals is below 5;
- 3)
- The values of kurtosis are independent of the geologic features and are only dependent on the feature of signals.
4. Conclusion
Acknowledgments
References and notes
- Shoji, Y.; Takasuka, T.; Yasukawa, H. Personal identification using footstep detection. In Intelligent Signal Processing and Communication Systems, Proceedings of 2004 International Symposium on, 18-19 Nov. 2004; ISPACS 2004, 2004; pp. 43–47. [Google Scholar]
- Lan, J.H.; Lan, T.; Nahavandi, S. A novel application of a microaccelerometer for target classification. IEEE Sensors J. 2004, 4, 519–524. [Google Scholar]
- Mazarakis, G.P.; Avaritsiotis, J.N. A prototype sensor node for footstep detection. In Wireless Sensor Networks. Proceeedings of the Second European Workshop on, 31 Jan.-2 Feb. 2005; 2005; pp. 415–418. [Google Scholar]
- Itai, A.; Yasukawa, H. Footstep Recognition with Psyco-acoustics Parameter. In Circuits and Systems, IEEE Asia Pacific Conference on, 4-7 Dec. 2006; APCCAS 2006, 2006; pp. 992–995. [Google Scholar]
- Pearson, K. “Das Fehlergesetz und seine Verallgemeinerungen durch Fechner und Pearson.” A Rejoinder. Biometrika 1905, 4, 169–212. [Google Scholar]
- Pearson, K. Contributions to the mathematical theory of evolution, II: Skew variation in homogeneous material. Proceedings of the Royal Society of London 1895, 186, 343–414. [Google Scholar]
- Richard, A.; Groeneveld, G. M. Measuring skewness and kurtosis. The Statistician 1984, 33, 391–399. [Google Scholar]
- Snedecor, G.W.; Cochran, W.G. Statistical Methods, 6th Edition ed; Ames; The Iowa State University Press, 1967. [Google Scholar]
- DeCarlo, L.T. On the meaning and use of kurtosis. Psychol. Methods 1997, 2, 292–307. [Google Scholar]
- Moors, J.J.A. The meaning of kurtosis: Darlington reexamined. Amer. Statist. 1986, 40, 283–284. [Google Scholar]
- Balanda, K.P.; MacGillivray, H.L. Kurtosis: A critical review. Amer. Statist. 1988, 42, 111–119. [Google Scholar]
- Richard, B. Darlington. Is Kurtosis Really “Peakedness?”. Amer. Statist. 1970, 24, 19–22. [Google Scholar]
- Ruppert, D. What Is Kurtosis?: An Influence Function Approach. Amer. Statist. 1987, 41, 1–5. [Google Scholar]
- Fiori, A.M.; Zenga, M. The meaning of kurtosis the influence function and an early intuition by L. Faleschini. Statistica 2005, 65, 135–144. [Google Scholar]
- Hopkins, K.D.; Weeks, D.L. Tests for normality and measures of skewness and kurtosis:Their places in research reporting. Educ. Psychol. Meas. 1990, 50, 717–729. [Google Scholar]
- Blest, D.C. A new measure of kurtosis adjusted for skewness. Aust. N. Z. J. Stat. 2003, 45, 175–179. [Google Scholar]
- Zhang, X.R. Discussions of kurtosis' statistical meanings. J. Yanshan Univ. 2006, 30, 57–60. [Google Scholar]
| X | freq A | freq B | freq C | freq D | freq E | freq F | freq G |
|---|---|---|---|---|---|---|---|
| 05 | 20 | 20 | 20 | 10 | 05 | 03 | 01 |
| 10 | 00 | 10 | 20 | 20 | 20 | 20 | 20 |
| 15 | 20 | 20 | 20 | 10 | 05 | 03 | 01 |
| Kurtosis | −2.0 | −1.75 | −1.5 | −1.0 | 0.0 | 1.33 | 8.0 |
| Variance | 25 | 20 | 16.6 | 12.5 | 8.3 | 5.77 | 2.27 |
| Distribution | Kurtosis excess |
|---|---|
| Bernoulli distribution | |
| Beta distribution | |
| Binomial distribution | |
| Chi-squared distribution | |
| Fisher-Tippett distribution | |
| Gamma distribution | |
| Geometric distribution | |
| Half-normal distribution | |
| Laplace distribution | 3 |
| Log normal distribution | e4S2 + 2e3S2 + 3e2S2 −6 |
| Maxwell distribution | |
| Negative binomial distribution | |
| Normal distribution | 0 |
| Poisson distribution | |
| Rayleigh distribution | |
| Student's t-distribution | |
| Continuous uniform distribution | |
| Discrete uniform distribution |
| X | Freq. A | Freq. B | Freq. C | Freq. D | Freq. E | Freq. F | Freq. G |
|---|---|---|---|---|---|---|---|
| –6.6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| –0.4 | 0 | 0 | 0 | 0 | 0 | 3 | 0 |
| 1.3 | 0 | 0 | 0 | 0 | 5 | 0 | 0 |
| 2.9 | 0 | 0 | 0 | 10 | 0 | 0 | 0 |
| 3.9 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| 4.4 | 0 | 20 | 0 | 0 | 0 | 0 | 0 |
| 5 | 20 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 10 | 20 | 20 | 20 | 20 | 20 |
| 15 | 20 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15.6 | 0 | 20 | 0 | 0 | 0 | 0 | 0 |
| 16.1 | 0 | 0 | 20 | 0 | 0 | 0 | 0 |
| 17.1 | 0 | 0 | 0 | 10 | 0 | 0 | 0 |
| 18.7 | 0 | 0 | 0 | 0 | 5 | 0 | 0 |
| 20.4 | 0 | 0 | 0 | 0 | 0 | 3 | 0 |
| 26.6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Kurtosis | −2.0 | −1.75 | −1.5 | −1.0 | 0.0 | 1.33 | 8.0 |
| Variance | 25 | 25.1 | 24.8 | 25.2 | 25.2 | 25.0 | 25.1 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liang, Z.; Wei, J.; Zhao, J.; Liu, H.; Li, B.; Shen, J.; Zheng, C. The Statistical Meaning of Kurtosis and Its New Application to Identification of Persons Based on Seismic Signals. Sensors 2008, 8, 5106-5119. https://doi.org/10.3390/s8085106
Liang Z, Wei J, Zhao J, Liu H, Li B, Shen J, Zheng C. The Statistical Meaning of Kurtosis and Its New Application to Identification of Persons Based on Seismic Signals. Sensors. 2008; 8(8):5106-5119. https://doi.org/10.3390/s8085106
Chicago/Turabian StyleLiang, Zhiqiang, Jianming Wei, Junyu Zhao, Haitao Liu, Baoqing Li, Jie Shen, and Chunlei Zheng. 2008. "The Statistical Meaning of Kurtosis and Its New Application to Identification of Persons Based on Seismic Signals" Sensors 8, no. 8: 5106-5119. https://doi.org/10.3390/s8085106




