A Polypyrrole-based Strain Sensor Dedicated to Measure Bladder Volume in Patients with Urinary Dysfunction
Abstract
:1. Introduction
2. Techniques to Measure Bladder Volume
2.1. Pressure Sensors
2.2. Ultrasound Measurements
2.3. Bioelectric Impedance Measurement
2.4. Electroneurogram Measurements
3. Mathematical Methodology of Proposed Strain Sensors
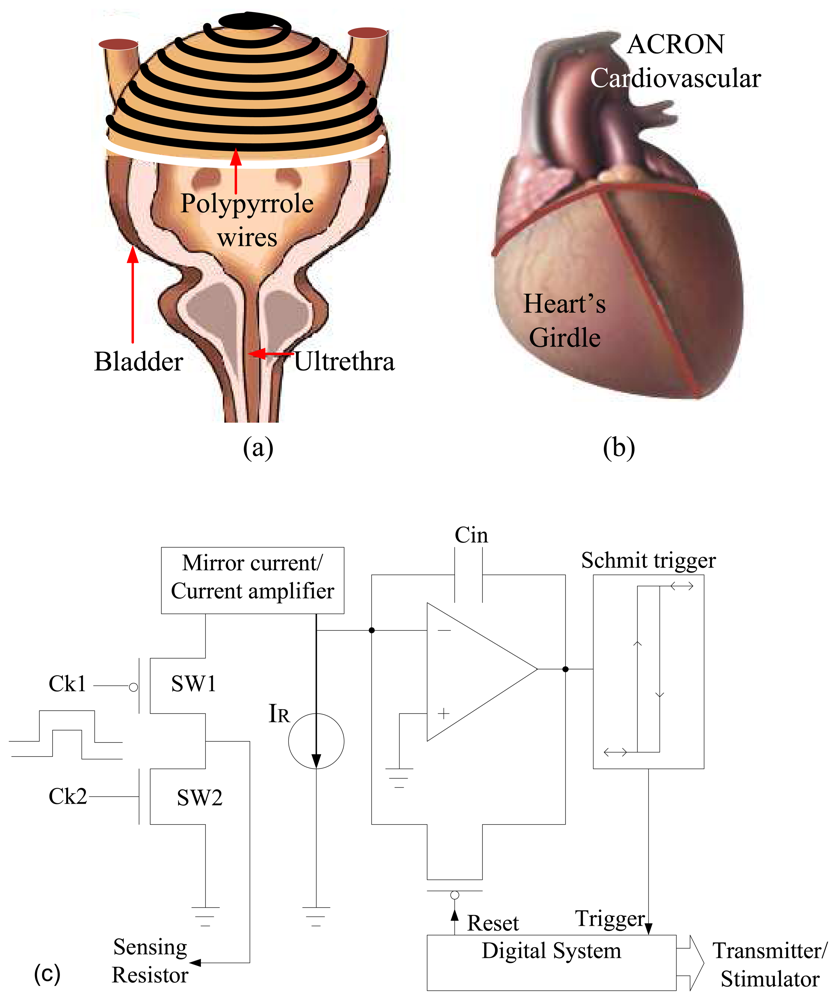
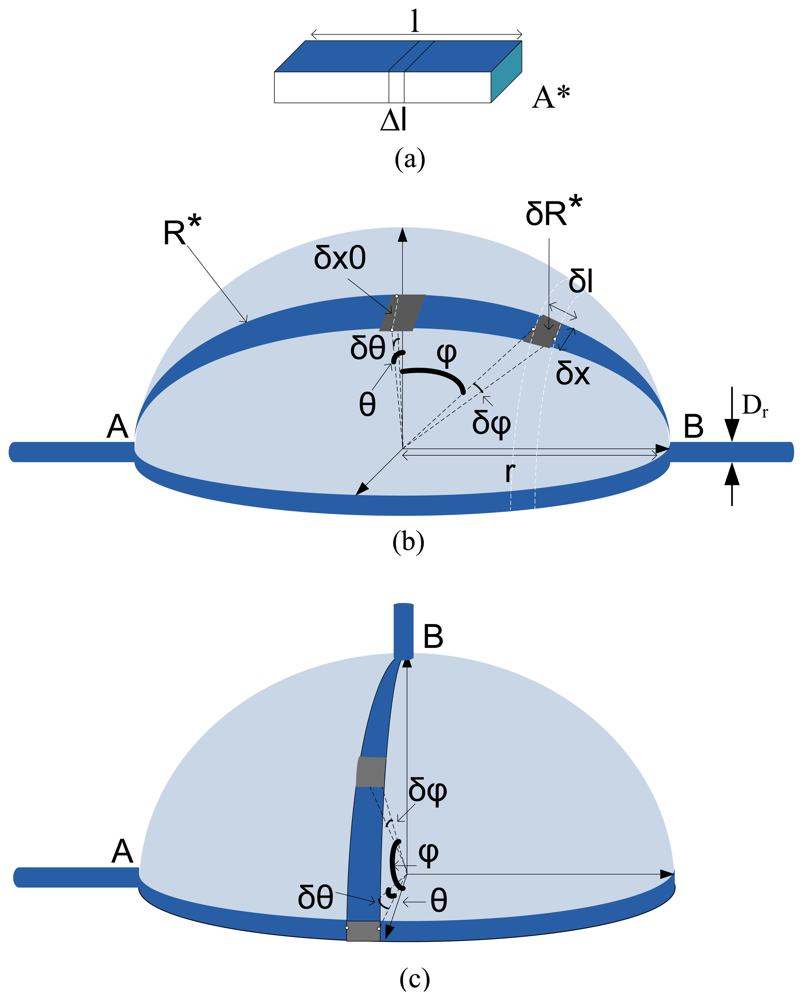
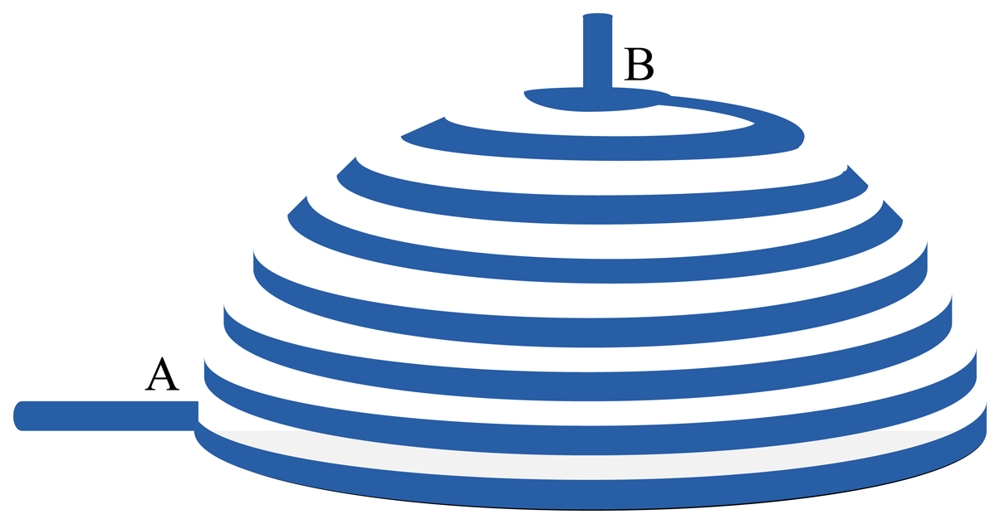
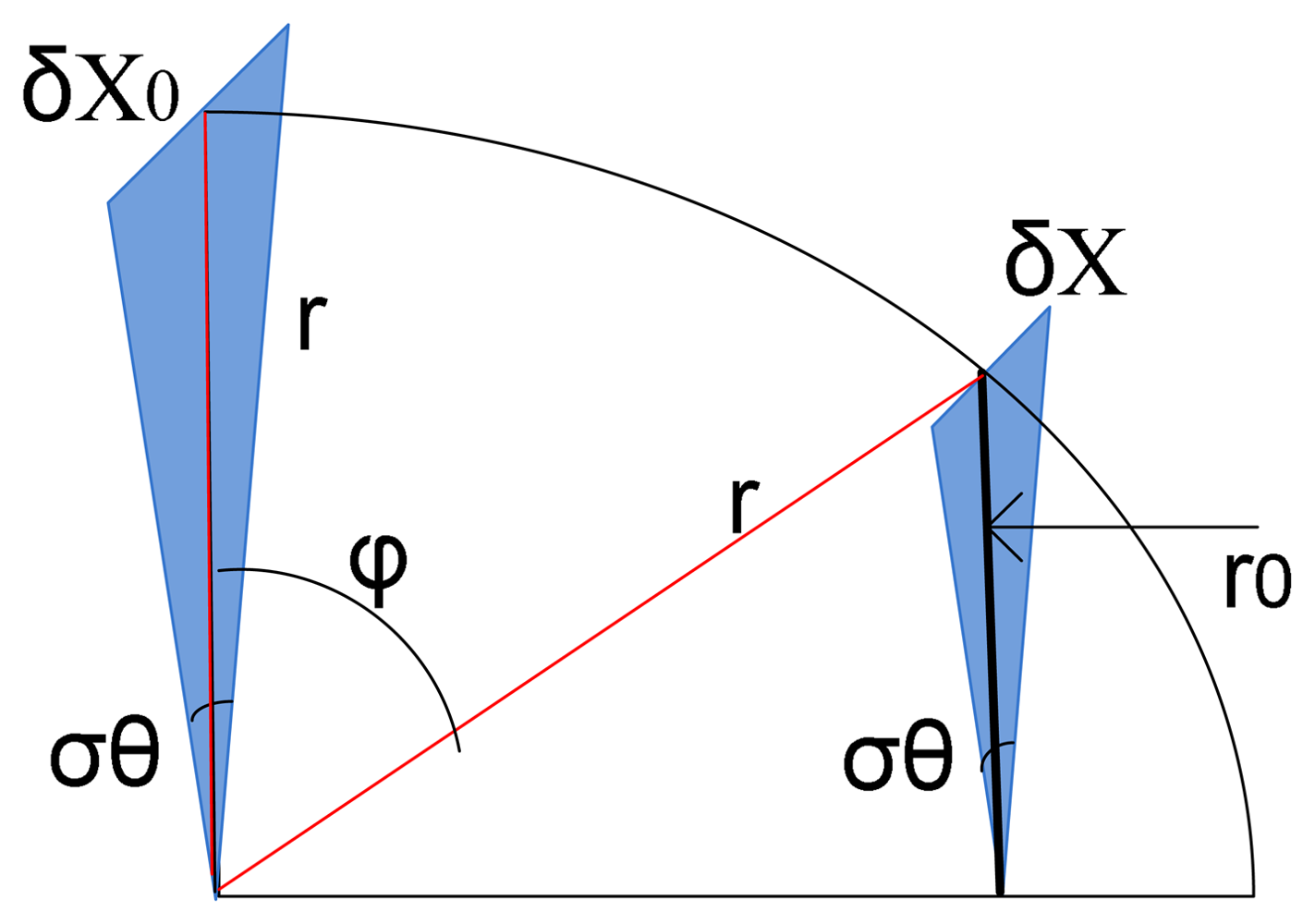
A. Strain Sensor Basics
B. Biomechanics of the Urinary Bladder
C. Minimum Design Requirements for Bladder Volume Sensor
- A non-linear viscoelastic fabric with a Young's modulus equal or greater than that of bladder tissue (as seen in result section)
- High gauge factor and low threshold volumes of detection (G≥1)
- Biocompatible and non-cytotoxic. ( PPY is biocompatible)
- Easily implanted surgically with minimal sutures (Based on explanation in Fabrication section).
4. Fabrication and Characterization of Sensor
4.1. Polypyrrole deposition
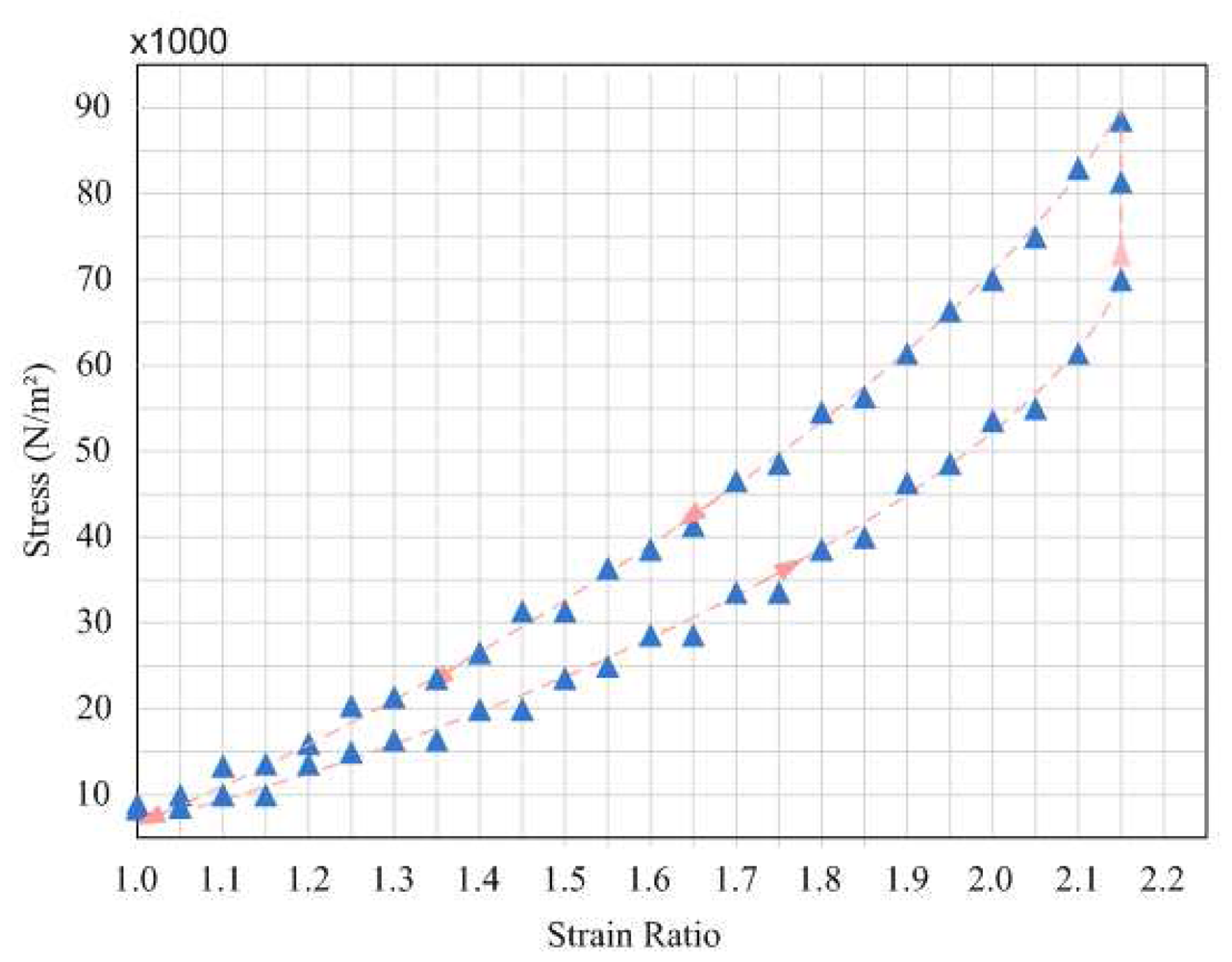
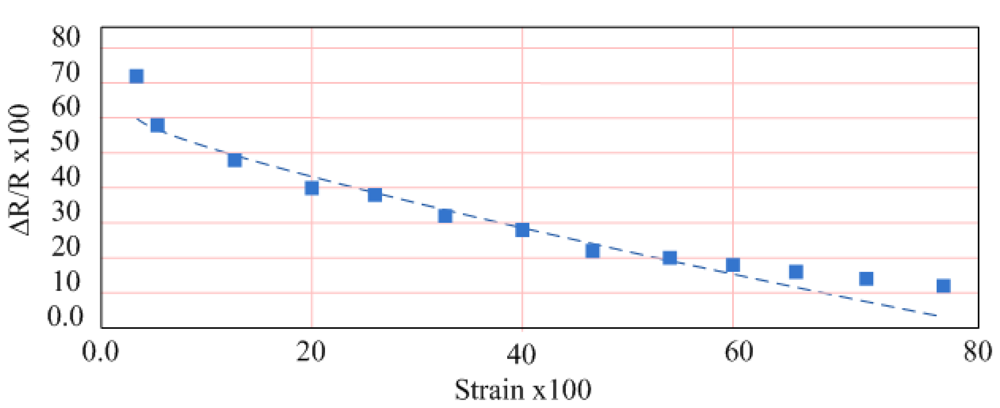
4.2. Tensile Properties of Strain Sensor
4.3. In-Vitro Testing of Strain Sensor on Bladder Volume
5. Discussion and Future Work
5.1. In-vivo consecrations
5.2. Strain sensor practical issues
6. Conclusions
Acknowledgments
Appendix A
References
- Gaunt, R.A.; Prochazka, A. Control of urinary bladder function with devices: successes and failures. Prog. Brain Res. 2006, 152, 163–194. [Google Scholar]
- Boyer, S.; Sawan, M.; Abdel-Gawad, M.; Robin, S.; Elhilali, M.M. Implantable selective stimulator to improve bladder voiding: design and chronic experiments in dogs. IEEE T. Neur. Sys. Reh. 2000, 8, 464–470. [Google Scholar]
- Arabi, K.; Sawan, M. Electronic design of a multichannel programmable implant for neuromuscular electrical stimulation. IEEE T. Neur. Sys. Reh. 1999, 6, 204–214. [Google Scholar]
- Ba, A.; Sawan, M. Integrated programmable neurostimulator to recuperate the bladder functions. IEEE CCECE Conf., Montreal 2003, 147–150. [Google Scholar]
- Gift, S.; Maundy, B. New configurations for the measurement of small resistance changes. IEEE T Circuits-II 2006, 53, 178–182. [Google Scholar]
- Grassi, M.; Malcovati, P.; Baschirotto, A. A 141-dB dynamic range CMOS gas-sensor interface circuit without calibration with 16-Bit digital output word. IEEE J. Solid-St. Circ. 2007, 42, 1543–1554. [Google Scholar]
- Ghafar-Zadeh, E.; Sawan, M. Charge-Based Capacitive Sensor Array for CMOS-Based Laboratory-on-Chip Applications. IEEE J. Sensors 2008, 8, 325–332. [Google Scholar]
- Smela, E. Conjugated Polymer Actuators for Biomedical Applications. Adv. Materials 2003, 15, 481–494. [Google Scholar]
- Koldewin, E.L. Bladder pressure sensors in an animal model. J. Urology 1994, 151, 1379–1384. [Google Scholar]
- Korkmazz, I.; Rogg, B. A simple fluid-mechanical model for the prediction of the stress-strain relation of the male urinary bladder. J. Biomech. 2007, 40, 663–668. [Google Scholar]
- Petrican, P.; Sawan, M.A. Design of a miniaturized ultrasonic bladder volume monitor and subsequent preliminary evaluation on 41 enuretic patients. IEEE T. Neur. Sys. Reh. 1994, 6, 66–74. [Google Scholar]
- Merks, E.J.W.J; Borsboom, M.G.; Bom, N.; van der Steen, A.F.W.; Jong, N. A KLM–circuit model of a multi-layer transducer for acoustic bladder volume measurements. Ultrasonics 2006, 44, 705–710. [Google Scholar]
- Craggs, M. Objective measurement of bladder sensation: use of a new patient-activated device and response to neuromodulation. BJU International 2005, 96, 29–36. [Google Scholar]
- Richard, Stein B.; Mushahwar, V. Reanimating limbs after injury or disease TRENDS in. Neurosciences 2005, 28, 518–524. [Google Scholar]
- Ghafar-Zadeh, E.; Sawan, M.; Therriault, D. A Microfluidic Packaging Technique for Lab-on-Chip Applications. IEEE T. Adv. Packaging. In Press.

© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rajagopalan, S.; Sawan, M.; Ghafar-Zadeh, E.; Savadogo, O.; Chodavarapu, V.P. A Polypyrrole-based Strain Sensor Dedicated to Measure Bladder Volume in Patients with Urinary Dysfunction. Sensors 2008, 8, 5081-5095. https://doi.org/10.3390/s8085081
Rajagopalan S, Sawan M, Ghafar-Zadeh E, Savadogo O, Chodavarapu VP. A Polypyrrole-based Strain Sensor Dedicated to Measure Bladder Volume in Patients with Urinary Dysfunction. Sensors. 2008; 8(8):5081-5095. https://doi.org/10.3390/s8085081
Chicago/Turabian StyleRajagopalan, Sumitra, Mohamad Sawan, Ebrahim Ghafar-Zadeh, Oumarou Savadogo, and Vamsy P. Chodavarapu. 2008. "A Polypyrrole-based Strain Sensor Dedicated to Measure Bladder Volume in Patients with Urinary Dysfunction" Sensors 8, no. 8: 5081-5095. https://doi.org/10.3390/s8085081
APA StyleRajagopalan, S., Sawan, M., Ghafar-Zadeh, E., Savadogo, O., & Chodavarapu, V. P. (2008). A Polypyrrole-based Strain Sensor Dedicated to Measure Bladder Volume in Patients with Urinary Dysfunction. Sensors, 8(8), 5081-5095. https://doi.org/10.3390/s8085081



