Estimation of Tree Size Diversity Using Object Oriented Texture Analysis and Aster Imagery
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
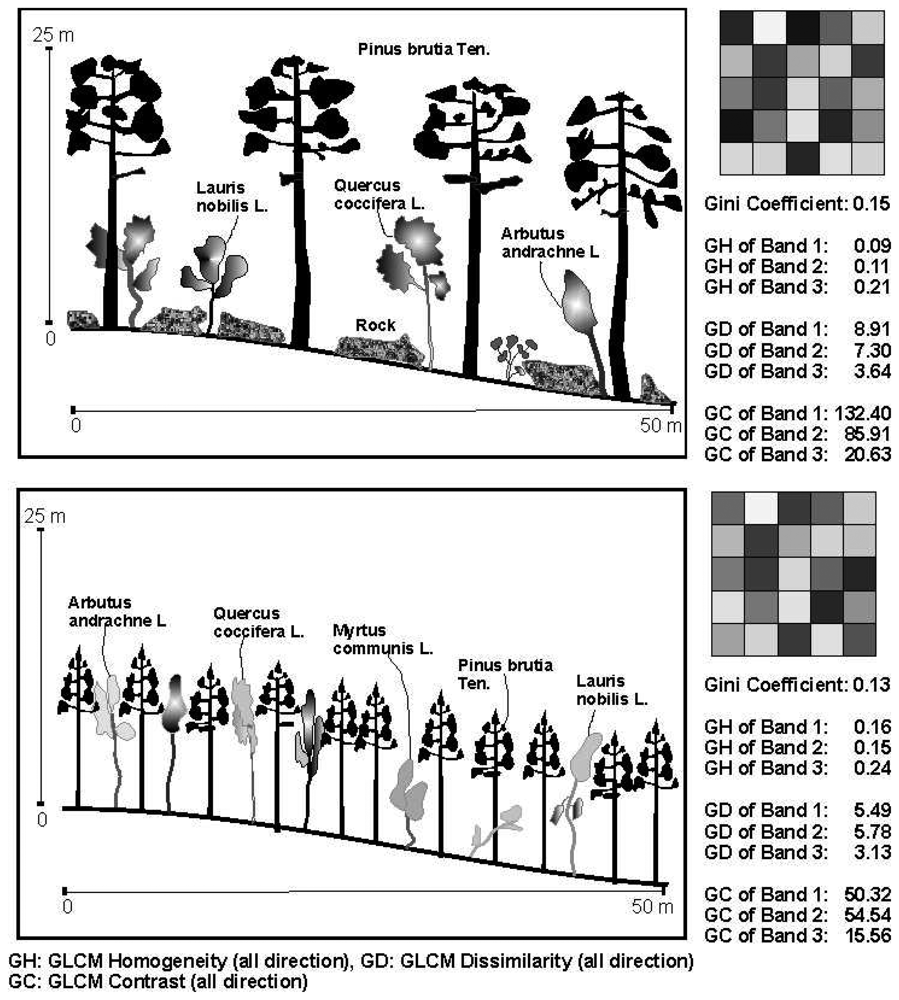
2.2. Creating of segmented images
2.3. The diversity indicates
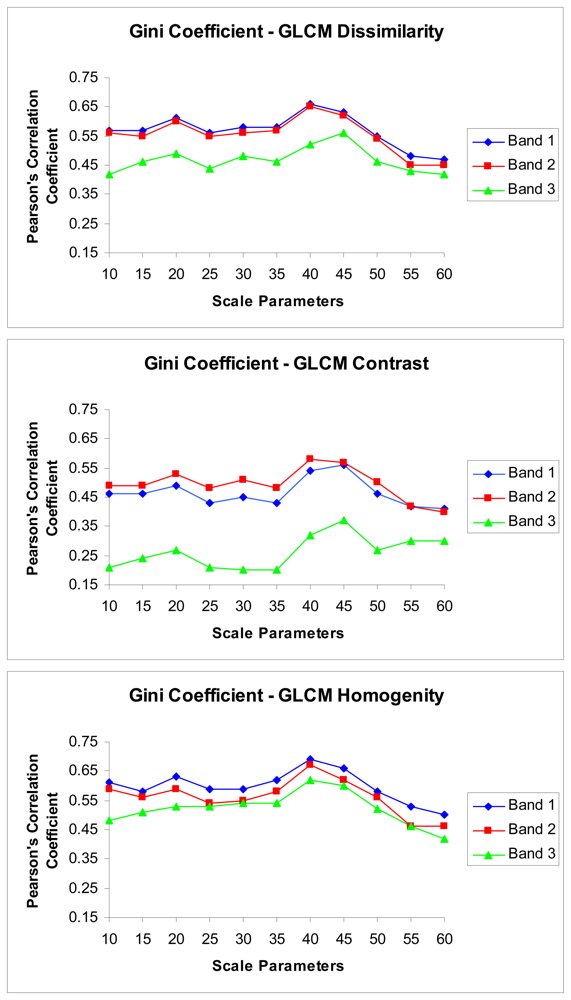
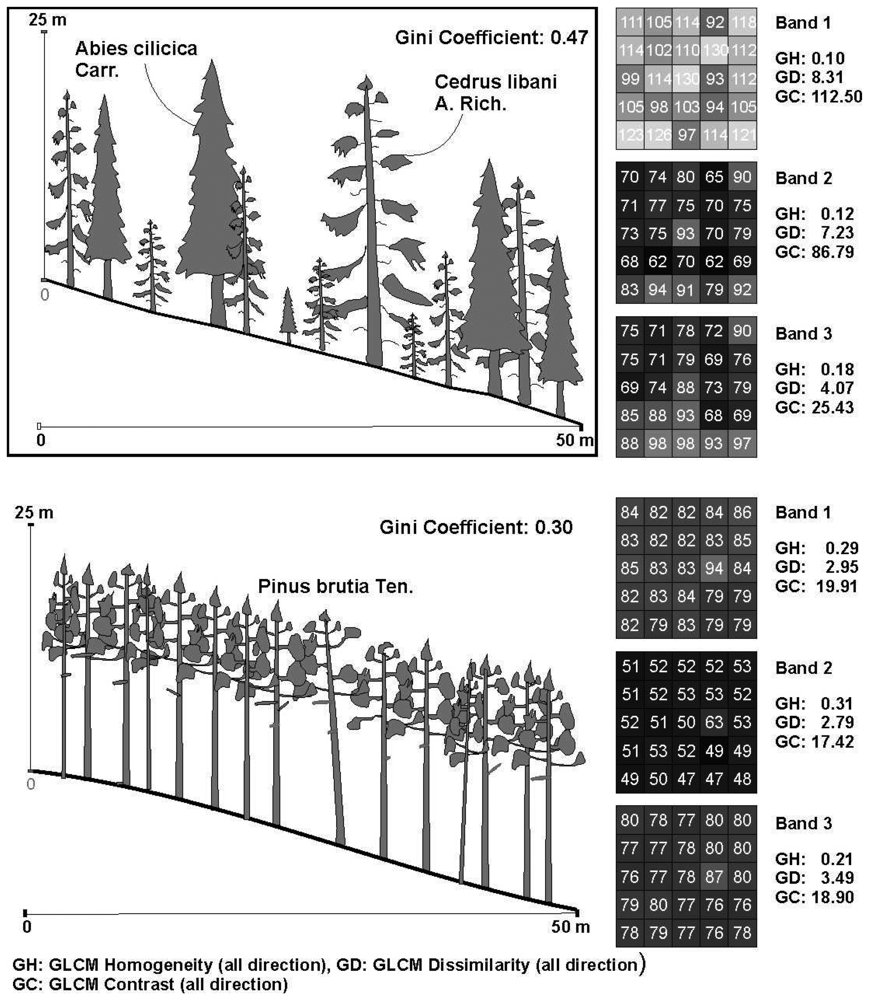
2.4. The texture variables
2.5. Statistical analysis
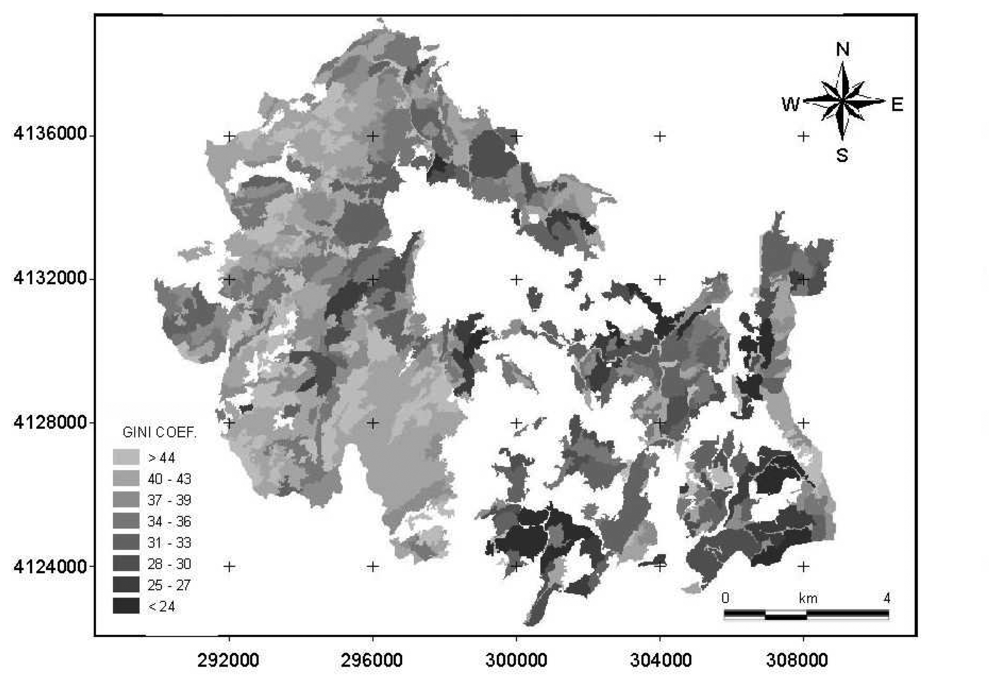
3. Results
4. Discussion and Conclusion
4.1. Comparison of Gini coefficient and Shannon index
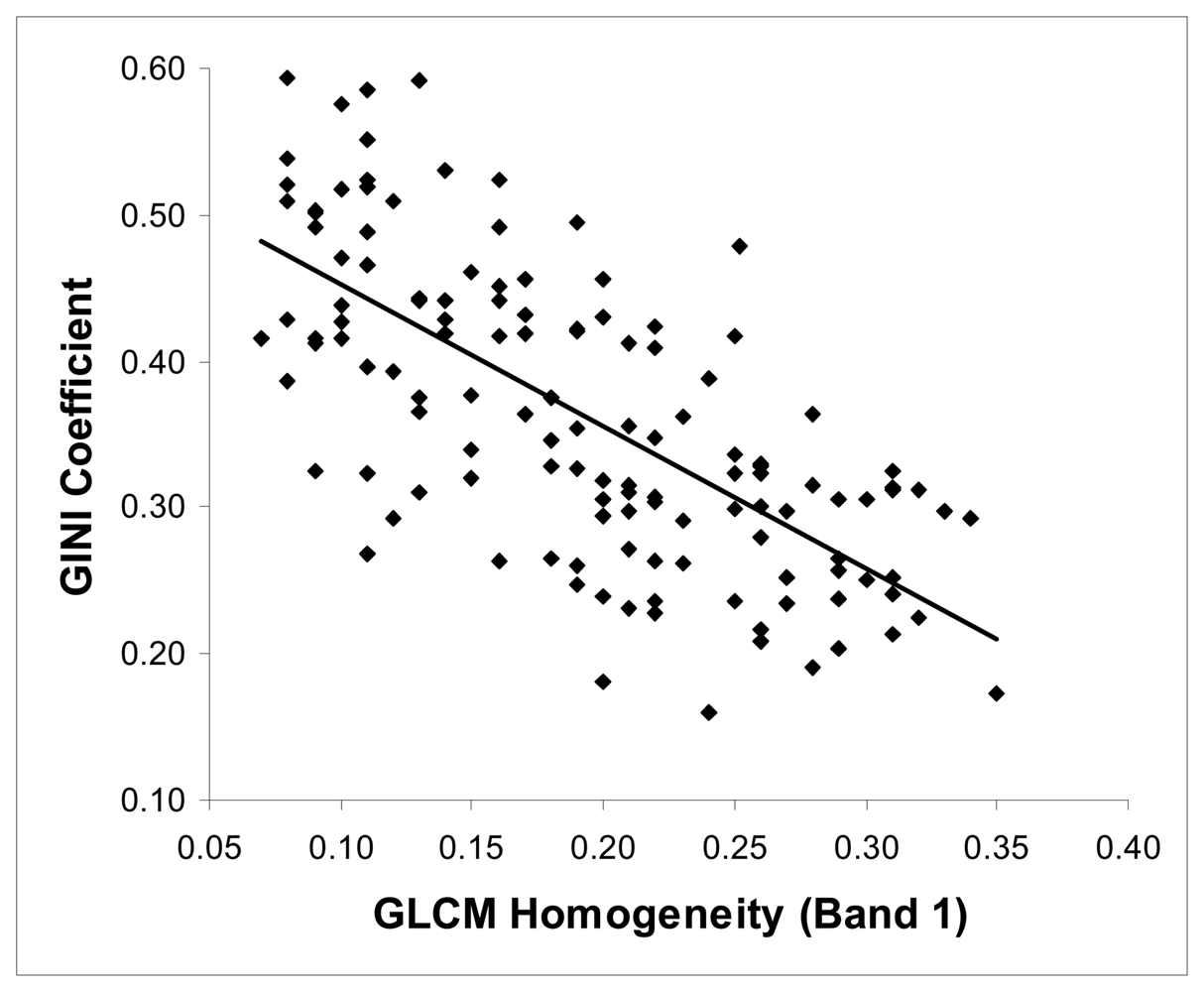
4.2. The relations between the texture parameters and Gini coefficient
Acknowledgments
References and Notes
- Seitz, B.; Katzel, R.; Kowarik, I.; Schulz, P.M. Method for identifying and recording harvest stands of regional provenances of indigenous woody species. Allg. Forst. Jagdztg. 2008, 179, 70–76. [Google Scholar]
- Baskent, E.Z.; Terzioglu, S.; Baskaya, S. Developing and implementing multiple-use forest management planning in Turkey. Environ. Manage. 2008, 42, 37–48. [Google Scholar]
- Lahde, E.; Laiho, O.; Norokorpi, Y.; Saksa, T. 1999. Stand structure as the basis of diversity index. Forest Ecol. Manag. 1999, 115, 213–220. [Google Scholar]
- Wikstrom, P.; Eriksson, L.O. Solving the stand management problem under biodiversity-related considerations. Forest Ecol. Manag. 2000, 126, 361–376. [Google Scholar]
- Anonymous. Stand Level Biodiversity-Web Based Training Course; Ministry of Forests: British Columbia. available at http://www.gov.bc.ca/for/.
- Spies, T.A. Forest structure: A key to the ecosystem. Northwest Sci. 1998, 72, 34–39. [Google Scholar]
- Lexerod, N.L.; Eid, T. An evaluation of different diameter diversity indices based on criteria related to forest management planning. Forest Ecol. Manag. 2006, 222, 17–28. [Google Scholar]
- Smith, W.R.; Farrar, R.M.; Murphy, P.A.; Yeiser, J.L.; Meldahl, R.S.; Kush, J.S. Crown area and basal area relationships for open-grown southern pines for modelling competition and growth. Can. J. Forest. Res. 1992, 22, 341–347. [Google Scholar]
- Norton, D.A.; Cochrane, C.H.; Reay, S.D. Crown-stem dimension relationships in two New Zealand native forests. New Zeal. J. Bot. 2005, 43, 673–678. [Google Scholar]
- Varga, P.; Chen, H.Y.H.; Klinka, K. Tree-size diversity between single- and mixed-species stands in three forest types in western Canada. Can. J. Forest. Res. 2005, 35, 593–601. [Google Scholar]
- Rouvinena, S.; Kuuluvainen, T. Tree diameter distributions in natural and managed old Pinus sylvestris-dominated forests. Forest Ecol. Manag. 2005, 208, 45–61. [Google Scholar]
- Sterba, H.; Zingg, A. Distance dependent and distance independent description of stand structure. Allg. Forst. Jagdztg. 2006, 177, 169–176. [Google Scholar]
- Chauhan, H.B.; Nayak, S. Land use/land cover changes near Hazira region, Gujarat using remote sensing satellite data. Photonirvachak-Journal of the Indian Society of Remote Sensing 2005, 33, 413–420. [Google Scholar]
- Ozdemir, I.; Koch, B.; Asan, U.; Gross, C.P.; Hemphill, S. Separation of citrus plantations from forest cover using landsat imagery. Allg. Forst. Jagdztg. 2007, 178, 208–212. [Google Scholar]
- Reddy, C.S.; Pattanaik, C.; Murthy, M.S.R. Assessment and monitoring of mangroves of Bhitarkanika Wildlife Sanctuary, Orissa, India using remote sensing and GIS. Curr. Sci. India 2007, 92, 1409–1415. [Google Scholar]
- Ismail, R.; Mutanga, O.; Bob, U. 2007. Forest health and vitality: the detection and monitoring of Pinus patula trees infected by Sirex noctilio using digital multispectral imagery. Southern Hemisphere Forestry Journal 2007, 69, 39–47. [Google Scholar]
- Kadiogullari, A.I.; Baskent, E.Z. Spatial and temporal dynamics of land use pattern in Eastern Turkey: a case study in Gumushane. Environ. Monit. Assess. 2008, 138, 289–303. [Google Scholar]
- Keles, S.; Sivrikaya, F.; Cakir, G.; Kose, S. Urbanization and forest cover change in regional directorate of Trabzon forestry from 1975 to 2000 using landsat data. Environ. Monit. Assess. 2008, 140, 1–14. [Google Scholar]
- McCleary, A.L.; Crews-Meyer, K.A.; Young, K.R. Refining forest classifications in the western Amazon using an intra-annual multitemporal approach. Int. J. Remote Sens. 2008, 29, 991–1006. [Google Scholar]
- St-Onge, B.; Hu, Y.; Vega, C. Mapping the height and above-ground biomass of a mixed forest using lidar and stereo Ikonos images. Int. J. Remote Sens. 2008, 29, 1277–1294. [Google Scholar]
- Gunlu, A.; Sivrikaya, F.; Baskent, E.Z.; Keles, S.; Cakir, G.; Kadiogullari, A.I. Estimation of stand type parameters and land cover using Landsat-7 ETM image: A case study from Turkey. Sensors 2008, 8, 2509–2525. [Google Scholar]
- Puhr, C.B.; Donoghue, D.N.M. Remote sensing of upland conifer plantations using Landsat TM data: a case study from Galloway, south-west Scotland. Int. J. Remote Sens. 2000, 21, 633–646. [Google Scholar]
- Innes, JL.; Koch, B. Forest biodiversity and its assessment by remote sensing. Global Ecol. Biogeogr. 1998, 7, 397–419. [Google Scholar]
- Aynekulu, E.; Kassawmar, T.; Tamene, L. Applicability of ASTER imagery in mapping land use/cover as a basis for biodiversity studies in drylands of northern Ethiopia. Afr. J. Ecol. 2008, 46, 19–23. [Google Scholar]
- Bawa, K.; Rose, J.; Ganeshaiah, K.N.; Barve, N.; Kiran, M.C.; Umashaanker, R. Assessing Biodiversity from Space: an Example from the Western Ghats, India. Conserv. Ecol. 2002, 6. article number 7. [Google Scholar]
- Levin, N.; Shmida, A.; Levanoni, O.; Tamari, H.; Kark, S. Predicting mountain plant richness and rarity from space using satellite-derived vegetation indices. Divers Distrib. 2007, 13, 692–703. [Google Scholar]
- Cho, V.H.K. Investigations for segment-based classification of satellite images for the purpose of forest mapping. Allg. Forst. Jagdztg. 2004, 175, 94–100. [Google Scholar]
- Ozdemir, I.; Asan, U.; Koch, B.; Yesil, A.; Ozkan, U.Y.; Hemphill, S. Comparison of Quickbird-2 and Landsat-7 ETM+ data for mapping of vegetation cover in Fethiye-Kumluova coastal dune in the Mediterranean region of Turkey. Fresen. Environ. Bull. 2005, 14, 823–831. [Google Scholar]
- Mallinis, G.; Koutsias, N.; Tsakiri-Strati, M.; Karteris, M. Object-based classification using Quickbird imagery for delineating forest vegetation polygons in a Mediterranean test site. Isprs J. Photogramm. 2008, 63, 237–250. [Google Scholar]
- Ozdemir, I. Estimating stem volume by tree crown area and tree shadow area extracted from pansharpened Quickbird imagery in open Crimean juniper forests. Int. J. Remote Sens. 2008. [Google Scholar] [CrossRef]
- Definiens, A.G. Definiens Professional 5 Reference Book; Definiens AG: Munich, Germany, 2006; p. 122. [Google Scholar]
- Baatz, M.; Benz, U.; Dehgani, S.; Heynan, M.; Holtje, A.; Hofmann, P.; Lingenfelder, I.; Mimler, M.; Sohlbach, M.; Weber, M.; Willhauck, G. eCognition Object Oriented Image Analysis User Guide; Munich, Germany, 2001; p. 483. [Google Scholar]
- Tian, J.; Chen, D.M. Optimization in multi-scale segmentation of high-resolution satellite images for artificial feature recognition. Int. J. Remote Sens. 2007, 28, 4625–4644. [Google Scholar]
- Shannon, C.E. The mathematical theory of communication. In In Mathematical Theory of Communication; Shannon, C.E., Weaver, W., Eds.; University of Illinois Press: Urbana, USA, 1948; pp. 29–125. [Google Scholar]
- Staudhammer, C.L.; LeMay, V.M. Introduction and evaluation of possible indices of stand structural diversity. Can. J. Forest. Res. 2001, 31, 1105–1115. [Google Scholar]
- Hall-Beyer, M. GLCM tutorial home page. 2007. available at http://www.fp.ucalgary/ca/mhallbey/tutorial.htm).
- Staupendahl, K. The modified six-tree-sample - a suitable method for forest stand assessment. Allg. Forst. Jagdztg. 2008, 179, 21–33. [Google Scholar]
| DBH (cm) | GINI coefficient | Shannon Index | ||||
|---|---|---|---|---|---|---|
| Diameter Class Width (cm) | ||||||
| 1 | 2 | 3 | 4 | |||
| Low tree size diversity | 20;20;21;22;23;24;25;26;26;26;27;28;28 29;30;30;31;31;31;32;32;32;32;33;33;33 | 0.167 | 2.367 | 1.705 | 1.462 | 1.293 |
| Moderate tree size diversity | 20;20;21;22;23;24;25;27;27;27;29;30;32 32;32;34;35;36;38;38;39;40;40;40;45;45 | 0.270 | 2.553 | 2.304 | 1.883 | 1.875 |
| High tree size diversity | 09;10;10;18;20;20;28;28;28;37;37;38;45 45;45;53;53;53;60;61;61;61;82;82;83;83 | 0.496 | 2.058 | 1.637 | 1.928 | 1.593 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ozdemir, I.; Norton, D.A.; Ozkan, U.Y.; Mert, A.; Senturk, O. Estimation of Tree Size Diversity Using Object Oriented Texture Analysis and Aster Imagery. Sensors 2008, 8, 4709-4724. https://doi.org/10.3390/s8084709
Ozdemir I, Norton DA, Ozkan UY, Mert A, Senturk O. Estimation of Tree Size Diversity Using Object Oriented Texture Analysis and Aster Imagery. Sensors. 2008; 8(8):4709-4724. https://doi.org/10.3390/s8084709
Chicago/Turabian StyleOzdemir, Ibrahim, David A. Norton, Ulas Yunus Ozkan, Ahmet Mert, and Ozdemir Senturk. 2008. "Estimation of Tree Size Diversity Using Object Oriented Texture Analysis and Aster Imagery" Sensors 8, no. 8: 4709-4724. https://doi.org/10.3390/s8084709
APA StyleOzdemir, I., Norton, D. A., Ozkan, U. Y., Mert, A., & Senturk, O. (2008). Estimation of Tree Size Diversity Using Object Oriented Texture Analysis and Aster Imagery. Sensors, 8(8), 4709-4724. https://doi.org/10.3390/s8084709




