Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters
Abstract
:1. Introduction
2. Sites and Methods
2.1. Study areas and field campaigns
- the southwest lagoon of New Caledonia, located between (22°10′S, 166°05′E) and (22°40′S, 166°40′E). New Caledonia is an approximately 450 km long × 50 km wide island, surrounded by the second largest coral reef lagoon in the world (22,175 km2). The waters in the New Caledonian lagoon are generally oligotrophic, except in the vicinity of Noumea, the main city of New Caledonia, due to anthropogenic disturbances (Torréton et al. 2007; Rochelle-Newall et al. 2008). River inputs are generally extremely low (i.e. < 5 m3 s-1), except during strong but short rainfall events. The lagoon is semi-enclosed and connected to the Coral Sea through a barrier reef segmented by narrow passes (Jouon et al. 2006). The measurements presented in this paper were performed between June 2002 and February 2006.
- the Cienfuegos Bay in Cuba, located between (22°12′N, 80°33′W) and (22°04′N, 80°22′W). This bay is almost enclosed, strongly influenced by urban and industrial activities, and connected to the Caribbean Sea by a narrow channel (Alonso-Hernandez et al. 2006, Perez-Santana et al. 2007). The measurements presented in this paper were performed in May 2006. TSM concentrations are, on average, bigger than at the New Caledonia site and smaller than at the Fiji site.
- the Suva Harbour and Laucala Bay south of Viti Levu, the biggest (10388 km2) of the 844 Fiji islands and islets, located between (18°00′S, 178°22′E) and (18°15′S, 178°35′E). The Rewa River, with mean monthly discharges in the range 45-210 m3 s-1, provides the Laucala Bay with a continuous high amount of suspended particles. Bay muds are about 25-40 m thick at Suva Harbour (Shorten 1993) and the area is also influenced by anthropogenic activities. This lagoon is connected to the Pacific Ocean through a coral barrier reef opened with wide passes (Singh 2007).
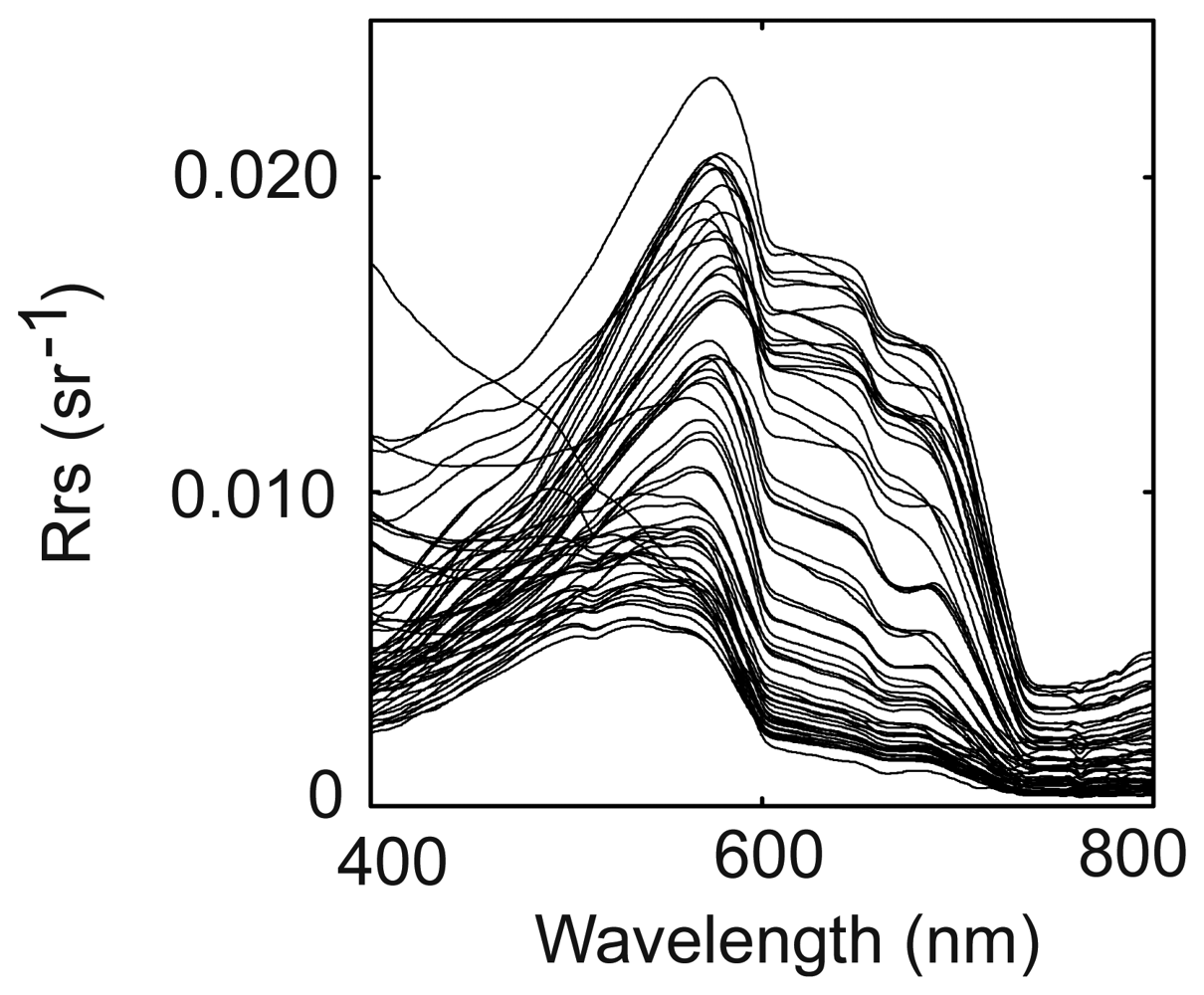
2.2. Instruments and Methods
3. Local algorithms for turbidity
3.1. New Caledonia
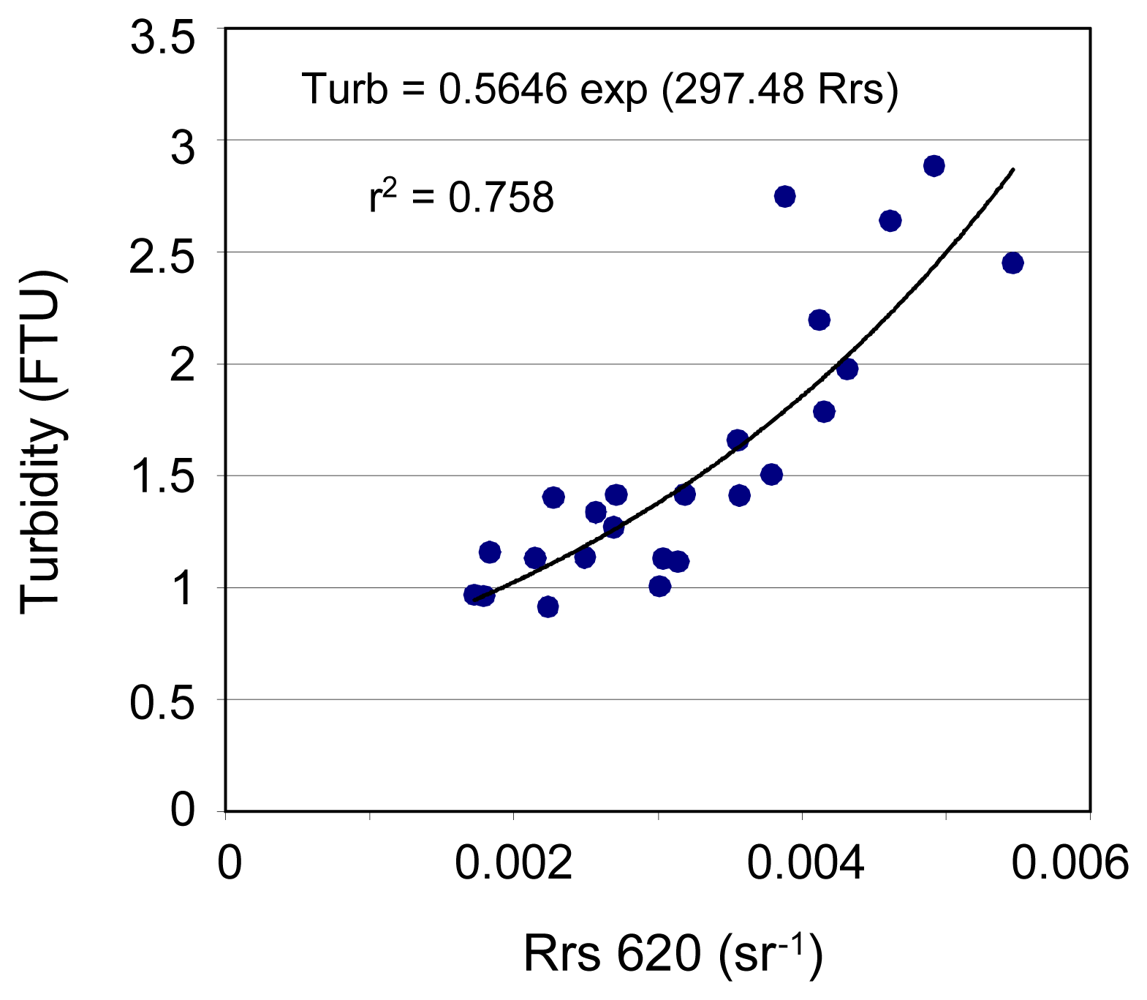
3.2 Cuba
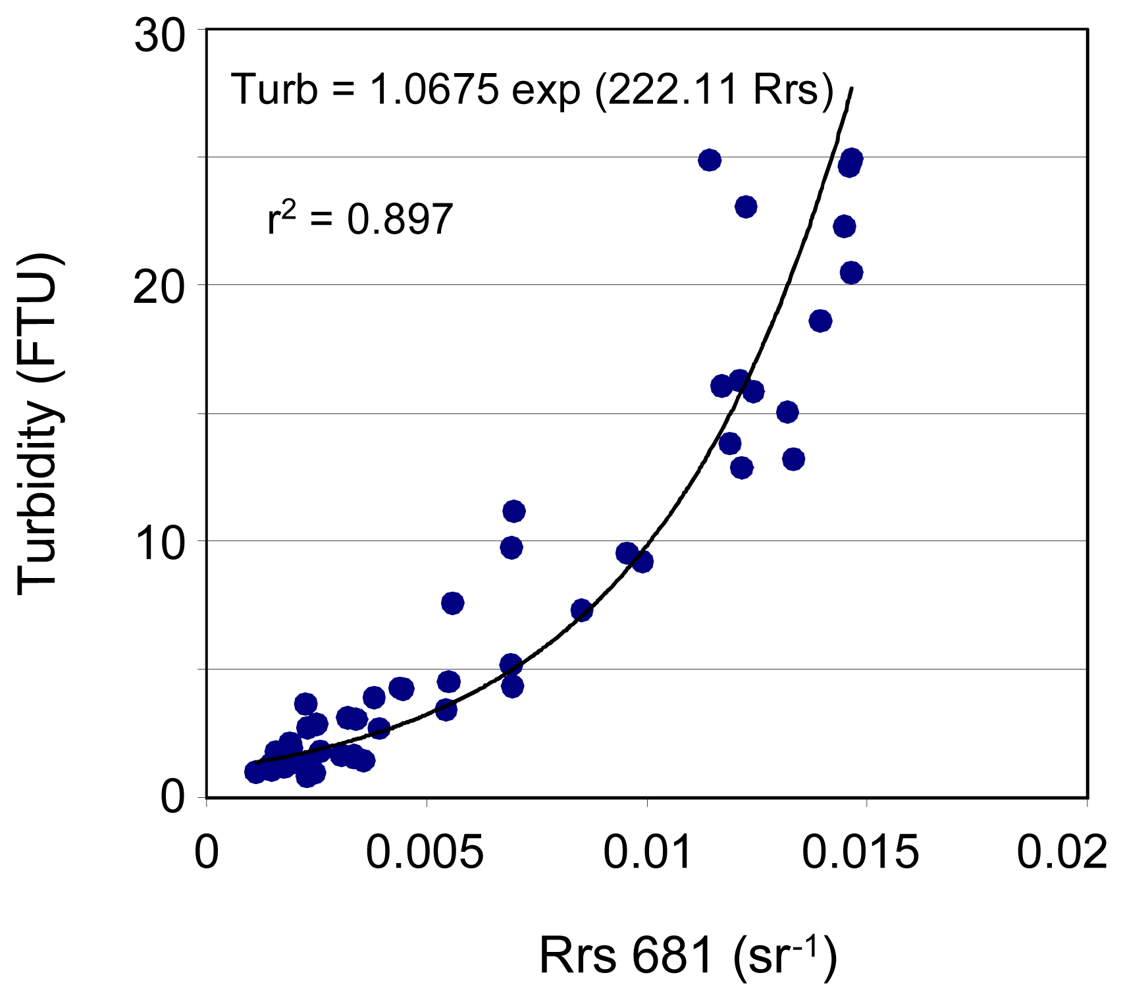
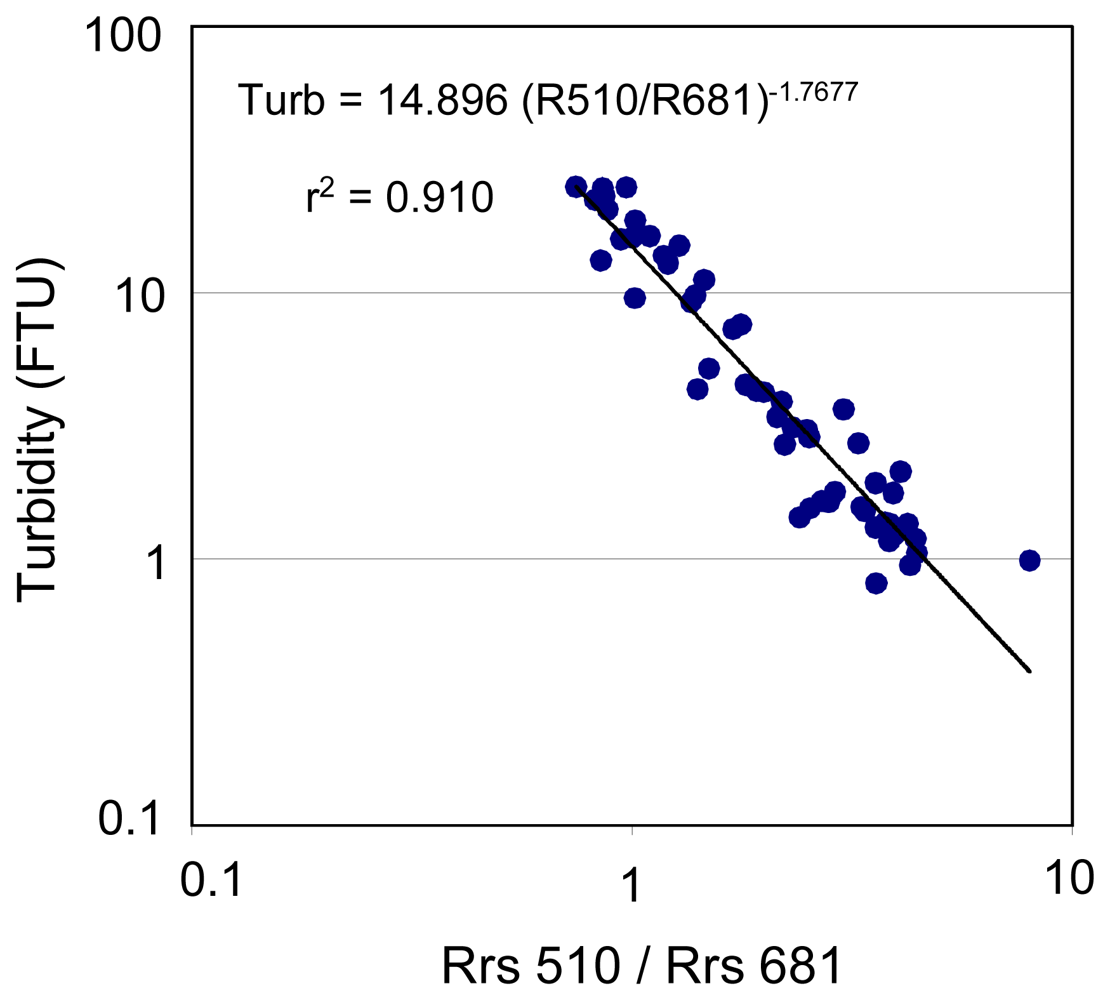
3.3 Fiji
4. Towards a global algorithm in tropical coastal waters
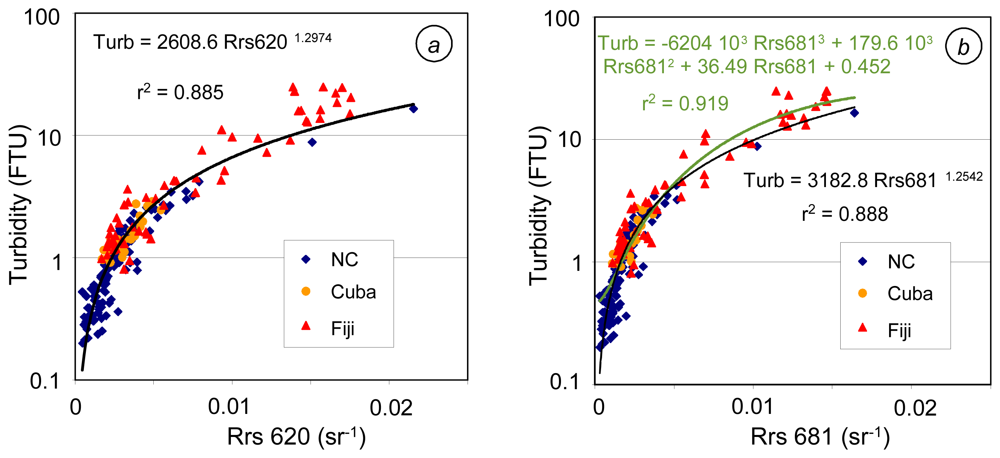
4.1 Correlation between surface turbidity and Rrs(λ), one-band algorithms
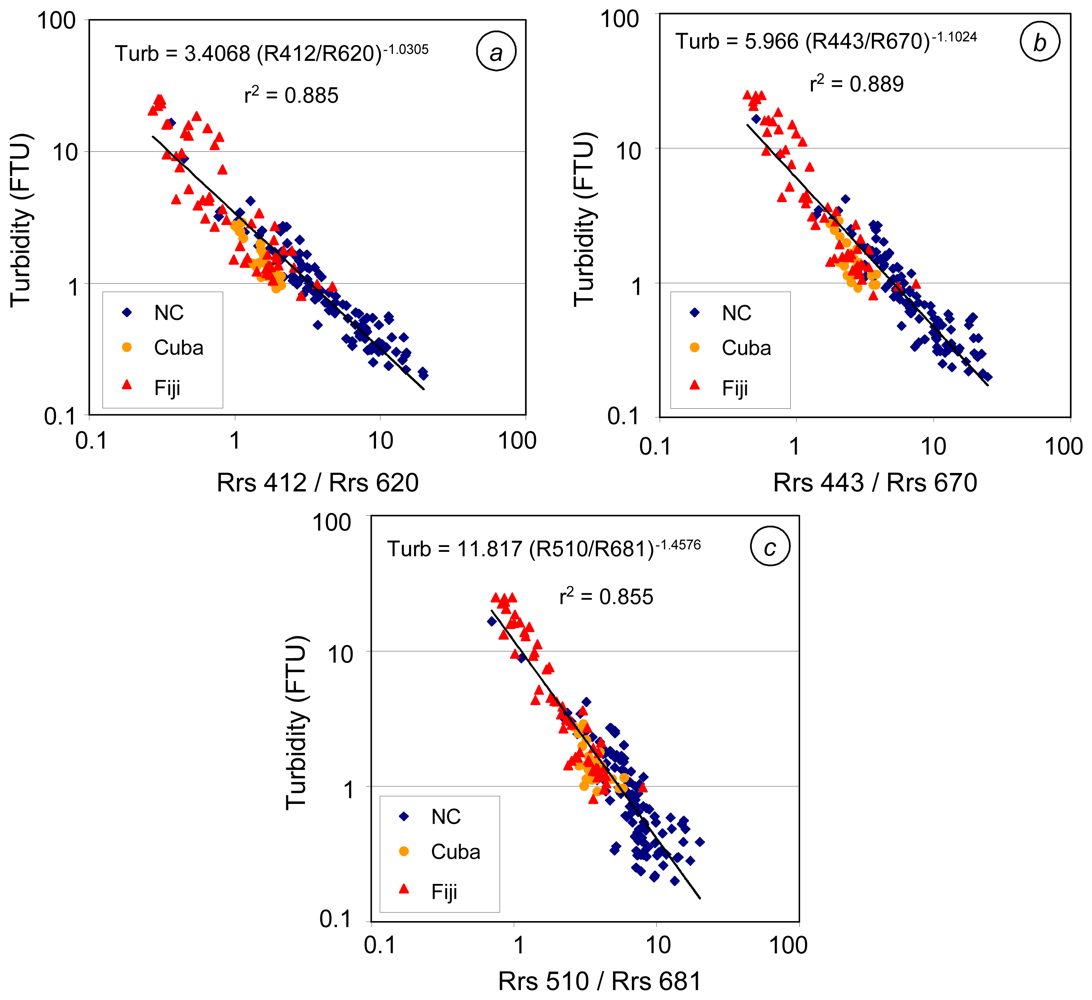
4.2 Two-band algorithms
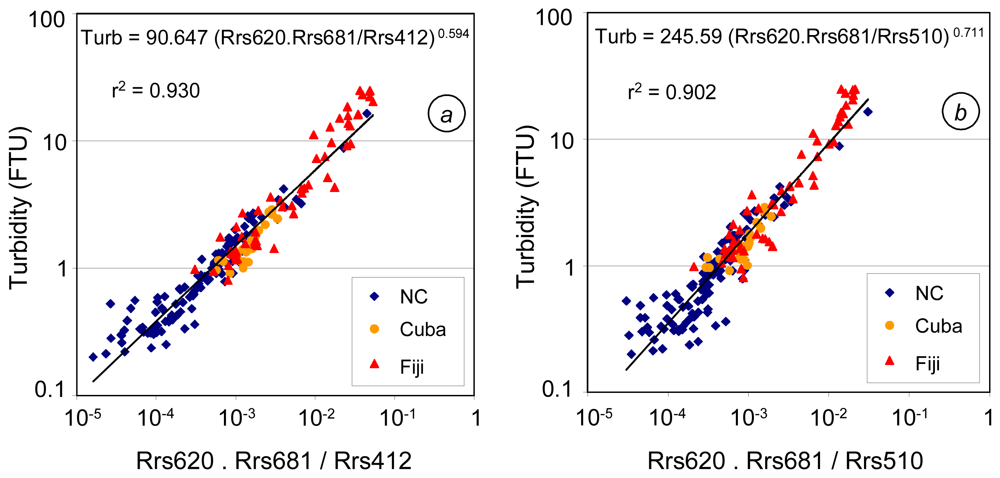
4.3 Three-band algorithms
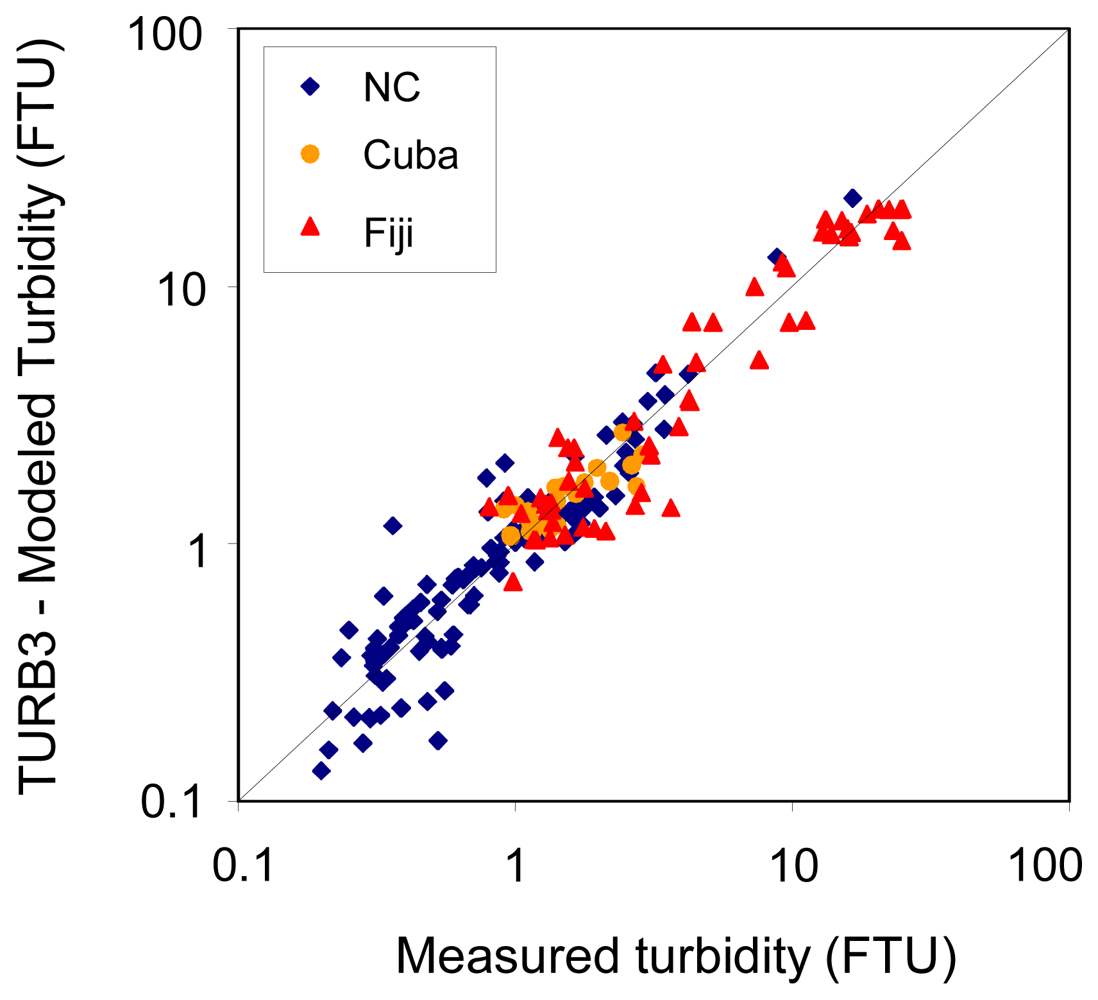
4.4 Proposal for a global algorithm with threshold
- (a)
- turbidity is calculated using algorithm 2:
- (b)
- if the resulting turbidity < 1 FTU, its calculation is replaced by algorithm 6:
5. Discussion and Conclusion
Acknowledgments
References and Notes
- Acker, J. Toward a working (and workable) definition of Total Suspended Matter. Total Suspended Matters 2006, 1(3), 1–2. [Google Scholar]
- Acker, J.; Ouillon, S.; Gould, R.W., Jr; Arnone, R.A. Measuring Marine Suspended Sediment Concentrations from Space: History and Potential. Proc. 8th Int. Conf. Remote Sensing for Marine and Coastal Environments(CD-ROM); Altarum/AMRS: Halifax, Canada, 2005. [Google Scholar]
- Ahn, Y.H.; Moon, J.E.; Gallegos, S. Development of suspended particulate matter algorithms for ocean color remote sensing. Korean J. Remote Sensing 2001, 17(4), 285–295. [Google Scholar]
- Ahn, Y.H.; Shanmugam, P.; Moon, J.E. Retrieval of ocean colour from high resolution multi-spectral imagery for monitoring highly dynamic ocean features. Int. J. Remote Sensing 2006, 27(2), 367–392. [Google Scholar]
- Alonso-Hernandez, C.M.; Diaz-Asencio, M.; Muñoz-Caravaca, A.; Delfanti, R.; Papucci, C.; Ferretti, O.; Crovato, C. Recent changes in sedimentation regime in Cienfuegos Bay, Cuba, as inferred from 210Pb and 137Cs vertical profiles. Continental Shelf Research 2006, 26, 153–167. [Google Scholar]
- Binding, C.E.; Bowers, D.G.; Mitchelson-Jacob, E.G. Estimating suspended sediment concentrations from ocean colour measurements in moderately turbid waters; the impact of variable particle scattering properties. Remote Sensing Env. 2005, 94(3), 373–383. [Google Scholar]
- Bowers, D.G.; Binding, C.E. The optical properties of mineral suspended particles: A review and synthesis. Estuarine Coastal and Shelf Science 2006, 67(1-2), 219–230. [Google Scholar]
- Bunt, J.A.C.; Larcombe, P.; Jago, C.F. Quantifying the response of optical backscatter devices and transmissometers to variations in suspended particulate matter. Cont. Shelf Res. 1999, 19, 1199–1220. [Google Scholar]
- Curran, P.J.; Novo, E.M.M. The relationship between suspended sediment concentration and remotely sensed spectral reflectance: a review. J. Coastal Research 1988, 4, 351–368. [Google Scholar]
- Darecki, M.; Stramski, D. An evaluation of MODIS and SeaWiFS bio-optical algorithms in the Baltic Sea. Remote Sensing Env. 2004, 89, 326–350. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sensing Env. 2002, 81(1), 149–161. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. Remote sensing reflectance of turbid sediment-dominated waters. Reduction of sediment type variations and changing illumination conditions effects by use of reflectance ratios. Applied Optics 2003, 42(15), 2623–2634. [Google Scholar]
- Estournel, C.; Kondrachoff, V.; Marsaleix, P.; Véhil, R. The plume of the Rhone: numerical simulation and remote sensing. Continental Shelf Research 1997, 17(8), 899–924. [Google Scholar]
- Forget, P.; Ouillon, S. Suspended matter off the Rhône river mouth from satellite imagery. Oceanologica Acta 1998, 21(6), 739–749. [Google Scholar]
- Han, L. Spectral reflectance with varying suspended sediment concentrations in clear and algae-laden waters. Photogr. Eng. Remote Sensing 1997, 63(6), 701–705. [Google Scholar]
- Holyer, R.J. Toward universal multispectral suspended sediment algorithms. Remote Sensing Env. 1978, 7, 323–338. [Google Scholar]
- Hu, C.; Chen, Z.; Clayton, T.D.; Swarzenski, P.; Brock, J.C.; Muller-Karger, F.E. Assessment of estuarine water-quality indicators using MODIS medium-resolution bands: Initial results from Tampa Bay, FL. Remote Sensing Env. 2004, 93(3), 423–441. [Google Scholar]
- Jin, J.Y.; Lee, D.Y.; Park, J.S.; Park, K.S.; Yum, K.D. Monitoring of suspended sediment concentration using vessels and remote sensing. In Coastal and Estuarine Fine Sediment Processes; McAnally, W.H., Mehta, A.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 287–299. [Google Scholar]
- Jouon, A.; Douillet, P.; Ouillon, S.; Fraunié, P. Calculations of hydrodynamic time parameters in a semi-opened coastal zone using a 3D hydrodynamic model. Continental Shelf Research 2006, 26, 1395–1415. [Google Scholar]
- Jouon, A.; Ouillon, S.; Douillet, P.; Lefebvre, J.P.; Fernandez, J.M.; Mari, X. Spatio-temporal variability in Suspended Particulate Matter concentration and size distribution in a coral reef lagoon. Marine Geology. submitted.
- Lahet, F.; Forget, P.; Ouillon, S. Application of a colour classification method to quantify the constituents of coastal waters from in situ reflectances sampled at satellite sensor wavebands. Int. J. Remote Sensing 2001a, 22(5), 909–914. [Google Scholar]
- Lahet, F.; Ouillon, S.; Forget, P. Colour classification of coastal waters of Ebro river plume from spectral reflectances. Int. J. Remote Sensing 2001b, 22(9), 1639–1664. [Google Scholar]
- Milliman, J.D.; Syvitski, J.P.M. Geomorphic/tectonic control of sediment discharge to the ocean: The importance of small mountainous rivers. Journal of Geology 1992, 100(5), 325–344. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Applied Optics 1999, 38, 7442–7455. [Google Scholar]
- Moore, G.F.; Aiken, J.; Lavender, S.J. The atmospheric correction of water colour and the quantitative retrieval of suspended particulate matter in Case II waters: application to MERIS. Int. J. Remote Sensing 1999, 20, 1713–1733. [Google Scholar]
- Mueller, J.L.; Davis, C.; Arnone, R.; Frouin, R.; Carder, K.; Lee, Z.P.; Steward, R.G.; Hooker, S.; Mobley, C.D.; McLean, S. Above-water radiance and remote sensing reflectance measurement and analysis protocols. In Ocean optics protocols for satellite ocean color sensor validation, rev. 4: radiometric measurements and data analysis protocols; Mueller, J.L., Fargion, G.S., McClain, C.R., Eds.; NASA; NASA/TM-2003-21621/REV-VolIII; 2003; Vol III, pp. 21–31. [Google Scholar]
- Neveux, J.; Lantoine, F. Spectrofluorometric assay of chlorophylls and phaeopigments using the least squares approximation technique. Deep Sea Research I 1993, 40(9), 1747–1765. [Google Scholar]
- Novo, E.M.M.; Hansom, J.D.; Curran, P.J. 1989. The effect of sediment type on the relationship between reflectance and suspended sediment concentration. Int. J. Remote Sensing 1989, 10(7), 1283–1289. [Google Scholar]
- Novo, E.M.M.; Steffen, C.A.; Braga, C.Z.F. Results of a laboratory experiment relating spectral reflectance to total suspended solids. Remote Sensing Env. 1991, 36, 67–72. [Google Scholar]
- O'Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. 1998, 103, 24937–24953. [Google Scholar]
- Ouillon, S. An inversion method for reflectance in stratified turbid waters. Int. J. Remote Sensing 2003, 24(3), 535–548. [Google Scholar]
- Ouillon, S.; Douillet, P.; Andréfouet, S. Coupling satellite data with in situ measurements and numerical modeling to study fine suspended sediment transport: a study for the lagoon of New Caledonia. Coral Reefs 2004, 23(1), 109–122. [Google Scholar]
- Ouillon, S.; Petrenko, A. Above-water measurements of reflectance and chlorophyll-aalgorithms in the Gulf of Lions,NW Mediterranean Sea. Optics Express. 2005, 13, pp. 2531–2548. http://www.opticsexpress.org/abstract.cfm?URI=OPEX-13-7-2531.
- Perez-Santana, S.; Pomares Alfonso, M.; Villanueva Tagle, M.; Peña Icart, M.; Brunori, C.; Morabito, R. Total and partial digestion of sediments for the evaluation of trace element environmental pollution. Chemosphere 2007, 66(8), 1545–1553. [Google Scholar]
- Puls, W.; Doerffer, R.; Sündermann, J. Numerical simulation and satellite observations of suspended matter in the North Sea. IEEE J. Ocean Eng. 1994, 19(9), 3. [Google Scholar]
- Rochelle-Newall, E.J.; Torréton, J.-P.; Mari, X.; Pringault, O. Phytoplankton-bacterioplankton coupling in the coastal sub-tropical South Pacific. Aquatic Microbial Ecology 2008, 50, 221–229. [Google Scholar]
- Shorten, G.G. Geotechnical analysis of recent estuarine organo-calcareous silts, Fiji: New considerations for investigations of soft marine clays. PhD thesis, University of Sydney, Australia, 1993. [Google Scholar]
- Siegel, H.; Gerth, M.; Mutzke, A. Dynamics of the Oder river plume in the southern Baltic Sea: satellite data and numerical modelling. Continental Shelf Research 1999, 19, 1143–1159. [Google Scholar]
- Singh, A.M. Transportation of fine suspended sediments in the Suva lagoon using numerical modelling. Msc thesis, The University of the South Pacific, Suva, Fiji, 2007. [Google Scholar]
- Sydor, M. Remote sensing of particulate concentrations in water. Applied Optics 1980, 19, 2794–2800. [Google Scholar]
- Teodoro, A.C.; Veloso-Gomes, F. Quantification of the total suspended matter concentration around the sea breaking zone from in situ measurements and TERRA/ASTER data. Marine Georesources & Geotechnology 2007, 25(2), 67–80. [Google Scholar]
- Toole, D.A.; Siegel, D.A.; Menzies, D.W.; Neumann, M.J.; Smith, R.C. Remote-sensing reflectance determinations in the coastal ocean environment: impact of instrumental characteristics and environmental variability. Applied Optics 2000, 39, 456–469. [Google Scholar]
- Topliss, B.J.; Amos, C.L.; Hill, P.R. Algorithms for remote sensing of high concentration, inorganic suspended sediment. Int. J. Remote Sensing 1990, 11(6), 947–966. [Google Scholar]
- Torréton, J.P.; Rochelle-Newall, E.; Jouon, A.; Faure, V.; Jacquet, S.; Douillet, P. Correspondance between the distribution of biological and chemical variables in a semi-enclosed coral reef lagoon. Estuarine Coastal and Shelf Science 2007, 74, 667–677. [Google Scholar]
- Wang, Y.J.; Yan, F.; Zhang, P.Q.; Dong, W.J. Experimental research on quantitative inversion model of suspended sediment concentration using remote sensing technology. Chinese geographical science 2007, 17(3), 243–249. [Google Scholar]
- Wernand, M.R.; Shimwell, S.J.; Boxall, S.; van Aken, H.M. Evaluation of specific semi-empirical coastal colour algorithms using historic data sets. Neth. J. Aquatic Ecology 1998, 32(1), 73–93. [Google Scholar]
- Wozniak, S.B.; Stramski, D. Modeling the optical properties of mineral particles suspended in seawater and their influence on ocean reflectance and chlorophyll estimation from remote sensing algorithms. Applied Optics 2004, 43(17), 3489–3503. [Google Scholar]
- Zhang, Y.Z.; Pulliainen, J.T.; Koponen, S.S.; Hallikainen, M.T. 2003. Water quality retrievals from combined Landsat TM data and ERS-2 SAR data, in the Gulf of Finland. IEEE Trans. Geosci. Remote Sens. 2003, 41(3), 622–629. [Google Scholar]
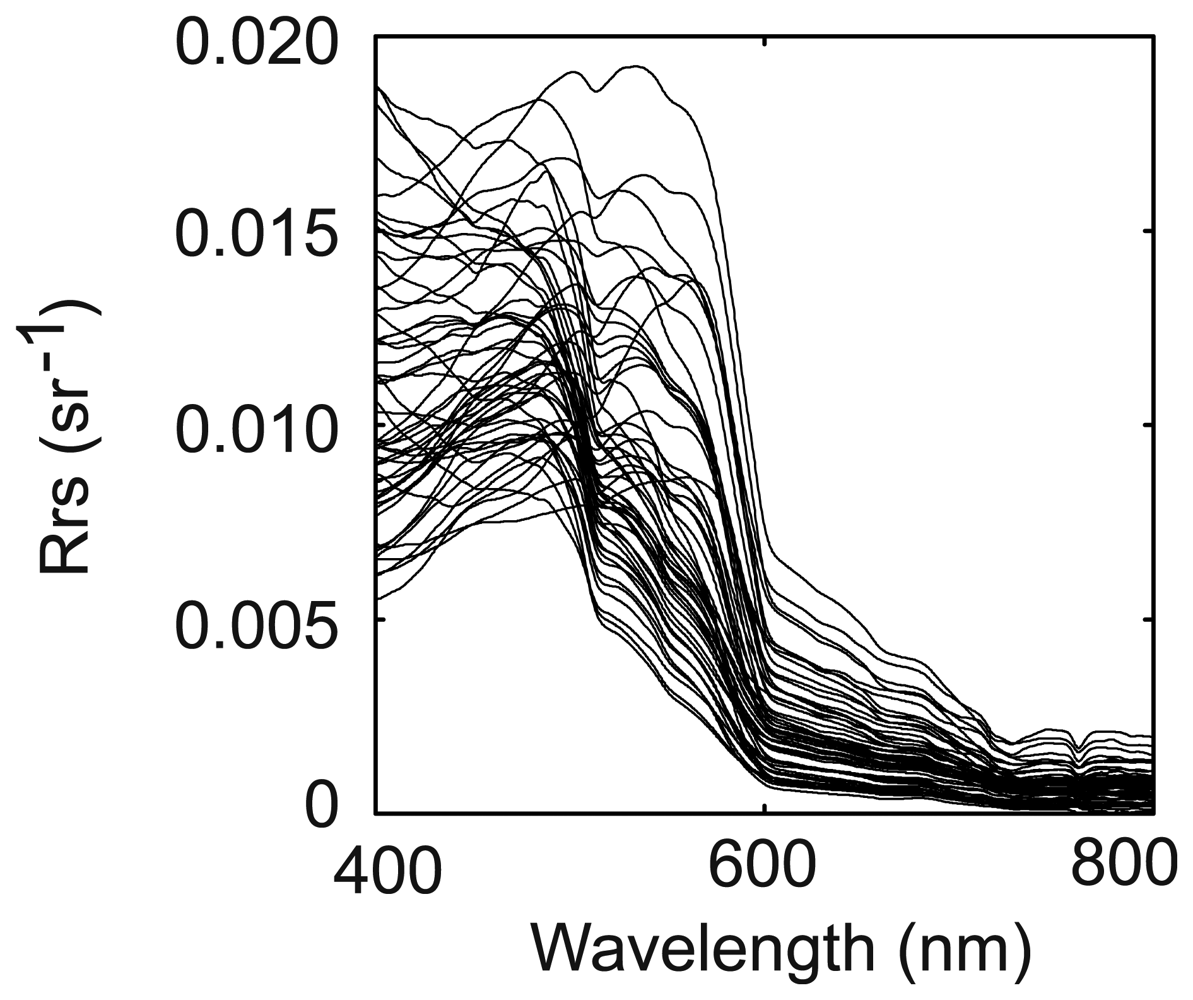
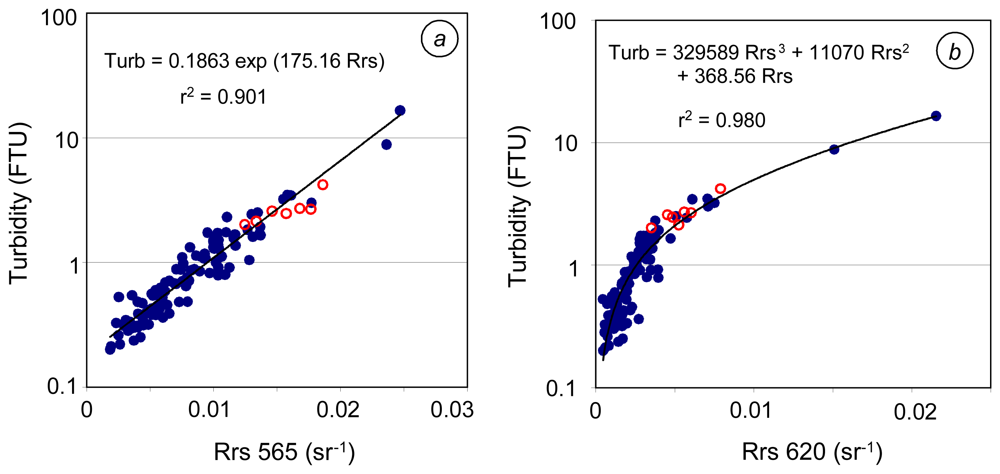
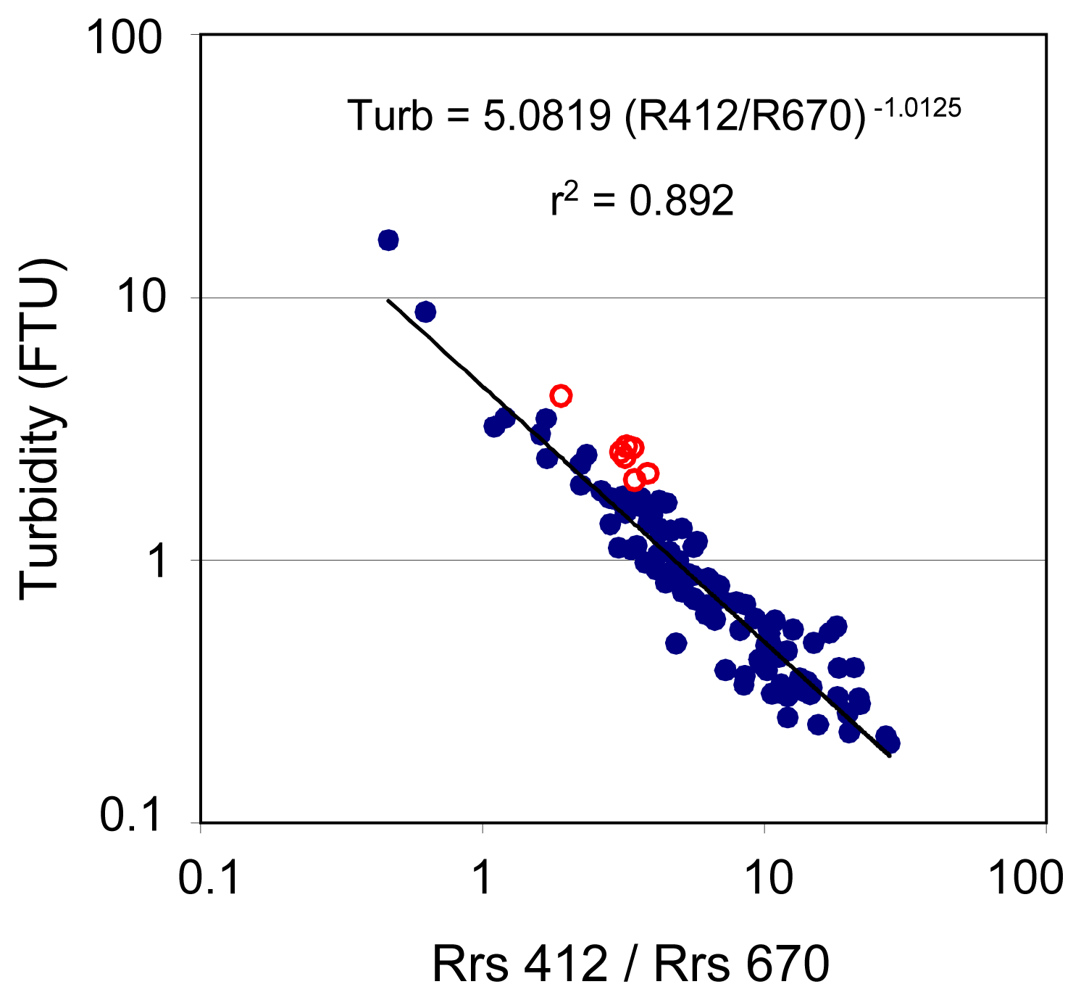
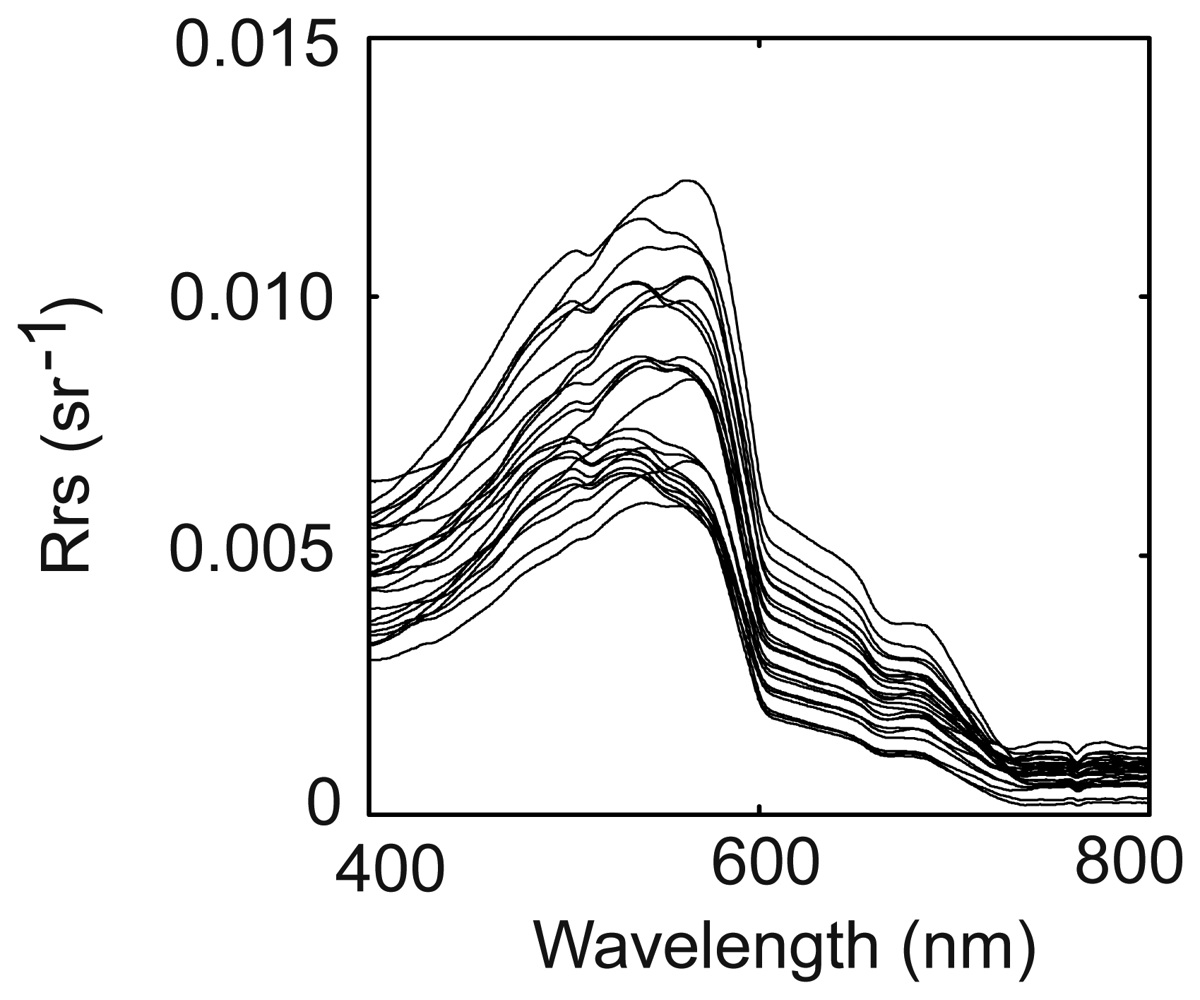
| Turbidity (FTU) | Chlorophyll a (mg m-3) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | Average (0-3 m) | SD (%) | Min | Max | N | Average (1.5 m) | SD (%) | Min | Max | |
| New Caledonia | 113 | 1.23 | 147.7 | 0.20 | 16.50 | 84 | 0.750 | 0.91 | 0.08 | 5.78 |
| Cuba | 24 | 1.57 | 38.4 | 0.91 | 2.88 | 0 | ||||
| Fiji | 56 | 7.08 | 106.0 | 0.81 | 24.90 | 49 | 2.25 | 1.47 | 0.55 | 9.14 |
| ALL | 193 | 2.96 | 168.8 | 0.20 | 24.90 | |||||
| Site | Local algorithm | MNB (%) | rms (%) | Mean quadr. error | Slope | Intercept | r2 |
|---|---|---|---|---|---|---|---|
| NC (a) | Turb=0.1863 exp(175.1 Rrs565) | 3.11 | 25.51 | 0.481 | 0.960 | 0.040 | 0.931 |
| NC (b) | 2.49 | 25.52 | 0.460 | 0.943 | 0.030 | 0.937 | |
| NC (a) | Turb=329589 Rrs6203+ 11070 Rrs6202 + 368.56 Rrs620 | 17.9 | 44.48 | 0.290 | 0.997 | 0.067 | 0.976 |
| NC (b) | 19.6 | 45.32 | 0.286 | 1.001 | 0.074 | 0.978 | |
| NC (a) | Turb=5.0819 (R412/R670) -1.0125 | 3.71 | 28.24 | 0.629 | 0.733 | 0.249 | 0.919 |
| NC (b) | 6.47 | 26.93 | 0.588 | 0.752 | 0.265 | 0.930 | |
| Cuba | Turb=0.565 exp(297.5 Rrs620) | 1.43 | 17.26 | 0.302 | 0.717 | 0.419 | 0.741 |
| Cuba | Turb=0.552 exp(441.4 Rrs681) | 1.83 | 19.83 | 0.336 | 0.632 | 0.543 | 0.681 |
| Fiji | Turb=0.928 exp(191.3 Rrs620) | 5.49 | 34.39 | 3.199 | 0.923 | 0.431 | 0.824 |
| Fiji | Turb=1.068 exp(222.1 Rrs681) | 5.90 | 35.41 | 2.892 | 1.019 | -0.113 | 0.871 |
| Fiji | Turb=14.896 (R510/R681) -1.768 | 5.44 | 35.90 | 2.399 | 0.828 | 0.743 | 0.904 |
| Global statistics | New Caledonia | Cuba | Fiji | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | MNB (%) | rms (%) | Mean quadr error | slope | Intercept | r2 | MNB (%) | rms (%) | Mean quadr error | MNB (%) | rms (%) | Mean quadr error | MNB (%) | rms (%) | Mean quadr error |
| (1) Turb=3183 (Rrs681) 1.254 | 7.6 | 45.2 | 1.832 | 0.716 | 0.478 | 0.913 | 17.50 | 50.4 | 0.411 | -1.4 | 24.0 | 0.350 | -8.7 | 34.9 | 3.342 |
| (2) Turb=-6204217(Rrs681)3 +179652 (Rrs681)2 +36.49 Rrs681 + 0.452 | 18.5 | 49.7 | 1.424 | 0.919 | 0.242 | 0.919 | 34.9 | 53.9 | 0.748 | -7.9 | 19.5 | 0.365 | -3.3 | 34.7 | 2.409 |
| (3) Turb=3.407 (R412/R620) -1.031 | 7.1 | 39.0 | 2.832 | 0.499 | 0.907 | 0.812 | -3.5 | 23.7 | 0.739 | 53.4 | 27.6 | 0.758 | 8.4 | 51.7 | 5.128 |
| (4) Turb=5.966 (R443/R670) -1.102 | 7.0 | 39.4 | 2.453 | 0.565 | 0.763 | 0.887 | -3.5 | 28.7 | 0.527 | 51.9 | 36.9 | 0.770 | 8.9 | 45.4 | 4.463 |
| (5) Turb=11.817 (R510/R681) -1.458 | 9.6 | 49.1 | 1.995 | 0.684 | 0.521 | 0.899 | 6.4 | 53.4 | 0.583 | 30.0 | 39.7 | 0.588 | 7.1 | 41.6 | 3.589 |
| (6) Turb=90.647 (Rrs620.Rrs681/Rrs412) 0.594 | 4.4 | 30.1 | 2.030 | 0.654 | 0.619 | 0.917 | 1.9 | 28.2 | 0.352 | 25.2 | 20.7 | 0.406 | 0.4 | 33.8 | 3.725 |
| (7) Turb=245.59 (Rrs620.Rrs681/Rrs510) 0.711 | 6.5 | 40.7 | 1.915 | 0.701 | 0.522 | 0.903 | 9.1 | 45.2 | 0.573 | 12.2 | 24.6 | 0.333 | -1.4 | 35.8 | 3.454 |
| (8) TURB3: (2) and if Turb < 1FTU, (6) | 3.6 | 35.0 | 1.416 | 0.923 | 0.201 | 0.920 | 5.0 | 38.3 | 0.731 | 1.6 | 19.8 | 0.350 | 1.5 | 33.4 | 2.405 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ouillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.-M.; Andréfouët, S.; Muñoz-Caravaca, A. Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters. Sensors 2008, 8, 4165-4185. https://doi.org/10.3390/s8074165
Ouillon S, Douillet P, Petrenko A, Neveux J, Dupouy C, Froidefond J-M, Andréfouët S, Muñoz-Caravaca A. Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters. Sensors. 2008; 8(7):4165-4185. https://doi.org/10.3390/s8074165
Chicago/Turabian StyleOuillon, Sylvain, Pascal Douillet, Anne Petrenko, Jacques Neveux, Cécile Dupouy, Jean-Marie Froidefond, Serge Andréfouët, and Alain Muñoz-Caravaca. 2008. "Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters" Sensors 8, no. 7: 4165-4185. https://doi.org/10.3390/s8074165





