Hydrologic Remote Sensing and Land Surface Data Assimilation
Abstract
:1. Introduction
2. Soil Moisture Observation
3. Snow Observations
- 1)
- The scanning Multichannel Microwave radiometer (SMMR), a 5 frequency radiometer providing observations from October 1978 to August 1987;
- 2)
- The Special Sensor Microwave Imager (SSM/I), providing observations from September 1987 until present; and
- 3)
- The Advanced Microwave Scanning Radiometer for the Earth Observing system (AMSR-E), providing observation from May 2002 until present.
4. Hydrologic Data Assimilation
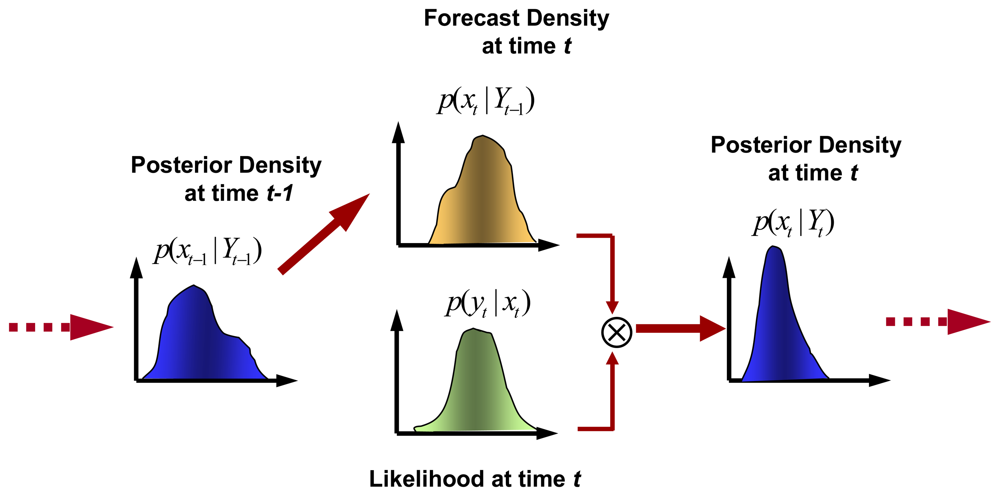
4.1. Sequential Bayesian Data Assimilation using Ensemble Filtering
4.1.1. Ensemble Kalman Filter
- 1)
- the forecasting step which is the transition of state variables from one observation time to the next represented through transition probability p(xt/xt-1) in eq. (5),
- 2)
- the analysis (updating) step which involves updating of the forecasted (propagated) states with the new observation.
4.1.2. Particle Filter
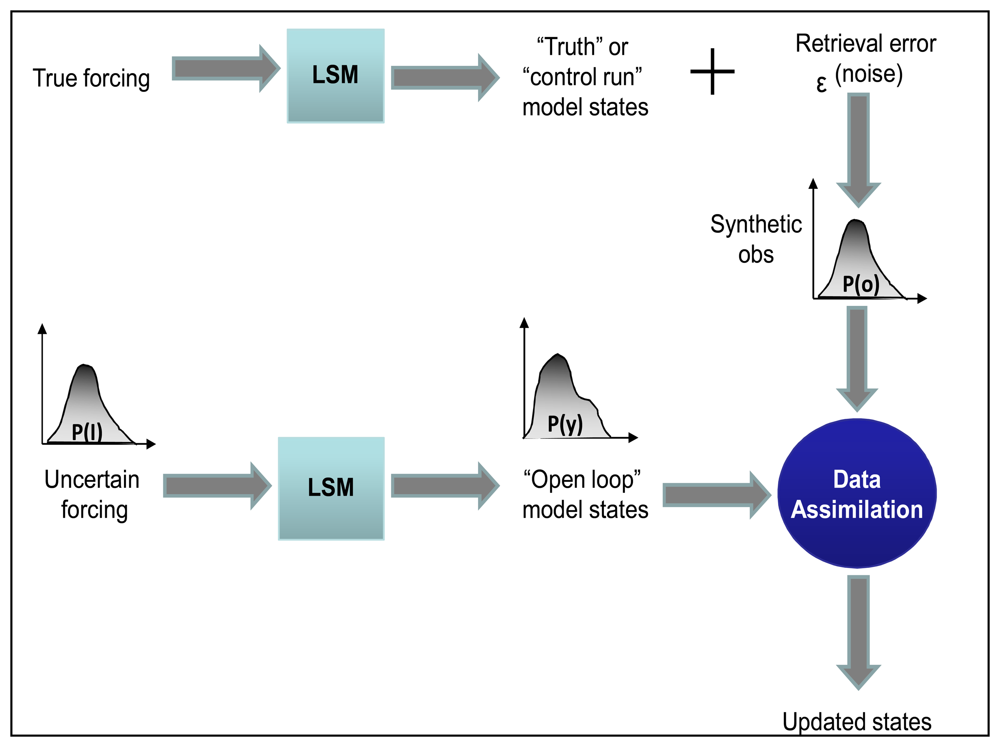
4.1.3. DA Experiment Setup through Observing System Simulation Experiment (OSSE)
5. Summary
Acknowledgments
References
- Andreadis, K.M.; Lettenmaier, D.P. Assimilating remotely sensed snow observations into a macroscale hydrology model. Adv. in Water Resour. 2006, 29, 872–886. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. Signal Processing, IEEE Transactions on Signal Processing 2002, 50, 174–188. [Google Scholar]
- Beljaars, A.C.M.; Viterbo, P.; Miller, M.J.; Betts, A.K. The Anomalous Rainfall over the United States during July 1993: Sensitivity to Land Surface Parameterization and Soil Moisture Anomalies. Mon. Weather Rev. 1996, 124, 362–383. [Google Scholar]
- Bindlish, R.; Jackson, T.J.; Gasiewski, A.; Stankov, B.; Klein, M.; Cosh, M.H.; Mladenova, I.; Watts, C.; Vivoni, E.; Lakshmi, V.; Bolten, J.; Keefer, T. Aircraft based soil moisture retrievals under mixed vegetation and topographic conditions. Remote Sensing of Environment 2008, 112, 375–390. [Google Scholar]
- Bindlish, R.; Jackson, T.J.; Gasiewski, A.J.; Klein, M.; Njoku, E.G. Soil moisture mapping and AMSR-E validation using the PSR in SMEX02. Remote Sensing of Environment 2006, 103, 127–139. [Google Scholar]
- Bosilovich, M.G.; Radakovich, J.D.; Silva, A.; Tooling, R.; Verter, F. Skin Temperature Analysis and Bias Correction in a Coupled Land-Atmosphere Data Assimilation System. J. of the Meteorological Soc. of Japan. Ser.II 2007, 85A, 205–228. [Google Scholar]
- Box, G.E.P.; Tiao, G.C. Bayesian Inference in Statistical Analysis; Addison-Wesley: Boston, MA, USA, 1973. [Google Scholar]
- Clark, M.P.; Slater, A.G.; Barrett, A.P.; Hay, L.E.; McCabe, G.J.; Rajagopalan, B.; Leavesley, G.H. Assimilation of snow covered area information into hydrologic and land-surface models. Adv. in Water Resour. 2006, 29, 1209–1221. [Google Scholar]
- Claussen, M. On multiple solutions of the atmosphere-vegetation system in present-day climate. Global Change Biol. 1998, 4, 549–559. [Google Scholar]
- Crow, W.T.; Wood, E.F. The assimilation of remotely sensed soil brightness temperature imagery into a land surface model using Ensemble Kalman filtering: a case study based on ESTAR measurements during SGP97. Adv. in Water Resour. 2003, 26, 137–149. [Google Scholar]
- Das, N.N.; Mohanty, B.P. Temporal dynamics of PSR-based soil moisture across spatial scales in an agricultural landscape during SMEX02: A wavelet approach. Remote Sensing of Environment 2008, 112, 522–534. [Google Scholar]
- Delworth, T.; Manabe, S. The Influence of Soil Wetness on Near-Surface Atmospheric Variability. J. of Climate 1989, 2, 1447–1462. [Google Scholar]
- Derber, J.C.; Parrish, D.F.; Lord, S.J. The New Global Operational Analysis System at the National Meteorological Center. Weather and Forecasting 1991, 6, 538–547. [Google Scholar]
- Dirmeyer, P.A. The Role of the Land Surface Background State in Climate Predictability. J. of Hydromet. 2003, 4, 599–610. [Google Scholar]
- Dong, J.; Walker, J.P.; Houser, P.R. Factors affecting remotely sensed snow water equivalent uncertainty. Remote Sensing of Environment 2005, 97, 68–82. [Google Scholar]
- Drusch, M. Initializing numerical weather prediction models with satellite derived surface soil moisture: Data assimilation experiments with ECMWF's integrated forecast system. J. of Geophysical Res. in press.
- Entekhabi, D.; Nakamura, H.; Njoku, E.G. Solving the inverse problem for soil moisture and temperature profiles by sequential assimilation of multifrequency remotely sensed observations. Geoscience and Remote Sensing, IEEE Transactions on 1994, 32, 438–448. [Google Scholar]
- Entin, J.K.; Robock, A.; Vinnikov, K.Y.; Hollinger, S.E.; Liu, S.; Namkhai, A. Temporal and spatial scales of observed soil moisture variations in the extratropics. J. of Geophysical Res. 2000, 105, 11865–11877. [Google Scholar]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar]
- Fennessy, M.J.; Shukla, J. Impact of Initial Soil Wetness on Seasonal Atmospheric Prediction. J. of Climate 1999, 12, 3167–3180. [Google Scholar]
- Foley, J.A. The sensitivity of the terrestrial biosphere to climatic change: A simulation of the middle Holocene. Global Biogeochem. Cycles 1994, 8, 505–525. [Google Scholar]
- Foster, J.L.; Sun, C.; Walker, J.P.; Kelly, R.; Chang, A.; Dong, J.; Powell, H. Quantifying the uncertainty in passive microwave snow water equivalent observations. Remote Sensing of Environment 2005, 94, 187–203. [Google Scholar]
- Galantowicz, J.F.; Entekhabi, D.; Njoku, E.G. Tests of sequential data assimilation for retrieving profile soil moisture and temperature from observed L-band radiobrightness. Geoscience and Remote Sensing, IEEE Transactions on 1999, 37, 1860–1870. [Google Scholar]
- Gallus, W.A.; Segal, M. Sensitivity of Forecast Rainfall in a Texas Convective System to Soil Moisture and Convective Parameterization. Weather and Forecasting 2000, 15, 509–525. [Google Scholar]
- Georgakakos, K.P.; Graham, N.E.; Carpenter, T.M.; Georgakakos, A.P.; Yao, H. Integrating Climate-Hydrology Forecasts and Multi-Objective Reservoir Management for Northern California. EOS 2005, 86, 122–127. [Google Scholar]
- Georgakakos, K.P.; Rajaram, H.; Li, S.G. On Improved Operational Hydrologic Forecasting of Streamflows. IIHR Report 1988, 325, 162. [Google Scholar]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS/Terra Snow Cover 8-day L3 Global 500 m Grid V004. Boulder CO, USA; In National Snow and Ice Data Center; 2000; digital media. [Google Scholar]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sensing of Environment 2002, 83, 181–194. [Google Scholar]
- Hoeben, R.; Troch, P.A. Assimilation of active microwave observation data for soil moisture profile estimation. Water Resour. Res. 2000, 36, 2805–2819. [Google Scholar]
- Houser, P.R.; Shuttleworth, W.J.; Famiglietti, J.S.; Gupta, H.V.; Syed, K.H.; Goodrich, D.C. Integration of soil moisture remote sensing and hydrologic modeling using data assimilation. Water Resour. Res. 1998, 34, 3405–3420. [Google Scholar]
- Jackson, T.J. Estimation of surface soil moisture using Microwave sensors. Encyclopedia of Hydrology 2005, 54, 799–809. [Google Scholar]
- Jackson, T.J.; Bindlish, R.; Gasiewski, A.J.; Stankov, B.; Klein, M.; Njoku, E.G.; Bosch, D.; Coleman, T.L.; Laymon, C.A.; Starks, P. Polarimetric scanning radiometer C- and X-band microwave observations during SMEX03. IEEE Transactions on Geoscience and Remote Sensing 2005, 43, 2418–2430. [Google Scholar]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Academic Press: New York, 1970; p. 376. [Google Scholar]
- Kitanidis, P.K.; Bras, R.L. Real-Time Forecasting With a Conceptual Hydrologic Model 2. Applications and Results. Water Resour. Res. 1980, 16, 1034–1044. [Google Scholar]
- Kitanidis, P.K.; Bras, R.L. Real-Time Forecasting With a Conceptual Hydrologic Model 1. Analysis of Uncertainty. Water Resour. Res. 1980, 16, 1025–1033. [Google Scholar]
- Koster, R.D.; Suarez, M.J.; Liu, P.; Jambor, U.; Berg, A.; Kistler, M.; Reichle, R.; Rodell, M.; Famiglietti, J. Realistic Initialization of Land Surface States: Impacts on Subseasonal Forecast Skill. J. of Hydromet. 2004, 5, 1049–1063. [Google Scholar]
- Kumar, S.V.; Peters-Lidard, C.D.; Tian, Y.; Houser, P.R.; Geiger, J.; Olden, S.; Lighty, L.; Eastman, J.L.; Doty, B.; Dirmeyer, P.; Adams, J.; Mitchell, K.; Wood, E.F.; Sheffield, J. Land information system: An interoperable framework for high resolution land surface modeling. Environmental Modeling & Software 2006, 21, 1402–1415. [Google Scholar]
- Li, X.; Koike, T.; Pathmathevan, M. A very fast simulated re-annealing (VFSA) approach for land data assimilation. Computers and Geosciences 2004, 30, 239–248. [Google Scholar]
- Margulis, S.A.; McLaughlin, D.; Entekhabi, D.; Dunne, S. Land data assimilation and estimation of soil moisture using measurements from the Southern Great Plains 1997 field experiment. Water Resour. Res. 2002, 38, 1299. [Google Scholar]
- Maurer, E.P.; Rhoads, J.D.; Dubayah, R.O.; Lettenmaier, D.P. Evaluation of the snow-covered area data product from MODIS. Hydrol. Process. 2003, 17, 59–71. [Google Scholar]
- McLaughlin, D.; O'Neill, A.; Derber, J.; Kamachi, M. Opportunities for enhanced collaboration within the data assimilation community. Quarterly Journal of the Royal Meteorological Society 2005, 131, 3683–3693. [Google Scholar]
- McLaughlin, D. An integrated approach to hydrologic data assimilation: interpolation, smoothing, and filtering. Adv. in Water Resour. 2002, 25, 1275–1286. [Google Scholar]
- Moradkhani, H.; Hsu, K.; Hong, Y.; Sorooshian, S. Investigating the impact of remotely sensed precipitation and hydrologic model uncertainties on the ensemble streamflow forecasting. Geophys. Res. Lett. 2006, 33, L12107. [Google Scholar]
- Moradkhani, H.; Hsu, K.L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, W05012. [Google Scholar]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state–parameter estimation of hydrological models using ensemble Kalman filter. Adv. in Water Resour. 2005, 28, 135–147. [Google Scholar]
- Njoku, E.G.; Chan, S.K. Vegetation and surface roughness effects on AMSR-E land observations. Remote Sensing of Environment 2006, 100, 190–199. [Google Scholar]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. Geoscience and Remote Sensing, IEEE Transactions on 2003, 41, 215–229. [Google Scholar]
- Njoku, E.G. AMSR-E/Aqua L2B surface soil moisture, ancillary parms, and QC EASE-Grids. Natl. Snow and Ice Data Cent. digital media: Boulder, CO, 2006. (Updated daily; available at http://nsidc.org/data/amsre/) June 2002 to May 2006.
- Njoku, E.G.; Entekhabi, D. Passive microwave remote sensing of soil moisture. J. of Hydrology 1996, 184, 101–129. [Google Scholar]
- Pfaendtner, J.; Bloom, S.; Lamich, D.; Seablom, M.; Sienkiewicz, M.; Stobie, J.; da Silva, A. Documentation of the Goddard Earth Observing System (GEOS) Data Assimilation System— Version 1. NASA Tech.Memo. 1995, 104606. [Google Scholar]
- Reichle, R.H.; Entekhabi, D.; McLaughlin, D.B. Downscaling of radio brightness measurements for soil moisture estimation: A four-dimensional variational data assimilation approach. Water Resour. Res. 2001, 37, 2353–2364. [Google Scholar]
- Reichle, R.H.; Koster, R.D. Global assimilation of satellite surface soil moisture retrievals into the NASA Catchment land surface model. Geophys. Res. Lett. 2005, 32. [Google Scholar]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SSMR). J. of Geophysical Res. 2007, 112, D09108. [Google Scholar]
- Reichle, R.H.; Walker, J.P.; Koster, R.D.; Houser, P.R. Extended versus Ensemble Kalman Filtering for Land Data Assimilation. J. of Hydromet. 2002, 3, 728–740. [Google Scholar]
- Rodell, M.; Houser, P.R. Updating a Land Surface Model with MODIS-Derived Snow Cover. J. of Hydrometorology 2004, 5, 1064–1075. [Google Scholar]
- Seo, D.; Koren, V.; Cajina, N. Real-Time Variational Assimilation of Hydrologic and Hydrometeorological Data into Operational Hydrologic Forecasting. J. of Hydromet. 2003, 4, 627–641. [Google Scholar]
- Slater, A.G.; Clark, M.P. Snow Data Assimilation via an Ensemble Kalman Filter. J. of Hydromet. 2006, 7, 478–493. [Google Scholar]
- Sun, C.J.; Walker, J.P.; Houser, P.R. A methodology for snow data assimilation in a land surface model. J. of Geophysical Res. 2004, 109, D08108. [Google Scholar]
- Texier, D.; de Noblet, N.; Harrison, S.P.; Haxeltine, A.; Jolly, D.; Joussaume, S.; Laarif, F.; Prentice, I.C.; Tarasov, P. Quantifying the role of biosphere-atmosphere feedbacks in climate change: coupled model simulations for 6000 years BP and comparison with palaeodata for northern Eurasia and northern Africa. Clim. Dyn. 1997, 13, 865–881. [Google Scholar]
- Vrugt, J.A.; Gupta, H.V.; Nualláin, B.Ó; Bouten, W. Real-Time Data Assimilation for Operational Ensemble Streamflow Forecasting. J. of Hydromet 2006, 7, 548–565. [Google Scholar]
- Walker, J.P.; Houser, P.R.; Reichle, R. New Technologies Require Advances in Hydrologic Data Assimilation. EOS 2003, 84, 545. [Google Scholar]
- Wang, J.R.; Choudhury, B.J. Passive microwave radiation from soil: examples of emission models and observations, in Passive microwave remote sensing of land-atmosphere interactions. VSP 1995, 423–460. [Google Scholar]
- Wang, J.R. The dielectric properties of soil-water mixtures at microwave frequencies. Radio Sci 1980, 15, 977–985. [Google Scholar]
- Weerts, A.H.; El Serafy, G.Y. H. Particle filtering and ensemble Kalman filtering for state updating with hydrological conceptual rainfall-runoff models. Water Resour. Res. 2006, 42, W09403. [Google Scholar]
- Zhou, Y.; McLaughlin, A.; Entekhabi, D. Assessing the Performance of the Ensemble Kalman Filter for Land Surface Data Assimilation. Mon. Weather Rev. 2006, 134, 2128–2142. [Google Scholar]
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the CreativeCommons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Moradkhani, H. Hydrologic Remote Sensing and Land Surface Data Assimilation. Sensors 2008, 8, 2986-3004. https://doi.org/10.3390/s8052986
Moradkhani H. Hydrologic Remote Sensing and Land Surface Data Assimilation. Sensors. 2008; 8(5):2986-3004. https://doi.org/10.3390/s8052986
Chicago/Turabian StyleMoradkhani, Hamid. 2008. "Hydrologic Remote Sensing and Land Surface Data Assimilation" Sensors 8, no. 5: 2986-3004. https://doi.org/10.3390/s8052986



