An Integrated MEMS Gyroscope Array with Higher Accuracy Output
Abstract
:1. Introduction
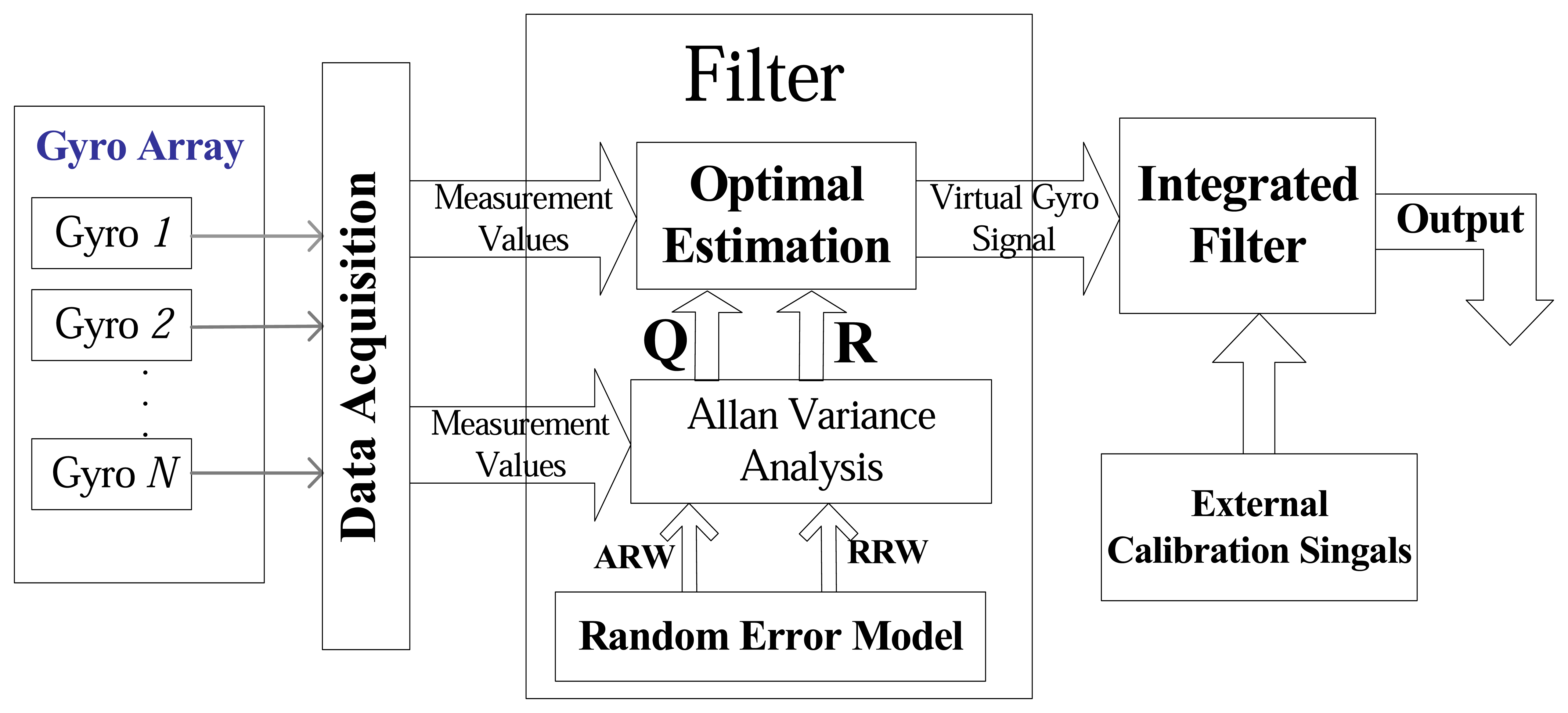
2. Working principle of the integrated gyroscope array
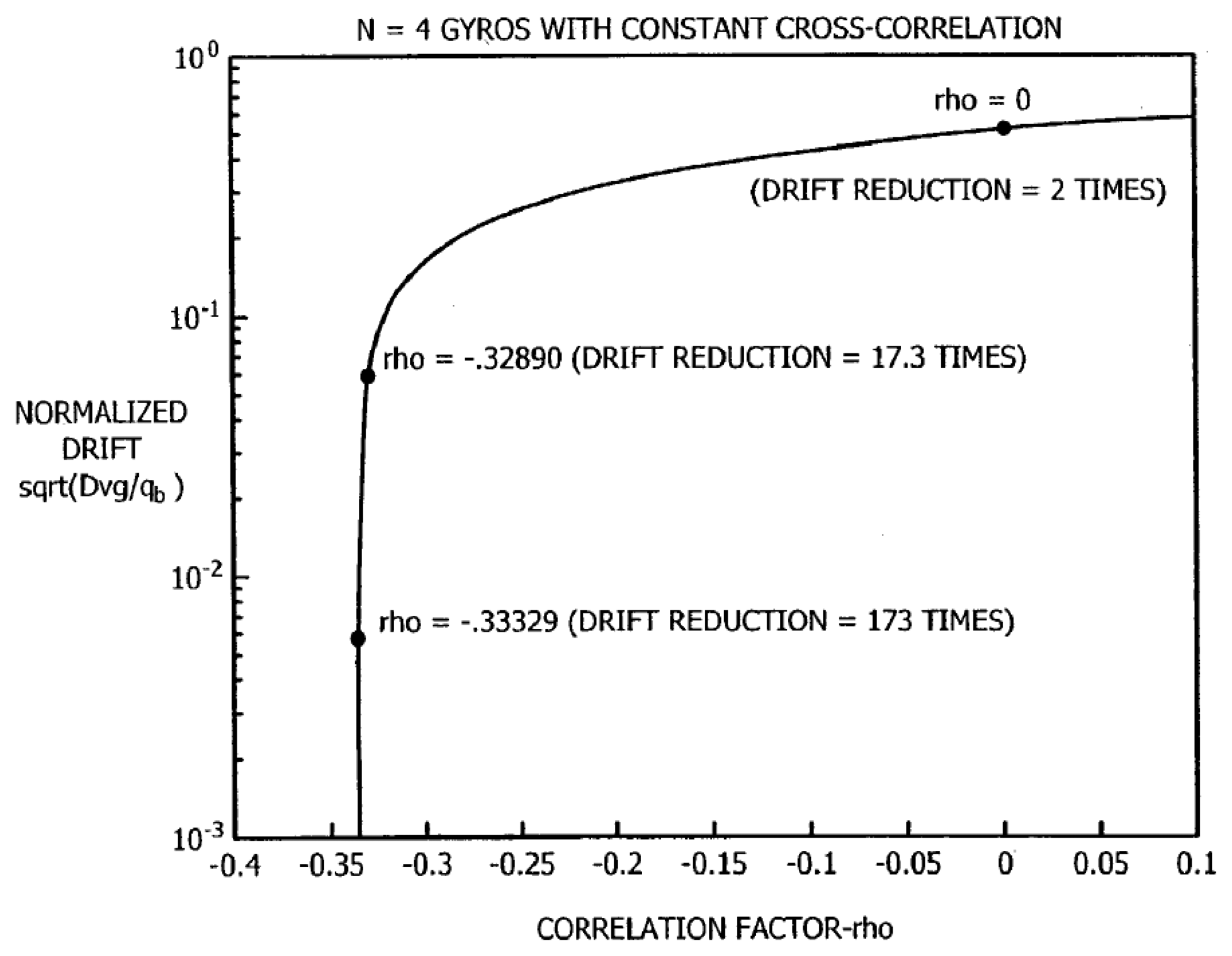
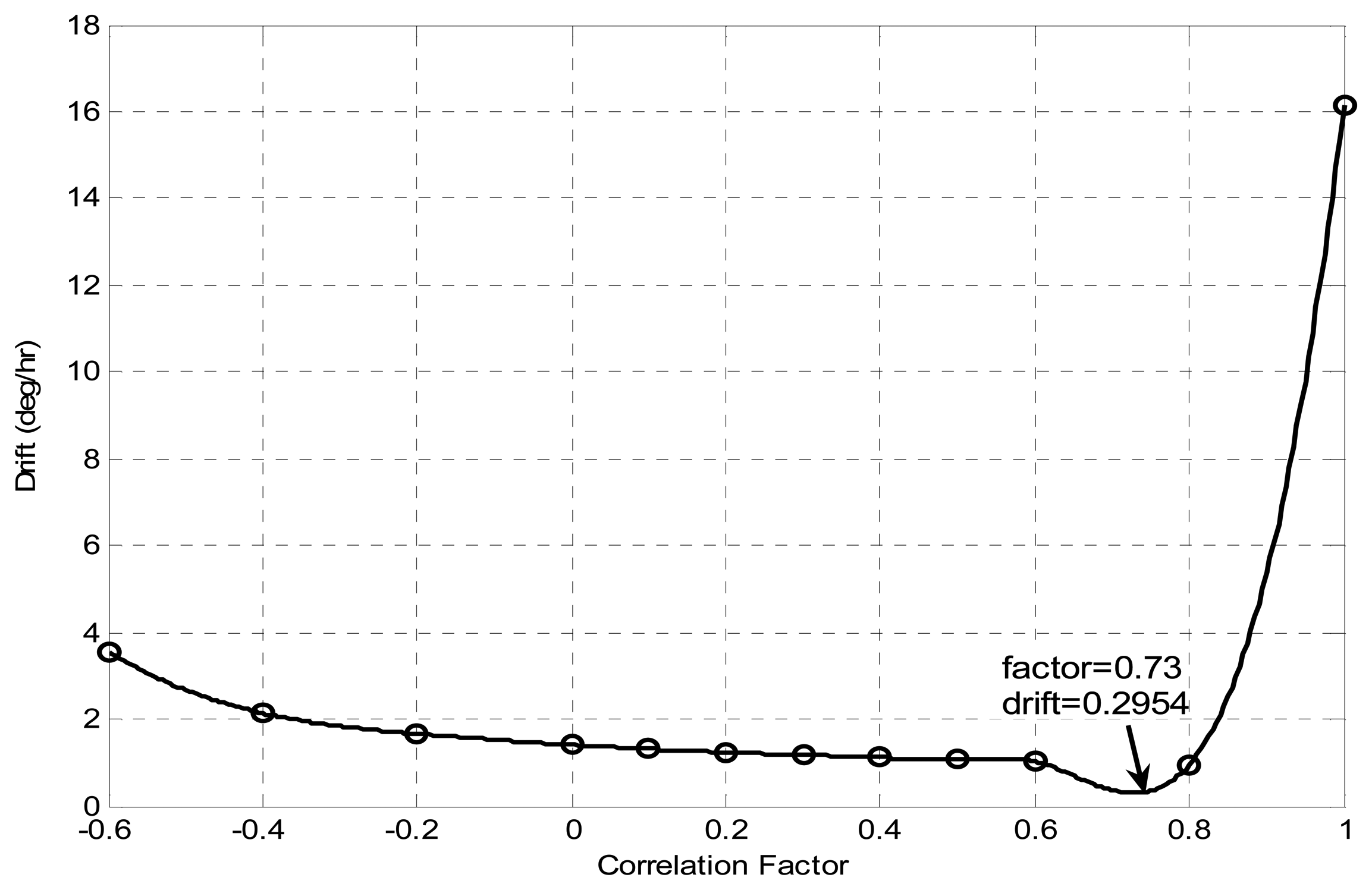
2.1 Correlations between the MEMS gyroscopes in the sensor array
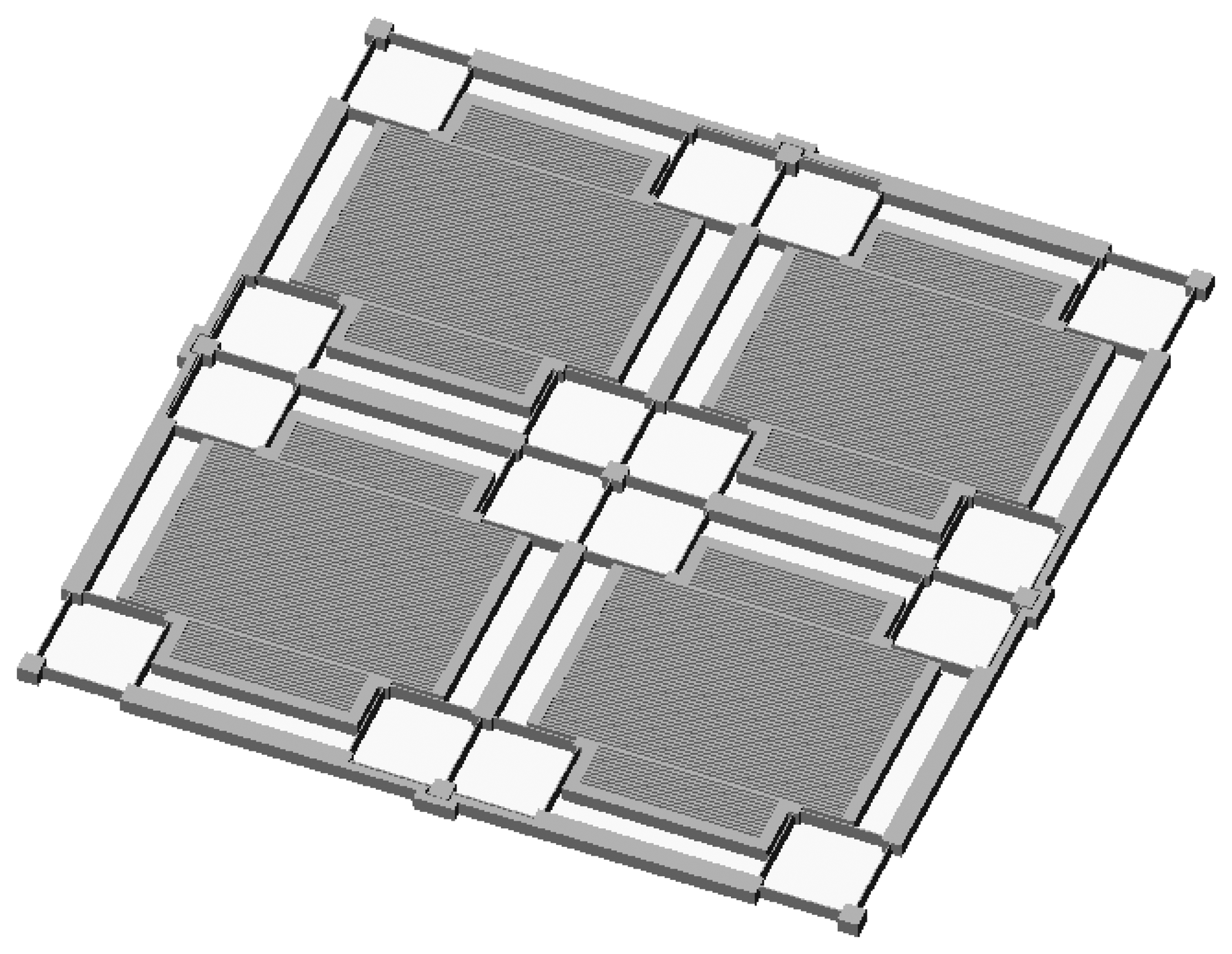
2.2 Structure of integrated MEMS gyroscope array
3. Design of integrated MEMS gyroscope array
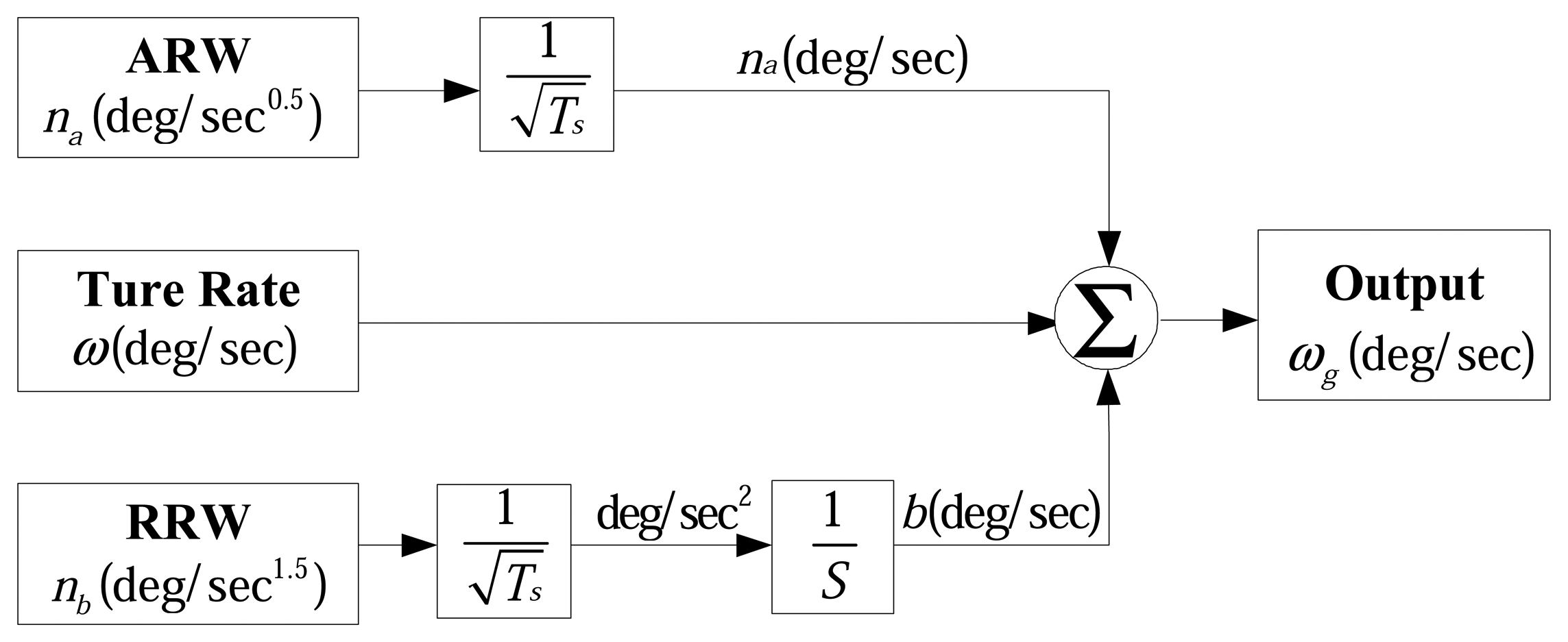
3.1 Random noise modeling for MEMS gyroscope
3.2 First-level optimal filter
3.3 Second-level integrated optimal filter
3.3.1 State equations derivation
3.3.2 Measurement equations derivation
3.3.3 Integrated optimal filter design
4. Experimental
4.1 Experiment setup
4.2 Experiment results
5. Conclusions
Acknowledgments
References and Notes
- Weinberg, M.S.; Kourepenis, A. Error sources in in-plane silicon tuning-fork MEMS gyroscopes. Journal of Microelectromechanical Systems 2006, 15, 479–491. [Google Scholar]
- Barbour, N.; Schmidt, G. Inertial Sensor Technology Trends. Proceedings of IEEE Workshop on Autonomous Underwater Vehicles, Cambridge, MA, August 1998; pp. 55–62.
- Lam, Q.M.; Wilson, T., Jr.; Contillo, R.; Buck, D. Enhancing MEMS sensors accuracy via random noise characterization and calibration. Proceedings of SPIE 2004, 5403, 427–438. [Google Scholar]
- Weis, M.; Allan, D. Smart Clock: A New Time. IEEE Transactions on Instrumentation and Measurement 1992, 41, 915–918. [Google Scholar]
- Bayard, D.S.; Ploen, S.R. High accuracy inertial sensors from inexpensive components. US Patent. US20030187623A1, 2003. [Google Scholar]
- Lam, Q.M.; Stamatakos, N.; Woodruff, C.; Ashton, S. Gyro modeling and estimation of its random noise sources. In AIAA Guidance, Navigation, and Control Conference and Exhibit; Austin, Texas, 2003; Volume 5562, pp. 1–11. [Google Scholar]
- Lam, Q.M.; Hunt, T.; Sanneman, P.; Underwood, S. Analysis and design of a fifteen state stellar inertial attitude determination system. In AIAA Guidance, Navigation, and Control Conference and Exhibit; Austin, Texas, 2003; Volume 5483, pp. 11–14. [Google Scholar]
- Kim, S.; Lee, B.; Lee, J. A gyroscope array with linked-beam structure. The 14th IEEE International Conference on Micro Electro Mechanical Systems, January 2001; pp. 30–33.
- Cardarelli, D. An integrated MEMS inertial measurement unit. IEEE Position Location and Navigation Symposium; 2002; pp. 314–319. [Google Scholar]
- Hou, H.; El-Sheimy, N. Inertial sensors errors modeling using Allan variance. Proc. ION GPS/GNSS 2003, 2860–2867. [Google Scholar]
- IEEE standard specification format guide and test procedure for single-axis laser gyros. IEEE Standard 1995, 647–1995.
- Grewal, M.S.; Andrews, A.P. Kalman filtering theory and practice using Matlab; John Wiley & Sons: New York, 2001. [Google Scholar]
- Doob, J.L. Stochastic Processes; John Wiley & Sons: New York, 1953. [Google Scholar]
- Hernandez, W. Robust multivariable estimation of the relevant information coming from a wheel speed sensor and an accelerometer embedded in a car under performance tests. Sensors 2005, 5, 488–508. [Google Scholar]
- Gebre-Egziabher, D.; Gabriel, H. A gyro-free quaternion-based attitude determination system suitable for implementation using low cost sensors. IEEE Position Location and Navigation Symposium 2000, 185–192. [Google Scholar]
- Gebre-Egziabher, D.; Hayward, R.C.; Powell, J.D. Design of multi-sensor attitude determination systems. IEEE Transaction on Aerospace and Electronic System 2004, 40, 627–649. [Google Scholar]
- Su, K.; Ren, D.H.; You, Z.; Zhou, Q. Application of MIMU/Magnetometer Integrated System on the Attitude Determination of Micro Satellite. Proceedings of the 2004 International Conference on intelligent Mechatronics and Automation, Chengdu, China; 2004. [Google Scholar]
- Rong, Z.; Zhaoying, Z. A MEMS-based attitude reference system. Measurement and Control Technology 2002, 21, 6–8. [Google Scholar]
- Caruso, M.J. Application of magneto resistive sensors in navigation systems. Sensors and Actuators 1997, 42, 15–21. [Google Scholar]
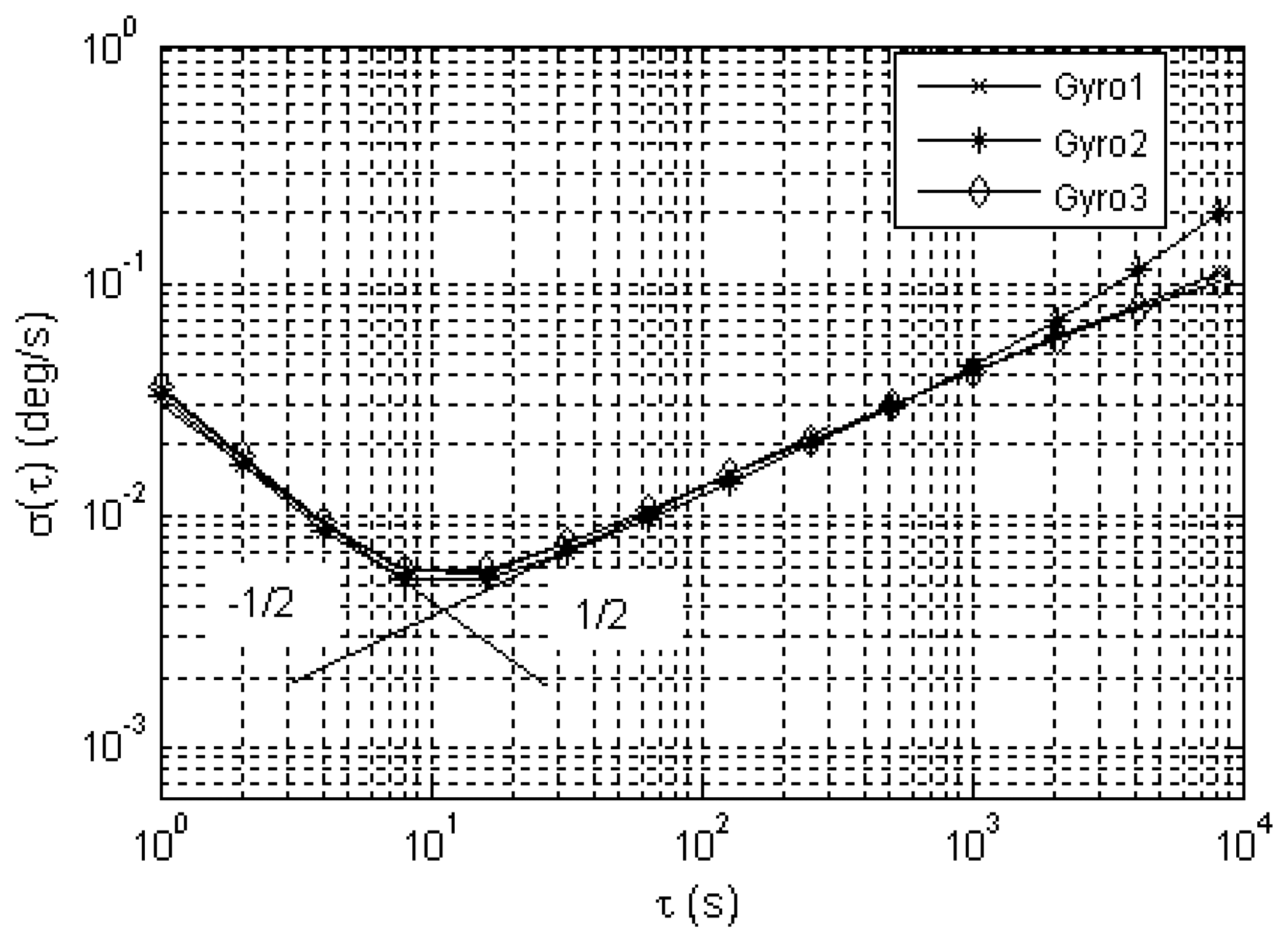
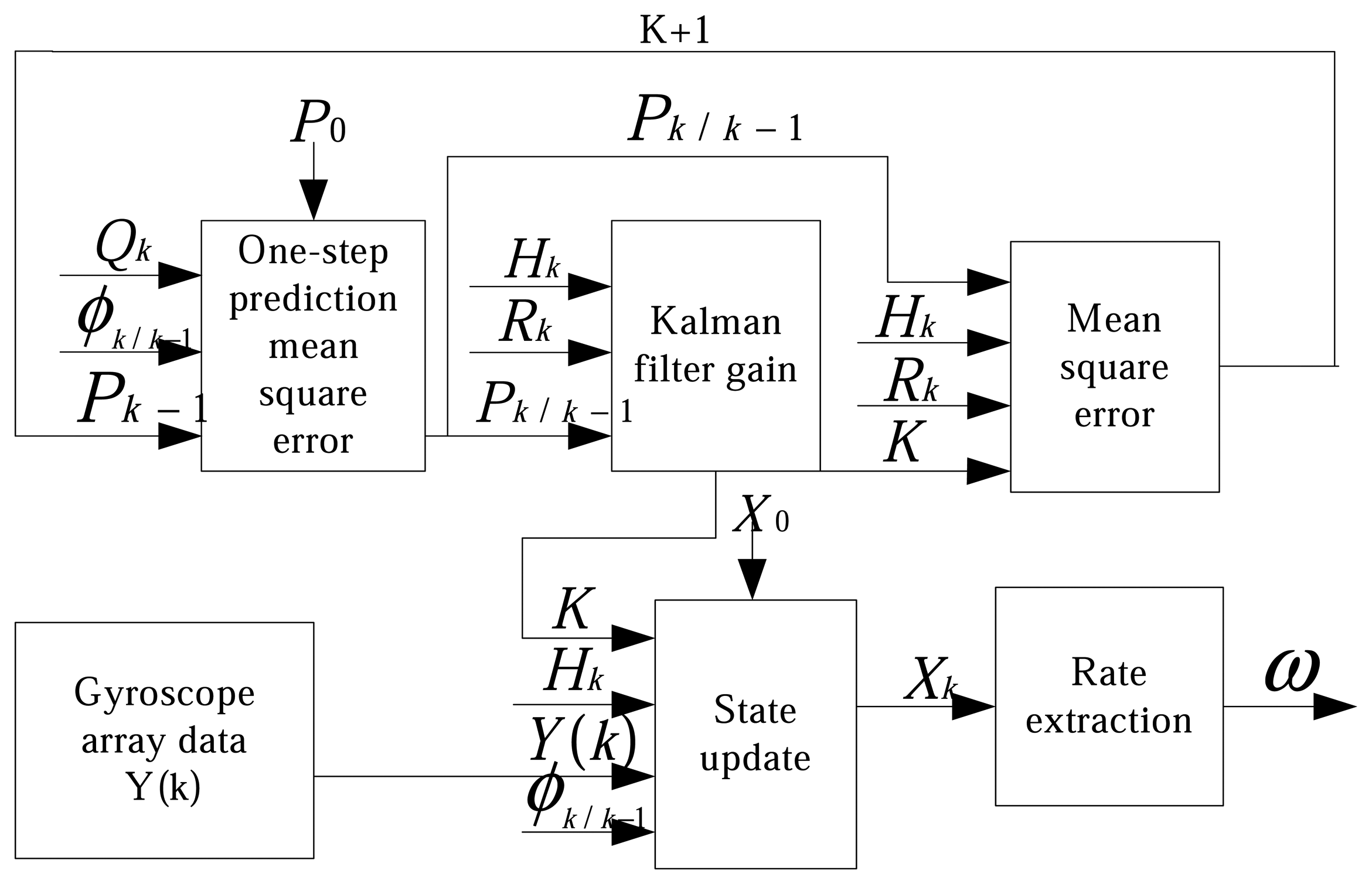
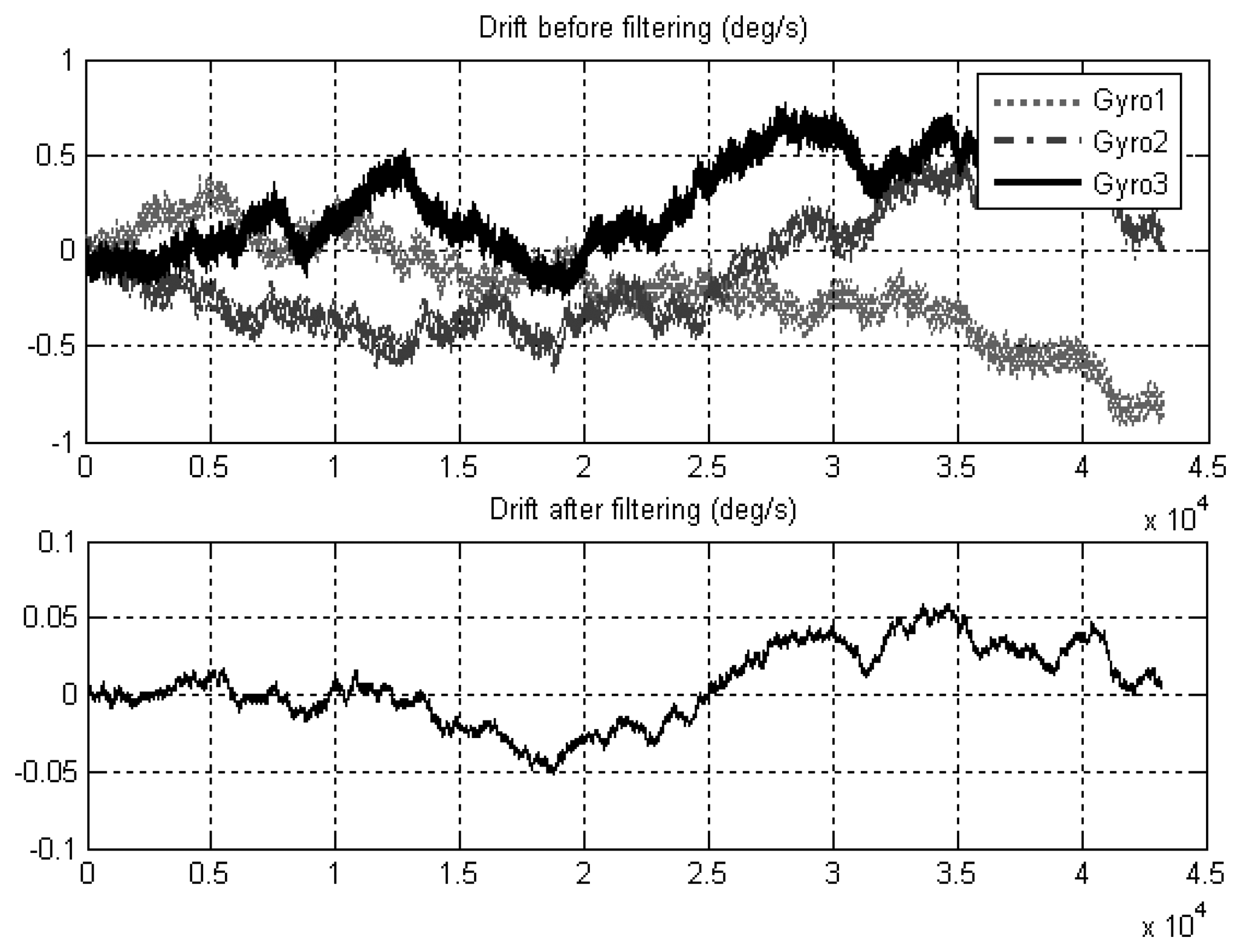
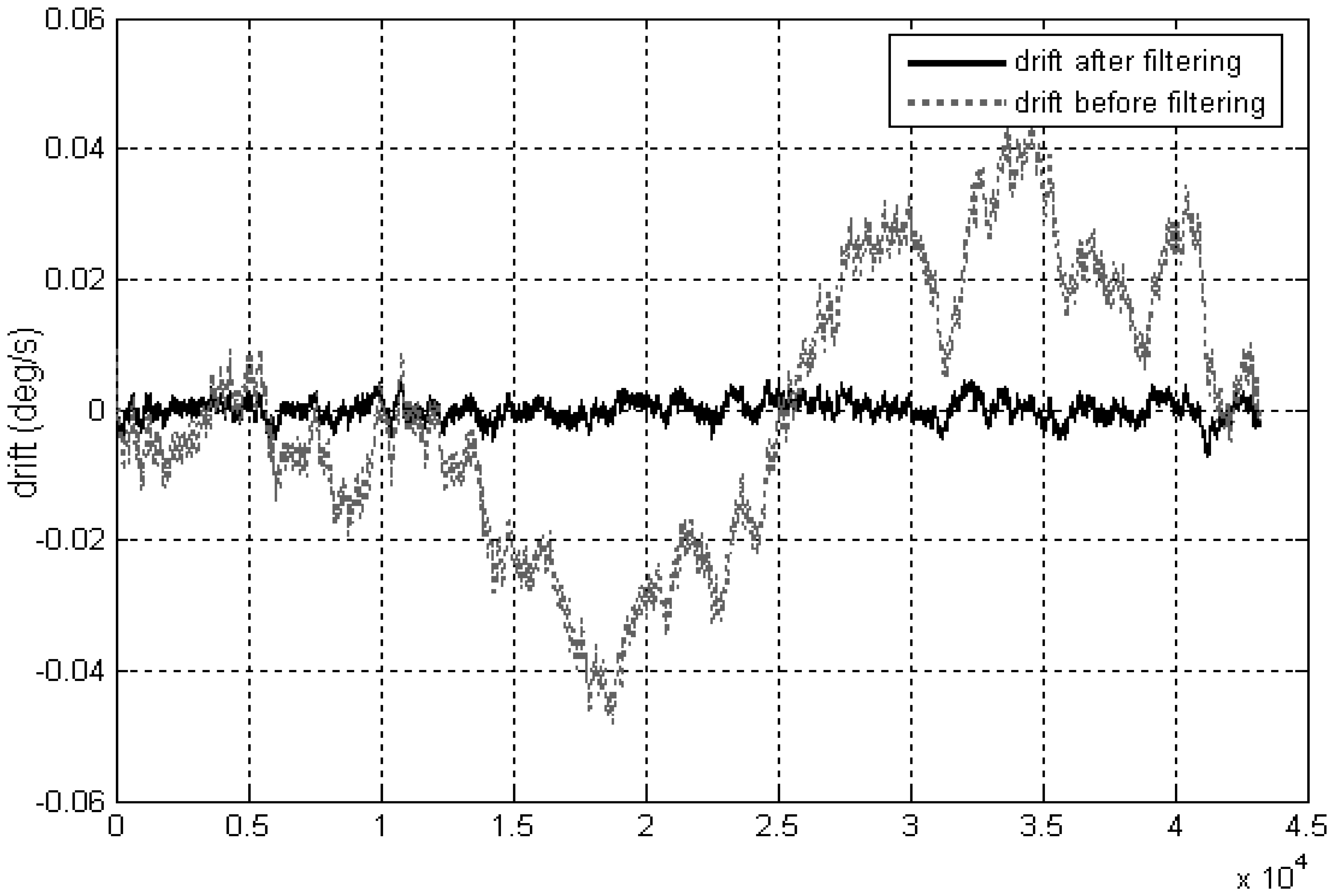
| Error terms | Allan variance | Unit | Slope |
|---|---|---|---|
| ARW | -1/2 | ||
| Bias Instability | deg/ hr | 0 | |
| RRW | deg/ hr1.5 | +1/2 |
| Symbols | Description |
|---|---|
| b | Body frame of aircraft |
| n | Navigation frame |
| Q | Attitude quaternion |
| Qe | Attitude error quaternion |
| Direction Cosine Matrix (DCM) | |
| m | Measurement value of Earth magnetic |
| a | Measurement value of gravity field |
| b̂ | Estimation of rate random walk |
© 2008 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Chang, H.; Xue, L.; Qin, W.; Yuan, G.; Yuan, W. An Integrated MEMS Gyroscope Array with Higher Accuracy Output. Sensors 2008, 8, 2886-2899. https://doi.org/10.3390/s8042886
Chang H, Xue L, Qin W, Yuan G, Yuan W. An Integrated MEMS Gyroscope Array with Higher Accuracy Output. Sensors. 2008; 8(4):2886-2899. https://doi.org/10.3390/s8042886
Chicago/Turabian StyleChang, Honglong, Liang Xue, Wei Qin, Guangmin Yuan, and Weizheng Yuan. 2008. "An Integrated MEMS Gyroscope Array with Higher Accuracy Output" Sensors 8, no. 4: 2886-2899. https://doi.org/10.3390/s8042886




