Two Improvements of an Operational Two-Layer Model for Terrestrial Surface Heat Flux Retrieval
Abstract
:1. Introduction
2. Model Descriptions
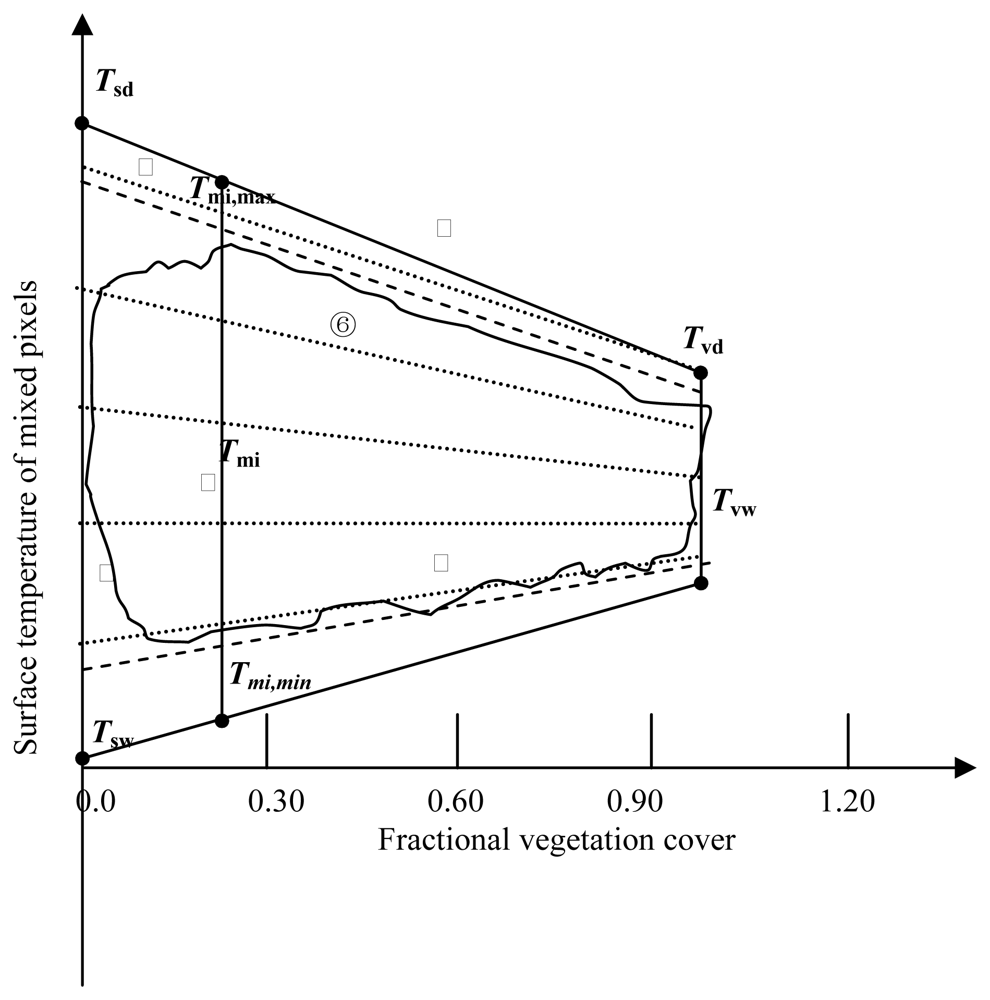
2.1 An interpretation of Tm – f space
2.2. PCACA Algorithm
2.3 Layered Energy-separating Algorithm
2.4 Estimation of Other Core Variables
3. Two improvements for the two-layer model
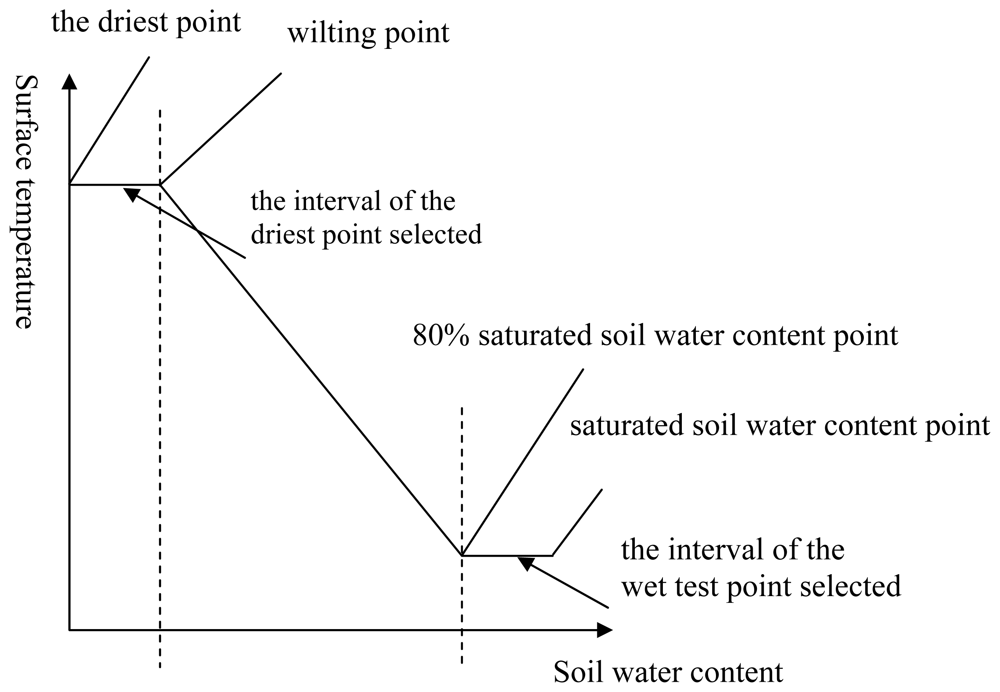
3.1 locating the true dry edge in Tm – f space
a) Estimation of air temperature (Ta)
b) Estimation of actual vapor pressure near surface (ea)
c) Estimation of surface resistance to evapotranspiration (rs)
d) Estimation of aerodynamic resistance (ra)
3.2 Locating the true wet edge in Tm – f space
3.3 Physical illustrations for the uncertainties using the above locating methods
3.4 Elimination of the effects of atmospheric conditions on surface evapotranspiration
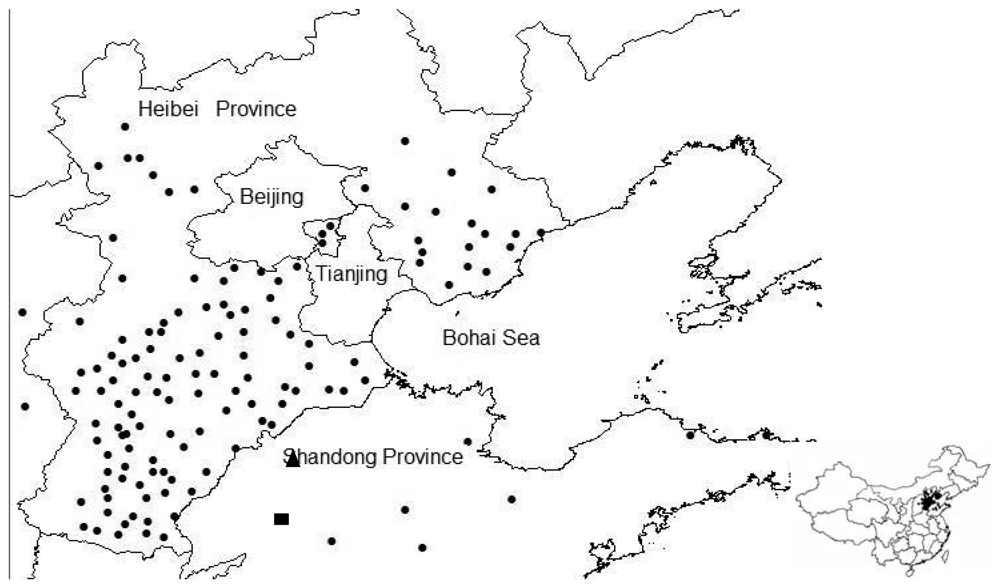
4. Study area and field measurements
5. Satellite data
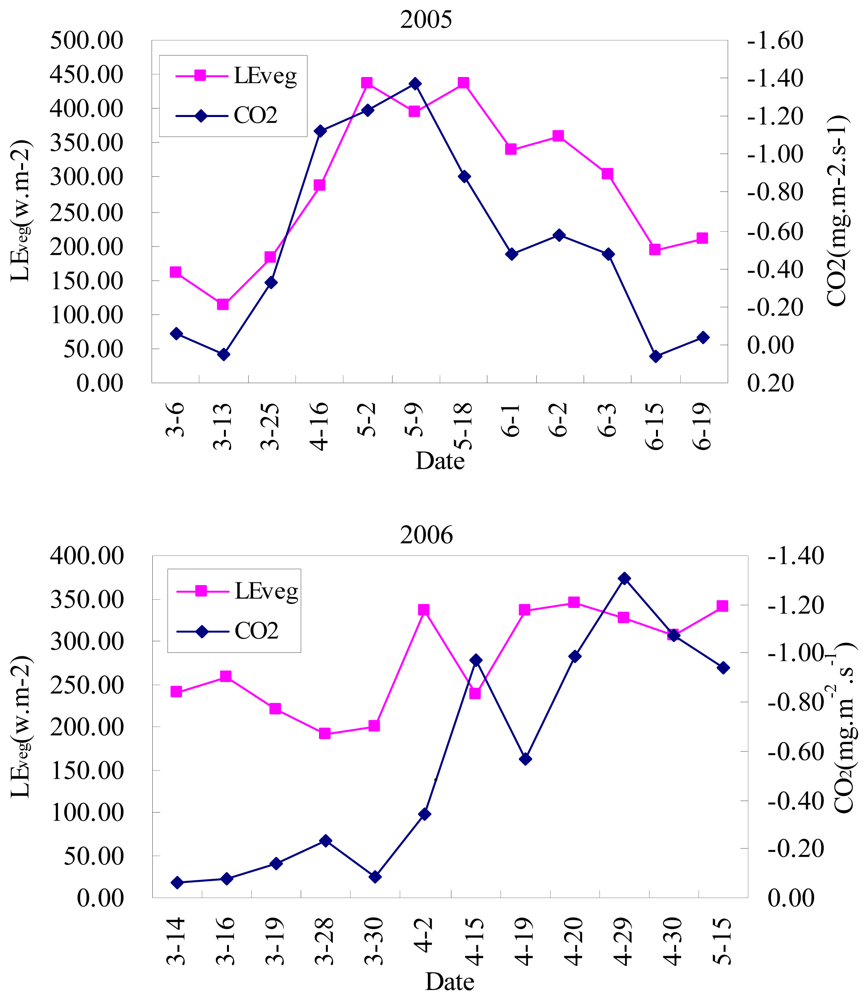
6. Results and Discussion
7. Conclusions
Acknowledgments
Appendix I
Appendix И
References and Notes
- Su, H.B.; McCabe, M.F.; Wood, E.F.; Su, Z.; Prueger, J.H. Modeling evapotranspiration during SMACEX: Comparing two approaches for local- and regional-scale prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar]
- Verhoef, A.; De Bruin, H.A.R.; Van den Hurk, B.J.I.M. Some practical notes on the parameter kB-1 for sparse vegetation. J. Appl. Meteor. 1997, 36, 560–572. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes from observation of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Evaluating the Effects of Subpixel Heterogeneity on Pixel Average Fluxes. Remote Sens. Environ. 2000, 74, 327–342. [Google Scholar]
- Zhang, R.H.; Sun, X.M.; Wang, W.M.; Xu, J.J.; Zhu, Z.L.; Tian, J. An operational two-layer remote sensing model to estimate surface flux in regional scale: physical background. Sci in China Ser. D. 2005, 48, 225–244. [Google Scholar]
- Gillies, R.R.; Carlson, T.N.; Cui, J.; Kustas, W.P.; Humes, K.S. A verification of the ‘triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface radiant temperature. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature / vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 13–224. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An Interpretation of Methodologies for Indirect Measurement of Soil-Water Content. Agric. For. Meteorol. 1995, 77, 191–205. [Google Scholar]
- Carlson, Toby. An Overview of the “Triangle Method” for Estimating Surface Evapotranspiration and Soil Moisture from Satellite Imagery. Sens. 2007, 7, 1612–1629. [Google Scholar]
- Stisen, S.; Sandholt, I.; Norgaard, A.; Fensholt, R.; Jensen. Combining the triangle method with thermal inertia to estimate regional evapotranspiration – Applied to MSG-SEVIRI data in the Senegal River basin. Remote Sens. Environ. 2008, 112, 1242–1255. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Perry, E.M. A Method to Make Use of Thermal Infrared Temperature and NDVI measurements to Infer Surface Soil Water Content and Fractional Vegetation Cover. Remote Sens. Rev. 1994, 9, 161–173. [Google Scholar]
- Valor, E.; Caselles, V. Mapping Land Surface Emissivity from NDVI: Application to European, African, and South American Areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar]
- Santanello, J.A.; Friedl, M.A. Diurnal covariation in soil heat flux and net radiation. J. Appl. Meteor. 2003, 42, 851–862. [Google Scholar]
- Kustas, W.P.; Li, F.; Jackson, T.J.; Prueger, J.H.; MacPherson, J.I.; Wolde, M. Effects of remote sensing pixel resolution on modeled energy flux variability of croplands in Iowa. Remote Sens. Environ. 2004, 92, 535–547. [Google Scholar]
- Batra, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, J. Estimation and comparison of evapotranspiration from MODIS and AVHRR sensors for clear sky days over the Southern Great Plains. Remote Sens. Environ. 2006, 103, 1–15. [Google Scholar]
- Zhang, R. Experimental Remote Sensing Modeling and Surface Foundations; Sciences Press: Beijing, 1996. [Google Scholar]
- On a derivable formula for long-wave radiation from clear skies. Water Resour. Res. 1975, 11, 742–744.
- Zhang, R.H.; Sun, X.M.; Zhu, Z.L.; Su, H.B.; Tang, X.Z. A remote sensing model for monitoring soil evaporation based on differential thermal inertia and its validation. Sci. China Ser. D. 2003, 46, 344–355. [Google Scholar]
- Qiu, G.Y.; Shi, P.J.; Wang, L.M. Theoretical analysis of a remotely measurable soil evaporation transfer coefficient. Remote Sens. Environ. 2006, 101, 390–398. [Google Scholar]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.-L. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens. 2004, 261–274. [Google Scholar]
- Justice, C.O.; Vermote, E.; Townshend, J.G.R.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; Lucht, W.; Myneni, R.B.; Yuri Knyazikhin, Y.; Running, S.W.; Nemani, R.R.; Wan, Z.; Huete, A.R.; van Leeuwen, W.; Wolfe, R.E.; Giglio, L.; Muller, J.P.; Lewis, P.; Barnsley, M.J. The Moderate Resolution Imaging Spectroradiometer (MODIS): land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar]
- Carlson, T.N.; Ripley, D.A.J. On the Relationship Between NDVI, Fractional Vegetation Cover and Leaf Area Index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar]
- Jiang, L.; Islam, S.; Carlson, T.N. Uncertainties in latent heat flux measurement and estimation: implications for using a simplified approach with remote sensing data. Can. J. Remote Sens. 2004, 30, 769–787. [Google Scholar]
- Prihodko, L.; Goward, S.N. Esitmation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar]
- Nishida, K.; Namani, R.R.; Running, S.W.; Glassy, J.M. An operational remote sensing algorithm of land surface evaporation. J. Geophys. Res. 2003, 108(D9), 42–70. [Google Scholar]
- Mo, X.; Liu, S.; Lin, Z.; Xu, Y.; McVicar, T.R. Prediction of crop yield, water consumption and water use efficiency with a SVAT-crop growth model using remotely sensed data on the North China Plain. Eco. Modelling 2005, 183, 301–322. [Google Scholar]
- Zhao, F.H.; Yu, G.R.; Li, S.G.; Ren, C.Y.; Sun, X.M.; Mi, N.; Li, J.; Zhu, Ouyang. Canopy water use efficiency of winter wheat in the North China Plain. Agric. Water. Manage. 2007, 93, 99–108. [Google Scholar]
- Rahman, H.; Dedieu, G. SMAC: a simplified method for the atmospheric correction of satellite measurements in the solar spectrum. Int. J. Remote Sens. 1994, 15, 123–143. [Google Scholar]
- Zhang, R.H.; Sun, X.M.; Zhu, Z.L.; Su, H.B.; Chen, G. A remote sensing model of CO2 flux for wheat and studying of regional distribution. Sci. in China Ser. D. 1999, 42, 325–336. [Google Scholar]
- Wang, S.S. Simulation of Evapotranspiration and Its Response to Plant Water and CO2 Transfer Dynamics. J. Hydrometeorol. 2008, 9, 426–443. [Google Scholar]
- Tilden, P.M.; Steven, E. H. An assessment of storage terms in the surface energy balance of maize and soybean. Agric. For. Meteorol. 2004, 125, 105–115. [Google Scholar]
- Tian, J.; Zhang, R.H.; Sun, X.M.; Zhu, Z.L.; Zhou, Y.L. Study of a model for correcting the effects of horizontal advection on surface fluxes measurement based on remote sensing. Sci in China Ser. D. 2006, 49, 273–280. [Google Scholar]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, Ch.; Ceulemans, R.; Dolman, H.; Field, C.; Grelle, A.; Law, B.; Meyers, T.; Moncrieff, J.; Monson, R.; Oechel, W.; Tenhunen, J.; Valentini, R.; Verma, S. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar]
- Su, Z.-B. The surface energy balance system (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–89. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land(SEBAL) 1. Formulation. J. Hydro. 1998, 212, 198–212. [Google Scholar]
- Jiang, L.; Islam, S. An intercomparison of regional latent heat flux estimation using remote sensing data. Int. J. Remote Sens. 2003, 24, 2221–2236. [Google Scholar]
- Wang, K.C.; Li, Z.Q.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: a new method to determine the Priestley–Taylor parameter. Remote Sens. Environ. 2006, 102, 293–305. [Google Scholar]




© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the CreativeCommons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, R.; Tian, J.; Su, H.; Sun, X.; Chen, S.; Xia, J. Two Improvements of an Operational Two-Layer Model for Terrestrial Surface Heat Flux Retrieval. Sensors 2008, 8, 6165-6187. https://doi.org/10.3390/s8106165
Zhang R, Tian J, Su H, Sun X, Chen S, Xia J. Two Improvements of an Operational Two-Layer Model for Terrestrial Surface Heat Flux Retrieval. Sensors. 2008; 8(10):6165-6187. https://doi.org/10.3390/s8106165
Chicago/Turabian StyleZhang, Renhua, Jing Tian, Hongbo Su, Xiaomin Sun, Shaohui Chen, and Jun Xia. 2008. "Two Improvements of an Operational Two-Layer Model for Terrestrial Surface Heat Flux Retrieval" Sensors 8, no. 10: 6165-6187. https://doi.org/10.3390/s8106165




