Comparison of Three Operative Models for Estimating the Surface Water Deficit Using ASTER Reflective and Thermal Data
Abstract
:1. Introduction
2. Description of the study region and data acquired
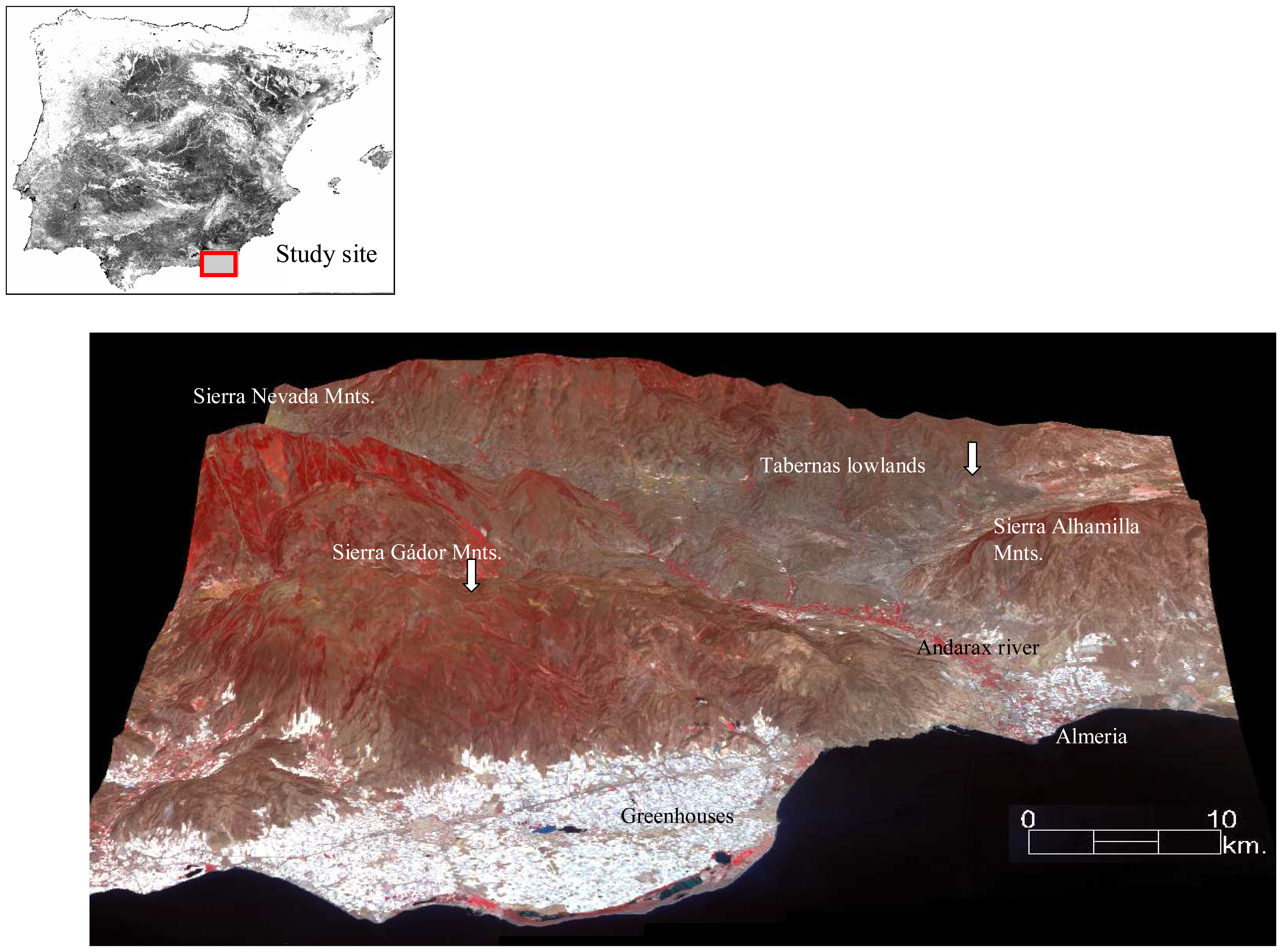
2.1. Study region
2.2. Field research sites in the study region
Llano de los Juanes research site
Rambla Honda research site
2.3. Remote sensing and spatial data
3. Methodology for estimating the non-evaporative fraction (NEF)
3.1. Estimating the non-evaporative fraction from the “Simplified Relationship”
Daily net radiation (Rnd)
Sensible heat flux (H)
Air temperature (Tair)
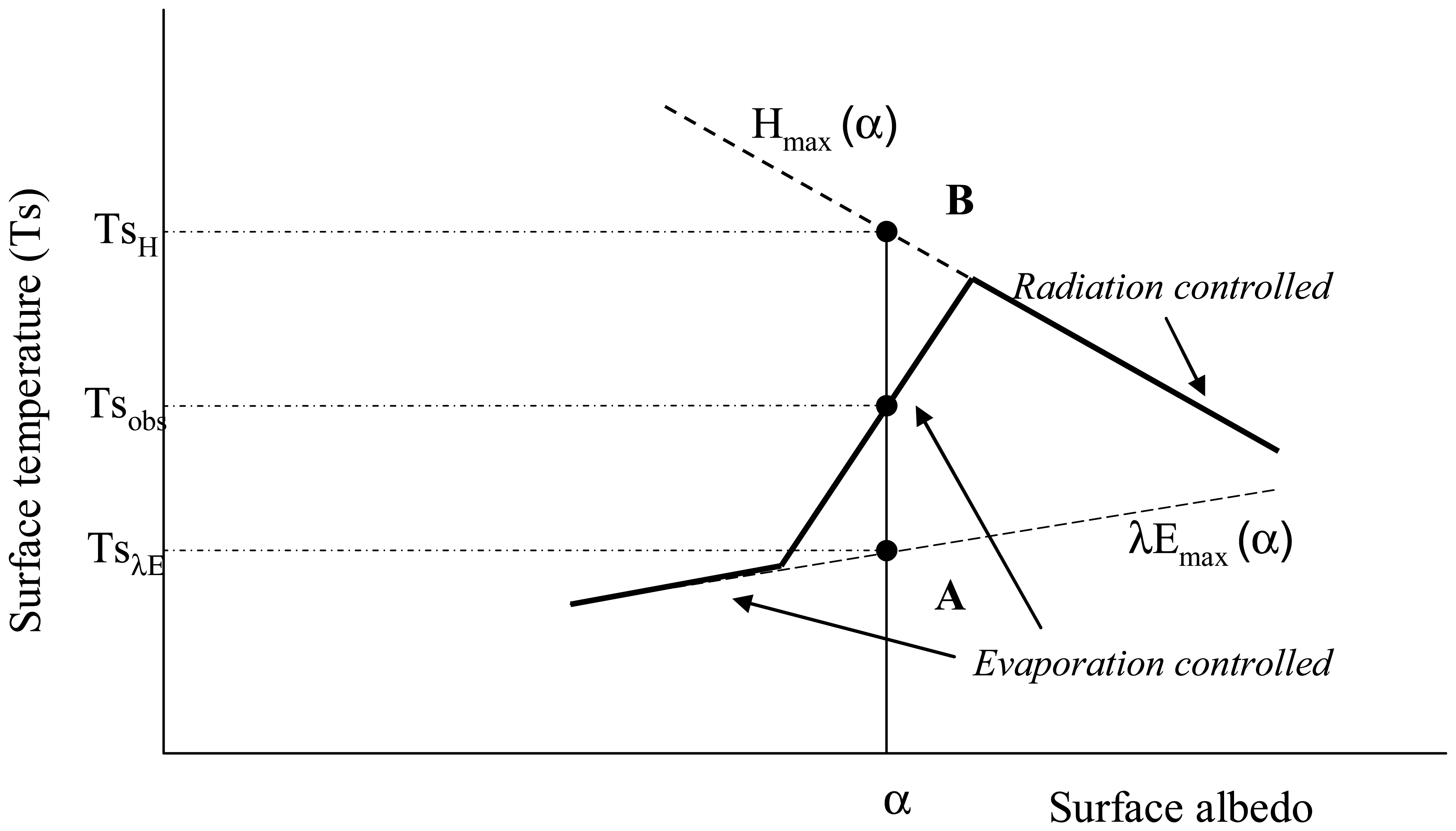
3.2. Estimating the non-evaporative fraction from S-SEBI (Simplified-Surface Energy Balance Index)
3.3. Validation of the non-evaporative fraction model results
4. Results and discussion
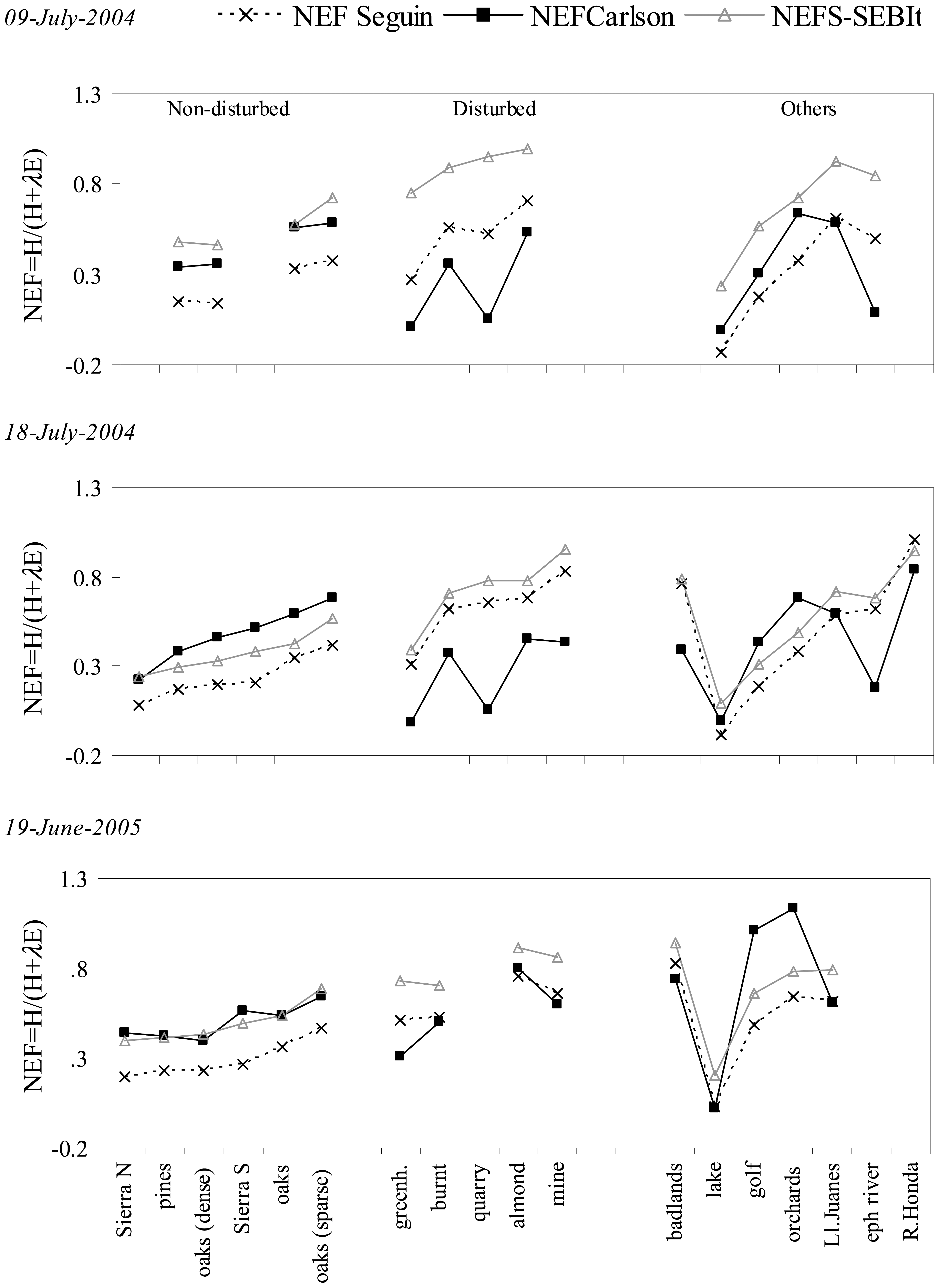
4.1. Comparison of models estimating the non-evaporative fraction (NEF)
4.2 Field validation of the non-evaporative fraction models
Air temperature
Daily net radiation (Rnd)
Sensible heat flux (H) and the non-evaporative fraction (NEF)
5. Conclusions
Acknowledgments
References
- Wilson, K. B.; Baldocchi, D. D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Dolman, H.; Falge, E.; Field, C.; Goldstein, A.; Granier, A.; Grelle, A.; Halldor, T.; Hollinger, D.; Katul, G.; Law, B. E.; Lindroth, A.; Meyers, T.; Moncrieff, J.; Monson, R.; Oechel, W.; Tenhunen, J.; Valentini, R.; Verma, S.; Vesala, T.; Wofsy, S. Energy Partitioning Between Latent and Sensible Heat Flux During the Warm Season at FLUXNET Sites. Water Resour. Res. 2002, 38. [Google Scholar]
- Kustas, W. P.; Norman, J. M. Use of Remote Sensing for Evapotranspiration Monitoring Over Land Surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar]
- Bastiaanssen, W. G. M.; Menenti, M.; Feddes, R. A.; Holtslag, A. A. M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL) - 1. Formulation. J. Hydrol. 1998, 213, 198–212. [Google Scholar]
- Roerink, G. J.; Su, Z.; Menenti, M. S-SEBI: A Simple Remote Sensing Algorithm to Estimate the Surface Energy Balance. Phys. Chem. Earth Pt. B. 2000, 25, 147–157. [Google Scholar]
- Domingo, F.; Villagarcía, L.; Boer, M. M.; Alados-Arboledas, L.; Puigdefábregas, J. Evaluating the Long-Term Water Balance of Arid Zone Stream Bed Vegetation Using Evapotranspiration Modelling and Hillslope Runoff Measurements. J. Hydrol. 2001, 243, 17–30. [Google Scholar]
- Moran, M. S.; Kustas, W. P.; Vidal, A.; Stannard, D. I.; Blanford, J. H.; Nichols, W. D. Use of Ground-Based Remotely-Sensed Data for Surface-Energy Balance Evaluation of A Semiarid Rangeland. Water Resour. Res. 1994, 30, 1339–1349. [Google Scholar]
- Jackson, R. D.; Reginato, R. J.; Idso, S. B. Wheat Canopy Temperature - Practical Tool for Evaluating Water Requirements. Water Resour. Res. 1977, 13, 651–656. [Google Scholar]
- Seguin, B.; Itier, B. Using Midday Surface-Temperature to Estimate Daily Evaporation From Satellite Thermal Ir Data. Int. J. Remote Sens. 1983, 4, 371–383. [Google Scholar]
- Carlson, T. N.; Capehart, W. J.; Gillies, R. R. A New Look at the Simplified Method for Remote-Sensing of Daily Evapotranspiration. Remote Sens. Environ. 1995, 54, 161–167. [Google Scholar]
- Pulido-Bosch, A.; Pulido-Leboeuf, P.; Molina-Sánchez, L.; Vallejos, A.; Martín-Rosales, W. Intensive Agriculture, Wetlands, Quarries and Water Management. A Case Study (Campo de Dalias, SE Spain). Environ. Geol. 2000, 40, 163–168. [Google Scholar]
- French, A. N.; Jacob, F.; Anderson, M. C.; Kustas, W. P.; Timmermans, W.; Gieske, A.; Su, Z.; Su, H.; Mccabe, M. F.; Li, F.; Prueger, J.; Brunsell, N. Surface Energy Fluxes With the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) at the Iowa 2002 SMACEX Site (USA). Remote Sens. Environ. 2005, 99, 55–65. [Google Scholar]
- Jacob, F.; Petitcolin, F.; Schmugge, T.; Vermote, E.; French, A.; Ogawa, K. Comparison of Land Surface Emissivity and Radiometric Temperature Derived From MODIS and ASTER Sensors. Remote Sens. Environ. 2004, 90, 137–152. [Google Scholar]
- López-Bermúdez, F.; Boix-Fayos, C.; Solé-Benet, A.; Albaladejo, J.; Barberá, G.C.; del Barrio, G.; Castillo, V.; García, J.; Lázaro, R.; Martínez-Mena, M.D.; Mosch, W.; Navarro-Cano, J.A.; Puigdefábregas, J.; Sanjuán, M. Landscapes and Desertification in South-East Spain: Overview and Field Sites. Field Trip Guide. A-5. In 6thInternational conference on Geomorphology; Sociedad Española de Geomorfología, 2005; p. 40. [Google Scholar]
- Oyonarte, C.; Perez- Pujalte, A.; Delgado, G.; Delgado, R.; Almendros, G. Factors Affecting Soil Organic-Matter Turnover in A Mediterranean Ecosystems From Sierra De Gador (Spain) - An Analytical Approach. Soil Sci. Plan. 1994, 25, 1929–1945. [Google Scholar]
- Contreras, S. Spatial Distribution of the Annual Water Balance in Semi-Arid Mountainous Regions: Application to Sierra de Gádor (Almería, SE Spain). Ph.D thesis, in spanish. Depto de Hidrogeología y Química Analítica. Universidad de Almería, 2006; pp. 41–69. [Google Scholar]
- Li, X Y.; Contreras, S.; Solé-Benet, A. Spatial Distribution of Rock Fragments in Dolines: a Case Study in a Semiarid Mediterranean Mountain-Range (Sierra Gádor, SE Spain). Catena 2007, in press. [Google Scholar]
- Puigdefábregas, J.; Delgado, L.; Domingo, F.; Cueto, M.; Gutiérrez, L.; Lázaro, R.; Nicolau, J.M.; Sánchez, G.; Solé-Benet, A.; Vidal, S.; Aguilera, C.; Brenner, A.; Clark, S.; Incoll, L. Mediterranean Desertification and Land Use; Brandt, J., Thornes, J., Eds.; John Wiley & Sons, Ltd., 1996; pp. 137–168. [Google Scholar]
- Puigdefábregas, J.; Sole, A.; Gutierrez, L.; del Barrio, G.; Boer, M. Scales and Processes of Water and Sediment Redistribution in Drylands: Results From the Rambla Honda Field Site in Southeast Spain. Earth-Sci. Rev. 1999, 48, 39–70. [Google Scholar]
- Puigdefábregas, J. The Role of Vegetation Patterns in Structuring Runoff and Sediment Fluxes in Drylands. Earth Surf. Proc. Land. 2005, 30, 133–147. [Google Scholar]
- Domingo, F.; Villagarcía, L.; Brenner, A. J.; Puigdefábregas, J. Evapotranspiration Model for Semi-Arid Shrub-Lands Tested Against Data From SE Spain. Agric. For. Meteorol. 1999, 95, 67–84. [Google Scholar]
- Domingo, F.; Brenner, A. J.; Gutierrez, L.; Clark, S. C.; Incoll, L. D.; Aguilera, C. Water Relations Only Partly Explain the Distributions of Three Perennial Plant Species in a Semi-Arid Environment. Biol. Plantarum 2003, 46, 257–262. [Google Scholar]
- Domingo, F.; Villagarcía, L.; Brenner, A. J.; Puigdefábregas, J. Measuring and Modelling the Radiation Balance of a Heterogeneous Shrubland. Plant Cell Environ. 2000, 23, 27–38. [Google Scholar]
- Domingo, F.; Villagarcía, L.; Boer, M. M.; Alados-Arboledas, L.; Puigdefábregas, J. Evaluating the Long-Term Water Balance of Arid Zone Stream Bed Vegetation Using Evapotranspiration Modelling and Hillslope Runoff Measurements. J. Hydrol. 2001, 243, 17–30. [Google Scholar]
- Domingo, F.; Gutierrez, L.; Brenner, A. J.; Aguilera, C. Limitation to Carbon Assimilation of Two Perennial Species in Semi-Arid South-East Spain. Biol. Plantarum 2002, 45, 213–220. [Google Scholar]
- Were, A.; Villagarcía, L.; Domingo, F.; Alados-Arboledas, L.; Puigdefábregas, J. Analysis of Effective Resistance Calculation Methods and Their Effect on Modelling Evapotranspiration in Two Different Patches of Vegetation in Semi-Arid SE Spain. HESSD. 2007, 4, 1–44. [Google Scholar]
- Hasse, P.; Pugnaire, F. I.; Clark, S. C.; Incoll, L. D. Photosynthetic Rate and Canopy Development in the Drought-Deciduous Shrub Anthyllis Cytisoides L. J. Arid Environ. 2000, 46, 79–91. [Google Scholar]
- Moro, M. J.; Pugnaire, F. I.; Haase, P.; Puigdefábregas, J. Mechanisms of Interaction Between a Leguminous Shrub and Its Understorey in a Semi-Arid Environment. Ecography 1997, 20, 175–184. [Google Scholar]
- Pugnaire, F. I.; Haase, P.; Puigdefábregas, J.; Cueto, M.; Clark, S. C.; Incoll, L. D. Facilitation and Succession Under the Canopy of a Leguminous Shrub, Retama Sphaerocarpa, in a Semi-Arid Environment in South-East Spain. Oikos 1996, 76, 455–464. [Google Scholar]
- Brenner, A. J.; Incoll, L. D. The Effect of Clumping and Stomatal Response on Evaporation From Sparsely Vegetated Shrublands. Agric. For. Meteorol. 1997, 84, 187–205. [Google Scholar]
- Shuttleworth, W. J.; Wallace, J. S. Evaporation From Sparse Crops - An Energy Combination Theory. Q. J. Roy.Meteor. Soc. 1985, 111, 839–855. [Google Scholar]
- Dolman, A. J. A Multiple-Source Land-Surface Energy-Balance Model for Use in General-Circulation Models. Agric. For. Meteorol. 1993, 65, 21–45. [Google Scholar]
- http://asterweb.jpl.nasa.gov/
- Fu, P. D.; Rich, P. M. A Geometric Solar Radiation Model With Applications in Agriculture and Forestry. Comput. Electron. Agr. 2002, 37, 25–35. [Google Scholar]
- Liang, S. L. Narrowband to Broadband Conversions of Land Surface Albedo I Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar]
- Van de Griend, A. A.; Owe, M. On the Relationship Between Thermal Emissivity and the Normalized Difference Vegetation Index for Natural Surfaces. Int. J. Remote Sens. 1993, 14, 1119–1131. [Google Scholar]
- Idso, S. B.; Jackson, R. D. Thermal Radiation From Atmosphere. J. Geophys. Res. 1969, 74, 5397–5403. [Google Scholar]
- Brutsaert, W. Evaporation into the Atmosphere. Theory, History, and Applications; Dordrecht; Holland, D. Reidel Publishing Company, 1982; p. 293. [Google Scholar]
- Jackson, R. D.; Moran, M. S.; Gay, L. W.; Raymond, L. H. Evaluating Evaporation From Field Crops Using Airborne Radiometry and Ground-Based Meteorological Data. Irrigation Sci. 1987, 8, 81–90. [Google Scholar]
- Kustas, W. P.; Perry, E. M.; Doraiswamy, P. C.; Moran, M. S. Using Satellite Remote-Sensing to Extrapolate Evapotranspiration Estimates in Time and Space Over A Semiarid Rangeland Basin. Remote Sens. Environ. 1994, 49, 275–286. [Google Scholar]
- Hall, F. G.; Huemmrich, K. F.; Goetz, S. J.; Sellers, P. J.; Nickeson, J. E. Satellite Remote-Sensing of Surface-Energy Balance - Success, Failures, and Unresolved Issues in Fife. J. Geophys. Res.-Atmos. 1992, 97, 19061–19089. [Google Scholar]
- Caselles, V.; Artigao, M. M.; Hurtado, E.; Coll, C.; Brasa, A. Mapping Actual Evapotranspiration by Combining Landsat TM and NOAA-AVHRR Images: Application to the Barrax Area, Albacete, Spain. Remote Sens. Environ. 1998, 63, 1–10. [Google Scholar]
- Sugita, M.; Brutsaert, W. Daily Evaporation Over A Region From Lower Boundary-Layer Profiles Measured With Radiosondes. Water Resour. Res. 1991, 27, 747–752. [Google Scholar]
- Prihodko, L.; Goward, S. N. Estimation of Air Temperature From Remotely Sensed Surface Observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar]
- Czajkowski, K. P.; Goward, S. N.; Mulhern, T.; Goetz, S. J.; Walz, A.; Shirey, D.; Stadler, S.; Prince, S. D.; Dubayah, R. O. Thermal remote sensing in land surface processes; Quattrochi, D. A., Luvall, J. C., Eds.; Boca Raton, Florida; CRC Press, 2000; pp. 11–32. [Google Scholar]
- Verstraeten, W. W.; Veroustraete, F.; Feyen, J. Estimating Evapotranspiration of European Forests From NOAA-Imagery at Satellite Overpass Time: Towards an Operational Processing Chain for Integrated Optical and Thermal Sensor Data Products. Remote Sens. Environ. 2005, 96, 256–276. [Google Scholar]
- Sobrino, J. A.; Gomez, M.; Jimenez-Munoz, J. C.; Olioso, A.; Chehbouni, G. A Simple Algorithm to Estimate Evapotranspiration From DAIS Data: Application to the DAISEX Campaigns. J. Hydrol. 2005, 315, 117–125. [Google Scholar]
- Gómez, M.; Olioso, A.; Sobrino, J. A.; Jacob, F. Retrieval of Evapotranspiration Over the Alpilles/ReSeDA Experimental Site Using Airborne POLDER Sensor and a Thermal Camera. Remote Sens. Environ. 2005, 96, 399–408. [Google Scholar]
- Koenker, R.; Hallock, K. F. Quantile Regression. J. Econ. Perspect. 2001, 15, 143–156. [Google Scholar]
- Villagarcía, L.; Domingo, F.; Alados-Arboledas, L.; Puigdefábregas, J. Modelización de la evapotranspiración real en rodales de tres especies vegetales del SE Español. In V Simposio sobre el agua en Andalucía.; Editorial de la Universidad de Almería, Almería, 2001; Volume 1, pp. 107–118. [Google Scholar]
- Paracuellos, M. How Can Habitat Selection Affect the Use of a Wetland Complex by Waterbirds? Biodivers. Conserv. 2006, 15, 4569–4582. [Google Scholar]
- Oswald, C. J.; Rouse, W. R. Thermal Characteristics and Energy Balance of Various-Size Canadian Shield Lakes in the Mackenzie River Basin. J. Hydrometeorol. 2004, 5, 129–144. [Google Scholar]
- Burba, G. G.; Verma, S. B.; Kim, J. Surface Energy Fluxes of Phragmites Australis in a Prairie Wetland. Agric. For. Meteorol. 1999, 94, 31–51. [Google Scholar]
- Rodríguez-Rodríguez, M.; Moreno-Ostos, E. Heat Budget, Energy Storage and Hydrological Regime in a Coastal Lagoon. Limnologica 2006, 36, 217–227. [Google Scholar]
- Sánchez-Carrillo, S.; Angeler, D. G.; Sanchez-Andres, R.; Alvarez-Cobelas, M.; Garatuza-Payan, J. Evapotranspiration in Semi-Arid Wetlands: Relationships Between Inundation and the Macrophyte-Cover: Open-Water Ratio. Adv. Water Resour. 2004, 27, 643–655. [Google Scholar]
- Burba, G. G.; Verma, S. B.; Kim, J. Energy Fluxes of an Open Water Area in a Mid-Latitude Prairie Wetland. Bound-Lay. Meteorol. 1999, 91, 495–504. [Google Scholar]
- Nosetto, M. D.; Jobbagy, E. G.; Paruelo, J. M. Land-Use Change and Water Losses: the Case of Grassland Afforestation Across a Soil Textural Gradient in Central Argentina. Glob. Change Biol. 2005, 11, 1101–1117. [Google Scholar]
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sc. s 2002, 6, 85–99. [Google Scholar]
- Jacob, F.; Olioso, A.; Gu, X. F.; Su, Z. B.; Seguin, B. Mapping Surface Fluxes Using Airborne Visible, Near Infrared, Thermal Infrared Remote Sensing Data and a Spatialized Surface Energy Balance Model. Agronomie 2002, 22, 669–680. [Google Scholar]
- Batra, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, J. Estimation and Comparison of Evapotranspiration From MODIS and AVHRR Sensors for Clear Sky Days Over the Southern Great Plains. Remote Sens. Environ. 2006, 103, 1–15. [Google Scholar]
- Timmermans, W. J.; Kustas, W. P.; Anderson, M. C.; French, A. N. An Intercomparison of the Surface Energy Balance Algorithm for Land (SEBAL) and the Two-Source Energy Balance (TSEB) Modeling Schemes. Remote Sens. Environ. In Press, Corrected Proof.
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the Net Radiation Using MODIS (Moderate Resolution Imaging Spectroradiometer) Data for Clear Sky Days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar]
- Rubio, E.; Caselles, V.; Badenas, C. Emissivity Measurements of Several Soils and Vegetation Types in the 8-14 Mu m Wave Band: Analysis of Two Field Methods. Remote Sens. Environ. 1997, 59, 490–521. [Google Scholar]
- Baldocchi, D.; Falge, E.; Gu, L. H.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; Fuentes, J.; Goldstein, A.; Katul, G.; Law, B.; Lee, X. H.; Malhi, Y.; Meyers, T.; Munger, W.; Oechel, W.; U, K. T. P.; Pilegaard, K.; Schmid, H. P.; Valentini, R.; Verma, S.; Vesala, T.; Wilson, K.; Wofsy, S. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-Scale Carbon Dioxide, Water Vapor, and Energy Flux Densities. B. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar]
- Nie, D.; Flitcroft, I. D.; Kanemasu, E. T. Performance of Bowen-Ratio Systems on A Slope. Agric. For. Meteorol. 1992, 59, 165–181. [Google Scholar]
- Gurney, R. J.; Sewell, I. J. Scaling-up: from cell to landscape; Van Gardingen, P. R., Foody, G. M., Curran, P. J., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 319–346. [Google Scholar]
- Seguin, B.; Becker, F.; Phulpin, T.; Gu, X. F.; Guyot, G.; Kerr, Y.; King, C.; Lagouarde, J. P.; Ottle, C.; Stoll, M. P.; Tabbagh, A.; Vidal, A. IRSUTE: A Minisatellite Project for Land Surface Heat Flux Estimation From Field to Regional Scale. Remote Sens. Environ. 1999, 68, 357–369. [Google Scholar]
- Wassenaar, T.; Olioso, A.; Hasager, C.; Jacob, F.; Chehbouni, A. Recent Advances in Quantitative Remote Sensing; Sobrino, J. A., Ed.; Universidad de Valencia, 2002; pp. 319–328. [Google Scholar]
- Humes, K.; Hardy, R.; Kustas, W.; Prueger, J.; Starks, P. Thermal remote sensing in land surface processes; Quattrochi, D.A., Luvall, J. C., Eds.; Boca Raton, Florida; CRC Press, 2000; pp. 110–132. [Google Scholar]
- Laymon, C. A.; Qattrochi, D. A. Thermal remote sensing in land surface processes; Quattrochi, D.A., Luvall, J. C., Eds.; Boca Raton, Florida; CRC Press, 2000; pp. 133–159. [Google Scholar]
- Chehbouni, A.; Nouvellon, Y.; Lhomme, J. P.; Watts, C.; Boulet, G.; Kerr, Y. H.; Moran, M. S.; Goodrich, D. C. Estimation of Surface Sensible Heat Flux Using Dual Angle Observations of Radiative Surface Temperature. Agric. For. Meteorol. 2001, 108, 55–65. [Google Scholar]
- Bastiaanssen, W. G. M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J. F.; Roerink, G. J.; van der Wal, T. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL) - 2. Validation. J. Hydrol. 1998, 213, 213–229. [Google Scholar]
- Jiang, L.; Islam, S. Estimation of Surface Evaporation Map Over Southern Great Plains Using Remote Sensing Data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar]
| NEF models | Date | |||
|---|---|---|---|---|
| July 7, 2004 | July 18, 2004 | June 19, 2005 | ||
| NEFSeguinvs. NEFS-SEBIt | ||||
| R2 | 0.97 | 0.98 | 0.96 | |
| p | 0.0000 | 0.0000 | 0.0000 | |
| RMSE | 0.34 | 0.13 | 0.18 | |
| slope | 1.0 | 0.83 | 0.94 | |
| intercept | 0.34 | 0.18 | 0.20 | |
| NEFSeguinvs. NEFCarlson | ||||
| R2 | 0.51 | 0.47 | 0.50 | |
| p | 0.0000 | 0.0000 | 0.0000 | |
| RMSE | 0.34 | 0.73 | 0.21 | |
| slope | 0.49 | 0.66 | 0.84 | |
| intercept | 0.08 | 0.05 | 0.16 | |
| NEFCarlsonvs. NEFSSEBIt | ||||
| R2 | 0.43 | 0.46 | 0.51 | |
| p | 0.0000 | 0.0000 | 0.0000 | |
| RMSE | 0.45 | 0.67 | 0.22 | |
| slope | 0.24 | 0.34 | 0.58 | |
| intercept | -0-006 | 0.59 | 0.35 | |
| July 18, 2004 n=11 | July 7, 2004 n=10 | July 19, 2004 n=12 | |
|---|---|---|---|
| R2 (observed-predicted) | 0.61 | 0.74 | 0.67 |
| MAE before adjustment (°C) | 4.31 | 3.40 | 2.68 |
| MAE after adjustment (°C) | 1.96 | 2.07 | 1.93 |
| T apex (°C) | 24.0 | 24.61 | 23.39 |
| Reference altitude (m) | 1800 | 1833 | 1099 |
| Date | Surface type | Location | Field Rnd (Wm-2) | ASTER Rnd (Wm-2) | AE (Wm-2) | %Error |
|---|---|---|---|---|---|---|
| 09-07-04 | Shrubs | Llano Juanes | 188.70 | 184.21 | 4.49 | 1.30 |
| 18-07-04 | Shrubs | Llano Juanes | 179.71 | 189.70 | 9.99 | 5.30 |
| 19-06-05 | Shrubs | Llano Juanes | 183.40 | 192.40 | 9.00 | 4.90 |
| 18-07-04 | Retama | Rambla Honda | 166.53 | 152.53 | 14.00 | -8.41 |
| 18-07-04 | Anthyllis | Rambla Honda | 165.07 | 156.59 | 8.48 | -5.14 |
| 18-07-04 | Stipa | Rambla Honda | 159.28 | 155.97 | 3.31 | -2.08 |
| 18-07-04 | Bare soil | Rambla Honda | 112.68 | 110.19 | 2.49 | -2.21 |
| MAE | 7.39 | |||||
| RMSE | 8.94 | |||||
| Mean % error | 4.38 | |||||
| R2 | 0.91 | |||||
| p | 0.0008 | |||||
| slope | 1.09 | |||||
| intercept | -16.14 | |||||
| Date | Surface type | Location | Field | Seguin | Carlson | S-SEBIt | |||
|---|---|---|---|---|---|---|---|---|---|
| H (Wm-2) | H (Wm-2) | AE (Wm-2) | H (Wm-2) | AE (Wm-2) | H (Wm-2) | AE (Wm-2) | |||
| 09-07-04 | Shrubs | Llano Juanes | 158.77 | 110.29 | 48.48 | 107.69 | 51.07 | 169.48 | 10.71 |
| 18-09-04 | Shrubs | Llano Juanes | 154.94 | 106.70 | 48.24 | 107.58 | 47.36 | 130.40 | 24.54 |
| 19-06-05 | Shrubs | Llano Juanes | 157.43 | 115.99 | 41.44 | 114.42 | 43.01 | 150.19 | 7.24 |
| 18-09-04 | Retama | Rambla Honda | 157.34 | 152.39 | 4.95 | 109.56 | 47.78 | 143.78 | 13.55 |
| 18-09-04 | Anthyllis | Rambla Honda | 133.15 | 139.38 | 6.24 | 80.56 | 52.59 | 139.06 | 5.91 |
| 18-09-04 | Stipa | Rambla Honda | 122.54 | 126.16 | 3.62 | 106.29 | 16.24 | 124.75 | 2.21 |
| 09-07-04 | lake | Greenhouses | 0.00 | -27.33 | 27.33 | -0.93 | 0.93 | 46.61 | 46.61 |
| 18-09-04 | lake | Greenhouses | 0.00 | -19.07 | 19.07 | -1.34 | 1.34 | 21.54 | 21.54 |
| 19-06-05 | lake | Greenhouses | 0.00 | 7.06 | 7.06 | 5.01 | 5.01 | 49.41 | 49.41 |
| MAE | 22.94 | 29.48 | 20.19 | ||||||
| RMSE | 29.12 | 36.58 | 25.97 | ||||||
| R2 | 0.900 | 0.97 | 0.948 | ||||||
| p | 0.00009 | 0.000001 | 0.00001 | ||||||
| slope | 0.904 | 0.694 | 0.702 | ||||||
| intercept | -9.833 | 1.66 | 39.304 | ||||||
| Date | Surface | Location | Field | Seguin | Carlson | S-SEBIt | |||
|---|---|---|---|---|---|---|---|---|---|
| NEF | NEF | AE | NEF | AE | NEF | AE | |||
| 09-07-04 | Shrubs | Llano Juanes | 0.88 | 0.61 | 0.27 | 0.59 | 0.29 | 0.93 | 0.05 |
| 18-07-04 | Shrubs | Llano Juanes | 0.92 | 0.59 | 0.33 | 0.61 | 0.31 | 0.72 | 0.2 |
| 19-06-05 | Shrubs | Llano Juanes | 0.88 | 0.62 | 0.26 | 0.61 | 0.27 | 0.79 | 0.09 |
| 18-07-04 | Retama | Rambla Honda | 0.97 | 1.00 | 0.03 | 0.72 | 0.25 | 0.94 | 0.03 |
| 18-07-04 | Anthyllis | Rambla Honda | 0.83 | 0.89 | 0.06 | 0.51 | 0.32 | 0.89 | 0.06 |
| 18-07-04 | Stipa | Rambla Honda | 0.79 | 0.81 | 0.02 | 0.68 | 0.11 | 0.8 | 0.01 |
| 09-07-04 | Lake (G=50) | Greenhouses | 0.00 | -0.17 | 0.17 | -0.01 | 0.01 | 0.24 | 0.24 |
| 09-07-04 | Lake (G=-50) | Greenhouses | -0.11 | 0.11 | 0.00 | 0.00 | |||
| 18-07-04 | Lake (G=50) | Greenhouses | 0.00 | -0.12 | 0.12 | -0.01 | 0.01 | 0.10 | 0.10 |
| 18-07-04 | Lake (G=-50) | Greenhouses | -0.07 | 0.07 | -0.01 | 0.01 | |||
| 19-06-05 | Lake (G=50) | Greenhouses | 0.04 | 0.04 | 0.03 | 0.03 | |||
| 19-06-05 | Lake (G=-50) | Greenhouses | 0.00 | 0.02 | 0.02 | 0.02 | 0.02 | 0.21 | 0.21 |
| MAE Glake=50 (-50) | 0.14 (0.13) | 0.18 (0.17) | 0.11 | ||||||
| RMSE Glake=50 (-50) | 0.18 (0.17) | 0.22 (0.22) | 0.13 | ||||||
| R2 Glake=50 (-50) | 0.88 (0.89) | 0.97 (0.97) | 0.94 | ||||||
| 0.0002 | 0.000002 | 0.00001 | |||||||
| p Glake=50 (-50) | (0.0002) | (0.000000) | |||||||
| Slope Glake=50 (-50) | 0.94 (0.91) | 0.70 (0.70) | 0.75 | ||||||
| Intercept Glake=50 (-50) | -0.08 (-0.05) | 0.01 (0.00) | 0.18 | ||||||
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
García, M.; Villagarcía, L.; Contreras, S.; Domingo, F.; Puigdefábregas, J. Comparison of Three Operative Models for Estimating the Surface Water Deficit Using ASTER Reflective and Thermal Data. Sensors 2007, 7, 860-883. https://doi.org/10.3390/s7060860
García M, Villagarcía L, Contreras S, Domingo F, Puigdefábregas J. Comparison of Three Operative Models for Estimating the Surface Water Deficit Using ASTER Reflective and Thermal Data. Sensors. 2007; 7(6):860-883. https://doi.org/10.3390/s7060860
Chicago/Turabian StyleGarcía, Mónica, Luis Villagarcía, Sergio Contreras, Francisco Domingo, and Juan Puigdefábregas. 2007. "Comparison of Three Operative Models for Estimating the Surface Water Deficit Using ASTER Reflective and Thermal Data" Sensors 7, no. 6: 860-883. https://doi.org/10.3390/s7060860




