1. Introduction
One of generic algorithms for random access control in networked systems is the
p-persistent CSMA protocol. A node, contending for the shared channel according to the
p-CSMA algorithm, transmits with the probability
p, if the channel is idle, and defers a transmission with the probability (1-
p) [
12].
The channel utilization in the p-persistent CSMA is strongly affected by the p value which represents the persistence level of the protocol. In particular, large p values cause excessive collisions, while small p values degrade the bandwidth utilization forcing the channel to be idle. A tradeoff between large and small values is thus necessary to provide the bandwidth utilization at the satisfactory level. However, a given persistence level, p, maximizes the throughput only for a preselected number of contending nodes which significantly restricts the usefulness of the pure p-CSMA in practice. If a number of contenders is unknown a priori or varies in time, the p value cannot be set optimally, and consequently the performance of p-persistent CSMA may be considerably degraded. Therefore, the CSMA-based protocols with collision avoidance try to adapt to the number of contending nodes.
In the class of variable-window CSMA protocols, the persistence level, maintained by each node, is modified basing on the feedback information from the network. The modification of p value is usually accomplished by decreasing p in case of collisions, and by an increase of p after each successful transmission. The generic policies consist in additive or multiplicative tuning of p as a response to a result of a transmission attempt in the previous packet cycle. For example, most protocols halve the p value after collisions (e.g. 802.11, Ethernet) using the truncated exponential backoff.
The predictive
p-persistent CSMA is an adaptive, variable-window version of the pure
p-CSMA developed for systems of intelligent sensors and actuators. The probability
p is variable and dynamically adjusted to the expected traffic load using the additive increase/additive decrease scheme [
1]. This protocol has been designed for sensor/control networking [
1,
2] where the traffic produced by sensing devices might be bursty, especially if the application architecture is event-triggered, and data are transmitted in response to external events [
8,
11,22]. The predictive
p-persistent CSMA is commercially implemented in MAC sublayer of LonTalk protocol [
1] registered as ANSI/EIA 709.1 and ENV 13154-2 standards and exploited in Local Operating Networks (LonWorks) technology for communication between intelligent sensors and actuators [22].
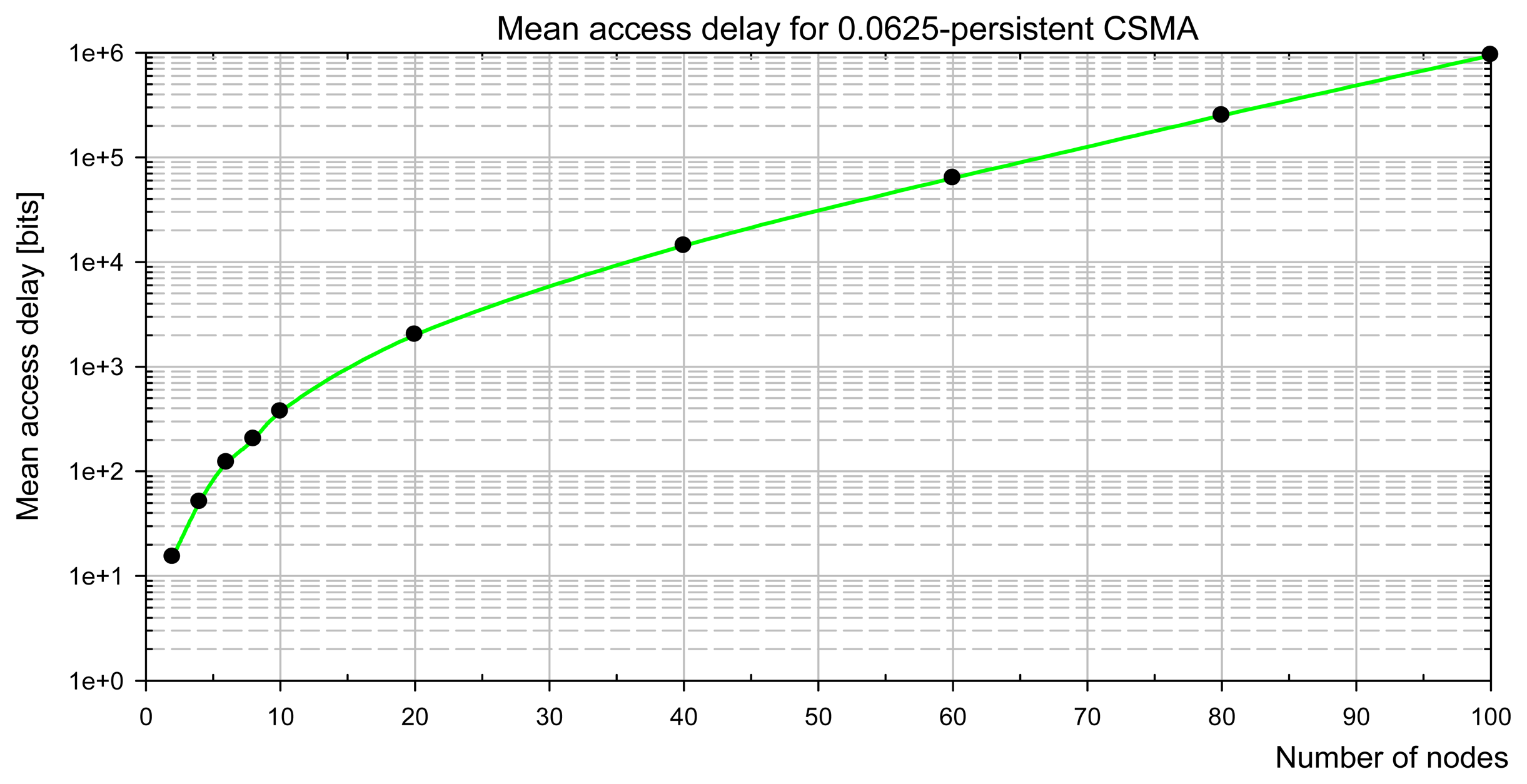
The present paper deals with the analytical evaluation of the mean access delay characteristic for the predictive p-persistent CSMA. In our approach, the analysis for the classical fixed-window p-CSMA is introduced firstly, and further the extension for the variable-window system is developed. We derive the analytical formulas for the medium access delay in term of the network load.
A delay in accessing the channel is one of the principal measures of real-time sensor/control networks. Undoubtedly, the medium access delay increases with the growing number of contending nodes. Due to the randomization of the access latency, a node that tries to send data according to the classical p-persistent CSMA defers a transmission even if only a single node wants to transmit. If more than one node tries to send their packets, the access delay increases due to collisions, and because of sharing the channel bandwidth among the contenders. As the maximum access delay in CSMA is generally unbounded, the mean access delay is chosen usually to evaluate the network access latency.
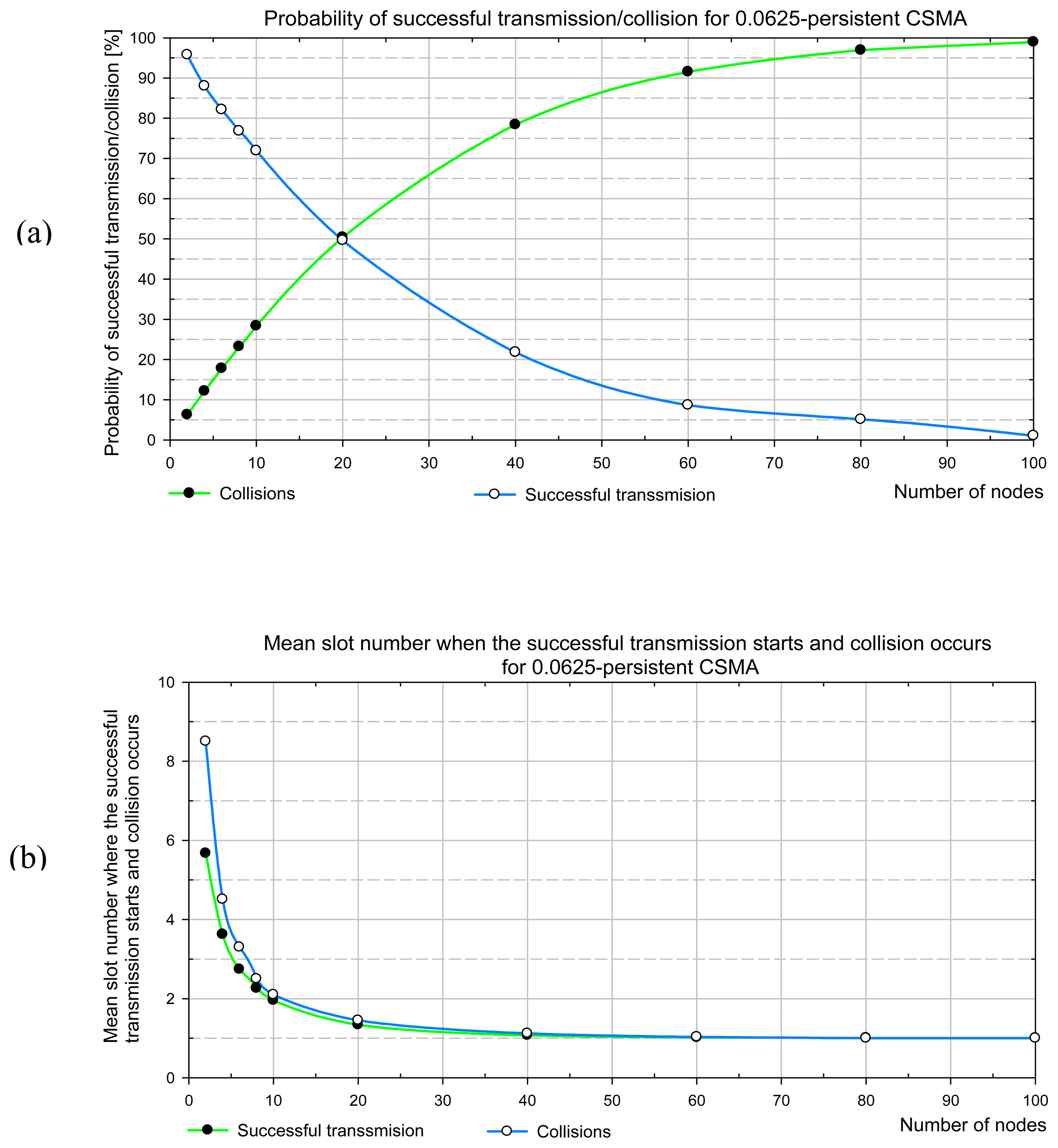
The method that we apply consists in an analytical evaluation of the expected number of trails in accessing the channel before a successful transmission, and the mean length of a packet cycle. The analytical method utilizing discrete-time Markov chains is applied. The results are reported first for the 0.0625-persistent CSMA which approximates the predictive p-persistent CSMA performance for light channel load. Next, the mean access delay for the predictive CSMA is presented.
The evaluation of the random MAC performance is a complex task since an analytical model has to follow random protocol behavior. Therefore, the stochastic analysis presented in this study is carefully explained and includes all the necessary analytical derivations of analytical steps. This feature facilitates the adaptation of the analytical procedure developed in the paper to the other adaptive random access MAC protocols.
Several papers deal with performance analysis of the predictive
p-persistent CSMA protocol. Main benefits of the predictive
p-CSMA scheme have been displayed in LonWorks Engineering Bulletin [
3]. The simulation analyses are carried out in [
7,
19]. The analytical approaches are reported in [
4,
10].
The latter follows the classical approach developed for
p-CSMA by Kleinrock and Tobagi in the seventies [
12]. The former is based on the queuing theory where the offered load is modelled by a number of stochastically distributed independent stimuli characterized by the corresponding packet arrival rates. The analysis developed in [
4] includes the evaluation of the mean access delay and belongs to the node-centric approaches. In the present study, we have developed a
channel-
centric analysis with a model of an offered load different than that used in [
4]. Namely, we define the offered load by a number of active nodes contending for the medium access. Such a model is widely used in CSMA performance analyses, e.g. in [
5,
6]. The motivation to use such a workload model is clear, since the purpose of the prediction built into the variable-window CSMA with collision avoidance is to reduce the contention among the nodes and to adapt the size of the contention window to the channel load, the number of nodes contending for the medium access is a more useful definition of the offered load for analyzing the protocol behavior. Roughly speaking, in order to recognize ability of the protocol to cope with congestion, we assume that a channel is heavily loaded since under light traffic workload the prediction mechanism is inactive. Furthermore, the backlog counting algorithm that we use in the protocol specification is slightly different than that analyzed in [
4].
The paper is structured as follows. In Section 2, we present the predictive p-CSMA specification and the backlog counting algorithm. Section 3 describes the network model. The definition and the analytical derivation of the mean access delay characteristics is presented in Section 4. In Section 5, the analysis of a fixed window p-CSMA using the stochastic analysis, is carried out. The Markov-based extension of the analytical approach for the predictive p-CSMA is introduced in Section 6. The numerical results are reported in Section 7. The validation of the developed analytical approach by simulation with the comparison of sample results are reported in Section 8. Finally, the conclusions are drawn.
2. Protocol Specification
2.1. Packet Cycle
The predictive p-persistent CSMA belongs to slotted-CSMA protocols. The algorithm operates in the following way. A node (an intelligent sensor or actuator) attempting to transmit monitors the state of the channel. If the channel is busy, the node continues sensing. When the node detects no transmission during the minimum interpacket space of β1 period, it delays a random number of contention slots of β2 duration.
If the channel is still idle when the random delay expires, the node transmits. Otherwise, the node receives incoming packet and competes for the channel access again. If more than one node choose the same slot number, and when that slot has the lowest number selected by any node with a packet to send, then a collision happens. All the packets involved in a collision are corrupted.
The backoff time is expressed as a pseudorandom number of contention slots drawn from the uniform distribution between 0 and
W, where
W is the
size of the contention window. The predictive
p-CSMA is an adaptive version of
p-CSMA, where a window size is dynamically adjusted to the current channel load. If the channel is idle, the contention window consists of 16 time slots. When the channel load increases, the number of slots grows by factor
BL, called the
estimated backlog. The backlog
BL can range from 1 to 63 and the size of the window varies from 16 to 1008 slots, since
where
Wbase is the size of the
basic contention window (16 slots). Thus, the level of the persistence of
p-CSMA equals 1/(16
BL), is variable, and has either the lower (1/16=0.0625), or the upper bound (1/1008=0.0009).
In the predictive p-CSMA, the optional collision detection can be introduced. The aim of the collision detection in the control networked systems is that the sender does not have to wait for time-out before attempting to resend the messages. By comparison, a goal of the collision detection in data networks is to improve the total channel utilization by interrupting the transmission of packets involved in a collision. It is because the packet lengths in networked control systems are short and usually range from ten to twenty bytes.
2.2. Backlog Counting Algorithm
The backlog estimation is based on the calculation of the number of packets expected in a competition for the channel during the next packet cycle. The current value of the backlog counter
BL varies from one to the next packet cycle and relies on the accumulation of consecutive backlog increments and decrements [
1,
2]. Backlog counting built in the node firmware, relies on the following principles [
2]:
- -
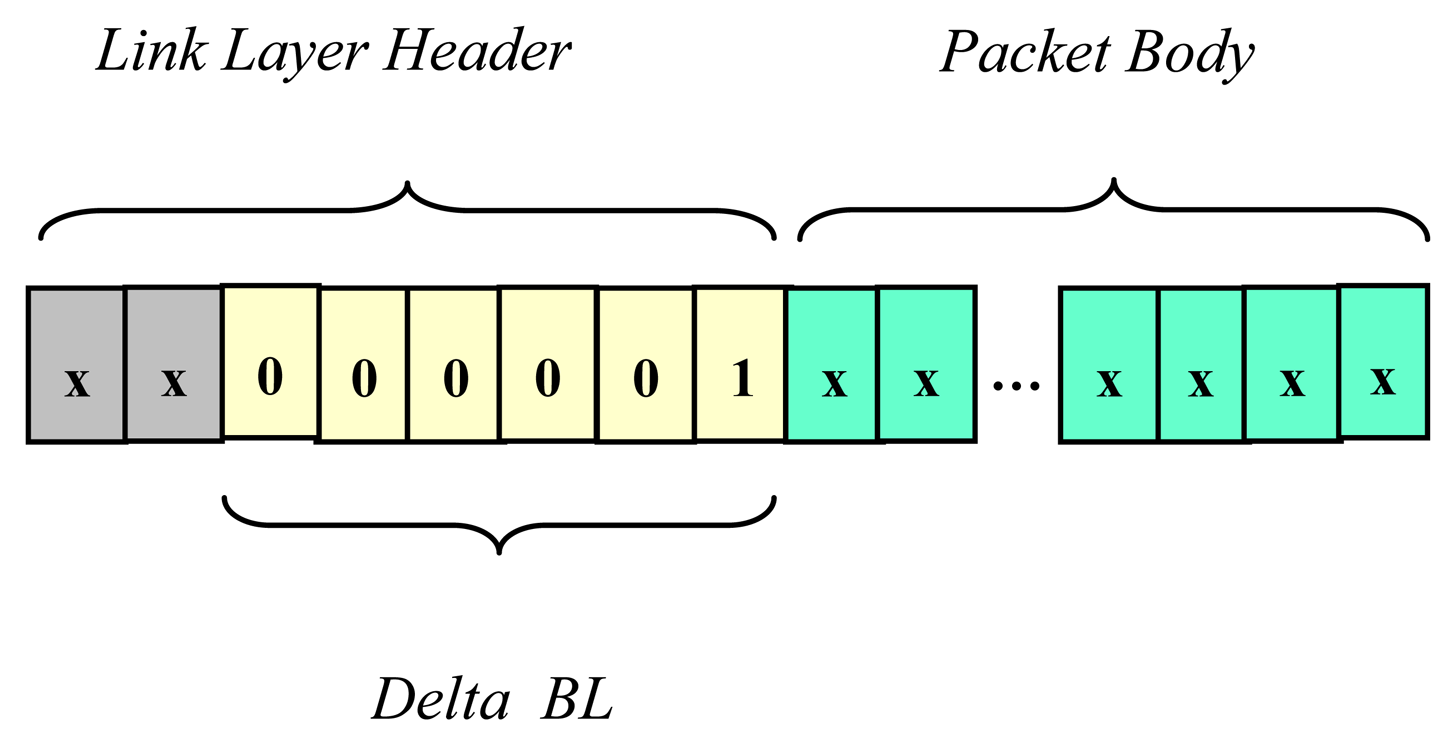
successive backlog increments are based on the information included in the header of each packet that is sent or successfully received by a particular node; this information is encoded in the 6-bit long field Delta_BL;
- -
successive backlog decrements by one occurring at the end of successful or idle packet cycles.
Both backlog modifications are independent of each other and occur in every cycle. Optionally, the backlog counter might be incremented by one in case of collision if the nodes are equipped with the collision detection [
1,
2]. Dedicated hardware in the transceiver is needed to detect collisions.
A number encoded in the Delta_BL data field represents the number of acknowledgements that will be generated by receiver(s) as a result of packet reception. This number equals one for unicast messages. Similarly, for multicast messages the number encoded in the Delta_BL is greater than one, but does not exceed 63, so the maximum size of a group of receiving nodes addressed by a single message equals 63. In the predictive p-CSMA, acknowledgement packets are not privileged in the channel access, and compete for the channel jointly with messages.
On the basis of the backlog counting algorithm we can conclude that after a successful transmission of a message the backlog
BL is incremented by a number of (
Delta_BL - 1). It is a resultant of the increment by a number of
Delta_BL, and the decrement by one at the end of a packet cycle. Comparing to the other congestion avoidance network protocols, the predictive
p-CSMA uses a kind of additive increase/additive decrease window scheme (AIAD) [
18], whereas IEEE 802.11 takes advantage of the truncated exponential backoff [
17].
2.3. Backlog Consistency
Each node calculates the channel backlog autonomously based on the backlog counter implemented in LonWorks node firmware. To keep the consistency of backlog states, all the nodes in the network should modify their backlog counters in the same way.
The consistency is kept if each node is able to detect unsuccessful transmissions in the channel because all the recipients can increment their backlog counters by Delta_BL only if a received packet has correct CRC. Note that recipients mean all the nodes in a network segment where a packet is broadcasted, not only message destination nodes addressed by a sender.
If transceivers, for example, enable only senders to detect possible packet collisions and increment their backlog counters, the backlog can lose its global character and becomes a local node-specific parameter. Any inconsistency in backlog counting among nodes causes unfairness in channel access.
3. Network Model
To recognize the predictive CSMA performance, we introduce some simplifications to the real network model. Below, we list the assumed simplifications in LonTalk/EIA-709.1 specification, and discuss how these simplifications may influence the obtained results.
3.1. Saturation Network Status
In our approach, we suppose that the network is at the saturation status where each node has a packet to send. To be precise, we assume that the network consists of n, a fixed number of nodes, and each node after the completion of a successful transmission immediately has a new packet available for sending. Thus, idle packet cycles do not occur in a saturated network. If an acknowledged message has been received by its recipient, this node generates an acknowledgement packet and places it in the output queue before messages waiting for a transmission. Throughout this paper the particular load scenario is considered, where the nodes are able to detect collisions, the acknowledged message service is used and all the transactions are unicast.
The validity of saturation performance analysis can be extended and treated more generally. Namely, the results derived for saturation workload are valid also for the network that is at non-saturated status but the number of transmitting nodes is constant.
3.2. Network Model
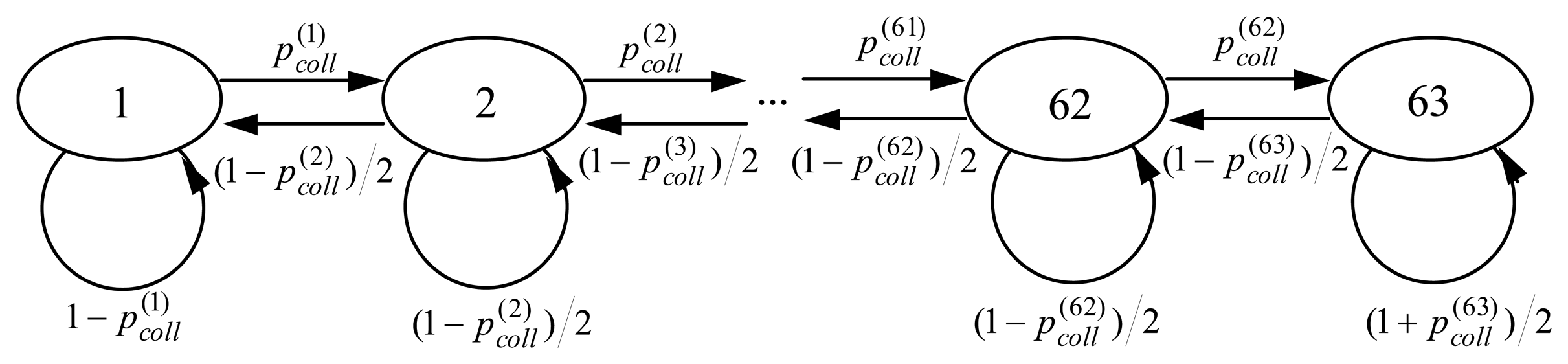
Unlike the classical p-CSMA, the predictive p-CSMA behavior is forced not only by the traffic rate but also by the structure of the traffic transmitted in the channel. In order to make the analysis tractable, we assume that each node is a source of messages unless it receives an acknowledged message. Then, it generates an acknowledgement packet and switches its status to the source of acknowledgements (i.e. schedules acknowledgement packet as the next packet for a transmission). According to the assumed load scenario all the messages are acknowledged and addressed to a single recipient (unicast). A key assumption we make is that the destination address(es) of transmitted messages are uniformly distributed in such a way that each message is sent to the node that currently possesses a status of a source of messages. The protocol performance analysis deals with the steady state of the network when the mean size of the contention window reaches asymptotically a constant value. The proportion between the number of sources of messages and the number of sources of acknowledgements in the steady state of the network determines the transition probabilities between backlog stages which are evaluated in Sect. 6.3. This proportion, however, does not influence the performance of the pure p-persistent CSMA because its behavior does not depend on the network traffic structure.
3.3. Network Segment
We assume that a network consists of a single segment that does not contain store-and-forward routers. The transceivers available on the market limit the segment size usually to 64 devices, although the LonTalk/EIA-709.1 can operate with segments containing hundreds of nodes [
1].
3.4. Backlog as the Global Measure of Channel
We assume that either Physical Layer, or Link Layer of the protocol do not introduce the backlog inconsistency, i.e. either the transmitting node, or the receiver(s) modify their backlog counter(s) in the same way. It is achieved if the channel can be assumed to be noise-free and all the transceivers are able to detect collisions even if they are not senders of colliding packets. Then, backlog might be considered as a
global channel measure. The similar assumption is adopted in [
4].
3.5. The Number of Outgoing Transactions
We assume that the number of concurrent outgoing transactions being in progress is unlimited (i.e. each node tries to send a new packet even if acknowledgement(s) of previously sent packets have not been successfully received yet). As a result of this assumption, the number of contenders in each packet cycle equals the number of nodes in the network.
In the LonTalk/EIA-709.1 protocol, the number of active outgoing non-priority transactions is limited by the Transport Layer implemented on the top of the predictive CSMA and equals one. As a result, a node awaiting the acknowledgement packet after the successful message transmission does not try to send the next message until this acknowledgement is received. Consequently, in the saturated status of the real LON network the mean number of contenders is lower than the number of nodes in the network since some nodes do not compete for the channel due to awaiting the acknowledgement.
3.6. CPU Processing Power vs. Channel Bit Rate
We suppose that the processing speed of the node is infinite. In other words, we assume that the communication channel is not too fast for the node CPU. The limitation of transmitted packets due to finite CPU speed does not appear for relatively low channel bit rates or long packets [
15].
3.7. Collision Detection
In LonTalk/EIA-709.1, the collision might be detected at the end of the packet preamble, or at the end of the packet transmission [
1]. We assume that the collision is detected at the end of the packet transmission and the preamble preceding the packet transmission is assumed to be of zero length. Note that as a result of this assumption, the whole packets are in fact transmitted either in successful, or in unsuccessful packet cycles.
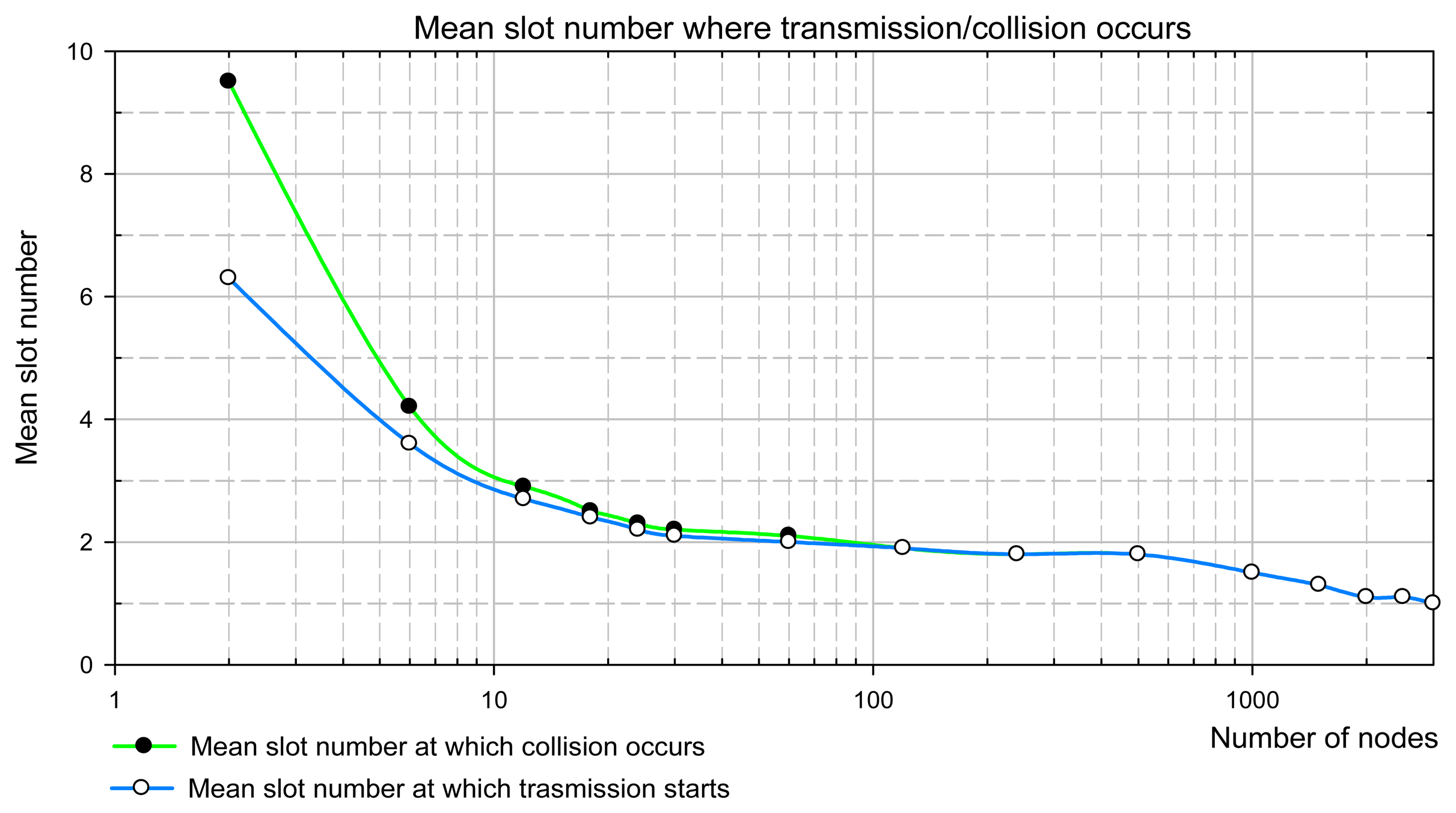
8. Simulative Validation of Analytical Approach
In order to verify the analytical approach we have run the simulations for the network containing selected number of nodes. The simulation model implemented in LabView corresponds to the analytical model specified in Section 3.
The simulation starts when the channel is idle. Next, the transient zone appears, when the nodes permanently try to access the channel and the mean channel backlog grows, but does not reach the steady-state value. Since the simulation model belongs to non-terminating systems and the steady state theoretically is never reached, we detect it with a finite accuracy. The detection relies on the search of the constant value of the mean backlog, rather than of the constant value of the current backlog. Therefore, we used the moving averages defined over a window of observations (i.e. a certain number of packet cycles, increasing with the number of nodes). Moving averages filter the higher frequency components in the mean backlog, arisen from the random behavior of the CSMA algorithm on the one hand, and remove also the influence of the transient zone on the estimation of saturation backlog on the other. The saturation backlog is found under quasi steady-state conditions when the moving average of the channel backlog is kept inside of 5% wide confidence interval.
Simulation outputs are the saturation channel backlog, the relative frequencies of successful/unsuccessful transmissions (as the experimental equivalents of the appropriate probabilities), and the mean access delay.
8.1. Validation of Transition Probabilities
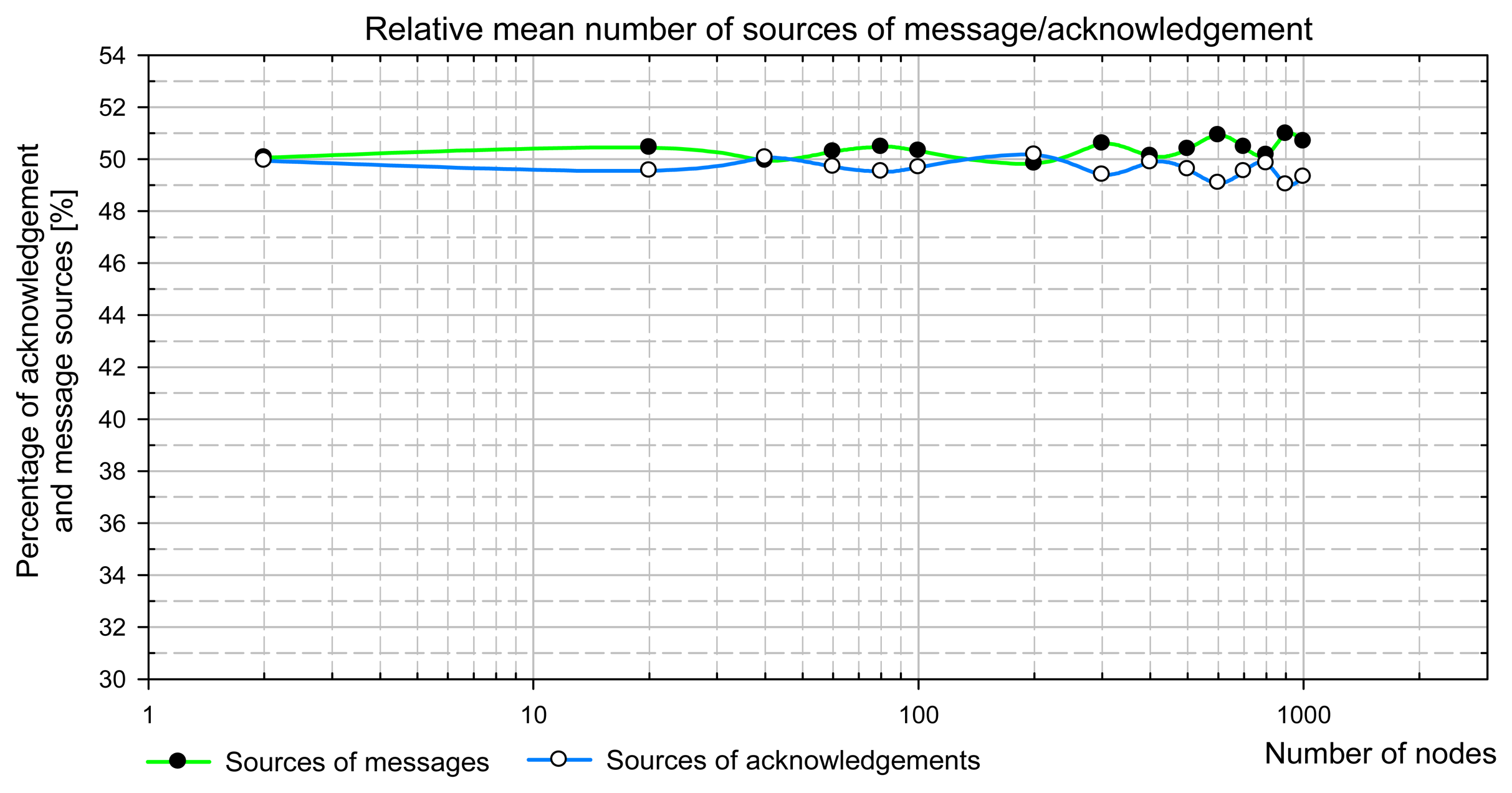
The transition probabilities in Markov model have been derived basing on the equality of the probabilities of the successful transmission of a message and an acknowledgement (see Sections 6.3). This assumption is true if the mean number of nodes having a message waiting for a transmission (i.e. message sources) equals the mean number of nodes that possesses an acknowledgement ready for sending (i.e. acknowledgement sources).
A uniform distribution of destination addresses has been implemented in the simulation model as stated in Sect. 3.2. The assignment of recipient addresses is controlled by the simulator. First, the simulator tries to assign a recipient that is a source of messages to every message sender. In case of the lack of sufficient number of message sources, the sender sends a message to itself (by the way such transmissions occur sometimes in real LON systems during turnaround network variable updates, see [
15]).
Fig. 9 presents simulation results showing the mean number of message and acknowledgement sources in the network steady state. It is clear that both numbers are equal to 50% with finite simulation accuracy. It was checked that these results are independent of initial conditions, i.e. the proportion between the number of message and acknowledgement sources at the simulation beginning.
8.2 Simulation versus Numerical Results
The comparison of simulation and numerical results for the saturation backlog, the probability of collision
Pcoll and its experimental measure (i.e. collision percentage
P'
coll), and the mean access delay, are presented in
Table 1. Since both results are very close to each other and the corresponding graphs overlap, they are not shown on the plots together. The comparison shows a good conformity of simulation and Markov chain-based analytical approach. The difference between the results obtained in both approaches stems from:
- -
the finite accuracy of backlog estimation and the steady state detection in the simulation,
- -
the inaccuracy (non-uniformity) of the pseudorandom generator in the simulation,
- -
the finite precision of complex analytical computations.