Modelling a Peroxidase-based Optical Biosensor
Abstract
:1. Introduction
2. Mathematical Model
3. Digital Simulation
4. Results and Discussion
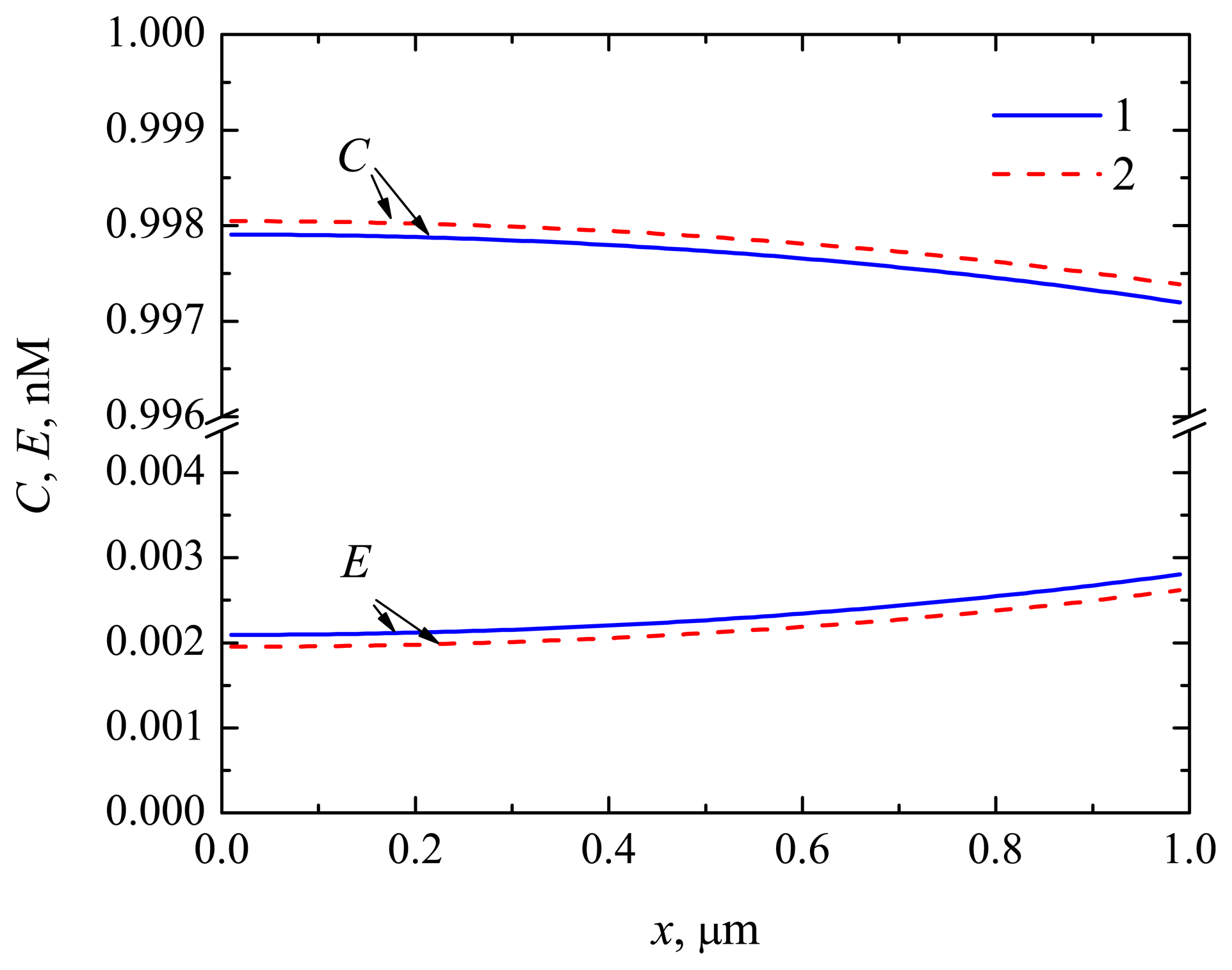
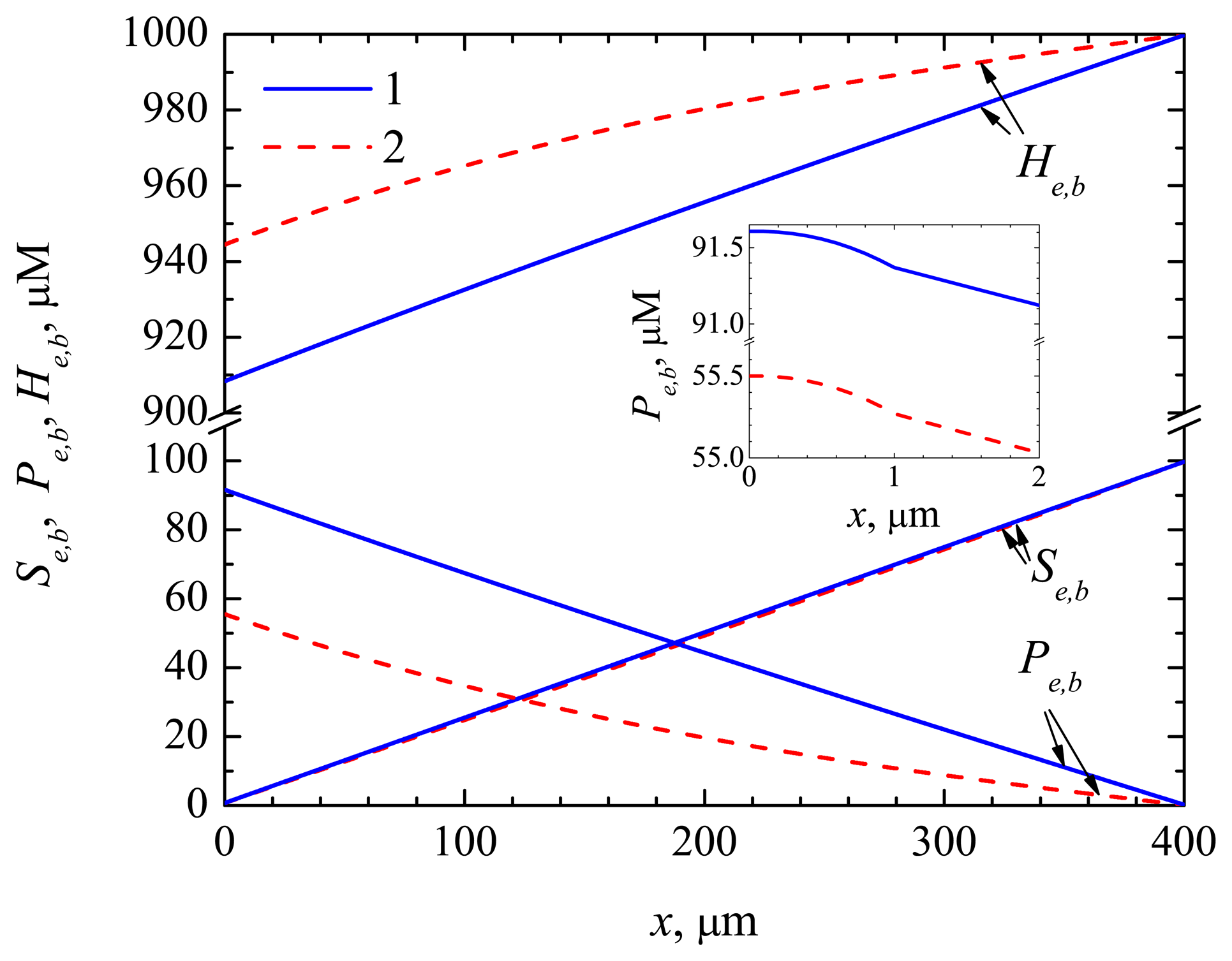
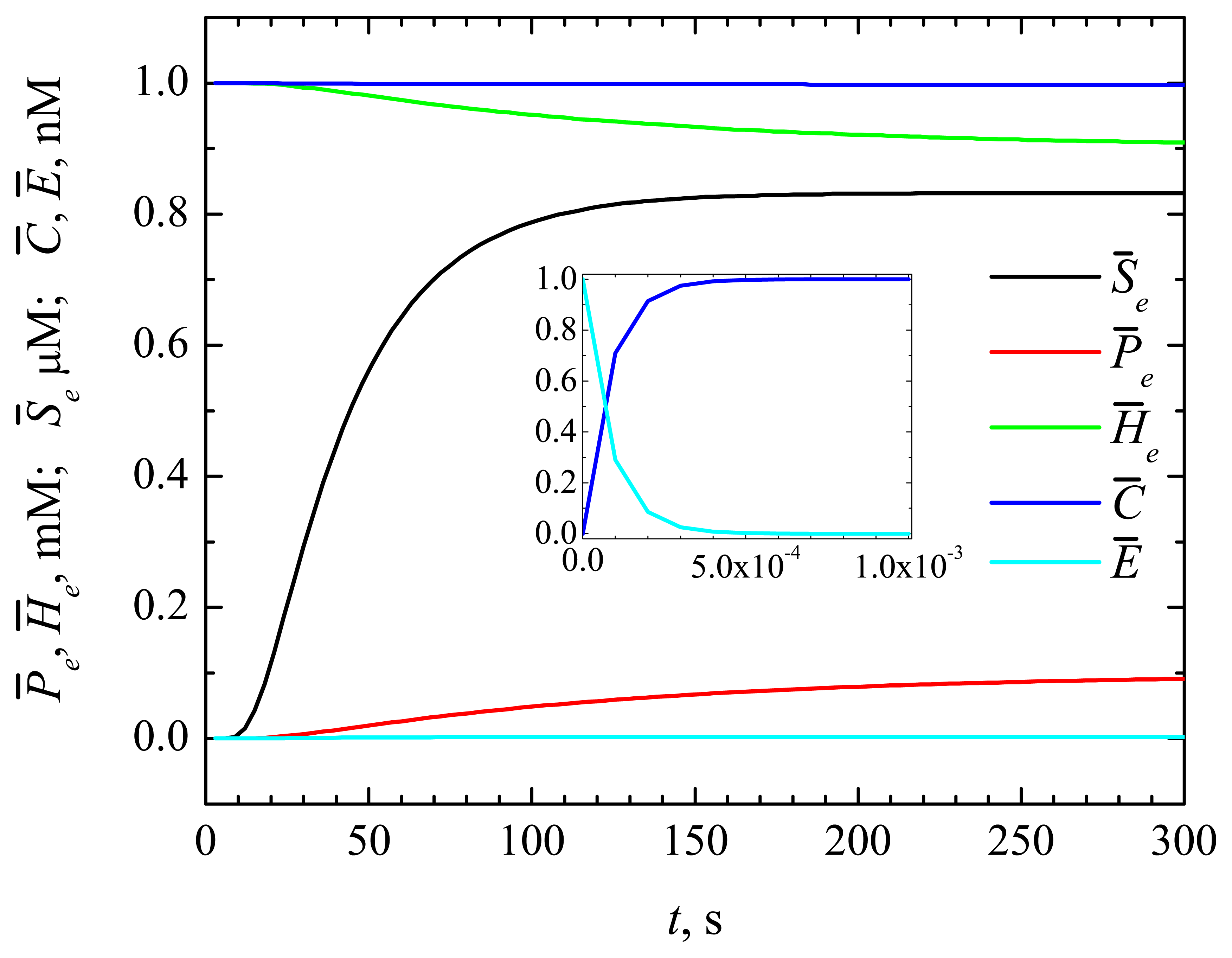
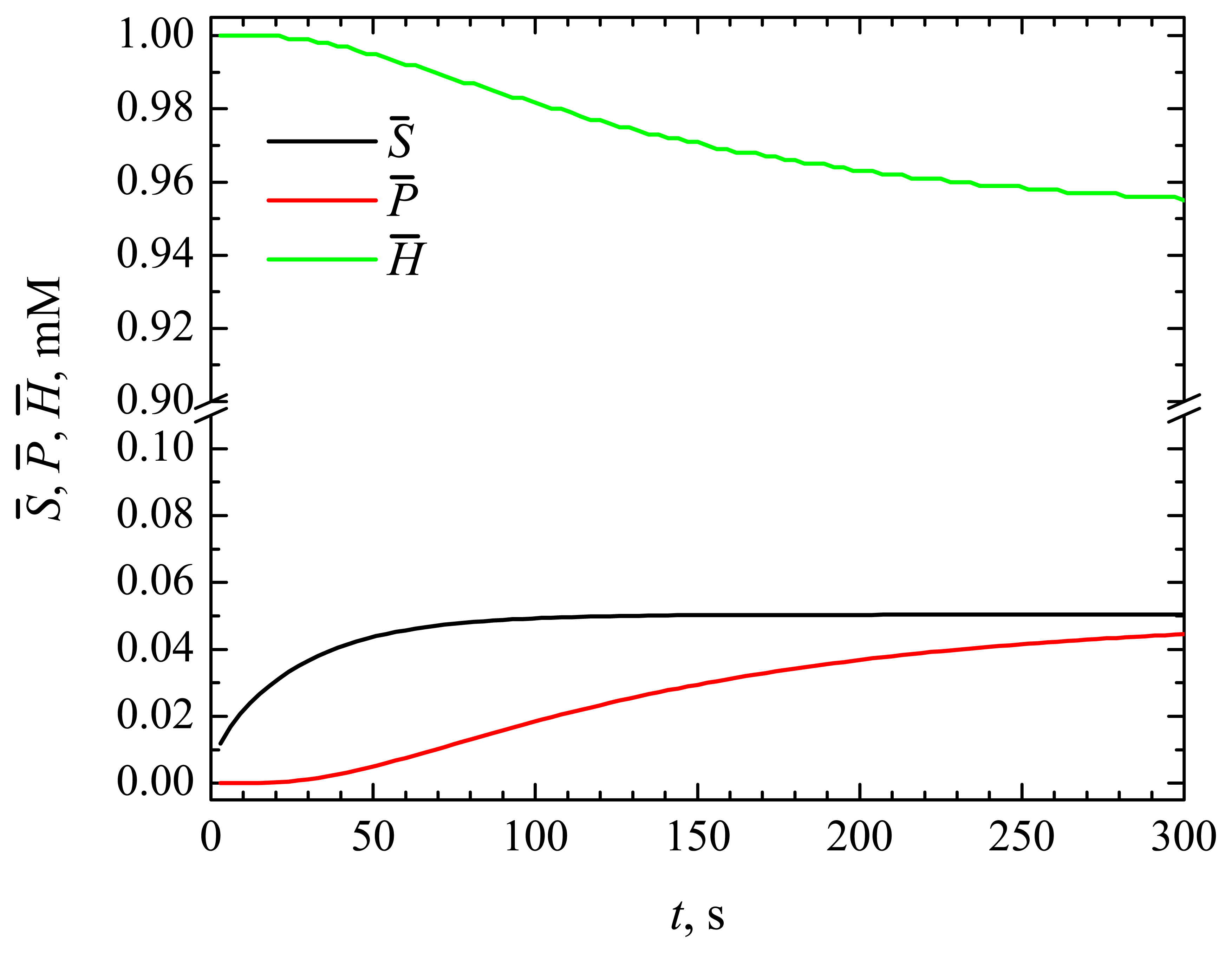
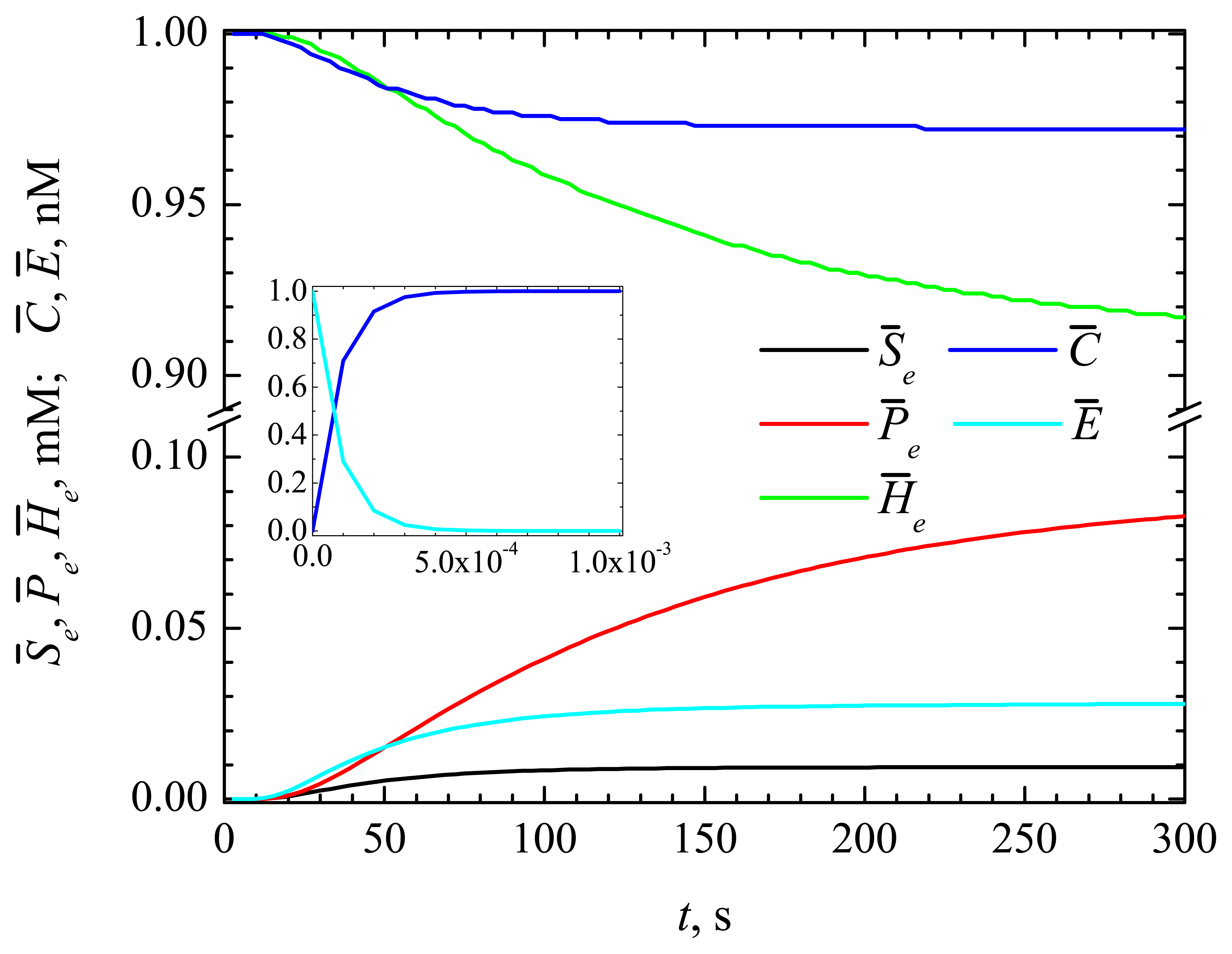
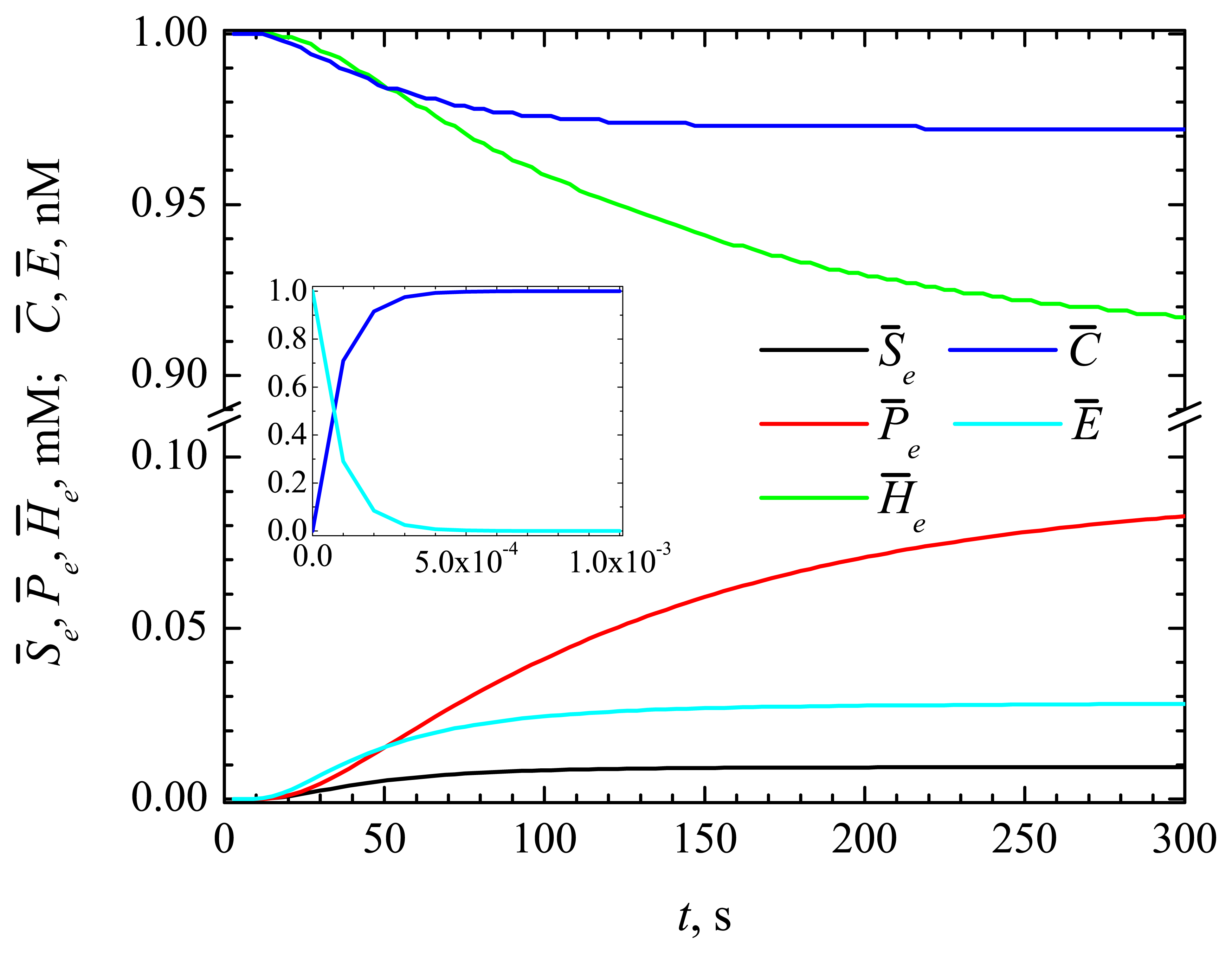
4.1. The Dynamics of the Concentrations of the Compounds
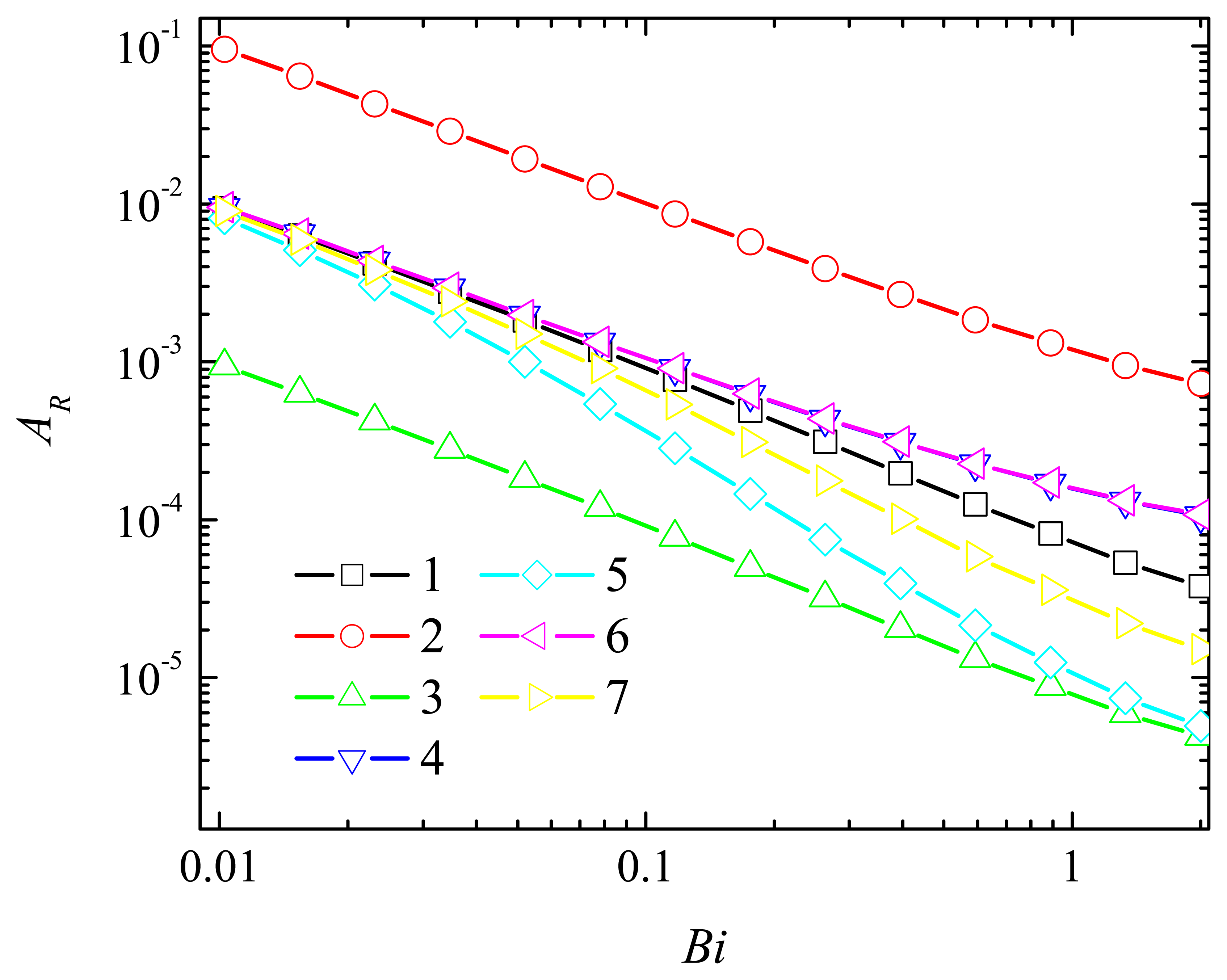
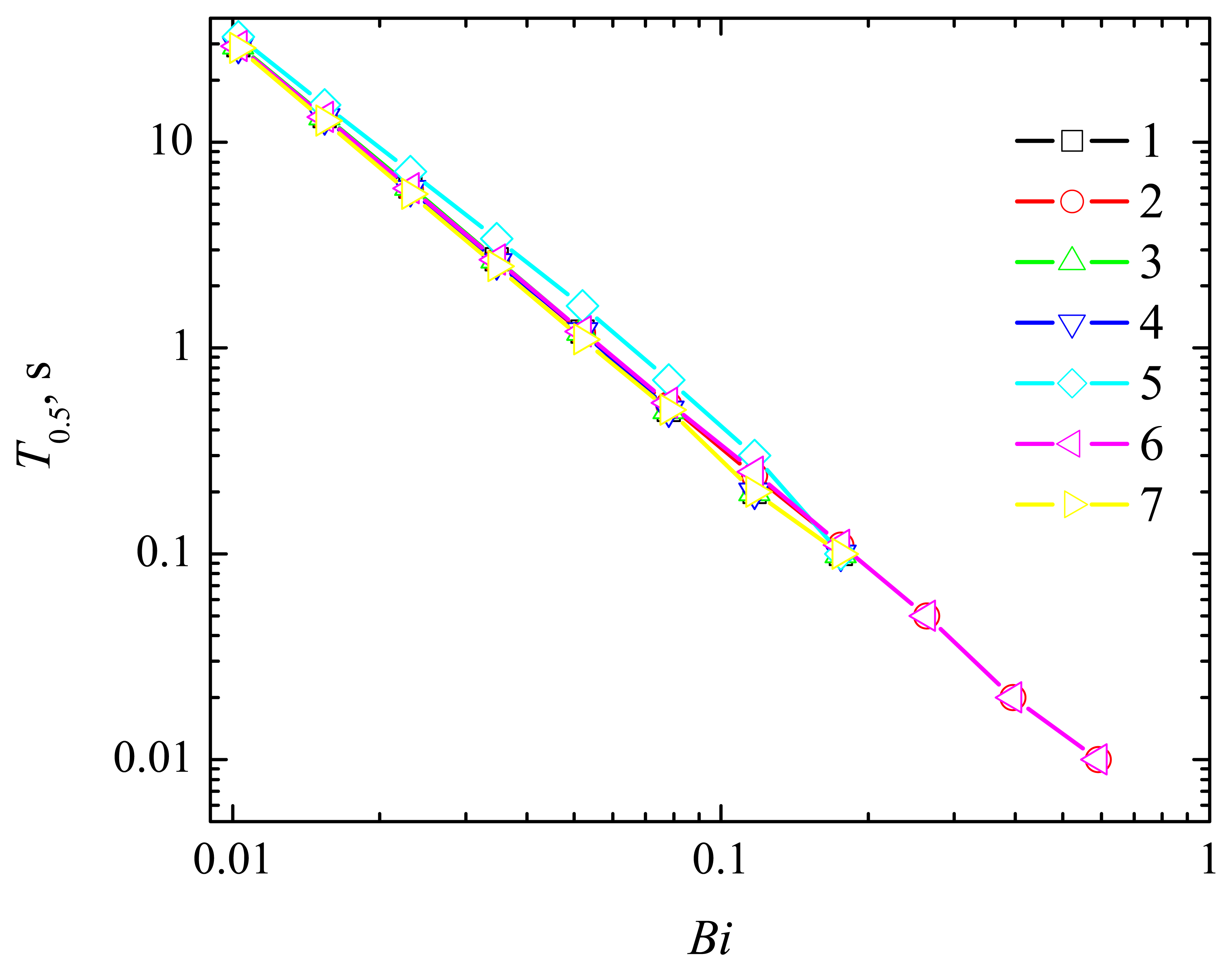
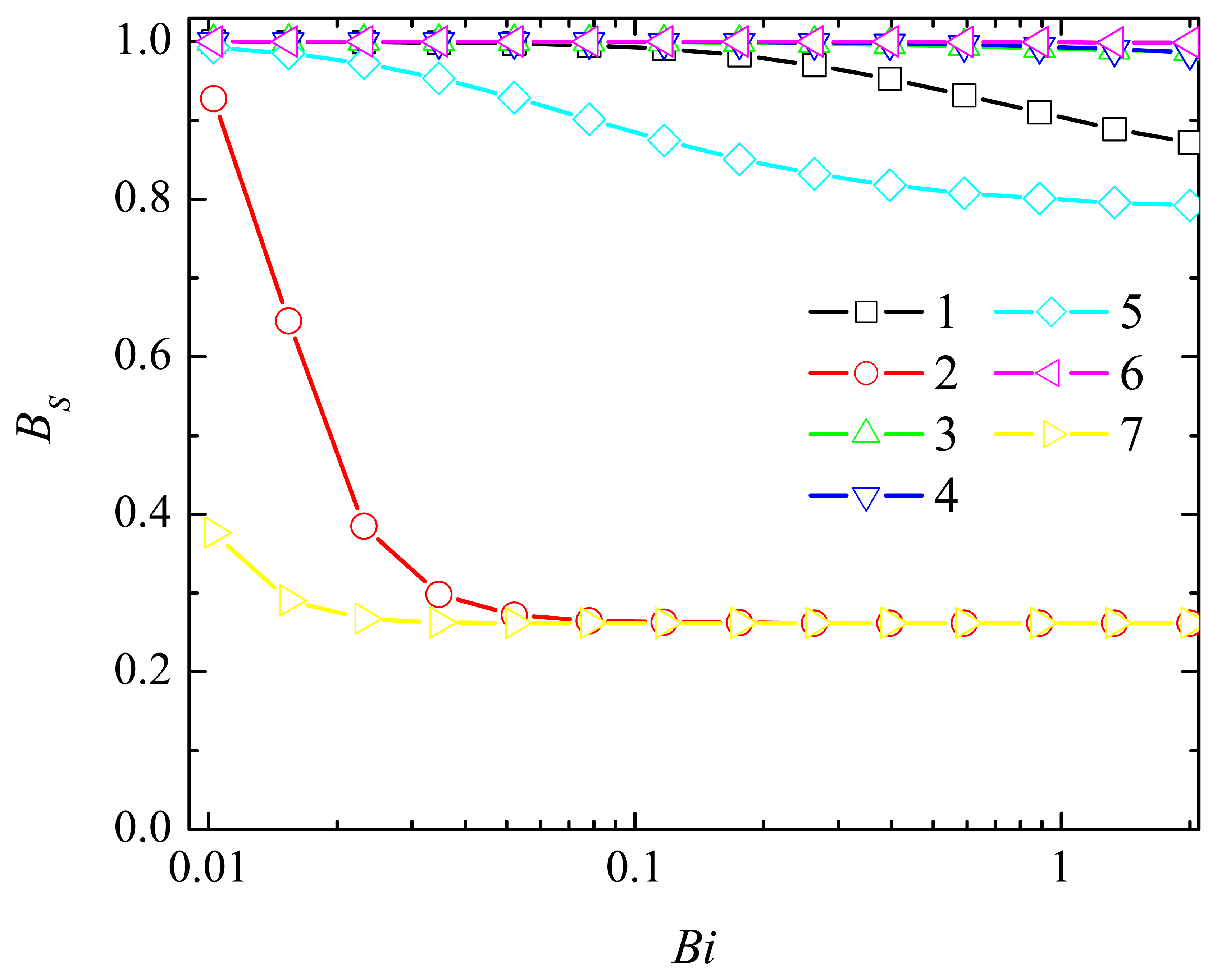
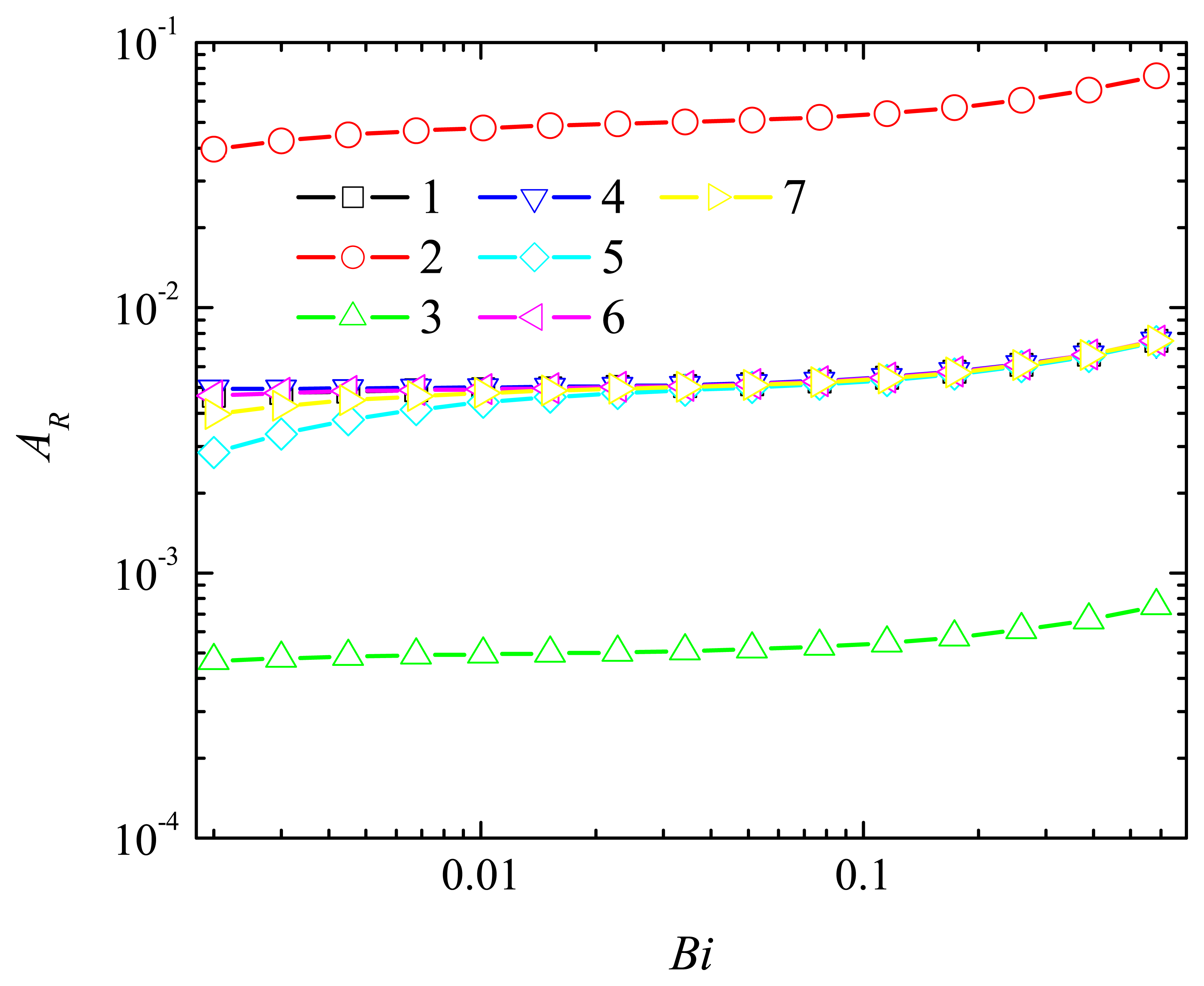
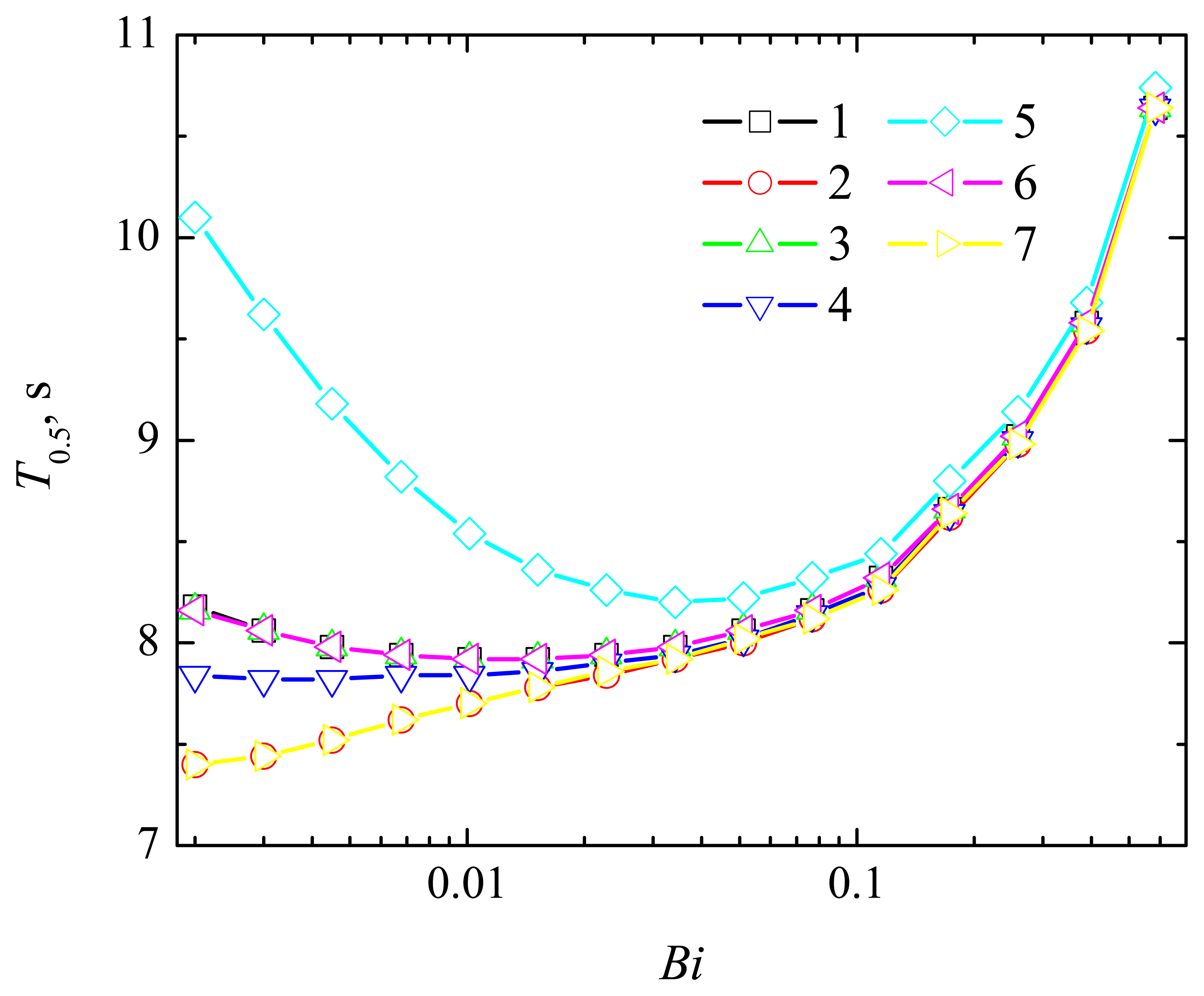
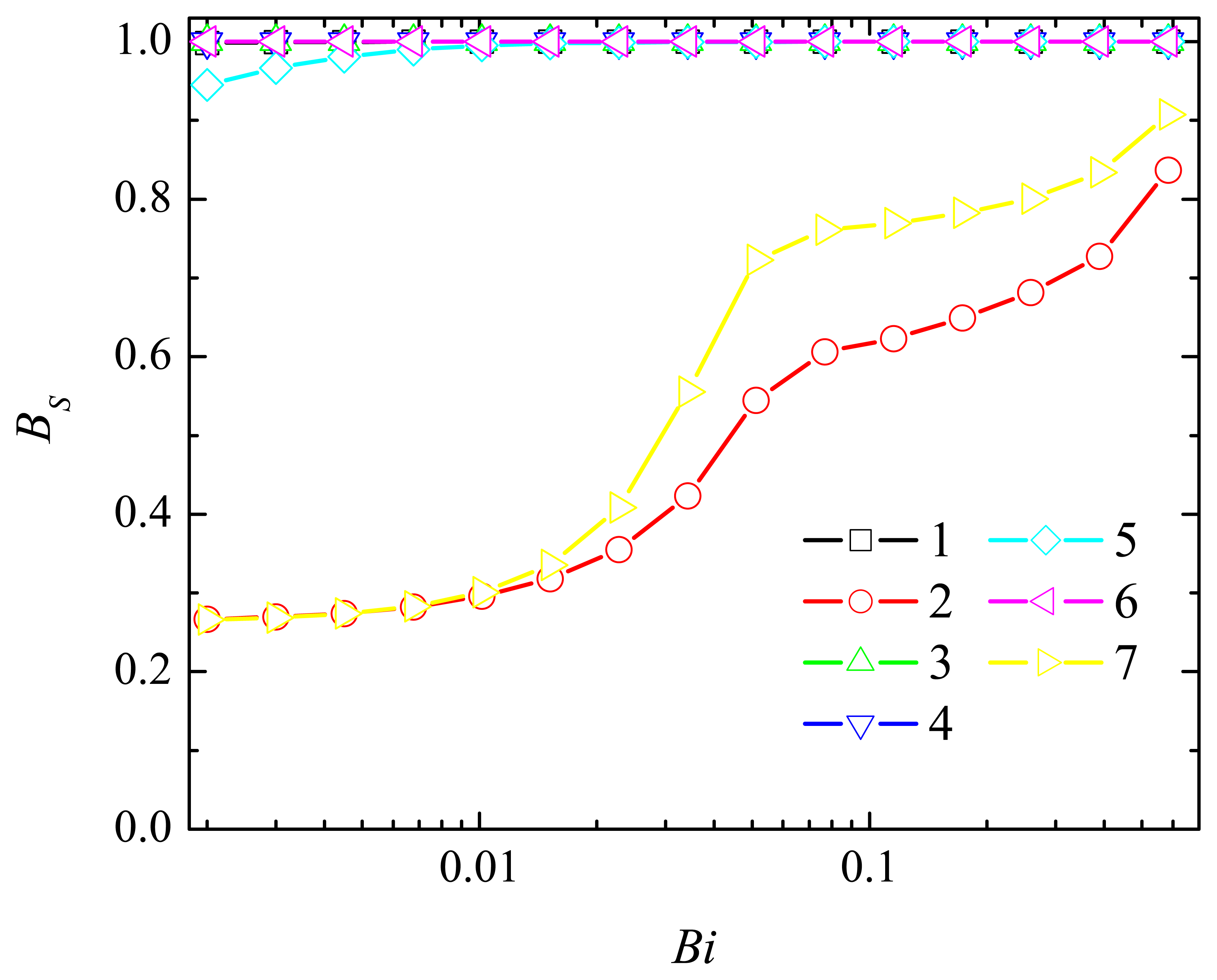
4.2. The Impact of the Thickness of the Diffusion Layer
4.3. The Impact of the Thickness of the Enzyme Layer
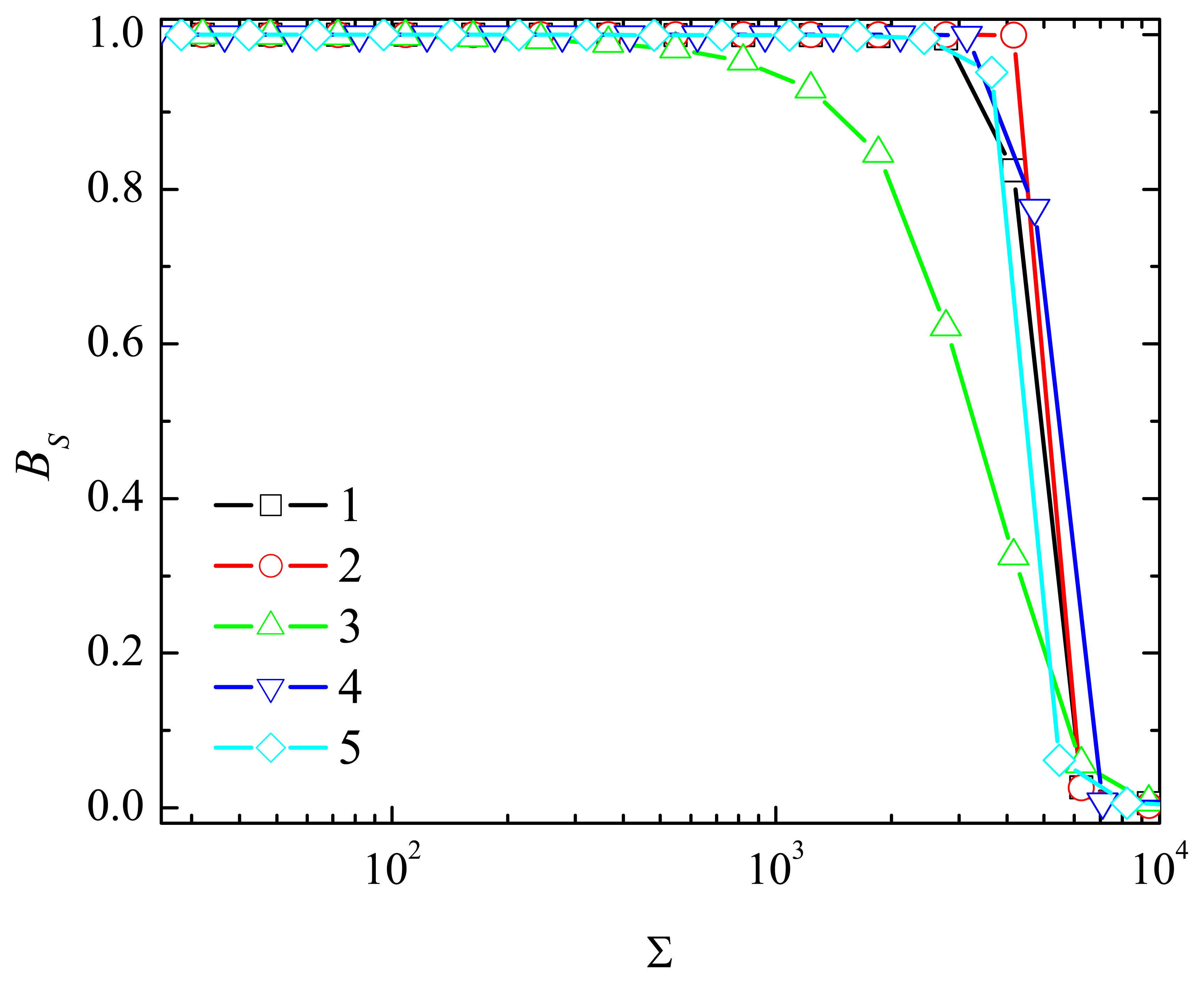
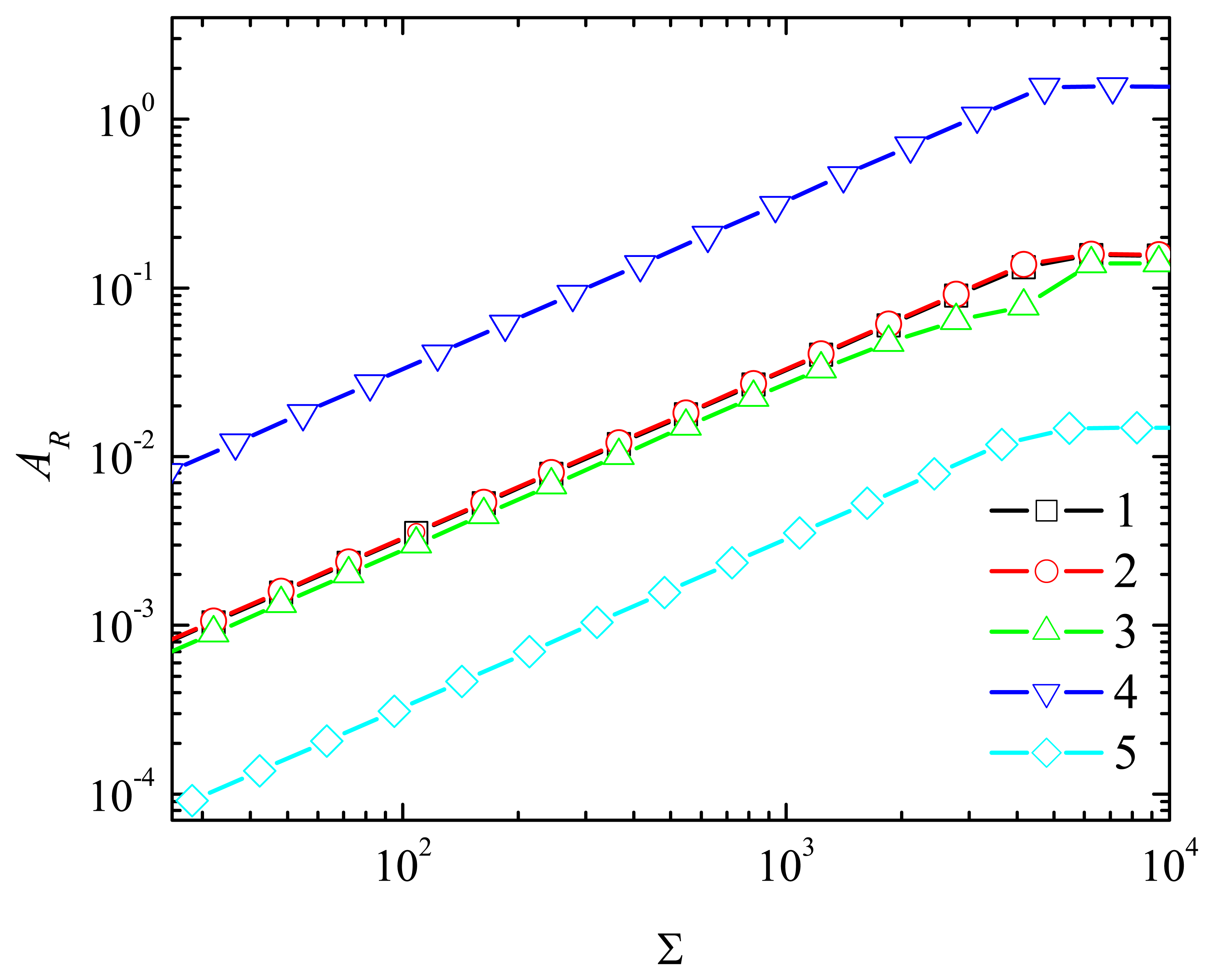
4.4. The Impact of the Outer Substrate Concentration
5. Conclusions
Acknowledgments
References
- Scheller, F.; Schubert, F. Biosensors; Elsevier: Amsterdam, 1992. [Google Scholar]
- Turner, A. P. F.; Karube, I.; Wilson, G. S. Biosensors: Fundamentals and Applications; Oxford University Press: Oxford, 1987. [Google Scholar]
- Chaubey, A.; Malhotra, B. D. Mediated biosensors. Biosens. Bioelectron. 2002, 17(6), 441–456. [Google Scholar]
- Ligler, F. S.; Taitt, C. R. Optical Biosensors: Present and Future; Elsevier Science: Amsterdam, 2002. [Google Scholar]
- Choi, M. M. F. Progress in enzyme-based biosensors using optical transducers. Microchimica Acta 2004, 148(3-4), 107–132. [Google Scholar]
- Bosch, M. E.; Sánchez, A. J. R.; Rojas, F. S.; Ojeda, C. B. Recent development in optical fiber biosensors. Sensors 2007, 7(6), 797–859. [Google Scholar]
- Wollenberger, U.; Lisdat, F.; Scheller, F. W. Frontiers in Biosensorics 2. Practical Applications; Birkhauser Verlag: Basel, 1997. [Google Scholar]
- Leatherbarrow, R. J.; Edwards, P. R. Analysis of molecular recognition using optical biosensors. Curr. Opin. Chem. Biol. 1999, 3(5), 544–547. [Google Scholar]
- Ojeda, C. B.; Rojas, F. S. Recent development in optical chemical sensors coupling with flow injection analysis. Sensors 2006, 6(10), 1245–1307. [Google Scholar]
- Wu, B.; Wang, Y.; Li, J.; Song, Z.; Huang, J.; Wang, X.; Chen, Q. An optical biosensor for kinetic analysis of soluble interleukin-1 receptor i binding to immobilized interleukin-1α. Talanta 2006, 70(3), 485–488. [Google Scholar]
- Stefano, L. D.; Arcari, P.; Lamberti, A.; Sanges, C.; Rotiroti, L.; Rea, I.; Rendina, I. DNA optical detection based on porous silicon technology: from biosensors to biochips. Sensors 2007, 7(2), 214–221. [Google Scholar]
- Passaro, V. M. N.; Dell’olio, F.; Casamassima, B.; Leonardis, F. D. Guided-wave optical biosensors. Sensors 2007, 7(4), 508–536. [Google Scholar]
- Sanz, V.; de Marcos, S.; Galbán, J. Direct glucose determination in blood using a reagentless optical biosensor. Biosens. Bioelectron. 2007, 22(12), 2876–2883. [Google Scholar]
- Ferreira, L. S.; Souza, M. B. D.; Trierweiler, J. O.; Broxtermann, O.; Folly, R. O. M.; Hitzmann, B. Aspects concerning the use of biosensors for process control: experimental and simulation investigations. Comp. Chem. Engng. 2003, 27(8), 1165–1173. [Google Scholar]
- Corcuera, J. R. D.; Cavalieri, R.; Powers, J.; Tang, J. Amperometric enzyme biosensor optimization using mathematical modeling. Proceedings of the 2004 ASAE / Csae Annual International Meeting, page Paper No. 047030. Ottawa, Ontario, Canada, (August 1-4 2004); American Society of Agricultural Engineers.
- Mell, C.; Maloy, J. T. A model for the amperometric enzyme electrode obtained through digital simulation and applied to the glucose oxidase system. Anal. Chem. 1975, 47, 299–307. [Google Scholar]
- Kulys, J. The development of new analytical systems based on biocatalysts. Anal. Lett. 1981, 14, 377–397. [Google Scholar]
- Bartlett, P. N.; Pratt, K. F. E. Modelling of processes in enzyme electrodes. Biosens. Bioelectron. 1993, 8(9-10), 451–462. [Google Scholar]
- Schulmeister, T.; Pfeiffer, D. Mathematical modelling of amperometric enzyme electrodes with perforated membranes. Biosens. Bioelectron. 1993, 8(2), 75–79. [Google Scholar]
- Yokoyama, K.; Kayanuma, Y. Cyclic voltammetric simulation for electrochemically mediated enzyme reaction and determination of enzyme kinetic constants. Anal. Chem. 1998, 70(16), 3368–3376. [Google Scholar]
- Lyons, M. E. G.; Murphy, J.; Rebouillat, S. Theoretical analysis of time dependent diffusion, reaction and electromigration in membranes. J. Solid State Electrochem. 2000, 4, 458–472. [Google Scholar]
- Baronas, R.; Ivanauskas, F.; Kulys, J. The influence of enzyme membrane thickness on the response of amperometric biosensors. Sensors 2003, 3(7), 248–262. [Google Scholar]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Modelling amperometric enzyme electrode with substrate cyclic conversion. Biosens. Bioelectron. 2004, 19(8), 915–922. [Google Scholar]
- Baronas, R.; Ivanauskas, F.; Kulys, J. Computer simulation of the respose of amperometric biosensors in stirred and non stirred solution. Nonlinear Anal. Model. Control 2003, 8(1), 3–18. [Google Scholar]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Mathematical model of the biosensors acting in a trigger mode. Sensors 2004, 4(4), 20–36. [Google Scholar]
- Lyons, M. E. G. Modelling the transport and kinetics of electroenzymes at the electrode/solution interface. Sensors 2006, 6(12), 1765–1790. [Google Scholar]
- Baronas, R.; Kulys, J.; Ivanauskas, F. Computational modelling of biosensors with perforated and selective membranes. J. Math. Chem. 2006, 39(2), 345–362. [Google Scholar]
- Kulys, J.; Baronas, R. Modelling of amperometric biosensors in the case of substrate inhibition. Sensors 2006, 6(11), 1513–1522. [Google Scholar]
- Popovtzer, R.; Natan, A.; Shacham-Diamand, Y. Mathematical model of whole cell based bio-chip: an electrochemical biosensor for water toxicity detection. J. Electroanal. Chem. 2007, 602(1), 17–23. [Google Scholar]
- Baronas, R.; Ivanauskas, F.; Kulys, J. Computational modelling of the behaviour of potentiometric membrane biosensors. J. Math. Chem. 2007, 42(3), 321–336. [Google Scholar]
- Schulmeister, T. Mathematical modelling of the dynamic behaviour of amperometric enzyme electrodes. Selective Electrode Rev. 1990, 12, 203–260. [Google Scholar]
- Merino, S.; Grinfeld, M.; McKee, S. A degenerate reaction diffusion system modelling an optical biosensor. Z. angew. Math. Phys. 1998, 49(1), 46–85. [Google Scholar]
- Rickus, J. L. Impact of coenzyme regeneration on the performance of an enzyme based optical biosensor: a computational study. Biosens. Bioelectron. 2005, 21(6), 965–972. [Google Scholar]
- Aris, R. The Mathematical Theory of Diffusion and Reaction in Permeable Catalysts. The Theory of the Steady State; Clarendon Press: Oxford, 1975. [Google Scholar]
- Carr, P. W.; Bower, L. D. Immobilized Enzymes in Analytical and Clinical Chemistry: Fundamentals and Applications; John Wiley: New York, 1980. [Google Scholar]
- Kernevez, J. P. Enzyme Mathematics. Studies in Mathematics and its Applications; Elsevier Science: Amsterdam, 1980. [Google Scholar]
- Vo-Dinh, T. Biomedical Photonics Handbook; CRC Press LLC: New York, 2003. [Google Scholar]
- Wang, J. Analytical Electrochemistry, 2nd Ed. ed; Springer-Verlag: Berlin, 1988. [Google Scholar]
- Britz, D. Digital Simulation in Electrochemistry, 3rd Ed. ed; Springer-Verlag: Berlin, 2005. [Google Scholar]
- Samarskii, A. A. The Theory of Difference Schemes; Marcel Dekker: New York-Basel, 2001. [Google Scholar]
- Moreira, J. E.; Midkiff, S. P.; Gupta, M.; Artigas, P. V.; Snir, M.; Lawrence, R. D. Java programming for high-performance numerical computing. IBM Systems Journal 2000, 39(6), 21–56. [Google Scholar]
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Baronas, R.; Gaidamauskait˙e, E.; Kulys, J. Modelling a Peroxidase-based Optical Biosensor. Sensors 2007, 7, 2723-2740. https://doi.org/10.3390/s7112723
Baronas R, Gaidamauskait˙e E, Kulys J. Modelling a Peroxidase-based Optical Biosensor. Sensors. 2007; 7(11):2723-2740. https://doi.org/10.3390/s7112723
Chicago/Turabian StyleBaronas, Romas, Evelina Gaidamauskait˙e, and Juozas Kulys. 2007. "Modelling a Peroxidase-based Optical Biosensor" Sensors 7, no. 11: 2723-2740. https://doi.org/10.3390/s7112723