1. Introduction
Recently, interest in the study of networked control system (NCS) and sensor networks has increased widely due to its low cost, high flexibility, simple installation and maintenance [
1]. In such systems, a center station has the task of receiving, processing and sending data to the slave nodes such as sensor nodes, actuator nodes, etc. over a serial network. It is easy to add or remove slave nodes in the network without changing the system structure much. Aside from the advantages as mentioned above, however, there are several problems affecting to the system such as bandwidth, network-induced delay, packet loss rate.
One of the most interesting problems is how to reduce network bandwidth when there are many nodes on the network. This can be achieved by reducing either data packet size or data packet transmission rate. In [
2], an adjustable deadband was defined on each node to reduce network traffic. The node does not broadcast a new message if its signal is within the deadband. In [
3], estimators were used at each sensor node instead. When the estimated value deviates from the actual output by more than a prespecified tolerance, the actual sensor data are transmitted. To overcome the limited network bandwidth, transmission data size reduction using a special encoder-decoder was considered in [
4]. Another method for reduction of data transmission rate called send-on-delta (SOD) transmission was explored in [
5-
8]. This method requires that a sensor node transmit data to the estimator node only if its measurement value changes more than a given specified
δ value. By adjusting the
δ value at each sensor node, data transmission rate is reduced so that the network bandwidth is increased and can be used for other traffic.
The purpose of this paper is to extend our work on the modified Kalman filter employing a SOD transmission method [
5], where the states are periodically estimated by the estimator node regardless of whether the sensor nodes transmit data or not. A challenging issue is how the estimator node determines the measurement value at a sensor node if it does not send data. If this problem is well solved, the estimation performance will be significantly improved. In this paper, we examine and evaluate the measurement output value as well as measurement noise arising when a sensor node does not transmit data. Then, a computed output with the new measurement value and new noise covariance is compensated to the system in order to reduce estimation error. Through simulations, we show that the proposed method gives better estimation performance than that of [
5].
2. Sensor Output Evaluation
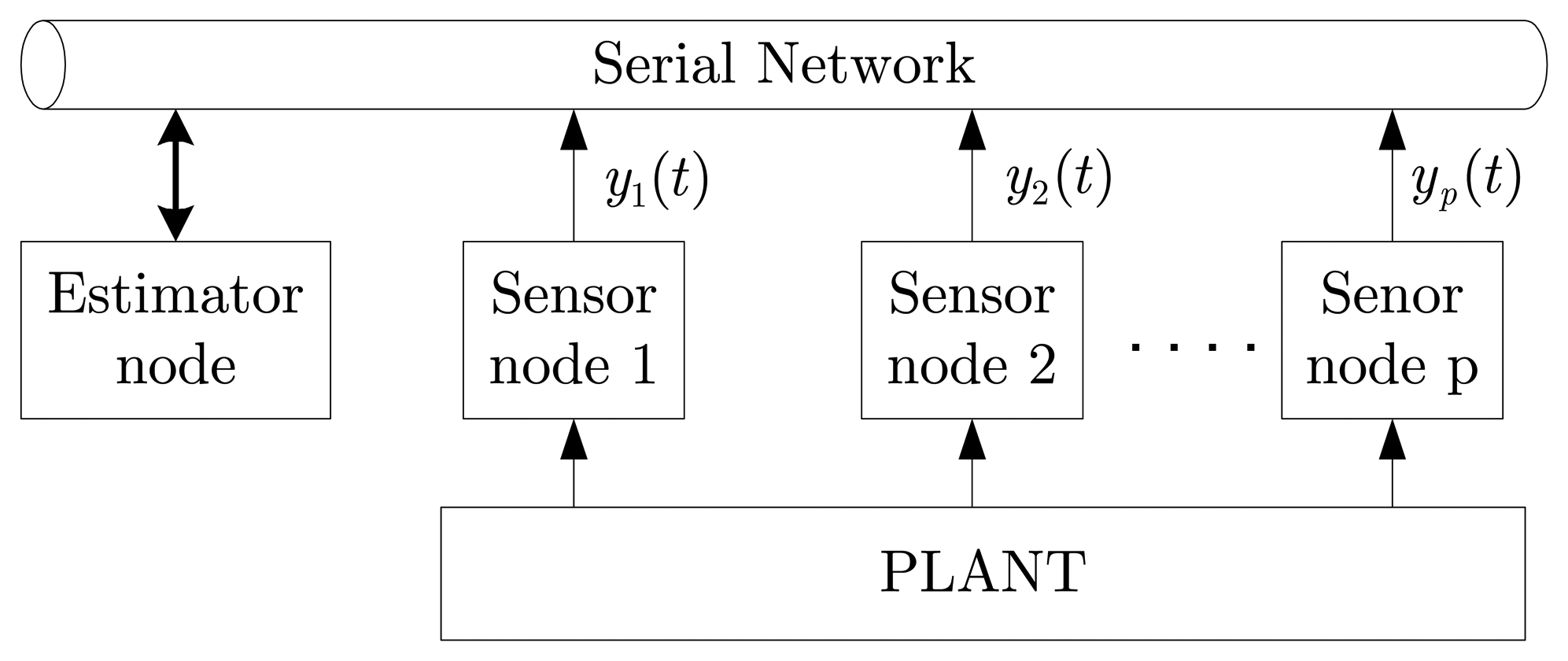
Consider a networked control system illustrated as in
Figure 1, where the linear continuous-time system is described as:
where
x ∈
Rn is the state of the plant,
u is the deterministic input signal,
y ∈
Rp is the measurement output which is sent to the estimator node by the sensor nodes.
w(
t) is the process noise with covariance
Q, and
v(
t) is the measurement noise with covariance
R.
w(
t) and
v(
t) are uncorrelated, zero mean white Gaussian random processes.
The following assumptions are made on the data transmission over network:
Measurement outputs are s yi(1 ≤ i ≤ p) are sampled at period T, but their data are only transmitted to the estimator node when the difference between the current value and the previously transmitted one is greater than δi.
For simplicity in problem formulation, any transmission delay from the sensor nodes to the estimator node is ignored.
The estimator node estimates the states of the plant regularly at period T, regardless of whether or not any sensor data arrive. If the i-th sensor data do not arrive, the estimator node knows that the current value of i-th sensor output has not changed more than the range (−δi,+δi), compared with the last arriving one. This implicit information is used to estimate the current states in case i-th sensor data do not arrive.
Let the last received value of
i-th sensor output be
ylast,i, at time
tlast,i. If there is no sensor data received for
t >
tlast,i, the estimator node considers that the measurement value of the
i-th sensor output
yi(
t) is still equal to
ylast,i but the measurement noise is increased from
vi(
t) to
vn,i(
t) =
vi(
t) + Δ
i(
t,
tlast,i), where Δ
i(
t,
tlast,i) is defined [
5]:
In [
5], it was assumed that Δ
i(
t,
tlast,i) had a uniform distribution with zero mean and a variance
. However, this assumption is incorrect in some cases where that measurement noise
R(i,i) is smaller than
, where
R(i,i) is the (
i,i)-th element of
R. To illustrate this, assume that there is no measurement noise (i.e.,
R=0). Then 0 ≤ Δ
i(
t,
tlast,i) <
δi if
Cx(
t) is increasing and −
δi <
Δi (
t,
tlast,i) ≤ 0 if
Cx(
t) is decreasing. In this case, a reasonable assumption is that the mean of Δ
i(
t,
tlast,i) is
δi /2 if
Cx(t) is increasing and −
δi /2 if
Cx(
t) is decreasing. This trend is preserved as long as the measurement covariance
R ≪
δ2. When the measurement covariance is large, then Δ
i(
t,
tlast,i) in [
5] is more likely affected by the zero-measurement noise
v(
t); thus zero mean assumption is a more valid assumption.
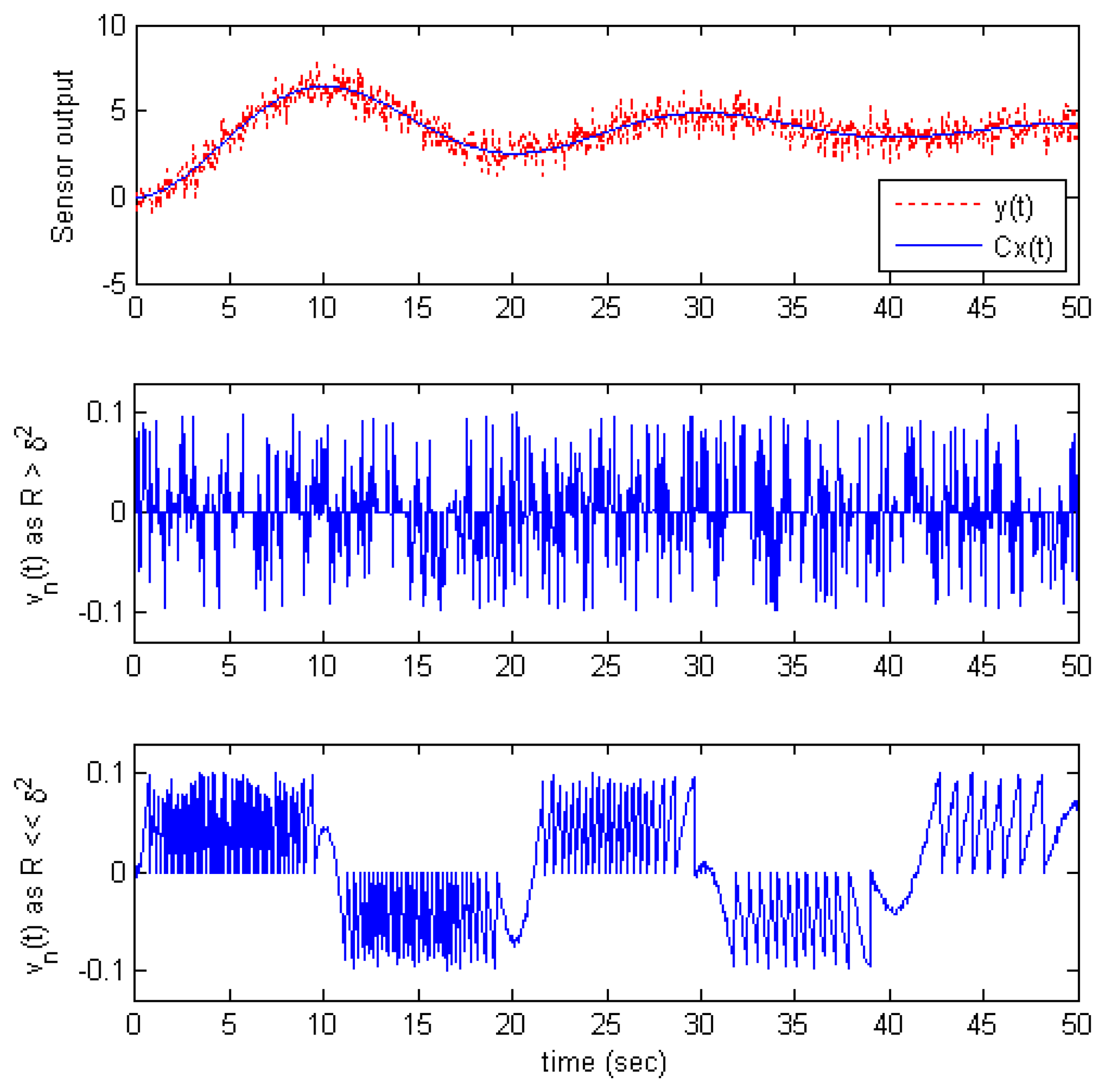
To demonstrate this argument, consider an example of the output response of an 2
nd order system with step input shown in
Figure 2. The top graph is the output signal without noise
Cx(
t) and the measurement output
y(
t). In this example,
y(
t) is sampled by the send-on-delta scheme with
δ = 0.1. The new measurement noise
vn(
t) is shown in the middle and bottom graphs for two cases:
R >
δ2 and
R ≪
δ2, respectively. Obviously, the waveform of
vn(
t) is rather different in two cases: It is a uniform distribution with zero mean in the first case, but with non zero mean in the second case. For example,
vn(
t) has a positive mean value in time range (0,10
s) but a negative mean value in (10,20
s).
Therefore, the assumption in [
5] is only correct in the case
R >
δ2. Furthermore, in realistic systems, measurement noise is normally small, while
δ is set to a greater value to reduce data transmission rate. For some types of digital sensor such as encoders, measurement noise is even equal to zero. This means that the second case (non-zero mean case) happens more usually than the first case in the real applications. We propose an estimation algorithm which exploits this non-zero mean case in order to improve the estimation performance.
Now we compute the mean value and variance of vn,i(t). Notice that the new measurement noise vn,i(t) only exists when the estimator node does not receive data from the i-th sensor node at instant t. Otherwise, measurement noise is still vi(t).
We see that variance of
vn,i(
t) in the second case
(4) is smaller than in
(3) which was used in [
5].
3. State estimation with the SOD transmission method
In this section, we propose a method to adaptively use
(3) or
(4) in the modified Kalman filter for the state estimation problem. The main issue here is when we should use
(4) instead of
(3)? And if
(4) is used, how then to determine when the mean value of
vn,i(
t) is positive or negative?
Firstly, we compute the mean value of
vn,i(
t) when
(4) is used. Let two latest consecutive
i-th sensor output values received at the estimator node be
ylast−1,i,
ylast,i at time
tlast−1,i,
tlast,i, respectively. Derivative of
yi at time
tlast,i is approximately calculated as follows:
where
ŷlast,i is the estimated value of
yi(
t) at instant
tlast,i, and
ki is number of sampling times. We use
ŷlast,i instead of
ylast,i to reduce measurement noise effects. If the
i-th sensor node does not send data at instant
t >
tlast,i, it is more likely that the output value
yi(
t) will satisfy:
Therefore, mean value of the new measurement noise
vn,i(
t) is computed:
Once
E{
vn,i(
t)} is obtained in
(6), to satisfy zero mean noise condition in the Kalman filter, we just add this value to the measurement value
ylast,i.
Now we investigate the system response to determine when
(3) or
(4) is chosen to the filter. The basic principle is that if it is certain that
yi(
t) is increasing or decreasing, we should use
(4). And if it is not certain, we should use
(3). This decision is made based on the absolute value of
as follows:
where
εi > 0 is a sufficiently small threshold. If
is small, it is difficult to draw a meaningful conclusion about whether
yi(
t) is increasing or decreasing, so in that case, we use
(3). Otherwise, we could be fairly certain about whether
yi(
t) is increasing or decreasing; in that case, we use
(4). Some remarks about the parameter
εi are warranted. If
εi = ∞,
(3) is always used in the filter as in [
5]. Therefore, in case
, the proposed filter will become to the filter in [
5] if setting
εi = ∞. It is very flexible to switch the filter to [
5] or to the the proposed filter so that estimation performance is improved in both case
R >
δ2 and
R ≪
δ2.
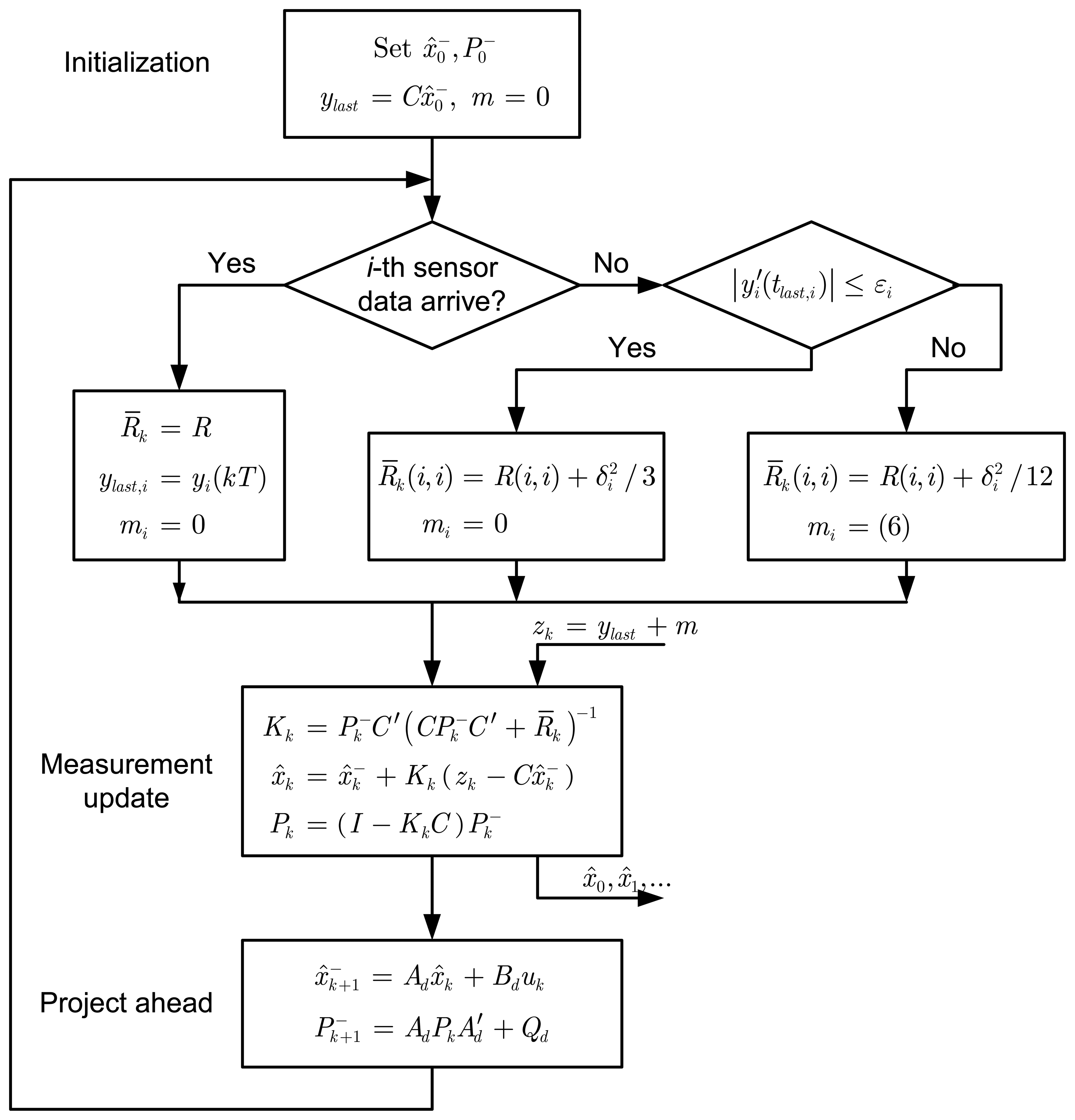
A modified Kalman filter for state estimation at step
k, where there is a change in the measurement update part of the discrete Kalman filter algorithm, is given as in the
Fig.3 when both
(3) and
(4) are used in case
R ≪
δ2. Basic principle of Kalman filters could be found in [
10,
11]. In
Fig.3, we use the discretized plant model is sampled at period
T:
Qd is the process noise covariance of the discretized plant:
ylast is the vector of
p last received sensor values:
and
m is the vector of
p men values:
In the modified filter above, vector
m presents mean value of
vn(
t) for all
p measurement outputs. In case the filter uses
(4) for estimation,
m becomes non-zero. In order to satisfy zero mean noise condition, we add
m to
ylast and consider (
ylast+
m) as the measurement values.
The
εi thresholds determine when the filter uses
(4) instead of
(3). The smaller
εi is, the more the filter relies on
(4). In practical systems,
εi thresholds could be determined by monitoring derivative of the sensor output
.
It is difficult to derive an explicit expression of performance improvement. However, we could say that the error covariance
Pk becomes smaller when
(4) is used more often. This is because smaller
R̅ value in the Kalman filter results in smaller
Pk value. We note that
(4) is more often used if
y(
t) is either monotonically increasing or decreasing.
4. Simulation
To verify the proposed filter, we consider an example of the step response of a second-order system where the output is sampled by the SOD method:
The system parameters are given in 3 following cases for performance evaluation:
M = 30, a =10, b = 10 : overdamped system
M = 30, a =5, b = 1 : underdamped system
M = 30, a =5, b = 0 : undamped system
The simulation process is implemented for 50 seconds, and
ε = 0.001 for all cases. In each case, we use 3 filters for performance comparison: the filter using
(3) only, the filter using
(4) only, and the proposed filter. Estimation error is evaluated by the criterion:
where
x1 is the reference state,
N=5000.
Estimation errors for different
δ values in 3 cases, where the condition
R ≪
δ2 is satisfied, are given in
Table 1,
2, and
3. We see that estimation performance of the proposed filter is the best and significantly improved in comparison with the filter using
(3). For example, in the case of
δ = 0.2, estimation error of the proposed filter is reduced 36.75% compared to the filter using
(3) in case 1, reduced 0.88% in case 2, and reduced 7.49% in case 3.
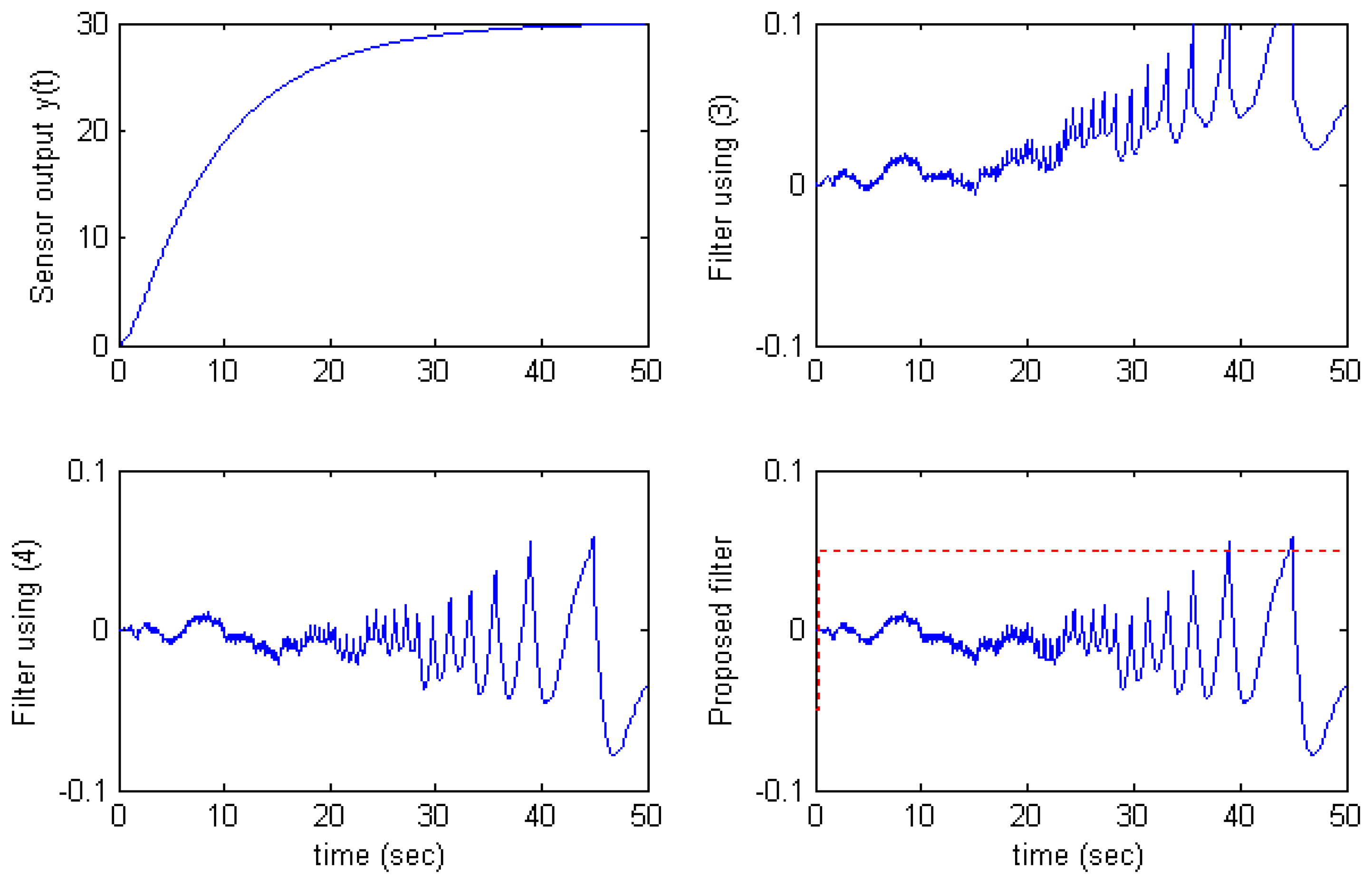
The results also show that the filter using
(4) is better than the filter using
(3) in case 1, but worse in case 2 and case 3. In theory, the filter using
(4) must be always better than the filter using
(3). This happens because there exists a delay between the sensor output signal
y′(
t) and the computed value
y′(
tlast) in
(5). Therefore, if
y′(
t) changes sign while condition |
y(
t) −
y(
tlast)| <
δ still holds, the estimator keeps using the old value
y′(
tlast) whose sign is incorrect compared with
y′(
t). This makes
(6) incorrect, and leads to increase of estimation error. As we see in the
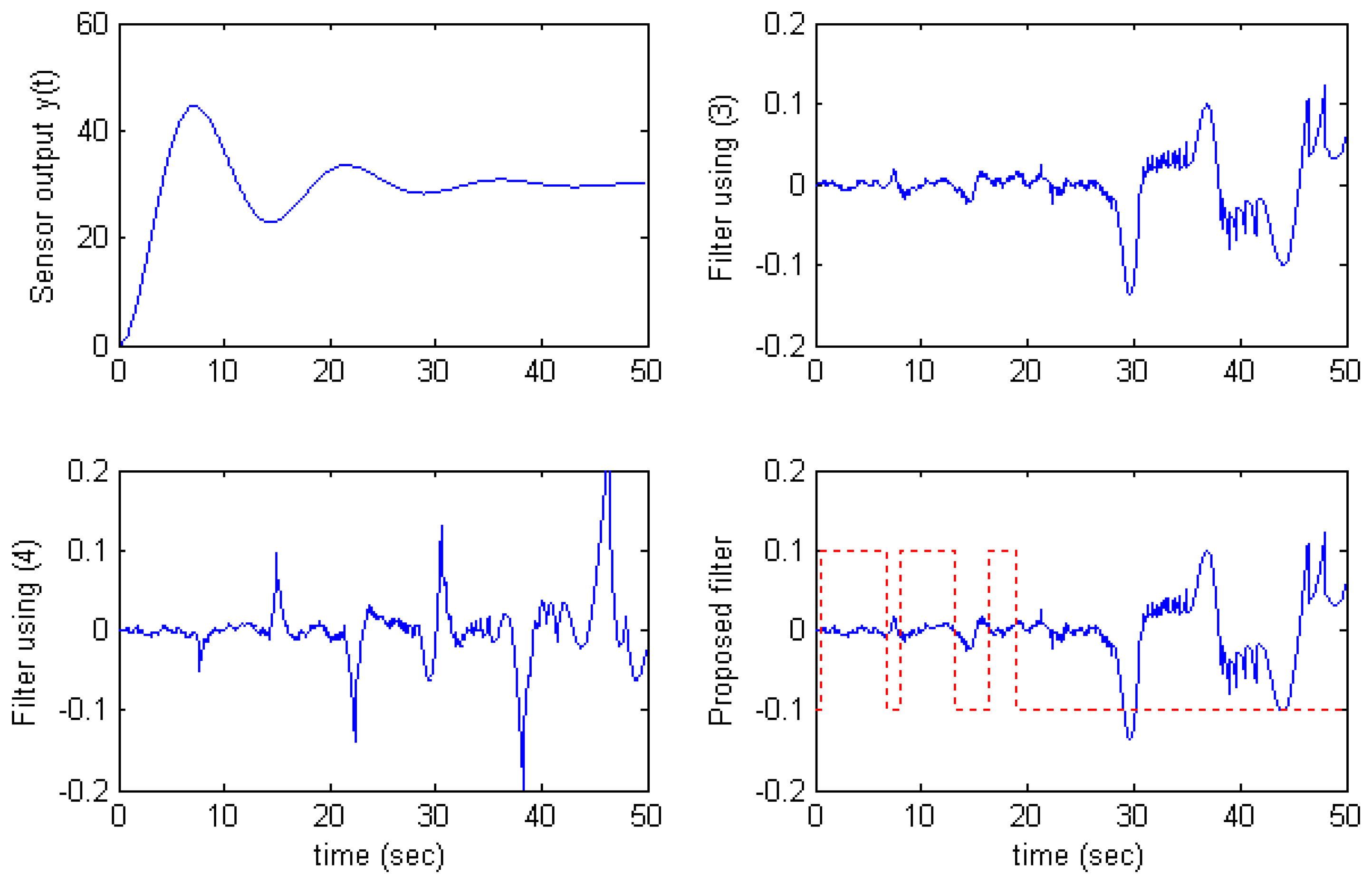
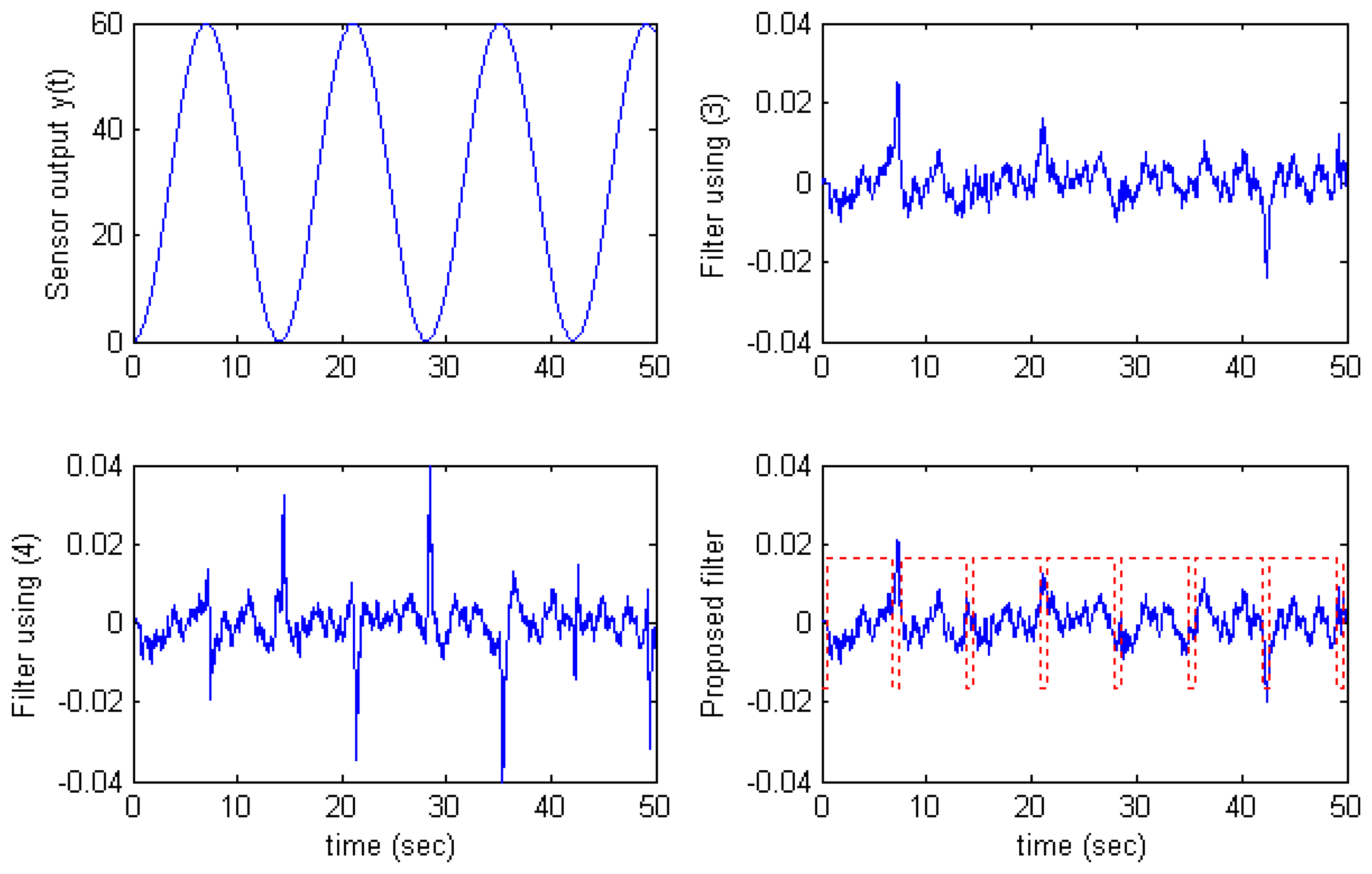
Fig.5 and
Fig.6, the estimation error of the filter using
(4) becomes large at time
y′(
t) changes the sign.
The proposed filter overcomes this situation by applying the algorithm
(7) in which the filter uses
(3) at time
y′(
t) changes sign and uses
(4) at other time. The solid line on the proposed filter graphs in
Fig.4,
Fig.5, and
Fig.6 presents the sign of
Selector (7). That is,
Selector > 0 denotes that the filter uses
(4) and
Selector < 0 denotes that the filter uses
(3).