1. Introduction
The primary objective of sensor networks is to sample the residing environment and send updates with the most recent information to data collecting center(s) for further processing. As is well-known, a main constraint of wireless sensor devices is limited battery life. Usually it is either impossible or impractical to replace batteries so the operational lifetime of the sensor device is equal to its battery life. The only option to lengthen the sensor lifetime is to reduce the waste of energy in device operation.
Wireless communication is a major source of energy consumption. Since every message uses up the low device energy resources, the number of messages sent through the sensor network should be as low as possible. It is worth being aware that
every bit transmitted can reduce the lifetime of the wireless sensor network [
12]. Wireless communication consumes more energy than information processing. In a typical scenario, a sensor node can execute 3000 instructions for the same energy cost of sending a single bit at the distance of 100 meters by radio [
15]. Therefore, in order to maximize the lifetime of the sensor devices, it is critical to maximize the usefulness of
every bit transmitted or received [
12].
The effective way to decrease energy consumption is the reduction of the network traffic originated out of a sensor node without degrading the resolution of observations reported from the environment. It is possible by a use of signal-dependent sampling schemes, where sampling occurs “when it is required” rather than in equidistant time intervals.
Basing on both data collection paradigms, a classification of sensor networks into
proactive and
reactive ones has been proposed [
16].
Proactive networks continuously monitor the environment and thus have data to be sent at a constant rate. In the
reactive network, nodes send new reports only when the variable being monitored increases or decreases beyond a threshold. The latter is sometimes called the
send-on-delta scheme.
The paper addresses the issue of send-on-delta data collecting strategy to capture information from the environment. Send-on-delta concept is the most natural signal-dependent temporal sampling scheme. According to this scheme the sampling is triggered if the signal deviates by delta, defined as a significant change of its value (e.g. 1°C) in relation to the most recent sample. Thus, the sensor node does not broadcast a new message until the input signal remains within a certain interval of confidence.
The level-crossing sampling is not new and has been known at least since the late 1950s, when Ellis noticed, that “the most suitable sampling is by transmission of only significant data, as the new value obtained when the signal is changed by a given increment” [
20]. Consequently, “it is not necessary to sample periodically, but only when quantized data change from one possible value to the next” [
20]. Various terms are used to express such a sampling strategy: the event-based sampling [
1,
2,
3,
17], the level-crossing sampling [
5,
18,
24], the magnitude-driven sampling [
3], and sometimes, the sampling in the amplitude domain. Recently, Aström and Bernhardsson suggest a term Lebesgue sampling, since the discrete representation of a continuous-time signal by levels equally distributed in the amplitude domain resembles the Lebesgue method of integration in mathematics [
22]. Using the same convention of terminology the periodic scheme is called Riemann sampling [
22]. The variety of existing terminology shows that it is really a generic concept adapted to a broad spectrum of technology and applications. In the sensor/control networking community the magnitude-driven/level-crossing sampling is known as the
send-on-delta [
6,
7,
13] or
deadbands [
11].
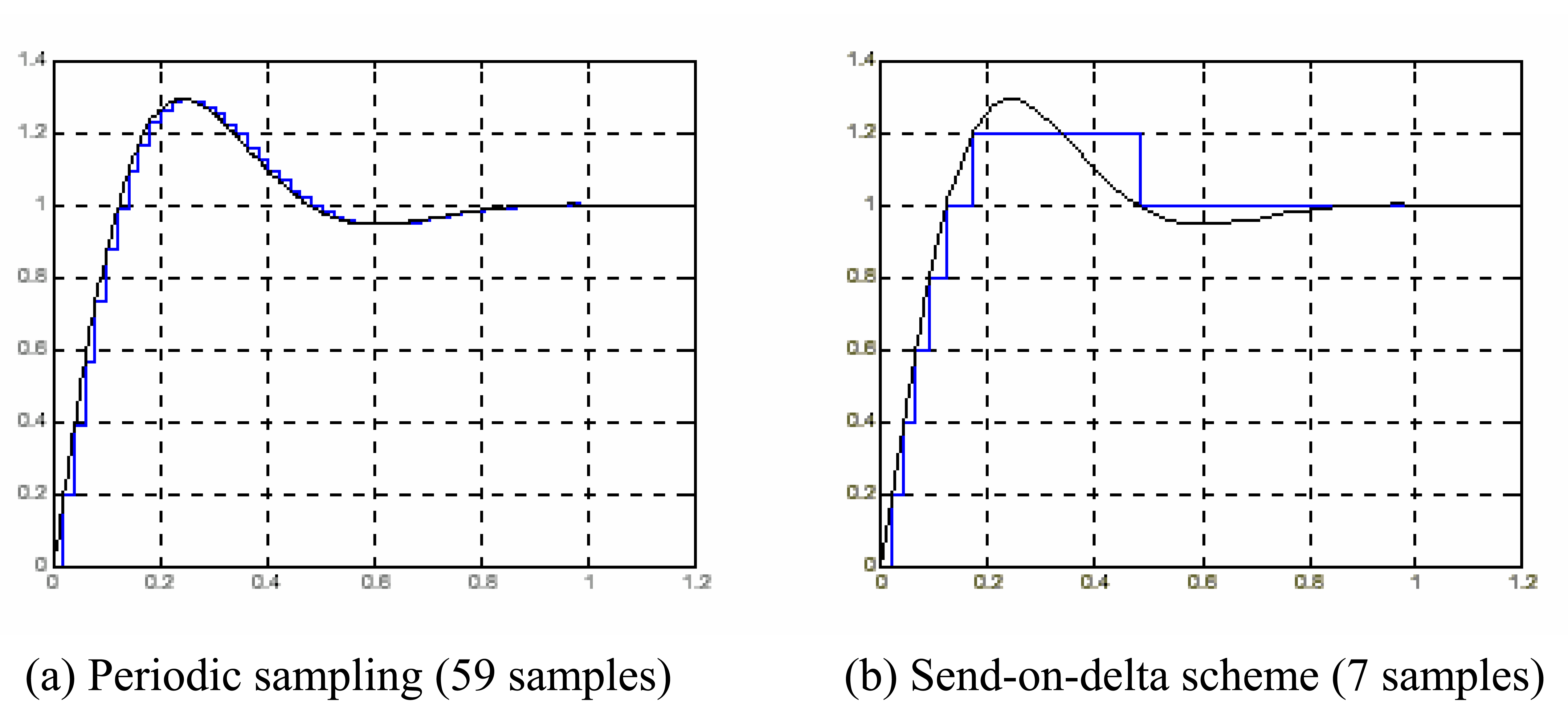
The send-on-delta scheme is used in many wireless sensor network applications. It is intuitively comprehensible that a use of the send-on-delta concept instead of traditional periodic updates reduces the mean rate of messages generated by a sensor node [
3]. The reduction is significant for
burst signals, defined as a type of signals that do not change, much or at all, for most of the time. Hence, the send-on-delta data collection is less demanding in terms of wireless communication since only significant changes of the input signal are propagated to a higher processing infrastructure.
The problem of waste of energy due to the transmission of redundant data is characterized in [
6] as
overtransmitting. This term has been developed following the convention of terminology used in the sensor network protocols, where
overhearing describes the effect of packets reception by nodes that are not their intended recipients.
The send-on-delta-based data acquisition might be used together with switching the sensor node to low-power state and the event-driven wake up to reduce waste of energy when the input signal is lazy. The analysis of energy savings and possible sensor lifetime increase in send-on-delta-based reporting is presented in [
6].
The send-on-delta strategy of the environmental monitoring is often a built-in feature of smart sensor devices. Some sensor/control networking technologies with the event-triggered architecture is equipped with the magnitude-driven input perception. A typical example is LonWorks/EIA-709 technology supporting programming resources for event detection and processing [
8,
13,
14].
LonWorks technology allows a node to go to sleep and to wake up if specified events occur. Each node sleeps autonomously calling sleep() function [
8]. The node can wake up when some activity in local environment (on I/O port), or in the communication channel is detected. However, the node can be configured to ignore incoming messages, e.g. when a sensor node is programmed as a source of messages only, and is not interested in message receiving.
The research area related to the send-on-delta sampling scheme is the
level-crossing problem, i.e. the evaluation of statistical temporal properties of crossings of a certain level by random signals [
23]. However, the results derived for the level-crossing problem cannot be applied directly to the send-on-delta scheme since the former deals with the issue of the single level crossings, and the latter concerns the crossings of multiple levels distributed in the amplitude domain.
Recently, the new research areas related to the level-crossing sampling have been initiated. A new type of signal processing problem related to the send-on-delta/event-based sampling is studied in [
17], where the purpose of
spectral analysis in the signal amplitude domain is introduced and exemplified. Finally, a new promising application of the level-crossing sampling is the
asynchronous analog-to-digital conversion [
18,
21], where the intersampling intervals instead of the signal amplitude are quantized according to the resolution of a timer, the purpose of which is only to date the samples. It announces a drastic change in the standard signal and data processing and the development of a new research area –
asynchronous signal processing [
21].
In this paper, the quantitative evaluations of the send-on-delta scheme for a general type continuous-time bandlimited signal are presented. First, Section 2 highlights the motivation of using the send-on-delta paradigm. In Section 3, the lower and the upper bounds on the mean traffic of messages for a given signal, and assumed sampling resolution, are evaluated. The analytic expressions estimate a balance between the traffic rate and the send-on-delta sampling resolution. Furthermore, in Section 4, the send-on-delta effectiveness, defined as the reduction of the mean rate of messages in comparison to the periodic sampling for a given resolution, is derived. In particular, it is shown that the lower bound of the send-on-delta effectiveness (i.e. the guaranteed reduction) is independent of the sampling resolution, and constitutes the built-in feature of the input signal. The calculation of the effectiveness for standard signals, that model the state evolution of dynamic environment in time, is exemplified. Finally, the example of send-on-delta programming is shown.
2. Motivation of use of the periodic sampling and the send-on-delta concept
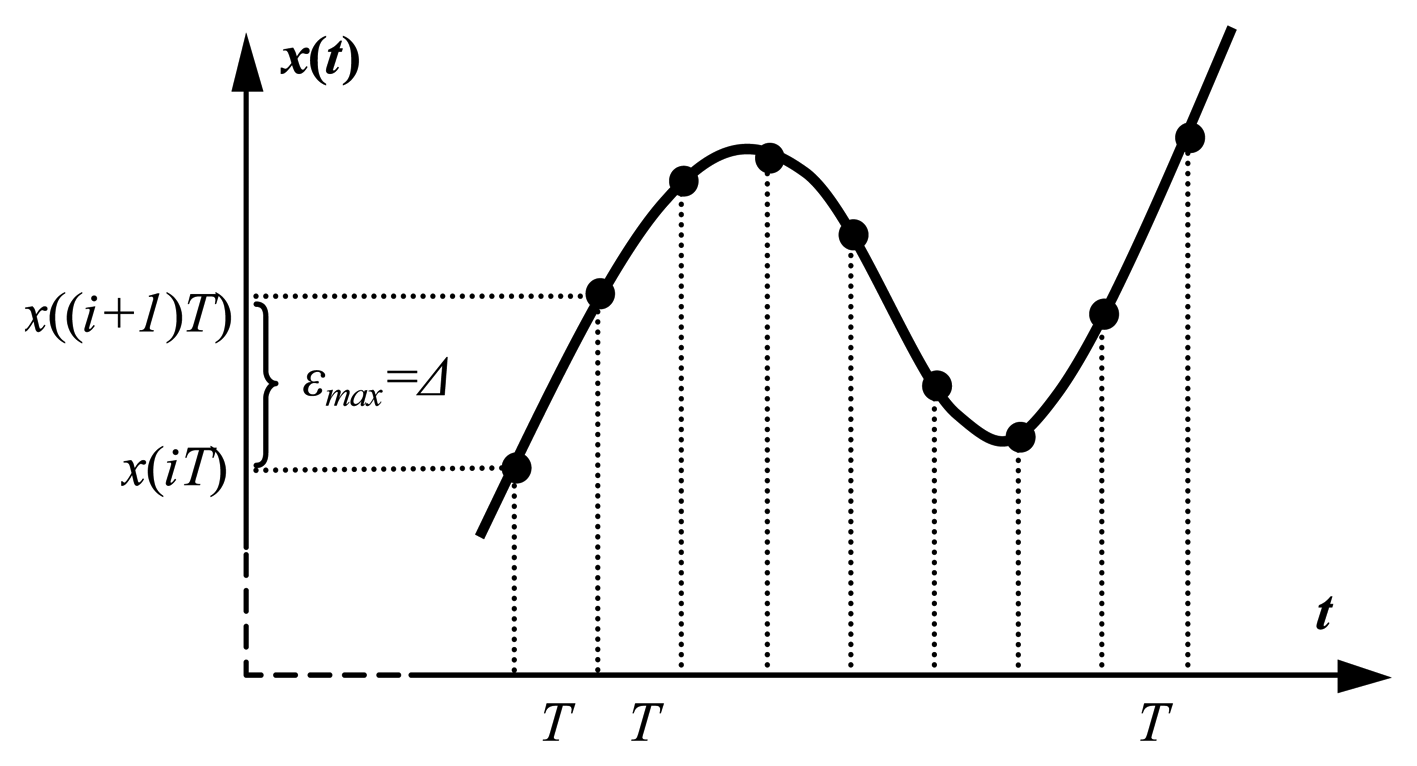
One of the most prominent and comprehensive ways of data collection in sensor networks is to extract raw sensor readings periodically. The uniform time-triggered data collection is assumed by most current protocols for wireless sensor networks. The sampling period depends mainly on how fast process can vary and what characteristics need to be captured. The selection of sampling period bases on the worst-case approach, and is adjusted to the fastest possible signal change.
2.1. Typical applications of the periodic data collection
Since the concepts of time and speed play a major role in the process control area, the synchronous sampling is natural in real-time control applications, where the system interacts in a feedback with the controlled object within imposed time constraints. The important reason is the existence of a well-established and mature system theory for periodic sampled control systems. The analysis and design of such sampled systems are relatively simple because the closed-loop system becomes linear and periodic for linear time-invariant processes [
19]. Reservation protocols are natural for message transport in the sensor network with equidistant sampling data collection.
From the point of view of real-time software, the periodic sampling supports the time-triggered architecture (TTA). Time is indeed a critical issue for real-time applications so the explicit management of time at the basic level supports the evaluation of the temporal properties of real-time software [
9]. Thus, recommendations for software architecture harmonize with control theory issues.
Although periodic sampling is a crucial approach in most sensor/control and signal processing applications, the implicit idea of its use relying on the assumption about regularity of environment evolution in the time, is usually invalid. Sensor networks have to deal with high system dynamics. The environment being sensed is bursty by nature so sending data periodically when nothing significant has happened in the process seems to be an evident waste of communication, processing and energy resources. Significant oversampling occurs, for example, when the controlled object is in the equilibrium and state variables do not change considerably.
The other problem associated with synchronous sampling applications is the phase relation of sampling instants among multiple sensor nodes. A random access sensor network is prone to repeated collisions if more than one node operates with the same or similar sampling frequencies. Thus, the instants when data reports are triggered in several nodes, should be distributed in the time in order to desynchronize the traffic.
Finally, it is no point to sample environment in the strict uniform time-triggered regime if the jitter of transmission delay is greater than the sampling period since temporal order of observations can be disturbed. Delay jitter is significant in random access networks with the backoff-based collision avoidance, or when messages are transmitted across field buses, computer networks, or even the Internet.
2.3. Problems of send-on-delta-based acquisition
A sensor network is essentially an event-based system. Events of interest occur in a sensor field asynchronously with regard to a priori selected sampling points. Therefore, the signal-dependent schemes, where the sampling instants are correlated with the stimuli coming from the environment, are more natural than the time-triggered ones, which periodic sampling exemplifies. In the signal-dependent sampling, the system input is fed by signal amplitude variations so the temporal density of sampling operations varies in the time, and is determined by input signal changes.
The send-on-delta concept might be used with several network protocols. For example, in LonWorks systems, the send-on-delta-based reports are transmitted over the CSMA-based channel [
5]. On the other hand, the FDMA scheme is proposed for a protocol presented in [
6]. In general, the send-on-delta concept corresponds well to the event-based nature of random access protocols, where every node decides to transmit autonomously “when it is required”.
Send-on-delta strategy is sometimes implemented in sensor devices using the
compound architecture for data acquisition. First, the continuous-time signal is sampled using the periodic scheme. On the top of it, the event-triggered communication and processing activities are implemented, that is, a detection of a significant change in a set of samples is performed. The compound approach, where the asynchronous events are presynchronized by background periodic sampling, is called the “
upward”
event-driven architecture [
9]. Such a compound architecture of send-on-delta implementation is used in many sensor networking applications, e.g. in LonWorks technology.
3. Send-on-delta principle
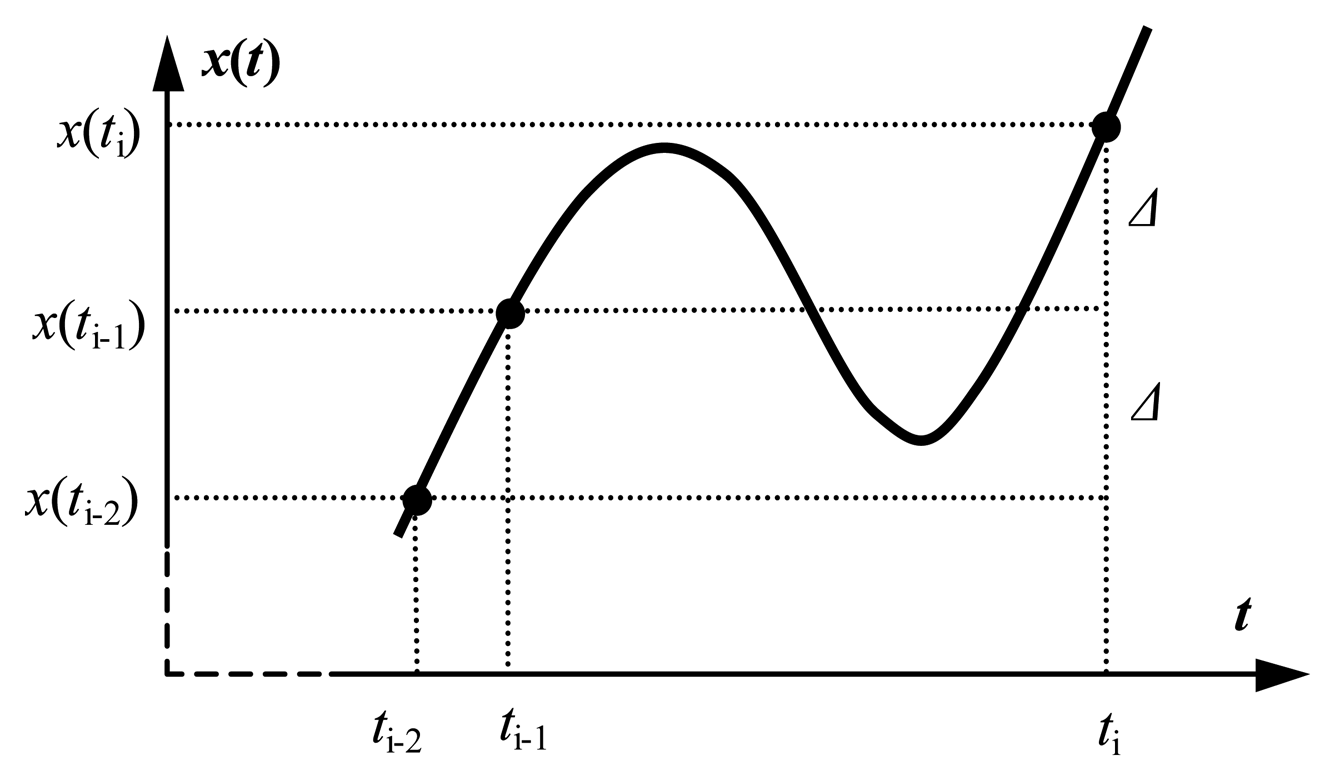
Using the
send-on-delta concept, a continuous-time bandlimited signal
x(
t) is sampled and a new report is sent, when the value of the physical variable being sensed deviates from the value included in the most recent report by an interval of confidence ± Δ, called the
threshold, or
delta, where Δ > 0 (
Fig. 1).
Thus, there is a constant difference equal to Δ between signal values included in consecutive updates:
where
x(
ti) is the
ith signal sample;
i = 1,2,…,
n.
The threshold Δ is a design parameter that determines the resolution of signal observations. The smaller threshold Δ, the higher resolution of input signal tracking. The digitized samples including the current signal value x(ti) and the protocol overhead are sent in messages through the sensor network.
Since by definition, the send-on-delta sampling is triggered by asynchronous events (crossings of the sampling levels), the time is the dependent variable in system modelling. Meanwhile, the communication requirements relate to temporal properties, e.g. measures that evaluate demands for the required network communication bandwidth.
3.2. Communication Bandwidth Requirements
One of the main parameters describing the send-on-delta concept is the mean rate of messages, λ, originated out of a node sensing a particular continuous-time physical variable with the resolution in the value domain equal to Δ. The mean rate of messages is simply defined as the mean number of samples per a unit of time calculated for a certain time interval (t0,tn).
The mean rate of messages
λ cannot be estimated analytically for a general type signal. However, either the
upper bound λmax, or the
lower bound λmin of
λ might be evaluated according to the following expression [
4]:
where
v,
v ∈
R is the
local extrema density, i.e. the average number of signal
peaks (maxima and minima) in a time unit.
3.2.1. Upper bound on the mean rate of messages
The upper bound
λmax equals
λ ′, which is defined as follows [
3]:
where
is the
average slope of the signal, that is, the mean of the absolute value of the first time-derivative of the signal
x(
t) in a time interval (
t0,
tn):
By the definition (see
(3)), the measure
λ′ is expressed by two factors:
- -
the mean of the absolute value of the first signal time-derivative during a time interval (
t0,
tn):
- -
the
resolution Δ
of the sampling in the value domain, or the
threshold, which is a difference between the consecutive sampling levels, see
(1).
As expected, the larger threshold Δ, the lower sensing resolution, and the lower mean rate of messages
λ. The measure
λ′ has highly intuitive interpretation. Namely, it is the average slope of the sampled signal
x(
t) normalized to the threshold Δ. Since
λ′ overestimates
λ, it represents the
worst-case mean rate of messages for a certain threshold Δ. Next, as follows from the formula
(2) and
(3),
λ approaches
λ′, if the threshold Δ is small, because:
Finally, if Δ→ 0, then
λ→
λ′, because:
Thus, if the threshold Δ approaches zero, then the mean observation rate λ converges to its upper bound λ′.
3.2.2. Lower bound on the mean rate of messages
The lower bound
λmin on mean rate of messages equals to (
λ′ − 2
v) and depends on the density of peaks in the signal being sensed by the sensor node. To be precise, the lower bound
λmin is defined for such a threshold Δ that:
If this inequality is violated, the level-crossing sampling might not be triggered since the signal value can vary within a region between two consecutive sampling levels.
The
uncertainty (
λmax −
λmin) of the analytic evaluation of the mean rate of messages
λ in send-on-delta data collecting strategy in the presented approach defined as:
is a function of the mean density of peaks in the signal.
In particular, if v = 0 (i.e. the signal x(t) is a monotone increasing of decreasing function of the time), the mean rate of messages λ is perfectly evaluated (λmax =λ = λmin) and equal to λ′. Some signals in dynamic systems meet this assumption, e.g. the first-order or higher order over-damped or critically damped step-responses.
Note that in order to estimate all the parameters λ, λmin, λmax, only the average slope of the signal
, and the mean peak density v have to be calculated since the threshold is a design parameter. Both parameters,
and v, can be found analytically for many common signals, either deterministic, or random ones.
Summing up, the mean rate of messages λ in send-on-delta concept, cannot be estimated perfectly using the analytic approach for a general type signal. However, the upper bound, and the lower bound on λ can be found basing on signal parameters. Moreover, if the sampling resolution is high (i.e. the threshold Δ is small), the mean sampling rate λ approaches asymptotically λ′. On the other hand, if the signal x(t) is a monotone increasing of decreasing function of the time, the mean rate of messages λ is perfectly evaluated and equal to λ′.