A High-Quality Sample Generation Method for Improving Steel Surface Defect Inspection
Abstract
:1. Introduction
2. Related Works
2.1. Defect Inspection Approaches
2.2. Sample Generative Models
2.3. Defect Sample Generation Methods Based on GANs
3. Methodology
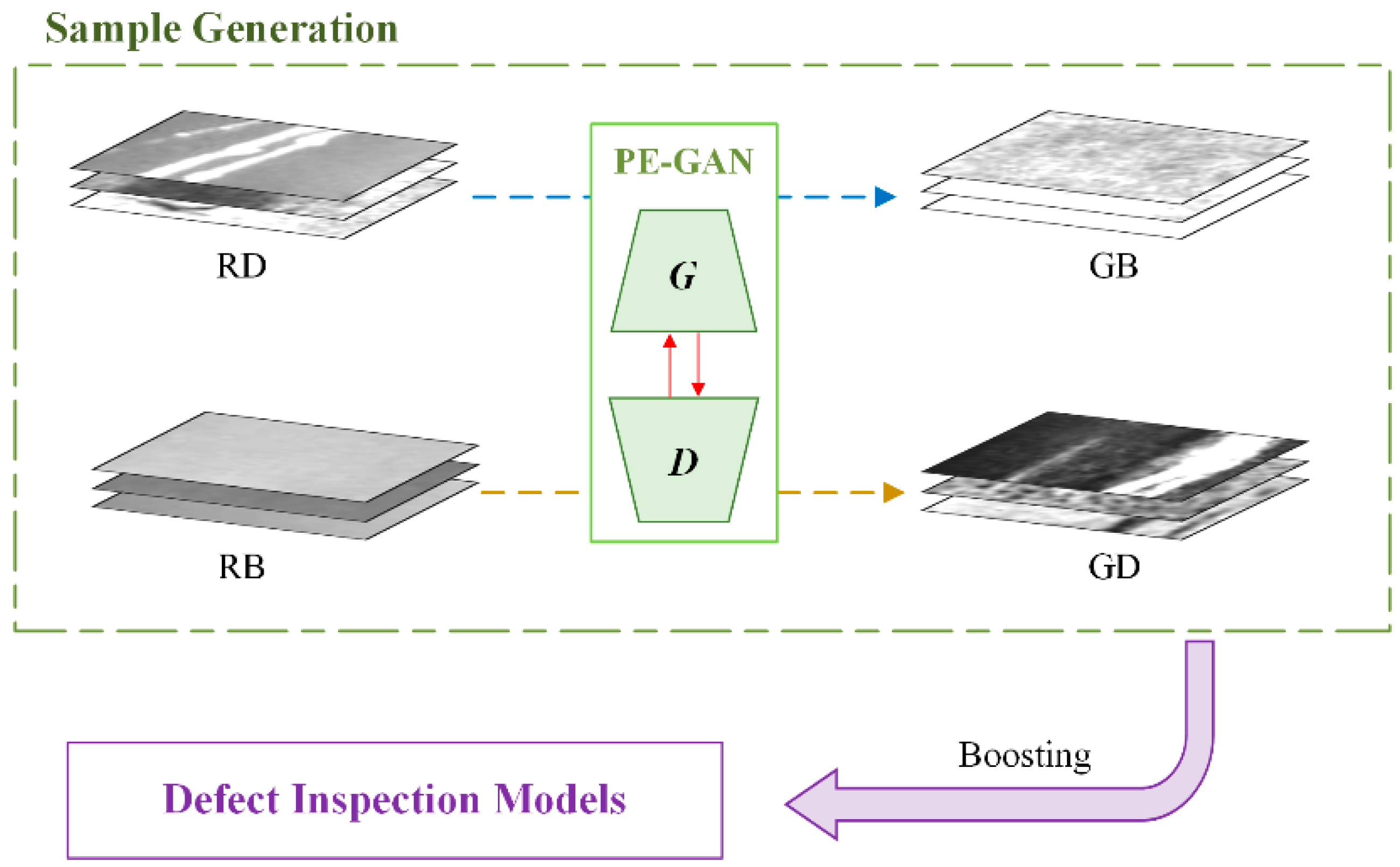
3.1. The Network Framework of the Proposed PE-GAN
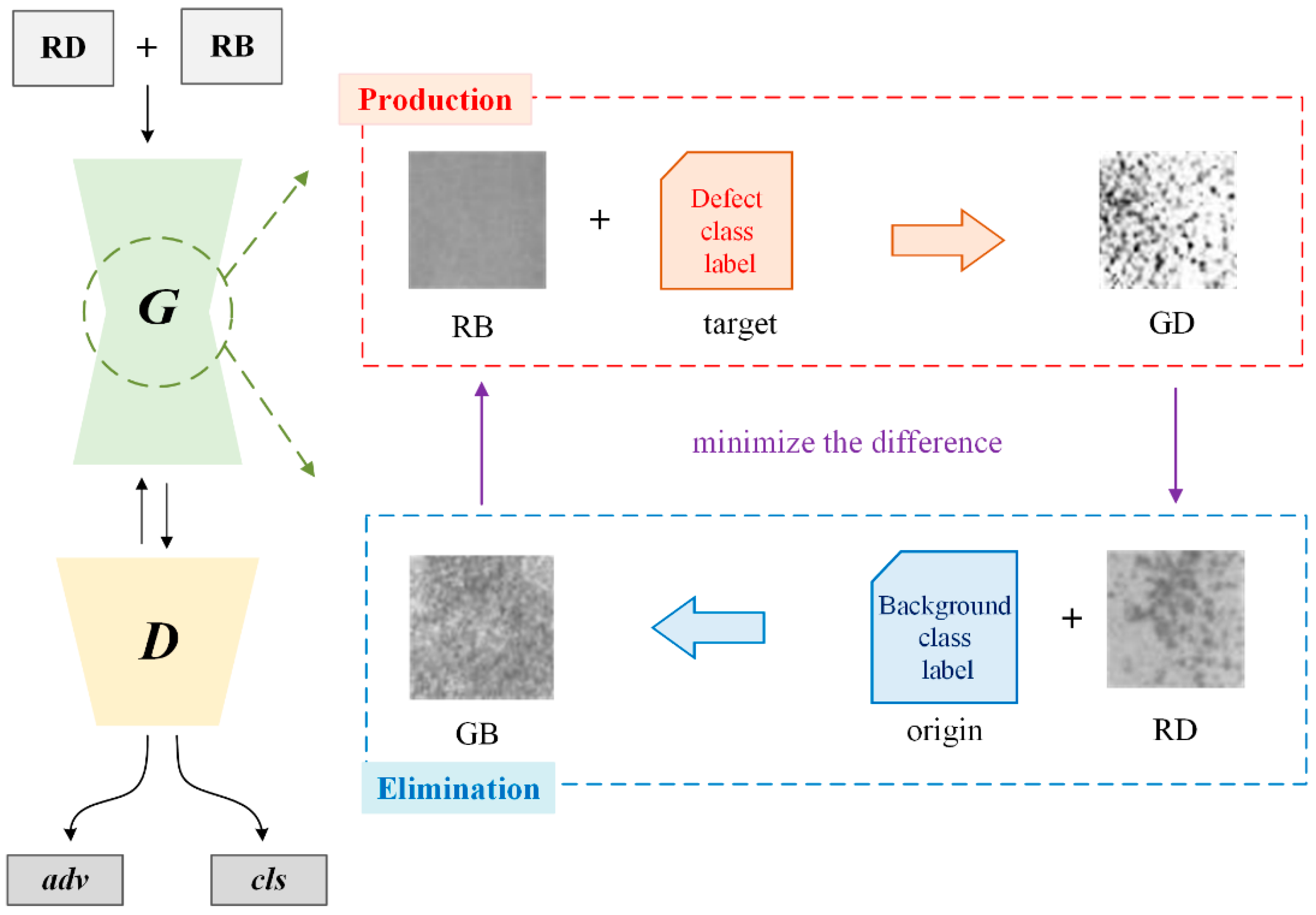
3.2. PE-GAN for Defect Sample Generation
3.3. Training Implementation
4. Experiments
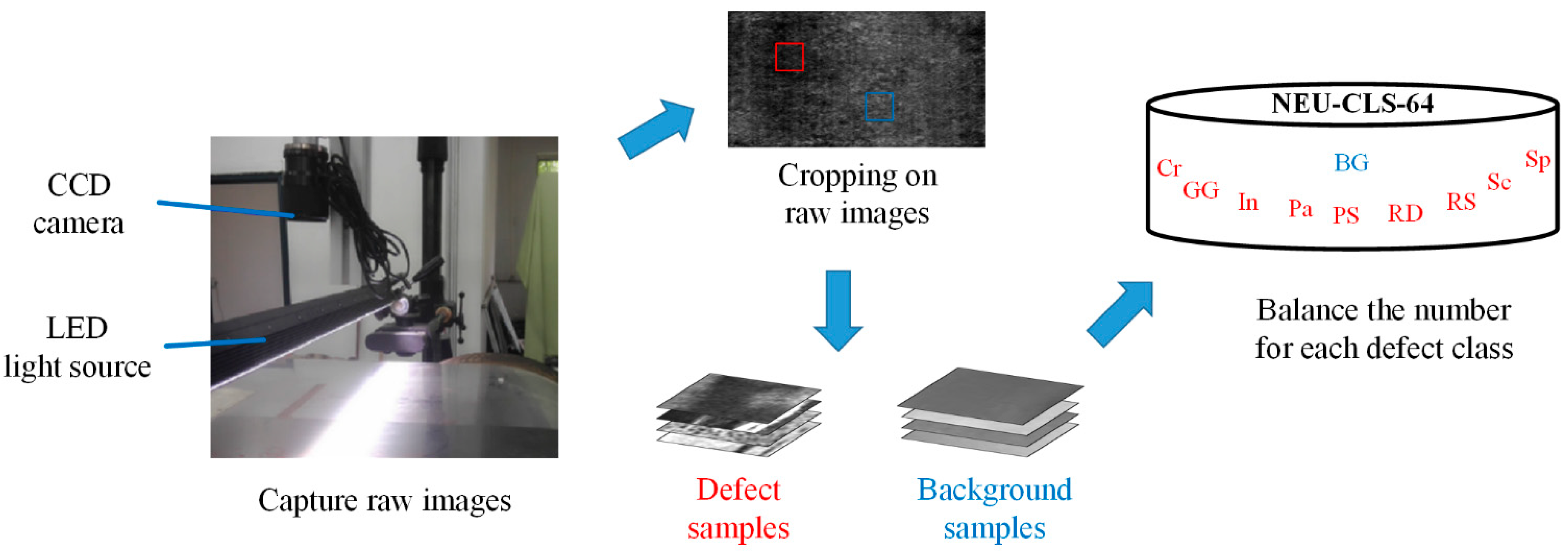
4.1. Defect Dataset and Metrics
4.2. Defect Dataset and Metrics
4.3. Defect Inspection Results with Generated Samples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wen, X.; Shan, J.; He, Y.; Song, K. Steel surface defect recognition: A survey. Coatings 2023, 13, 17. [Google Scholar] [CrossRef]
- Chu, M.; Zhao, J.; Liu, X. Multi-class classification for steel surface defects based on machine learning with quantile hyper-spheres. Chemom. Intell. Lab. Syst. 2017, 168, 15–27. [Google Scholar] [CrossRef]
- Wen, X.; Li, S.; Yu, H.; He, Y. Multi-scale context feature and cross-attention network-enabled system and software-based for pavement crack detection. Eng. Appl. Artif. Intell. 2024, 127 Pt B, 107328. [Google Scholar] [CrossRef]
- Dong, Y.; Tao, D.; Li, X.; Ma, J.; Pu, J. Texture classification and retrieval using shearlets and linear regression. IEEE Trans. Cybern. 2015, 45, 359–369. [Google Scholar]
- He, Y.; Wen, X.; Xu, J. A semi-supervised inspection approach of textured surface defects under limited labeled samples. Coatings 2022, 12, 1707. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, L.; Li, X. A generative adversarial network based deep learning method for low-quality defect image reconstruction and recognition. IEEE Trans Ind. Inf. 2021, 17, 3231–3240. [Google Scholar] [CrossRef]
- Jain, S.; Seth, G.; Paruthi, A.; Soni, U.; Kumar, G. Synthetic data augmentation for surface defect detection and classification using deep learning. J. Intell. Manuf. 2022, 33, 1007–1020. [Google Scholar] [CrossRef]
- Bau, D.; Zhu, J.Y.; Wulff, J.; Peebles, W.; Strobelt, H.; Zhou, B.; Torralba, A. Seeing what a gan cannot generate. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2019, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4502–4511. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 6–12 December 2020; pp. 6840–6851. [Google Scholar]
- Niu, S.; Li, B.; Wang, X.; Lin, H. Defect image sample generation with GAN for improving defect recognition. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1611–1622. [Google Scholar] [CrossRef]
- Liu, K.; Wang, H.; Chen, H.; Qu, E.; Tian, Y.; Sun, H. Steel surface defect detection using a new haar–weibull-variance model in unsupervised manner. IEEE Trans. Instrum. Meas. 2017, 66, 2585–2596. [Google Scholar] [CrossRef]
- Luo, Q.; Sun, Y.; Li, P.; Simpson, O.; Tian, L.; He, Y. Generalized Completed Local Binary Patterns for Time-Efficient Steel Surface Defect Classification. IEEE Trans. Instrum. Meas. 2019, 68, 667–679. [Google Scholar] [CrossRef]
- Ghorai, S.; Mukherjee, A.; Gangadaran, M.; Dutta, P.K. Automatic defect detection on hot-rolled flat steel products. IEEE Trans. Instrum. Meas. 2013, 62, 612–621. [Google Scholar] [CrossRef]
- Song, K.; Yan, Y. A noise robust method based on completed local binary patterns for hot-rolled steel strip surface defects. Appl. Surf. Sci. 2013, 285 Pt B, 858–864. [Google Scholar] [CrossRef]
- Zhou, S.; Chen, Y.; Zhang, D.; Xie, J.; Zhou, Y. Classification of surface defects on steel sheet using convolutional neural networks. Mater. Tehnol. 2017, 51, 123–131. [Google Scholar] [CrossRef]
- Huang, H.-W.; Li, Q.-T.; Zhang, D.-M. Deep learning based image recognition for crack and leakage defects of metro shield tunnel. Tunn. Undergr. Space Technol. 2018, 77, 166–176. [Google Scholar] [CrossRef]
- Yi, L.; Li, G.; Jiang, M. An end-to-end steel strip surface defects recognition system based on convolutional neural networks. Steel Res. Int. 2017, 88, 1600068. [Google Scholar] [CrossRef]
- Ren, R.; Hung, T.; Tan, K.C. A generic deep-learning-based approach for automated surface inspection. IEEE Trans. Cybern. 2018, 48, 929–940. [Google Scholar] [CrossRef]
- He, Y.; Song, K.; Meng, Q.; Yan, Y. An end-to-end steel surface defect detection approach via fusing multiple hierarchical features. IEEE Trans. Instrum. Meas. 2020, 69, 1493–1504. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, L.; Li, X. A hierarchicalI feature fusion-basedmethod for defect recognition with a small sample. In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Macau, China, 15–18 December 2019; pp. 1048–1052. [Google Scholar]
- Guo, Z.; Wang, C.; Yang, G.; Huang, Z.; Li, G. MSFT-YOLO: Improved YOLOv5 based on transformer for detecting defects of steel surface. Sensors 2022, 22, 3467. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Q.; Lau, D. Real-time detection of cracks in tiled sidewalks using YOLO-based method applied to unmanned aerial vehicle (UAV) images. Autom. Constr. 2023, 147, 104745. [Google Scholar] [CrossRef]
- Vincent, P.; LaRochelle, H.; Bengio, Y.; Manzagol, P.-A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Montreal, QC, Canada, 11–15 April 2016. [Google Scholar]
- Sohn, K.; Lee, H.; Yan, X. Learning structured output representation using deep conditional generative models. In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 7–12 December 2015; pp. 3483–3491. [Google Scholar]
- Oord, A.; Vinyals, O.; Kavukcuoglu, K. Neural discrete representation learning. In Proceedings of the Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Cao, H.; Tan, C.; Gao, Z.; Xu, Y.; Chen, G.; Heng, P.-A.; Li, S.Z. A survey on generative diffusion models. IEEE Trans. Knowl. Data Eng. 2024. [Google Scholar] [CrossRef]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional generative adversarial nets. In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- He, Y.; Song, K.; Dong, H.; Yan, Y. Semi-supervised defect classification of steel surface based on multi-training and generative adversarial network. Opt. Lasers Eng. 2019, 122, 294–302. [Google Scholar] [CrossRef]
- Hao, Z.; Li, Z.; Ren, F.; Lv, S.; Ni, H. Strip steel surface defects classification based on generative adversarial network and attention mechanism. Metals 2022, 12, 311. [Google Scholar] [CrossRef]
- Chang, J.; Guan, S.Q.; Shi, H.Y. Strip defect classification based on improved generative adversarial networks and MobileNetV3. Laser Optoelectron. Prog. 2021, 58, 221–226. [Google Scholar]
- Su, S.; Du, S.; Lu, X. Geometric constraint and image inpainting-based railway track fastener sample generation for improving defect inspection. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23883–23895. [Google Scholar] [CrossRef]
- Larsen, A.; Larochelle, H.; Winther, O. Auto-encoding beyond pixels using a learned similarity metric. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016; pp. 2341–2349. [Google Scholar]
- Huang, H.; He, R.; Sun, Z.; Tan, T. IntroVAE: Introspective variational autoencoders for photographic image synthesis. In Proceedings of the Neural Information Processing Systems (NIPS), Montreal, QC, Canada, 3–8 December 2018; pp. 52–63. [Google Scholar]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Choi, Y.; Choi, M.; Kim, M.; Ha, J.W.; Kim, S.; Choo, J. StarGan: Unified generative adversarial networks for multi-domain image-to-image translation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 8789–8797. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Instance normalization: The missing ingredient for fast stylization. arXiv 2016, arXiv:1607.08022. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A.C. Improved training of wasserstein GANs. In Proceedings of the Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 5767–5777. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980v9. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 6626–6637. [Google Scholar]
- Mao, X.; Li, Q.; Xie, H.; Lau, R.Y.; Wang, Z.; Smolley, S.P. Least squares generative adversarial networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2813–2821. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]




| Type | Filters | Size/Stride | Activation Function |
|---|---|---|---|
| CONV | 32 | 7 × 7/1 | ReLU |
| CONV | 64 | 5 × 5/2 | ReLU |
| CONV | 128 | 5 × 5/2 | ReLU |
| RB | 128 | 3 × 3/1 | ReLU |
| RB | 128 | 3 × 3/1 | ReLU |
| RB | 128 | 3 × 3/1 | ReLU |
| RB | 128 | 3 × 3/1 | ReLU |
| RB | 128 | 3 × 3/1 | ReLU |
| RB | 128 | 3 × 3/1 | ReLU |
| DECONV | 64 | 5 × 5/2 | ReLU |
| DECONV | 32 | 5 × 5/2 | ReLU |
| CONV | 3 | 7 × 7/1 | Tanh |
| Type | Filters | Size/Stride | Activation Function |
|---|---|---|---|
| CONV | 32 | 5 × 5/2 | Leaky ReLU |
| CONV | 64 | 5 × 5/2 | Leaky ReLU |
| CONV | 128 | 5 × 5/2 | Leaky ReLU |
| CONV | 256 | 5 × 5/2 | Leaky ReLU |
| CONV | 512 | 5 × 5/2 | Leaky ReLU |
| Output (adv) | 1 | 3 × 3/1 | Leaky ReLU |
| Output (cls) | c + 1 | W × h/1 | Softmax |
| Methods | DCGAN | LSGAN | CycleGAN | StarGAN | PE-GAN |
|---|---|---|---|---|---|
| Cr | 188.62 | 176.53 | 180.12 | 142.33 | 120.06 |
| GG | 256.00 | 222.07 | 205.69 | 180.34 | 184.67 |
| In | 288.35 | 291.42 | 240.16 | 210.71 | 192.43 |
| Pa | 199.07 | 162.33 | 140.07 | 121.88 | 117.00 |
| PS | 255.81 | 156.91 | 186.34 | 144.32 | 126.97 |
| RD | 300.70 | 193.65 | 151.13 | 134.90 | 108.45 |
| RS | 340.52 | 223.45 | 177.79 | 179.42 | 180.21 |
| Sc | 273.49 | 253.04 | 227.88 | 194.51 | 200.99 |
| Sp | 308.96 | 240.08 | 190.20 | 188.39 | 147.54 |
| Avg | 267.95 | 213.28 | 188.82 | 166.31 | 153.15 |
| Inspection Models | Source of Generated Samples | Accuracy (%) |
|---|---|---|
| Resnet-18 | None | 93.24 |
| DCGAN | 96.64 | |
| LSGAN | 97.67 | |
| CycleGAN | 98.89 | |
| StarGAN | 99.12 | |
| PE-GAN | 99.79 | |
| MobileNet | None | 91.26 |
| DCGAN | 95.92 | |
| LSGAN | 96.61 | |
| CycleGAN | 99.16 | |
| StarGAN | 99.29 | |
| PE-GAN | 99.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Li, S.; Wen, X.; Xu, J. A High-Quality Sample Generation Method for Improving Steel Surface Defect Inspection. Sensors 2024, 24, 2642. https://doi.org/10.3390/s24082642
He Y, Li S, Wen X, Xu J. A High-Quality Sample Generation Method for Improving Steel Surface Defect Inspection. Sensors. 2024; 24(8):2642. https://doi.org/10.3390/s24082642
Chicago/Turabian StyleHe, Yu, Shuai Li, Xin Wen, and Jing Xu. 2024. "A High-Quality Sample Generation Method for Improving Steel Surface Defect Inspection" Sensors 24, no. 8: 2642. https://doi.org/10.3390/s24082642






